What is ab initio in nuclear theory?

Ab initio has been used as a label in nuclear theory for over two decades. Its meaning has evolved and broadened over the years. We present our interpretation, briefly review its historical use, and discuss its present-day relation to theoretical uncertainty quantification.

1 Introduction

The literal meaning of the latin term ab initio implies that one starts from the beginning. In computations of atomic nuclei, this means that the relevant degrees of freedom should be quarks and gluons. However, the history of physics tells us that we do not need to know everything to describe something and that we have some freedom in choosing the starting point. As such, we do not necessarily have to employ Standard Model degrees of freedom. In fact, many nuclear properties were successfully analyzed in terms of hadronic degrees of freedom before we even knew about the existence of quarks [1–3]. Today, we know how to explain this using renormalization group (RG) ideas [4, 5]. One may wonder about the exact meaning of the ab initio method and what should constitute the beginning. However, it is safe to say that a hallmark of this approach is its promise of precise and accurate predictions, with quantified uncertainties, across the multiple energy scales relevant to nuclei. Examples range from low-energy collective phenomena such as deformation and rotation [6–10], to loosely bound and unbound nuclei [11–16], and to lepton nucleus scattering in the quasi-elastic energy regime [17–19]. We expect the ab initio method to reliably extrapolate, in a controlled and systematic way, to regions outside the ones used for inferring the model parameters. Following the ideas from effective field theory (EFT) [20], we interpret the ab initio method to be a systematically improvable approach for quantitatively describing nuclei using the finest resolution scale possible while maximizing its predictive capabilities. A key part of this interpretation is the possible tension between the two latter aspects. In a nuclear physics context, we therefore let nucleons, and possibly other relevant hadronic degrees of freedom, define the beginning. Lattice quantum chromodynamics (QCD) might one day be the optimal starting point for predicting nuclear phenomena. Presently, Lattice QCD continues to provide useful input for EFTs based on hadronic degrees of freedom. However, it currently lacks predictive power for describing atomic nuclei [21–25].

We acknowledge that the ab initio method is interpreted differently by different people; see, e.g., Refs. [26–33]. In nuclear physics, the evolution of ab initio and its wide application reflect the creativity and innovation of the scientists who perform ab initio computations. In this sense, ab initio is unlike Tennessee Whiskey or French Champagne, which are internationally protected labels, but rather like Gruyère cheese, i.e., a generic expression that benefits a “vibrant, competitive marketplace”¹. In this review we provide a brief history of ab initio nuclear physics (Section 2), clarify our interpretation of this label (Section 3), explain how this approach creates an inferential advantage (Section 4), and provide examples in connection with some remaining challenges (Section 5).

2 A brief history of ab initio nuclear physics

A search of the term ab initio in the title on arXiv:nucl-th returns about 300 papers, with the earliest one by Navrátil, Vary, and Barrett (Ref. [34]) dating back to the year 2000. When the search includes abstracts, the count increases to more than 700, and papers by Leinweber (Ref. [35]) and Friar (Ref. [36]) are the earliest published in the mid-1990s. Since then, an ever-increasing number of authors have used the term ab initio to characterize their work. In Figure 1, we show a plot of the data for the yearly use of this term in titles and abstracts.

FIGURE 1

FIGURE 1. Number of times the term ab initio appears in the abstract (red circles) and titles (blue squares) of papers on arXiv:nucl-th in a given year.

The authors of Ref. [34] did not explain what distinguished their ab initio no-core shell model computations from quite similar earlier approaches [37, 38] (see also Ref. [39]). Whatever the reason, the term ab initio stuck and has been popular ever since. Colloquially, we often use ab initio to label theoretical analyses of nuclei based on “realistic” nucleon-nucleon, and three-nucleon potentials, with solutions to the nuclear many-body problem obtained either “virtually” exactly or with controlled approximations. Over the years, however, the small number of available “realistic” or “high-precision” nucleon-nucleon potentials [40, 41] have been replaced by nucleon-nucleon potentials plus three-nucleon potentials from chiral effective field theories (χEFTs) of QCD [42–44].

Because of the power counting in χEFT the potentials are recognized as approximate with a fidelity that presumably increases with increasing chiral order. This presented an opportunity for systematically improvable many-body methods that scale polynomially with increasing mass number [26, 30, 45–52]. Why solve an approximate potential virtually exactly? This class of gently-scaling methods has now extended the reach of many-body calculations to medium-mass and heavy-mass nuclei [13, 53–58]. The computational cost of these calculations is kept manageable by also approximating three-nucleon potentials as normal-ordered, i.e., “density-dependent,” two-body potentials [53, 57, 59, 60], and using the intrinsic kinetic energy alleviated problems with the center of mass in the laboratory system [61–63]. These efforts also revealed the need for nuclear potentials that accurately reproduce bulk observables beyond the lightest-mass nuclei [64, 65]. This spurred the development of many new potentials differing by the degrees of freedom they used, how the numerical values of the low-energy constants (LECs) were determined, the choice of regulator function, power counting, and degree of locality [64–79].

Since the mid-to-late 1990s, this two-decades-long struggle to describe nuclei has brought nuclear structure and reactions closer together [11, 12, 80, 81]. Ideas from EFT [82] and RG [83, 84] have changed our views on what is observable [85], the importance of understanding the intrinsic resolution-scale and scheme dependencies [86, 87], how we can systematically account for finite-size corrections [88, 89], and estimate the effects of truncating the EFT expansion [69, 72, 90, 91]. These ideas have also led to the advent of the in-medium similarity renormalization group [49, 51, 52] and nuclear lattice EFT [92, 93] as the latest many-body methods. What we nowadays refer to as ab initio computations of nuclei [16, 56, 58, 94] is intimately linked to the ideas of EFT and uncertainty quantification. Clearly, what we considered ab initio two decades ago does not necessarily pass as ab initio today, and vice versa.

3 Our interpretation of the ab initio method

The methods of EFT [82] and RG [83, 84] provide a valuable foundation for the idea that the physics at a given energy scale does not explicitly depend on the details at much higher energies. The beginning can therefore be marked by identifying a scale separation, specifying the relevant degrees of freedom and symmetries, and allowing interactions accordingly. A power counting facilitates meaningful truncations.

We interpret the ab initio method as employing Lagrangians, Hamiltonians, or energy density functionals based on EFT principles and with degrees of freedom chosen such that it maximizes our predictive capabilities. Ab initio descriptions of atomic nuclei concern the physics of multi-hadron systems in an energy range from keV to a few hundreds of MeV. As such, it is reasonable to start from hadronic degrees of freedom with interactions derived from the Standard Model using the principles of EFT. While hadrons are composite systems, and QCD is the underlying theory of the strong nuclear force, Lattice QCD calculations of two-hadron systems are not yet under control [21, 22]. This might change, and one could imagine computing nuclei ab initio from QCD. Moving the beginning from hadronic degrees of freedom to quarks and gluons would extend the upper limit of the applicable energy scale by several orders of magnitude and thus increase predictive capabilities significantly. It is, however, an open question whether this ansatz will capture emergent phenomena like the saturation of nuclear forces [95]. Even if this were possible, it is another question how much understanding would be gained about emergent phenomena that involve novel (low-resolution) degrees of freedom from such a high-resolution perspective. The usefulness of the tower of EFTs will most likely remain [96].

Assuming that ab initio descriptions of nuclei inherit the physics of the Standard Model via EFT methods, we expect to obtain more reliable predictions compared to complementary and phenomenological approaches. Also, building on an EFT, the ab initio method should be systematically improvable, organizing the relevant physics according to importance following the principles of power counting. To use this advantage, we must obtain observables using numerically exact methods or, if necessary, using controlled approximations that allow for a systematic analysis. By controlled approximations, we mean ignoring, in a graded way, what we believe to be less essential physics. Doing so, we obtain a handle on what we discard and a more meaningful estimate of our prediction uncertainty. We would like to emphasize the distinction between ignored physics and unresolved physics. An example of the latter is short-range physics that, although unresolved, is accounted for in the Hamiltonian via contact interactions [97].

It is pivotal to incorporate and declare our knowledge base and assumptions in analyzing uncertainties. The ab initio method does not emerge from a vacuum. That would be an ex nihilo method, of which we cannot find any example in science. Quantifying theoretical uncertainties grounded in systematicity should create an advantage when assessing discrepancies between theory and experiment. Note that according to our interpretation, the ab initio method does not guarantee that we can find absolute bounds on the theoretical uncertainties nor that we approach the true data-generating mechanism by gradually reducing all truncations. Indeed, should tensions between experiment and theory remain despite our best efforts to quantify uncertainties and keep the truncations at a minimum, we obtain quantitative evidence that we should contest at least one of our assumptions.

4 How the ab initio method creates an inferential advantage

The use of probability theory to quantify uncertainty plays a central role in the scientific endeavor of inferring new knowledge about the Universe. In this context, the ab initio method has evolved significantly over the last few years and now offers a distinct advantage. However, before we can elaborate on the topic of inductive inference and its relation to the ab initio method, we must briefly discuss the nature of science in terms of data, theories, and models. This topic is expanded upon in the context of EFTs much more thoroughly in, e.g., Refs. [98, 99].

Let us start with the data $\mathcal{D}$ obtained through a measurement process. All data are equipped with uncertainties of various origins; let us denote this $\delta \mathcal{D}$. Given some data $\mathcal{D}$, one could ask what this data can tell us about future data $\mathcal{F}$. At present, the future data is uncertain and must therefore be described with a conditional probability $p(\mathcal{F}|\mathcal{D},I)$ [100]. Here I denotes all available background information. The obvious question is: How does one go from this abstract probability to something that can be evaluated quantitatively? The answer is to develop a theory within which we can formulate a model that allows for numerical evaluation.

In physics, a theory is very often some framework that postulates or deduces from some foundational principles the spacetime dependence of a system of interacting bodies, e.g., Einstein’s field equations in the general theory of relativity or Heisenberg’s equations of motion in quantum mechanics. A physical theory always comes with some prior probability of being wrong and this probability should never be exactly zero or one. Otherwise no new evidence/data will ever influence the validity of the theory. In this sense, all theories are wrong, i.e., never correct with absolute certainty. This provocative statement is designed to draw attention to the fact that all theories can be improved or replaced as we progress and gather more data.

A physical model M allows quantitative evaluation of the system under study. Any model we employ will always depend on model parameters θ with uncertain numerical values. Moreover, like theories: “all models are wrong” [101]. Indeed, there will always be some physics that we still need to include or are unaware of today. If we denote the mismatch between model predictions and data as δM, we can write

$\mathcal{D}=M\left(\mathit{\theta }\right)+\delta \mathcal{D}+\delta M.(1)$

We often refer to the mismatch term δM as the model discrepancy [102]. Naturally, we are uncertain about this term, so we represent it by a probability distribution following our beliefs about the limitations of M. It is no trivial task to incorporate model discrepancies in the analysis of scientific models and data. Nevertheless, it is crucial to avoid overfitting the model parameters θ and making overly confident model predictions [103]. It is in this context that the ab initio method creates an inferential advantage. The promise of systematicity grounded in EFT, and the controlled approximations underlying the computation of nuclear observables, allows us to be quantitative about the distribution that governs δM as we increase the fidelity of M. For simplicity we sometimes refer to EFTs as models. However, an EFT is more than a physical model in the traditional sense. Indeed, within its domain of applicability an EFT prediction reflects the underlying theory up to a truncation error. In this sense, the EFT is complete, which is a distinct advantage compared to traditional models. This is sometimes referred to as model-independence. Of course, the underlying theory might be wrong, and such model discrepancies cannot be remedied at the level of the EFT.

For example, assume that we operate with an EFT of QCD to derive the potential for the nuclear interaction up to some order in the relevant power counting. In addition, suppose that we use a systematically improvable many-body method at some well-defined truncation level to solve the many-body Schrödinger equation for the ground-state energy in our favorite nucleus. Then we can say more about δM than if we use a shell model description grounded in phenomenologically defined interaction matrix elements tailored to a specific model space. We are not saying that the latter calculation cannot provide valuable guidance or insight. However, we are saying that it is possible to systematically test the underlying assumptions within the ab initio method. Having quantified δM also tells us the significance of a possible discrepancy or tension between experiment and theory.

The distribution of future data conditioned on past data and background information I, i.e., $p(\mathcal{F}|\mathcal{D},I)$, is referred to as a posterior predictive distribution (PPD). Assuming that we have a model M (θ) for the data-generating mechanism, then we can express the PPD by marginalizing over the uncertain model parameters θ belonging to some parameter space Ω

$p\left(\mathcal{F}|\mathcal{D},I\right)={\int }_{\mathrm{\Omega }}p\left(\mathcal{F}|\mathit{\theta },I\right)p\left(\mathit{\theta }|\mathcal{D},I\right)\mathrm{d}\mathit{\theta }.(2)$

By performing this integral, we average all predictions with respect to our uncertainty of the model parameters θ. To evaluate the posterior probability density function (PDF) $p(\mathit{\theta }|\mathcal{D},I)$ for the model parameters, we can employ Bayes’ theorem, i.e.,

$p\left(\mathit{\theta }|\mathcal{D},I\right)=\frac{p\left(\mathcal{D}|\mathit{\theta },I\right)p\left(\mathit{\theta }|I\right)}{p\left(\mathcal{D}|I\right)}.(3)$

This requires a likelihood function $p(\mathcal{D}|\mathit{\theta },I)$ and a prior distribution of the model parameters p(θ|I). The denominator, $p(\mathcal{D}|I)$, does not explicitly depend on θ and is only needed for proper normalization. Quantifying the posterior is called Bayesian parameter estimation and is a staple of Bayesian inference. It is a probabilistic generalization of parameter optimization and maximum likelihood estimation.

In the historical developments of “high-precision” nucleon-nucleon potentials, one often employed a χ²-measure to quantify the goodness of fit to nucleon-nucleon scattering data [40, 41]. Although such an approach has several drawbacks, most notably its limited use in uncertainty quantification and non-trivial incorporation of prior knowledge and model discrepancy, it is undoubtedly less demanding computationally than quantifying a multi-dimensional posterior PDF. Evaluating the posterior requires numerical methods like Markov Chain Monte Carlo [104, 105], which is no silver bullet and by no means guaranteed to succeed. To compute the denominator in Eq. (3), i.e., the marginal likelihood, is even more difficult. There is significant progress in linking ab initio methods to the Bayesian inferential approach in the nucleon-nucleon and few-nucleon sectors [106]. The development of efficient and accurate emulators [107–110] should provide us with sufficient leverage to continue applying Bayesian methods for analyzing and quantifying uncertainties for non-trivial nuclear structure observables and reaction cross sections. Access to emulators also opens the door to detailed experimental design studies [111–116].

5 A few examples

We will briefly discuss a few examples and highlight some remaining challenges to clarify our interpretation of the ab initio method to analyze nuclei.

For light-mass nuclei, methods like the Faddeev-Yakubovsky equations [117], hyperspherical harmonics expansion [27], no-core shell model [39], and quantum Monte Carlo [118] yield virtually exact solutions to the many-body Schrödinger equation [119], barring systematic truncations of the single-particle basis and the Hilbert space of many-body wave functions, or limited sampling statistics. As such, the fidelity of the prediction is mainly limited by the available computational resources [120]. When we employ these methods with interactions that can be systematically improved, we obtain the prototypical ab initio calculation of a nucleus. As an example, in Figure 2, we show the predictions for ground-state energies in selected nuclei with mass numbers A = 4–12 as obtained in a systematic study [77] of light nuclei using two-plus three-nucleon interactions up to next-to-next-to-leading order in χEFT. The parameters of the employed interactions, i.e., the LECs, were calibrated to reproduce selected two- and three-nucleon data. The authors of that study recognized the well-known trend [54] of over-binding starting at A ≈ 10 and increasing with A. Whether going to higher orders in χEFT ameliorates this issue remains to be understood. A recent paper [122] shows that ground-state energies are better reproduced when going to the next order, but nuclear radii remain challenging to describe.

FIGURE 2

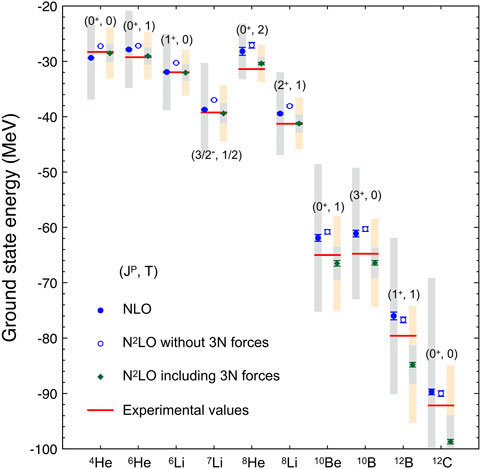
FIGURE 2. Predictions for ground-state energies of selected light nuclei using interactions up to next-to-next-to-leading order in χEFT. The grey (coral) bands indicate 68% (95%) credible intervals for the theoretical uncertainty stemming from truncating the χEFT expansion. Figure from Ref. [121], where additional details can be found.

In contrast to increasing the chiral order of the nuclear potential, which also introduces additional LECs to be inferred, it was demonstrated in Ref. [64] that one could obtain accurate predictions for binding energies and nuclear radii in medium-mass nuclei using a chiral interaction at next-to-next-to-leading order (NNLO_sat), which is calibrated to reproduce data for bulk observables in nuclei with A = 2–16, see Figure 3, in addition to nucleon-nucleon scattering cross sections. Calibrating the LECs to reproduce this wider class of nuclear data residing in the domain of applicability of χEFT, has been very fruitful and informative. This approach was expanded upon in Ref. [65] by exploiting empirical information from nuclear matter at saturation densities and including the Δ(1232)-isobar in the chiral expansion of the nuclear interaction. The strategy of inferring LECs to also reproduce bulk properties of medium-mass nuclei runs the risk of overfitting but there are Bayesian methods to mitigate this, as discussed in the next paragraph. The interactions in Refs. [64, 65] account for rudimentary theory and method errors and can be systematically improved. Therefore we characterize them, and ensuing predictions utilizing controlled approximations, as ab initio. On the contrary, nuclear interactions designed to maximize the data likelihood of nucleon-nucleon scattering cross sections at any cost, invoking, e.g., unphysical parameters of the regulator for fitting purposes [78], cannot be considered as an ab initio approach despite being based on EFT Lagrangians. A smaller χ²-value does not imply greater ab initio content.

FIGURE 3

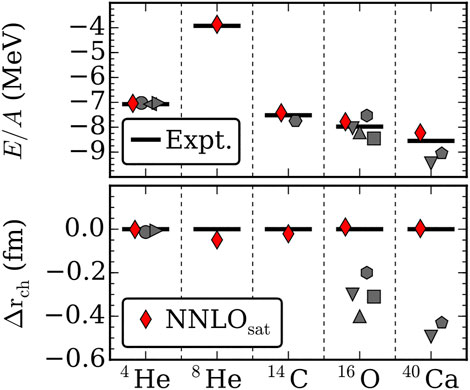
FIGURE 3. Ground-state energy (negative of binding energy) per nucleon (top), and residuals (differences between computed and experimental values) of charge radii (bottom) for selected nuclei computed with chiral interactions. In most cases, theory predicts too-small radii and too-large binding energies. Figure from Ref. [123], where additional details can be found.

Utilizing Bayesian inference methods, one can express the PDF for the LECs conditioned on low-energy data while accounting for the truncation errors of χEFT and our knowledge about the accuracy of the employed many-body methods. The challenge, however, is to quantify these uncertainties. There are methods based on, e.g., Gaussian processes to account for correlated EFT truncation errors in nucleon-nucleon scattering [124] and nuclear matter predictions [125]. However, studies of the χEFT truncation error for finite nuclei deserve more attention [126]. Hu et al. [58] took the first step in this direction to analyze heavy-mass nuclei, where they quantified an ab initio PPD for the neutron-skin thickness in ²⁰⁸Pb. This distribution is conditioned on low-energy data from light- and medium-mass nuclei together with assigned uncertainties of the employed nuclear interactions and the many-body methods.

To enable predictions for nuclei with A ≳ 10, one must use methods whose computational complexity scales gently with A and the size of the single-particle basis. Still, these methods must retain essential many-body physics to describe the observable of interest. Three-nucleon interactions can be challenging to handle computationally [127]. Operating with truncated model spaces and normal-order-approximated interactions goes well with the ideas of the ab initio method. Here, we exemplify our discussion using the coupled cluster method [30] with polynomial scaling in A, but we note that several methods [128, 129] of this kind exist. The coupled cluster method exploits an exponentiated cluster operator $\widehat{T}$ expanded on particle-hole excitations of some many-body reference state. Truncating the expansion of $\widehat{T}$ at some level of n-particle n-hole excitations, and solving for the remaining excitation amplitudes, constitutes a systematically improvable description of the many-body wave function. Although a formal bound on the effect of higher-order particle-hole excitations is lacking, it is clear how to improve. This recipe for improvement is what we seek in an ab initio method. Unfortunately, the convergence pattern might be irregular and vary significantly depending on the observable considered. For example, a rapid convergence for the ground- and first excited-state energies does not imply that their respective wave functions yield a converged description of non-stationary observables [130]. Convergence must be inspected empirically by either gradually increasing the number of particle-hole excitations, or defining a more appropriate starting point (reference state) for the expansion, see, e.g., Ref. [131]. Understanding this kind of convergence pattern is important for proper uncertainty quantification and remains an open question that requires significant domain knowledge.

In Figure 4, we show how the 2p-2h and 3p-3h excitations of the coupled-cluster method contribute to the correlation energy of various closed-shell nuclei. The correlation energy is defined as the difference between the predicted binding energies and the Hartree-Fock energy. Here, the correlation energy $E_{\text{corr}}^{(2+3)}$ is the sum of the 2p-2h correlation energy from CCSD and the 3p-3h correlation energy from the triples, namely the Λ-CCSD(T) approximation [133] (for the 1.8/2.0 (EM) interaction of Ref. [67]) and the CCSDT-1 approximation [134] (for the interaction of Ref. [65]). We see that CCSD accounts for about 90% of the correlation energy for different nuclei and interactions. Various quantum chemistry applications [135] have obtained similar results. This strongly suggests that coupled-cluster theory provides us with a systematic approximation when truncated at the doubles, triples, etc levels. While we do not (yet), have an understanding of the hierarchy (i.e. triples yield much smaller energy contributions than doubles) shown in Figure 4, Sun et al. [132] proposed RG arguments as a possible explanation: Lowering the resolution scale in the three-body subsystems of a many-body system corresponds to removing (short-ranged) triples excitations. Extending the arguments by Lepage [5] and Bogner and Roscher [136] from two to three-body systems then suggests that removal of short-ranged triples excitation can be compensated by a renormalization of the three-body contact.

FIGURE 4

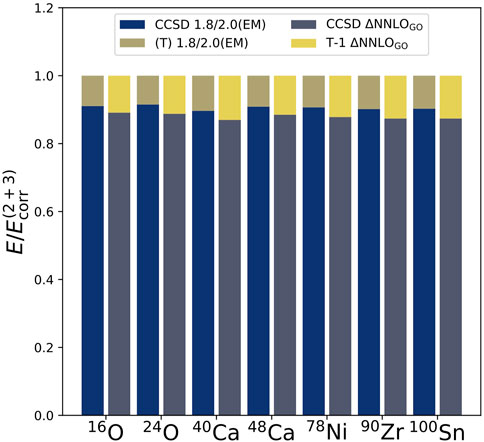
FIGURE 4. Relative contributions to the correlation energy $E_{\text{corr}}^{(2+3)}$ of several closed-shell nuclei from coupled cluster with singles and doubles (CCSD) and triples using the CCSD(T) approximation for the 1.8/2.0 (EM) interaction of Ref. [67] (left bars) and CCSDT-1 for the ΔNNLO_GO (394) interaction of Ref. [65] (right bars). The CCSD result accounts for about 90% of the correlation energy for different nuclei and interactions, and this visualizes the systematic improvements of the coupled-cluster expansion. The data is taken from Ref. [132].

As discussed, the ab initio method aims at maximizing its predictive power over multiple energy scales relevant to nuclei. If we increase the resolution scale to resolve quarks and gluons, we can use Lattice QCD to study nuclear interactions [137, 138] and currents [139, 140]. However, the method is not yet operational for accurate predictions of atomic nuclei [21-25] at physical quark masses. Nevertheless, short of practical and computational challenges, some of the pion-nucleon couplings of χEFT have been computed on the lattice [141]. Although still operating at unphysical pion masses, lattice results can be extrapolated in the infrared using EFT methods [142]. This extrapolative approach has turned out to be particularly valuable in the data-scarce hyperon sector [143] to, e.g., elucidate the role of strangeness in dense nuclear matter [144]. If we instead decrease the resolution scale, likely at the cost of predictive power, we can integrate out the pion to obtain a systematically improvable pionless EFT [145, 146] for which we can solve the Schrödinger equation and perform ab initio computations of processes at very low external momenta. Continuing in this direction, one can devise halo EFT [147, 148], and EFTs for collective phenomena [149–153]. Although these latter two methods are systematically improvable, i.e., they are equipped with a power-counting scheme, they have even less predictive power because they exhibit a relatively small breakdown scale and are tailored to analyze a particular class of low-energy phenomena.

The traditional shell model can be formulated as an ab initio approach if one derives the valence-space interaction from a few-nucleon Hamiltonian, based on χEFT, using a systematically improvable prescription [52, 154–156]. Likewise, coarse-grained representations of nuclear phenomena, like those provided by density functional theory, might be cast as an ab initio method one day if we can link them to low-energy interactions derived from χEFT [157, 158]. However, this has not yet come to fruition [159, 160].

Finally, it is essential to point out that different and sometimes conflicting assumptions regarding the power counting scheme and its meaning are in use. Besides the foundations, which are covered at length in, e.g., Refs. [79, 161–165], all power counting schemes strive to furnish an EFT description of the nuclear interaction that become increasingly refined at higher orders of the expansion. To test this, we must perform calculations to predict nuclear observables. This is an important example of how the nuclear ab initio method and nuclear EFTs are intimately connected and how they can benefit from each other.

6 Summary

The ab initio method should not be confused with nuclear EFT. The ab initio method includes the ideas of EFT in the sense that it is systematically improvable, and one starts from degrees of freedom determined by the relevant scale separation and resolution. However, the ab initio method is also something more. What this “more” is, has not been specified or discussed much in our community. Naturally, misunderstandings and controversies often arise, and one may meet questions like: “Is this really ab initio?” With this paper we hope to bring some clarity to that question.

In our view, the ab initio method should set the beginning at a resolution scale that maximizes the method’s predictive power and enables reliable predictions for phenomena at multiple energy scales ranging from a few tens of keV’s to hundreds of MeV’s. This implies that nucleons are currently the appropriate degrees of freedom for the ab initio method. However, it is an open question whether the beginning can be shifted to an even finer resolution scale, e.g., quarks and gluons while increasing the predictive power across energy scales significantly. We interpret the ab initio method as a systematically improvable approach employing Lagrangians, Hamiltonians, or energy density functionals derived from the Standard Model according to the principles of EFT. Subsequently solving for observables using numerically exact methods or, if necessary, controlled approximations that allow for systematic predictions with quantified uncertainties.

Despite our best efforts, tensions between theoretical predictions and experimental results remain. It is however clear that the ab initio method offers a unique advantage for estimating the uncertainties necessary for assessing the significance of discrepancies between theory and experiment.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant agreement No. 758027), the Swedish Research Council (Grants Nos. 2017-04234, 2020-05127, and 2021-04507), the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Award Nos. DE-FG02-96ER40963 and DE-SC0018223. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.nytimes.com/2022/01/12/business/gruyere-cheese-us-court-ruling.html

References

1. Bethe HA, Bacher RF. Nuclear physics a. stationary states of nuclei. Rev Mod Phys (1936) 8:82–229. doi:10.1103/RevModPhys.8.82

CrossRef Full Text | Google Scholar

2. Bethe HA. Nuclear physics b. nuclear dynamics, theoretical. Rev Mod Phys (1937) 9:69–244. doi:10.1103/RevModPhys.9.69

CrossRef Full Text | Google Scholar

3. Livingston MS, Bethe HA. Nuclear physics c. nuclear dynamics, experimental. Rev Mod Phys (1937) 9:245–390. doi:10.1103/RevModPhys.9.245

CrossRef Full Text | Google Scholar

4. Wilson KG. The renormalization group: Critical phenomena and the kondo problem. Rev Mod Phys (1975) 47:773–840. doi:10.1103/RevModPhys.47.773

CrossRef Full Text | Google Scholar

5. Lepage GP. How to renormalize the schrodinger equation. 8th jorge andre swieca summer school on nuclear physics (1997), 135–180. doi:10.48550/arXiv.nucl-th/9706029

CrossRef Full Text | Google Scholar

6. Caprio MA, Maris P, Vary JP. Emergence of rotational bands in ab initio no-core configuration interaction calculations of light nuclei. Phys Lett B (2013) 719:179–84. doi:10.1016/j.physletb.2012.12.064

CrossRef Full Text | Google Scholar

7. Dytrych T, Launey KD, Draayer JP, Maris P, Vary JP, Saule E, et al. Collective modes in light nuclei from first principles. Phys Rev Lett (2013) 111:252501. doi:10.1103/PhysRevLett.111.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hagen G, Novario SJ, Sun ZH, Papenbrock T, Jansen GR, Lietz JG, et al. Angular-momentum projection in coupled-cluster theory: Structure of ³⁴Mg. Phys Rev C (2022) 105:064311. doi:10.1103/PhysRevC.105.064311

CrossRef Full Text | Google Scholar

9. Yuan Q, Fan SQ, Hu BS, Li JG, Zhang S, Wang SM, et al. Deformed in-medium similarity renormalization group. Phys Rev C (2022) 105:L061303. doi:10.1103/PhysRevC.105.L061303

CrossRef Full Text | Google Scholar

10. Frosini M, Duguet T, Ebran JP, Bally B, Mongelli T, Rodríguez TR, et al. Multi-reference many-body perturbation theory for nuclei. The Eur Phys J A (2022) 58:63. doi:10.1140/epja/s10050-022-00693-y

CrossRef Full Text | Google Scholar

11. Nollett KM, Pieper SC, Wiringa RB, Carlson J, Hale GM. Quantum Monte Carlo calculations of neutron-α scattering. Phys Rev Lett (2007) 99:022502. doi:10.1103/PhysRevLett.99.022502

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Quaglioni S, Navrátil P. Ab initio many-body calculations of n −³H, n −⁴He, p −^3,4He, and n −¹⁰Be scattering. Phys Rev Lett (2008) 101:092501. doi:10.1103/PhysRevLett.101.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hagen G, Jansen GR, Papenbrock T. Structure of ⁷⁸Ni from first-principles computations. Phys Rev Lett (2016) 117:172501. doi:10.1103/PhysRevLett.117.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li JG, Michel N, Hu BS, Zuo W, Xu FR. Ab initio no-core gamow shell-model calculations of multineutron systems. Phys Rev C (2019) 100:054313. doi:10.1103/PhysRevC.100.054313

CrossRef Full Text | Google Scholar

15. Li JG, Michel N, Zuo W, Xu FR. Resonances of a = 4t = 1 isospin triplet states within the ab initio no-core gamow shell model. Phys Rev C (2021) 104:024319. doi:10.1103/PhysRevC.104.024319

CrossRef Full Text | Google Scholar

16. Stroberg SR, Holt JD, Schwenk A, Simonis J. Ab initio limits of atomic nuclei. Phys Rev Lett (2021) 126:022501. doi:10.1103/PhysRevLett.126.022501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Neutral weak current two-body contributions in inclusive scattering from ¹²C. Phys Rev Lett (2014) 112:182502. doi:10.1103/PhysRevLett.112.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lovato A, Carlson J, Gandolfi S, Rocco N, Schiavilla R. Ab initio study of (ν_ℓ, ℓ⁻) and (ν¯ℓ,ℓ⁺) inclusive scattering in ¹²C: Confronting the miniboone and t2k ccqe data. Phys Rev X (2020) 10:031068. doi:10.1103/PhysRevX.10.031068

CrossRef Full Text | Google Scholar

19. Sobczyk JE, Acharya B, Bacca S, Hagen G. Ab initio computation of the longitudinal response function in ⁴⁰Ca. Phys Rev Lett (2021) 127:072501. doi:10.1103/PhysRevLett.127.072501

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Weinberg S. Phenomenological Lagrangians. Physica A (1979) 96:327–40. doi:10.1016/0378-4371(79)90223-1

CrossRef Full Text | Google Scholar

21. Drischler C, Haxton W, McElvain K, Mereghetti E, Nicholson A, Vranas P, et al. Towards grounding nuclear physics in qcd. Prog Part Nucl Phys (2021) 121:103888. doi:10.1016/j.ppnp.2021.103888

CrossRef Full Text | Google Scholar

22. Nicholson A, Berkowitz E, Bulava J, Cheng Chang C, Clark K, Hanlon A, et al. Toward a resolution of the NN controversy. In: PoS LATTICE 2021 (2022). p. 098. doi:10.22323/1.396.0098

CrossRef Full Text | Google Scholar

23. Barnea N, Contessi L, Gazit D, Pederiva F, van Kolck U. Effective field theory for lattice nuclei. Phys Rev Lett (2015) 114:052501. doi:10.1103/PhysRevLett.114.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

24. McIlroy C, Barbieri C, Inoue T, Doi T, Hatsuda T. Doubly magic nuclei from Lattice QCD forces at M_PS =469 MeV/c². Phys Rev C (2018) 97:021303. doi:10.1103/PhysRevC.97.021303

CrossRef Full Text | Google Scholar

25. Bansal A, Binder S, Ekström A, Hagen G, Jansen GR, Papenbrock T. Pion-less effective field theory for atomic nuclei and lattice nuclei. Phys Rev C (2018) 98:054301. doi:10.1103/PhysRevC.98.054301

CrossRef Full Text | Google Scholar

26. Hagen G, Papenbrock T, Dean DJ, Hjorth-Jensen M. Ab initio coupled-cluster approach to nuclear structure with modern nucleon-nucleon interactions. Phys Rev C (2010) 82:034330. doi:10.1103/PhysRevC.82.034330

CrossRef Full Text | Google Scholar

27. Leidemann W, Orlandini G. Modern ab initio approaches and applications in few-nucleon physics with A ≥ 4. Prog Part Nucl Phys (2013) 68:158–214. doi:10.1016/j.ppnp.2012.09.001

CrossRef Full Text | Google Scholar

28. Roth R, Calci A, Langhammer J, Binder S. Ab initio nuclear structure theory: From few to many. Few Body Syst (2014) 55:659–65. doi:10.1007/s00601-014-0860-0

CrossRef Full Text | Google Scholar

29. Roth R. Ab initio approaches to nuclear structure. Lect Notes Phys (2022) 1005:87–139. doi:10.1007/978-3-031-10751-1_3

CrossRef Full Text | Google Scholar

30. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rep Prog Phys (2014) 77:096302. doi:10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Launey KD, Dytrych T, Draayer JP. Symmetry-guided large-scale shell-model theory. Prog Part Nucl Phys (2016) 89:101–36. doi:10.1016/j.ppnp.2016.02.001

CrossRef Full Text | Google Scholar

32. Somà V. Self-consistent green’s function theory for atomic nuclei. Front Phys (2020) 8:340. doi:10.3389/fphy.2020.00340

CrossRef Full Text | Google Scholar

33. Coraggio L, Itaco N. Perturbative approach to effective shell-model Hamiltonians and operators. Front Phys (2020) 8:345. doi:10.3389/fphy.2020.00345

CrossRef Full Text | Google Scholar

34. Navrátil P, Vary JP, Barrett BR. Properties of ¹²c in the ab initio nuclear shell model. Phys Rev Lett (2000) 84:5728–31. doi:10.1103/PhysRevLett.84.5728

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Leinweber DB. Essential strangeness in nucleon magnetic moments. Nucl Phys A (1995) 585:341C–2. doi:10.1016/0375-9474(94)00597-G

CrossRef Full Text | Google Scholar

36. Friar JL. Nuclear forces and chiral theories. Few Body Syst Suppl (1995) 8:471–482. doi:10.48550/arXiv.nucl-th/9601012

CrossRef Full Text | Google Scholar

37. Zheng DC, Barrett BR, Vary JP, Haxton WC, Song CL. Large-basis shell model studies of light nuclei with a multivalued g-matrix effective interaction. Phys Rev C (1995) 52:2488–98. doi:10.1103/PhysRevC.52.2488

CrossRef Full Text | Google Scholar

38. Navrátil P, Barrett BR. Large-basis shell-model calculations for p-shell nuclei. Phys Rev C (1998) 57:3119–28. doi:10.1103/PhysRevC.57.3119

CrossRef Full Text | Google Scholar

39. Barrett BR, Navrátil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys (2013) 69:131–81. doi:10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

40. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C (1995) 51:38–51. doi:10.1103/PhysRevC.51.38

CrossRef Full Text | Google Scholar

41. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys Rev C (2001) 63:024001. doi:10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

42. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

43. Machleidt R, Entem D. Chiral effective field theory and nuclear forces. Phys Rep (2011) 503:1–75. doi:10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

44. Hammer HW, König S, van Kolck U. Nuclear effective field theory: Status and perspectives. Rev Mod Phys (2020) 92:025004. doi:10.1103/RevModPhys.92.025004

CrossRef Full Text | Google Scholar

45. Mihaila B, Heisenberg JH. Microscopic calculation of the inclusive electron scattering structure function in ¹⁶O. Phys Rev Lett (2000) 84:1403–6. doi:10.1103/PhysRevLett.84.1403

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Dickhoff W, Barbieri C. Self-consistent green’s function method for nuclei and nuclear matter. Prog Part Nucl Phys (2004) 52:377–496. doi:10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

47. Dean DJ, Hjorth-Jensen M. Coupled-cluster approach to nuclear physics. Phys Rev C (2004) 69:054320. doi:10.1103/PhysRevC.69.054320

CrossRef Full Text | Google Scholar

48. Epelbaum E, Krebs H, Lee D, Meißner UG. Lattice calculations for a = 3, 4, 6, 12 nuclei using chiral effective field theory. Eur Phys J A (2010) 45:335–52. doi:10.1140/epja/i2010-11009-x

CrossRef Full Text | Google Scholar

49. Tsukiyama K, Bogner SK, Schwenk A. In-medium similarity renormalization group for nuclei. Phys Rev Lett (2011) 106:222502. doi:10.1103/PhysRevLett.106.222502

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Somà V, Barbieri C, Duguet T. Ab initio gorkov-green’s function calculations of open-shell nuclei. Phys Rev C (2013) 87:011303. doi:10.1103/PhysRevC.87.011303

CrossRef Full Text | Google Scholar

51. Hergert H, Bogner SK, Morris TD, Schwenk A, Tsukiyama K. The in-medium similarity renormalization group: A novel ab initio method for nuclei. Phys Rep (2016) 621:165–222. doi:10.1016/j.physrep.2015.12.007

CrossRef Full Text | Google Scholar

52. Stroberg SR, Calci A, Hergert H, Holt JD, Bogner SK, Roth R, et al. Nucleus-dependent valence-space approach to nuclear structure. Phys Rev Lett (2017) 118:032502. doi:10.1103/PhysRevLett.118.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Roth R, Binder S, Vobig K, Calci A, Langhammer J, Navrátil P. Medium-mass nuclei with normal-ordered chiral NN+3N interactions. Phys Rev Lett (2012) 109:052501. doi:10.1103/PhysRevLett.109.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys Lett B (2014) 736:119–23. doi:10.1016/j.physletb.2014.07.010

CrossRef Full Text | Google Scholar

55. Lähde TA, Epelbaum E, Krebs H, Lee D, Meißner UG, Rupak G. Lattice effective field theory for medium-mass nuclei. Phys Lett B (2014) 732:110–5. doi:10.1016/j.physletb.2014.03.023

CrossRef Full Text | Google Scholar

56. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest tin isotopes. Phys Rev Lett (2018) 120:152503. doi:10.1103/PhysRevLett.120.152503

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Miyagi T, Stroberg SR, Holt JD, Shimizu N. Ab initio multishell valence-space Hamiltonians and the island of inversion. Phys Rev C (2020) 102:034320. doi:10.1103/PhysRevC.102.034320

CrossRef Full Text | Google Scholar

58. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Ab initio predictions link the neutron skin of 208pb to nuclear forces. Nat Phys (2022) 18:1196–200. doi:10.1038/s41567-022-01715-8

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Hagen G, Papenbrock T, Dean DJ, Schwenk A, Nogga A, Włoch M, et al. Coupled-cluster theory for three-body Hamiltonians. Phys Rev C (2007) 76:034302. doi:10.1103/PhysRevC.76.034302

CrossRef Full Text | Google Scholar

60. Ripoche J, Tichai A, Duguet T. Normal-ordered k-body approximation in particle-number-breaking theories. Eur Phys J A (2020) 56:40. doi:10.1140/epja/s10050-020-00045-8

CrossRef Full Text | Google Scholar

61. Hagen G, Papenbrock T, Dean DJ. Solution of the center-of-mass problem in nuclear structure calculations. Phys Rev Lett (2009) 103:062503. doi:10.1103/PhysRevLett.103.062503

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Parzuchowski NM, Stroberg SR, Navrátil P, Hergert H, Bogner SK. Ab initio electromagnetic observables with the in-medium similarity renormalization group. Phys Rev C (2017) 96:034324. doi:10.1103/PhysRevC.96.034324

CrossRef Full Text | Google Scholar

63. Djärv T, Ekström A, Forssén C, Jansen GR. Normal-ordering approximations and translational (non)invariance. Phys Rev C (2021) 104:024324. doi:10.1103/PhysRevC.104.024324

CrossRef Full Text | Google Scholar

64. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C (2015) 91:051301. doi:10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

65. Jiang WG, Ekström A, Forssén C, Hagen G, Jansen GR, Papenbrock T. Accurate bulk properties of nuclei from a = 2 to ∞ from potentials with Δ isobars. Phys Rev C (2020) 102:054301. doi:10.1103/PhysRevC.102.054301

CrossRef Full Text | Google Scholar

66. Roth R, Langhammer J, Calci A, Binder S, Navrátil P. Similarity-transformed chiral NN + 3N interactions for the ab initio description of ¹²C and ¹⁶O. Phys Rev Lett (2011) 107:072501. doi:10.1103/PhysRevLett.107.072501

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C (2011) 83:031301. doi:10.1103/PhysRevC.83.031301

CrossRef Full Text | Google Scholar

68. Ekström A, Baardsen G, Forssén C, Hagen G, Hjorth-Jensen M, Jansen GR, et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys Rev Lett (2013) 110:192502. doi:10.1103/PhysRevLett.110.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett (2015) 115:122301. doi:10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Piarulli M, Girlanda L, Schiavilla R, Pérez RN, Amaro JE, Arriola ER. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange includingΔresonances. Phys Rev C (2015) 91:024003. doi:10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

71. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C (2016) 94:054007. doi:10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

72. Carlsson BD, Ekström A, Forssén C, Strömberg DF, Jansen GR, Lilja O, et al. Uncertainty analysis and order-by-order optimization of chiral nuclear interactions. Phys Rev X (2016) 6:011019. doi:10.1103/PhysRevX.6.011019

CrossRef Full Text | Google Scholar

73. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys Rev C (2018) 97:024332. doi:10.1103/PhysRevC.97.024332

CrossRef Full Text | Google Scholar

74. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A (2018) 54:86. doi:10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

75. Lu BN, Li N, Elhatisari S, Lee D, Epelbaum E, Meißner UG. Essential elements for nuclear binding. Phys Lett B (2019) 797:134863. doi:10.1016/j.physletb.2019.134863

CrossRef Full Text | Google Scholar

76. Somà V, Navrátil P, Raimondi F, Barbieri C, Duguet T. Novel chiral Hamiltonian and observables in light and medium-mass nuclei. Phys Rev C (2020) 101:014318. doi:10.1103/PhysRevC.101.014318

CrossRef Full Text | Google Scholar

77. Maris P, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, Huther T, et al. Light nuclei with semilocal momentum-space regularized chiral interactions up to third order. Phys Rev C (2021) 103:054001. doi:10.1103/PhysRevC.103.054001

CrossRef Full Text | Google Scholar

78. Nosyk Y, Entem DR, Machleidt R. Nucleon-nucleon potentials from Δ-full chiral effective-field-theory and implications. Phys Rev C (2021) 104:054001. doi:10.1103/PhysRevC.104.054001

CrossRef Full Text | Google Scholar

79. Yang CJ, Ekström A, Forssén C, Hagen G. Power counting in chiral effective field theory and nuclear binding. Phys Rev C (2021) 103:054304. doi:10.1103/PhysRevC.103.054304

CrossRef Full Text | Google Scholar

80. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha–alpha scattering. Nature (2015) 528:111–4. doi:10.1038/nature16067

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Navrátil P, Quaglioni S, Hupin G, Romero-Redondo C, Calci A. Unified ab initio approaches to nuclear structure and reactions. Physica Scripta (2016) 91:053002. doi:10.1088/0031-8949/91/5/053002

CrossRef Full Text | Google Scholar

82. Bedaque PF, van Kolck U. Effective field theory for few-nucleon systems. Annu Rev Nucl Part Sci (2002) 52:339–96. doi:10.1146/annurev.nucl.52.050102.090637

CrossRef Full Text | Google Scholar

83. Bogner SK, Kuo TTS, Schwenk A. Model-independent low momentum nucleon interaction from phase shift equivalence. Phys Rep (2003) 386:1–27. doi:10.1016/j.physrep.2003.07.001

CrossRef Full Text | Google Scholar

84. Bogner SK, Furnstahl RJ, Perry RJ. Similarity renormalization group for nucleon-nucleon interactions. Phys Rev C (2007) 75:061001. doi:10.1103/PhysRevC.75.061001

CrossRef Full Text | Google Scholar

85. Furnstahl R, Hammer HW. Are occupation numbers observable? Phys Lett B (2002) 531:203–8. doi:10.1016/S0370-2693(01)01504-0

CrossRef Full Text | Google Scholar

86. Jurgenson ED, Navrátil P, Furnstahl RJ. Evolution of nuclear many-body forces with the similarity renormalization group. Phys Rev Lett (2009) 103:082501. doi:10.1103/PhysRevLett.103.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

87. More SN, Bogner SK, Furnstahl RJ. Scale dependence of deuteron electrodisintegration. Phys Rev C (2017) 96:054004. doi:10.1103/PhysRevC.96.054004

CrossRef Full Text | Google Scholar

88. Furnstahl RJ, Hagen G, Papenbrock T. Corrections to nuclear energies and radii in finite oscillator spaces. Phys Rev C (2012) 86:031301. doi:10.1103/PhysRevC.86.031301

CrossRef Full Text | Google Scholar

89. König S, Lee D. Volume dependence of n-body bound states. Phys Lett B (2018) 779:9–15. doi:10.1016/j.physletb.2018.01.060

CrossRef Full Text | Google Scholar

90. Schindler MR, Phillips DR. Bayesian methods for parameter estimation in effective field theories. Ann Phys (2009) 324:682–708. doi:10.1016/j.aop.2008.09.003

CrossRef Full Text | Google Scholar

91. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev C (2015) 92:024005. doi:10.1103/PhysRevC.92.024005

CrossRef Full Text | Google Scholar

92. Lee D. Lattice simulations for few- and many-body systems. Prog Part Nucl Phys (2009) 63:117–54. doi:10.1016/j.ppnp.2008.12.001

CrossRef Full Text | Google Scholar

93. Lähde TA, Meißner UG. Nuclear lattice effective field theory: An introduction. Berlin: Springer (2019). doi:10.1007/978-3-030-14189-9

CrossRef Full Text | Google Scholar

94. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the ⁴⁸Ca nucleus. Nat Phys (2016) 12:186–90. doi:10.1038/nphys3529

CrossRef Full Text | Google Scholar

95. Hagen G, Hjorth-Jensen M, Jansen GR, Papenbrock T. Emergent properties of nuclei from ab initio coupled-cluster calculations. Phys Scr (2016) 91:063006. doi:10.1088/0031-8949/91/6/063006

CrossRef Full Text | Google Scholar

96. Bontems V, Duguet T, Hagen G, Somà V. Topical issue on the tower of effective (field) theories and the emergence of nuclear phenomena. Eur Phys J A (2021) 57:42. doi:10.1140/epja/s10050-021-00356-4

CrossRef Full Text | Google Scholar

97. Tropiano AJ, Bogner SK, Furnstahl RJ. Short-range correlation physics at low renormalization group resolution. Phys Rev C (2021) 104:034311. doi:10.1103/PhysRevC.104.034311

CrossRef Full Text | Google Scholar

98. Hartmann S. Effective field theories, reductionism and scientific explanation. Stud Hist Philos Sci B: Stud Hist Philos Mod Phys (2001) 32:267–304. doi:10.1016/s1355-2198(01)00005-3

CrossRef Full Text | Google Scholar

99. Rivat S, Grinbaum A. Philosophical foundations of effective field theories. Eur Phys J A (2020) 56:90. doi:10.1140/epja/s10050-020-00089-w

CrossRef Full Text | Google Scholar

100. Lindley D. The philosophy of statistics. J R Stat Soc Ser D (The Statistician) (2000) 49:293–337. doi:10.1111/1467-9884.00238

CrossRef Full Text | Google Scholar

101. Box GEP. Science and statistics. J Am Stat Assoc (1976) 71:791–9. doi:10.1080/01621459.1976.10480949

CrossRef Full Text | Google Scholar

102. Kennedy MC, O’Hagan A. Bayesian calibration of computer models. J R Stat Soc Ser B (Statistical Methodology) (2001) 63:425–64. doi:10.1111/1467-9868.00294

CrossRef Full Text | Google Scholar

103. Brynjarsdóttir J, O’Hagan A. Learning about physical parameters: The importance of model discrepancy. Inverse Probl (2014) 30:114007. doi:10.1088/0266-5611/30/11/114007

CrossRef Full Text | Google Scholar

104. Brooks S, Gelman A, Jones G, Meng XL. Handbook of Markov chain Monte Carlo. Florida: CRC Press (2011).

Google Scholar

105. Svensson I, Ekström A, Forssén C. Bayesian parameter estimation in chiral effective field theory using the Hamiltonian Monte Carlo method. Phys Rev C (2022) 105:014004. doi:10.1103/PhysRevC.105.014004

CrossRef Full Text | Google Scholar

106. Wesolowski S, Svensson I, Ekström A, Forssén C, Furnstahl RJ, Melendez JA, et al. Rigorous constraints on three-nucleon forces in chiral effective field theory from fast and accurate calculations of few-body observables. Phys Rev C (2021) 104:064001. doi:10.1103/PhysRevC.104.064001

CrossRef Full Text | Google Scholar

107. König S, Ekström A, Hebeler K, Lee D, Schwenk A. Eigenvector continuation as an efficient and accurate emulator for uncertainty quantification. Phys Lett B (2020) 810:135814. doi:10.1016/j.physletb.2020.135814

CrossRef Full Text | Google Scholar

108. Ekström A, Hagen G. Global sensitivity analysis of bulk properties of an atomic nucleus. Phys Rev Lett (2019) 123:252501. doi:10.1103/PhysRevLett.123.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Witała H, Golak J, Skibiński R. Efficient emulator for solving three-nucleon continuum Faddeev equations with chiral three-nucleon force comprising any number of contact terms. Eur Phys J A (2021) 57:241. doi:10.1140/epja/s10050-021-00555-z

CrossRef Full Text | Google Scholar

110. Furnstahl R, Garcia A, Millican P, Zhang X. Efficient emulators for scattering using eigenvector continuation. Phys Lett B (2020) 809:135719. doi:10.1016/j.physletb.2020.135719

CrossRef Full Text | Google Scholar

111. Chaloner K, Verdinelli I. Bayesian experimental design: A review. Statist Sci (1995) 10:273–304. doi:10.1214/ss/1177009939

CrossRef Full Text | Google Scholar

112. Santner TJ, Williams BJ, Notz WI. The design and analysis of computer experiments. Berlin: Springer (2003). doi:10.1007/978-1-4757-3799-8

CrossRef Full Text | Google Scholar

113. Farrow M, Goldstein M. Trade-off sensitive experimental design: A multicriterion, decision theoretic, bayes linear approach. J Stat Plan Inference (2006) 136:498–526. doi:10.1016/j.jspi.2004.07.008

CrossRef Full Text | Google Scholar

114. Vernon I, Liu J, Goldstein M, Rowe J, Topping J, Lindsey K. Bayesian uncertainty analysis for complex systems biology models: Emulation, global parameter searches and evaluation of gene functions. BMC Syst Biol (2018) 12:1. doi:10.1186/s12918-017-0484-3

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Melendez JA, Furnstahl RJ, Griesshammer HW, McGovern JA, Phillips DR, Pratola MT. Designing optimal experiments: An application to proton compton scattering. Eur Phys J A (2021) 57:81. doi:10.1140/epja/s10050-021-00382-2

CrossRef Full Text | Google Scholar

116. Pablo G, Jorge P. From noise to information: The transfer function formalism for uncertainty quantification in reconstructing the nuclear density. Phys Rev C (2021) 104:024301. doi:10.1103/PhysRevC.104.024301

CrossRef Full Text | Google Scholar

117. Glöckle W. The quantum mechanical few-body problem. Berlin: Springer-Verlag (1983).

Google Scholar

118. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys (2015) 87:1067–118. doi:10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

119. Kamada H, Nogga A, Glöckle W, Hiyama E, Kamimura M, Varga K, et al. Benchmark test calculation of a four-nucleon bound state. Phys Rev C (2001) 64:044001. doi:10.1103/PhysRevC.64.044001

CrossRef Full Text | Google Scholar

120. Forssén C, Carlsson BD, Johansson HT, Sääf D, Bansal A, Hagen G, et al. Large-scale exact diagonalizations reveal low-momentum scales of nuclei. Phys Rev C (2018) 97:034328. doi:10.1103/PhysRevC.97.034328

CrossRef Full Text | Google Scholar

121. Maris P, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, Hüther T, et al. Light nuclei with semilocal momentum-space regularized chiral interactions up to third order. arXiv:nucl-th 2012.12396 (2020). doi:10.48550/arXiv.2012.12396

CrossRef Full Text | Google Scholar

122. Maris P, Roth R, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Nuclear properties with semilocal momentum-space regularized chiral interactions beyond N2LO. Phys Rev C (2022) 106:064002. doi:10.1103/PhysRevC.106.064002

CrossRef Full Text | Google Scholar

123. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. arXiv:nucl-th 1502.04682 (2015). doi:10.48550/arXiv.1502.04682

CrossRef Full Text | Google Scholar

124. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys Rev C (2019) 100:044001. doi:10.1103/PhysRevC.100.044001

CrossRef Full Text | Google Scholar

125. Drischler C, Furnstahl RJ, Melendez JA, Phillips DR. How well do we know the neutron-matter equation of state at the densities inside neutron stars? A bayesian approach with correlated uncertainties. Phys Rev Lett (2020) 125:202702. doi:10.1103/PhysRevLett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Tews I, Davoudi Z, Ekström A, Holt JD, Lynn JE. New ideas in constraining nuclear forces. J Phys G (2020) 47:103001. doi:10.1088/1361-6471/ab9079

CrossRef Full Text | Google Scholar

127. Miyagi T, Stroberg SR, Navrátil P, Hebeler K, Holt JD. Converged ab initio calculations of heavy nuclei. Phys Rev C (2022) 105:014302. doi:10.1103/PhysRevC.105.014302

CrossRef Full Text | Google Scholar

128. Hergert H. A guided tour of ab initio nuclear many-body theory. Front Phys (2020) 8:379. doi:10.3389/fphy.2020.00379

CrossRef Full Text | Google Scholar

129. Tichai A, Roth R, Duguet T. Many-body perturbation theories for finite nuclei. Front Phys (2020) 8:164. doi:10.3389/fphy.2020.00164

CrossRef Full Text | Google Scholar

130. Stroberg SR, Henderson J, Hackman G, Ruotsalainen P, Hagen G, Holt JD. Systematics of e2 strength in the sd shell with the valence-space in-medium similarity renormalization group. Phys Rev C (2022) 105:034333. doi:10.1103/PhysRevC.105.034333

CrossRef Full Text | Google Scholar

131. Novario SJ, Hagen G, Jansen GR, Papenbrock T. Charge radii of exotic neon and magnesium isotopes. Phys Rev C (2020) 102:051303. doi:10.1103/PhysRevC.102.051303

CrossRef Full Text | Google Scholar

132. Sun ZH, Bell CA, Hagen G, Papenbrock T. How to renormalize coupled cluster theory. Phys Rev C (2022) 106:L061302. doi:10.1103/PhysRevC.106.L061302

CrossRef Full Text | Google Scholar

133. Taube AG, Bartlett RJ. Improving upon ccsd(t): Lambda ccsd(t). i. potential energy surfaces. J Chem Phys (2008) 128:044110. doi:10.1063/1.2830236

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Lee YS, Kucharski SA, Bartlett RJ. A coupled cluster approach with triple excitations. J Chem Phys (1984) 81:5906–12. doi:10.1063/1.447591

CrossRef Full Text | Google Scholar

135. Bartlett RJ, Musiał M. Coupled-cluster theory in quantum chemistry. Rev Mod Phys (2007) 79:291–352. doi:10.1103/RevModPhys.79.291

CrossRef Full Text | Google Scholar

136. Bogner SK, Roscher D. High-momentum tails from low-momentum effective theories. Phys Rev C (2012) 86:064304. doi:10.1103/PhysRevC.86.064304

CrossRef Full Text | Google Scholar

137. Illa M, Beane SR, Chang E, Davoudi Z, Detmold W, Murphy DJ, et al. Low-energy scattering and effective interactions of two baryons at m_π ∼ 450 MeV from lattice quantum chromodynamics. Phys Rev D (2021) 103:054508. doi:10.1103/PhysRevD.103.054508

CrossRef Full Text | Google Scholar

138. Aoki S, Doi T. Lattice qcd and baryon-baryon interactions: Hal qcd method. Front Phys (2020) 8:307. doi:10.3389/fphy.2020.00307

CrossRef Full Text | Google Scholar

139. Davoudi Z, Detmold W, Shanahan P, Orginos K, Parreño A, Savage MJ, et al. Nuclear matrix elements from lattice qcd for electroweak and beyond-standard-model processes. Phys ReportsNuclear matrix Elem lattice QCD electroweak beyond–Standard-Model Process (2021) 900:1–74. doi:10.1016/j.physrep.2020.10.004

CrossRef Full Text | Google Scholar

140. Parreño A, Shanahan PE, Wagman ML, Winter F, Chang E, Detmold W, et al. Axial charge of the triton from lattice qcd. Phys Rev D (2021) 103:074511. doi:10.1103/PhysRevD.103.074511

CrossRef Full Text | Google Scholar

141. Chang CC, Nicholson AN, Rinaldi E, Berkowitz E, Garron N, Brantley DA, et al. A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics. Nature (2018) 558:91–4. doi:10.1038/s41586-018-0161-8

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Eliyahu M, Bazak B, Barnea N. Extrapolating lattice qcd results using effective field theory. Phys Rev C (2020) 102:044003. doi:10.1103/PhysRevC.102.044003

CrossRef Full Text | Google Scholar

143. Beane SR, Chang E, Cohen SD, Detmold W, Lin HW, Luu TC, et al. Light nuclei and hypernuclei from quantum chromodynamics in the limit of SU(3) flavor symmetry. Phys Rev D (2013) 87:034506. doi:10.1103/PhysRevD.87.034506

CrossRef Full Text | Google Scholar

144. Beane SR, Chang E, Cohen SD, Detmold W, Lin HW, Luu TC, et al. Hyperon-nucleon interactions from quantum chromodynamics and the composition of dense nuclear matter. Phys Rev Lett (2012) 109:172001. doi:10.1103/PhysRevLett.109.172001

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Kaplan DB, Savage MJ, Wise MB. Two-nucleon systems from effective field theory. Nucl Phys B (1998) 534:329–55. doi:10.1016/S0550-3213(98)00440-4

CrossRef Full Text | Google Scholar

146. van Kolck U. Effective field theory of short-range forces. Nucl Phys A (1999) 645:273–302. doi:10.1016/S0375-9474(98)00612-5

CrossRef Full Text | Google Scholar

147. Bertulani CA, Hammer HW, van Kolck U. Effective field theory for halo nuclei: Shallow -wave states. Nucl Phys A (2002) 712:37–58. doi:10.1016/S0375-9474(02)01270-8

CrossRef Full Text | Google Scholar

148. Hammer HW, Ji C, Phillips DR. Effective field theory description of halo nuclei. J Phys G: Nucl Part Phys (2017) 44:103002. doi:10.1088/1361-6471/aa83db

CrossRef Full Text | Google Scholar

149. Coello Pérez EA, Papenbrock T. Effective field theory for nuclear vibrations with quantified uncertainties. Phys Rev C (2015) 92:064309. doi:10.1103/PhysRevC.92.064309

CrossRef Full Text | Google Scholar

150. Papenbrock T. Effective theory for deformed nuclei. Nucl Phys A (2011) 852:36–60. doi:10.1016/j.nuclphysa.2010.12.013

CrossRef Full Text | Google Scholar

151. Chen QB, Kaiser N, Meißner UG, Meng J. Effective field theory for triaxially deformed nuclei. Eur Phys J A (2017) 53:204. doi:10.1140/epja/i2017-12404-5

CrossRef Full Text | Google Scholar

152. Alnamlah IK, Coello Pérez EA, Phillips DR. Effective field theory approach to rotational bands in odd-mass nuclei. Phys Rev C (2021) 104:064311. doi:10.1103/PhysRevC.104.064311

CrossRef Full Text | Google Scholar

153. Papenbrock T. Effective field theory of pairing rotations. Phys Rev C (2022) 105:044322. doi:10.1103/PhysRevC.105.044322

CrossRef Full Text | Google Scholar

154. Jansen GR, Engel J, Hagen G, Navratil P, Signoracci A. Ab initio coupled-cluster effective interactions for the shell model: Application to neutron-rich oxygen and carbon isotopes. Phys Rev Lett (2014) 113:142502. doi:10.1103/PhysRevLett.113.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Sun ZH, Morris TD, Hagen G, Jansen GR, Papenbrock T. Shell-model coupled-cluster method for open-shell nuclei. Phys Rev C (2018) 98:054320. doi:10.1103/PhysRevC.98.054320

CrossRef Full Text | Google Scholar

156. Sun ZH, Hagen G, Jansen GR, Papenbrock T. Effective shell-model interaction for nuclei “southeast” of ¹⁰⁰Sn. Phys Rev C (2021) 104:064310. doi:10.1103/PhysRevC.104.064310

CrossRef Full Text | Google Scholar

157. Bogner SK, Furnstahl RJ, Platter L. Density matrix expansion for low-momentum interactions. Eur Phys J A (2009) 39:219–41. doi:10.1140/epja/i2008-10695-1

CrossRef Full Text | Google Scholar

158. Dobaczewski J. Ab initio derivation of model energy density functionals. J Phys G: Nucl Part Phys (2016) 43:04LT01. doi:10.1088/0954-3899/43/4/04lt01

CrossRef Full Text | Google Scholar

159. Furnstahl RJ. Turning the nuclear energy density functional method into a proper effective field theory: Reflections. Eur Phys J A (2020) 56:85. doi:10.1140/epja/s10050-020-00095-y

CrossRef Full Text | Google Scholar

160. Salvioni G, Dobaczewski J, Barbieri C, Carlsson G, Idini A, Pastore A. Model nuclear energy density functionals derived from ab initio calculations. J Phys G: Nucl Part Phys (2020) 47:085107. doi:10.1088/1361-6471/ab8d8e

CrossRef Full Text | Google Scholar

161. Nogga A, Timmermans RGE, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev C (2005) 72:054006. doi:10.1103/PhysRevC.72.054006

CrossRef Full Text | Google Scholar

162. Epelbaum E, Meißner UG. On the renormalization of the one–pion exchange potential and the consistency of weinberg’s power counting. Few-Body Syst (2013) 54:2175–90. doi:10.1007/s00601-012-0492-1

CrossRef Full Text | Google Scholar

163. Epelbaum E, Gasparyan AM, Gegelia J, Meißner UG. How (not) to renormalize integral equations with singular potentials in effective field theory. Eur Phys J A (2018) 54:186. doi:10.1140/epja/i2018-12632-1

CrossRef Full Text | Google Scholar

164. Yang CJ. Do we know how to count powers in pionless and pionful effective field theory? Eur Phys J A (2020) 56:96. doi:10.1140/epja/s10050-020-00104-0

CrossRef Full Text | Google Scholar

165. van Kolck U. The problem of renormalization of chiral nuclear forces. Front Phys (2020) 8:79. doi:10.3389/fphy.2020.00079

CrossRef Full Text | Google Scholar