- 1COSS, DGESS, ETHZ, Zurich, Switzerland
- 2Humanities and Social Sciences, California Institute of Technology, Pasadena, CA, United States
This study investigates the effects of temporal changes at the individual and social levels and their impact on cooperation in social networks. A theoretical framework is proposed to explain the probability of cooperation as a function of endogenously driven periodic temporal variation and neural synchrony modeled as a diffusion process. Agents are simulated playing a prisoner’s dilemma game, with and without evolution, in a two-player setting and on networks. Most importantly, we find that temporal variation and synchrony influence cooperation patterns in a non-trivial way and can enhance or suppress cooperation, depending on exact parameter values. Furthermore, some of our results point to promising future research on human subjects. Specifically, we find that cooperators can dramatically increase their payoff—as opposed to defectors—if neural synchrony is present. Furthermore, the more heterogeneous the synchrony between two agents, the less they cooperate. In a network setting, neural synchrony inhibits cooperation, and variation in circadian patterns counteracts this effect.
Call: Hidden Order Behind Cooperation in Social Systems.
1 Introduction
The ability to cooperate on a large scale has been highlighted as the strongest competitive advantage we—the human species—have in the animal kingdom. In today’s closely networked society, daily (cooperative) encounters with other individuals are a normal part of life.
Although often omitted in analyses and models, environmental and cognitive variations affect each individual’s decision process, thus shaping cooperation at large. One example of such an environmental variable is the rising and setting of the sun. It profoundly impacts various physiological processes, some of which a person experiences consciously, such as sleep, drive, and appetite. For some other behaviors, such as the tendency to cooperate, a causal link to circadian or neuromodulatory variation is less evident. To make matters more complicated, the act of social interaction itself also directly impacts the brain’s decision-making abilities, as individuals that engage in a social encounter experience a higher correlation in brain activity—the so-called neural synchrony or inter-brain synchrony. Knowledge of a link between these time-varying cognitive patterns and cooperation at large would be extremely powerful, enabling us to time interactions to maximize a specific outcome, such as cooperation.
It is well-known that neuronal communication is mediated by a range of neurotransmitters and neuromodulators that shape behavior during decision-making processes [1]. Studies have shown that various neurotransmitters, such as dopamine and serotonin, show rhythmic variations in concentration in many neuronal nuclei and centers of the brain [2,3]. Moreover, light, a major environmental cue, plays a central role in setting circadian cycles, which in turn impact body temperature, melatonin, cortisol, and cortical activity (as seen through EEG recordings [4–7] and biological clock neurons [8]). Additionally, the circadian system has been linked to various aspects of physiology and cognitive processes, such as learning, memory, attention, mood, and reaction time [9]. These cognitive variations resulting from circadian cycles can ultimately affect social phenomena globally.
On the other hand, social interactions also influence the dynamics of the brain. Recent developments in neuroimaging have enabled measurements of the activity of two or more brains simultaneously, a process known as “hyperscanning” [10,11]. This has allowed for the exploration of inter-brain synchrony, which has been linked to joint attention, interpersonal communication, coordination, and decision-making (for review, see [11]). Studies have revealed that higher inter-brain synchrony is associated with successful cooperation [12–17]. Intra-person variation, such as circadian variation in the expression of specific genes in the prefrontal cortex [18], is also believed to play a role in these interactions. Altogether, social dynamics are intricately linked with the dynamical system of the brain.
Classical social network analysis, a branch in sociology [19], typically assumes that the only essential elements that define societies are interactions—links—between individuals and their interacting units—people or animals—where the latter is modeled as internally monolithic entities. Researchers have only now begun appreciating the importance of the potentially heterogeneous internal structure of an individual in the fabric of society. These ideas are being explored in new fields of the network [20] and social [21] neuroscience and have already yielded knowledge fruits. So far, building upon the social brain hypothesis [22], these fields have mainly focused on associations between neural dynamics and structural properties of social networks, such as density [23], centrality, and homophily [24], or linking the neuroendocrine system with the structure of a social network [25]. However, the effects that neurocognitive dynamics may have on global socio-dynamic processes that take place in a network have been researched far less. Some of the examples in this direction are research on potential interventions, such as giving oxytocin to central individuals in a social network to increase their trust and enforcement of cooperation norms through peer punishment, thereby enabling cooperation [26], or linking temporal connectivity in a social network with a circadian rhythm [27]. However, the most common focus in the field is on the effects that temporal changes in interactions, such as bursty patterns [28], have on cooperation [29] rather than the temporal variability that is intrinsic to an individual, such as variation at a cognitive level.
To fill this gap, this study investigates the impact that temporal changes at the individual level may have on cooperation in a social network. We specifically concentrate on two sources of temporality, namely, the behavioral variations caused by circadian or other periodic variations in the concentration of (neuro) hormones, and neural synchrony, namely, a transition from a less- to more-correlated inter-brain activity, as a direct consequence of social interaction itself. In Section 2, we incorporate individuality in evolutionary game theory models on graphs and allow individual preferences and tendencies to be time-varying, e.g., within a 24-h rhythm, and converging to a global mean, thereby mimicking neural synchrony. We then study the model’s predictions within the framework of a social dilemma game: the prisoner’s dilemma. At first, we introduce the game as a non-evolutionary game and then proceed with implementing evolution. Subsequently, we add another layer of complexity and consider the game to be played in a pair and then on a network. Our simulation results are discussed in Section 3. We conclude and suggest steps for future research in Section 4.
2 Methods: Theorizing cooperation as temporal variation and synchrony
We established a link between circadian rhythms, inter-person neural synchrony, and cooperation preferences in the introduction. In this section, we develop a theoretical framework that aims to quantitatively elucidate this link. Many neuromodulators posit cyclic patterns; therefore, we model decision preferences as periodic functions and dependent on neural synchrony. Subsequently, we describe the game within which we consider the cooperative action to take place. Lastly, we describe the evolutionary mechanisms introduced, the types of networks, and the metrics we will investigate after obtaining simulation results.
2.1 Periodic variability and synchrony in decision preferences
To incorporate an individual’s periodic variability caused by circadian rhythms and temporal changes due to neural synchrony into our model, we proceed as follows. First, we allow the probability associated with a random variable of cooperation to be time-varying and composed of two individual parts:
i.e., for each individual i, the probability to cooperate at round t is composed of a time-varying part fi(t, Θi) that reflects the person’s circadian rhythm or any other internal influences that affect a person without interaction with a human-populated environment and a time-varying part gi that corresponds to that individual’s inter-person neural synchrony (interaction with a human-populated environment). Here, Θ is a set of parameters for f and similarly for g. For simplicity, we will consider fi = f, gi = g ∀i. It should be noted that
The periodic variability part is modeled as the sum of periodic functions1. For instance, if there is one time-varying influence,
where ai is the amplitude of a sine wave, Ti is its period, and θi is the phase and δi is a shift. Both t and Ti are expressed in equivalent units of time. Such variability is akin to periodic changes in personal preferences that one would expect due to changes in the activity of a single neuromodulator. In the case of Q influences, f can be defined as
Next, we move on to a model of neural synchrony. Generally, synchronization is a temporal phenomenon whereby a system transitions from a less ordered state to a more ordered state. In cooperation dynamics, an ordered state would be a state where all individuals partake in the same decision to cooperate or to defect [10]. Therefore, a natural candidate for modeling the neural synchrony part is a simple diffusion model where individuals converge toward the same probability to cooperate over time. A diffusion model is defined as
The equilibrium solution depends on K, f, while the dynamics over time depend on the network structure and assortativity in δi. If Ki = k ∀ i, then
2.2 Non-evolutionary prisoner’s dilemma
The prisoner’s dilemma is a two-player game where each player has to choose one of two possible strategies (to cooperate or to defect). The payoff for each individual depends on the strategy taken by her and another player. Specifically, when both agents cooperate, they both receive a payoff R, whereas when a cooperator interacts with a defector, she receives a payoff S, and the defector gets T. Lastly, when both agents defect, they receive a payoff of value P. A matrix often represents the payoff
Different values of parameters R, S, T, and P bring about different dilemmas with different equilibrium points. A prisoner’s dilemma is defined with values such that T > R > P > S. The payoff relationship R > P implies that mutual cooperation is superior to mutual defection, while the payoff relationships T > R and P > S imply that defection is the dominant strategy for both agents. The game can be iterated, known as the iterated prisoner’s dilemma. We also require that 2R > T + S to prevent alternating cooperation and defection, giving a greater reward than cooperation. In this study, we set the payoff matrix to values R = 3, S = 0, T = 5, p = 1.
In a pure strategy game, each agent chooses one fixed strategy. It can be changed throughout the game (evolve), and the change in strategies is typically based on a comparison of recent payoffs. In a mixed strategy game, an agent’s strategy is a random variable with a probability of cooperating p. Therefore, a pure strategy game is a special (deterministic) case of a mixed (stochastic) strategy game where p ∈ {0, 1} [30,31]. At each round, each player i plays an independent game with each of its ki neighbors and accumulates a total payoff
2.3 Evolution, networks, and metrics
The evolution proceeds following the Fermi rule. Specifically, each node imitates the strategy pl(t) adopted by one of its neighbors, l, chosen at random2. The node i updates its strategy with probability [32].
Here KF is the Fermi temperature, set to 0.1 if not otherwise stated.
To explore the proposed theoretical model, we choose several different network topologies, namely, Erdős–Rényi (ER) [33], Barabási–Albert (BA) [34], and Watts–Strogatz [35] (WS) random graphs.
To analyze the impact of neural synchrony on cooperation, we consider the following two metrics:
The fraction of mutually cooperative steps fC is the number of games in which both players adopted a cooperative strategy as a fraction of all games that were played during timesteps [tτ, tτ+1, tτ+2, …, tτ+n−1] between times tτ and tτ+n−1:
where aij(tk) is the decision of a node i (either to cooperate—C or to defect—D) in the game with j at time tk,
We will also study the standard deviation in payoffs across a network at a particular timestep of the simulation t. The second moment of the distribution is of particular importance, computed as the standard deviation in the payoffs obtained by agents in a graph,
3 Simulation results
Throughout this section, we simulate a mixed-strategy of prisoner’s dilemma. In all cases, we considered integration timesteps of length 0.1 units of time, and unless otherwise stated, the simulation lengths are 40 units of time (400 timesteps) and the periods of sine waves are set to 5 units of time. First, we study the results of a non-evolutionary game and then proceed with interpreting an evolutionary game, both in a 2-player scenario. We then expand the two-player game to a networked game.
3.1 Two-player game
3.1.1 Non-evolutionary game
In the simulated mixed strategy game, the first player begins as a “cooperator,” signified by an initial value of p(0) = 1. The second player begins as a “defector” since its p(0) =03.
Specifically, the functional form we study is
where we study the cases when θ = 0 (the agents are “in-phase”) or θ = T/2 (the agents are “out-of-phase”). We will refer to K1 and K2 simply as K when K = K1 = K2.
Figure 1 illustrates the effects of variability in p(t) without an evolutionary process. Here, the “cooperator’s” results are shown in yellow, whereas the “defector’s” results are in green. Both agents are defined as having the same amplitude, a1 = a2 = 0.2. The figure has two columns: the left column denotes the absence of neural synchrony (K = 0), and the right one denotes the presence of neural synchrony (K = 0.03). Each column has two rows, differing in in-phase neural oscillations (|θ1 − θ2| = 0, top row) and out-of-phase4 neural oscillations (|θ1 − θ2| = T/2, bottom row)5. The most prominent difference that a switch from K = 0 to K = 0.03 (left versus right column) introduces is observed concerning p(t): neural synchrony induces agents to gravitate toward the same probability of cooperating p(t). This change in p(t) is followed by a change in the strategies adopted: while the cooperator only rarely defects under K = 0, she defects far more often under K = 0.03. This shift in strategies chosen, in turn, affects the payoff: while under K = 0, the cooperator and defector gain similar payoffs, and the cooperator is far better off under K = 0.03. In other words, neural synchrony leads to the redistribution of the payoffs in an unequal manner in which the cooperating entity is better off.
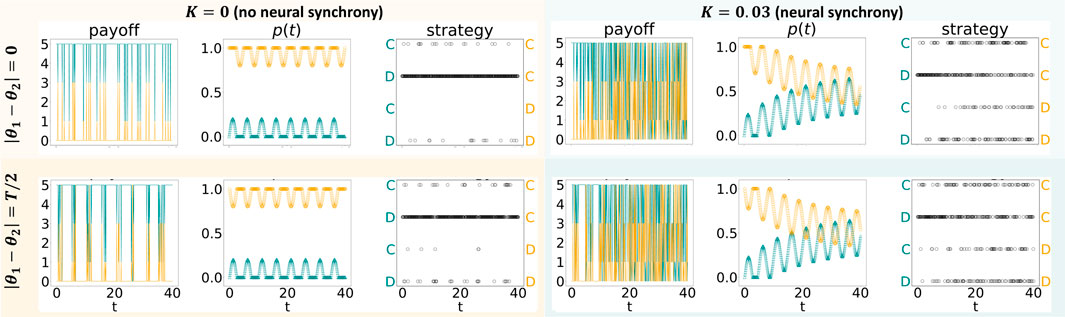
FIGURE 1. Iterated prisoner’s dilemma game played by two agents, whose probability of cooperating varies in time according to Eq. 4, with f defined in the main text and K1 = K2. For each agent, we show the changes over time of a payoff (left), a probability to cooperate p (middle), and a strategy (right). Depending on the phase difference, |θ1 − θ2|, the agents’ probabilities to cooperate are either simultaneously higher/lower than their baselines or are asynchronous.
In Figure 1, we investigate only two values of K, while we vary K in a more fine-grained way in Figure 2. Specifically, we study the case where K1 = K2; therefore, the average probability to cooperate
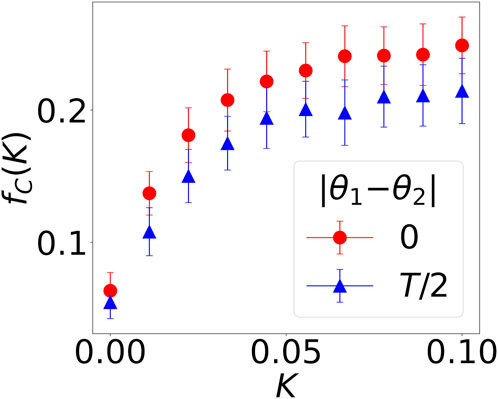
FIGURE 2. The fraction of mutually cooperative steps out of all games in the last 100 steps as a function of neural synchrony K, fC(K), in the two-player iterated prisoner’s dilemma game. Out-of-phase agents are indicated by blue triangles; in-phase ones, by red dots.
Interestingly, the blue and red curves are both concave, indicating that small values of synchrony have a profound effect. The curve flattens earlier when the interacting agents are out of phase (|θ1 − θ2| = T/2, blue triangles); it is steeper (|θ1 − θ2| = 0, red circles) when the oscillations are in phase. In other words, phase alignment is not as important as achieving a small degree of synchrony. This is because when K1 = K2 = a1 = a2 = 0, fC = 0, meaning that mutual cooperation is only possible through temporal variation (non-zero a1, a2). However, cooperation achieved in this way is much smaller than when K1, K2 are non-zero.
In Figure 1, we study the case where the value of neural synchrony is the same for both agents K1 = K2. In Figure 3, by contrast, we investigate the case where K1 ≠ K2. Therefore, the
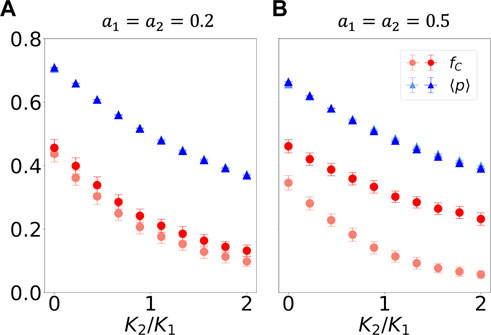
FIGURE 3. Iterated prisoner’s dilemma game played by two agents, whose probability of cooperating varies in time according to Eq. 4 with f defined in the main text and K1 ≠ K2, K1 = 0.05, and K2 is varied. As in Figure 1, agent 1 tends to be a cooperator, and agent 2 tends to be a defector. In (A), small-amplitude a variations in cooperation preference take place, whereas in (B), the amplitude is increased. The blue triangles showcase the time- and agent-average probabilities of cooperating, p; the red circles show the fraction of mutually cooperative steps, fC. Lighter-colored datapoints indicate results from out-of-phase simulations; saturated points show results from in-phase simulations. All values are calculated for the last 100 out of 400 steps in the simulation. The statistics were obtained from 100 independent simulations.
We see that when K1 > K2,
3.1.2 Evolutionary game
In Figure 4, we introduce an evolution in this two-player game. Specifically, we study the fraction of mutually cooperative games, fC, in the evolutionary game at varied Fermi temperatures KF. Low values of KF can be interpreted as the agents adopting the advantageous, payoff-increasing strategy in most evolutionary steps. Large values of KF describe an agent making mistakes more often by adopting a disadvantageous strategy at evolutionary steps. The heatmaps in Figure 4 relate the fraction of mutually cooperative games, fC, to neural synchrony K on the y-axis and τ, the integration timesteps after which the player updates her strategy, on the x-axis. Here, we study a fraction of which the nominator refers to the fraction of cooperative games in which neural synchrony is present (K ≠ 0 and K1 = K2). Still, there are no temporal variations (a1 = a2 = 0). In contrast, the denominator refers to the fraction of cooperative games in the absence of neural synchrony (K = 0). Consequently,
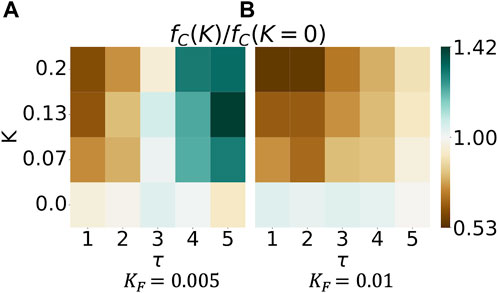
FIGURE 4. Neural synchrony can increase the abundance of mutually cooperative games in an evolutionary two-player iterated prisoner’s dilemma game. The heatmap shows the magnitude of fC(K)/fC(K = 0) in two dimensions. The numerator fC(K) refers to neural synchrony of strength K; K1 = K2, and the denominator fC(K = 0) denotes the absence of neural synchrony. The figure plots the last 50 out of 200 simulation steps, averaged over 2000 simulations.
We observe that the hue changes from blue to brown with increasing Fermi temperature KF; higher Fermi temperature KF reduces the fraction of mutually cooperative games played by synced agents. In other words, if agents are more likely to make mistakes, it is advantageous to not have neural synchrony. Simply put, who cooperates depends on the likelihood of making mistakes. The left heatmap shows darker shades of green at the top right, implying that more intense neural synchrony K increases cooperation fC the longer a specific strategy is kept (increasing values of τ). Who cooperates, however, changes in the right heatmap: darker shades of brown are found in the top left of the figure, implying that more intense neural synchrony K increases cooperation fC, the shorter a specific strategy is kept (smaller values of τ). All in all, the effect of neural synchrony depends on the likelihood of agents making irrational decisions and the frequency of evolutionary steps.
3.2 Expanding the game on a network
We now expand the game to a network scenario. More precisely, we investigate the Erdös–Rényi, Barabási–Albert, and Watts–Strogatz graphs.
We begin with a case where neural synchrony is present, but otherwise, there are no periodic variations. Namely, we study the case where
Figure 5 shows how the standard deviation in the payoffs of agents
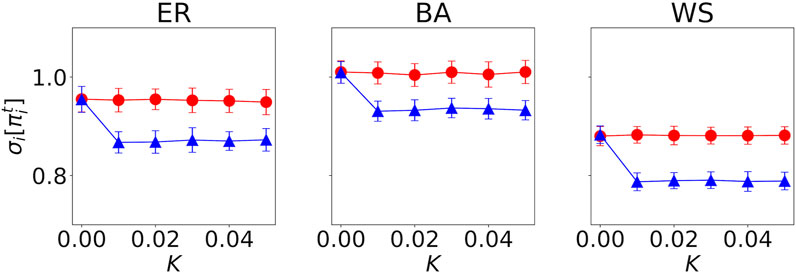
FIGURE 5. Standard deviation in the payoffs
Next, we include the influence of temporal variations on the cooperation patterns in the network scenario. While in the two-agent case there are these two distinct cases (namely, in-phase and out-of-phase); in a network where N > 2, we are concerned with the variance in the distribution of the parameters of f, namely, θi, Ti. In the current study, we assume that T = const and concentrate on heterogeneity in phases. Specifically, we considered three cases where the distribution of phases has varied amounts of variance. First, a case where θi = 0 ∀i; second, sampled from a beta distribution
In Figure 6, we show the effect of heterogeneity in phases for various amounts of neural synchrony K. In Figure 6A, we consider no evolutionary process, whereas in Figure 6B, we study the case where evolution takes place at every simulation step: τ = 1. Similarly, as in Figure 4, we contrast the fraction of mutually cooperative games in simulations with a given variance in phases and strength of neural synchrony (fC(a = 0.1, K), emphasizing that the amplitude parameter a is set to this value for all nodes) with the values of the same measure, observed in simulations without temporal variability, namely, fC(a = 0, K = 0). We restrict the study to the case of an ER ensemble with N = 100 nodes and an average degree of 3, since the network structure influences the time evolution of the dynamics but not the time-averaged results.
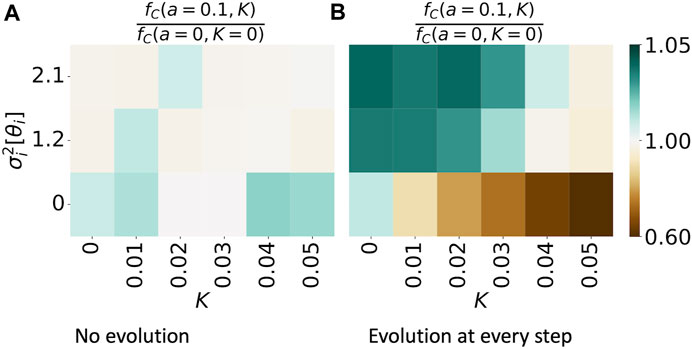
FIGURE 6. Synchronization of periodic patterns of agents’ tendency to cooperate, Eq. 2, enhances cooperation in a network when cooperation has no evolutionary process (A) and supresses cooperation if an evolutionary process exists (B). The figures show the magnitude of fC(a = 0.1, K)/fC(a = 0, K = 0). The denominator refers to the fraction of mutually cooperative games observed in simulations without neural synchrony (K = 0) and without intrinsic temporal variability in cooperative preferences (f(t) = δ, a = 0). The numerator shows the same observation in the simulations where f(t) is varied; there is variance in the phase parameter θ and of strength K in the neural synchrony. The results are obtained from 100 simulations on an ER graph ensemble, with N = 100 and an average node degree of 3.
Figure 6A shows that as variance in phases increases, mutual cooperation is suppressed. Surprisingly, the cooperation is minimal yet enhanced in cases when neural synchrony is present, and there is no phase difference, i.e., θi = const ∀i with respect to the fraction of mutually cooperative games observed in the baseline case.
However, as evolution is introduced, the effect of neural synchrony and variance in phases changes. Since an increase in K leads to the convergence of individual strategies to a global mean, K acts as an attractor to a suboptimal strategy for maximizing payoffs. With the presence of evolution, nodes can adopt the optimal strategy pi = 1 ∀i, and neural synchrony acts as a negative force to reach this goal. In the case where K is non-zero, variance in phases brings value by increasing the diversity of strategies at each t and allowing for the evolutionary process to override the effect of neural synchrony.
4 Conclusion
In this study, we investigate how intra-individual temporal variation impacts cooperation on a social level. To that end, we proposed a theoretical framework to explain the probability of cooperation as a function of intra-personal temporal variation due to circadian variations and neural synchrony. We simulated agents playing a prisoner’s dilemma game, without and with evolution, in a two-player setting and on networks. Our simulations revealed a diverse set of insights that enrich our understanding of how temporality and individuality shape cooperation.
We find that when agents experience synchrony and gravitate toward the same probability of cooperating, there is a change in the strategies adopted, which in turn affects agents’ payoffs. Interestingly, neural synchrony leads to redistribution of the payoffs in an unequal manner in which the cooperating entity is better off. This finding is highly interesting: in human subject experiments, cooperating entities are on average worse off than freeriders and defectors. Our results further allow us to comment on the intensity of synchrony: we find that transitioning from no synchrony to a tiny degree of synchrony profoundly and positively affects cooperation in a two-player game. Furthermore, we implemented a variation that behavioral experimentalists so far have overlooked: understanding synchrony as either a directed or an undirected phenomenon. The more heterogeneous the synchrony between two agents, the less they cooperate; large amplitudes aggravate this phenomenon. Our simulations with evolution produce further interesting results: if a pair of agents is more likely to make mistakes in choosing an advantageous strategy, not experiencing synchrony positively impacts cooperation. In other words, synchrony is not always desirable; instead, its quality is context dependent.
Lastly, we extend our simulations to networks. We find that in the later stages of the game, the agents’ payoffs become more similar when they switch from no synchrony to synchrony. This can lead to enhanced cooperation if the game is non-evolutionary. However, in an evolutionary game, neural synchrony acts as a suppressor of cooperation, while the variance in phases of individual temporal variability counteracts the inhibitory effect of synchrony.
5 Discussion
Our aim was to extend a model of cooperation by incorporating individual- and group-level dynamics of tendencies to cooperate that are not driven solely by the goal of maximizing a payoff. In this way, we were able to compare the strength of endogenous influences and conscious decisions, such as mimicking others’ strategies in order to obtain a larger individual payoff, to that of endogenous processes.
We concentrated on a case where f(t) mimics circadian rhythms [36], known to impact decision-making. Regarding neural synchrony, we acknowledge that alternative mathematical models could have sufficed; e.g., models of coupled oscillators such as the Kuramoto model [37] have been used in several studies to study the emergence of synchronization and cooperation in networked populations of coupled oscillators [38]. We, by contrast, chose to use a diffusion model as it is more appropriate for our specific research question: while a coupled oscillator model would seem a natural fit, it assumes that circadian rhythms and neuromodulation are impacted by social interactions. In a context where such a coupling is desired, one would replace g with Θ in the diffusion model and set g = 0 in Eq. 1.
Furthermore, it should be acknowledged that the proposed model is simplistic and does not account for all aspects of brain physiology. For example, it does not capture intrinsic fluctuations at the cellular level or the need for sleep itself, which is a limitation that future research should address. Furthermore, the exact functional forms and parameter values of functions in our model should be calibrated for particular circadian and neuromodulatory causes of variability in decision-making. Social memory [39] may also be a crucial element incorporated in the future.
The results we report are a source of inspiration for investigating the phenomenon of cooperation in the real world. First, we report that cooperators can dramatically increase their payoff—as opposed to defectors—if neural synchrony is present. Experimental studies could exogenously vary synchrony levels and incentivize different groups to adopt a certain type of strategy. Furthermore, we experiment with different levels of synchrony among agents. So far, in behavioral studies, the variable of interest has been where in the brain(s) the neural synchrony occurs. However, our findings suggest that enormous value lies in investigating in more detail the quality of this synchrony. Lastly, the behavioral literature on neural synchrony almost exclusively investigates the interaction between two participants. Repeating those experiments on networks might allow for an even deeper understanding of cooperation as a temporal phenomenon. On the other hand, experimental data from a networked study would also guide a decision as to how important it is to incorporate cognitive properties into computational social science models.
Additionally, the results on networks should be studied in greater depth, e.g., by exploring how our results translate to real-world networks, temporal networks [29], simplicial complexes [32], or hypergraphs [40], and looking in greater depth at how network structure impacts the trajectory of a dynamical process in a cooperative game. Furthermore, we did not analyze the impact of assortative mixing [41], e.g., cooperation probability. The last variation left for future research to study is a redefinition of the coupling of agents, where neural synchrony affects the parameters of the functions that govern their internal periodicity patterns, as explained earlier in this section.
In conclusion, this paper advances our understanding of cooperation as a temporal phenomenon. We introduce a mathematical framework that couples individual endogenous influences with conscious decisions in order to explain the probability of cooperation. More broadly, our work suggests that cognitive processes are linked with the social phenomenon: for cognitive science, social interactions may not be just an end goal, but an active variable; on the other hand, to understand group dynamics, neuroscientific explanations may be crucial.
Data availability statement
The data simulated during the study, together with the simulation codes are available on github at the link https://github.com/vv2246/temporal_cooperation.
Author contributions
VV: conceptualization, methodology, software, validation, formal analysis, investigation, visualization, and writing—original draft-review and editing. CH: conceptualization, writing—original draft, and writing—review and editing.
Funding
Open access funding is provided by the Swiss Federal Institute of Technology Zürich. VV acknowledges the support of the European Union—Horizon 2020 Program under the scheme “INFRAIA-01-2018-2019—Integrating Activities for Advanced Communities,” Grant Agreement no. 871042, “SoBigData++: European Integrated Infrastructure for Social Mining and Big Data Analytics” (http://www.sobigdata.eu).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Other researchers have also described the rhythmic properties of the circadian system as sinusoidal functions [42].
2Updating in line with the Fermi rule has been found in behavioral data: payoff-based learning—not fairness preferences—best explains the rate of decline in cooperation across a large set of experimental data on social dilemma games [43].
3We study the extreme cases of p1(0) = 0 and p2(0) = 1 to maximize the visibility of the effects being studied. The choice of these specific values for p is made to demonstrate the most prominent results possible. As the difference between p1(0) and p2(0) decreases, the differences observed are expected to decrease.
4The expression “out-of-phase” refers to the state when the phases of the circadian rhythms of two individuals are shifted. As light is a key cue that helps to reset and synchronize circadian rhythms, it is possible for two individuals to become out-of-phase if they are not exposed to the same light cues at the same time [44].
5We study the extreme cases of θ = 0 and θ = T/2 to maximize the visibility of the effects being studied. The choice of these specific values for θ was made to demonstrate the most prominent results possible. As the difference between θ1 and θ2 decreases, the differences observed in the study are expected to decrease.
References
1. Grossman CD, Cohen JY. Neuromodulation and neurophysiology on the timescale of learning and decision-making. Annu Rev Neurosci (2022) 45:317–37. doi:10.1146/annurev-neuro-092021-125059
2. Lambert GW, Reid C, Kaye DM, Jennings GL, Esler MD. Effect of sunlight and season on serotonin turnover in the brain. The Lancet (2002) 360:1840–2. doi:10.1016/s0140-6736(02)11737-5
3. Smith A, Olson R, Justice J. Quantitative microdialysis of dopamine in the striatum: Effect of circadian variation. J Neurosci Methods (1992) 44:33–41. doi:10.1016/0165-0270(92)90111-p
4. Jung CM, Khalsa SBS, Scheer FA, Cajochen C, Lockley SW, Czeisler CA, et al. Acute effects of bright light exposure on cortisol levels. J Biol rhythms (2010) 25:208–16. doi:10.1177/0748730410368413
5. Hughes S, Jagannath A, Hankins MW, Foster RG, Peirson SN. Photic regulation of clock systems. Methods Enzymol (2015) 552:125–43. doi:10.1016/BS.MIE.2014.10.018
6. Cajochen C, Kräuchi K, Danilenko KV, Wirz-Justice A. Evening administration of melatonin and bright light: Interactions on the EEG during sleep and wakefulness. J Sleep Res (1998) 7:145–57. doi:10.1046/J.1365-2869.1998.00106.X
7. Badia P, Myers B, Boecker M, Culpepper J, Harsh JR. Bright light effects on body temperature, alertness, EEG and behavior. Physiol Behav (1991) 50:583–8. doi:10.1016/0031-9384(91)90549-4
8. Ramkisoensing A, Meijer JH. Synchronization of biological clock neurons by light and peripheral feedback systems promotes circadian rhythms and health. Front Neurol (2015) 6:128. doi:10.3389/FNEUR.2015.00128
9. Burke TM, Scheer FA, Ronda JM, Czeisler CA, Wright KP. Sleep inertia, sleep homeostatic and circadian influences on higher-order cognitive functions. J Sleep Res (2015) 24:364–71. doi:10.1111/JSR.12291
10. Dumas G, Nadel J, Soussignan R, Martinerie J, Garnero L. Inter-brain synchronization during social interaction. PLOS ONE (2010) 5:e12166. doi:10.1371/JOURNAL.PONE.0012166
11. Czeszumski A, Eustergerling S, Lang A, Menrath D, Gerstenberger M, Schuberth S, et al. Hyperscanning: A valid method to study neural inter-brain underpinnings of social interaction. Front Hum Neurosci (2020) 14:39. doi:10.3389/fnhum.2020.00039
12. Wikström V, Saarikivi K, Falcon M, Makkonen T, Martikainen S, Putkinen V, et al. Inter-brain synchronization occurs without physical co-presence during cooperative online gaming. Neuropsychologia (2022) 174:108316. doi:10.1016/j.neuropsychologia.2022.108316
13. Szymanski C, Pesquita A, Brennan AA, Perdikis D, Enns JT, Brick TR, et al. Teams on the same wavelength perform better: Inter-brain phase synchronization constitutes a neural substrate for social facilitation. Neuroimage (2017) 152:425–36. doi:10.1016/j.neuroimage.2017.03.013
14. Cui X, Bryant DM, Reiss AL. NIRS-based hyperscanning reveals increased interpersonal coherence in superior frontal cortex during cooperation. NeuroImage (2012) 59:2430–7. doi:10.1016/J.NEUROIMAGE.2011.09.003
15. Zhang M, Jia H, Zheng M. Interbrain synchrony in the expectation of cooperation behavior: A hyperscanning study using functional near-infrared spectroscopy. Front Psychol (2020) 11:542093. doi:10.3389/fpsyg.2020.542093
16. Behrens F, Snijdewint JA, Moulder RG, Prochazkova E, Sjak-Shie EE, Boker SM, et al. Physiological synchrony is associated with cooperative success in real-life interactions. Scientific Rep (2020) 10(1):19609–9. doi:10.1038/s41598-020-76539-8
17. Czeszumski A, Liang SHY, Dikker S, König P, Lee CP, Koole SL, et al. Cooperative behavior evokes interbrain synchrony in the prefrontal and temporoparietal cortex: A systematic review and meta-analysis of fnirs hyperscanning studies. eNeuro (2022) 9:ENEURO.0268-21.2022. doi:10.1523/ENEURO.0268-21.2022
18. Chen CY, Logan RW, Ma T, Lewis DA, Tseng GC, Sibille E, et al. Effects of aging on circadian patterns of gene expression in the human prefrontal cortex. Proc Natl Acad Sci United States America (2016) 113:206–11. doi:10.1073/PNAS.1508249112
21. Cacioppo JT, Berntson GG, Adolphs R, Carter CS, McClintock MK, Meaney MJ, et al. Foundations in social neuroscience. Cambridge, MA, USA: MIT press (2002).
22. Dunbar RI. The social brain hypothesis. Evol Anthropol Issues News Rev Issues News Rev (1998) 6:178–90. doi:10.1002/(sici)1520-6505(1998)6:5<178:aid-evan5>3.0.co;2-8
23. Schmälzle R, O’Donnell MB, Garcia JO, Cascio CN, Bayer J, Bassett DS, et al. Brain connectivity dynamics during social interaction reflect social network structure. Proc Natl Acad Sci United States America (2017) 114:5153–8. doi:10.1073/pnas.1616130114
24. Baek EC, Hyon R, López K, Finn ES, Porter MA, Parkinson C. In-degree centrality in a social network is linked to coordinated neural activity. Nat Commun (2022) 13:1118–3. doi:10.1038/s41467-022-28432-3
25. Han M, Jiang G, Luo H, Shao Y. Neurobiological bases of social networks. Front Psychol (2021) 12:626337. doi:10.3389/fpsyg.2021.626337
26. Li S, Ma S, Wang D, Zhang H, Li Y, Wang J, et al. Oxytocin and the punitive hub—Dynamic spread of cooperation in human social networks. J Neurosci (2022) 42:5930–43. doi:10.1523/jneurosci.2303-21.2022
27. Alakörkkö T, Saramäki J. Circadian rhythms in temporal-network connectivity. Chaos (2020) 30:093115. doi:10.1063/5.0004856
29. Li A, Zhou L, Su Q, Cornelius SP, Liu YY, Wang L, et al. Evolution of cooperation on temporal networks. Nat Commun (2020) 11:2259. doi:10.1038/s41467-020-16088-w
30. Beersma DG, Daan S. Generation of activity-rest patterns by dual circadian pacemaker systems: A model. J Sleep Res (1992) 1:84–7. doi:10.1111/J.1365-2869.1992.TB00015.X
31. Cimini G, Sánchez A. How evolution affects network reciprocity in prisoner’s dilemma (2014). arXiv preprint arXiv:1403.3043.
32. Miyaji K, Tanimoto J. A co-evolutionary model combined mixed-strategy and network adaptation by severing disassortative neighbors promotes cooperation in prisoner’s dilemma games. Chaos, Solitons and Fractals (2021) 143:110603. doi:10.1016/J.CHAOS.2020.110603
33. Burton-Chellew MN, West SA. Payoff-based learning best explains the rate of decline in cooperation across 237 public-goods games. Nat Hum Behav (2021) 5:1330–8. doi:10.1038/s41562-021-01107-7
34. Guo H, Jia D, Sendiña-Nadal I, Zhang M, Wang Z, Li X, et al. Evolutionary games on simplicial complexes. Chaos, Solitons and Fractals (2021) 150:111103. doi:10.1016/j.chaos.2021.111103
35. Erdős P, Rényi A. On the evolution of random graphs. Publ Math Inst Hung Acad Sci (1960) 5:17–60.
36. Barabási AL, Albert R. Emergence of scaling in random networks. Science (1999) 286:509–12. doi:10.1126/science.286.5439.509
37. Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’networks. Nature (1998) 393:440–2. doi:10.1038/30918
38. Davidson AJ, Menaker M. Birds of a feather clock together – sometimes: Social synchronization of circadian rhythms. Curr Opin Neurobiol (2003) 13:765–9. doi:10.1016/J.CONB.2003.10.011
39. Asgari-Targhi A, Klerman EB. Mathematical modeling of circadian rhythms. Wiley Interdiscip Rev Syst Biol Med (2019) 11:e1439. doi:10.1002/wsbm.1439
40. Kuramoto Y. International symposium on mathematical problems in theoretical physics. Lecture Notes Phys (1975) 30:420.
41. Antonioni A, Cardillo A. Coevolution of synchronization and cooperation in costly networked interactions. Phys Rev Lett (2017) 118:238301. doi:10.1103/PhysRevLett.118.238301
42. Oliva A. Neuronal ensemble dynamics in social memory. Curr Opin Neurobiol (2023) 78:102654. doi:10.1016/j.conb.2022.102654
43. Alvarez-Rodriguez U, Battiston F, Ferraz de Arruda G, Moreno Y, Perc M, Latora V. Collective games on hypergraphs. In: F Battiston, and G Petri, editors. Higher-order systems. Understanding complex systems. Cham: Springer (2022). p. 377–88. doi:10.1007/978-3-030-91374-8_15
Keywords: Cooperation, neural synchrony, temporal variation, neural activity, networks, circadian rhythms
Citation: Vasiliauskaite V and Hausladen CI (2023) How do circadian rhythms and neural synchrony shape networked cooperation?. Front. Phys. 11:1125270. doi: 10.3389/fphy.2023.1125270
Received: 16 December 2022; Accepted: 20 February 2023;
Published: 15 March 2023.
Edited by:
Dun Han, Jiangsu University, ChinaReviewed by:
Hang-Hyun Jo, Catholic University of Korea, Republic of KoreaPer Sebastian Skardal, Trinity College, United States
Copyright © 2023 Vasiliauskaite and Hausladen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vaiva Vasiliauskaite, dnZhc2lsaWF1QGV0aHouY2g=
 Vaiva Vasiliauskaite
Vaiva Vasiliauskaite Carina I. Hausladen
Carina I. Hausladen