Numerical study on the aerodynamic performance of the three-dimensional wing of a jellyfish-like flyer

The jellyfish-like flying machine is a new development direction of the future bionic flapping-wing aircraft besides the insect-mimic and bird-mimic micro air vehicles (MAVs). To better understand the underlying fluid mechanisms of the jellyfish-like flyer, we numerically simulated the aerodynamic forces of the three-dimensional flapping wings under different control parameters. The effects of flapping amplitude, vortex wake, up-flight speed, and wing–wing interaction on aerodynamic performance were investigated. The results show that, at hovering, the mean lift rises rapidly at first and then tends to be stable with the increase in flapping amplitude. The vortex wake can improve the lift at large flapping amplitudes, while it reduces the lift at very small flapping amplitudes. With the increase in up-flight speed, the lift decreases. However, the sources of lift reduction are different for different flapping amplitudes. When the two wings flap together and the distance between the wings is small enough, the wing–wing interaction can improve the lift by about 15% compared with that of a single wing, but much higher power is required, resulting in lower efficiency. The results of this study provide new insights into the flight mechanism of the jellyfish-like aircraft and have important guiding significance for the design and optimization of the jellyfish-like flying machine.

1 Introduction

After hundreds of millions of years of evolution, flying creatures can obtain astonishing aerodynamic performance by flapping wings, which has become the inspiration for designing bionic aircraft. The design of bionic aircraft is generally based on two typical types of motion: the lift-based stroke in a horizontal plane (also termed the normal mode) [1], like that of the hummingbird, and the drag-based paddling stroke in a vertical plane [2], like that of the dragonfly. Since the conventional steady-state aerodynamic theory is insufficient to explain the high aerodynamic force coefficients required by these small creatures [3], much endeavor has been put into obtaining the unsteady aerodynamic interpretations. The revealed unsteady aerodynamic mechanisms include delayed stall, rapid pitching rotation, rapid acceleration (or added mass), clap and fling, and wake capture [4–7]. Although the flapping-powered robotic flyer shows great potential in producing high aerodynamic forces and energy efficiency relying on these unsteady mechanisms, it also needs to be equipped with feedback control systems to maintain stable flight due to its inherent instability [8–11].

In an experimental study, Childress et al. [12] observed that a pyramid-shaped flexible body with an array of four wings can achieve a stable hovering within a vertically oscillating airflow. Motivated by this experiment, Ristroph and Childress [13] developed a prototype of the jellyfish-like flying machine. This flapping-wing air vehicle can achieve self-righting hovering by opening and closing four downward-pointing wings, without relying on additional aerodynamic surfaces and without feedback control. Each wing of the aircraft was hinged on the upper horizontal loop and rotates around a pivot point, which is very similar to the simple pitching motion. This provides a new way of movement for designing bionic aircraft.

This intrinsically stable jellyfish-like flying machine and the relatively simple actuation motion attracted the attention of researchers, prompting them to carry out more detailed research on the aerodynamics and flows of such flyers. Using two-dimensional (2D) models, Fang et al. [14] and Zhang et al. [15] explored the aerodynamics and flight dynamics of the flying machine with theoretical and numerical methods, respectively. Both studies found that pitching amplitude and wing separation played a determining role in the locomotion state and aerodynamic performance. In addition, Zhang et al. [16] simulated the passive flight of a pair of 2D flexible pitching foils with a concave-down configuration in the vertically oscillating airflow. It was shown that flexibility can strongly affect the weight-supporting capability and stability of the flyer.

It is worth noting that all the aforementioned studies that were carried out on the jellyfish-like aircraft are 2D studies. More recently, Liu et al. [17] experimentally investigated the effect of the time asymmetric pitching motion on the lift generation and the flow-field characteristics of this kind of ornithopters, which is the only three-dimensional (3D) research on hovering. They found that the fast downstroke and slow upstroke pitching pattern was superior to symmetric pitching. Although the flow-field was 3D in their study, the vortex structures were still displayed by the 2D PIV measurement. The evolution of the side-edge vortex was not considered, and its effect on the forces of the wing remains unclear so far. The experimental study by Buchholz and Smits [18] demonstrated that the streamwise vorticity formed at the 3D panel edges tended to dominate the wake formation. Other studies [19–21] have also demonstrated that the 3D effect plays a key role in the formation of vortices and the aerodynamic performance of the flapping wings. Therefore, with respect to this jellyfish-like flyer, it is still far from being possible to fully understand the details of 3D vortex evolution and aerodynamics, especially the vortex structures around all edges of the wing.

In contrast to the previous 2D studies, this paper numerically investigated the aerodynamics of 3D flapping wings employing the locomotion of the jellyfish-like flyer. The hovering was emphasized because it is an indispensable flight mode for MAVs to perform special tasks. This is also different from most other works, which studied the pitching wing in an incoming flow [18–21]. The aerodynamic performance under some key motion parameters was examined and related to the flow fields. In addition, the wing–wake interaction was also considered, which was neglected in previous studies. The remainder of the paper is organized as follows: the wing motion and the numerical method with its validation are described in Section 2. The simulated results are presented in Section 3. In Section 3.1, the influence of flapping amplitude on the aerodynamics of a single wing under hovering conditions is studied first, and then the vortex structures are examined in detail. The role of vortex wake is also emphasized in Section 3.2. Next, the effect of up-flight speed on aerodynamic performance is investigated in Section 3.3. Finally, in Section 3.4, the interference effect between wings is studied and comparisons with relevant biological data are presented. In Section 4, we summarize the conclusions and discuss future research avenues.

2 Methodology

2.1 Wing model and motion

In this work, the wing was modeled as a flat plate with rounded edges. The wing shape is similar to the teardrop-shaped wing of the jellyfish-like aircraft manufactured by Ristroph and Childress [13] (Figure 1A). The aspect ratio $R/c$ of the wing is 2.25, where R and c are the wing length and mean chord length, respectively. The radius of gyration r₂ of the wing is 0.62R.

FIGURE 1

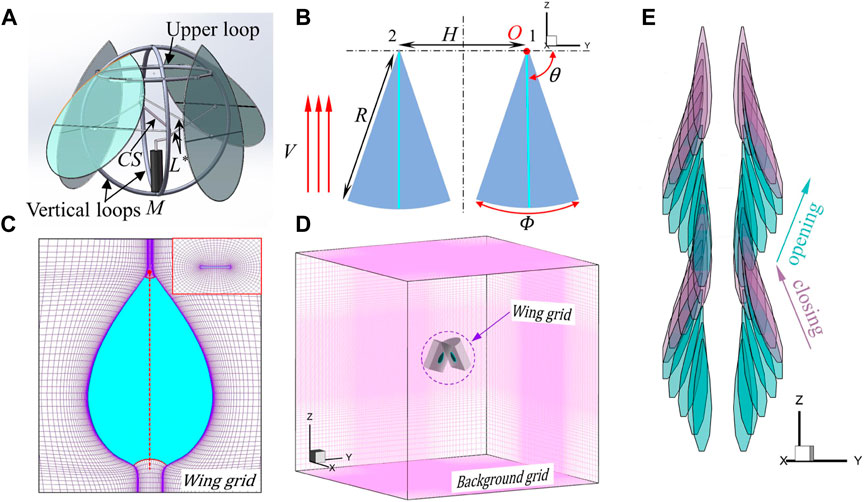
FIGURE 1. (A) Three-dimensional model of the jellyfish-like flying machine manufactured by Ristroph and Childress [13]. The prototype pulls in and pushes out four wings by using a motor (M) to rotate a crankshaft (CS) that connects via a link (L^*) to each wing. The body of the flyer consists of two crossed vertical loops that support the motor below and a horizontal upper loop. More detailed information about this flyer can be found in [13]. (B) Simplified wing-pair model. Here, V is the up-flight speed; $\theta$ represents the wings’ base opening angle; R and H denote the wing length and the distance between the two pivot points, respectively. Two rigid plates are driven to flap with prescribed mirror-symmetric sinusoidal pitching motions of peak-to-peak amplitude $\mathrm{\Phi }$. (C) Wing grid with an inset showing the grid at a half wing length section. (D) Over-set grid system. (E) Instantaneous snapshots of the flapping wings during ascending flight. The prototype in (A) achieves upward flight by closing and opening an opposing pair of wings, just like the jellyfish which periodically contract and expand their bell-shaped structure.

To facilitate the flow-field analysis, one opposing pair of wings was used instead of the bell-like configuration of four pieces of wings in the original prototype of the ornithopter. It should also be noted that the simple drive mechanism shown in Figure 1A does not close all four wings simultaneously but rather causes one opposing pair to lead the other by a quarter period. Figure 1B illustrates the pitching motion. The two wings flap about the wing root with a mirror-symmetric sinusoidal pitching motion in time. The origin of the Cartesian coordinates OXYZ coincides with the pivot of the right wing, with the Y-axis passing through the two wing roots and the Z-axis pointing vertically upward (Figure 1B). The wings can move upward at a speed of V, and $V=0$ represents the hovering state. The separation distance between the two wings’ hinge points is H. $\theta$ and $\mathrm{\Phi }$ represent the opening angle and peak-to-peak flapping amplitude, respectively (see Figure 1B). The pitching angles of the right (${\varphi }_1$) and left (${\varphi }_2$) wings are expressed as follows:

${\varphi }_{\mathrm{1,2}}\left(t\right)=\pm \left(\frac{\pi }{2}-\theta +0.5\mathrm{\Phi }\mathit{cos}\left(2\pi nt\right)\right),(1)$

where n is the wingbeat frequency and t is the time. A dimensionless time (τ) is defined as that varies between 0 and 1 for each flapping cycle. One flapping cycle includes two strokes, with $\tau =0$ and $\tau =1$ representing the start of the first right-to-left stroke and the end of the second left-to-right stroke, respectively.

This paper first studied the aerodynamics of a single wing (the right wing) at different flapping amplitudes and up-flight speeds, assuming that the wing–wing spacing is large enough and there is no interference between the left and right wings. The opening angle for the single wing was set at $\theta =90°$ to ensure that the resultant force of the wing points vertically upward [22]. Then, the interference effect of two wings at different distances was studied. It should be noted that to avoid collision between wings, the opening angle was no longer 90° when the wing–wing interaction was considered.

2.2 Numerical methods

The flows and aerodynamic forces were computed using the method of computational fluid dynamics (CFD), and the laminar flow model was used due to the low Reynolds number. The governing equations of the flow are the three-dimensional incompressible unsteady Navier–Stokes (N–S) equations:

$\nabla \bullet \mathit{u}=0,(2)$

$\frac{\partial \mathit{u}}{\partial t}+\mathit{u}\bullet \nabla \mathit{u}=-\frac{1}{\rho }\nabla p+v{\nabla }^2\mathit{u}.(3)$

In the aforementioned equations, $\mathit{u}$, $t$, and $p$ represent dimensional fluid velocity, time, and pressure, respectively. $\nabla$ is the gradient operator, and ${\nabla }^2$ is the Laplacian operator. $v$ and $\rho$ are the kinematics viscosity and density of the fluid, respectively. In the non-dimensionalization, $U$, c, and $c/U$ are taken as reference velocity, length, and time, respectively. $U$ is the mean flapping velocity at the radius of gyration of the wing, $U=2\mathrm{\Phi }n{r}_2$. Thus, the non-dimensional parameters involve: ${\mathit{u}}^{*}=\frac{\mathit{u}}{U}$, $t^{*}=\frac{tU}{c}$, $p*=\frac{p}{\rho U^2}$, $\frac{\partial }{\partial t^{*}}=\frac{c}{U}\frac{\partial }{\partial t},{\nabla }^{*}=c\nabla .$ The non-dimensional wingbeat cycle is written as $T^{*}=2\mathrm{\Phi }{r}_2/c$, which is proportional to the peak-to-peak amplitude. Then, the dimensionless form of the N–S equations can be deduced as follows:

$\nabla \bullet {\mathit{u}}^{*}=0,(4)$

$\frac{\partial {\mathit{u}}^{*}}{\partial t^{*}}+{\mathit{u}}^{*}\bullet {\nabla }^{*}{\mathit{u}}^{*}=-\nabla p^{*}+\left(\frac{1}{Re}\right){{\nabla }^{*}}^2{\mathit{u}}^{*}.(5)$

Here, Re is the Reynolds number, and $Re=cU/v$. Its value is set at 200 in the following simulations.

The method for solving the N–S equations is the same as that in the previous studies [23, 24]. The algorithm is based on the method of artificial compressibility developed by Rogers et al. [25] and Rogers and Pulliam [26]. To discretize the time derivative of the momentum equations, a three-point backward differencing formula with second-order accuracy is used. Moreover, a pseudo-time and a pseudo-time derivative of pressure are introduced into the continuity equation. The resulting system of equations is iterated in pseudo-time. As long as the pressure derivative in pseudo-time approaches zero, the velocity divergence at the new time level approaches zero. The derivatives of the viscous fluxes in the momentum equation are approximated using second-order central differences. The upwind differencing method based on the flux-difference splitting technique is used for the derivatives of convective fluxes. For points located close to boundaries, the second-order upwind differencing is employed; for points located toward the interior, the third-order upwind differencing is used. This algorithm was described in detail in [25, 26]. Under the far-field boundary conditions, at the inflow boundary, the relative velocity at the boundary is used to determine the velocity components, while pressure is extrapolated from the interior; at the outflow boundary, the velocity is extrapolated from the interior, and pressure is set to be equal to the static pressure of the still air. On the wing surfaces, impermeable wall and no-slip boundary conditions are applied, and the pressure on the boundary is obtained through the normal component of the momentum equation written in the moving coordinate system.

To facilitate the study of the wing–wing interaction, the technique of moving overset grids was employed. Figures 1C, D show the grid system that consists of two body-fitted curvilinear wing grids that extend a relatively short distance from the wing surfaces and a Cartesian background grid that extends to the domain’s far-field boundaries. The wing grid captures features such as boundary layers, separated vortices, and vortex–wing interactions, and the background grid captures the vortex wake and carries the solution to the far field. Data are interpolated from one grid to another at the inter-grid boundary points using tri-linear interpolation. The wing grid (O-H type) was created using a Poisson solver, which was based on the work of Hilgenstock [27]. It allows fast generation of the three-dimensional wing grid with full boundary control. The background grid was generated algebraically. The non-dimensional time step ($∆t^{*}$) is equal to $T^{*}/440$. The wing grid has dimensions 43 × 71 × 70 in the normal direction, around the wing, and in the spanwise direction, respectively (the first grid layer thickness is 0.001c). The outer boundary of the wing grid is 2.5c from the wing spanwise axis in the normal direction and 1.5c from the wing root and tip in the spanwise direction. The background grid has dimensions 121 × 121 × 121 in the X, Y, and Z directions, respectively, and its boundaries are 20c away from the wing root. To accurately capture the vortex structure, the background grid is refined in the regions covered by the wing grid motion and the main development region of the vortex wake. In these regions, the background grid is evenly distributed, and the grid spacing is approximately the same as that of the outer part of the wing grid. A detailed study of the variables such as time step, domain size, and grid dimensions was conducted, and the values mentioned previously are appropriate for the present study.

After the pressure and velocity of the fluid are obtained, the aerodynamic forces are calculated by integrating the pressure and the viscous stresses on the wing surface. The lift ($L$) and drag force ($D$) of the wing are defined as the force components along the Z and Y axes, respectively. The pressure, lift, and drag coefficients are defined as $C_p=\left(p-p_{\infty }\right)/\left(0.5\rho {\left(U\right)}^2\right),C_L=L/\left(0.5\rho {\left(U\right)}^{2}S\right)$, and $C_D=D/\left(0.5\rho {\left(U\right)}^{2}S\right)$, respectively. Here, $p$ is the pressure, $p_{\infty }$ is the pressure at infinity, and $S$ is the area of one wing. The aerodynamic power (P_a) required to overcome the aerodynamic moments is determined by the aerodynamic torque and angular velocity of the wing. The aerodynamic power coefficient is calculated as $C_{P,a}{=P}_a/\left(0.5\rho {\left(U\right)}^{3}S\right)$. The propulsion efficiency $\eta$ is given as $\eta =\overline{C_L}/\overline{C_{P,a}}$. $\overline{C_L}$ and $\overline{C_{P,a}}$ are cycle-averaged $C_L$ and $C_{P,a}$, respectively.

The code has been verified by comparing the calculated forces with those of experimental measurement of flapping insect wings [28]. It showed that the calculated results matched the experimental measurements closely. To further ensure that our code is correct, Figure 2 compares our calculations with the work of Li and Lu [29], which studied the forces of pitching and heaving flat plates in an incoming flow. Again, the aerodynamic data are in good agreement. In addition, according to the previous research of our group [24], this flow solver can accurately predict the wing–wing or wing–wake interactions.

FIGURE 2

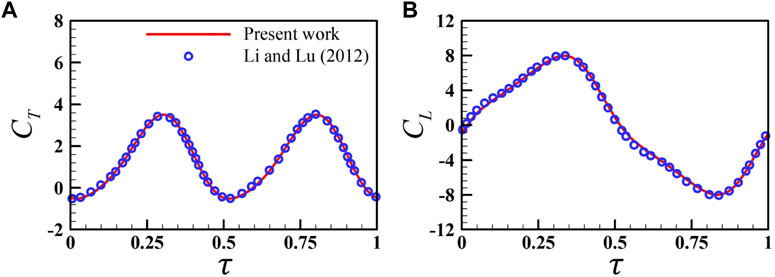
FIGURE 2. Comparison of the present instantaneous lift coefficient (A) and drag coefficient (B) with previous data obtained by Li and Lu [29] for a rectangular plate with an aspect ratio of 0.5 at $Re=500$.

3 Results and discussion

3.1 Effect of flapping amplitude

As mentioned in Section 2.2, the non-dimensional wingbeat period ($T^{*}=2\mathrm{\Phi }{r}_2/c$) is proportional to the peak-to-peak amplitude $\mathrm{\Phi }$. Thus, the mean angular velocity is the same for different amplitudes. The main purpose of changing $\mathrm{\Phi }$ is to compare the difference in aerodynamic performance between smaller, faster motions and larger, slower motions.

In this section, the aerodynamics and flow structures of a single wing under the condition of hovering are simulated first because hovering is an important flight mode for the MAVs to perform specific tasks. The amplitude of pitching is varied from $\mathrm{\Phi }=10°$ to 80° at intervals of 10°. It should be noted that the range of pitching amplitude investigated in this study is larger than those in previous works [18–21]. The transient lift and drag coefficients of the wing after the flow reached a stable periodic state are shown in Figure 3. It is seen that there are two positive crests and two negative troughs of lift in one cycle for each curve (Figure 3A). The magnitude of positive crests is larger than that of the negative troughs, which ensures that the wing is subjected to an upward average lift. With the increase in $\mathrm{\Phi }$, the peak of lift increases and shifts slightly rightward in phase. The curve of drag for each flapping amplitude has only one crest and one trough with equal magnitude, which results in zero cycle-averaged drag (Figure 3B). As shown in Figure 3B, the crest and trough of the drag increase as $\mathrm{\Phi }$ decreases.

FIGURE 3

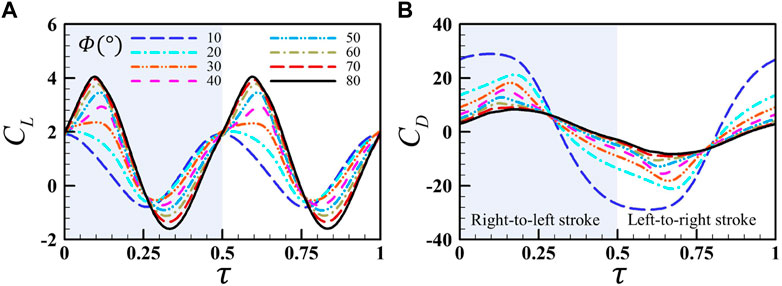
FIGURE 3. Comparison of the instantaneous lift coefficient (A) and drag coefficient (B) of a single wing for different flapping amplitudes $\mathrm{\Phi }$ within one flapping cycle.

$\overline{C_L}$, $\overline{C_{P,a}}$, and $\eta$ of the wing as a function of $\mathrm{\Phi }$ are shown in Figure 4. It shows that $\overline{C_L}$ increases with the enlargement of $\mathrm{\Phi }$ at first, and then it remains approximately stable when $\mathrm{\Phi }$ is larger than 30°. Since $\overline{C_{P,a}}$ decreases gradually, $\eta$ shows a general trend of continuous growth as $\mathrm{\Phi }$ increases. It indicates that a larger, slower flapping motion can improve the efficiency of the wing compared to a smaller, faster flapping motion. This is also consistent with the findings of Van Buren et al. [30] in the study of a heaving and pitching wing in an incoming flow.

FIGURE 4

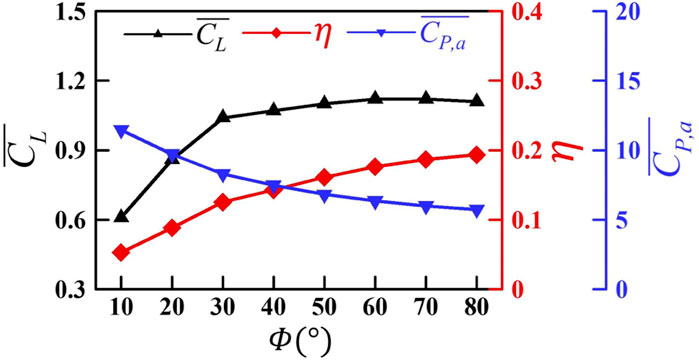
FIGURE 4. Variation in the mean lift coefficient $\overline{C_L}$, mean aerodynamic power coefficient $\overline{C_{P,a}}$, and propulsive efficiency $\eta$ as a function of the flapping amplitude $\mathrm{\Phi }$ for a single wing at hovering.

Next, we further discuss the vortex structures around the wing under different flapping amplitudes. Figure 5 illustrates the evolution of the vortex structures around the wing at eight typical instants during one flapping cycle at $\mathrm{\Phi }=40°$. The vortex is visualized by the Q criterion, and the oblique view is used to facilitate the identification of different vortices. The vortex structures at $\tau =0$ (the beginning of the right-to-left stroke) and $\tau =0.5$ (the beginning of the left-to-right stroke) in Figure 5 can be viewed as mirror images of each other due to the symmetry in the wing kinematics. The “mirrored image” is of help to clearly demonstrate the vortex structures around the wing.

FIGURE 5

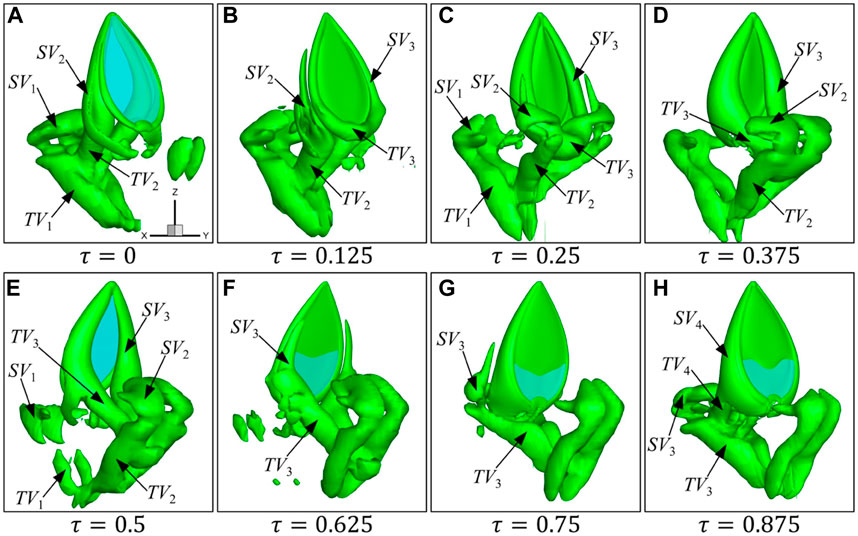
FIGURE 5. Formation and evolution of vortices at eight typical instants (A–H) during one flapping cycle for a single wing at $\mathrm{\Phi }=40°$. In all snapshots, the iso-surface of the Q criterion with $\mathrm{Q}=2$ is shown.

As shown in Figure 5, when the wing starts to flap from right to left ($\tau =0$), the main vortex structures are two curved vortex rings. One is composed of the side-edge vortices (SV₂) and the wingtip vortex (TV₂) formed in the preceding left-to-right stroke, and the other is composed of SV₁ and TV₁ formed in the earlier right-to-left stroke. At $\tau =0$, SV₂ is still attached to the wing surface, but TV₂ has shed away from the wing, resulting in the curved shape of the vortex ring. At $\tau =0.125$, the new side and tip vortices (SV₃ and TV₃₎ are gradually generated at the wing edge, forming a new vortex ring. At this instant, the wing as well as the newly formed SV₃ bypasses SV₂, providing an opportunity for the wing–wake interaction. At $\tau =0.25$ (Figure 5C), SV₃ and TV₃ become stronger, and SV₂ is distorted due to the induction of the newly generated vortex ring. From $\tau =0.375$ to 0.5, TV₃ detaches away from the wing, resulting in a gradually bent vortex ring. In addition, the vortex ring formed by SV₂ and TV₂ has been seriously distorted, mainly because SV₂ is further entrained and induced by TV₃. It should be noted that SV₁ and TV₁ gradually dissipate from $\tau =0$ to 0.5 and finally disappear in the following process. In the subsequent stroke (from $\tau =0.5$ to 0.875), the formation and evolution of vortex structures are similar to those in the preceding stroke (from $\tau =0$ to 0.375), that is, the formation of SV₄ and TV₄ and their entraining and inducing effect on SV₃. By 2D PIV measurement, Liu et al. [17] showed that the flow field for the wing of the jellyfish-like flyer is characterized as the consecutive shedding of two vortices at the wingtip with an opposite rotation sense, which are generated during the downstroke and upstroke, respectively. This is similar to the generation and shedding of TV₃ and TV₄ in the present study, although the Reynolds numbers are different in the two studies.

The vortex structures under different flapping amplitudes at $\tau =0.5$ are shown in Figure 6. It should be noted that the wing begins to flap from left to right at this moment. When $\mathrm{\Phi }$ is smaller than 40°, the vortex structures become more complex, although they show similar topology. It is seen that SV₃ and TV₃ become larger gradually with the increase in $\mathrm{\Phi }$ (Figures 6A–D). Due to the short dissipation time, the vortex structures generated by the previous strokes for small flapping amplitude can still be displayed. When $\mathrm{\Phi }$ is larger than 40°, the strength of the side vortices changes little, which is consistent with the cycle-averaged lift force performance in Figure 4. Because of the long dissipation time at the large flapping amplitude, SV₂ and TV₂, which can be observed for $\mathrm{\Phi }=40°$, have almost disappeared for $\mathrm{\Phi }=70°$ and 80°.

FIGURE 6

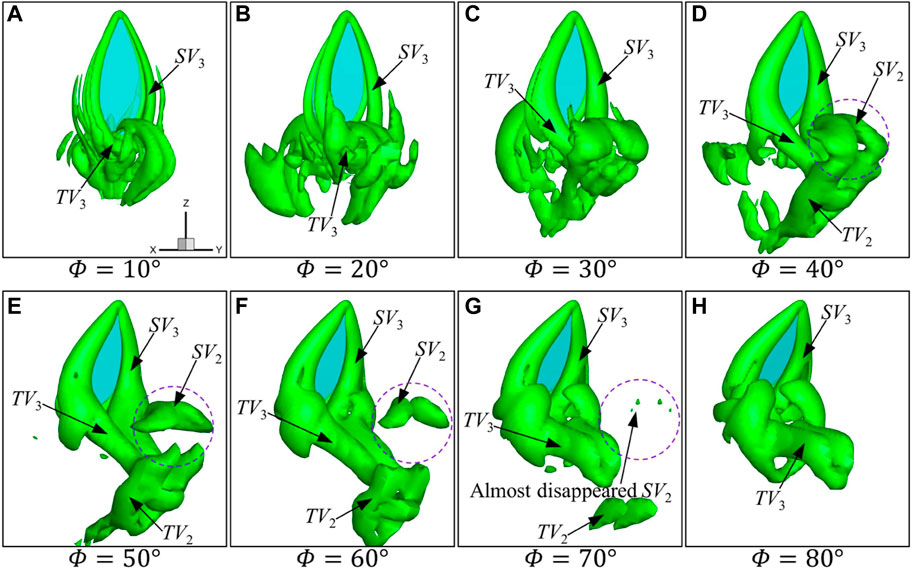
FIGURE 6. Instantaneous vortex structure of the wing for different amplitudes at Φ (A–H) $\tau =0.5$. In all snapshots, the iso-surface of the Q criterion with $\mathrm{Q}=2$ is shown.

The iso-surfaces of time-averaged velocity $\overline{u_Z}$ in the flow field for different $\mathrm{\Phi }$ cases are shown in Figure 7. The iso-surfaces in gray with a threshold of $\overline{u_Z}=0.2$ indicate the unfavorable upwash for propulsion, while those in blue with $\overline{u_Z}=-0.3$ represent the favorable downwash for propulsion. The upwash is supposed to be generated by the part of the distorted vortex ring (SV₂), which is labeled in Figure 6. As shown in Figure 7, the downwash concentrates near the wing at hovering. This is different from the case with incoming flow, in which the wakes developed into bifurcated jets [21, 31]. The downwash is distributed under and on both sides of the wing, while the upwash is mainly concentrated on both sides of the wing. As $\mathrm{\Phi }$ increases from 10° to 40°, the downwash region becomes significantly wider in the Y-axis direction and longer in the Z-axis direction (Figures 7A–D). The longer downwash in the vertical direction indicates a larger lift. As $\mathrm{\Phi }$ increases further, the width of the downwash keeps increasing, but the length changes little (Figures 7E–H), so the overall downwash beneficial for lift generation is basically unchanged. This is consistent with the results in Figure 4, which shows that the mean lift increases rapidly first and then stabilizes approximately. Meanwhile, the upwash on both sides of the wing decreases continuously. As $\mathrm{\Phi }$ reaches 80°, the upwash has nearly disappeared. This is because the distorted part of the vortex wake (SV₂) dissipates faster for larger $\mathrm{\Phi }$, which can also be observed in the circled part in Figure 6.

FIGURE 7

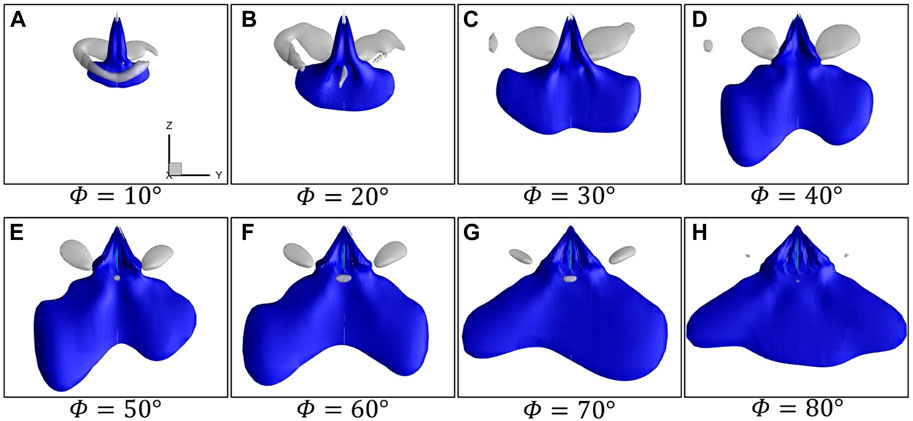
FIGURE 7. Iso-surfaces of time-averaged velocity $\overline{u_Z}$ thresholded at 0.2 (gray) and -0.3 (blue) of a single wing for different flapping amplitudes Φ (A–H).

According to the vortex structures and downwash in Figure 6 and Figure 7, it can be summarized that with the increase in the flapping amplitude from 10° to 40°, SV and TV on the wing surface are significantly enhanced, forming a stronger vortex ring to induce stronger downwash, thus causing a larger lift. As the flapping amplitude increases further, the vortex wake, as well as the accompanying downwash, mainly widens in the horizontal direction, but the strength of the vortex and the downwash in the vertical direction changes little, resulting in basically no change in the lift.

3.2 Wake effect

For flapping wings at hovering, the vortices are convected away from the wing at a very small speed due to the lack of incoming flow. Hence, as a wing decelerates and reverses to start the next stroke, the wing inevitably captures and interacts with the remaining wake from the previous stroke. It is necessary to explore the wake effect under different amplitudes at hovering, which has not been examined for the jellyfish-like wing motion in previous studies.

The contribution of wake capture to the aerodynamic force is isolated by comparing the averaged lift force of the first stroke when the wing starts to flap in a quiescent fluid and the wake effect is absent, with that of the ninth stroke after the periodic flow field has been established. The results are shown in Figure 8. It is seen that with the increase in $\mathrm{\Phi }$, the effect of wake capture changes from reducing lift to increasing lift, and the improvement of lift keeps increasing (see the solid and dashed black lines with delta symbols). Also displayed in Figure 8 are the two components of lift contributed by friction and pressure, respectively. For all $\mathrm{\Phi }$ considered, whether there is wake or not, the friction-based lift (denoted as C_L(F)) is always negative, while the pressure-based lift (denoted as C_L(P)) is always positive. The wake effect is to increase C_L(P) and decrease C_L(F). As $\mathrm{\Phi }$ increases, the improvement in C_L(P) caused by the wake effect becomes larger (compare the solid and dashed red lines with diamond symbols), while the reduction in C_L(F) due to the wake effect becomes smaller (compare the solid and dashed red lines with gradient symbols). As a result, the combined effect of the wake becomes larger with the increase in $\mathrm{\Phi }$. It should be noted that at $\mathrm{\Phi }=10°$, the wake effect on C_L(P) is negligibly small, but its reduction effect on C_L(F) is much larger, so the wake effect is to decrease C_L at this small flapping amplitude.

FIGURE 8

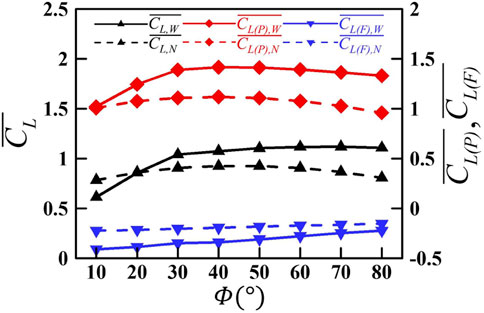
FIGURE 8. Variation in the mean lift and the pressure- and friction-based lift of the wing as a function of the flapping amplitude $\mathrm{\Phi }$ with/without wake effect. Subscripts “P” and “F” in the symbols represent the pressure- and friction-based components of the lift, respectively. Subscripts “W” and “N” in the symbols represent the cases with and without wake effect, respectively.

Next, we analyzed the case of $\mathrm{\Phi }=40°$ in detail to explore the reason why the pressure-based lift was enlarged by the vortex wake. Figure 9 shows the spanwise component of vorticity (${\omega }_S$) and pressure contours of the wing at the 0.7R section at $\tau =0.125$ for the first stroke and the ninth stroke. The vortex structures and the location of the section are also displayed in the figure to assist the analysis. Compared with the result in the first stroke, not only the positive pressure on the lower wing surface in the ninth stroke is larger, but the negative pressure on the upper wing surface is also lower, which makes the pressure-based lift larger (see Figures 9A, B).

FIGURE 9

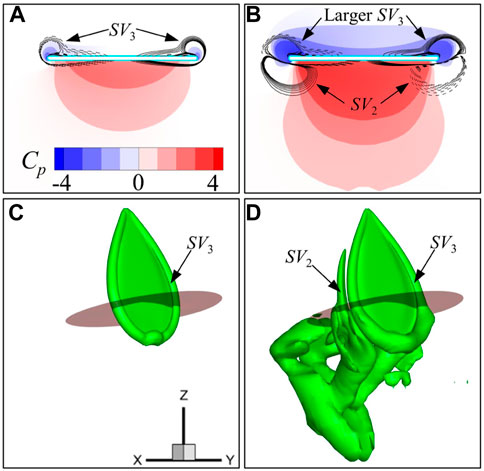
FIGURE 9. Pressure and spanwise vorticity (${\omega }_S$) contours at the 0.7 R wing section, as well as the instantaneous vortex structure ($\mathrm{Q}=2$) of the wing at $t^{*}/T^{*}=0.125$ (A,C) and $t^{*}/T^{*}=4.125$ (B,D) (solid and broken lines indicate positive and negative vorticity, respectively).

For the first stroke, only SV₃ is generated at this time instant (Figures 9A, C). In contrast, for the ninth stroke in Figures 9B, D, besides the newly generated SV₃ on the upper wing surface, two edge vortices (SV₂) can be seen on the lower surface of the wing, and they are part of the vortex ring generated in the preceding stroke (Figure 9D). The two edge vortices (SV₂) or the previous vortex ring can induce favorable fluid velocity toward the lower surface of the wing, resulting in higher pressure as shown in Figure 9B. Furthermore, it is noted that on both edges of the wing, the vorticity signs of the newly generated vortex and wake vortex are opposite (Figure 9B). Therefore, as the wing approaches the vortex wake, narrow channels are formed between SV₃ and SV₂, which will accelerate the fluid in the middle and promote the strength of SV₃ at the same time. As a result, larger side-edge vortices (SV₃) are generated on the upper wing surface, resulting in lower pressure. This wake capture effect is similar to the findings of Birch and Dickinson [32], and Lua et al. [33]. These findings indicated that the wake capture can improve the lift of insect wings. However, it is somewhat different from the study of Wu and Sun [34], which shows that the vortex wake can reduce the lift of the wing by generating a downwash.

It has been shown in Figure 6 that with the decrease in flapping amplitude, the strength of the vortex gets weaker. At $\mathrm{\Phi }=10°$, SV₂ and TV₂ generated in the preceding stroke are very small (Figure 6A), so the surface pressure profit is small. Moreover, because the wing is more vertically placed, the contribution of the change in surface pressure to the lift can be almost ignored. At larger $\mathrm{\Phi }$, not only does the effective horizontal projection area of the wing increase, but the stronger SV₂ and TV₂ also prompt more favorable changes in surface pressure, so the effect of the wake capture on enlarging the C_L(P) becomes larger.

The reason for the negative C_L(F) is easy to understand. The flapping wing obtains upward reaction force by driving the fluid to convect downward. The downward movement of fluid causes a velocity gradient near the wing surface, which can result in the negative lift. When there is a vortex wake, the downward velocity will be enhanced by the downwash, leading to an increase in the friction force. Thus, the negative friction-based lift becomes smaller when there is a vortex wake.

3.3 The effect of up-flight speed

By changing the flapping amplitude, the jellyfish-like aircraft can switch between hovering, ascending, and forward flight states [13]. In this section, we further explored the aerodynamic performance of a single wing at different up-flight speeds (V, see Figure 1B). Figure 10 plots the mean lift coefficient $\overline{C_L}$ of the wing flying upward at $V=0$, 0.25V₀, 0.50V₀, 0.75V_0, and 1.00V₀, respectively. It should be noted that V₀ is defined as the mean velocity of the wingtip at $\mathrm{\Phi }=40°$. It is seen that for a specific ascending speed, $\overline{C_L}$ rises rapidly at first and then tends to be stable with the increase in flapping amplitude. When the flapping amplitude is fixed, $\overline{C_L}$ decreases gradually with the increase in up-flight speed. The smaller the flapping amplitude is, the faster the $\overline{C_L}$ drops, and even negative average lift values appear in some cases.

FIGURE 10

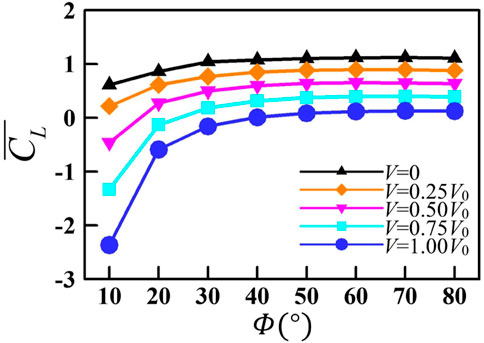
FIGURE 10. Variation in the mean lift coefficient $\overline{C_L}$ as a function of the flapping amplitude $\mathrm{\Phi }$ of the wing at different up-flight speeds V.

The vortex structures of the wing with different up-flight speeds at $\tau =0$ for three cases ($\mathrm{\Phi }=10°$, 40°, and 70°) are shown in Figure 11. To show more vortex structures, the criterion of $\mathrm{Q}=0.5$ is used in these images. For $\mathrm{\Phi }=10°$ (left column in Figure 11), the wake under the wing consists of two sets of vortex rings (shed a vortex ring in each half-cycle). This is similar to the work of Buchholz and Smits [18] in which a rectangular plate conducting pitching motion was studied and a series of “horseshoe vortices” was observed in the wake. With the increase in the up-flight speed, the vortex street becomes longer. As the vortices convect downward and dissipate gradually, the vortex ring breaks and forms two separate branches. When $\mathrm{\Phi }$ increases to 40°, the vortex rings become larger, and they are no longer concentrated in the vertical direction but convect downstream at an oblique angle relative to the wake centerline. For $\mathrm{\Phi }=70°$, the vortex rings are further enhanced and the inclination angle becomes larger.

FIGURE 11

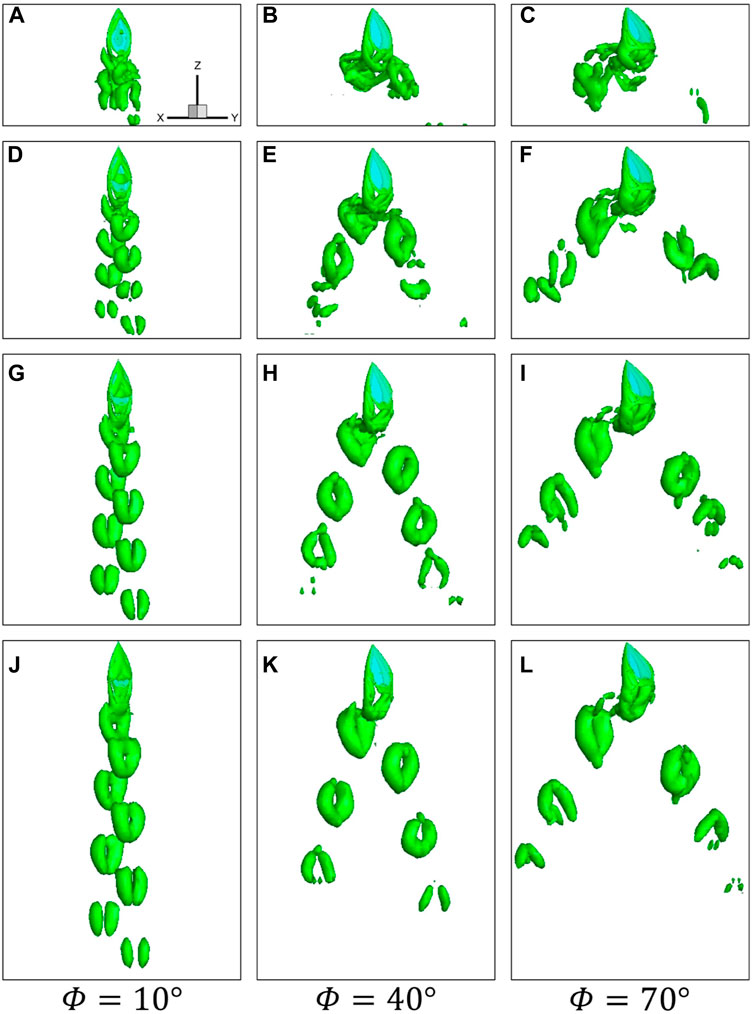
FIGURE 11. Instantaneous vortical structures visualized by the iso-surface of $\mathrm{Q}=0.5$ for the wing at $V=0.25V_0$ (A–C), $0.50V_0$ (D–F), $0.75V_0$ (G–I), and $1.00V_0$ (J–L) for different flapping amplitudes Φ.

Figure 12 plots the instantaneous lift coefficients and its two components (C_L, C_L(P), and C_L(F)) of the wing for $\mathrm{\Phi }=10°$, 40°, and 70° cases at different up-flight speeds. At $\mathrm{\Phi }=10°$, the change in C_L(P) with the increase in V is relatively small (Figure 12B), but C_L(F) obviously decreases (Figure 12C). This leads to the rapid decrease in $\overline{C_L}$ with the up-flight speed for the $\mathrm{\Phi }=10°$ case, as shown in Figure 12A. The study by Floryan et al. [35] on the heaving or pitching foils also showed that viscous drag added an approximately constant negative offset to the thrust coefficient. Our results show that this constant negative offset increases rapidly with the increase in the up-flight speed at a very small flapping amplitude. Considering that the flapping wing is approximately vertical for the $\mathrm{\Phi }=10°$ case, the larger up-flight speed will cause a bigger velocity gradient in the normal direction at the wing surface, resulting in a greater frictional force.

FIGURE 12

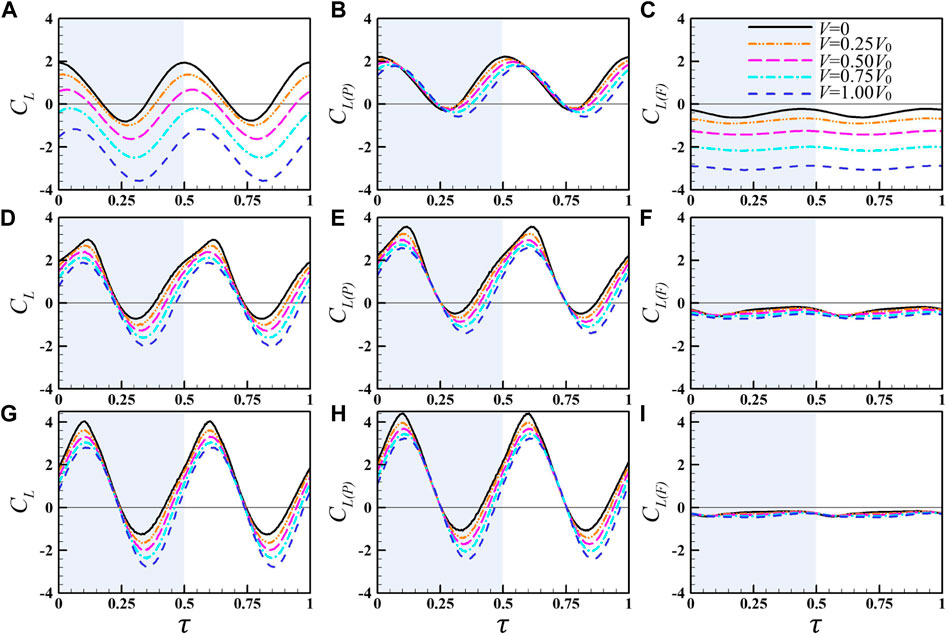
FIGURE 12. Instantaneous lift coefficients and its two components (the pressure-based lift and friction-based lift) of the wing for $\mathrm{\Phi }=10°$ (A–C), $\mathrm{\Phi }=40°$ (D–F), and $\mathrm{\Phi }=70°$ (G–I) at different up-flight speeds V. Subscripts “P” and “F” in the symbols represent the pressure- and friction-based components of the lift, respectively.

When $\mathrm{\Phi }$ increases to 40° and 70°, C_L(F) is essentially unchanged at different up-flight speeds (Figures 12F, I), while C_L(P) decreases (Figures 12E, H), resulting in the reduction of C_L with the increase in V. The change in C_L(P) is caused by the velocity change in the incoming flow relative to the wing surface. When the wing moves up at a certain speed, the lower wing surface will face a lower relative inflow velocity as the wing flaps downward, while the upper wing surface will face a higher relative inflow velocity as the wing flaps upward. This opposite change in the relative inflow velocity can reduce the magnitude of positive C_L(P) at about $\tau =0.125$ and increase the magnitude of negative C_L(P) at around $\tau =0.375$ (Figures 12E, H). Since the effective horizontal projection area of the wing also becomes larger following the increase in the flapping amplitude, the reduction in C_L(P) would be further amplified at larger $\mathrm{\Phi }$.

3.4 The effect of wing–wing interaction

Using the wing-pair model in Section 2.1, we explored the effect of the aerodynamic interaction between two wings at different separations (H, see Figure 1B) at the hovering state. The opening angle $\theta =80°$ and the flapping amplitude $\mathrm{\Phi }=20°$ were selected to ensure that the two wings would parallel with each other at the end of the downstroke. Here, the process of two wings approaching is called downstroke, and the process of moving apart is called upstroke. Figure 13 displays the instantaneous lift and drag coefficients of the right wing at different wing–wing spacings, along with those of a single wing for comparison. It is seen that the magnitudes of the peak and trough of lift and drag of the wing pair are larger than those of the single wing, and they increase with the decrease in H. Since the opening angle is now $80°$, the setting of the relative position of the pair of wings in this section is similar to that of Liu et al. [17] Therefore, the change trends of the forces in both studies for the symmetric pitching motion are also similar, that is, the downstroke mainly produces positive lift and the upstroke produces negative lift (see Figure 3A in Ref. [17]).

FIGURE 13

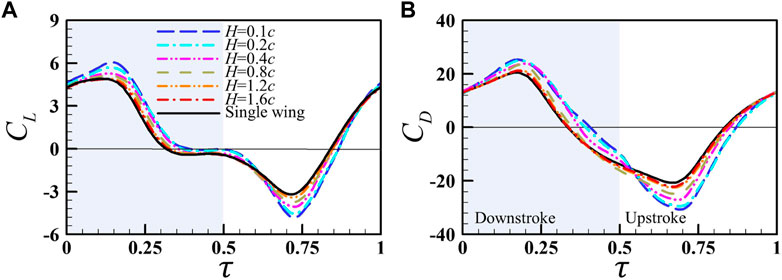
FIGURE 13. Instantaneous (A) lift and (B) drag coefficients of the right wing of the wing pair at different wing–wing separations (H), with the results of the single wing for comparison.

The flow-field information of two wing-pair cases ($H=0.1c$ and $H=1.2c$) and the single wing case was selected for analysis and comparison. The pressure distributions and the velocity vectors in the YOZ plane at $\tau =0.125$ and $\tau =0.75$ are plotted in Figure 14. At $H=0.1c$, it is seen that as the wings move close to each other, the fluid between them is “squeezed” and the pressure significantly increases compared with that of the single wing (Figures 14A, C), indicating that the larger force is caused by the squeezed air between the two wings. During the upstroke, the “moving apart” of the wings in the opposite direction increases the gap between the wings and creates a larger suction pressure there (Figures 14B, D). This suction pressure produces a larger negative lift and drag than that of the single wing to keep the wings from moving apart. The large aerodynamic forces due to the wing–wing interaction are also similar to those of wings conducting clap and fling motion [36, 37]. When the separation increases to $H=1.2c$ (Figures 14E, F), the pressure and the velocity vectors of the wing pair are not very different from those of the single wing, leading to almost the same aerodynamic force of the two cases. It should be noted that a favorable strong downward jet is generated under the two wings at $H=0.1c$ (Figure 14C), while no jet but downwash is generated in the other cases. Therefore, we can deduce that when multiple flapping wings are arranged at the distance of the prototype of the jellyfish-like aircraft, which is about 1.2c, the wing–wing interaction is very small.

FIGURE 14

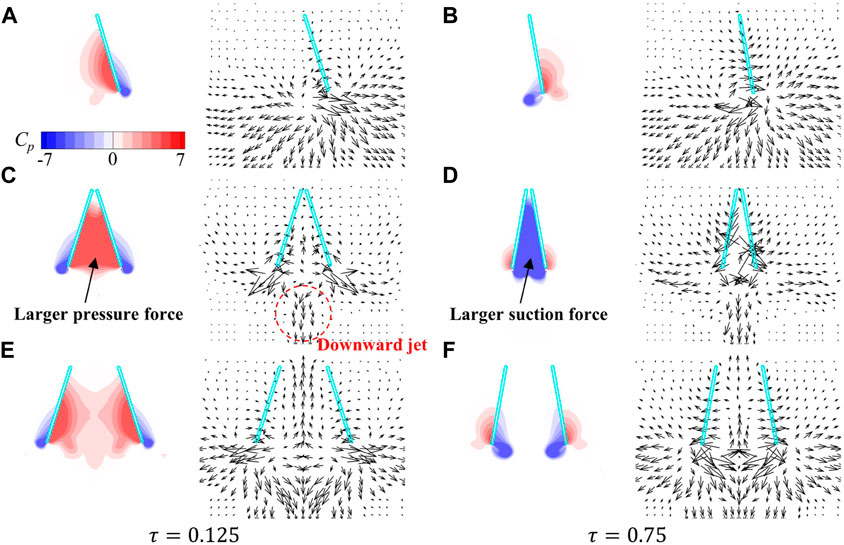
FIGURE 14. Pressure contours and the velocity vectors around the wings in the YOZ plane for the (A,B) single wing case, (C,D) $H=0.1c$ case, and (E,F) $H=1.2c$ case at $\tau =0.125$ and $\tau =0.75$. H is the distance between two wing roots.

The variation in $\overline{C_L}$, $\overline{C_{P,a}}$, $\eta$, and the mean absolute value of the drag $\overline{{\mid C}_D\mid }$ of the right wing as a function of H is displayed in Figure 15. It shows that $\overline{C_L}$, $\overline{C_{P,a}}$, and $\overline{{\mid C}_D\mid }$ increases with the decrease in H, but $\eta$ has the opposite changing trend. At $H=1.2c$, the average lift is almost the same as that of a single wing, which indicates that the interference effect between the two wings becomes negligibly small when H reaches 1.2 c or larger. Compared with the single wing, $\overline{C_L}$ and $\overline{{\mid C}_D\mid }$ of the wing at $H=0.1c$ are increased by 15.5% and 24.7%, respectively, but at the same time, $\overline{C_{P,a}}$ is enlarged by 66.3%, resulting in a 30.1% decrease in efficiency. Although reducing the distance between wings can improve the lift to a certain extent, it requires more energy consumption and becomes less efficient, which is not beneficial to the economic flight of this jellyfish-like flyer. Dewey et al. [38] found a thrust enhancement of about 70% for the out-of-phase 2D foils in a side-by-side configuration compared to an isolated foil with no observable change in the propulsive efficiency. Fang et al. [14] found that efficiency increased as the wings get closer due to a mirror-image “ground effect” between the wings. The differences in the results between our current research and the previous two research studies may lie in the difference in wing models (2D vs 3D), and/or the incoming flow settings (with vs without incoming flow).

FIGURE 15

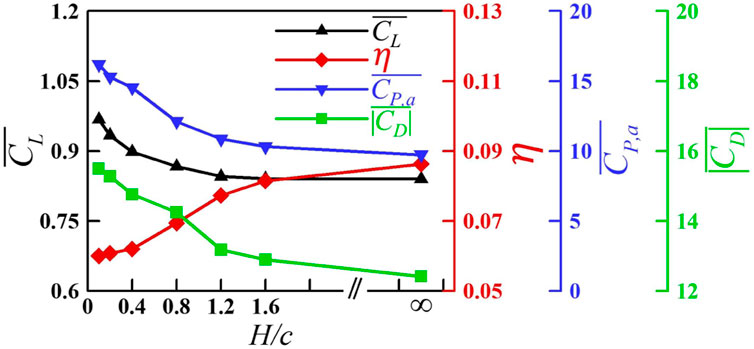
FIGURE 15. Variation in $\overline{C_L}$, $\overline{C_{P,a}}$, $\eta$, and the mean absolute value of the drag $\overline{{\mid C}_D\mid }$ of the wing as a function of wing–wing separations (H). The symbol “∞” indicates the single wing case.

It is instructive to test our calculation results against biological observations. For real jellyfish, there are two main mechanisms for propulsion [39]. One is the jet propulsion mechanism used by the elongated jellyfish. During the contraction stroke of the elongated jellyfish, it drives the entire bell and creates a powerful jet in the subumbrellar cavity. Periodic bell contractions cause the ejected jets to form a series of uniform vortex rings with the same rotational direction in the wake. This motion can produce rapid acceleration and swimming speed but require high energy expenditure. The other is the “rowing mechanism” used by the oblate jellyfish [40]. For oblate jellyfish, contractions occur primarily at the bell margin, which is similar to using paddles (the bell margin) to row a boat (the body). An oblate jellyfish produced periodic vortex wake instead of strong jets. A train of closely spaced vortex ring pairs was formed in the wake and convected downstream. This motion was more efficient in propulsion. For the numerical results in this study, the velocity fields at $H=0.1c$ and $H=1.2c$ correspond well to those of elongated and oblate jellyfish, respectively. At $H=0.1c$, although wings can gain a larger aerodynamic force and generate a favorable jet, the efficiency is lower. At $H=1.2c$, although the force on the wings is small and no jet is generated, the efficiency is higher. Therefore, the real jellyfish-like flyer is closer to a simplified rowing model without the interference effect between multiple wings.

4 Conclusion

By solving the incompressible Navier–Stokes equation, we numerically investigated the aerodynamic performance of the flapping wing of the jellyfish-like flyer under some control parameters, including the flapping amplitude, up-flight speed, and the spacing of the wing pair. The wake capture effect and wing–wing interaction were emphasized and discussed. Different from previous 2D models, the 3D wing model with a shape similar to that of the jellyfish-like aircraft wing was used in this study.

With the increase in the flapping amplitude, the lift of the wing first rises rapidly and then becomes approximately stable. As the flapping amplitude increases from 10° to 40°, the vortices generated at the wing edge are significantly enhanced, forming an intenser vortex ring to induce stronger downwash. When the flapping amplitude increases further, the vortex wake, as well as the accompanying downwash, mainly widens in the horizontal direction, but the strength of the vortex and the downwash in the vertical direction changes little, resulting in basically no change in lift.

The wake capture effect changes from reducing the lift at $\mathrm{\Phi }=10°$ to increasing the lift when $\mathrm{\Phi }$ is larger than 20°, and with the increase in $\mathrm{\Phi }$, the improvement of lift caused by the vortex wake keeps increasing. The vortex wake improves the lift mainly by inducing a larger fluid velocity relative to the lower wing surface and inducing larger edge vortices on the upper wing surface, making the positive pressure and suction force on both wing sides larger.

When the wing has an up-flight speed, the variation in lift with amplitude is similar to the results at hovering. At a specific $\mathrm{\Phi }$, the mean lift gradually decreases with the increase in up-flight speed. It is also found that the viscous drag accounts for the reduction in lift at small flapping amplitude, while the change in surface pressure dominates the force variation for large flapping amplitude.

The aerodynamic effect of the wing–wing interaction was also studied. It is found that when the distance between wings is small enough, the wing–wing interaction can improve the lift of the wing, but it requires more power consumption and results in lower efficiency, which is unfavorable to the aircraft. When the wings’ spacing is the same as that of the prototype of the jellyfish-like flyer, the aerodynamic interference between multiple wings can be neglected.

The findings in this study may shed some light on further understanding of the aerodynamics of the jellyfish-like flapping wing and provide useful insights into the future design of jellyfish-like aircraft. While the flyer is described as being “jellyfish-like”, there are some apparent differences between the kinematics of its wings and that of a jellyfish’s bell. During swimming, jellyfish contracts and expands the soft deformable bell very complicatedly, with asymmetries in the contraction and expansion phases. Therefore, it is necessary to consider the effects of flexibility and time asymmetry motion while adopting the 3D wing model, as well as to evaluate the postural stability of the air vehicle.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XM, DW, and SJ conceived the project. CD carried out the simulations. All the authors performed the data analyses. XM wrote the manuscript with contributions from CD, DW, and SJ.

Funding

This research was sponsored by grants from the National Natural Science Foundation of China (No. 12172276), the Foundation of National Key Laboratory of Science and Technology on Aerodynamic Design and Research (No. 614220121020116), and the Laboratory of Aerodynamic Noise Control (No. 2101ANCL20210101) governed by China Aerodynamics Research and Development Center.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wood RJ. The first takeoff of a biologically inspired at-scale robotic insect. IEEE Trans Rob (2008) 24:341–7. doi:10.1109/TRO.2008.916997

CrossRef Full Text | Google Scholar

2. Ratti J, Vachtsevanos G. A biologically-inspired micro aerial vehicle: Sensing, modeling and control strategies. J Intell Rob Syst (2010) 60:153–78. doi:10.1007/s10846-010-9415-x

CrossRef Full Text | Google Scholar

3. Ellington CP. The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Philos Trans R Soc B (1984) 305:79–113. doi:10.1098/rstb.1984.0052

CrossRef Full Text | Google Scholar

4. Ellington CP, Van Den Berg C, Willmott AP, Thomas ALR. Leading-edge vortices in insect flight. Nature (1996) 384:626–30. doi:10.1038/384626a0

CrossRef Full Text | Google Scholar

5. Dickinson MH, Lehmann FO, Sane SP. Wing rotation and the aerodynamic basis of insect flight. Science (1999) 284:1954–60. doi:10.1126/science.284.5422.1954

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sun M, Tang J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J Exp Biol (2002) 205:55–70. doi:10.1242/jeb.205.1.55

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lighthill MJ. On the Weis-Fogh mechanism of lift generation. J Fluid Mech (1973) 60:1–17. doi:10.1017/S0022112073000017

CrossRef Full Text | Google Scholar

8. Lyu YZ, Sun M. Dynamic stability in hovering flight of insects with different sizes. Phys Rev E (2022) 105:054403. doi:10.1103/PhysRevE.105.054403

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Taylor GK, Krapp HG. Sensory systems and flight stability: What do insects measure and why? Adv Insect Physiol (2007) 34:231–316. doi:10.1016/S0065-2806(07)34005-8

CrossRef Full Text | Google Scholar

10. Ma KY, Chirarattananon P, Fuller SB, Wood RJ. Controlled flight of a biologically inspired, insect-scale robot. Science (2013) 340:603–7. doi:10.1126/science.1231806

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ristroph L, Bergou AJ, Ristroph G, Coumes K, Berman GJ, Guckenheimer J, et al. Discovering the flight autostabilizer of fruit flies by inducing aerial stumbles. Proc Natl Acad Sci U S A (2010) 107:4820–4. doi:10.1073/pnas.1000615107

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Childress S, Vandenberghe N, Zhang J. Hovering of a passive body in an oscillating airflow. Phys Fluids (2006) 18:117103. doi:10.1063/1.2371123

CrossRef Full Text | Google Scholar

13. Ristroph L, Childress S. Stable hovering of a jellyfish-like flying machine. J R Soc Interf (2014) 11:20130992. doi:10.1098/rsif.2013.0992

CrossRef Full Text | Google Scholar

14. Fang F, Ho KL, Ristroph L, Shelley MJ. A computational model of the flight dynamics and aerodynamics of a jellyfish-like flying machine. J Fluid Mech (2017) 819:621–55. doi:10.1017/jfm.2017.150

CrossRef Full Text | Google Scholar

15. Zhang X, He G, Wang S, Zhang X. Locomotion of a bioinspired flyer powered by one pair of pitching foils. Phys Rev Fluids (2018) 3:013102. doi:10.1103/PhysRevFluids.3.013102

CrossRef Full Text | Google Scholar

16. Zhang X, He G, Wang S, Zhang X. Passive hovering of a flexible Λ-flyer in a vertically oscillating airflow. J Fluid Mech (2019) 878:113–46. doi:10.1017/jfm.2019.633

CrossRef Full Text | Google Scholar

17. Liu YY, Pan C, Liu Y. Propulsive performance and flow-field characteristics of a jellyfish-like ornithopter with asymmetric pitching motion. Phys Fluids (2020) 32:071904. doi:10.1063/5.0010938

CrossRef Full Text | Google Scholar

18. Buchholz JHJ, Smits AJ. The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J Fluid Mech (2008) 603:331–65. doi:10.1017/S0022112008000906

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Buchholz JHJ, Smits AJ. On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J Fluid Mech (2006) 546:433–43. doi:10.1017/S0022112005006865

CrossRef Full Text | Google Scholar

20. Green MA, Smits AJ. Effects of three-dimensionality on thrust production by a pitching panel. J Fluid Mech (2008) 615:211–20. doi:10.1017/S0022112008003583

CrossRef Full Text | Google Scholar

21. Li GJ, Kemp G, Jaiman RK, Khoo BC. A high-fidelity numerical study on the propulsive performance of pitching flexible plates. Phys Fluids (2021) 33:051901. doi:10.1063/5.0049217

CrossRef Full Text | Google Scholar

22. Sarkar S, Venkatraman K. Numerical simulation of thrust generating flow past a pitching airfoil. Comput Fluids (2006) 35:16–42. doi:10.1016/j.compfluid.2004.10.002

CrossRef Full Text | Google Scholar

23. Meng XG, Sun M. Aerodynamics and vortical structures in hovering fruitflies. Phys Fluids (2015) 27:031901. doi:10.1063/1.4914042

CrossRef Full Text | Google Scholar

24. Meng XG, Chen ZS, Zhang Y, Chen G. Aerodynamic performance and flow mechanism of multi-flapping wings with different spatial arrangements. Phys Fluids (2022) 34:021907. doi:10.1063/5.0080395

CrossRef Full Text | Google Scholar

25. Rogers SE, Kwak D, Kiris C. Steady and unsteady solutions of the incompressible Navier–Stokes equations. AIAA J (1991) 29:603. doi:10.2514/3.10627

CrossRef Full Text | Google Scholar

26. Rogers SE, Pulliam TH. Accuracy enhancements for overset grids using a defect correction approach. AIAA J (1994) 94:0523.

CrossRef Full Text | Google Scholar

27. Hilgenstock A. A fast method for the elliptic generation of three-dimensional grids with full boundary control. Numer Grid Gen Comput Fluid Mech (1988) 88:137.

Google Scholar

28. Meng XG. Ceiling effects on the aerodynamics of a flapping wing at hovering condition. Phys Fluids (2019) 31:051905. doi:10.1063/1.5094661

CrossRef Full Text | Google Scholar

29. Li GJ, Lu XY. Force and power of flapping plates in a fluid. J Fluid Mech (2012) 712:598–613. doi:10.1017/jfm.2012.443

CrossRef Full Text | Google Scholar

30. Van Buren T, Floryan D, Smits AJ. Scaling and performance of simultaneously heaving and pitching foils. AIAA J (2019) 57:3666–77. doi:10.2514/1.J056635

CrossRef Full Text | Google Scholar

31. Zhang CY, Huang HB, Lu XY. Effect of trailing-edge shape on the self-propulsive performance of heaving flexible plates. J Fluid Mech (2020) 887:A7. doi:10.1017/jfm.2019.1076

CrossRef Full Text | Google Scholar

32. Birch JM, Dickinson MH. The influence of wing-wake interactions on the production of aerodynamic forces in flapping flight. J Exp Biol (2003) 206:2257–72. doi:10.1242/jeb.00381

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lua KB, Lim TT, Yeo KS. Effect of wing-wake interaction on aerodynamic force generation on a 2D flapping wing. Exp Fluids (2011) 51:177–95. doi:10.1007/s00348-010-1032-8

CrossRef Full Text | Google Scholar

34. Wu JH, Sun M. The influence of the wake of a flapping wing on the production of aerodynamic forces. Acta Mech Sin (2005) 21:411–8. doi:10.1007/s10409-005-0064-4

CrossRef Full Text | Google Scholar

35. Floryan D, Van Buren T, Rowley CW, Smits AJ. Scaling the propulsive performance of heaving and pitching foils. J Fluid Mech (2017) 822:386–97. doi:10.1017/jfm.2017.302

CrossRef Full Text | Google Scholar

36. Cheng X, Sun M. Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J Fluid Mech (2018) 855:646–70. doi:10.1017/jfm.2018.668

CrossRef Full Text | Google Scholar

37. Lyu YZ, Sun M. Power requirements for the hovering flight of insects with different sizes. J Insect Physiol (2021) 134:104293. doi:10.1016/j.jinsphys.2021.104293

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Dewey PA, Quinn DB, Boschitsch BM, Smits AJ. Propulsive performance of unsteady tandem hydrofoils in a side-by-side configuration. Phys Fluids (2014) 26:041903. doi:10.1063/1.4871024

CrossRef Full Text | Google Scholar

39. Peng JF, Alben S. Effects of shape and stroke parameters on the propulsion performance of an axisymmetric swimmer. Bioinspiration Biomimetics (2012) 7:016012. doi:10.1088/1748-3182/7/1/016012

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jo D, Colin SP, Costello JH, Gharib M. Flow patterns generated by oblate medusan jellyfish: Field measurements and laboratory analyses. J Exp Biol (2005) 208:1257–65. doi:10.1242/jeb.01519

PubMed Abstract | CrossRef Full Text | Google Scholar