
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 07 March 2023
Sec. Mathematical Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1123370
This article is part of the Research TopicSymmetry and Exact Solutions of Nonlinear Mathematical Physics EquationsView all 20 articles
 R. A. Alharbey1*
R. A. Alharbey1* S. S. Hassan2†
S. S. Hassan2†The critical slowing down (CSD) phenomenon of the switching time in response to perturbation β (0 < β < 1) of the control parameters at the critical points of the steady state bistable curves, associated with two biological models (the spruce budworm outbreak model and the Thomas reaction model for enzyme membrane) is investigated within fractional derivative forms of order α (0 < α < 1) that allows for memory mechanism. We use two definitions of fractional derivative, namely, Caputo’s and Caputo-Fabrizio’s fractional derivatives. Both definitions of fractional derivative yield the same qualitative results. The interplay of the two parameters α (as memory index) and β shows that the time delay τD can be reduced or increased, compared with the ordinary derivative case (α = 1). Further, τD fits: (i) as function of β the scaling inverse square root formula
Bistable systems in many branches of sciences (physics, biology, … ) and engineering are characterized by the co-existence of two stable states, where the system switches from one stable state to other state by means of changing one or some of the system control parameters [1–4]. The associated transient phenomena of lengthening the switching time between these two stable states, called critical slowing down (CSD), happens upon perturbing one of the parameters at the critical (switching-on or -off) points of the charactertistic bistable curve [5–8]. It has been suggested that, CSD may serve as a universal indicator of how a complex physical system (such as brain, ecosystems, climate and financial markets) approaches a threshold [9–12], and as well serving as an indicator of transitions in two-species biological models, which exhibit Hopf bifurcation or hysteresis transition [13]. For our specific current concern, the CSD phenomenon has recently been investigated by us in [14] for some biological bistable models, namely.
(a) The spruce budworm outbreak model [3, 4, 15];
(b) The Thomas-reaction (enzyme membrane) model [4, 16].
Specifically, our investigation in [14] was concerned with the nature of transition between the two stable states, and the verification of the inverse square root scaling law, for the switching time delay (τD) at the critical switching-on and -off points, independent of the type of non-linearity in the model rate equations. The model rate equation in model a) is of first order ordinary differential equation (ODE), while in model b) the model rate equations are coupled first order ODEs.On the other hand, fractional calculus, a field of mathematics that deals with the analysis of derivatives and integrals of fractional (or even complex) order, has its applications in diverse areas of science and engineering. The associated fractional differential equations (FDEs) are widely and successfully used in mathematical modelling in a variety of fields. We refer the reader to the extensive list of major works and applications in the area of fractional calculus cited in ([17–20] and refs. therein). In ordinary calculus, the first order derivative of a function f(t), namely
Experimentally speaking, fractional derivative models (FDMs) are in excellent agreement with experimental data in many branches of science and engineering. Two specific examples we quote.
1. A recent experimental study of viscoelastic properties of some soft biological tissues under harmonic mechanical loading shows that the FD Voigt model performed better, compared with integer order derivative models [29].
2. FDM (Maxwell’s model) describing the viscoelastic Creep damage of some fruits is more efficient and well fitted with experimental data [30].
Further, CSD or more generally instability mechanism and chaos, have been investigated at large in fractional order dynamical systems in fields, like, fluid flow [31–35], neurology and biological phenomena ([36–38]; refs. therein) to account successfully for memory (time-delay) and special non-local effects. For example.
1. The Landau model that describes the fluid flow from laminar to turbulent has been examined within a fractional rate equation model [35] in order to account for memory effect. This transition to turbulence due to CSD shows that the turbulent fluctuations depend on memory of inverse power law decay in agreement with experiment [39]-slower than in the case of no memory (ordinary derivative case) of turbulent fluctuations decaying exponentially,
2. Capacitive memory due to fractional order cardiomyocyte dynamical model [37] alters the electrical signaling in cardiac cells in a manner that promote or suppress electrical instability (known as alternans).
3. The use of a fractional order mathematical model to study the signaling process in nerve cells (like, neuron) due to incorporated strong memory effects [36] has been interpreted as a neuronal disorder (Parkinson disease).
The concern of the present paper is to adopt the corresponding FDEs in both models a) [3, 4, 15] and b) [4, 16], referred to above, in order to incorporate for memory effects and examine effects of the fractional derivative order parameter (α), (0 < α < 1) on the time delay (τD) associated with the CSD phenomena examined in the no-memory case [14]. We use and compare two definitions of fractional derivatives, namely, Caputo’s [40] and Caputo-Fabrizio’s [21, 22] definitions. Both definitions have the advantage of dealing with initial conditions of the variables and their integer derivatives suitable in most physical processes, like models a) [3, 4, 15] and b) [4, 16] referred to above. As a main result, it is found that Caputo’s and Caputo-Fabrizio’s definitions of fractional derivatives yield the same qualitative results of reduced time delay τD at fixed perturbation of the concerned control parameter, with smaller values of the fractional derivative order α. The small quantitative difference in τD is due to the different convoluted kernels (that model the memory or delay effect) in [21, 22, 40].This paper is presented as follows. In section 2), we present the model differential equations in both ordinary and Caputo’s fractional derivative forms, for both models. In section 3), we present the computational results for the transient switching. Section 4) presents a summary of the results. In Supplementary Appendix A, a brief background of the model ODEs (eqa (1) and. 2) below) representing the two biological models referred to above is given, while Supplementary Appendix B presents a guideline for Euler’s numerical method to solve fractional FDE.
Here, we first present the model DEs of the two biological models (the Spruce-budworm and Thomas reaction models) in their ordinary derivative forms. (A brief background of these model ODEs are given in Supplementary Appendix A). Second, we present the corresponding fractional derivative forms, according to the two formulations of Caputo’s [40] and Caputo-Fabrizio’s definitions [21].
This model ([3, 4, 15]) provides a good example for understanding the dynamics of the interaction between trees and insects. The model rate equation for the insect (budworms) population has the form:
where N(τ) is the budworm’s population, τ = rt is normalised time, r is the linear birth rate and K is the constant carrying capacity which is related to the foliage (food) available on the trees in the absence of birds. The constant F = poA/r is the predation population with rate po and A is the (positive) predator attack rate and B is the threshold measure of the budworm population. The predation will approach an upper level value,
The mechanism of this model is based on a basic reaction in an enzyme membrane, between the substrate oxygen and uric acid. The model equations of the system in a dimensionless form are [4, 16]:
Here, u and v represent the uric acid and the oxygen being supplied at constant rates a and γb, respectively, where, a, ℓ, k, γ and b are all positive real constants. The factor
In [14], the model Equations 1, 2 were analysed in detail (theoretically and computationally) regarding regions of bistability, the CSD phenomenon at the critical (switch-up and -down) points of the bistable curves and the verification of the inverse square root scaling law of the switching time delay [7, 41].
In this case, Equations 1, 2 take the following forms;
and,
respectively, where
Caputo’s fractional derivative of f(τ) is defined as the convolution of the kernel power function τ−α, 0 < α < 1 with the first order (ordinary derivative) f′τ) on the closed interval [0, τ],
with Γ(x) is the gamma function.
This fractional derivative of f(τ) is defined as the convolution of the kernel exponential function e−ατ/(1−α), 0 < α < 1, with f′(τ) on the closed interval [0, τ],
The switching time at the critical (switch-on and -off) points of the characteristic steady state bistable curves (N vs K) according to the FDE 3), or (u and v vs a) according to the FDEs 4) with both Caputo’s and Caputo-Fabrizio’s fractional derivatives, Eqs. 5 and 6, respectively, are investigated by solving these FDEs numerically using the fractional Euler’s method developed in [28, 48] (see Supplementary Appendix B for guidelines). This is done by replacing the control (input) parameter K in Equations 1–3) by Kc ± β, or a in Equations 2, 4 by ac ± β, where β (0 < β < 1) is a small real perturbation of the relevant control parameter, and Kc, ac are the initial (switch-on or switch-off) points of the bistable curves. Results are compared with the ordinary derivatives case (α = 1) [14].
The switching-on and off -points, Aon and Aoff, respectively, of the steady state bistable curve (N vs. K) according to the ODE, Eq. 1, or the FDE; Eq. 3, i. e.,
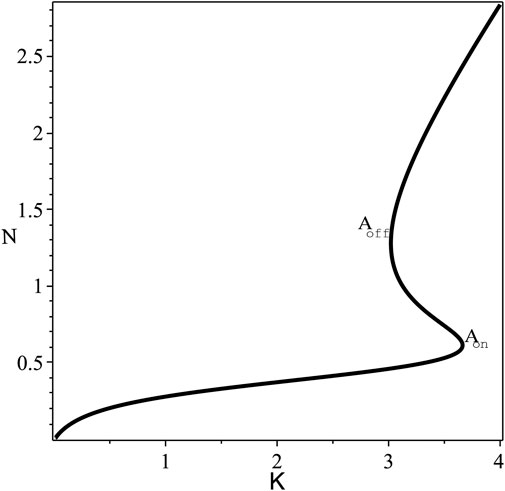
FIGURE 1. The steady state bistable curve of N against K, at fixed values of the parameters F =0.85, B =0.5. The switching-on and -off points: Aon =(3.6631,0.61299) and Aoff =(3.0199,1.2793).
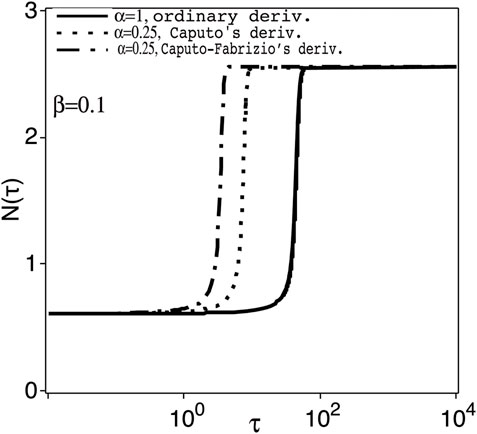
FIGURE 2. The transient population N(τ) versus the normalised time τ = γt (as log scale), for control parameter with positive perturbation, K = Kc + β; Kc =3.6631 at the switching-on point, Aon, of Figure 1 and fixed β =0.1, and for α =1 (ordinary derivative) and 0.25 (Caputo’s and Caputo-Fabrizio’s fractional derivatives).
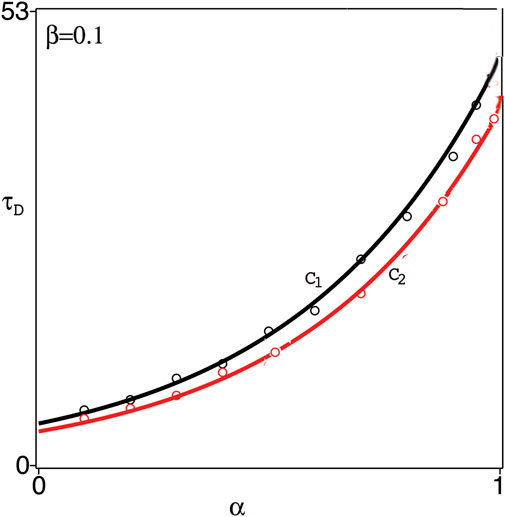
FIGURE 3. Time-delay, τD, versus the fractional derivative parameter α at fixed β =0.1. Circles represent the numerical results and the solid lines C1, C2 represent the exponential fitting, 4.9e2.2α in the case of Caputo’s derivative, and 3.8e2.3α in the case of Caputo-Fabrizio’s derivative, respectively.

FIGURE 4. As Figure 2, but at fixed value of α =0.25, and different β =0.01,0.3 in the case of: (A) Caputo’s, and (B) Caputo-Fabrizio’s, fractional derivatives.

FIGURE 5. Data as in Figure 2, but with negative perturbation, Kc − β at Aoff, where Kc =3.0199.
In both cases of positive and negative perturbations β) at the switching-on and -off points, Aon and Aoff, respectively, the time delay formula τD ∼|β|−1/2 (inverse square root scaling law) essentially holds in the both cases of Caputo’s and Caputo-Fabrizio’s fractional derivatives (0 < α < 1), Figure 6, similar to the ordinary derivative case (α = 1) [14], but with different proportionality factor.

FIGURE 6. Time-delay, τD, versus the perturbation parameter β at the switching-on point Aon in Figure 1. Circles represent the numerical results and the dashed lines represent the corresponding fittings,
The steady state bistable curves for the Oxygen and uric acid concentrations u, v, respectively, against the supplied rate a, according to Eq. 2 or 4) are shown in Figure 7, for fixed values of other system parameters [14]. For positive perturbation β in the ordinary derivative case (α = 1) at the switching-on point, Aon in Figure 7, the transient oxygen concentration u(τ), Figure 8, shows similar qualitative behaviour of reducing τD in both cases of Caputo’s and Caputo-Fabrizio’s fractional derivatives, but with smaller quantitive difference. The same behaviour occurs with negative perturbation at the switching-off point Aoff in Figure 7. Similar qualitative behaviour is also exhibited for the transient uric acid concentration v(t) for α = 1 [14] and α < 1. The time delay τD in both cases of u(τ) and v(τ) against the fractional parameter α and the perturbation parameter β shows similar qualitative behaviour as in Figures 3, 6, respectively.
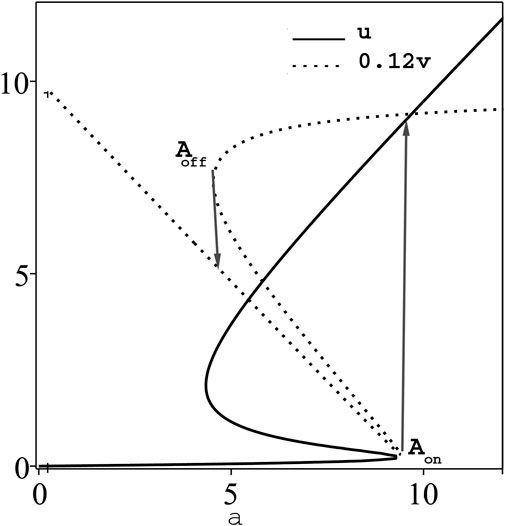
FIGURE 7. The steady state bistable curves, u and 0.12v, versus the control parameter, a, for fixed parameters K =20, B =100, γ = l =1.
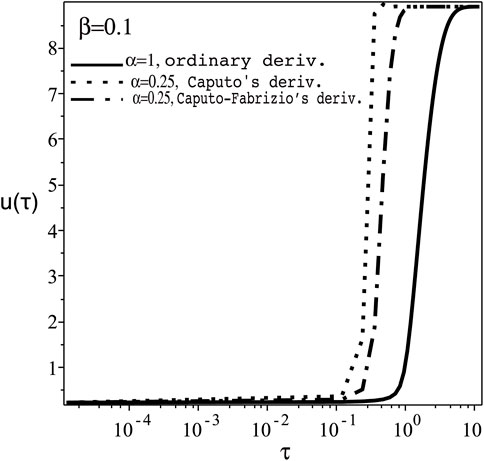
FIGURE 8. The transient Oxygen concentration, u(τ), versus the normalised time, τ with positive perturbation, κ = ac + β, ac =9.3643, at the switching-on point Aon of Figure 7 with fixed β =0.1 for α =1 (ordinary derivative) and 0.25 (Caputo’s and Caputo-Fabrizio’s fractional derivatives).
Fractional order mathematical models generalise the concept of ordinary differentiation to incorporate memory (time delay) and spatial non-local effects, and hence provide extra fractional parameters to interpret/predict the dynamical behaviour of the concerned model and capture more of its details.In this paper, we have investigated the switching time response at the critical switching-on and -off points of the bistable curves related to two biological models, namely, the spruce budworm outbreak model [3, 4, 15] and the Thomas reaction model for enzyme membrane [4, 16] within fractional order models. Two definitions of fractional derivatives of order α, (0 < α < 1) have been used, namely, Caputo’s [40] and Caputo-Fabrizio’s [21, 22] fractional derivatives. Our study shows the following.
(i) The two definitions use convolution kernels of different variability that model the memory effect, namely, as power function [40] and as exponential function [21]. Both definitions yield the same qualitative results, (ii)-(iv) below, for the two biological models referred to above. The small quantitative variance in the results is due to the different mathematical forms for the memory or delay effect.
(ii) The switching time τD due to the perturbation in the control (input) parameter, at the critical points of the bistable curves, is reduced further in the fractional derivative case (0 < α < 1), compared with the ordinary derivative case (α = 1) [14],
(iii) For fixed perturbation β, τD as a function of the fractional derivative parameter, α, (0 < α < 1) fits an exponential form, i.e., τD is reduced with strong memory index (α ≪ 1) and,
(iv) The switching time τD as a function of the perturbation parameter β fits the scaled inverse square root law
In general, fractional order models provide deeper insight into the system dynamics with memory taken, into effect and further motivate for experimental observation.Finally, we refer to some very recent works [43, 44] on biological models of COVID-19. In [43], the authors investigated various parameter estimation methods of COVID-19 incubation period using lognormal and Gamma distribution assumptions. The expressions for the maximum likelihood estimation, expectation maximisation algorithm and newly proposed algorithm [43] are termed as double or single (Riemann) integrals: these integral expressions can be converted to fractional integrals (i.e usual Riemann integral with memory or non-local, convolution kernel of fractional index, e.g. [23]), and so to have extra fractional order parameter. The other biological model of COVID-19 [44] is concerned with the stability and sensitivity analysis, and optimal control strategies of a suggested epidemic control of COVID-19. The adopted model of ODEs can be converted to FDEs and so to investigate the memory effect in this epidemic model. The formulation of the models in [43, 44] within fractional calculus will certainly add details concerning memory/non-local effects.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
RA: Conceptualization, Methodology, Software SH: Data curation, Writing- Original draft preparation. RA: Visualization, Investigation. SH: Supervision: RA: Software, Validation: SH: Writing- Reviewing and Editing. All authors contributed to the article and approved the submitted version.
The authors received the fund by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah under grant No. (G-184-247-1443).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1123370/full#supplementary-material
1. Gibbs HM. Optical bistability: Controling light with light. In: Quantum electronics-principles and applications. Massachusetts, United States: Academic Press (1985).
2. Mandel P, Erneux T. Nonlinear control in optical bistability. IEEE J Quan Electron (1985) 21:1352–5. doi:10.1109/jqe.1985.1072832
3. May RM. Thresholds and break points in ecosystems with a multiplicity of stable states. Nature (1977) 289:471–7. doi:10.1038/269471a0
5. Cribier S, Giacobino E, Grynberg G. Quantitative investigation of critical slowing down in all-optical bistability. Opt Commun (1983) 47:170–2. doi:10.1016/0030-4018(83)90109-8
6. Garmire E, Marburger JH, Allen SD, Winful HG. Transient response of hybrid bistable optical devices. Appl. Phys Lett (1979) 34:374–6.
7. Shu Q, Rand SC. Critical slowing down and dispersion of avalanche upconversion dynamics. Phys Rev B (1997) 55:8776–83. doi:10.1103/physrevb.55.8776
8. Boettner C, Boers N. Critical slowing down in dynamical systems driven by nonstationary correlated noise. Phys Rev Res (2022) 4:013230–7. doi:10.1103/physrevresearch.4.013230
9. Wolchover N. Nature’s critical warning system (2015). Available at https://www.quantamagazine.org/20151117-natures-critical-warning-system/ Accessed 2015.
10. Carpenter SR, Brock WA. Rising variance: A leading indicator of ecological transition. Ecol Lett (2006) 9:311–8. doi:10.1111/j.1461-0248.2005.00877.x
11. Dakos V, Scheffer M, van Nes EH, Brovkin V, Petoukhov V, Held H. Slowing down as an early warning signal for abrupt climate change. Proc Natl Acad Sci (2008) 105:14308–12. doi:10.1073/pnas.0802430105
12. Ditlevsen PD, Johnsen SJ. Tipping points: Early warning and wishful thinking. Geophys Res Lett (2010) 37:L19703. doi:10.1029/2010gl044486
13. Chisholm RA, Filotas E. Critical slowing down as an indicator of transitions in two-species models. J Theor Biol (2009) 257:142–9. doi:10.1016/j.jtbi.2008.11.008
14. Alharbey RA, Nejad LAM, Lynch S, Hassan SS. Critical slowing down in biological bistable models. Int J. Pure Appl. Math. (2014) 93:581–602. doi:10.12732/ijpam.v93i4.8
15. Ludwig D, Jones DD, Holling CS. Qualitative analysis of insect outbreak systems: The spruce budworm and forest. J Anim Ecol (1978) 47:315–32. doi:10.2307/3939
16. Thomas D. Artificial enzyme membranes, transport, memory and oscillation. In: D Thomas, and JP Kernevez, editors. Analysis and control of immobilized enzyme systems. Berlin Heidelberg New York: Springer (1975). p. pp115–150.
17. Machado JAT, Kiryakova V, Mainardi F. Recent history of fractional calculus. Commun. Nonlinear Sci Numer Simulat (2011) 16:1140–53.
18. Du M, Wong Z, Hu H. Measuring memory with the order of fractional derivative. Scientific Rep (2013) 3:3431–3. doi:10.1038/srep03431
19.De Oliveira, Edmundo CapelasJos Antnio Tenreiro Machado. A review of definitions for fractional derivatives and integral. Math Probl Eng (2014) 2014:1–6. doi:10.1155/2014/238459
20. Teodoro GS, Machado JT, De Oliveira EC. A review of definitions of fractional derivatives and other operators. J Comput Phys (2019) 388:195–208. doi:10.1016/j.jcp.2019.03.008
21. Caputo M, Fabrizio’s M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl (2015) 2:73–85.
22. Caputo M, Fabrizio M. Applications of new time and spatial fractional derivatives with exponential kernels. Progr Fract Differ Appl (2016) 2:1–11. doi:10.18576/pfda/020101
23. Podlubny I. Fractional differential euqations. Massachusetts, United States: Academic Press (1999).
24. Caputo M, Mainardi F. A new dissipation model based on memory mechanism. Pure Appl Geophys (1971) 91:134–47. doi:10.1007/bf00879562
25. Anastasio TJ. The fractional-order dynamics of brainstem vestibulo-oculomotor neurons. Biol Cybernet (1994) 72:69–79. doi:10.1007/bf00206239
27. Sweilam NH, Khader MM, Mahdy AMS. Computational methods for fractional differential equations generated by optimization problem. J Fractional Calculus Appl (2012) 3:1–12.
28. Tong P, Feng Y, Lv H. Euler’s method for fractional differential equations. WSEAS Transaction Maths (2013) 12:1146–53.
29. Meral FC, Royston TJ, Magin R. Fractional calculus in viscoelasticity: An experimental study. Commun Nonlinear Sci Numer Simulation (2010) 15:939–45. doi:10.1016/j.cnsns.2009.05.004
30. Xu Z, Chen W. A fractional-order model on new experiments of linear viscoelastic Creep of hami melon. Comput Maths Appl (2013) 66:677–81. doi:10.1016/j.camwa.2013.01.033
31. Scheidegger AE, Johnson EF. The statistical behavior of instabilities in displacement processes in porous media. Can J Phys (1961) 39:326–34. doi:10.1139/p61-031
32. Verma AP. Statistical behavior of fingering in a displacement process in heterogeneous porous medium with capillary pressure. Can J Phys (1969) 47:319–24. doi:10.1139/p69-042
33. Bhathawala PH, Parveen S. Analytic study of three phase flow through porous media. J Indian Acad Math (2001) 23:17–24.
34. Prajapati JC, Patel AD, Pathak KN, Shukla AK. Fractional calculus approach in the study of instability phenomenon in fluid dynamics. Palestine J Maths (2012) 2:95–105.
35. West BJ, Turalska M. The fractional Landau model. IEEE/CAA J Automatica Sinica. (2016) 3:257–60.
36. Joshi H, Jha BK. Fractional-order mathematical model for calcium distribution in nerve cells. Comput Appl Maths (2020) 39:56–22. doi:10.1007/s40314-020-1082-3
37. Comlekoglu T, Weinberg SH. Memory in a fractional-order cardiomyocyte model alters voltage-and calcium-mediated instabilities. Commun Nonlinear Sci Numer Simulation (2020) 89:105340. doi:10.1016/j.cnsns.2020.105340
38. Ionescu C, Lopes A, Copot D, Machado JT, Bates JH. The role of fractional calculus in modeling biological phenomena: A review. Commun Nonlinear Sci Numer Simulation (2017) 51:141–59. doi:10.1016/j.cnsns.2017.04.001
40. Caputo M. Linear models of dissipation whose Q is almost frequency independent, Part II. J Roy Astr Soc (1967) 13:529–39.
41. Alistair Steyn-Ross D, Steyn-Ross M. Modeling phase transition in the brain, Springer series in computational neuroscience, Springer, NewYork, NY, 2010.
42. Al-Attar HA, MacKenzie HA, Firth WJ. Critical slowing-down phenomena in an InSb optically bistable etalon. JOSA B (1986) 3:1157–63. doi:10.1364/josab.3.001157
43. Yin MZ, Zhu QW, L X. Parameter estimation of the incubation period of COVID-19 based on the doubly interval-censored data model. Nonlinear Dyn (2021) 106:1347–58. doi:10.1007/s11071-021-06587-w
44. L X, Hui HW, Liu F, Bai YL. Stability and optimal control strategies for a novel epidemic model of COVID-19. Nonlinear Dyn (2021) 106:1491–507. doi:10.1007/s11071-021-06524-x
45. Fowler AC. Mathematical models in the applied sciences. Cambridge, United Kingdom: Cambridge University Press (1997).
46. Barbotin JN, Thomas D. Electron microscopic and kinetic studies dealing with an artificial enzyme membrane. Application to a cytochemical model with the horseradish peroxidase-3,3’-diaminobenzidine system. J Histochem Cytochem (1974) 11:1048–59. doi:10.1177/22.11.1048
47. Chan YH, Boxer SG. Model membrane systems and their applications. Curr Opin Chem Biol (2007) 11:581–7. doi:10.1016/j.cbpa.2007.09.020
Keywords: critical slowing down, Caputo’s and Caputo-Fabrizio’s fractional derivatives, switching timedelay, bistable behaviour, mathematical models in biology
Citation: Alharbey RA and Hassan SS (2023) Fractional critical slowing down in some biological models. Front. Phys. 11:1123370. doi: 10.3389/fphy.2023.1123370
Received: 14 December 2022; Accepted: 23 January 2023;
Published: 07 March 2023.
Edited by:
Samir A. El-Tantawy, Port Said University, EgyptCopyright © 2023 Alharbey and Hassan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: R. A. Alharbey, cmFuaWEubWF0aEBnbWFpbC5jb20=
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.