Deep learning based registration for head motion correction in positron emission tomography as a strategy for improved image quantification

Objectives: Positron emission tomography (PET) is affected by various kinds of patient movement during a scan. Frame-by-frame image registration is one of the most practiced motion correction techniques. In recent years, deep learning has shown a remarkable ability to quickly and accurately register images once trained. This paper studies the feasibility of using a deep learning framework to correct 3D positron emission tomography image volumes for head motion in routine positron emission tomography imaging to improve quantification in motion impacted data.

Materials and Methods: A neural network was trained with 3D positron emission tomography image volumes in an unsupervised manner to predict transformation parameters required to perform image registration. A multi-step convolutional neural network (CNN) was combined with a spatial transform layer. Pairs of target and source images were used as input to the network. To prepare the training dataset, a previously published TOF-PEPT algorithm was applied to automatically detect static frames where the patient remained in a relatively steady position and transitional frames where they underwent abrupt motion. A single image volume was reconstructed for each static frame. The image reconstructed from the first static frame served as the target image with images from subsequent static frames being used as source images. The trained neural network predicted transformation parameters that could be used to perform frame-by-frame image-based motion correction but also enabled raw listmode positron emission tomography data correction where individual line-of-responses were repositioned. Line profiles and ROIs were drawn across the reconstructed image volumes to compare performance and quantitative results between standard registration tools and the deep learning technique. Corrected volumes were further compared to motion free images quantitatively using Dice indices.

Results: In total, one hundred 3D positron emission tomography image volumes were used to train the network. Cross-validation was carried out using a 4:1 ratio for the training and test data. A conventional algorithm for affine registration from the Advanced Normalization Tools (ANTs) software package served as a baseline. To evaluate the correction performance, the mean Dice index and standardized uptake value (SUV) were used. Application of the algorithm to clinical data showed good performance with respect to registration accuracy as well as processing time. The neural network yielded a mean Dice index of ∼0.87 which was similar to the advanced Normalization Tools algorithm and did so ∼3x faster using a multi-core CPU and ∼20x faster with a GPU. Standardized uptake value analysis showed that quantitative results were 30%–60% higher in the motion-corrected images, and the neural network performed better than or close to the advanced Normalization Tools.

Conclusion: The aim of this work was to study the quantitative impact of using a data-driven deep learning motion correction technique for positron emission tomography data and assess its performance. The results showed the technique is capable of producing high quality registrations that compensate for patient motion that occurs during a scan and improve quantitative accuracy.

1 Introduction

Positron emission tomography (PET) is a non-invasive nuclear medicine imaging procedure that uses radioactive tracers to visualize biochemical changes such as metabolism. Quantitative and qualitative assessment of PET data is affected by various kinds of patient movement such as respiratory and cardiac motion which are non-rigid and periodic by nature, head and whole-body motion which are rigid/affine and irregular by nature, etc. Patient movement leads to degraded image quality, e.g., in the form of blurring, which impacts diagnostic image analysis including but not limited to quantification of standardized uptake values (SUV) and measurement of lesion intensity, size, and location.

Use of external devices constitutes one of the most widely practiced approaches for motion correction. However, the use of such devices is limited by several constraints such as device cost and setup, necessary training, regular maintenance, and, most importantly, retroactive data correction. Attention has therefore shifted toward data-driven motion correction which typically either performs frame-by-frame image registration [1] or event-based correction [1–5]. In frame-based image registration, the listmode data is divided into a sequence of motion-free frames. Images are reconstructed for each frame of data, aligned with a reference frame, and then summed together to create the final image volume. In event-based correction, individual lines of response (LOR) in each frame are repositioned, thereby allowing a single image to be reconstructed from all the raw data. In most cases, registration is carried out by optimizing different similarity criteria in the image domain, e.g., mutual information [6–8], cross-correlation [6, 7, 9], the sum of absolute differences [9, 10], or standard deviation of the ratio of two image volumes [9, 10].

Several traditional methods exist that facilitate image registration [11–14]. These methods aim to numerically solve the optimization problem in an iterative manner over pairs of images. The computation can be very intensive, depending on the complexity of the task. More recently, deep learning has received significant attention as it allows a neural network to learn the underlying patterns of the registration task thereby replacing the costly optimization computation with an inexpensive forward pass of the trained network.

To date, many different deep learning approaches have been proposed, e.g., Convolutional Neural Network (CNN) [15–20], Generative Adversarial Network (GAN) [21–23], and reinforcement learning [24–26]. The neural network can be trained in a supervised or unsupervised way. Supervised learning relies on ground truth transformation parameters [20, 24–28]. In such cases, the network is either trained with simulated images with known ground truth information, or the ground truth information is extracted by applying other methods for the training dataset. In routine clinical applications, it is very difficult to acquire accurate ground truth information which makes supervised learning of a neural network a challenging task. Thus, for medical image applications, unsupervised and self-supervised learning is desired [29].

In 2015, Jaderberg et al. [30] introduced their Spatial Transform Network (STN), which allowed unsupervised image registration. STN consisted of three modules, namely, a neural network, a grid generator, and a sampler. Firstly, the neural network was used to learn features from input images and estimate a mapping between them, the grid generator was then used to compute the sampling grid based on the derived transformation parameters, and the sampler finally generated a warped/moved image by carrying out the sampling operation using interpolation. The loss between the warped and target image thus could be used to train the neural network in an end-to-end unsupervised manner. Later, other papers explored similar approaches with different neural networks, such as the use of a Fully Convolutional Network (FCN) by Li et al. [19], de Vos et al. [15] and the use of a U-net-like architecture by Balakrishnan et al. [17] Research on the application of the deep learning approach has continued to enhance the registration performance using a number of different approaches including but not limited to multi-step recurrent network [31], cascaded network [16, 32], multi-scale estimation [18, 33, 34], diffeomorphic registration [35, 36], reducing negative Jacobian determinant [37], and encouraging invertibility [31, 32].

Most of the above-mentioned papers focused on CT and/or MRI image registration. Neural network-based PET image registration, on the other hand, has only been addressed in a limited scope [38–40]. This paper studies deep learning based motion correction for PET with the aim of achieving computational efficiency compared to the conventional iterative approach ensuring the consistency of performance. The multi-step recurrent network by Shen et al. [31] formed the basis for the work as it has demonstrated superior performance, particularly for affine registration. We introduced a few modifications as described below. The paper will mainly focus on rigid head motion correction of brain PET data using the more general affine model. The following sections provide a detailed overview of the approach.

2 Materials and methods

2.1 Overview of the image registration approach

The task of image registration can be considered as warping a source image $I_{src}$ to a target image $I_{tgt}$ defined in the spatial domain $\mathrm{\Omega }\in R^{h\times w\times d}$. The objective is to find a mapping function $f:I_{src}\to I_{tgt}$. Letting $I_{wrpd}$ and $\mathrm{\Phi }$ denote the warped image and the transformation parameters, respectively, the warping operation can be expressed as:

$I_{wrpd}=f\left(I_{src},\mathrm{\Phi }\right)(1)$

The neural network parameters θ are then optimized in a way that minimizes the dissimilarities between the warped image and fixed images. The network learns by optimizing the image dissimilarity metric denoted by $S$ as follows. That is:

${\theta }^{*}={\mathit{argmin}}_{\theta }S\left(I_{wrpd},I_{tgt}\right)(2)$

Ultimately, the network is trained to predict the transformation parameters which for a 3D affine registration include transform matrix $A\in R^{3x3}$ and translation vector $t\in R^{3\times 1}$.

2.2 Network architecture

We adopted a multi-step recurrent approach that includes a CNN [31] and a spatial transform layer [30] to train the network in an unsupervised manner. Pairs of source and target images were fed as input to the network and the network made predictions of transformation parameters, which were then passed along with the source image to the spatial transform layer. The grid generator of the spatial transform layer created a sampling grid to warp the moving source image according to the transformation parameters predicted by the network. The sampler then performed linear interpolation to sample and provide the warped image.

With reference to Figure 1, prediction and correction took place in a recurrent manner by repeatedly feeding the warped image back to the same CNN as a new source image which was then registered with the target image. The process is repeated for $k$ number of steps. For the results reported here, we used $k=3$ and an analysis is presented in Section 3.2 as a support of this choice. The composition of the parameters obtained at each step was used as the final transformation parameters. Letting $A_1$, $A_2$, and $A_3$ denote the affine transform matrices and $t_1$, $t_2$, and $t_3$ the translation vectors, the final solution can be expressed as:

$A^{\prime }=A_3{A}_2{A}_1(3)$

$t^{\prime }=A_3{A}_2{t}_1+A_3{t}_2+t_3$

FIGURE 1

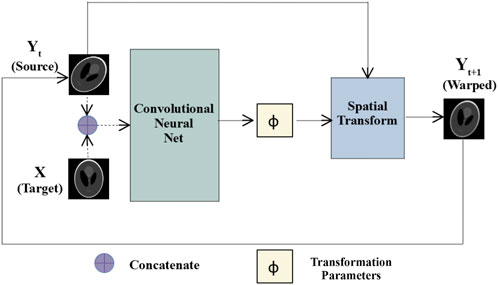
FIGURE 1. Multi-step affine registration network: Initially, source and target images are concatenated and passed as input to a convolutional neural network. The network predicts transformation parameters that are passed along with the source images to a spatial transform layer. The layer generates warped images, which at the next step are passed as the source images to the same network, and the process repeats for $k$ number of steps.

Figure 2 shows the CNN architecture, which was inspired by work by Zhao et al. [32] and consisted of a series of convolutional and pooling layers. Except for the final layer, the convolution operations were performed using kernel size 3, stride 1, and a ReLU [41] activation function. At the final layer, two convolution operations were performed to predict the transform matrix and translation vector using kernel size 3 and linear activation functions. In selected layers after convolution, average pooling with kernel size 2 was performed. Section 3.2 speaks to the choice of the network architecture.

FIGURE 2

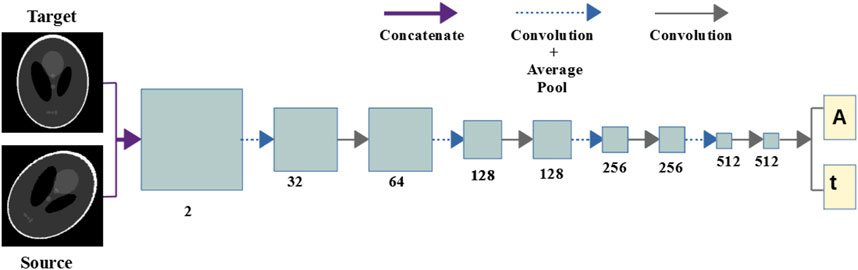
FIGURE 2. Convolutional neural network: The network consists of a series of convolutional and pooling layers after selected convolution operations. Two convolution operations are carried out at the final layer to output the transform matrix and the translational parameters.

2.3 Loss functions

Image dissimilarity loss was modeled by the negative normalized cross-correlation [42] given by:

$L_{img}=-\frac{{\displaystyle \sum }_{i\in \mathrm{\Omega }}\left(I_{wrpd}^i-\underset{\_}{I_{wrpd}}\right)\left(I_{tgt}^i-\underset{\_}{I_{tgt}}\right)}{\sqrt{{\displaystyle \sum }_{i\in \mathrm{\Omega }}{\left(I_{wrpd}^i-\underset{\_}{I_{wrpd}}\right)}^2\sqrt{{\displaystyle \sum }_{i\in \mathrm{\Omega }}{\left(I_{tgt}^i-\underset{\_}{I_{tgt}}\right)}^2}}}(4)$

where $\underset{\_}{I_{wrpd}}$ and $\underset{\_}{I_{tgt}}$ denote the mean of the warped image and the target image, respectively.

To prevent the transform parameters from overshooting, the following regularizing loss function was used [1]:

$L_{reg}={\left|\left|A-I\right|\right|}_F^2+{\left|\left|t\right|\right|}_2^2(5)$

where subscript $F$ denotes the Frobenius norm and I is the identity matrix.

These loss functions were combined to form a total loss:

$L_{total}={{\lambda }_{img}L}_{img}+{\lambda }_{reg}{L}_{reg}(6)$

where ${\lambda }_{img}$ and ${\lambda }_{reg}$ denote image dissimilarity loss and regularization weighting factors set to 1 and 0.01, respectively, with the values determined empirically. Future work will explore this aspect in-depth.

2.4 Data preparation and training details

To prepare the dataset, the PET listmode data was sorted into motion-free static frames using the previously published TOF-PEPT algorithm [43–46]. An image was reconstructed for each frame using the OSEM algorithm available on the 64-slice Biograph mCT Flow PET/CT scanner. We used our institution’s standard clinical protocol that calls for $3$ iterations, $24$ subsets and $5\times 5$ Gaussian post-smoothing. The Siemens e7 processing tools (Siemens Healthineers, Knoxville) were used for all data processing and reconstruction. The image volume reconstructed from the first static frame was used as the reference/target image while image volumes reconstructed from subsequent static frames were used as source images.

Five patient studies were conducted in compliance with an Institutional Review Board approved protocol (IRB #3941) using full 64-bit listmode data acquisition. During a 3-min scan, patients rested their heads in random positions and orientations at random time points. Each study thus exhibited a different range of movements and therefore yielded different numbers of static frames.

In order to expand the limited amount of data available to form an adequately large dataset for training the neural network, image volumes were further synthesized from the five patient studies. In total, one hundred 3D PET image volumes were simulated by applying random transformations to the LOR data. Each transformed raw listmode dataset was then histogrammed and sent to the reconstruction algorithm as previously mentioned to create image volumes. To reduce the computational cost associated with the neural network training, images were resized from $400\times 400\times 109$ to $128\times 128\times 96$ by cropping background with zero-valued voxels and rescaling the result. Cross-validation was used with a 4:1 ratio for the training and test data. Training spanned 100 epochs with 20 steps per epoch and using a batch size of 4. The learning rate was fixed at 1e-4. The network was trained using a computer equipped with a 32-core Intel Xeon E5-2670 CPU and a Tesla V100S GPU.

2.5 Validation and evaluation

Pairs of source and target image volumes were passed to the trained neural network. The network outputted the transformation parameters along with a warped image from the spatial transform layer. An overall motion-corrected image was then produced by registering the source image from each motion-free static frame for the whole scan duration and summing them together. Additionally, the transformation parameters predicted by the trained neural network were applied to the raw listmode data. The LORs within each static frame were all aligned to the reference frame using the predicted transformation parameters. The transformed listmode data was then histogrammed and reconstructed using the Siemens e7 processing tools (Siemens Healthineers, Knoxville).

To evaluate the neural network’s image registration capabilities quantitatively, the Dice index was used to measure the similarity between warped and target images:

$Dice\left(A,B\right)=\frac{2\left|A\cap B\right|}{\left|A\right|+\left|B\right|}(6)$

A higher value of the index indicates better performance. The processing time needed for a trained network to perform the registration was used to evaluate the computational efficiency. Lastly, in order to evaluate the motion correction from a clinical perspective, the standardized uptake value (SUV) was studied. The conventional iterative registration algorithm (typeofTransform = “Affine”) from the Advanced Normalization Tools (ANTs) software package [11] was used as a baseline against which the performance of the neural network could be compared.

Quantitative analysis of the image data were performed using comparison of line profiles across the brain from each of the image volumes created using a commercial analysis software (Inveon Research Workplace, Siemens Healthineers, Knoxville, TN). Data were loaded into the software, geometric alignment verified, and linear regions of interest were drawn across the brain with line profiles plotted along the direction of the line width. This enabled comparison of SUVs along the profile but to also gave a measure of signal-to-background variance across regions of high and minimal uptake across the region. Peak-to-valley ratios were calculated to provide an estimation of signal-to-noise ratio to more quantitatively illustrate whether the corrected data improved upon the uncorrected images.

3 Results

3.1 Qualitative and quantitative evaluation of the performance of neural network

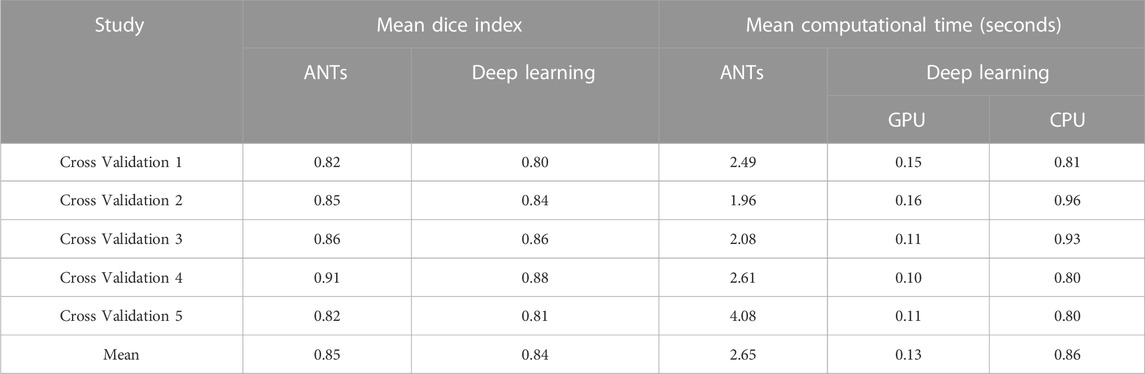
Table 1 compares the neural network performance in individual image registration in terms of mean Dice index and computational time against the ANTs algorithm for the synthesized dataset. The neural network performed close to the conventional iterative algorithm but did so ∼3x and ∼20x faster, respectively, using the multi-core CPU and the GPU.

TABLE 1

TABLE 1. Comparison of performance in image registration.

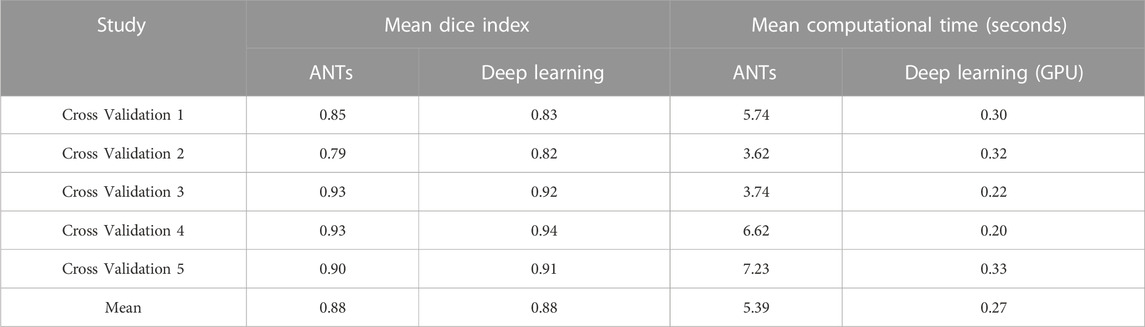
The ability to generate motion-corrected images was also studied. Figures 3, 4 show motion-free static frames for two patient studies. The trained network was used to register “Frame 2” and “Frame 3” to reference frame “Frame 1.” The three frames were then summed to create a motion-corrected image. For comparison, motion-corrected images were created using the ANTs algorithm as well. Figures 5, 6 show axial, coronal, and sagittal slices of the original uncorrected image and motion-corrected images using the neural network and ANTs software. The qualitative improvement in the motion-corrected images is readily apparent with the neural network and ANTs showing comparable performance. Table 2 compares the neural network performance in producing overall motion-corrected image volumes by means of mean Dice index and computational time. Both qualitative and quantitative reviews show that the deep learning and conventional iterative approaches performed similarly; however, the former provided final results ∼20 times faster with the use of a GPU.

FIGURE 3

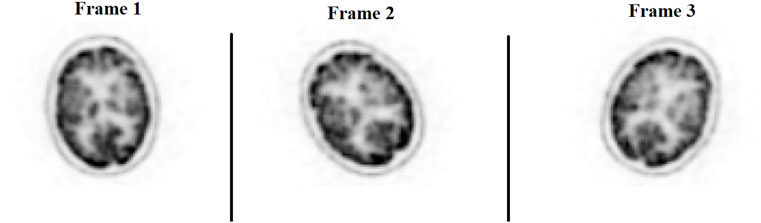
FIGURE 3. Patient Study 1: Illustration of the three motion-free static frames where the patient placed their head in three different positions. A slice of the 3D PET image volume in the axial plane is shown in the figure.

FIGURE 4

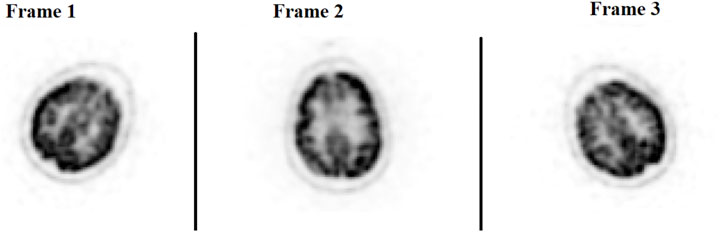
FIGURE 4. Patient Study 2: Illustration of the three motion-free static frames where the patient placed their head in three different positions. A slice of the 3D PET image volume in the axial plane is shown in the figure.

FIGURE 5

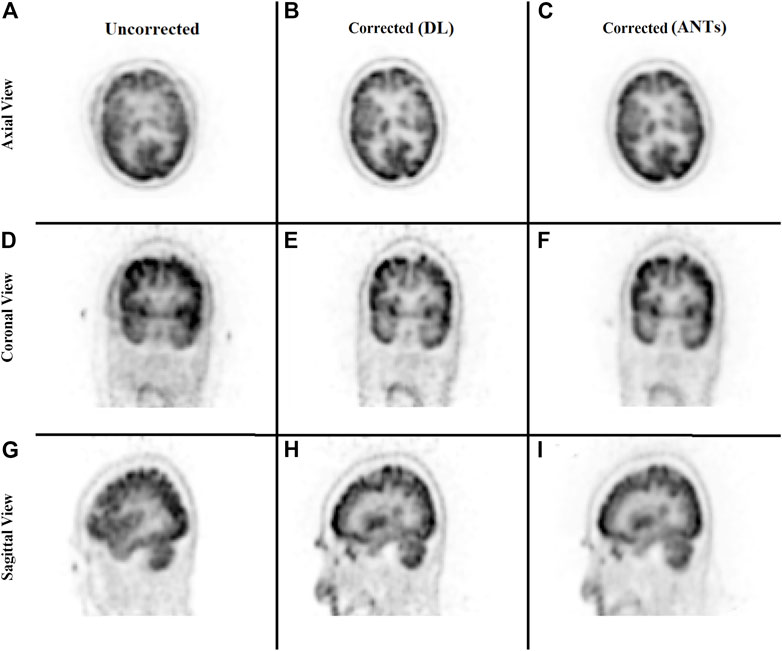
FIGURE 5. Qualitative comparison of the neural network performance in motion correction by means of frame-by-frame image registration. Rows from top to bottom show the sum of the three frames without any correction (A, D, G), correction using the deep learning approach (B, E, H), and the ANTs iterative algorithm (C, F, I), respectively, in the axial, coronal, and sagittal view.

FIGURE 6

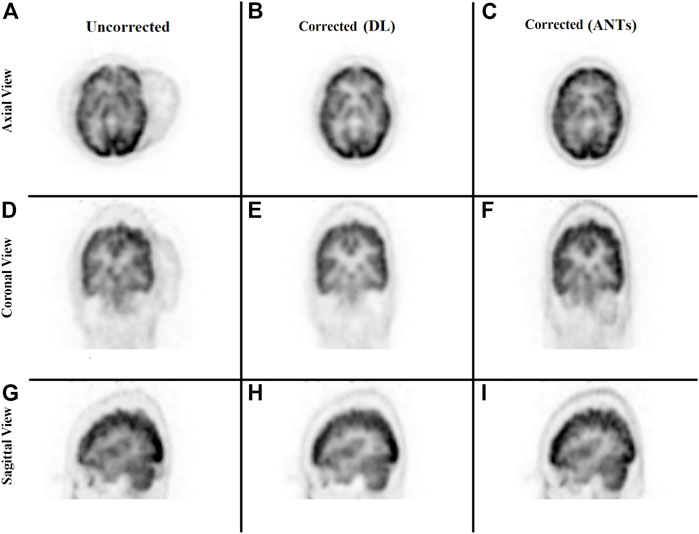
FIGURE 6. Qualitative comparison of the neural network performance in motion correction by means of frame-by-frame image registration. Rows from top to bottom show the sum of the three frames without any correction (A, D, G), correction using the deep learning approach (B, E, H), and the ANTs iterative algorithm (C, F, I), respectively, in the axial, coronal, and sagittal view.

TABLE 2

TABLE 2. Comparison of performance in producing motion corrected images.

Quantitative assessments showed good SUV agreement across the methods. As illustrated by Figures 7, 8, the peak-to-valley ratios of SUVs were 30%–60% higher in the motion-corrected images, with the neural network performing better or similar to ANTs. Good peak-to-valley improvement helps confirm that the correction method is appropriately aligning the data so that regions of uptake are not motion-blurred into areas of lower uptake.

FIGURE 7

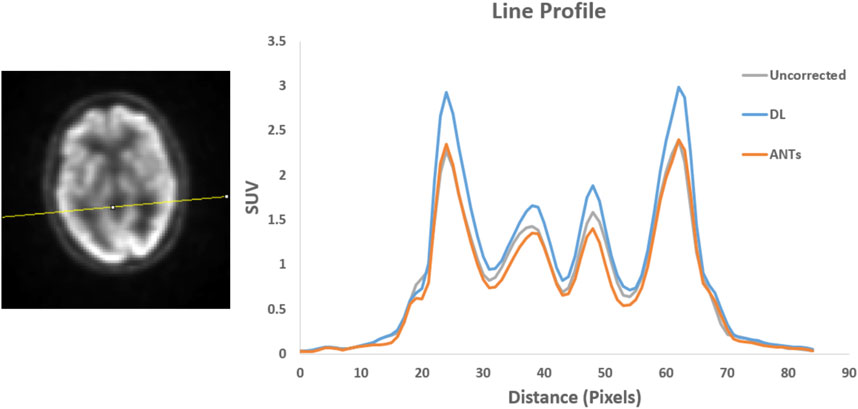
FIGURE 7. Patient Study 1: A region in the brain area (left) where a line profile (right) was manually drawn. The peak-to-valley ratio for the motion-corrected data with the deep learning (DL) approach is shown to be higher than the ANTs method.

FIGURE 8

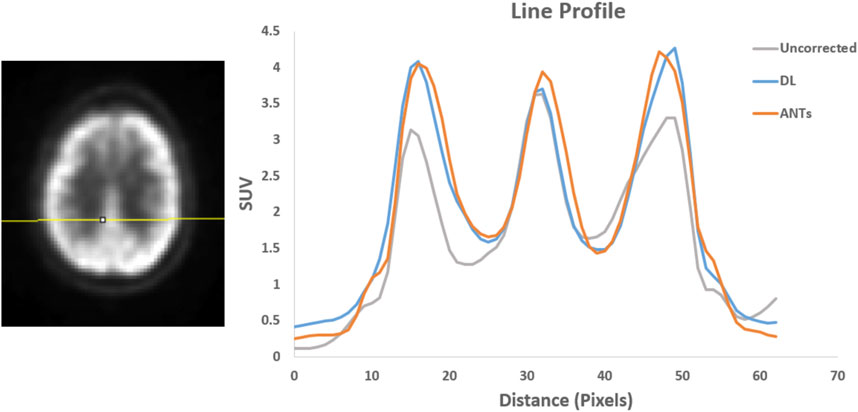
FIGURE 8. Patient Study 2: A region in the brain area (left) where a line profile (right) was manually drawn. The peak-to-valley ratio for the motion-corrected data with the deep learning (DL) approach is close to the ANTs method.

Lastly, a study was conducted to evaluate the correction of the original raw listmode data by repositioning the LORs with the transformation parameters estimated by the trained neural network. Figure 9 provides a qualitative comparison of the uncorrected and motion-corrected image volumes reconstructed from the repositioned listmode data. Motion-corrected image volume achieved sharper details compared to the uncorrected data.

FIGURE 9

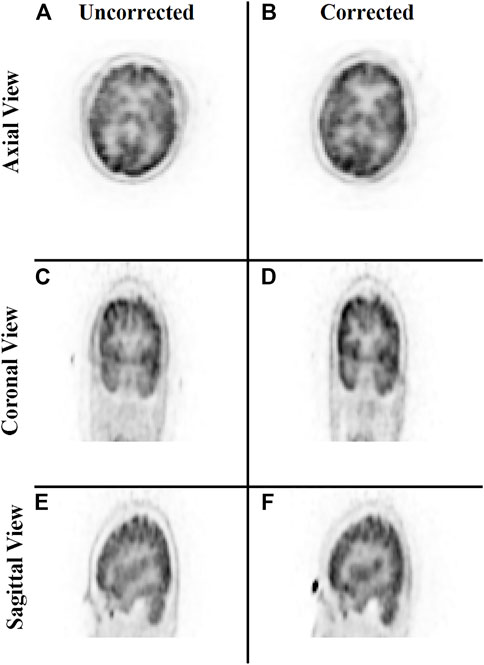
FIGURE 9. Qualitative comparison of the neural network performance in motion correction by remapping raw listmode data. Rows from top to bottom show the sum of the three frames without any correction (A,C,E) and correction using the deep learning approach (B,D,F), respectively, in the axial, coronal, and sagittal view.

3.2 Analysis of the choice of network architecture

The choice of the network and the step size of the multi-step architecture (defined in Section 2.2) were analyzed by means of two studies. Figure 10 shows the training loss versus epoch with varying step sizes: 1, 2, 3, and 4. We observed that the network learned faster with increasing step size but saturated at step size 4. Thus, a step size of 3 was chosen for network training.

FIGURE 10

FIGURE 10. The plot of training loss versus epoch demonstrates the neural network performance with changing step sizes from 1 to 4. The network learned faster with increasing step size but saturated at step size 4 for the dataset used.

The network performance in image registration was studied by means of Dice scores for four different architectures: 5 convolution stages with 32, 64, 128, 256, and 512 features; 5 convolution stages with 16, 32, 64, 128, and 256 features; 4 convolution stages with 32, 64, 128, and 256 features; and 4 convolution stages with 16, 32, 64, and 128 features. Figure 11 shows the results. The configuration with 5 convolution stages led to better learning, possibly due to having deeper layers with more abstraction. The network, on the other hand, performed better when more features were used.

FIGURE 11

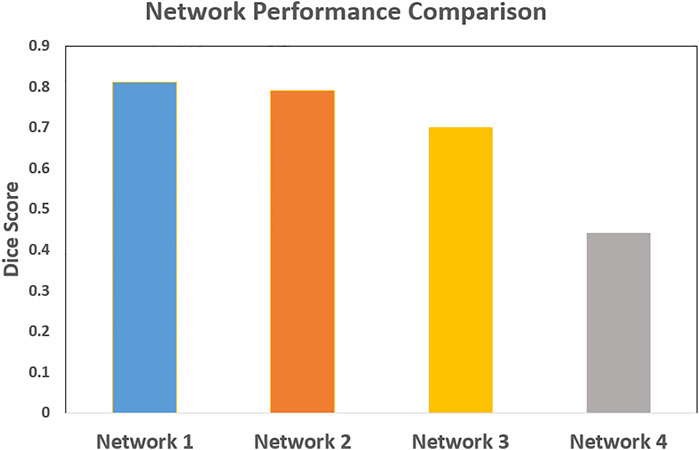
FIGURE 11. The comparison of the neural network performance for four different network architectures by means of Dice score. Network 1: 5 levels of convolution with 32, 64, 128, 256, and 512 features; Network 2: 5 levels of convolution with 16, 32, 64, 128, and 256 features; Network 3: 4 levels of convolution with 32, 64, 128, and 256 features; and Network 4: 4 levels of convolution with 16, 32, 64, and 128 features. The network performed better with 5 levels of convolution, and a higher number of features.

4 Discussion

This paper focused on studying and presenting the application of deep learning for data-driven PET motion correction.

The deep learning approach for image registration has demonstrated promising performance over the years. Here, a modified version of a multi-step recurrent deep learning approach was adopted to train a neural network for affine registration. The network was trained on a synthesized dataset to predict required transformation parameters in an unsupervised manner using a spatial transform layer that provided warped images to supervise the training.

To prepare the training data, multiple motion-free static frames were identified from the whole scan duration using the previously published motion detection algorithm TOF-PEPT. Images reconstructed from these static frames were used as input to train the network along with a target image reconstructed from a reference frame. The final goal was to perform motion correction by means of frame-by-frame registration with the trained network. The registered image frames were summed together to create the final motion-corrected image. To evaluate against a baseline, the frame-by-frame registration was implemented with the ANTs algorithm as well. Mean Dice indices and manually drawn line profiles across brain regions were used to compare the motion-corrected images from the two methodologies against the uncorrected data. With respect to the iterative algorithm, the neural network yielded comparable and reliable performance both from qualitative and quantitative perspectives with significant improvements in speed. The neural network performed ∼3x faster when using a multi-core CPU and ∼20x faster with a GPU.

Additionally, the correction of the raw listmode data itself was studied by repositioning the LORs within each static frame according to the transformation parameter predictions by the neural network. A final motion-corrected image volume was created by sending the remapped listmode data to the image reconstruction tools. With this approach, a reasonable correction could be achieved as presented in this paper. Further improvement in mapping from the image domain to actual scanner geometry and more precise transformation prediction will make it possible to produce more clinically suitable motion-corrected data.

Our group works heavily with radiation oncology supporting various advanced therapy workflows using PET/CT, where multimodal registration can certainly result in mismatches [47]. Although this work focused on our single modality head registration results that typically might only need rigid models, the full intent was to have a generalizable process that can support multimodal PET/CT registration. Ireland, et. Al. presented a study that specifically focused on multimodal head and neck registration showing improvements when using a non-rigid model [48]. Since geometric mismatches between the modalities can occur due to voxel variations, etc. We decided to test the robustness of the deep learning technique using an affine model. This also enabled some level of testing for this specific set of cases as we expected mostly rigid transformation within the same modality and our registration scaling factors were in fact unity indicating confirmation of a rigid transformation.

Lastly, the paper presented two studies that supported and evaluated the choice of network architecture. The first study analyzed the choice of step size, whereas the second study was evaluated four different network architectures with respect to their performance in image registration. The network choice with deeper layers and a higher number of features was found to perform better.

This work aimed to study the feasibility of applying deep learning to correction of affine/rigid motion during routine clinical brain PET imaging. Notwithstanding using a limited amount of real data augmented by synthesized data, results showed promising performance with a reduced computational cost once the neural network has been trained. Limitations of neural network methods such as the one studied here include the general need for large amounts of data and computational resources for training. Future work will aim to further enhance the network performance, study use of a larger amount of real data, and extend application to non-rigid cases, such as respiratory motion correction.

5 Conclusion

This paper explored an unsupervised deep learning approach for PET motion correction by means of 3D image registration. The feasibility of the proposed deep learning approach in the application of motion correction was studied by means of both frame-by-frame image registration and remapping of raw listmode data. Both approaches yielded reasonable corrections. The network performance was compared both qualitatively and quantitatively against a conventional iterative algorithm from the Advanced Normalization Tools (ANTs) software package. The deep learning approach performed on par with the iterative approach, but ∼3x faster when using a multi-core CPU and ∼20x with a GPU. This work is expected to aid to address the application of a deep learning approach for routine PET motion correction.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by University of Tennessee Graduate School of Medicine Institutional Review Board. The patients/participants provided their written informed consent to participate in this study.

Author contributions

TT: Graduate student, manuscript writing, data processing, analysis, code development JG: Student advisor, manuscript writing and revision, mentoring and code development SA: Patient recruitment, data management, clinical acquisition of data DO: Principle investigator, mentor, manuscript writing and revision, code/model development, clinical data acquisition, and recruiting.

Funding

This work is supported by the University of Tennessee Graduate School of Medicine, Knoxville.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Montgomery AJ, Thielemans K, Mehta MA, Turkheimer F, Mustafovic S, Grasby PM. Correction of head movement on PET studies: Comparison of methods. J Nucl Med (2006) 47:1936–44.

PubMed Abstract | Google Scholar

2. Jin X, Mulnix T, Gallezot JD, Carson RE. Evaluation of motion correction methods in human brain PET imaging-A simulation study based on human motion data. Med Phys (2013) 40:102503. doi:10.1118/1.4819820

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bloomfield PM, Spinks TJ, Reed J, Schnorr L, Westrip AM, Livieratos L, et al. The design and implementation of a motion correction scheme for neurological PET. Phys Med Biol (2003) 48:959–78. doi:10.1088/0031-9155/48/8/301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Menke M, Atkins MS, Buckley KR. Compensation methods for head motion detected during PET imaging. IEEE Trans Nucl Sci (1996) 43:310–7. doi:10.1109/23.485971

CrossRef Full Text | Google Scholar

5. Picard Y, Thompson CJ. Motion correction of PET images using multiple acquisition frames. IEEE Trans Med Imaging (1997) 16:137–44. doi:10.1109/42.563659

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Perruchot F, Reilhac A, Grova C Motion correction of multi-frame PET data. IEEE symposium conference record nuclear science 2004., IEEE, pp. 3186–90.

Google Scholar

7. Costes N, Dagher A, Larcher K, Evans AC, Collins DL, Reilhac A. Motion correction of multi-frame PET data in neuroreceptor mapping: Simulation based validation. Neuroimage (2009) 47:1496–505. doi:10.1016/j.neuroimage.2009.05.052

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wardak M, Wong K-P, Shao W, Dahlbom M, Kepe V, Satyamurthy N, et al. Movement correction method for human brain PET images: Application to quantitative analysis of dynamic 18F-fddnp scans. J Nucl Med (2010) 51:210–8. doi:10.2967/jnumed.109.063701

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lin K-P, Huang S-C, Yu D-C, Melega W, Barrio JR, Phelps ME. Automated image registration for FDOPA PET studies. Phys Med Biol (1996) 41:2775–88. doi:10.1088/0031-9155/41/12/014

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Andersson JL. How to obtain high-accuracy image registration: Application to movement correction of dynamic positron emission tomography data. Eur J Nucl Med Mol Imaging (1998) 25:575–86. doi:10.1007/s002590050258

CrossRef Full Text | Google Scholar

11. Avants BB, Tustison N, Song G. Advanced normalization tools (ANTS). Insight j (2009) 2:1–35.

Google Scholar

12. Klein S, Staring M, Murphy K, Viergever M, Pluim J. Elastix: A toolbox for intensity-based medical image registration. IEEE Trans Med Imaging (2010) 29:196–205. doi:10.1109/tmi.2009.2035616

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Thirion J-P. Image matching as a diffusion process: An analogy with maxwell's demons. Med Image Anal (1998) 2:243–60. doi:10.1016/s1361-8415(98)80022-4

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage (2009) 45:S61–S72. doi:10.1016/j.neuroimage.2008.10.040

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Vos BDD, Berendsen FF, Viergever MA, Staring I, Ivana I, et al. End-to-end unsupervised deformable image registration with a convolutional neural network. Deep learning in medical image analysis and multimodal learning for clinical decision support. Springer (2017). p. 204–12. doi:10.1007/978-3-319-67558-9_24

CrossRef Full Text | Google Scholar

16. de Vos BD, Berendsen FF, Viergever MA, Sokooti H, Staring M, Išgum I. A deep learning framework for unsupervised affine and deformable image registration. Med Image Anal (2019) 52:128–43. doi:10.1016/j.media.2018.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, Dalca AV, et al. An unsupervised learning model for deformable medical image registration. Proc IEEE Conf Comput Vis pattern recognition (2018) 9252–60. doi:10.1109/cvpr.2018.00964

CrossRef Full Text | Google Scholar

18. Fan J, Cao X, Yap P-T, Shen D. BIRNet: Brain image registration using dual-supervised fully convolutional networks. Med Image Anal (2019) 54:193–206. doi:10.1016/j.media.2019.03.006

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Li H, Fan Y. Non-rigid image registration using self-supervised fully convolutional networks without training data. 2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018), IEEE, pp. 1075–8.doi:10.1109/isbi.2018.8363757

CrossRef Full Text | Google Scholar

20. Sokooti H, de Vos BD, Berendsen F, Lelieveldt BPF, Išgum I, Staring M. Nonrigid image registration using multi-scale 3D convolutional neural networks. International conference on medical image computing and computer-assisted intervention. Springer (2017). p. 232–9. doi:10.1007/978-3-319-66182-7_27

CrossRef Full Text | Google Scholar

21. Mahapatra D, Antony B, Sedai S, Garnavi R, et al. Deformable medical image registration using generative adversarial networks. 2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018), IEEE, pp. 1449–53.doi:10.1109/isbi.2018.8363845

CrossRef Full Text | Google Scholar

22. Fan J, Cao X, Wang Q, Yap PT, Shen D. Adversarial learning for mono- or multi-modal registration. Med Image Anal (2019) 58:101545. doi:10.1016/j.media.2019.101545

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yan P, Xu S, Rastinehad AR, Wood BJ. workshop on machine learning in medical imaging. Springer (2018). p. 197–204. doi:10.1007/978-3-030-00919-9_23

CrossRef Full Text | Google Scholar

24. Krebs J, Mansi T, Delingette H, Zhang L, Ghesu FC, Miao S, et al. Robust non-rigid registration through agent-based action learning. International conference on medical image computing and computer-assisted intervention. Springer (2017). p. 344–52. doi:10.1007/978-3-319-66182-7_40

CrossRef Full Text | Google Scholar

25. Ma K, Wang J, Singh V, Tamersoy B, Chang Y-J, Wimmer A, et al. International conference on medical image computing and computer-assisted intervention. Springer (2017). p. 240–8. doi:10.1007/978-3-319-66182-7_28Multimodal image registration with deep context reinforcement learning

CrossRef Full Text | Google Scholar

26. Liao R, Miao S, de Tournemire P, Grbic S, Kamen A, Mansi T, et al. An artificial agent for robust image registration. Proceedings of the AAAI conference on artificial intelligence (2017). doi:10.1609/aaai.v31i1.11230

CrossRef Full Text | Google Scholar

27. Yang X, Kwitt R, Styner M, Niethammer M. Quicksilver: Fast predictive image registration - a deep learning approach. NeuroImage (2017) 158:378–96. doi:10.1016/j.neuroimage.2017.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Rohé M-M, Datar M, Heimann T, Sermesant M, Pennec X, et al. SVF-net: Learning deformable image registration using shape matching. International conference on medical image computing and computer-assisted intervention. Springer (2017). p. 266–74.

Google Scholar

29. Fu Y, Lei Y, Wang T, Curran WJ, Liu T, Yang X. Deep learning in medical image registration: A review. Phys Med Biol (2020) 65:20TR01. doi:10.1088/1361-6560/ab843e

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jaderberg M, Simonyan K, Zisserman A. Spatial transformer networks. Adv Neural Inf Process Syst (2015) 28.

Google Scholar

31. Shen Z, Han X, Xu Z, Xu H, Marc N, et al. Networks for joint affine and non-parametric image registration. Proc IEEE/CVF Conf Comput Vis Pattern Recognition (2019) 4224–33. doi:10.1109/cvpr.2019.00435

CrossRef Full Text | Google Scholar

32. Zhao S, Lau T, Luo J, Chang EIC, Xu Y. Unsupervised 3D end-to-end medical image registration with volume tweening network. IEEE J Biomed Health Inform (2020) 24:1394–404. doi:10.1109/jbhi.2019.2951024

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Krebs J, Delingette H, Mailhe B, Ayache N, Mansi T. Learning a probabilistic model for diffeomorphic registration. IEEE Trans Med Imaging (2019) 38:2165–76. doi:10.1109/tmi.2019.2897112

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Guo Y, Bi L, Ahn E, Feng D, Wang Q, Kim J, et al. A spatiotemporal volumetric interpolation network for 4D dynamic medical image. Proc IEEE/CVF Conf Comput Vis Pattern Recognition (2020) 4726–35. doi:10.1109/cvpr42600.2020.00478

CrossRef Full Text | Google Scholar

35. Dalca AV, Balakrishnan G, Guttag J, Sabuncu MR. Unsupervised learning for fast probabilistic diffeomorphic registration. International conference on medical image computing and computer-assisted intervention. Springer (2018). p. 729–38. doi:10.1007/978-3-030-00928-1_82

CrossRef Full Text | Google Scholar

36. Krebs J, Mansi T, Mailhé B, Ayache N, Delingette H. Unsupervised probabilistic deformation modeling for robust diffeomorphic registration. Deep learning in medical image analysis and multimodal learning for clinical decision support. Springer (2018). p. 101–9. doi:10.1007/978-3-030-00889-5_12

CrossRef Full Text | Google Scholar

37. Kuang D, Schmah T. Faim - a ConvNet method for unsupervised 3D medical image registration. International workshop on machine learning in medical imaging. Springer (2019). p. 646–54. doi:10.1007/978-3-030-32692-0_74

CrossRef Full Text | Google Scholar

38. Xia K-j, Yin H-s, Wang J-q. A novel improved deep convolutional neural network model for medical image fusion. Cluster Comput (2019) 22:1515–27. doi:10.1007/s10586-018-2026-1

CrossRef Full Text | Google Scholar

39. Yu H, Zhou X, Jiang H, Kong H, Wang Z, Hara T, et al. Learning 3D non-rigid deformation based on an unsupervised deep learning for PET/CT image registration. Medical imaging 2019: Biomedical applications in molecular, structural, and functional imaging. SPIE (2019). p. 439–44. 10.1117/12.2512698.

CrossRef Full Text | Google Scholar

40. Yu H, Jiang H, Zhou X, Hara T, Yao YD, Fujita H. Unsupervised 3D PET-CT image registration method using a metabolic constraint function and a multi-domain similarity measure. IEEE Access (2020) 8:63077–89. doi:10.1109/access.2020.2984804

CrossRef Full Text | Google Scholar

41. Nair V, Hinton GE. Rectified linear units improve restricted Boltzmann machines. ICML (2010).

Google Scholar

42. Penney GP, Weese J, Little JA, Desmedt P, Hill D, hawkes D. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Trans Med Imaging (1998) 17:586–95. doi:10.1109/42.730403

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Tumpa TR. Qualitative and quantitative improvements for positron emission tomography using different motion correction methodologies (2021).

Google Scholar

44. Osborne D, Acuff S, Tumpa T, Hu D, et al. Respiratory motion correction using novel particle tracking techniques. J Nucl Med (2017) 58:1362.

Google Scholar

45. Tumpa TR, Acuff SN, Gregor J, Lee S, Hu D, Osborne DR, et al. Respiratory motion correction using A novel positron emission particle tracking technique: A framework towards individual lesion-based motion correction. 2018 40th annual international conference of the IEEE engineering in medicine and biology society (EMBC), IEEE, pp. 5249–52.doi:10.1109/embc.2018.8513486

CrossRef Full Text | Google Scholar

46. Tumpa TR, Acuff SN, Gregor J, Lee S, Hu D, Osborne DR. A data-driven respiratory motion estimation approach for PET based on time-of-flight weighted positron emission particle tracking. Med Phys (2021) 48:1131–43. doi:10.1002/mp.14613

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Beyer D, Boellaard T, De Ruysscher R, Grgic D, Lee A, Pietrzyk JA, et al. Integration of FDG- PET/CT into external beam radiation therapy planning. Nuklearmedizin (2012) 51(4):140–53. Epub 2012 Apr 3. PMID: 22473130. doi:10.3413/Nukmed-0455-11-12

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ireland RH, Dyker KE, Barber DC, Wood SM, Hanney MB, Tindale WB, et al. Nonrigid image registration for head and neck cancer radiotherapy treatment planning with PET/CT. Int J Radiat Oncology*Biology*Physics (2007) 68(3):952–7. Epub 2007 Apr 18. PMID: 17445999; PMCID: PMC2713594. doi:10.1016/j.ijrobp.2007.02.017

CrossRef Full Text | Google Scholar