- 1Institute of Theoretical Physics and Department of Physics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, China
- 2State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan, China
- 3School of Physical Sciences, University of Chinese Academy of Sciences, Beijing, China
- 4Hefei National Research Center for Physical Sciences at the Microscale and School of Physical Sciences, Department of Modern Physics, University of Science and Technology of China, Hefei, China
- 5Center for Advanced Material Diagnostic Technology, College of Engineering Physics, Shenzhen Technology University, Shenzhen, China
In this work, we theoretically investigate the ellipticity dependence of the Rydberg state excitation (RSE) and ionization of noble gas atoms subject to strong laser fields at a series of intensities and wavelengthes by a semiclassical model, where the nonadiabtic effect is considered or ignored. Our results demonstrate that, if the nonadiabatic effect has been ignored, the ratio between RSE and ionization yields exhibits an anomalous maximum at a nonzero ellipticity. On the other hand, if the nonadiabatic effect has been considered, this anomalous behavior disappears. The analysis indicates that the absence of this anomalous behavior can be attributed to the nonadiabatic corrections of instantaneous ionization rate and the initial photoelectron momentum distribution at the tunnel exit.
1 Introduction
For an atom or molecule subject to a strong laser field, the valence electron can be released via tunneling [1, 2] if the electric field strength of the laser pulse is comparable to that of the Coulomb field of the ionic core. The ionization dynamics may be comprehended with either multiphoton ionization (MPI) or tunneling ionizaiton (TI) [3, 4]. To indicate the transition between these two limits, a pivotal role is given to the Keldysh parameter
After tunneling of the electron, the electron motion in a strong laser field can be described by a semiclassical model [14]. In this model, driven by the oscillating laser field, part of the tunneled electron wavepacket may return to the ionic core, resulting in a variety of interesting physical phenomena, such as high-order harmonic generation (HHG) [15, 16], nonsequential double ionization (NSDI) [17], and high-order above-threshold ionization (HATI) [18], etc. In contrast to the phenomena mentioned above, if the electron does not gain enough drift energy from the laser pulse, it will eventually be captured by the Coulomb field, leading to Rydberg state excitation (RSE) of neutral atoms. This process can be comprehended by the mechanism of frustrated tunneling ionization (FTI) [19]. The application of Rydberg atoms is very attractive in many fields [20].
In addition to the works on RSE process in linearly polarized strong laser fields (see, e.g. [21–27]), studies on the ellipticity dependence of RSE have attracted attention. Experimentally, Nubbemmeyer et al. demonstrated a dramatic decrease of RSE yields for He with increasing laser ellipticity, as expected with a rescattering picture [19]. An experimental investigation of high-lying Rydberg state excitation of diatomic atoms and their companion atoms with comparable ionization potentials shows a similar trend [28]. Theoretically, Landsman et al. well reproduced the results in [19] by the semiclassical model [29]. Zhao et al. found that the decline of the RSE yields with increasing ellipticity can be attributed to a decrease of low-energy electrons that could be captured in the Rydberg states by the Coulomb potential [30]. Recently, an astonishing maximum of the ratio between the RSE and the ionization yields at a nonzero ellipticity was found, based on a 2-dimensional semiclassical calculation [31]. Note that the results in [31] are inconsistent to a more recent time-dependent Schr
Except for RSE and ionization, the high-order harmonic generation (HHG) of atoms and molecules in elliptically polarized laser field has also been studied intensively [33–36]. Although many interesting phenomena, e.g., HHG from N2 can be strongly elliptically polarized even when driven by linearly polarized laser fields [35], the polarization of HHG depends strongly on the molcular alignment and laser ellipticity [36], have been documented, technically, it is very difficult to measure the HHG and ionization yields with the same spectrometer simultaneously because the sample pressure in the HHG experiments is usually much higher [35]. On the contrary, the ionization yields can be measured easily along with the RSE yields by the identical spectrometer simultaneously [19]. Thus, the investigation of correlation of RSE and ionization yields could be more significant due to the possibility of comparison with experimental results.
In this work, we study the RSE and ionization processes for atoms subject to elliptically polarized laser fields by a semiclassical model, where the nonadiabatic effect can be considered or ignored. Our results demonstrate that, if the nonadiabatic effect has been ignored, the ratio between RSE and ionization yields exhibits an anomalous maximum at a nonzero ellipticity, which is consistent to the results of Ref. [31]. On the other hand, if the nonadiabatic effect has been considered, this anomalous behavior disappears, which matches the results of Ref. [32]. By tracing back the initial photoelectron momenta and the coordinates of the photoelectron trajectories based on the semiclassical calculations, we found that the absence of this anomalous behavior can be attributed to the nonadiabatic corrections of the instantaneous ionization rate and the initial photoelectron momentum distribution at the tunnel exit.
2 Adiabatic model
The excitation and ionization dynamics are numerically simulated by a semiclassical model, which is shown to be invaluable and efficient in providing intuitive understanding and predictive power for the ultrafast dynamics of atoms and molecules subject to strong laser field [37–41]. In this model, it can be chosen to include the nonadiabatic effect or not. According to the documented works (see, e.g., [2, 12]), the nonadiabatic effect can be safely ignored if the Keldysh parameter is much less than unity [2], i.e., the laser intensity is strong enough or the laser wavelength is long enough. In these cases, the semiclassical model ignoring the nonadiabatic effect can be termed the classical-trajectory Monte Carlo (CTMC) model, which has already been widely applied in studying RSE based on the FTI mechanism [19, 29–32]. In contrast, if the above conditions cannot be well satisfied and the Keldysh parameter is close to unity, the nonadiabatic effect [9, 12, 42, 43] of electron tunneling could be too strong to be ignored. In these cases, the semiclassical model including the nonadiabatic effect will be coined the nonadiabatic model in this work.
In the CTMC model, the RSE and ionization processes in elliptically polarized laser field include two steps, i.e., tunneling ionization and classical evolution of the tunneled electron in a combination of the laser field and ionic Coulomb field. In the first step, it is assumed that the electron is adiabatically released from the groundstate to a continuum state through tunneling [44, 45]. The elliptically polarized laser electric field employed in this work can be given by F(t) = (Ex(t), 0, Ez(t)) (atomic units are used unless stated otherwise),
where
where N is the number of the laser cycles. In this work, N = 30 corresponds to the pulse duration (full width at half maximum) of around 30 fs, which is a typical parameter of the multi-cycle laser pulses generated by the commercial Ti:Sapphire laser system.
In the case of elliptical polarization, in the x-z plane, the laser electric field rotates successively with a period of
In the laboratory coordinate system, the initial spatial coordinates of the tunneled electron are given by x0 = −η0 cos[arctan[ɛ tan(ωt0)]], y0 = 0, z0 = −η0 sin[arctan[ɛ tan(ωt0)]] and the initial momenta are given by px0 = p⊥ cos θ cos[arctan[ɛ tan(ωt0)]], py0 = p⊥ sin θ, pz0 = −p⊥ cos θ sin[arctan[ɛ tan(ωt0)]], where t0 is photoelectron tunneling instant. The weight of the trajectory can be determined by [44, 46].
In the second step, the dynamics after tunneling can be described by a classical Newtonian equation [47–52],
where the effective potential, V(r), exerted on the tunneled electron is given by
where
To numerically identify the electron trajectories contributed to RSE yields, along which the electrons will be captured by the Coulomb potential after the laser pulse ends, we search for the electron trajectories with the energies of Ef = P2/2 − Zeff/r < 0, where
3 Nonadiabatic model
Compared to the CTMC model described above, in our nonadiabatic model, the initial photoelectron momenta, tunnel exit, and instantaneous ionization rate have been further corrected by the nonadiabatic effect [9, 12, 42, 43]. Based on the S-Matrix theory [53, 54], the transition probability from the groundstate to a continuum state can be described by
The initial photoelectron momentum, p = (px, py, pz), satisfies p = P + A(t0). Thus, one can obtain
In the plane of the polarization ellipse, pz and px relate to the initial photoelectron longitudinal (p‖) and transverse (p⊥) momentum, where the subscript ‖ (⊥) indicates the direction parallel (perpendicular) to the transient laser polarization direction, in the rotating coordinate system by
where
where
In the SFA theory, the electron sub-barrier trajectory can be described by
The ionization probability can be obtained by,
where
In our calculations, the tunneling time t0 and the initial transverse momentum p⊥ are given randomly in their corresponding parameter spaces. While, the initial longitudinal momentum, ti, tunnel exit and instantaneous ionization probability rate can be obtained with Eqs 12–15, respectively. The following evolution of the photoelectron can be achieved by numerically solving the Newtonian equation Eq 7. The electron trajectories relevant to the RSE and ionization processes are found by the identical procedures described in the last section.
4 Results and discussion
The typical CTMC calculation results for Ar subject to strong elliptically polarized laser fields at a series of laser wavelengthes and intensities are presented in Figure 1A, where a maximum of the ratio between RSE and ionization yields at ɛ = 0.3 can be identified in the case of the laser pulse with an intensity of 0.4 × 1014W/cm2 and a wavelength of 800 nm. Moreover, the ratio maximum at a nonzero ellipticity disappears at the higher laser intensity or the longer wavelength in Figure 1A. The result is similar to the adiabatic semiclassical calculations in [31], except that the anomalous ratio maximum at a nonzero ellipticity persists at a higher intensity of 0.8 × 1014W/cm2 at 800 nm in [31]. The difference can be attributed to the fact that, compared to the 2-dimensional adiabatic semiclassical model employed in [31], where the influence of Coulomb potential has been overestimated, a 3-dimensional adiabatic semiclassical model, which could be closer to the real physical scenario, is employed in this work. The numerical results in [31] can be well reproduced if the photoelectron dynamics in our model are confined in the 2-dimensional polarization ellipse plane at y = 0.
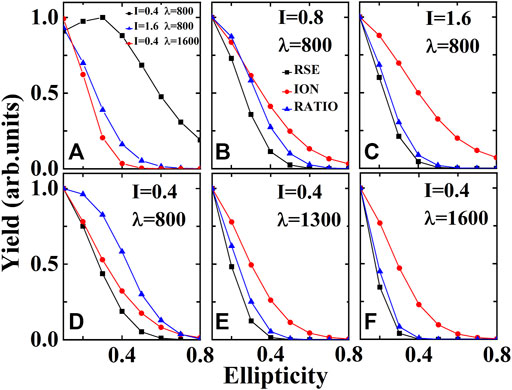
FIGURE 1. (A) The calculated ratio between the yields of RSE and ionization processes as a function of the ellipticity by the adiabatic semiclassical model. The laser intensities are indicated in the unit of 1014W/cm2. The laser wavelengthes are 800 nm (black squares and blue triangles) and 1,600 nm (red circles). (B–F) The calculations by the nonadiabatic semiclassical model. The calculated normalized yields of RSE (black squares), ionization (red circles) and the ratio between them (blue triangles) as a function of the ellipticity at the intensities of (D) 0.4, (B) 0.8 and (C) 1.6 (in the unit of 1014W/cm2) at 800 nm. The ellipticity dependence of the corresponding normalized yields at the wavelengthes of 800 nm (D), 1300 nm (E), 1600 nm (F) at 0.4×1014W/cm2 have also been presented.
In order to comprehend the ellipticity dependence of the ratio between the RSE and the ionization yields, based on the calculations of adiabatic model, we present the laser phase dependence of the initial photoelectron transverse momentum distributions at ɛ = 0, ɛ = 0.1, ɛ = 0.3 for tunneling (including the contributions of both ionization and RSE processes) (Figures 2A–C), ionization (Figures 2F–H) and RSE (Figures 2K–M), respectively. In addition, the distributions of the RSE process with V(r) = 0 applied in Eq. 7 except in the calculation of the final energy of the electron are depicted in Figures 2P–T. In this case, since the final kinetic energy of the tunneled electron is solely determined by the initial transverse momentum and tunneling phase which gives the acceleration p = −A(ti), the distribution shows a symmetric filled circle in Figure 2P) for ɛ = 0. When the ellipticity increases, the initial transverse momentum shifts toward positive direction to compensate the additional acceleration due to the increasing minor axis of the laser field. The distribution becomes asymmetric with respect to p⊥ considering the Guassian distribution Eq. 6 (see Figures 2P, Q)). If the Coulomb potential is included in the calculation, comparing Figure 2P) with Figure 2K, the distribution is modified significantly. Firstly, the distribution region is enlarged prominently due to attraction of the Coulomb potential which reduces the final kinetic energy of the electron. Secondly, different regions inside the circle are modified in different manner due to influence of the Coulomb potential. The regions denoted by A and C, which possess large initial transverse momentum and tunneling moment near the crest of the field, are affected by the Coulomb potential most slightly because of relatively large initial transverse momentum which makes the electron move far away from the core during evolution after tunneling. When the tunneling phase moves away from the crest of the laser field, i. e., entering region B, the electron will move closer to the core due to relatively small initial transverse momentum and hence interact strongly with the Coulomb potential, resulting in decreased capture probability. Especially, according to the simple-man picture, electron tunneled out with positive phase (ωt0 > 0) will return to the core or return to re-cross the x-y plane if the initial transverse momentum of the electron is considered in the 3-dimensional case [55]. Rescattering of the electron upon the core, or in other words, strong interaction between the electron and the core, will significantly increase the kinetic energy that the electron gains in the field. This effect leads to missing upper part of the circle, especially for the small initial transverse momentum region, resulting in two symmetric hook-like structures shown in Figure 2K. For the region of negative tunneling phase (ωt0 < 0) considered here, the electron will also return to re-cross the x-y plane due to attraction of the Coulomb potential though it should directly move out without return according to the simple-man picture which does not take into account the Coulomb potential. Depending on the initial condition, some of the tunneled electrons will interact with the core strongly, gains large kinetic energy and escapes. It is noteworthy that the overall shape of the RSE region is very similar to that obtain by the 2-dimensional simulation in Ref. [31], the distribution inside the RSE region possesses more structures for the 3-dimensional calculation while it is almost empty for the 2-dimensional simulation. This difference can be attributed to that, in 2-dimensional case, the electron will interact with the core much strongly and then gains enough energy to escape, resulting in two symmetric crescent-like structures, while, in the 3-dimensional case, the situation is much more complicated. Note that there are even more structures near the center of the RSE region which can be ascribed to chaotic behavior of the electron moving in the combined Coulomb potential and external laser field. Many electrons will experience multiple returns and some may even circle around the core many time before they move away from the core [56], giving rise to complex structures in the region. When the ellipticity increases, the RSE region shifts to the positive direction of the initial transverse momentum for the same reason as that in the calculation without considering Coulomb potential (Figures 2P–R). To show the ellipticity dependent probabilities more clearly, we plot the distributions of initial transverse momentum (integral over tunneling phase) and tunneling phase (integral over initial transverse momentum) in the right two columns in Figure 2. One can find that all the distributions of tunneling phase are symmetric with respect to the crest of the laser field and hardly change with increasing ellipticity while the distributions of initial transverse momentum change noticeably with ellipticity. For the calculation without taking into account the Coulomb potential in evolution, the distribution of RSE shifts toward positive momentum but the shape keeps unchanged (see Figure 2S). When the Coulomb potential is fully considered, the distribution of RSE becomes much broader and possesses multi-peak structure for ɛ = 0. It shifts toward positive momentum and changes to a single-peak distribution with increasing ellipticity. This can be understood that since the distribution of the tunneling hardly changes with ellipticity, the regions B and C drop fast when the distribution of RSE shifts, so only the peak in region A remains. In addition, when the ellipticity increases, the peak in the region A shift toward the peak of the distribution of tunneling and coincides with the peak of tunneling at ɛ = 0.3, thus the ratio between RSE and ionization yields increases and reaches maximum at ɛ = 0.3. If the ellipticity increases further, the peak in the region A shifts away from the peak of tunneling distribution and thus drops quickly (see black squares in Figure 1A).
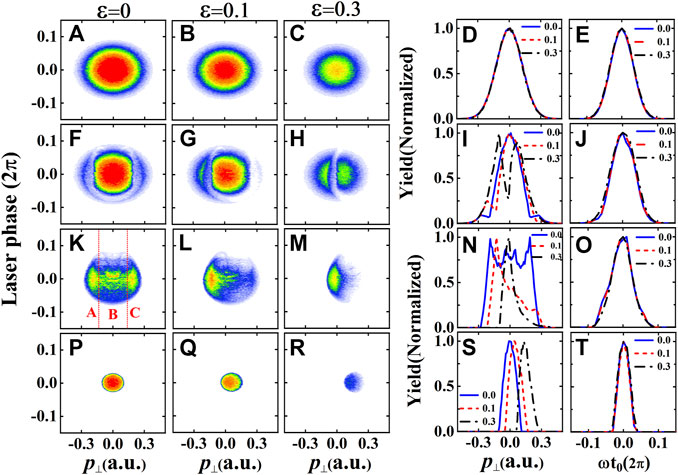
FIGURE 2. The laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling (A–C), ionization (F–H) and RSE (K–M), (P–R) processes at the ellipticities of ɛ =0 (A, F, K, P), ɛ =0.1 (B, G, L, Q), ɛ =0.3 (C, H, M, R). The initial photoelectron transverse momentum distributions in (D, I, N,S) and laser phase distributions in (E, J, O, T) are extracted from the data of (A–C), (F–H), (K–M) and (P–R), respectively. These data are calculated by the CTMC model with the laser intensity of 4×1013W/cm2 and the wavelength of 800 nm. For the data in (P–R), the Coulomb potential corrections of the photoelectron trajectories are ignored. Please find more details in the text.
To understand the laser intensity and wavelength dependence of the ratio between the RSE yields and the ionization yields in Figure 1A, the laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling, ionization and RSE processes at the ellipticities of 0.1 and 0.3 at a higher intensity of 1.6 × 1013W/cm2 (at 800 nm) and a longer wavelength of 1,600 nm (at 0.4 × 1014W/cm2) are given in Figure 3. Firstly, we concentrate on the laser intensity dependence of the ratio between RSE and ionization yields. When the intensity increases, the tunneling exit shifts toward the core and hence leads to stronger rescattering effect of the tunneled electron. Moreover, considering that the kinetic energy of the electron gained from the laser field is proportional to the intensity, the tunneling phase will be reduced significantly in the positive direction for the initial phase distribution of RSE. In the negative direction of the tunneling phase, since these electrons interact with the core softly, the distribution also shrinks but not so prominently as that in the positive direction. Therefore, the maximum of the RSE distribution shifts to negative tunneling phase as can be seen in Figures 3I–L) which show clear asymmetry with respect to the crest of the laser field. In this case, when the ellipticity increases, the RSE distribution shifts toward positive momentum but the maximum will miss the peak of the tunneling phase distribution (see Figures 3I, J), resulting in decreasing ratio of RSE/Ion as shown in Figure 1A (blue triangles) for high intensity. The same analysis given above can also be applied to the case of longer wavelength (1,600 nm) depicted in Figure 3. It should be noted that, since the intensity of the laser field is the same as that used in Figure 2, the tunneling exit does not shift but the kinetic energy gained by the electron, which is proportional to Up ∝ Iλ2, is the same as that of the high intensity case for 800 nm, so the asymmetry in the tunneling phase direction is less pronounced than that of the former case (comparing Figure 3X) with Figure 3L)). However, the maximum is still in the negative tunneling phase and it will also miss the peak of the tunneling phase distribution with increasing ellipticity, giving rise to decreasing ratio of RSE/Ion shown in Figure 1A (red circles).
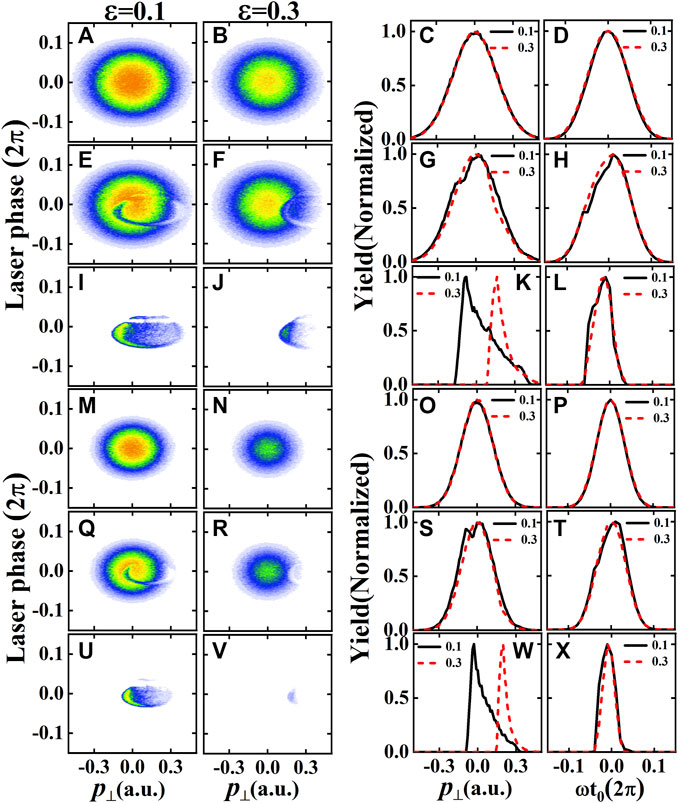
FIGURE 3. The laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling (A, B, M, N), ionization (E, F, Q, R) and RSE (I, J, U, V) processes at the ellipticities of ɛ =0.1 (A, E, I, M, Q, U), ɛ =0.3 (B, F, J, N, R, V). The initial photoelectron transverse momentum distributions in (C, G, K, O, S, W) and laser phase distributions in (D, H, L, P, T, X) are extracted from the data of (A, B, E, F, I, J, M, N, Q, R, U, V), respectively. The laser intensities are 1.6×1014W/cm2 (A–L) and 0.4×1014W/cm2 (M–X). The laser wavelengthes are 800 nm (A–L) and 1,600 nm (M–X). These data are calculated by the CTMC model.
Based on the above analysis of the CTMC calculation results, we further investigate the nonadiabatic effect on the ratio of RSE yields over ionization yields. The calculations with the nonadiabatic model are presented in Figures 1B–F). As shown in these panels, with rising ellipticity, both the ionization and RSE yields decrease rapidly. With closer inspection, the RSE yields decrease even faster than the ionization yields for all the laser intensities and wavelengthes investigated in this work. It can be found that the slope of the ellipticity dependence of RSE (ionization) yields becomes more and more steep (flat) for higher laser intensities or longer wavelengthes. As a result, the ratios between the RSE yields and the ionization yields become steeper with rising ellipticity for stronger laser intensities or longer wavelengthes. Therefore, the ratio maximum at a nonzero ellipticity disappear if the nonadiabatic effect has been considered in the semiclassical model.
The calculation results of the nonadiabatic model are in stark contrast to those in [31] (and also the data in Figure 1A), where a radical maximum of the ratio can be identified at ɛ ≈ 0.2 (or ɛ = 0.3) at 800 nm. On the contrary, the calculation results of nonadiabatic model are qualitatively consistent to those in [32], where the RSE yields also decrease faster at higher laser intensity. Considering that our CTMC calculations qualitatively match the results in [31] where the nonadiabatic effect has been ignored, we can conclude that the nonadiabatic effect must be the physical origin behind the difference between the results of [31, 32].
To comprehend the influence of the nonadiabatic effect on the ellipticity dependence of the ratio, we present the laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling, ionization and RSE processes at the ellipticities of ɛ = 0.1 and ɛ = 0.3 in Figure 4. Although the laser parameters of Figure 4 is identical to those of Figure 2, as well documented (see, e.g., [9]), the nonadiabatic effect will lead to a shift of the tunneling exit to the core, compared to its adiabatic counterpart. Therefore, the contribution of the rescattering process could be significantly enhanced, giving rise to the shift of the RSE area to the negative direction of the laser phase. Furthermore, in contrast to the zero photoelectron longitudinal momentum employed in the CTMC model, a significant nonzero photoelectron longitudinal momentum is introduced by the nonadiabatic effect. As shown in Ref. [54], the initial longitudinal momentum is always along the direction of -A(t), i. e., the final kinetic energy of the tunneled electron will be increased if the initial longitudinal momentum is taken into account. So the RSE distribution shrinks in the direction of tunneling phase. In addition, in the falling edge of the laser field where the electron is expected to return to the x-y plane in the simple-man picture, the initial longitudinal momentum always points to the core, so the rescattering effect is also enhanced, which will reduce the distribution in the positive initial longitudinal momentum region. As shown in Figures 4K, L), strong asymmetry can be found in the distributions of initial longitudinal momentum and tunneling phase for RSE process. Therefore, the nonadiabatic modification of the tunneling exit and the initial photoelectron longitudinal momentum lead to that laser phase range of RSE area in Figures 4I–LJ) becomes narrower and shifts to the negative direction of laser phase, if compared to the results in Figures 2L, M, O. Meanwhile, the laser phase range of the tunneling areas in Figures 4A, B, D is still symmetric (close to that of Figures 2A, B, D). Thus, with rising ellipticity, the dominant yields of RSE distribution will miss the peak of the tunneling distribution (Figure 4A), which, in turn, leads to the absence of the ratio maximum at a nonzero ellipticity.
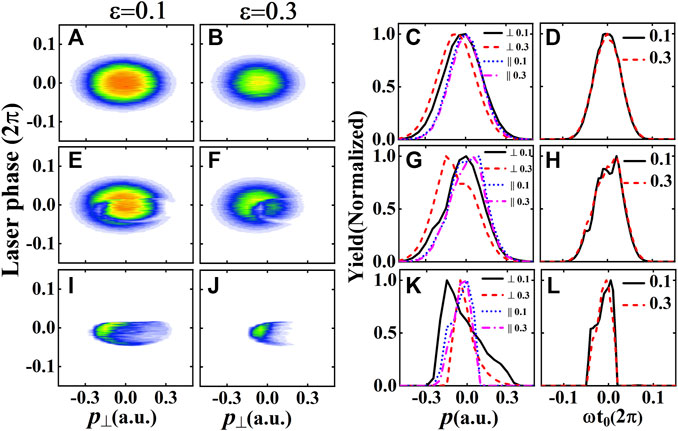
FIGURE 4. The laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling (A, B), ionization (E, F) and RSE (I, J) processes at the ellipticities of ɛ =0.1 (A, E, I), ɛ =0.3 (B, F, J). The initial photoelectron transverse momentum distributions in (C, G, K) and laser phase distributions in (D, H, L) are extracted from the data of (A, B), (E, F), and (I, J), respectively. The initial photoelectron longitudinal momentum distributions for tunneling (C), ionization (G) and RSE (K) are also presented. These data are calculated by the nonadiabatic model with the laser intensity of 4×1013W/cm2 and the wavelength of 800 nm.
In Figure 5, calculation results by the nonadiabatic model at a higher laser intensity and a longer wavelength are presented. At a higher intensity, as shown in Figures 5A, B, D, the laser phase ranges of the tunneling areas become wider, compared to its lower intensity counterpart (see Figures 4A, B, D). In the meantime, at the higher intensity, the width of lase phase range of the RSE distribution hardly changes and but its peak shifts to the negative direction of laser phase due to the larger contribution of rescattering process, resulting from shift of tunneling exit towards the core at higher laser intensity. Thus, the peak of the RSE distribution shifts by passing the region farther away from the tunneling distribution with rising ellipticity than that in the lower intensity case, which, in turn, leads to a monotonous faster decrease of the ratio (comparing Figures 1C, D). In the case of a longer wavelength, in Figures 5M, N, P, the laser phase ranges of the tunneling areas are close to the case of 800 nm (see Figures 4A, B, D). However, the laser phase ranges of the RSE areas become obviously narrower and shifts to negative laser phase compared to the case of 800 nm due to the larger photoelectron acceleration by the laser field at the longer wavelength. In addition, since the acceleration of the field is proportional to E0/ω, the RSE distribution shifts much faster in the initial transverse momentum axis for long wavelength case comparing with the shorter wavelength with the same intensity (comparing Figures 5U–W with Figures 4I–K). Thus, the ratio of RSE/Ion decreases faster with rising ellipticity for longer wavelength than that in the 800 nm case which can be clearly seen by comparing Figures 1D, F).
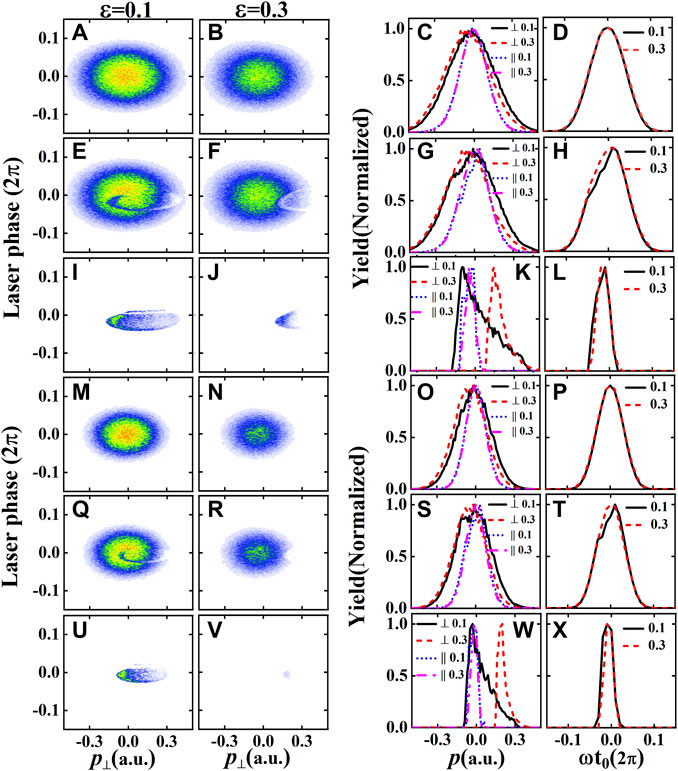
FIGURE 5. The laser phase dependence of the initial photoelectron transverse momentum distributions for tunneling (A, B, M, N), ionization (E, F, Q, R) and RSE (I, J, U, V) processes at the ellipticities of ɛ =0.1 (A, E, I, M, Q, U) and ɛ =0.3 (B, F, J, N, R, V). The initial photoelectron transverse momentum distributions in (C, G, K, O, S, W) and laser phase distributions in (D, H, L, P, T, X) are extracted from the data of (A, B, (E, F, I, J, M, N, Q, R, U, V), respectively. The initial photoelectron longitudinal momentum distributions for tunneling (C,O), ionization (G, S) and RSE (K, W) are also presented. The laser intensities are 1.6×1014W/cm2 (A–L) and 0.4×1014W/cm2 (M–X). The laser wavelengthes are 800 nm (A–L) and 1,600 nm (M–X). These data are calculated by the nonadiabatic model.
5 Conclusion
Using a semiclassical model where the nonadiabatic effect can be chosen to be included or ignored, we found that the documented anomalous behavior of the ratio between RSE and the ionization yields, which maximizes at a nonzero ellipticity, is absent when the nonadiabatic effects are taken into account. Our analysis indicates that this result can be attributed to the nonadiabatic modification of the tunneling exit and the initial momentum distribution of the tunneled electron at the tunneling exit.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material further inquiries can be directed to the corresponding authors.
Author contributions
ZW and WQ performed the calculations; ZW, WQ, JC, XH, and XL performed the data analysis; WQ, JC, and XH. planned the calculations and supervised the work; all authors contributed to the discussion of the results; the manuscript was prepared by ZW, WQ, JC, XH, and XL.
Funding
This work is supported by the National Key Research and Development Program (No. 2019YFA0307700), the National Natural Science Foundation of China (Nos. 11834015, 11974383, 12121004 and 12274273), the Science and Technology Department of Hubei Province (No. 2020CFA029).
Acknowledgments
We thank Prof. Y. M. Zhou for his help and stimulating discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Protopapas M, Keitel C, Knight P. Atomic physics with super-high intensity lasers. Rep.Prog.Phys. (1997) 60:389–486. doi:10.1088/0034-4885/60/4/001
2. Keldysh L. Ionization in the field of a strong electromagnetic wave. Sov.Phys.JETP. (1965) 20(5):1307–14.
3. Milosevic DB, Fritz E. Scattering and reaction processes in powerful laser fields. Adv.At.Mol.Opt.Phys. (2003) 49:373–532. doi:10.1016/S1049-250X(03)80007-1
4. Agostini P, DiMauro L. Atoms in high intensity mid-infrared pulses. Contemp.Phys. (2008) 49:179–97. doi:10.1080/00107510802221630
5. Walker B, Mevel E, Yang B, Breger P, Chambaret J, Antonetti A, et al. Double ionization in the perturbative and tunneling regimes. Phys.Rev.A (1993) 48:R894–R897. doi:10.1103/PhysRevA.48.R894
6. Mevel E, Breger P, Trainham R, Petite G, Agostini P, Migus A, et al. Atoms in strong optical fields: Evolution from multiphoton to tunnel ionization. Phys.Rev.Lett. (1993) 70:406–9. doi:10.1103/PhysRevLett.70.406
7. Chaloupka J, Rudati J, Lafon R, Agostini P, Kulander K, DiMauro L. Observation of a transition in the dynamics of strong-field double ionization. Phys.Rev.Lett. (2003) 90:033002. doi:10.1103/PhysRevLett.90.033002
8. Colosimo P, Doumy G, Blaga C, Wheeler J, Hauri C, Catoire F, et al. Scaling strong-field interactions towards the classical limit. NaturePhysics (2008) 4:386–9. doi:10.1038/nphys914
9. Yudin G, Ivanov M. Nonadiabatic tunnel ionization: Looking inside a laser cycle. Phys.Rev.A (2001) 64:013409. doi:10.1103/PhysRevA.64.013409
10. Boge R, Cirelli C, Landsman A, Heuser S, Ludwig A, Maurer J, et al. Probing nonadiabatic effects in strong-field tunnel ionization. Phys.Rev.Lett. (2013) 111:103003. doi:10.1103/PhysRevLett.111.103003
11. Ni H-C, Eicke N, Ruiz C, Cai J, Oppermann F, Nikolay I, et al. Tunneling criteria and a nonadiabatic term for strong-field ionization. Phys.Rev.A (2018) 98:013411. doi:10.1103/PhysRevA.98.013411
12. Landsman A, Keller U. Attosecond science and the tunnelling time problem. Phys.Rep. (2015) 547:1–24. doi:10.1016/j.physrep.2014.09.002
13. Klaiber M, Hatsagortsyan K, Keitel C. Tunneling dynamics in multiphoton ionization and attoclock calibration. Phys.Rev.Lett. (2015) 114:083001. doi:10.1103/PhysRevLett.114.083001
14. Corkum P. Plasma perspective on strong field multiphoton ionization. Phys.Rev.Lett. (1993) 71:1994–7. doi:10.1103/physrevlett.71.1994
15. Shiner A, Schmidt B, Trallero H, Wörner H, Patchkovskii S, Corkum PB, et al. Probing collective multi-electron dynamics in xenon with high-harmonic spectroscopy. Nat.Phys. (2011) 7:464–7. doi:10.1038/NPHYS1940
16. Gao X-Z, Landsman AS, Cao H-B, Zhang Y-P, Wang Y-S, Fu Y-X, et al. Influence of initial tunneling step on the return energy of high-order harmonic generation. Phys.Rev.A (2022) 106:053105. doi:10.1103/PhysRevA.106.053105
17. Becker W, Liu X-J, Ho P, Eberly J. Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev.Mod.Phys. (2012) 84:1011–43. doi:10.1103/RevModPhys.84.1011
18. Paulus GG, Nicklich W, Xu H, Lambropoulos P, Walther H. Plateau in above threshold ionization spectra. Phys.Rev.Lett. (1994) 72:2851–4. doi:10.1103/PhysRevLett.72.2851
19. Nubbemeyer T, Gorling K, Saenz A, Eichmann U, Sandner W. Strong-field tunneling without ionization. Phys.Rev.Lett. (2008) 101:233001. doi:10.1103/PhysRevLett.101.233001
20. Zhang Z-Y, Guo J, Gu B-L, Hao L, Yang G-G, Wang K, et al. Parametric amplification of Rydberg six- and eight-wave mixing processes. PhotonicsResearch (2018) 6:000713. doi:10.1364/PRJ.6.000713
21. Eichmann U, Nubbemeyer T, Rottke H, Sandner W. Acceleration of neutral atoms in strong short-pulse laser fields. Nature (2009) 461(7268):1261–4. doi:10.1038/nature08481
22. Shomsky K, Smith Z, Haan S. Frustrated nonsequential double ionization: A classical model. Phys.Rev.A (2009) 79:061402(R). doi:10.1103/PhysRevA.79.061402
23. Manschwetus B, Nubbemeyer T, Gorling K, Steinmeyer G, Eichmann U, Rottke H, et al. Strong laser field fragmentation ofH2: Coulomb explosion without double ionization. Phys.Rev.Lett. (2009) 102:113002. doi:10.1103/PhysRevLett.102.113002
24. McKenna J, Gaire CK, Esry B, Ben I, Zohrabi M, Johnson NG, et al. Frustrated tunneling ionization during laser-induced D2 fragmentation: Detection of excited metastable D* atoms. Phys.Rev.A (2011) 84:043425. doi:10.1103/PhysRevA.84.043425
25. Hu S-L, Hao X-L, Lv H, Liu M-Q, Yang T-X, Xu H-F, et al. Quantum dynamics of atomic Rydberg excitation in strong laser fields. Opt.Express. (2019) 27:031629. doi:10.1364/OE.27.031629
26. Liu M, Xu S, Hu S, Becker W, Quan W, Liu X, et al. Electron dynamics in laser-driven atoms near the continuum threshold. Optica (2021) 8:765. doi:10.1364/optica.418636
27. Xu S, Liu M, Hu S, Shu Z, Quan W, Xiao Z, et al. Observation of a transition in the dynamics of strong-field atomic excitation. Phys.Rev.A (2020) 102:043104. doi:10.1103/PhysRevA.102.043104
28. Sun F-H, Lu C-X, Ma Y-Z, Pan S-Z, Wang J-W, Zhang W, et al. Orbital effects in strong-field Rydberg state excitation of N2, Ar, O2 and Xe. Opt.Express. (2021) 29:31240. doi:10.1364/OE.437437
29. Landsman A, Pfeiffer A, Hofmann C, Smolarski M, Cirelli C, Keller U. Rydberg state creation by tunnel ionization. NewJ.Phys. (2013) 15:013001. doi:10.1088/1367-2630/15/1/013001
30. Zhao L, Dong J-W, Lv H, Yang T-X, Lian Y, Jing M-X, et al. Ellipticity dependence of neutral Rydberg excitation of atoms in strong laser fields. Phy.Rev.A (2016) 94:053403. doi:10.1103/PhysRevA.94.053403
31. Zhao Y, Zhou Y, Liang J, Zeng Z, Ke Q, Liu Y, et al. Frustrated tunneling ionization in the elliptically polarized strong laser fields. Opt.Express. (2019) 27:21689. doi:10.1364/OE.27.021689
32. Pauly T, Bondy A, Hamilton K, Douguet N, Tong X-M, Chetty D, et al. Ellipticity dependence of excitation and ionization of argon atoms by short-pulse infrared radiation. Phy.Rev.A (2020) 102:013116. doi:10.1103/PhysRevA.102.013116
33. Nagai M, Mukai N, Minowa Y, Ashida M, Takayanagi J, Ohtake H. Achromatic THz wave plate composed of stacked parallel metal plates. Opt.Letters. (2014) 39:146. doi:10.1364/OL.39.000146
34. Strelkov VV. Theory of high-order harmonic generation and attosecond pulse emission by a low-frequency elliptically polarized laser field. Phys.Rev.A (2006) 74:013405. doi:10.1103/PhysRevA.74.013405
35. Zhou X-B, Lock R, Wagner N, Li W, Kapteyn H, Murnane MM. Elliptically polarized high-order harmonic emission from molecules in linearly polarized laser fields. Phys.Rev.Lett. (2009) 102:073902. doi:10.1103/PhysRevLett.102.073902
36. Sun F-J, Chen C, Li W-Y, Liu X, Li W, Chen Y-J. High ellipticity of harmonics from molecules in strong laser fields of small ellipticity. Phy.Rev.A (2021) 103:053108. doi:10.1103/PhysRevA.103.053108
37. Chen J, Liu J, Chen S-G. Rescattering effect on phase-dependent ionization of atoms in two-color intense fields. Phy.Rev.A (2000) 61:033402. doi:10.1103/PhysRevA.61.033402
38. Hao X-L, Wang G-Q, Jia X-Y, Li W-D, Liu J, Chen J. Nonsequential double ionization of Ne in an elliptically polarized intense laser field. Phys.Rev.A (2009) 80:023408. doi:10.1103/PhysRevA.80.023408
39. Quan W, Lin Z, Wu M, Kang H, Liu H, Liu X, et al. Classical aspects in above-threshold ionization with a midinfrared strong laser field. Phys.Rev.Lett. (2009) 103:093001. doi:10.1103/PhysRevLett.103.093001
40. Wang Y-L, Xu S-P, Chen Y-J, Kang H-P, Lai X-Y, Quan W, et al. Wavelength scaling of atomic nonsequential double ionization in intense laser fields. Phys.Rev.A (2017) 95:063415. doi:10.1103/PhysRevA.95.063415
41. Quan W, Hao X, Chen Y, Yu S, Xu S, Wang Y, et al. Long-range Coulomb effect in intense laser-driven photoelectron dynamics. Sci.Rep. (2016) 6:27108. doi:10.1038/srep27108
42. Trabert D, Anders N, Brennecke S, chöffler M, Jahnke T, Schmidt L, et al. Nonadiabatic strong field ionization of atomic hydrogen. Phys.Rev.Lett. (2021) 127:273201. doi:10.1103/PhysRevLett.127.273201
43. Xiao Z, Quan W, Yu S, Lai X, Liu X, Wei Z, et al. Nonadiabatic strong field ionization of noble gas atoms in elliptically polarized laser pulses. Opt.Express. (2022) 30:14873. doi:10.1364/OE.454846
44. Ammosov M, Delone N, Krainov V. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Sov.Phys.JETP. (1986) 64(6):2008–13.
45. Delone N, Krainov V. Energy and angular electron spectra for the tunnel ionization of atoms by strong low-frequency radiation. J.Opt.Soc.Am.B. (1991) 8:1207. doi:10.1364/JOSAB.8.001207
46. Perelomov A, Popov V, Terent’ev M. Ionization of atoms in an alternating electric field. Sov.Phys.JETP. (1967) 24:207.
47. Brabec T, Ivanov MY, Corkum P. Coulomb focusing in intense field atomic processes. Phys.Rev.A (1996) 54:R2551–4. doi:10.1103/PhysRevA.54.R2551
48. Chen J, Liu J, Fu L-B, Zheng WM. Interpretation of momentum distribution of recoil ions from laser-induced nonsequential double ionization by semiclassical rescattering model. Phys.Rev.A (2000) 63:011404(R). doi:10.1103/PhysRevA.63.011404
49. Fu L-B, Liu J, Chen J, Chen S-G. Classical collisional trajectories as the source of strong-field double ionization of helium in the knee regime. Phys.Rev.A (2001) 63:043416. doi:10.1103/PhysRevA.63.043416
50. Chen J, Liu J, Zheng W-M. Characteristic photoelectron spectra and angular distributions of single and double ionization. Phys.Rev.A (2002) 66:043410. doi:10.1103/PhysRevA.66.043410
51. Ye D-F, Liu X, Liu J. Classical trajectory diagnosis of a fingerlike pattern in the correlated electron momentum distribution in strong field double ionization of helium. Phys.Rev.Lett. (2008) 101:233003. doi:10.1103/PhysRevLett.101.233003
52. Xia Q-Z, Ye D-F, Fu L-B, Han X-Y, Liu J. Momentum distribution of near-zero-energy photoelectrons in the strong-field tunneling ionization in the long wavelength limit. Sci.Rep. (2015) 5:11473. doi:10.1038/srep11473
53. Becker W, Grasbon F, Kopold R, Milošević D, Paulus G, Walther H. Above-threshold ionization: From classical features to quantum effects. Adv.At.Mol.Opt.Phys. (2002) 48:35–98. doi:10.1016/S1049-250X(02)80006-4
54. Li M, Liu M, Geng J, Han M, Sun X, Shao Y, et al. Experimental verification of the nonadiabatic effect in strong-field ionization with elliptical polarization. Phys.Rev.A (2017) 95:053425. doi:10.1103/PhysRevA.95.053425
55. Paulus G, Becker W, Nicklich W, Walther H. Rescattering effects in above-threshold ionization: A classical model. J.Phys.B (1994) 27:L703–8. doi:10.1088/0953-4075/27/21/003
Keywords: rydberg state excitation, elliptically polarized laser field, ultrafast ionization, nonadiabatic effect, electron tunneling
Citation: Wang Z, Quan W, Hao X, Chen J and Liu X (2023) The ellipticity dependence of Rydberg state excitation of noble gas atoms subject to strong laser fields. Front. Phys. 11:1120654. doi: 10.3389/fphy.2023.1120654
Received: 10 December 2022; Accepted: 03 March 2023;
Published: 21 March 2023.
Edited by:
Yiqi Zhang, Xi’an Jiaotong University, ChinaReviewed by:
Yanpeng Zhang, Xi’an Jiaotong University, ChinaWeibin Li, University of Nottingham, United Kingdom
Copyright © 2023 Wang, Quan, Hao, Chen and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Quan, Y2hhcmx5d2luZ0B3aXBtLmFjLmNu; Xiaolei Hao, eGxoYW9Ac3h1LmVkdS5jbg==; Jing Chen, Y2hlbmppbmdAdXN0Yy5lZHUuY24=
 Zhiqiang Wang
Zhiqiang Wang Wei Quan
Wei Quan Xiaolei Hao1*
Xiaolei Hao1* Jing Chen
Jing Chen