Abstract
We report on the direct generation of the high-power optical vortices at ∼2.7 μm from an Er:Y2O3 ceramic laser end-pumped by an annular pump beam using a simple capillary fiber-based pump beam conditioning scheme. Taking advantage of the thermal gradient on the gain medium and mode matching between the pump and oscillating modes, vortex beams with a controllable topological charge order of l = 1 and l = 2 were successfully achieved. The laser yields 4.65 W of output power at an absorbed power of 19.8 W, corresponding to a slope efficiency of 25.9% with respect to the absorbed pump power. Adaptable beam profiles from a shallow crater-shape to quasi-top-hat intensity patterns were directly produced by actively defining the gain distribution in the ceramic, generating 4-W shallow crater-shape beams and 3.9-W quasi-top-hat beams, corresponding to a slope efficiency of 22.0% and 22.7%, respectively. Such optical vortices and tailored spatial intensity profiles in the 3-µm spectral region will enable novel applications, such as super-resolution molecular spectroscopy and material processing.
1 Introduction
Optical vortices characterized by a helical phase variation and a donut intensity spatial distribution carry orbital angular momentum (OAM) of lħ per photon in the beam, where l is the topological charge or vortex order [1–3]. Coherent sources of the vortex at different wavelengths have found widespread applications in science and technology, including the presence of an extra degree of freedom for improving the channel capacity in optical communications [4], quantum communications [5], super-resolution optical microscopy [6], optical trapping, and manipulation [7, 8]. In particular, optical vortex sources that operate in the mid-infrared region, where rich spectroscopic signatures exist [9, 10], will open up the prospects for super-resolution molecular spectroscopy and microstructure fabrication. Common methods used for generating optical vortices are mainly based on external mode converters, such as spiral phase plates (SPPs) [11], q-plates [12], cylindrical lenses [13], or spatial light modulators (SLMs) [4]. These techniques suffer from at least one of the common drawbacks, such as low wavelength coverage, power handling limitation, and high cost. For example, material dispersion restricts SPP’s effectiveness to discrete wavelengths, and thus, it is difficult to produce broadband vortices. SLMs and q-plates usually suffer from a low damage threshold and thus are difficult for high-power operation. Non-linear frequency conversion techniques [14–16], i.e., optical parametric oscillators (OPO) or optical parametric amplifiers (OPAs), could be an alternative way, providing high power and wavelength-versatile vortices, while the generated topological charge depends highly on the input near-infrared vortex beams [16].
In recent years, “direct generation” techniques have evolved as a simple and efficient route for producing optical vortices [17–20]. Employing a spatially structured pump beam based on a mode-matching principle, optical vortices can be directly generated in a robust laser resonator with advantages of power scalability and high beam quality [18–20]. So far, great efforts have been made to produce optical vortices in the visible and near-infrared spectral regions [18–22], while the exploitation of vortex beams in the mid-infrared spectral region is relatively scarce. In 2019, the first 2.7-μm optical vortex beam was directly generated from an Er:Y2O3 ceramic laser and due to the additional insertion loss and serious thermal issues, the output power of the LG01 mode was less than 125 mW [23]. Recently, by using polycrystalline Fe:ZnSe as a saturable absorber (SA), the Q-switched LG01 mode from a 2.7-µm Er:YAP laser was demonstrated [24].
In this paper, we demonstrate the high-power optical vertex operation of an Er:Y2O3 ceramic laser at ∼2.7 μm. A ring-shaped pump beam was employed to spatially match the desired LG0l mode in the laser resonator. Benefits from mode matching between the pump and lasing mode and proper thermal gradient on the ceramic, controllable topological charge order of l = 1 and l = 2 are successfully produced. The laser generated 4.65 W of output power for an absorbed power of 19.8 W, corresponding to a slope efficiency of 25.9% with respect to the absorbed pump power. Direct generation of adaptable beam profiles from a shallow crater shape to quasi-top-hat intensity patterns are achieved by actively defining the gain distribution in the ceramic. The laser produced 4 W of output with shallow crater-shape intensity profiles and 3.9 W of quasi-top-hat intensity profiles, corresponding to a slope efficiency of 22.0% and 22.7%, respectively. This study, to the best of our knowledge, represents the highest output power of optical vortices directly generated from a solid-state oscillator in the 3-μm region and the first direct generation of adaptable beam profiles in this spectral region.
2 Experimental setup
Schematic representation of the experimental setup is shown in Figure 1. An Er:Y2O3 ceramic which was grown in the house via co-precipitation with an Er3+ doping level of 7.0 at% and length 13.5 mm was used as the gain medium. Furthermore, details can be found in [25]. The ceramic was water-cooled using a copper heat sink maintained at a temperature of 15°C to alleviate thermal loading. The pump source was provided by a high-brightness 976-nm laser diode with a delivery fiber of 105-µm core and 0.22 NA. The output of the laser diode was spectrally narrowed, and the wavelength was stabilized with a volume Bragg grating to have a line width of ∼0.3 nm. To produce the required ring-shaped beam profile, the output from the laser diode was launched into the annular waveguide of a capillary fiber with a 300-μm diameter inner-cladding and a 110-μm-diameter air-hole in the center. The reformatted pump beam from the capillary fiber was imaged into the Er:Y2O3 ceramic using a telescope configuration with a waist outer radius of ∼320 μm and an inner “hole” radius of ∼110 μm. The inset of Figure 1 shows the spatial pattern evolution of the pump beam after passing through F2. The pump beam has an expected annular near-field intensity distribution and which could maintain at a distance of ∼14 mm, covering the entire length of the ceramic. At the position away from the focal plane, the pump beams gradually evolve into a Gaussian-like profile (see the inset of Figure 1). Thus, to spatially match the intensity distribution for the desired LG0l mode, the ceramic was located at the position where the pump beam with the annular intensity distribution could preserve over the entire length of the ceramic.
FIGURE 1
Schematic diagram of the Er:Y2O3 ceramic laser.
The Er:Y2O3 ceramic laser resonator comprised a plane input coupler (IC, anti-reflective coated of T >85% at ∼980 nm and high reflectivity R >99.8% at 2.65–2.95 μm) and a plane output coupler (OC) with 10% transmission at the lasing wavelength and a transmission of T >85% at the pump wavelength. A 45° dichroic mirror (DM) was used as a beam splitter to filter the residual pump light in the output beam. Output power and spectrum were recorded using a power meter (Ophir, 3 A-PF-12) and an optical spectrum analyzer of 50-p.m. resolution (AQ6375B, Yokogawa). The pump and output beam profiles were monitored with the aid of an infrared CCD (Xeva-1.7) and a mid-infrared CCD camera (WinCamD-IR-BB), respectively.
3 Results and discussion
The Er:Y2O3 ceramic laser output power, as a function of absorbed pump power, is shown in Figure 2. The laser reaches a threshold at an absorbed pump power of ∼1.53 W and generated 4.65 W of output power at an absorbed power of 19.8 W, giving a slope efficiency of 25.9% with respect to the absorbed pump power. In comparison with the performance of a previously reported 2.7-µm vortex laser oscillator [23, 24], the output power achieved in the present study was improved by one order of magnitude and the high slope efficiency could be attributed to the mode matching between the annular pump beam and the LG0,l mode [26]. We monitored the stability of the output transverse modes and found that it was not maintained with increasing pump power. The inset in Figure 2 shows the output transverse mode profiles at different pump powers. Near the lasing threshold, we observed that output beam profiles were not stable but changed over time. The TEM00 mode occasionally appeared, but the primary pattern was a petal-like structure with two lobes, which was a result of the coherent superposition of the LG01 modes with opposite helicity [23]. By further increasing the pump power and slightly misaligning the resonator, a clear donut-shaped intensity profile was successfully generated, which is indicative of the single LG0,1 mode and which was sustained in the pump range from 3.4 to 15.7 W. As the absorbed pump power increased to over 15.7 W, the higher-order LG02 mode was excited.
FIGURE 2
Dependence of the output power and transverse patterns on the absorbed pump power.
The underlying mechanism for generation of LG0,l modes in an annular pumping scheme can be explained by the mode selection rule. According to the relationship Pth ∝ Aeff [26], the lasing mode that better matches a smaller effective pump (Aeff) area exhibits a lower laser threshold and, thus, preferentially oscillates. The effective pump area Aeff for the LG0,l modes can be given by [26] where is the TEM00 mode waist radius, and a and b are the inner and outer radii of the ring-shaped pump beam, respectively. Figure 3 shows the calculated Aeff values for the LG0,l (l = 0, 1, and 2) modes with respect to the TEM00 mode waist (ω0) using the pump size in our case (an inner radius of 110 µm and an outer radius of 320 µm). As can be seen, for ω0>∼ 290 μm, a TEM00 mode has the lowest Aeff value and, thus, will be excited preferentially. Decreasing the beam waist to the range of 205 µm <ω0 < 290 μm, the LG0,1 mode will be excited. Furthermore, reducing the beam waist to ω0 < 205 μm, a higher-order LG0,2 mode can be produced. Therefore, the observed higher modes, i.e., LG02, could be explained by that the increased thermal gradient at high pump powers gives rise to serious thermal lens effects, which reduces the sizes of oscillating modes and makes the higher-order mode match well with the pump beam [27].
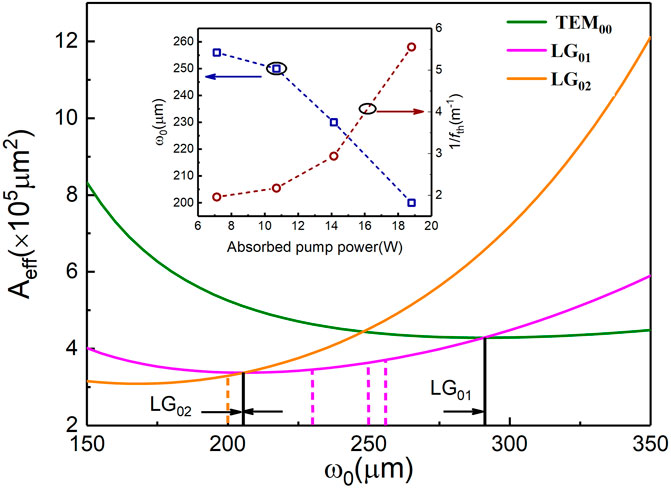
FIGURE 3
Simulated effective pump area for TEM00, LG01, and LG02 modes. Inset: dependence of the TEM00 mode radius and the optical power thermal lens on the absorbed pump power.
To confirm this assumption, we measured the thermal focal length (fth) at different ranges of the absorbed pump power. The inset of Figure 3 shows the optical power thermal lens (1/fth) at an absorbed pump power of 7.1 W, 10.7 W, 14.1 W (experimental LG01 mode output), and 18.8 W (LG02 mode output). As can be seen, the thermally induced focal length fth decreased with the increase of the pump power, and consequently, the beam size of the TEM00 mode was calculated and found to be decreased monotonically based on the ABCD matrix, as shown in the inset of Figure 3. To be clear, the calculated mode sizes are depicted in Figure 3 as orange and red dotted lines. As can be seen, the experimentally observed LG01 mode (red dotted line) and LG02 mode (orange dotted lines) fall into the theoretical modeled mode region of the LG01 mode and LG02 mode, respectively. The close agreement between experimental results and the theoretical model is indicative of the LG0,l mode excitation and was selected by mode matching, and the topological charge orders were thermally driven.
The normalized transverse intensity distributions of the LG01 mode and LG02 mode output, as a function of the radial position, are shown in Figure 4A. According to the radial intensity distributions for the LG0,l mode, is obtained as follows [28]where w(z) is the transverse beam radius, and the theoretical intensity distributions of the LG01 mode and LG02 mode are depicted as green and black curves, respectively, in Figure 4A. As can be seen, the measured transverse intensity is in close agreement with the theoretical intensity profiles, which further confirmed the excited laser modes are indeed LG0,1 and LG0,2 modes. Typical lasing spectra of the ceramic laser are shown in Figure 4B, and dual wavelength operation at ∼2,717 nm and ∼2,740 nm was observed. To select a pure LG0,+1, LG0,+2, (or LG0,−1, LG0,−2) mode, an asymmetric cavity loss was introduced by slightly misaligning the OC [29, 30]. The helicity was confirmed by detecting its interference pattern by using the homemade Mach–Zehnder interferometer. As seen in the inset of Figure 4B, the typical fork-shape stripes with one fork indicate that the laser beam oscillated in a pure LG0,1 mode with l = +1. We also tried to fine-tune the OC to obtain the LG0,−1 mode and LG0,±2 mode, while they were detected but difficult to be maintained over time. Furthermore, the LG0,−1 and LG0,±2 mode output with stable well-defined helicity could be achievable by inserting an etalon in the laser resonator to additionally introduce distinguishable loss for the opposite helicity [18, 23].
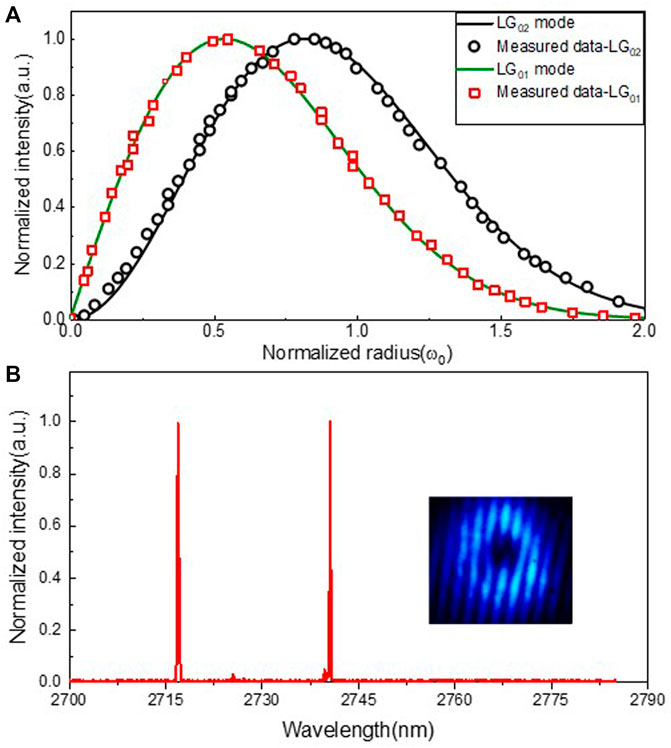
FIGURE 4
(A) Theoretical and measured transverse intensity distributions for the LG01 and LG02 mode (B) output spectra of the vortex laser. Inset: intensity interference pattern of the produced LG0,+1 mode.
To further explore the tunability on output beam profiles, we then carefully define the gain distribution in the laser ceramic. This is achieved by adjusting the location of lens F2 against the pump direction to actively control the pump beam intensity distribution in the ceramic, as shown in Figure 1. In other words, benefitting from the pump beam intensity distribution evolution dynamics, the pump region in the ceramic will be fulfilled from annular pump intensity distribution to the existed partial Gaussian-like intensity distribution with gradually translating F2. This combined pump intensity provides available gain in the central volume of the pumped region, which has the highest overlap with TEM00 modes. Therefore, under appropriate pump conditions, the laser will operate in the multimode and the output intensity profile depends on the pump intensity profiles in the ceramic. By continuously translating F2, we observed that the produced beam profiles ranged from the annular intensity pattern, to a shallow crater-shape distribution and, finally, to a quasi-top-hat distribution. Figures 5A, B show the produced shallow crater-shape distribution pattern and quasi-top-hat distribution pattern, respectively. By fitting the normalized transverse intensity distributions with the theoretical model [31], it is indicative that the output profiles are an incoherent superposition of the TEM00 and LG02 modes. The laser output power as a function of absorbed pump power for both beams is shown in Figure 5C. The laser yielded 4 W and 3.9 W of output power for shallow crater-shape beams and quasi-top-hat beams, respectively, at an absorbed pump power of 19.8 W. The corresponding slope efficiency was 22.0% and 22.7%, respectively, with respect to absorbed pump power. The tailored spatial intensity profiles in the 3-μm spectral region will benefit a range of novel applications, such as scientific research and material processing technology.
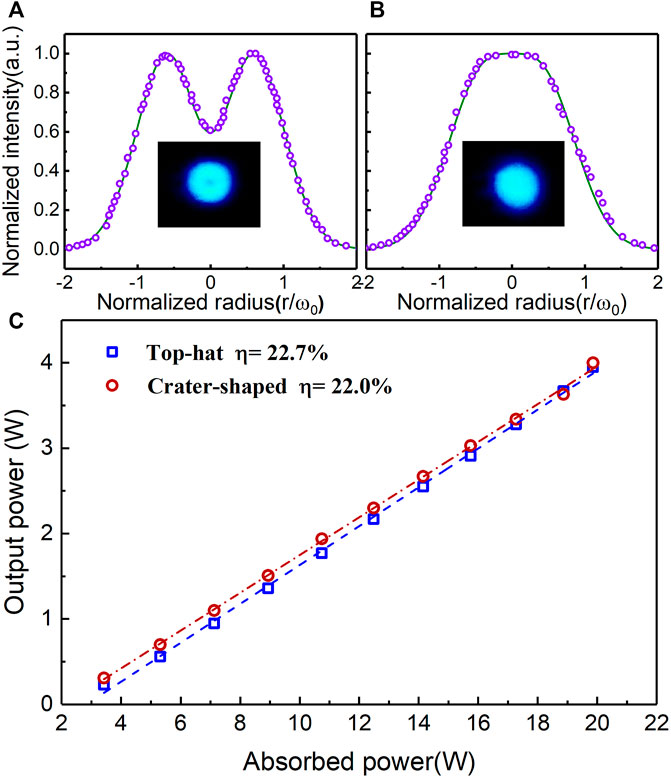
FIGURE 5
Beam profiles and measured transverse intensity distributions of the (A) shallow crater-shape mode and (B) quasi-top-hat mode. The solid lines are the normalized theoretical intensity distribution. (C) Laser output power as a function of the absorbed pump power for the shallow crater-shape and quasi-top-hat modes.
4 Conclusion
In summary, we have demonstrated the direct generation of high-power LG0,l beams (l = 1, 2) from an Er:Y2O3 ceramic laser in the 3-µm spectral region. The pump beams were tailored to possess an annular intensity distribution using a simple capillary fiber to spatially match the desired LG0l mode in the laser resonator. Based on the theoretical model for mode selection, we show that the laser was thermally driven and a proper thermal gradient on the ceramic enable the generation of vortex beams with controllable topological charge orders of l = 1 and l = 2, and no obvious reduction in optical efficiency is observed. The laser generated 4.65 W of output power for an absorbed power of 19.8 W, corresponding to a slope efficiency of 25.9% with respect to the absorbed pump power. Using a simple strategy to define the appropriate gain distribution in the ceramic, spatial intensity distributions ranging from a shallow crater-shape to a distribution with a quasi-top-hat profile were successfully produced. The laser generated 4 W of output with a shallow crater-shape and 3.9 W of quasi-top-hat intensity profiles, corresponding to a slope efficiency of 22.0% and 22.7%, respectively. Such optical vortices and tailored spatial intensity profiles in the 3-µm spectral region will benefit a range of novel applications, such as super-resolution molecular spectroscopy and fabrication of chiral organic materials.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the manuscript and approved it for publication.
Funding
This work is supported by the National Natural Science Foundation of China (62105130, 62035007, and 61875078).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Allen L Beijersbergen MW Spreeuw RJC Woerdman JP . Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45(11):8185–9. 10.1103/PhysRevA.45.8185
2.
He C Shen YJ Forbes A . Towards higher-dimensional structured light. Light Sci Appl (2022) 11(1):205–17. 10.1038/s41377-022-00897-3
3.
Shen YJ Wang XJ Xie ZW Min C Fu X Liu Q et al Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci Appl (2019) 8(1):90–29. 10.1038/s41377-019-0194-2
4.
Wang J Yang JY Fazal IM Ahmed N Yan Y Huang H et al Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat Photon (2012) 6(7):488–96. 10.1038/NPHOTON.2012.138
5.
Barreiro JT Paul TW Kwiat G . Beating the channel capacity limit for linear photonic superdense coding. Nat Phys (2008) 4(4):282–6. 10.1038/nphys919
6.
Heller I Sitters G Broekmans OD Farge G Menges C Wende W et al STED nanoscopy combined with optical tweezers reveals protein dynamics on densely covered DNA. Nat Methods (2013) 10(9):910–6. 10.1038/nmeth.2599
7.
Grier DG . A revolution in optical manipulation. Nature (2003) 424(6950):810–6. 10.1038/nature01935
8.
Franke-Arnold S Allen L Padgett M . Advances in optical angular momentum. Laser&photon Rev (2008) 2(4):299–313. 10.1002/lpor.200810007
9.
Huth F Govyadinov A Amarie S Nuansing W Keilmann F Hillenbrand R . Nano-FTIR absorption spectroscopy of molecular fingerprints at 20 nm spatial resolution. Nano Lett (2012) 12:3973–8. 10.1021/nl301159v
10.
Tittel FK Richter D Fried A . Mid-Infrared laser applications in spectroscopy. In: SorokinaITVodopyanovKL, editors. Solid-state mid-infrared laser sources. Charm: Springer (2003). p. 458–529. 10.1007/3-540-36491-9_11
11.
Beijersbergen MW Coerwinkel RPC Kristensen M Woerdman JP . Helical-wavefront laser beams produced with a spiral phaseplate. Opt Commun (1994) 112(5-6):321–7. 10.1016/0030-4018(94)90638-6
12.
Marrucci L Manzo C Paparo D . Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett (2006) 96(16):163905. 10.1103/physrevlett.96.163905
13.
Bai YH Lv HR Fu X Yang YJ . Vortex beam: Generation and detection of orbital angular momentum [invited]. Chin Opt Lett (2022) 20(1):012601. 10.3788/COL202220.012601
14.
Aadhi A Sharma V Samanta GK . High-power, continuous-wave, tunable mid-IR, higher-order vortex beam optical parametric oscillator. Opt Lett (2018) 43(10):2312–5. 10.1364/OL.43.002312
15.
Furuki K Horikawa MT Ogawa A Miyamoto K Omatsu T . Tunable mid-infrared (6.3-12 μm) optical vortex pulse generation. Opt Express (2014) 22(21):26351–7. 10.1364/OE.22.026351
16.
Camper A Park H Lai YH Kageyama H Li S Talbert BK et al Tunable mid-infrared source of light carrying orbital angular momentum in the femtosecond regime. Opt Lett (2017) 42(19):3769–72. 10.1364/OL.42.003769
17.
Wang YB Shen YJ Meng Y Gong M . Generation of 1535-nm pulsed vortex beam in a diode-pumped Er, Yb: Glass microchip laser. IEEE Photon Technol Lett (2018) 30(10):891–4. 10.1109/LPT.2018.2822838
18.
Kim DJ Kim JW . Direct generation of an optical vortex beam in a single-frequency Nd: YVO4 laser. Opt Lett (2015) 40(3):399–402. 10.1364/ol.40.000399
19.
Lin D Daniel JMO Clarkson WA . Controlling the handedness of directly excited Laguerre-Gaussian modes in a solid-state laser. Opt Lett (2014) 39(13):3903–6. 10.1364/OL.39.003903
20.
Fang ZQ Yao Y Xia KG Li JL . Actively Q-switched and vortex Nd:YAG laser. Opt Commun (2015) 347:59–63. 10.1016/j.optcom.2015.02.037
21.
Ma Y Vallés A Tung JC Chen YF Miyamoto K Omatsuet T . Direct generation of red and orange optical vortex beams from an off-axis diode-pumped Pr3+: YLF laser. Opt Express (2019) 27(13):18190–200. 10.1364/OE.27.018190
22.
Shen YJ Meng Y Fu X Gong M . Wavelength-tunable hermite-Gaussian modes and an orbital-angular-momentum-tunable vortex beam in a dual-off-axis pumped Yb: CALGO laser. Opt Lett (2018) 43(2):291–4. 10.1364/OL.43.000291
23.
Ding MM Chen Y Wang J Yin DL Zhao YG Shen DY et al 2.7 µm optical vortex beam directly generated from an Er:Y2O3 ceramic laser. Opt Lett (2019) 44(20):4973–6. 10.1364/OL.44.004973
24.
Gao QG Zhou JJ Jia DW Wang YY Chen B Zhao YG et al Direct generation of mid-infrared pulsed optical vortices at∼ 2.7 µm. Opt Express (2021) 29(25):41842–50. 10.1364/OE.444033
25.
Ding MM Li XX Wang F Shen DY Wang J Tang DY et al Power scaling of diode-pumped Er: Y2O3 ceramic laser at 2.7 μm. Appl Phys Express (2022) 15(6):062004. 10.35848/1882-0786/ac6da3
26.
Kim JW Clarkson WA . Selective generation of laguerre-Gaussian (LG0n) mode output in a diode-laser pumped Nd: YAG laser. Opt Commun (2013) 296:109–12. 10.1016/j.optcom.2013.01.046i
27.
Ding YT Xu MM Zhao YG Yu HH Zhang HJ Wang ZP et al Thermally driven continuous-wave and pulsed optical vortex. Opt Lett (2014) 39(8):2366–9. 10.1364/OL.39.002366
28.
Zhang J Huang SJ Zhu FQ Shao W Chen MS . Dimensional properties of Laguerre–Gaussian vortex beams. Appl Opt (2017) 56(12):3556–61. 10.1364/AO.56.003556
29.
Lu JL Lin FHF Zhang G Li BX Zhang LZ Chen YF et al Direct generation of an optical vortex beam from a diode-pumped Yb:MgWO4 laser. Laser Phys Lett (2017) 14:085807. 10.1088/1612-202X/aa7878
30.
Chen YF Lan YP . Dynamics of the Laguerre Gaussian TEM0,l* mode in a solid-state laser. Phys Rev A (2001) 63:063807. 10.1103/physreva.63.063807
31.
Kim DJ Mackenzie JI Kim JW . Adaptable beam profiles from a dual-cavity Nd:YAG laser. Opt Lett (2016) 41(8):1740–3. 10.1364/OL.41.001740
Summary
Keywords
optical vortices, 2.7 μm, high-power laser, Er:Y2O3 ceramic, annular puming
Citation
Ding M, Wang J, Wang F, Shen D, Tang D and Zhu H (2023) High-power Er:Y2O3 ceramic laser with an optical vortex beam output at ∼ 2.7 μm. Front. Phys. 11:1119263. doi: 10.3389/fphy.2023.1119263
Received
08 December 2022
Accepted
13 January 2023
Published
02 February 2023
Volume
11 - 2023
Edited by
Houkun Liang, Sichuan University, China
Reviewed by
Yijie Shen, University of Southampton, United Kingdom
Chaoliang Ding, Luoyang Normal University, China
Updates
Copyright
© 2023 Ding, Wang, Wang, Shen, Tang and Zhu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Deyuan Shen, mrde@jsnu.edu.cn
This article was submitted to Optics and Photonics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.