Numerical investigation of non-linear inverse Compton scattering in double-layer targets

Non-linear inverse Compton scattering (NICS) is of significance in laser-plasma physics and for application-relevant laser-driven photon sources. Given this interest, we investigated this synchrotron-like photon emission in a promising configuration achieved when an ultra-intense laser pulse interacts with a double-layer target (DLT). Numerical simulations with two-dimensional particle-in-cell codes and analytical estimates are used for this purpose. The properties of NICS are shown to be governed by the processes characterizing laser interaction with the near-critical and solid layers composing the DLT. In particular, electron acceleration, laser focusing in the low-density layer, and pulse reflection on the solid layer determine the radiated power, the emitted spectrum, and the angular properties of emitted photons. Analytical estimates, supported by simulations, show that quantum effects are relevant at laser intensities as small as $\sim 10^{21}$ W/cm² Target and laser parameters affect the NICS competition with bremsstrahlung and the conversion efficiency and average energy of emitted photons. Therefore, DLT properties could be exploited to tune and enhance photon emission in experiments and future applications.

1 Introduction

In the field of ultra-high intensity ($>10^{18}$ W/cm²) laser–plasma interactions, high-energy photon (x-rays and γ-rays) production has become of great interest for its impact on plasma dynamics (e.g., effects of radiation reaction on particles [1–4]), for fundamental studies (e.g., investigation of quantum-electrodynamics (QED) in strong fields [5] and plasmas [6, 7]), and for several potential applications. Some of these are plasma diagnostics [8], interrogation of nuclear materials [9], radiography [10], tomography [11], and imaging [12] for industrial and medical purposes, as well as photo-nuclear spectroscopy [13, 14].

Photon emission by electrons in the laser–plasma interaction occurs mainly through two processes: bremsstrahlung mediated by high-Z atoms in dense-plasma regions [15, 16], and non-linear inverse Compton scattering (NICS) mediated by strong electromagnetic fields [5]. NICS is expected to be the dominant emission process at very high intensities when a₀ = eE₀/(m_eω₀c) ≥ 100, where a₀ is the normalized vector potential defined with the electron charge e, the electric field peak amplitude E₀, the electron mass m_e, the laser frequency ω₀, and the speed of light c. Instead, bremsstrahlung strongly depends on the target atomic number Z, density, and geometry. Thus, it is expected to dominate for thick enough, high-Z-material targets [17].

NICS is the process in which an electron absorbing multiple laser photons emits a high-energy photon [5]. It is the quantum version of synchrotron emission important in the regime in which the ultra-high intensities of the electromagnetic fields and the high energy of the electron make relevant spin effects and the discrete stochastic nature of the emitted radiation [3, 4]. The main parameter to describe this emission is a Lorentz invariant, usually referred to as the electron quantum parameter:

$\chi =\frac{\gamma }{E_s}\sqrt{{\left(\mathbf{E}+\mathbf{v}\times \mathbf{B}\right)}^2-{\left(\frac{\mathbf{E}\cdot \mathbf{v}}{c}\right)}^2},(1)$

where γ is the emitting electron Lorentz factor, $E_s=m_e^2{c}^3/(\hslash e)=1.3\cdot 10^{18}$ V/m is the Schwinger field with ℏ being the reduced Planck constant, v is the electron velocity, and E and B are the electromagnetic fields at the electron position. χ is related to the transverse acceleration exerted instantaneously by the electromagnetic field on the electron and determines the emission rate and the radiated power by the electron. χ → 0 is the classical limit of continuous emission in which the instantaneous power radiated away is given by the Larmor formula P_rad = 2m_ec²α²χ²/(3τ_e) with τ_e = e²/(4πϵ₀m_ec³) being the time for light to cross the classical radius of the electron, ϵ₀ is the vacuum permittivity, and α is the fine structure constant. For χ ∼ 1, quantum effects become important. In particular, a single emitted photon carries a significant fraction of the electron energy, and the classical emitted power is corrected by a factor $g\left(\chi \right)$ (see Equation (4) in Section 3.2) that reduces the radiated power, albeit letting it always increase with χ. From Eq. 1, it is easy to deduce that χ assumes large values when the electromagnetic field propagation direction k and the electron velocity v are anti-parallel. In this condition, χ ≈ 2γE_⊥/E_s [18], where E_⊥ is the electric field perpendicular to the electron motion. In general, the emission is enhanced by this condition of counter-propagation and the combination of energetic electrons (γ ≫ 1) and intense fields (a₀ ≫ 1).

The first experiments on NICS have been performed by colliding a high-intensity laser pulse with a relativistic electron beam from a conventional linear accelerator [19]. In all-optical setups, NICS has been observed in several cases exploiting laser wakefield acceleration (LWFA) with either two counter-propagating laser beams [1, 2] or only one laser beam reflected from a plasma mirror [20]. However, the low density of the gas target in these schemes and, consequently, the limited number of high-energy electrons (bunch charge around tens of pC) limit the conversion efficiency from laser to photons [21, 22]. Higher efficiencies would be possible at higher densities in solid foils [6] or, even better, in near-critical targets [23], that is, targets approaching the critical density $n_c=m_e{\omega }_0^2{ϵ}_0/e^2$ and granting efficient laser–plasma coupling. Nevertheless, simple solid or near-critical slabs cannot easily ensure both efficient electron generation and the condition of laser propagating against electrons. Therefore, these cases have not yet been studied thoroughly in experiments, and numerical studies have revealed that they would require extreme intensities ($>10^{22}-10^{23}$ W/cm²) to make the process efficient (conversion from laser to photons ≥5%) [24–32].

A highly developed target concept, like a double-layer target (DLT), could allow exploiting NICS more efficiently than the LWFA case and performing more accessible studies for current laser facilities. The DLT we consider here consists of a low-density layer placed on a solid substrate. The low-density layer is near-critical at a laser wavelength of around 1 µm and can be obtained by growing a nanostructured material (foam) on the substrate [33–35]. Laser propagating against electrons is achieved in DLTs thanks to the substrate acting as a plasma mirror like in [20]. At the same time, the near-critical layer enhances the hot-electron generation producing a high-charge (tens of nC) population of energetic electrons during the interaction [36]. The substrate reflects the laser pulse creating an overlap between the reflected field and the hot electrons efficiently accelerated before reflection by the laser itself. The fulfilment of the counter-propagation condition makes the DLT a promising scheme for NICS, as proved by some numerical studies [37–42] and preliminarily investigated by some of us as supervisors of [43]. Consequently, as demonstrated in [44], DLTs could become interesting for electron-positron pair generation at extreme intensities ($\sim 10^{23}$ W/cm²). At the same time, by choosing a micrometric DLT with low-Z layers, we can focus on NICS also in non-extreme regimes of laser–plasma interaction (a₀ ∼ 20–60) since bremsstrahlung production yield has proven to be low in this case [45, 46]. Very recently, proof of highly efficient photon generation via NICS in DLTs has been obtained experimentally [47], confirming the expectations and relevance of this approach.

The micrometric target case and the time scales of NICS, which follow the typical laser pulse time scales of tens of fs, are accessible to particle-in-cell (PIC) simulations. PIC codes, well-established tools to simulate collisionless plasmas in self-consistent electromagnetic fields, have been recently enriched with several packages to simulate additional physics, including synchrotron-like emission. One of the most feasible and accurate ways to simulate photon emission via NICS inside PIC codes is a Monte Carlo method [48]. This strategy adopts a semi-classical approach using emission rates calculated in the locally constant crossed field approximation (LCFA), which assumes only first-order QED processes and is now standard in many PIC codes [49–51].

An in-depth numerical investigation of NICS during the laser–DLT interaction is preparatory to any experimental campaign. Some numerical studies of NICS in DLTs or similar targets [37, 38, 41, 44] focus on the very high-intensity regime, a₀ ∼ 100–300, which is not ordinary in current laser facilities and was only recently achieved experimentally [52]. For these reasons, in this work, we study NICS in DLTs at non-extreme intensities (a₀ ∼ 20–60) with a sizeable numerical scan of 2D PIC simulations performed with Smilei [53], a PIC code capable of simulating NICS. Some existing studies focus on non-extreme intensities similar to ours but with different objectives or target properties [39, 40, 42]. We want to contribute novel aspects with respect to these investigations, specifying that, on the comparable parts, our findings are compatible with the results of these works. We focus first on the physical aspects of interaction and, in particular, of emission. Second, we reconstruct some photon emission properties analytically to test the numerical tool and evaluate the impact of quantum effects in this regime. Then, we compare NICS and bremsstrahlung in some selected cases to estimate the possible competition between the two processes in an experimental framework. Finally, we analyze the emission properties considering all the laser intensities and target parameters (foam density and length) studied in the simulation scan.

2 Materials and methods

We have investigated NICS in DLTs with the PIC code Smilei. This code embarks a Monte Carlo module for NICS based on the approach presented in [50]. This approach relies on the emission rates obtained within the LCFA (see discussion in [3]) and allows treating high-energy photons as macro-photons. When emitted, these macro-photons are created with a momentum pointing in the direction of the emitting electron, an approximation valid in the relativistic limit [54].

We have performed 2D simulations of a laser pulse interacting with a DLT. The simulation resolution is 62.5 points per µm in a box of 40.96 µm in y and variable in x from 34 to 74 µm according to the target length. The simulation duration also changes according to the target length from 138 fs to 272 fs. The laser pulse peak enters the simulation box from the x = 0 boundary nearly 20 fs after the beginning of the simulation. The laser pulse has wavelength λ = 2πc/ω₀ = 0.8 µm, a sin² temporal profile in intensity with FWHM = 20 fs and a Gaussian spatial profile with a waist (radius at which the field amplitudes fall to 1/e) of 3 μm, corresponding approximately to an f/4 focusing aperture. The laser is linearly polarized in the y plane of the box. These laser parameters have been chosen to be a characteristic of forthcoming experiments on multi-petawatt, ultrashort, Ti:Sapphire laser systems such as Apollon [55]. The target is a DLT with a fully ionized homogeneous carbon (Z = 6, A = 12) foam on top of a fully ionized aluminum (Z = 13, A = 27) layer of 2 µm thickness and density 450 n_c. The choice of fully ionized target layers results from having tested, considering field ionization in additional simulations, that the target atoms involved in the interaction rapidly get fully ionized at a₀ ≥ 20. The foam electrons are represented with up to 10 particles per cell (ppc) according to the layer density, foam ions with 1 ppc, substrate electrons with 32 ppc, and substrate ions with 3 ppc. Electrons are initialized with a temperature of 10 eV, and ions are initialized cold. Photon generation via NICS is switched on only for photon energies above 0.25 m_ec² and for χ > 10^–4. NICS is simulated with the default tables of Smilei, and pair production is neglected. We have performed 80 simulations exploring all the combinations of the following parameters: foam density n_e = 1, 2, 5, 10 n_c, foam thickness = 5, 10, 15, 20, 25 μm, and intensity I = 0.87, 3.46, 5.41, 7.79 ⋅ 10²¹ W/cm² (a₀ = 20, 40, 50, 60). A special simulation, called simulation A, characterized by a₀ = 50, foam thickness = 15 µm and foam density = 2 n_c was performed with a high temporal resolution of the diagnostics. We will use it in Section 3 to describe the physics of the interaction and the main properties of NICS in DLTs.

3 Results and discussion

3.1 Description of interaction and emission

We start reporting the results of simulation A (see Section 2). We use this simulation to describe the main aspects of the laser–DLT interaction and the consequent NICS emission. Figure 1 helps visualize the behavior of the laser and hot electrons during the simulation.

FIGURE 1

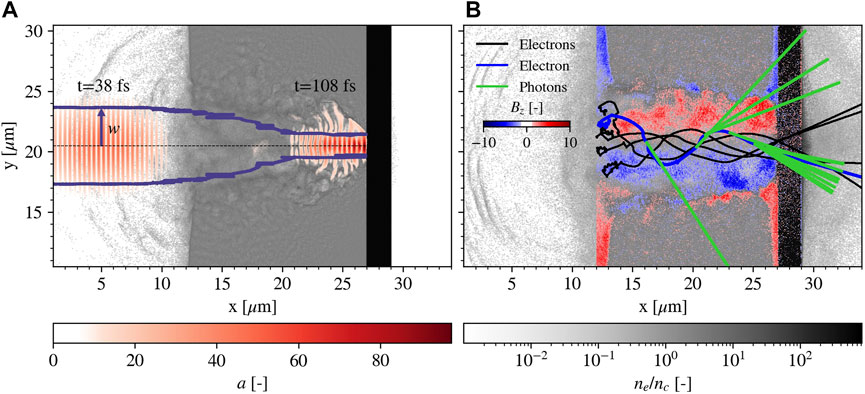
FIGURE 1. Evolution of the laser and trajectories of some electrons in simulation A. Plot (A) shows in blue lines the laser waist limits, calculated as the points where the field amplitude falls to 1/e of its maximum, and two snapshots of a = e|E|/(m_eω₀c) at 38 fs and 108 fs. The black dashed line indicates the center of the box in y. Plot (B) shows some trajectories of electrons and photons and the field B_z normalized to the code units at 204 fs. The represented electrons (black and blue lines) are characterized by a final value of kinetic energy above 60 MeV. The photons (green lines) are emitted by the electron represented in blue. In the background of both plots, the electron density normalized to n_c at 108 fs in (A) and 204 fs in (B).

Before the interaction, the laser pulse focused on the target left boundary undergoes free-propagation (Figure 1A laser snapshot at 38 fs). When the interaction with the low-density layer starts, the pulse experiences a progressive alteration of its spatial and temporal shape, and a gradual absorption [56]. The near-critical plasma behaves as a lens causing relativistic self-focusing [57–59]. This phenomenon induces the reduction of the laser spot size, the increase of the laser pulse intensity, and, consequently, the pulse confinement in a channel in which the electron density is depleted because of the ponderomotive force. As shown by the blue line in Figure 1A, the laser waist is decreased symmetrically inside the foam from 3 µm down to nearly 1 µm. During the interaction with the near-critical layer, a = e|E|/(m_eω₀c) increases from 50 to 70 and goes above 100 when the laser is reflected on the substrate (Figure 1A laser snapshot at 108 fs). As a consequence of reflection, the electromagnetic field strength is further enhanced due to the superposition of the incident and reflected pulse. A temporary standing wave builds in front of the substrate, and the peaks of the normalized electric field e|E|/(m_eω₀c) and magnetic field e|B|/(m_eω₀) alternatively grow up to 150 at the nodes and antinodes of this wave. Self-focusing and superposition can thus significantly boost NICS. Another phenomenon is the magnetization of the channel [60]: following the laser pulse propagation, the B_z component of the field fills the channel in two symmetric regions of opposite signs (Figure 1B).

The channel dug by the laser inside the plasma has a variable diameter that follows the reduction of the laser size during propagation. Hot electrons are generated in this channel with a broad energy spectrum with maximum energies up to 460 MeV. Indeed, when the interaction starts, electrons are rapidly accelerated via direct laser acceleration [61]. The trajectories of the most energetic electrons, black and blue lines in Figure 1B, show that, at the beginning of the interaction, the electrons are pushed backwards and then are accelerated into the channel following the laser pulse and co-moving with it. Simultaneously, the electrons experience betatron oscillations in the transverse direction driven by the magnetization of the channel, which, in addition, constrains electrons to be confined in the channel itself [61].

Some examples of the higher-energy emission are presented in Figure 1B, where the emitted photons are shown in green, and the emitting electron appears in blue. In general, we can distinguish two emission phases. Photons are produced firstly during the laser propagation through the foam; we call this the ramp phase [43] because emission occurs at a constant rate and the energy radiated away grows linearly. Then, a peak of emission happens in front of the substrate (burst phase [43]) when electrons see the counterpropagating reflected laser field. In Figure 2A, the number density of all emitted photons is reported. The emission occurs predominantly in the channel region of the foam, where most energetic electrons are confined. In Figure 2B, all the emitted photons are represented as arrows directed according to their momentum and colored according to their energy. We can recognize low-energy backward emitted photons, especially in the early phase of interaction (left side of the channel), and higher-energy forward emission due to oscillating electrons in the channel. Most photons and the most energetic ones are emitted before the substrate during the burst phase. The distributions in Figure 2C describe the directionality of photon emission in more detail. Although a background of emission is present at all angles due to the chaotic motion of electrons, photons are mainly emitted backwards during the ramp phase (blue curve) and in a cone of 30° around the forward direction during the burst phase (green curve). The energy distribution in the ramp phase (yellow curve) shows a more relevant contribution in energy by the forward emission due to electrons undergoing oscillations and following the laser pulse, as recognized in Figure 2B. During the burst phase, the emission shows two lobes peaked at 15°. This bilobal structure is typically observed when emitting electrons accelerated by a linearly polarized laser undergo oscillations in a near-critical plasma channel [23, 25, 27, 29, 62, 63]. The peak angle of the bilobal structure is determined by the angular deviation of betatron oscillations at the instant of copious burst emission. This angle is given by ϕ ∼ r_βω_β/c [63, 64], where r_β is the amplitude of the oscillations which is approximately given by the channel radius, and ${\omega }_{\beta }={\omega }_p/\sqrt{2\gamma }$ with ω_p the plasma frequency. Approximating r_β to the minimum waist achieved by the laser, that is 1 µm, and γ to 800, which is a value achieved by the most energetic electrons in the simulation, the angular deviation of oscillations results in 15,9°, which is in good agreement with what we see in Figure 2C.

FIGURE 2

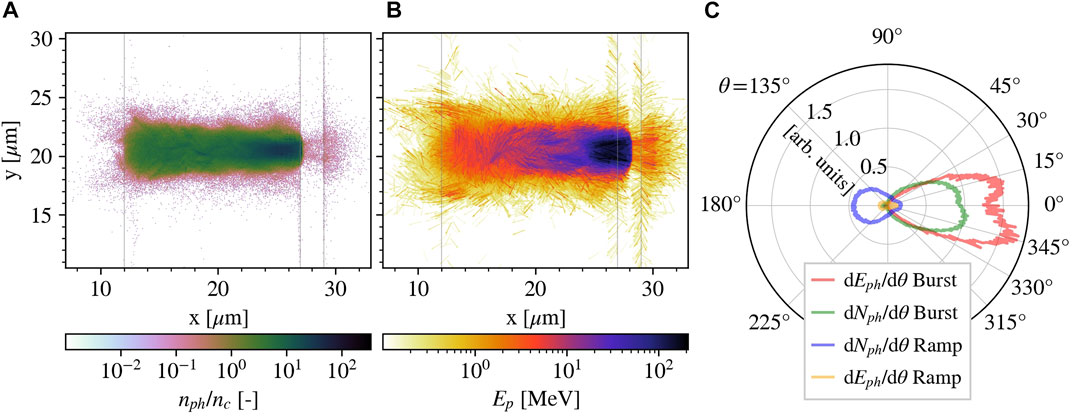
FIGURE 2. Spatial and angular information on photon emission: the distribution in space of photon number density normalized to n_c (A), the emitted photons represented as arrows directed according to their momentum and colored according to their energy E_p (B), and the photon angular distribution in number and energy (C) for the two phases of emission, that is, ramp (before 110 fs) and burst (after 110 fs). The three plots consider all the photons emitted in simulation A. In plots (A) and (B), photons are fixed in their emission position and grey lines indicate the target limits at the beginning of the simulation. The angle θ of the distribution in (C) is zero in the laser propagation direction.

The maximum values of χ reached by electrons are around 0.04 in the ramp phase and up to 0.33 in the burst phase. Since electron χ goes above 0.1 in this phase, we expect to see the impact of quantum effects [3, 48]. Using the approximation for χ mentioned in Section 1 for the counterpropagation condition, we can simply estimate the maximum value for this parameter in the burst phase using χ ≈ 2γa_fℏω₀/(m_ec²), where a_f is the maximum normalized vector potential achieved by self-focusing. We can check that using γ ≈ 800 and a_f ≈ 75, which are reasonable values for simulation A, this formula gives a χ value around 0.33. More insights are gained by discussing a more specific approximation for χ. Since the most relevant fields in the physical system are the laser ones, E_y and B_z, and the electrons are mainly accelerated in the forward direction, we can evaluate χ using this approximation of formula 1:

$\chi \simeq \frac{\gamma }{a_s}|E_y-{\beta }_x{B}_z|,(2)$

where a_s = mc²/(ℏω₀), β_x = v_x/c with v_x the electron velocity component in the laser propagation direction, and E_y and B_z are normalized by m_eω₀c/e and m_eω₀/e, respectively. As shown in Figure 3A by the red line, this approximated formula describes well the maximum value of χ achieved during the simulation. An improvement in the agreement is obtained considering also the term ${\beta }_y^2(B_z^2-E_y^2)$ due to the transversal motion of electrons (Figure 3A blue line). This panel helps understand which fields are determining the emission. Electric and magnetic fields’ contributions appear with opposite signs in formula 2, meaning that if the two fields are in phase, they cancel each other, and the emission is low unless β_x is negative (counterpropagating electron). This case occurs in the ramp phase in which emission is mainly due to low-energy electrons travelling against the laser (see backward emission in Figure 2). Furthermore, the rising quasi-electrostatic fields and a relevant y component of electron velocity lead to further emission during the ramp phase (Figure 3A blue line). In the burst phase, when reflection occurs, superposition leads to alternatively maximizing one field amplitude while lowering the other, and the E_y and B_z fields are phase-shifted. This effect is reported in Figure 3B. In the region between 110 and 130 fs, E_y and B_z values on the macroelectron with maximum χ at each timestep (represented by connected dots) are alternatively large and small, and their signs end up being opposite. The electric and magnetic fields’ contributions are not cancelling out, and χ reaches the maximum possible values as long as hot forward-propagating electrons are available to experience these fields.

FIGURE 3

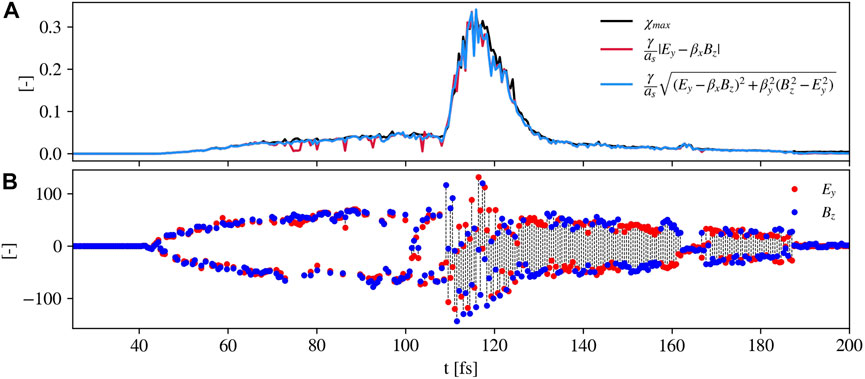
FIGURE 3. In (A), maximum values of χ obtained during the simulation: in black, the simulation values; in red, the values computed with formula 2 considering the macroelectrons with the maximum χ, and in blue the values calculated in the same way but with an additional correction. In (B), the electric field normalized by m_eω₀c/e in the y direction (red dots) and the magnetic field normalized by m_eω₀/e in the z direction (blue dots) felt by the macroelectron with the maximum χ at each timestep of the simulation diagnostic. The two field values for each macroelectron are connected with a dashed black line.

3.2 Comparison with analytical estimates

We compare some properties of emitted photons in simulation A with analytical results. Since Smilei simulates emission according to the LCFA and, thus, using the results for NICS in constant crossed fields, that is, when E⊥B and |E| = c|B|, we can use the results of this theory [3, 65–68] to estimate the evolution of the emitted power and the final spectrum of all emitted photons. We rearrange the formulas of this theory as functions of macro-electron properties: parameter χ, kinetic energy E_e, and numerical weight w_e. The instantaneous emitted power by all electrons is given by the summation of their contributions at a given time:

$P_{\mathit{rad}}=\frac{2{\alpha }^2{m}_e{c}^2}{3{\tau }_e}\sum _e{\chi }^{2}g\left(\chi \right)w_e,(3)$

where $g\left(\chi \right)$ is equal to 1 in the classical limit and given by the following expression in the general case:

$g\left(\chi \right)=\frac{9\sqrt{3}}{8\pi }{\int }_0^{\infty }\left[\frac{2{\xi }^2}{{\left(2+3\chi \xi \right)}^2}{K}_{5/3}\left(\xi \right)+\frac{36{\chi }^2{\xi }^3}{{\left(2+3\chi \xi \right)}^4}{K}_{2/3}\left(\xi \right)\right]d\xi ,(4)$

where K_v are the modified Bessel functions of the second kind, and ξ is the variable of integration. In Figure 4A, we have plotted the evolution of the emitted power in the simulation (black) compared with the same quantity obtained from formula 3 in the classical case (red) and with the quantum correction of formula 4 (blue). More precisely, the plotted quantities are power densities due to the reduced dimensionality of the simulations. The evolution of emitted power shows the two distinct phases we have highlighted in Section 3.1. The emitted power is nearly constant from 60 fs to 110 fs; thus, the energy converted in photons linearly increases: ramp phase. Instead, around 120 fs, the peak of emission characteristic of the burst phase occurs. While emission in the ramp phase is well-described in a classical framework of synchrotron emission, the emission peak in front of the substrate needs quantum corrections to be estimated correctly. This fact indicates that the quantum regime of synchrotron emission is observed here. The plot confirms that the quantum effects arising when χ approaches one reduce the emitted power against the classical case.

FIGURE 4

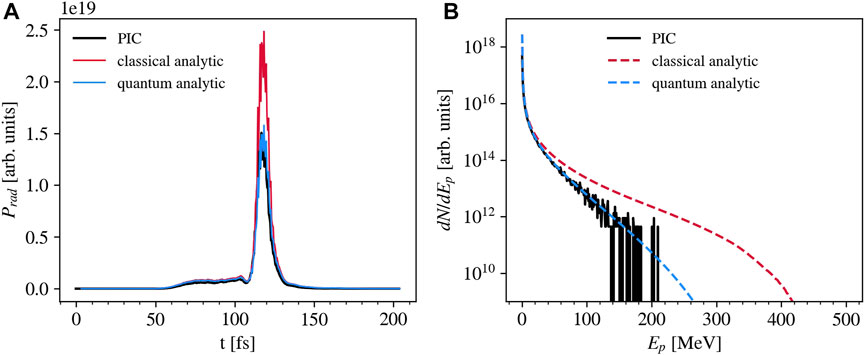
FIGURE 4. Comparison among emission properties obtained in simulation A and estimated analytically considering synchrotron emission classically or including quantum effects. Plot (A) shows the evolution in time of the emitted power densities. Plot (B) shows the final photon spectrum.

The energy spectrum of all emitted photons during the simulation is given analytically by a summation of electrons contributions integrated in time:

$\frac{dN}{d{E}_p}=\frac{{\alpha }^2{m}_e{c}^2}{\sqrt{3}\pi {\tau }_e}{\int }_{t_0}^{t_1}\sum _{E_e\ge E_p}\left\{w_e\frac{1}{E_e^2}\left[\frac{E_p^2}{E_e\left(E_e-E_p\right)}{K}_{2/3}\left(y\right)+{\int }_y^{\infty }{K}_{5/3}\left(x\right)dx\right]\right\}dt,(5)$

where t₀ and t₁ are the starting and ending time of the simulation, respectively, E_p is the photon energy, and y is given by the following equation:

$y=\frac{2E_p}{3\left(E_e-E_p\right)\chi }.(6)$

It is worth noting that E_e, χ, and, consequently, y are time-dependent quantities. The classical limit, corresponding to the usual synchrotron emission formula [54], is obtained neglecting the recoil of the radiating electrons, that is, by taking E_p ≪ E_e in Eqs. 5, 6:

$\frac{dN}{d{E}_p}=\frac{{\alpha }^2{m}_e{c}^2}{\sqrt{3}\pi {\tau }_e}{\int }_{t_0}^{t_1}dt\sum _{E_e\ge E_p}\left[w_e\frac{1}{E_e^2}{\int }_y^{\infty }{K}_{5/3}\left(x\right)dx\right],(7)$

$y=\frac{2E_p}{3E_e\chi }.(8)$

In Figure 4B, we compare the spectrum obtained in the simulation (solid black line) with those analytically estimated in the classical case (dashed red line) and with quantum corrections (dashed blue line). The NICS spectrum is broad with an exponential shape. This shape is expected considering the typically broad, nearly exponential spectra obtained for electrons in DLTs [69–71]. The quantum corrections change the slope and cut-off of the estimated spectrum at high energy since the most energetic emission is expected to come from electrons with higher χ and thus more affected by these corrections. The cut-off of the simulated spectrum is not present in the estimated ones. This effect is due to the reduced number of particles per cell used for macro-electrons in our simulations. If this number is low, reduced sampling affects the high-energy electrons and the photons they emit. We have tested that a visible improvement in the high-energy sampling in this plot occurs only by strongly increasing the number of macro-electrons by at least two orders of magnitude, making the simulation more expensive in computational resources.

The procedure described in this section is similar to some strategies reported in literature [72, 73] evaluating photon emission without using a Monte Carlo approach. Our estimates were performed after the simulation using the macro-electron properties saved by the diagnostics with a high time resolution. Even if the stochasticity of emission is not considered, formulas 3 and 5 can be valuable tools to check and estimate emission after PIC simulations in any case of interest and not only in the DLT case. Furthermore, this procedure can be used to recognize and evaluate the impact of quantum effects of NICS emission according to the laser and target configurations, as we have demonstrated in the DLT case.

3.3 Comparison with bremsstrahlung

Using analytical formulas and simulations, we can compare NICS and bremsstrahlung in the range of parameters explored in this work. Similarly to Eq. 5, we can estimate bremsstrahlung generated in the substrate, which is the target region with higher density and atomic number, thus the most relevant for this type of emission. We use a generalization of Eq. 7 of Ref. [46]:

$\frac{dN}{d{E}_p}=n_i{\int }_{t_0}^{t_1}dt{\int }_{E_p}^{\infty }d{E}_e\left[\frac{dN}{d{E}_e}{v}_e\frac{a{Z}^2}{E_p}\left(1-\frac{b{E}_p}{E_e}\right)\right],(9)$

where n_i is the ion density of the substrate, dN/dE_e is the time-dependent spectrum in energy of electrons inside the substrate, a = 11 ⋅ 10^–31 m² and b = 0.83. In Figure 5, we report NICS-bremsstrahlung comparisons in the case of foam thickness 25 µm and foam density 1 n_c varying the parameter a₀ (20–40-50–60). We show the NICS spectra obtained with Smilei (green), the bremsstrahlung spectra from analogous simulations using the PIC code EPOCH [74] that allows for Monte Carlo evaluation of bremsstrahlung [46] (blue), and the analytical estimates of bremsstrahlung using formula 9 (red). Due to the lower efficiencies of the two processes, we consider them independent, and we do not activate NICS emission in EPOCH. When a₀ = 40, 50, 60, bremsstrahlung is lower than NICS by at least two orders of magnitudes on the whole range of the spectrum. Instead, at a₀ = 20, NICS contribution is strongly reduced due to the relatively low laser intensity and becomes closer to the bremsstrahlung contribution. In this case, the two processes contribute similarly: the high-energy spectrum is dominated by bremsstrahlung, while in the low-energy portion, synchrotron radiation prevails. Overall, we deduce that the impact of NICS in our DLTs in non-extreme laser regimes is remarkably relevant. The results of Figure 5 can be discussed considering that NICS and bremsstrahlung have a different dependence on laser intensity. Bremsstrahlung depends on the electron energy achieved during the laser-driven acceleration of electrons and, thus, indirectly on laser intensity. On the other hand, NICS has an explicit dependence on intensity and the production yield goes approximately as $a_0^3$ as demonstrated for different target cases [25, 40, 75] and approximately valid also in our parametric scan (see Figure 7A). Increasing the intensity at a fixed target thickness, NICS will ultimately prevail on bremsstrahlung. Even if we are considering a foam-attached target, our results are consistent with the bare-aluminum case of [76]: in a micrometric target of aluminum, bremsstrahlung can be ignored for intensities $>10^{21}$ W/cm². Practically, only in the case a₀ = 20, among those presented, NICS and bremsstrahlung are comparable. In this case, the competition between the two processes could be discussed in detail with more accurate simulations, for example, in 3D geometry. If the thickness and/or the atomic number of the solid substrate are changed, the bremsstrahlung contribution becomes much more important [17, 76, 77], and the threshold to ignore bremsstrahlung shifts at higher intensities.

FIGURE 5

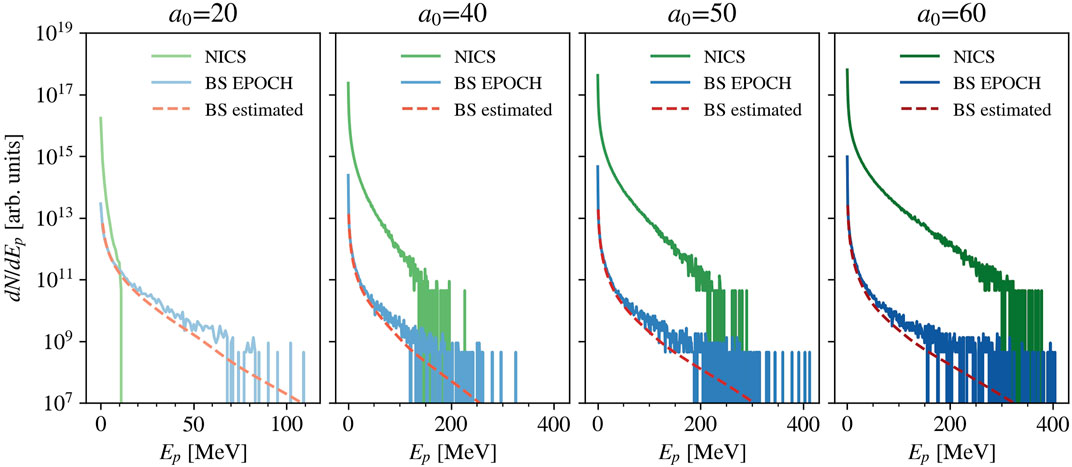
FIGURE 5. Spectra of emitted photons in the case of foam thickness 25 µm and foam density 1 n_c varying the parameter a₀ (20–40–50–60). The reported spectra refer to NICS emission from Smilei simulations (solid lines in green), bremsstrahlung (BS) emission simulated with the PIC code EPOCH (solid lines in blue) and estimated analytically (dashed lines in red).

3.4 Dependence on target and laser parameters

We report results from the whole simulation scan focusing on the dependencies of NICS emission properties on the laser and target parameters. We have chosen two properties for this analysis: the conversion efficiency from laser energy into photon energy and the average energy of all emitted photons (Figure 6). These quantities are expected to be useful in assessing the feasibility of applications and can be quantitatively evaluated in 2D simulations avoiding units altered by the reduced dimensionality. The conversion efficiencies represent the ratio between the energy in photons generated in the simulation, which have energy above 0.25 m_ec², and the laser energy. The presence of this cut-off reduces the conversion efficiency since only the high-energy portion of the electromagnetic spectrum is considered but avoids generating a lot of low-energy photons, which can be computationally heavy to handle. Furthermore, as noted in Section 3.2, low-energy emission is not affected by quantum effects and, thus, less relevant to be simulated with a Monte Carlo approach.

FIGURE 6

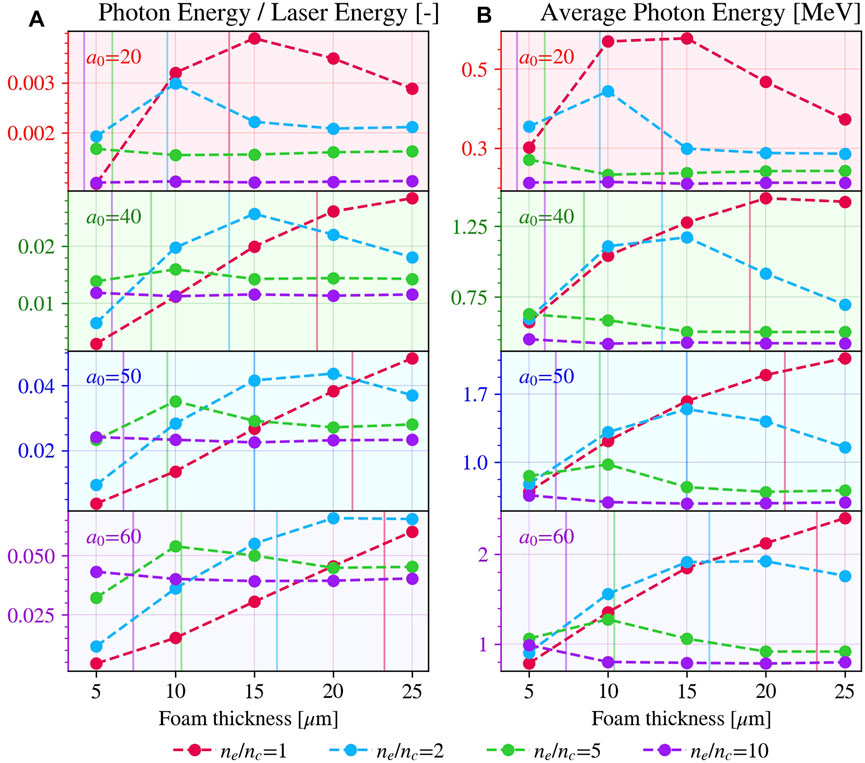
FIGURE 6. Conversion efficiency of photon energy in laser energy (A) and average energy of all emitted photons (B) in all the simulations performed varying a₀, foam thickness and density (n_e/n_c). Every circle represents a simulation. Vertical lines colored according to the density values indicate the self-focusing length.

In Figure 6A, we observe that the conversion efficiencies tend to show an optimum case in thickness for fixed a₀ and the foam density. Exceptions are the low-density cases at high a₀ where probably the scan is not covering the optimal cases corresponding to higher foam lengths, as shown by [40]. By decreasing a₀ or increasing the foam density, this optimum tends to shift toward lower lengths, and its value decreases. This effect is due to the lower transparency of the plasma to the laser. Shorter foams grant that the laser can reach the reflection on the substrate and thus the counter-propagation condition of the burst phase that enhances the efficiency and energy of emission. Contrarily, the cases with dense and long foams tend to suppress the burst emission because of relevant laser absorption during the propagation, a phenomenon evidenced in [78]. Because of this, the conversion efficiencies in long foam cases increase by lowering the density. However, denser cases can become optimal at shorter foam lengths.

The average photon energy (Figure 6B) shows similar optimal lengths once fixed a₀ and the density. The same comments on efficiencies are valid for the average photon energy, although dense foam cases have lower performance considering this parameter even in thinner foams.

The processes involving the laser pulse, in particular, the self-focusing and the consequent electron heating, directly impact NICS and its dependence on target parameters. 3D PIC simulations have revealed that the self-focusing effect generated by the near-critical target is representable as the action of a lens [56]. A thin-lens model can be used to obtain the focal length f of the near-critical layer and to describe the self-focusing process. This model gives $f\approx w_0/\sqrt{\bar{n}}$ with the transparency factor $\bar{n}=n_e/({\gamma }_0{n}_c)$ and ${\gamma }_0=\sqrt{1+a_0^2/2}$, where $w_0$ is the beam waist [59]. f gives the rule to calculate the distance inside the foam at which the laser reaches its maximum focusing before being absorbed considerably. For example, if a₀ = 50, $w_0$ = 3 µm, and n_e/n_c = 2, the self-focusing length is equal to 12.6 µm. Therefore, in simulation A the foam is long enough to reach the maximum possible focalization of the laser pulse. Since absorption and filamentation prevail for propagation longer than the self-focusing length, the foam thickness must be tuned to maximize the intensity when the substrate is reached, which means roughly having a foam length equal to the self-focusing length f. Despite relativistic self-focusing being an inherent 3D process, this reasoning is still valid in our 2D simulations when comparing the optimal values with the vertical lines corresponding to the self-focusing lengths in Figure 6. In many cases, the optimal length identified when fixing foam density and laser intensity is approximately the self-focusing length with a better matching when considering the average photon energy. Indeed, conversion efficiencies take advantage of laser absorption; thus, optimal values slightly longer than the self-focusing lengths are expected due to the increased laser absorption. With n_e/n_c = 1 at high intensities, the optimal lengths go beyond the self-focusing limit. This fact is reasonable since the transparency factor $\bar{n}$ becomes small in these cases, and, consequently, the thin-lens model starts to fail [59].

Figure 7 reports the conversion efficiency, panel (A), and the average photon energy, panel (B), varying a₀, thus making identifiable their dependence on this parameter. The simulations considered here are only those with foam thickness closest to the self-focusing length once fixed a₀ and n_e/n_c. This plot confirms a general trend reported in the literature according to which the conversion efficiency from the laser in photon energy goes approximately as $a_0^3$. Instead, the average photon energy shows a milder dependence going approximately as $a_0^{1.25}$. Overall, the laser intensity proves to be the essential parameter deciding the order of magnitude of the emission properties we focused on.

FIGURE 7

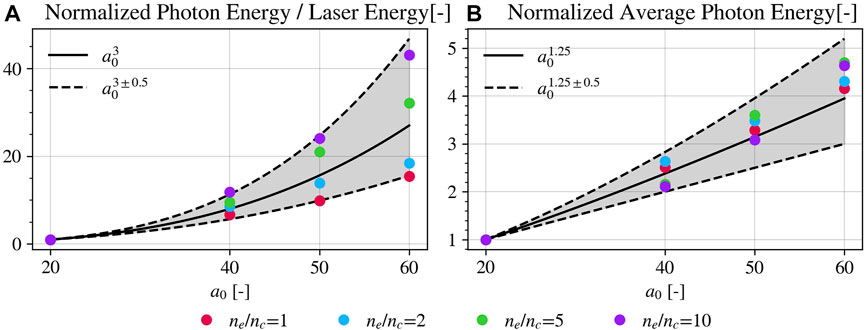
FIGURE 7. Normalized conversion efficiency of photon energy in laser energy (A) and average energy of all emitted photons (B) in the simulations with foam thickness closest to the self-focusing length f. Normalization is achieved by dividing by the value at a₀ = 20 once fixed the foam density n_e/n_c. Solid and dashed black lines represent powers of a₀ approximately matching the simulation point dependence.

Considering a nanostructured morphology for the target, the quantitative results reported in this section and the previous ones would be different. Alteration of the interaction processes due to the presence of the nanostructure is expected [79]. We mention that, as reported in [39, 43], including a nanostructured morphology for the foam in 2D simulations has mainly the impact of reducing the photon yield and maximum photon energy due to density dishomogeneities and more chaotic motion of electrons with respect to the uniform case, albeit remaining more efficient than the single layer. For this work, based on 2D simulations, we focus on something other than the detailed morphology expecting it to be worthy of consideration in more realistic 3D simulations. In addition, relatively high laser intensities tend to homogenize the nanostructure [79], and, if the laser contrast is not very high, the laser prepulse is expected to ionize and make the foam uniform before the interaction with the main laser peak.

4 Conclusion

In this work, we have investigated NICS occurring during the interaction of an intense laser pulse ($\sim 10^{21}$ W/cm²) with near-critical foam-based DLTs. We have focused on non-extreme laser intensities achievable in current laser facilities and on realistic target parameters. Using PIC simulations, we have recognized the main steps leading to high-energy photon emission in DLTs: laser shaping in the near-critical layer, electron heating, betatron oscillations, and laser reflection on the substrate. The photon production shows two phases of emission, one related to electron motion in the self-focusing channel (ramp phase) and the other associated with the scattering of electrons off the laser after reflection (burst phase). These two phases characterize the emission in DLTs unless the laser pulse absorption in the near-critical layer prevents reflection. We have checked the simulation results against theory using analytical estimates. The simulation gives what is expected by the theoretical scheme on which it is based. We have used these analytical formulas to evaluate the importance of using a quantum description of synchrotron radiation in the different emission phases. Emission during ramp phase is well-described in the classical framework, while burst emission in front of the substrate at laser reflection needs quantum corrections. This procedure of analytical estimates could be used to predict NICS emission and assess the impact of quantum effects after PIC simulations in any case of interest. We have compared bremsstrahlung and NICS in some selected cases proving the impact of this second type of emission also in non-extreme regimes of laser–plasma interaction. NICS prevails on bremsstrahlung increasing the intensity, and the two phenomena seem comparable only around a₀ = 20 with synchrotron-like emission strongly affecting the low-energy ($<$ 10 MeV) portion of emitted spectra also in this case. However, if the solid substrate properties are adequately selected, bremsstrahlung contribution becomes much more relevant at higher intensities. By looking at the conversion efficiencies and average photon energies in a large simulation scan, the most promising configurations for NICS emission seem characterized by low densities (1–2 n_c) and large foam thicknesses ($>$20 µm) or intermediate densities (∼ 5n_c) and short foam lengths (5–15 µm). Larger values of a₀ are always better to enhance the emission properties. The results show that the maximum conversion efficiencies in photon energy reached in all the simulations are around 5–6%, which is an interesting value considering the non-extreme intensities of this investigation. We conclude that DLTs are worth quantitative 3D numerical studies and, ultimately, experimental campaigns. On the one hand, 3D simulations, possibly including the nanostructured morphology, could more accurately evaluate NICS and bremsstrahlung competition at relatively low intensities, quantify the brilliance of a DLT photon source, and precisely describe relativistic self-focusing assessing the relationship between optimal emission cases and the self-focusing length. On the other hand, experiments are already planned to investigate this scenario of high-energy photons production at Apollon and assess the results obtained in this work. The DLT parameters could be used to tailor emission properties making NICS dominant in experiments and exploitable in the desired applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MGa, AF, MGr, and MP contributed to the conception and design of the study. MGa and AF performed the PIC simulations and the data analysis. MGa wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). This work was funded by the European Union (ERC, PANTANI, 101069171).

Acknowledgments

The authors thank Rafael Caprani for his master’s thesis [43] supervised by MGr, MP, and AF, which set the basis of this work and was preparatory to the analysis of results. They acknowledge the agreement between the Department of Energy at Politecnico di Milano and the Cineca consortium (Casalecchio di Reno, Italy) for access to the high-performance computing machines Marconi, Galileo, Galileo100, and Marconi100.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cole J, Behm K, Gerstmayr E, Blackburn T, Wood J, Baird C, et al. Experimental evidence of radiation reaction in the collision of a high-intensity laser pulse with a laser-wakefield accelerated electron beam. Phys Rev X (2018) 8:011020. doi:10.1103/physrevx.8.011020

CrossRef Full Text | Google Scholar

2. Poder K, Tamburini M, Sarri G, Piazza AD, Kuschel S, Baird C, et al. Experimental signatures of the quantum nature of radiation reaction in the field of an ultraintense laser. Phys Rev X (2018) 8:031004. doi:10.1103/physrevx.8.031004

CrossRef Full Text | Google Scholar

3. Niel F, Riconda C, Amiranoff F, Duclous R, Grech M. From quantum to classical modeling of radiation reaction: A focus on stochasticity effects. Phys Rev E (2018) 97:043209. doi:10.1103/physreve.97.043209

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Blackburn TG. Radiation reaction in electron–beam interactions with high-intensity lasers. Rev Mod Plasma Phys (2020) 4:5. doi:10.1007/s41614-020-0042-0

CrossRef Full Text | Google Scholar

5. Piazza AD, Müller C, Hatsagortsyan KZ, Keitel CH. Extremely high-intensity laser interactions with fundamental quantum systems. Rev Mod Phys (2012) 84:1177–228. doi:10.1103/revmodphys.84.1177

CrossRef Full Text | Google Scholar

6. Ridgers CP, Brady CS, Duclous R, Kirk JG, Bennett K, Arber TD, et al. Dense electron-positron plasmas and ultraintense γ rays from laser-irradiated solids. Phys Rev Lett (2012) 108:165006. doi:10.1103/physrevlett.108.165006

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhang P, Bulanov SS, Seipt D, Arefiev AV, Thomas AGR. Relativistic plasma physics in supercritical fields. Phys Plasmas (2020) 27:050601. doi:10.1063/1.5144449

CrossRef Full Text | Google Scholar

8. Daykin TS, Sawada H, Sentoku Y, Beg FN, Chen H, McLean HS, et al. Characterization of fast electron divergence and energy spectrum from modeling of angularly resolved bremsstrahlung measurements. Phys Plasmas (2018) 25:123103. doi:10.1063/1.5055257

CrossRef Full Text | Google Scholar

9. Geddes CG, Rykovanov S, Matlis NH, Steinke S, Vay JL, Esarey EH, et al. Compact quasi-monoenergetic photon sources from laser-plasma accelerators for nuclear detection and characterization. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2015) 350:116–21. doi:10.1016/j.nimb.2015.01.013

CrossRef Full Text | Google Scholar

10. Courtois C, Edwards R, Fontaine ACL, Aedy C, Barbotin M, Bazzoli S, et al. High-resolution multi-MeV x-ray radiography using relativistic laser-solid interaction. Phys Plasmas (2011) 18:023101. doi:10.1063/1.3551738

CrossRef Full Text | Google Scholar

11. Ma Y, Hua J, Liu D, He Y, Zhang T, Chen J, et al. Region-of-interest micro-focus computed tomography based on an all-optical inverse compton scattering source. Matter Radiat Extremes (2020) 5:064401. doi:10.1063/5.0016034

CrossRef Full Text | Google Scholar

12. Gruse JN, Streeter M, Thornton C, Armstrong C, Baird C, Bourgeois N, et al. Application of compact laser-driven accelerator x-ray sources for industrial imaging. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2020) 983:164369. doi:10.1016/j.nima.2020.164369

CrossRef Full Text | Google Scholar

13. Habs D, Tajima T, Schreiber J, Barty CP, Fujiwara M, Thirolf PG. Vision of nuclear physics with photo-nuclear reactions by laser-driven γ beams. The Eur Phys J D (2009) 55:279–85. doi:10.1140/epjd/e2009-00101-2

CrossRef Full Text | Google Scholar

14. Mirani F, Calzolari D, Formenti A, Passoni M. Superintense laser-driven photon activation analysis. Commun Phys (2021) 4:185. doi:10.1038/s42005-021-00685-2

CrossRef Full Text | Google Scholar

15. Kmetec JD, Gordon CL, Macklin JJ, Lemoff BE, Brown GS, Harris SE. MeV x-ray generation with a femtosecond laser. Phys Rev Lett (1992) 68:1527–30. doi:10.1103/physrevlett.68.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gahn C, Pretzler G, Saemann A, Tsakiris GD, Witte KJ, Gassmann D, et al. MeV γ-ray yield from solid targets irradiated with fs-laser pulses. Appl Phys Lett (1998) 73:3662–4. doi:10.1063/1.122855

CrossRef Full Text | Google Scholar

17. Martinez B, d'Humières E, Gremillet L. Synchrotron radiation from ultrahigh-intensity laser-plasma interactions and competition with bremsstrahlung in thin foil targets. Phys Rev Res (2020) 2:043341. doi:10.1103/physrevresearch.2.043341

CrossRef Full Text | Google Scholar

18. Bulanov SS, Schroeder CB, Esarey E, Leemans WP. Electromagnetic cascade in high-energy electron, positron, and photon interactions with intense laser pulses. Phys Rev A (2013) 87:062110. doi:10.1103/physreva.87.062110

CrossRef Full Text | Google Scholar

19. Bula C, McDonald KT, Prebys EJ, Bamber C, Boege S, Kotseroglou T, et al. Observation of nonlinear effects in compton scattering. Phys Rev Lett (1996) 76:3116–9. doi:10.1103/physrevlett.76.3116

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Phuoc KT, Corde S, Thaury C, Malka V, Tafzi A, Goddet JP, et al. All-optical compton gamma-ray source. Nat Photon (2012) 6:308–11. doi:10.1038/nphoton.2012.82

CrossRef Full Text | Google Scholar

21. Esarey E, Schroeder CB, Leemans WP. Physics of laser-driven plasma-based electron accelerators. Rev Mod Phys (2009) 81:1229–85. doi:10.1103/revmodphys.81.1229

CrossRef Full Text | Google Scholar

22. Chen S, Powers ND, Ghebregziabher I, Maharjan CM, Liu C, Golovin G, et al. MeV-energy x rays from inverse compton scattering with laser-wakefield accelerated electrons. Phys Rev Lett (2013) 110:155003. doi:10.1103/physrevlett.110.155003

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Brady CS, Ridgers CP, Arber TD, Bell AR. Gamma-ray emission in near critical density plasmas. Plasma Phys Controlled Fusion (2013) 55:124016. doi:10.1088/0741-3335/55/12/124016

CrossRef Full Text | Google Scholar

24. Nerush EN, Kostyukov IY, Ji L, Pukhov A. Gamma-ray generation in ultrahigh-intensity laser-foil interactions. Phys Plasmas (2014) 21:013109. doi:10.1063/1.4863423

CrossRef Full Text | Google Scholar

25. Ji LL, Pukhov A, Nerush EN, Kostyukov IY, Shen BF, Akli KU. Energy partition, γ-ray emission, and radiation reaction in the near-quantum electrodynamical regime of laser-plasma interaction. Phys Plasmas (2014) 21:023109. doi:10.1063/1.4866014

CrossRef Full Text | Google Scholar

26. Brady CS, Ridgers CP, Arber TD, Bell AR. Synchrotron radiation, pair production, and longitudinal electron motion during 10-100 PW laser solid interactions. Phys Plasmas (2014) 21:033108. doi:10.1063/1.4869245

CrossRef Full Text | Google Scholar

27. Wang HY, Liu B, Yan XQ, Zepf M. Gamma-ray emission in near critical density plasmas at laser intensities of 10²¹ w/cm². Phys Plasmas (2015) 22:033102. doi:10.1063/1.4913991

CrossRef Full Text | Google Scholar

28. Wu D, Qiao B, He XT. The radiation reaction effects in the ultra-intense and ultra-short laser foil interaction regime. Phys Plasmas (2015) 22:093108. doi:10.1063/1.4930111

CrossRef Full Text | Google Scholar

29. Huang TW, Robinson APL, Zhou CT, Qiao B, Liu B, Ruan SC, et al. Characteristics of betatron radiation from direct-laser-accelerated electrons. Phys Rev E (2016) 93:063203. doi:10.1103/physreve.93.063203

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Serebryakov DA, Nerush EN. Efficient gamma-ray generation by ultra-intense laser pulses obliquely incident on a planar plasma layer. Quan Elect (2016) 46:299–304. doi:10.1070/qel16051

CrossRef Full Text | Google Scholar

31. Chang HX, Qiao B, Zhang YX, Xu Z, Yao WP, Zhou CT, et al. Ultraintense laser absorption and γ-ray synchrotron radiation in near critical density plasmas. Phys Plasmas (2017) 24:043111. doi:10.1063/1.4981213

CrossRef Full Text | Google Scholar

32. Chang HX, Qiao B, Huang TW, Xu Z, Zhou CT, Gu YQ, et al. Brilliant petawatt gamma-ray pulse generation in quantum electrodynamic laser-plasma interaction. Scientific Rep (2017) 7:45031. doi:10.1038/srep45031

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zani A, Dellasega D, Russo V, Passoni M. Ultra-low density carbon foams produced by pulsed laser deposition. Carbon (2013) 56:358–65. doi:10.1016/j.carbon.2013.01.029

CrossRef Full Text | Google Scholar

34. Maffini A, Pazzaglia A, Dellasega D, Russo V, Passoni M. Growth dynamics of pulsed laser deposited nanofoams. Phys Rev Mater (2019) 3:083404. doi:10.1103/physrevmaterials.3.083404

CrossRef Full Text | Google Scholar

35. Maffini A, Orecchia D, Pazzaglia A, Zavelani-Rossi M, Passoni M. Pulsed laser deposition of carbon nanofoam. Appl Surf Sci (2022) 599:153859. doi:10.1016/j.apsusc.2022.153859

CrossRef Full Text | Google Scholar

36. Yang Y, Jiao J, Tian C, Wu Y, Dong K, Zhou W, et al. Near-microcoulomb multi-MeV electrons generation in laser-driven self-formed plasma channel. Laser Part Beams (2017) 35:476–82. doi:10.1017/s0263034617000490

CrossRef Full Text | Google Scholar

37. Gong Z, Hu RH, Lu HY, Yu JQ, Wang DH, Fu EG, et al. Brilliant GeV gamma-ray flash from inverse compton scattering in the QED regime. Plasma Phys Controlled Fusion (2018) 60:044004. doi:10.1088/1361-6587/aaa9b1

CrossRef Full Text | Google Scholar

38. Gu YJ, Klimo O, Bulanov SV, Weber S. Brilliant gamma-ray beam and electron–positron pair production by enhanced attosecond pulses. Commun Phys (2018) 1:93. doi:10.1038/s42005-018-0095-3

CrossRef Full Text | Google Scholar

39. Huang TW, Kim CM, Zhou CT, Ryu CM, Nakajima K, Ruan SC, et al. Tabletop laser-driven gamma-ray source with nanostructured double-layer target. Plasma Phys Controlled Fusion (2018) 60:115006. doi:10.1088/1361-6587/aadbeb

CrossRef Full Text | Google Scholar

40. Huang TW, Kim CM, Zhou CT, Cho MH, Nakajima K, Ryu CM, et al. Highly efficient laser-driven compton gamma-ray source. New J Phys (2019) 21:013008. doi:10.1088/1367-2630/aaf8c4

CrossRef Full Text | Google Scholar

41. Xue K, Dou ZK, Wan F, Yu TP, Wang WM, Ren JR, et al. Generation of highly-polarized high-energy brilliant γ-rays via laser-plasma interaction. Matter Radiat Extremes (2020) 5:054402. doi:10.1063/5.0007734

CrossRef Full Text | Google Scholar

42. Jirka M, Klimo O, Gu YJ, Weber S. Enhanced photon emission from a double-layer target at moderate laser intensities. Scientific Rep (2020) 10:8887. doi:10.1038/s41598-020-65778-4

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Caprani R. Compact photon sources in multi-PetaWatt facilities: A kinetic numerical investigation. Master’s thesis. Milano, Italy: University Politecnico di Milano (2020).

Google Scholar

44. Liu JX, Ma YY, Yu TP, Zhao J, Yang XH, Gan LF, et al. Enhanced electron–positron pair production by ultra intense laser irradiating a compound target. Plasma Phys Controlled Fusion (2016) 58:125007. doi:10.1088/0741-3335/58/12/125007

CrossRef Full Text | Google Scholar

45. Prencipe I, Metzkes-Ng J, Pazzaglia A, Bernert C, Dellasega D, Fedeli L, et al. Efficient laser-driven proton and bremsstrahlung generation from cluster-assembled foam targets. New J Phys (2021) 23:093015. doi:10.1088/1367-2630/ac1fcd

CrossRef Full Text | Google Scholar

46. Formenti A, Galbiati M, Passoni M. Modeling and simulations of ultra-intense laser-driven bremsstrahlung with double-layer targets. Plasma Phys Controlled Fusion (2022) 64:044009. doi:10.1088/1361-6587/ac4fce

CrossRef Full Text | Google Scholar

47. Shou Y, Wang P, Lee SG, Rhee YJ, Lee HW, Yoon JW, et al. Brilliant femtosecond-laser-driven hard x-ray flashes from carbon nanotube plasma. Nat Photon (2022) 17:137–142. doi:10.1038/s41566-022-01114-8

CrossRef Full Text | Google Scholar

48. Ridgers C, Kirk J, Duclous R, Blackburn T, Brady C, Bennett K, et al. Modelling gamma-ray photon emission and pair production in high-intensity laser–matter interactions. J Comput Phys (2014) 260:273–85. doi:10.1016/j.jcp.2013.12.007

CrossRef Full Text | Google Scholar

49. Gonoskov A, Bastrakov S, Efimenko E, Ilderton A, Marklund M, Meyerov I, et al. Extended particle-in-cell schemes for physics in ultrastrong laser fields: Review and developments. Phys Rev E (2015) 92:023305. doi:10.1103/physreve.92.023305

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Lobet M, d'Humières E, Grech M, Ruyer C, Davoine X, Gremillet L. Modeling of radiative and quantum electrodynamics effects in PIC simulations of ultra-relativistic laser-plasma interaction. J Phys Conf Ser (2016) 688:012058. doi:10.1088/1742-6596/688/1/012058

CrossRef Full Text | Google Scholar

51. Blackburn TG, Seipt D, Bulanov SS, Marklund M. Benchmarking semiclassical approaches to strong-field QED: Nonlinear compton scattering in intense laser pulses. Phys Plasmas (2018) 25:083108. doi:10.1063/1.5037967

CrossRef Full Text | Google Scholar

52. Yoon JW, Kim YG, Choi IW, Sung JH, Lee HW, Lee SK, et al. Realization of laser intensity over 10²3 w/cm². Optica (2021) 8:630. doi:10.1364/optica.420520

CrossRef Full Text | Google Scholar

53. Derouillat J, Beck A, Pérez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comp Phys Commun (2018) 222:351–73. doi:10.1016/j.cpc.2017.09.024

CrossRef Full Text | Google Scholar

54. Jackson J. Classical electrodynamics. Nashville, TN: John Wiley & Sons (1998).

Google Scholar

55. Cros B, Paradkar B, Davoine X, Chancé A, Desforges F, Dobosz-Dufrénoy S, et al. Laser plasma acceleration of electrons with multi-PW laser beams in the frame of CILEX. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 740:27–33. doi:10.1016/j.nima.2013.10.090

CrossRef Full Text | Google Scholar

56. Wang HY, Lin C, Sheng ZM, Liu B, Zhao S, Guo ZY, et al. Laser shaping of a relativistic intense, short Gaussian pulse by a plasma lens. Phys Rev Lett (2011) 107:265002. doi:10.1103/physrevlett.107.265002

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Sun GZ, Ott E, Lee YC, Guzdar P. Self-focusing of short intense pulses in plasmas. Phys Fluids (1987) 30:526. doi:10.1063/1.866349

CrossRef Full Text | Google Scholar

58. Ren C, Duda BJ, Hemker RG, Mori WB, Katsouleas T, Antonsen TM, et al. Compressing and focusing a short laser pulse by a thin plasma lens. Phys Rev E (2001) 63:026411. doi:10.1103/physreve.63.026411

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Pazzaglia A, Fedeli L, Formenti A, Maffini A, Passoni M. A theoretical model of laser-driven ion acceleration from near-critical double-layer targets. Commun Phys (2020) 3:133. doi:10.1038/s42005-020-00400-7

CrossRef Full Text | Google Scholar

60. Pukhov A, ter Vehn JM. Relativistic magnetic self-channeling of light in near-critical plasma: Three-dimensional particle-in-cell simulation. Phys Rev Lett (1996) 76:3975–8. doi:10.1103/physrevlett.76.3975

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Arefiev AV, Khudik VN, Robinson APL, Shvets G, Willingale L, Schollmeier M. Beyond the ponderomotive limit: Direct laser acceleration of relativistic electrons in sub-critical plasmas. Phys Plasmas (2016) 23:056704. doi:10.1063/1.4946024

CrossRef Full Text | Google Scholar

62. Stark D, Toncian T, Arefiev A. Enhanced multi-MeV photon emission by a laser-driven electron beam in a self-generated magnetic field. Phys Rev Lett (2016) 116:185003. doi:10.1103/physrevlett.116.185003

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Shen XF, Pukhov A, Günther MM, Rosmej ON. Bright betatron x-rays generation from picosecond laser interactions with long-scale near critical density plasmas. Appl Phys Lett (2021) 118:134102. doi:10.1063/5.0042997

CrossRef Full Text | Google Scholar

64. Esarey E, Shadwick BA, Catravas P, Leemans WP. Synchrotron radiation from electron beams in plasma-focusing channels. Phys Rev E (2002) 65:056505. doi:10.1103/PhysRevE.65.056505

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Ritus VI. Quantum effects of the interaction of elementary particles with an intense electromagnetic field. J Soviet Laser Res (1985) 6:497–617. doi:10.1007/bf01120220

CrossRef Full Text | Google Scholar

66. Baier VN, Katkov VM, Strakhovenko VM. Electromagnetic processes at high energies in oriented single crystals. Singapore, Singapore: World Scientific Publishing (1998). doi:10.1142/2216

CrossRef Full Text | Google Scholar

67. Sokolov A, Ternov I, Kilmister C. Radiation from relativistic electrons. American Institute of physics translation series. New York, NY: American Institute of Physics (1986).

Google Scholar

68. Berestetskii V, Lifshitz E, Pitaevskii L. Quantum Electrodynamics. 2nd ed. Translated by J. B. Sykes and J. S. Bell. Oxford, England: Butterworth-Heinemann (1982).

Google Scholar

69. Cialfi L, Fedeli L, Passoni M. Electron heating in subpicosecond laser interaction with overdense and near-critical plasmas. Phys Rev E (2016) 94:053201. doi:10.1103/physreve.94.053201

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Passoni M, Sgattoni A, Prencipe I, Fedeli L, Dellasega D, Cialfi L, et al. Toward high-energy laser-driven ion beams: Nanostructured double-layer targets. Phys Rev Acc Beams (2016) 19:061301. doi:10.1103/physrevaccelbeams.19.061301

CrossRef Full Text | Google Scholar

71. Passoni M, Arioli FM, Cialfi L, Dellasega D, Fedeli L, Formenti A, et al. Advanced laser-driven ion sources and their applications in materials and nuclear science. Plasma Phys Controlled Fusion (2019) 62:014022. doi:10.1088/1361-6587/ab56c9

CrossRef Full Text | Google Scholar

72. Martins JL, Vranic M, Grismayer T, Vieira J, Fonseca RA, Silva LO. Modelling radiation emission in the transition from the classical to the quantum regime. Plasma Phys Controlled Fusion (2015) 58:014035. doi:10.1088/0741-3335/58/1/014035

CrossRef Full Text | Google Scholar

73. Niel F, Riconda C, Amiranoff F, Lobet M, Derouillat J, Pérez F, et al. From quantum to classical modeling of radiation reaction: A focus on the radiation spectrum. Plasma Phys Controlled Fusion (2018) 60:094002. doi:10.1088/1361-6587/aace22

CrossRef Full Text | Google Scholar

74. Arber TD, Bennett K, Brady CS, Lawrence-Douglas A, Ramsay MG, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Controlled Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

75. Vyskočil J, Gelfer E, Klimo O. Inverse compton scattering from solid targets irradiated by ultra-short laser pulses in the 10²²-10²³ w/cm² regime. Plasma Phys Controlled Fusion (2020) 62:064002. doi:10.1088/1361-6587/ab83cb

CrossRef Full Text | Google Scholar

76. Wan F, Lv C, Jia M, Sang H, Xie B. Photon emission by bremsstrahlung and nonlinear compton scattering in the interaction of ultraintense laser with plasmas. Eur Phys J D (2017) 71:236. doi:10.1140/epjd/e2017-70805-7

CrossRef Full Text | Google Scholar

77. Chintalwad S, Krishnamurthy S, Ramakrishna B, Ridgers CP. Photon emission enhancement studies from the interaction of ultraintense laser pulses with shaped targets. Phys Rev E (2022) 105:025205. doi:10.1103/physreve.105.025205

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Fedeli L, Formenti A, Bottani CE, Passoni M. Parametric investigation of laser interaction with uniform and nanostructured near-critical plasmas. Eur Phys J D (2017) 71:202. doi:10.1140/epjd/e2017-80222-7

CrossRef Full Text | Google Scholar

79. Fedeli L, Formenti A, Cialfi L, Pazzaglia A, Passoni M. Ultra-intense laser interaction with nanostructured near-critical plasmas. Scientific Rep (2018) 8:3834. doi:10.1038/s41598-018-22147-6

PubMed Abstract | CrossRef Full Text | Google Scholar