A local community detection algorithm based on potential community exploration

Local community detection aims to detect local communities that have expanded from the given node. Because of the convenience of obtaining the local information of the network and nearly linear time complexity, researchers have proposed many local community detection algorithms to discover the community structure of real-world networks and have obtained excellent results. Most existing local community detection algorithms expand from the given node to a community based on an expansion mechanism that can determine the membership of nodes. However, when determining the membership of neighboring nodes of a community, previous algorithms only considered the impact from the current community, but the impact from the potential communities around the node was neglected. As the name implies, a potential community is a community structure hidden in an unexplored network around a node. This paper gives the definition of potential communities of a node for the first time, that is, a series of connected components consisting of the node’s neighbors that are in the unexplored network. We propose a three-stage local expansion algorithm, named LCDPC, that performs Local Community Detection based on Potential Community exploration. First, we search for a suitable node to replace the given node as the seed by calculating the node importance and the node similarity. Second, we form the initial community by combining the seed and its suitable potential community. Finally, the eligible nodes are selected by comparing the similarities between potential communities and the expanding community and nodes and adding them to the initial community for community expansion. The proposed algorithm is compared with eight state-of-the-art algorithms on both real-world networks and artificial networks, and the experimental results show that the performance of the proposed algorithm is better than that of the comparison algorithms and that the application of potential community exploration can help identify the community structure of networks.

1 Introduction

In recent years, there have been many changes in people’s lifestyles brought by the emergence of various kinds of complex networks in different domains, such as computer networks, social media networks, biological networks, and power system networks [1]. Research on complex networks, especially the community structure of complex networks, has received much attention in various fields and interdisciplinary subjects [2, 3]. In a real-world network, the node represents an entity and the edge represents the correlation among entities [4]. In addition, edges in the same community are connected densely, and edges between communities are sparse in contrast [3, 5].

The detection and analysis of community structure are helpful to discover the interaction between people in social networks, the function of proteins in protein networks, and the research fields of scholars in academic cooperation networks. These can help people solve practical problems in society, such as personalized recommendations of products and information in the commercial field, technological breakthroughs in the medical field, and expert mining in the academic field.

Research on community detection aims to detect the community structure in complex networks quickly and accurately. Girvan et al. [6] proposed the classic Girvan–Newman (GN) algorithm based on the Betweenness, which denotes the number of shortest paths between two nodes. The GN algorithm is a hierarchical clustering algorithm based on global information. The basic idea of GN is to delete edges in the network with the maximum Betweenness relative to all source nodes continuously and then recalculate the Betweenness of remaining edges in the network relative to all source nodes all edges in the network are deleted.

Subsequently, various excellent community detection algorithms that depend on the global information of the network were proposed [7]. However, accessing the global information of a real-world network is sometimes impossible and in some cases, unnecessary [8]. On the one hand, for large-scale or dynamic real-world networks, it is difficult and time-consuming to obtain global information [9]. On the other hand, in some practical applications, one does not need the global information of the entire network but just needs to obtain local information from a specific node [10]. Different from the algorithms based on global information, the local community detection algorithm is capable of obtaining the local community based on only local information around the target node. Therefore, an increasing number of local community detection algorithms based on local information have emerged over time.

Most existing local community detection algorithms expand from the given node to a community based on an expansion mechanism that can determine the membership of nodes. The expansion mechanism of previous algorithms is generally based on the relationship between the community under expansion and its neighboring nodes. However, the communities existing in the undetected area of the network also impact these neighboring nodes. It is arbitrary and inefficient to determine the membership of neighboring nodes based only on the relationship between the community and its neighboring nodes while ignoring the relationship between the neighboring nodes and these communities in the undetected area of the network. In addition, ignoring the communities in the undetected area of the network means that the lack of topological information about the node leads to a decline in the accuracy of node membership.

Accordingly, this paper introduces the concept of the potential community which represents the potential community structure hidden in the unexplored network, to solve the problem above. We define the potential communities of a node as a set of connected components composed of node neighbors. The connected component is a set of nodes, where there is a path between each of the two nodes. The consideration of the potential community serves to provide the suspicious node with the topological information of its neighboring communities in the undetected area of the network. We propose a three-stage local community detection algorithm named LCDPC, which performs Local Community Detection based on Potential Community exploration. The algorithmic process of LCDPC consists of three stages: the seed selection stage, the community initialization stage, and the community expansion stage. First, the seed selection searches for a suitable seed to replace the given node. Second, the community initialization process forms the initial community by combining the seed and its suitable potential community. Finally, the community expansion process adds eligible nodes to the initial community for community expansion. The main contributions of this paper are as follows.

• This paper gives the definition of the potential community. For the first time, the notion of potential community is applied to the process of node identification to increase the accuracy of the local community detection algorithm.

• In addition, we propose a three-stage local expansion algorithm based on potential community exploration, which performs seed selection, community initialization, and community expansion in order.

• Experimental results show that the application of potential community exploration can help identify the community structure of networks.

The rest of this paper is organized as follows. Section 2 reviews the basic theory and the related algorithms. The basic definitions and detailed description of the proposed algorithm are presented in Section 3. Experimental results are shown in Section 4. Section 5 concludes this paper and outlines future work.

2 Related works

A typical local community detection algorithm consists of two main processes: the seed selection process and community expansion process. The seed or the seed community generated by the seed selection process is the basis of the algorithm, which directly determines the quality of the result. The community expansion process takes the seed as the initial community and expands the community by optimizing the quality function or node similarity. This section outlines representative methods in terms of seed selection and community expansion as well as node centrality metrics and quality functions.

2.1 Seed selection

To obtain high-quality communities, the seed selection method is applied to detect the most appropriate node of the target community that contains the given node as the seed. In recent years, scholars have proposed a variety of local community detection algorithms based on local expansion. Lancichinetti et al. [11] developed an algorithm that takes random nodes as the seed. Although this method has a fast running time, it reduces the quality of the resulting community, and the test is unstable. Baumes et al. [12] proposed a robust algorithm, named IC (iterative scan), which takes a random edge as the seed. However, this method is time-consuming because it produces a great many duplicate communities when searching for seeds. Lee et al. [13] proposed a method named GCE (greedy clique expansion), which takes a k-clique as the seed. Whang et al. [14] proposed a new seeding strategy based on the same distance kernel and degree. Taking maximal cliques as the seed, Li et al. [15] introduced a deep and broad searching method to detect maximal cliques, where different communities are allowed to be merged into a larger subgraph according to some given rules. Li et al. [16] considered some eligible nodes as a seed community and expanded the seed community by absorbing adjacent nodes of the seed community based on the absorbing degree function. Zareie et al. [17] introduced a hierarchical community detection method, which proposed two indices, the topological location of a node and the closeness to the network graph core, to measure the influence of node and rank them based on these two indices. To solve the seed-dependent problem, Ding et al. [18] introduced a core detecting method to replace the seed with the core member of the target community. Mohammadi et al. [19] developed a new node ranking strategy based on nodes’ global potential values, such as influence and importance, to reveal the core of the community. Cheng et al. [20] proposed an algorithm that performs the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) to rank each node and take the node with the highest score as the seed. Rezaei et al. [21] proposed a non-heuristic algorithm EML (Extended Machine Learning-based vital node identification), which makes use of the vitality of a part of a network for training a SVR model and predicts the vitality of each node based on this trained SVR.

2.2 Community expansion

The community expansion method takes a seed or a seed community as the initial community and expands it by absorbing the appropriate neighboring nodes iteratively. There are two common ways to determine the fitness of a node: running a greedy optimization process for a quality function [22–26] and spreading the influence of the seed throughout the network [27–32]. The quality function evaluates the quality of the community partition, and the scores generated by it can be used for partition ranking [2]. In a study on 13 quality functions based on 230 large real-world social, collaboration, and information networks, Yang et al. distinguished quality functions from (1) only internal community connectivity, (2) only connectivity between internal nodes and external networks; (3) both internal and external community connectivity and (4) modularity [33].

Influence spreading is a method that spreads the seed influence throughout the entire network. Inspired by the epidemic spreading model, Raghavan et al. [34] proposed the classical LPA (Label Propagation algorithm). LPA initializes each node in the network with a unique label and propagates the label throughout the network. The method stops when the node label does not change. Gregory et al. [35] proposed an improved LPA algorithm, named COPRA (Community Overlap PRopagation Algorithm), which allows overlapping by multiple labels on each node. Tang [36] proposed an algorithm based on speaker-listener label propagation to detect overlapping nodes.

In recent years, some other excellent expansion methods have been proposed. Tao et al. [37] proposed a method based on local similarity, which expands the community by connecting the node of a small-scale community with the nodes that have a high degree. Li et al. [38] proposed an algorithm to detect overlapping communities by diffusing the local spectral which is simulated by short random walks. Based on the idea that walkers who follow the same node sets should be assigned to the same community, Makoto et al. [39] proposed a retrained random-walk similarity algorithm for community expansion. Taking advantage of NGC (Nearest Greater Centrality) nodes, Luo et al. [40] proposed a novel community expansion method that adds the node that has the largest fuzzy relation with its NGC nodes into the local community. Bahadori et al. [41] proposed a probabilistic overlapping community detection method called PODCD which addresses dynamic communities efficiently. PODDCD scans communities by a probabilistic generative model which is constructed by a multi-objective optimization evolutionary-based method.

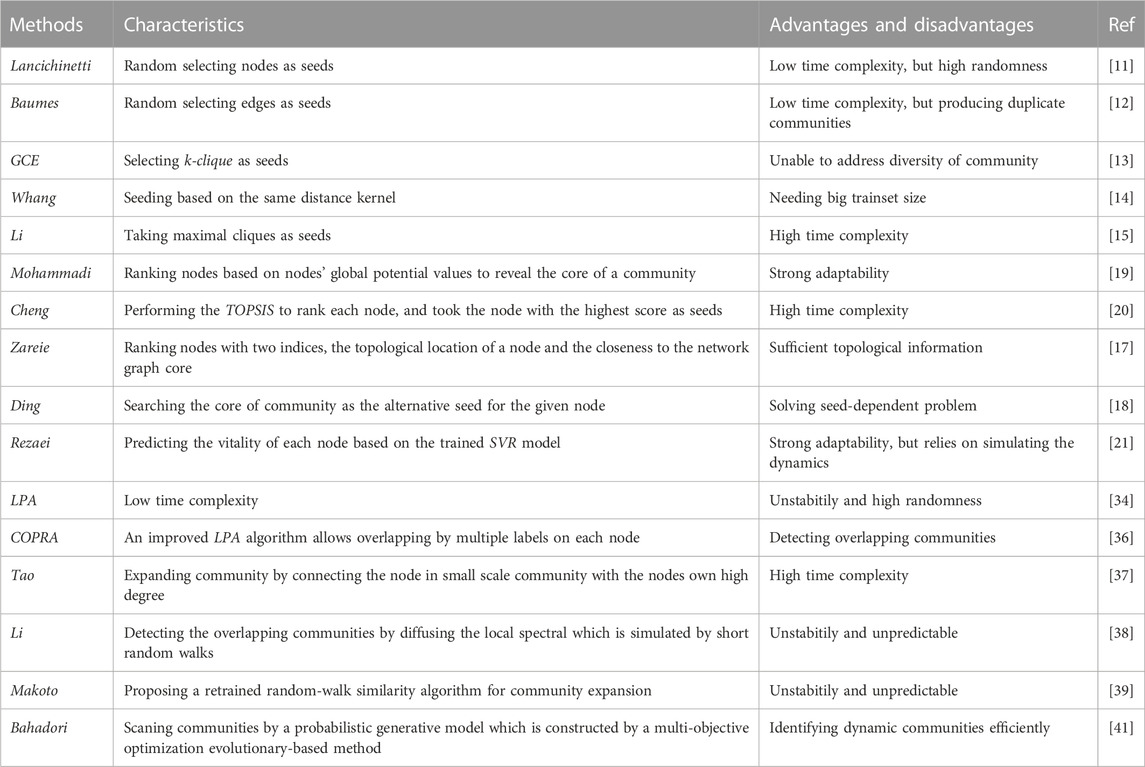
To enable readers to clearly understand recent achievements in the field of seed selection and community expansion, we summarize the characteristics, advantages, and disadvantages of the abovementioned methods in the following Table 1.

TABLE 1

TABLE 1. Pros and cons of common methods.

3 Basic definitions and algorithms

3.1 Motivation

As mentioned in Section 2, researchers have proposed many local expansion algorithms and made great progress in terms of seed selection and community expansion. However, there are still problems in local expansion algorithms when determining the membership of suspicious nodes. Previous algorithms only consider the relationship between the community and suspicious nodes while ignoring the relationship between the suspicious node and its potential communities.

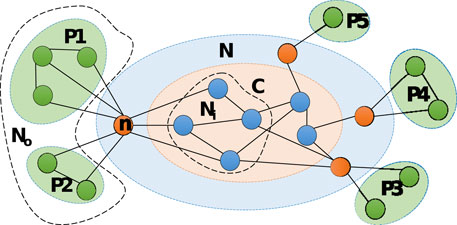
Let us take a brief figure legend of local community detection shown in Figure 1 to illustrate this problem. In Figure 1, subgraph C denotes the community under detection. Subgraph N denotes the neighboring nodes of C. The orange nodes in subgraph N denote the suspicious nodes of C. Subgraph P_{i(i∈{1−5})} denotes the potential communities of the suspicious nodes. The area N_o in the dotted line denotes the neighboring nodes outside C of suspicious node n. The area N_i in the dotted line denotes the neighboring nodes inside C of suspicious node n.

FIGURE 1

FIGURE 1. An example of local community detection and the potential communities of nodes.

Node n in Figure 1 is a suspicious node of community C that is under detection. The neighboring nodes of n can be divided into two parts: subgraph N_i located in community C and subgraph N_o located in the rest of the network. Most proposed algorithms determine the membership of suspicious node n on the basis of the relationship between N_i and n. Some algorithms take the relationship between N_o and node n into consideration, but they regard N_o as a whole. Actually, N_o is not an integrated whole, where nodes likely belong to different communities. As shown in Figure 1, N_o is composed of P₁ and P₂, which impact n. Therefore, treating adjacent nodes as a whole in undetected areas will lead to a reduction in the accuracy of node membership judgment in the process of community detection.

Topological structure refers to describing the entities and their relationships in complex networks by two basic graphic elements: nodes and links. The more topological structure information we have, the more precisely and rapidly we can detect the community structure from the complex network. Therefore, the motivation of this paper is to explore the topological structure information and subdivide the neighborhood of suspicious nodes. Therefore, we introduce the abstract concept of potential community into the local community detection algorithm. Detailed topological structure information can be obtained by exploring the potential communities of suspicious nodes to determine the membership of suspicious nodes accurately. As shown in Figure 1, P₁ and P₂ are the potential communities of node n. In our method, we first calculate the similarity between P₁, P₂, and n. Then calculate the similarity between N_i and n. Finally, we choose the most similar one from P₁, P₂, and n as the result community. Thus we can obtain a more accurate result on the basis of more topological structure information.

3.2 Problem definition

In this paper, we use a graph G = (V, E), where V is the node set and E is the link set. The graph G can be represented as an adjacency matrix A, where A_ij denotes the connection of node i and node j, if node i and node j are connected, A_ij = 1; otherwise A_ij = 0. The graph G consists of communities, where C = {C₁, C₂, … , C_i}(C₁ ∪ C₂, … , ∪ C_i ⊆ V). A community can be represented as a node set C = {v₁, v₂, … , v_j}(C ∈ C, v_i ∈ V). The given node v_g is the initial node for local community detection, where v_g ∈ V. The target community C_target is a community where the given node is located in the real network, where C_target ∈ C, v_g ∈ C_target. The local community detection aims to detect the most similar community to the target community based on the given node.

3.3 Basic definitions

The definitions related to this paper are presented in this subsection.

Definition 1. (Neighboring nodes). The neighboring nodes N(v) of node v is defined as follows:

$N\left(v\right)=\left\{u|\left(v,u\right)\in E,u\in V\right\},v\in V(1)$

where node v and node v_i are connected by a link. E is the link set and V is the node set of network G.

Definition 2. (Neighboring Community). The neighboring community Γ(v) of node v is defined as follows:

$\mathrm{\Gamma }\left(v\right)=N\left(v\right)\cup \left\{v\right\},v\in V(2)$

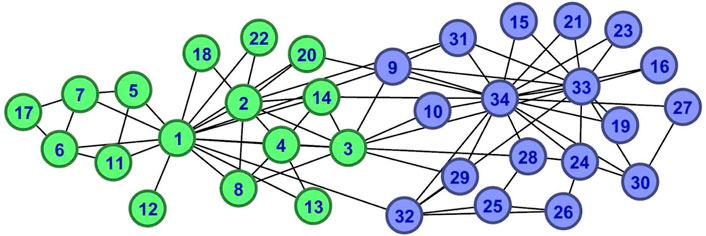
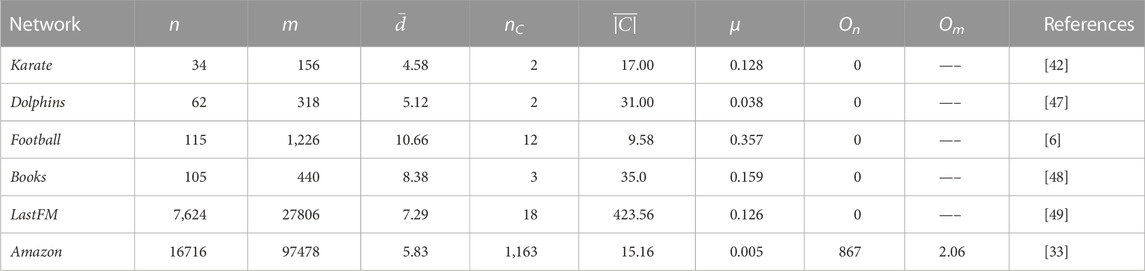
The neighboring community of a node is the union of the node and its neighboring nodes. Figure 2 displays the nodes distribution of Karate network, and Figure 3 displays a part of Karate network. For instance, all nodes in Figure 3A make up the neighboring community of node v₁, Γ(1) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 18, 20, 22, 32}. Our algorithm takes the neighboring community of the seed node as the initial community for expansion.

FIGURE 2

FIGURE 2. The node distribution of the Karate network.

FIGURE 3

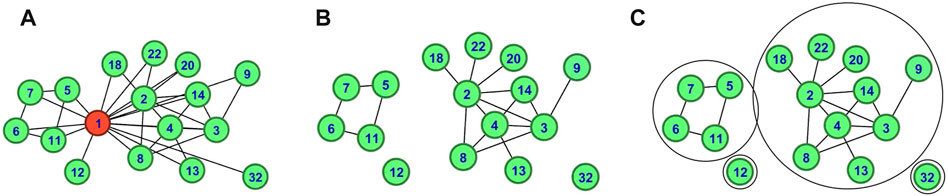
FIGURE 3. An example of exploring the potential community of node v₁. (A) The distribution of node v₁ and its neighbors. (B) Remove v₁ and its links between its neighbors. (C) Potential communities of v₁.

Definition 3. (Community Neighbors). The community neighbors N(C) of community C is defined as follows:

$N\left(C\right)=\left\{u|u\notin C,\exists v\in C,\left(u,v\right)\in E\right\},C\in V(3)$

The community neighbors are neighboring nodes of community members, which are not in the community. Our algorithm takes the community neighbors of the detected community as suspicious nodes.

Definition 4. (Connected component). The connected component is defined as follows:The connected component is a set of nodes, where there is a path between each pair of nodes. Nodes in the connected component are closely connected.

Definition 5. (Potential Community). The potential community of a node is defined as follows:The potential communities of a node are a series of connected components that consist of the node’s neighbors. That is, every pair of nodes in the adjacent node is connected to each other.We can search for the potential communities of node v by the following steps.

Step 1: Set up a subgraph G_v that is composed of node neighbors N(v) and links between them. That is, a tight node set formed by neighbors where each pair of nodes have a path, which is called the potential community.

Step 2: Starting from one node in G_v, the proposed algorithm walks along the link and records the nodes encountered. When a path ends, it continues to walk along the previous branch until no branch can be continued. The nodes recorded constitute a connected component (The subnetwork with only one node is also considered to be a connected component.)

Step 3: The connected component found in step 2 is one potential community of v, denoted by P(v)_i. Remove P(v)_i from G_v. The proposed algorithm iterates step 2 until there are no nodes left in G_v.

Note that ${\bigcup }_{P{(v)}_i\in P(v)}=N(v)$, and ∀P(v)_i, P(v)_j ∈ P(v), i ≠ j, P(v)_i ∩ P(v)_j = ∅, where P(v) represents the union of P(v)_i.Figure 3 displays the process of exploring the potential communities of node v₁ in the Karate Club Network [42]. We use all neighboring nodes of node v₁ to form a subgraph $G_{v_1}$. The connected components determined by the proposed algorithm are {2, 3, 4, 5, 13, 14, 18, 20, 22}, {5, 6, 7, 11}, {12} and {32}.

Definition 6. (Node Similarity). The similarity between a pair of nodes is defined as follows:

$NS\left(v_i,v_j\right)=\left|\frac{\mathrm{\Gamma }\left(v_j\right)\cap \mathrm{\Gamma }\left(v_i\right)}{\mathrm{\Gamma }\left(v_i\right)\cup \mathrm{\Gamma }\left(v_j\right)}\right|,v_i\in V,v_j\in V(4)$

The Jaccard similarity coefficient [43] is a common measure used to compare the similarity between two finite sets. It is easy to compute and has linear time complexity. Therefore, we use the Jaccard similarity coefficient value of two nodes’ neighboring communities to measure the similarity between the two nodes.

Definition 7. (Node Community Similarity). The similarity between community C and node v is defined as follows:

$NCS\left(v,C\right)=|\mathrm{\Gamma }\left(v\right)\cap C|\times \sum _{i,j\in \left(\mathrm{\Gamma }\left(v\right)\cap C\right)}{A}_{ij}\left(d\left(v_i\right)+d\left(v_j\right)\right),v\in V,C\in V(5)$

where |Γ(v) ∩ C| denotes the number of nodes in the intersection of the neighboring community of node v and community C and d(v) denotes the degree of node v.We use the internal links in the intersection of the neighboring community of the node and community as the measurement of similarity between the node and community. To distinguish the situation in which there is the same number of links in the intersection, we set the degree of nodes on both sides of the link as the weight of the link. In addition, a larger scale of intersection means a higher similarity between the node and community. Therefore, we add the number of nodes in the intersection to the formula.

Definition 8. (Fittest Community). The fittest community FC to which node v belongs is defined as follows:

$FC\left(v\right)=\arg \max \left(NCS\left(v,C\right)\right),C\in \left(\mathbf{P}\cup C_{\mathit{detected}}\right),v\in V(6)$

where P is the potential community set of node v.The fittest community to which a node belongs is the community that has the greatest similarity to the node among the potential communities of the node and the detected community. In the process of community expansion, nodes with the fittest community being the detected community will be added to the detected community. In addition, when the detected community and the potential communities have the greatest similarity to the node at the same time, we choose the detected community as the fittest community.

3.4 The proposed algorithm

The proposed algorithm named LCDPC includes three stages: seed selection, community initialization, and community expansion. In order to give readers a clear description of the proposed algorithm, we show an example on Karate Club Network in Figures 3, 4.

FIGURE 4

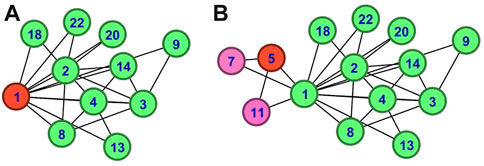
FIGURE 4. An example of community initialization and community expansion of seed v₁. (A) The initial community of seed v₁. (B) The process of identification on the membership of node v₅.

Figure 3 shows an example of exploring the potential community of node v₁. As described in Definition.5, we first get the network composed of the node v₁ and its neighboring nodes in Figure 3A. Second, we removed node v₁ and its links which is shown in Figure 3B. Third, each circle in Figure 3C is a connected component, the potential community of node v₁.

When node v₁ is the seed, the initial community of seed v₁ is shown in Figure 4A. We can get the connected components of node v₁ is {v₂, v₃, v₄, v₈, v₉, v₁₃, v₁₄, v₁₈, v₂₀, v₂₂} with similarity 3,784, {v₅, v₆, v₇, v₁₁} with similarity 450, {v₁₂} with similarity 30 and {v₃₂} with similarity 40 from Figure 3C. Therefore, we will form the initial community with node v₁ and the connected component that is most similar to node v₁.

Figure 4B shows the process of identification on the membership of node v₅. Note that, the value of node degree is in the whole network rather than in the subgraph. First, we get the neighboring nodes of v₅, where {v₁} is neighbor inside the community and {v₇, v₁₁} are neighbors outside the community. Then, we explore the potential community of v₅, {v₇} and {v₁₁}. The similarity between {v₇} and v₅ is (3 + 4)*2 = 14 is bigger than the similarity between {v₁₁} and v₅ is (3 + 3)*2 = 12. So the external similarity is 14 The internal similarity between {v₁} and v₅ is (16 + 3)*2 = 38 is bigger than 14. Therefore, node v₅ is assigned to the community. If we perform the process without the application of potential community, the external neighboring nodes are considered as a whole {v₇, v₁₁}. The similarity between {v₇, v₁₁} and v₅ is ((3 + 4) + (3 + 3))*2 = 39 which is bigger than internal similarity 38. Therefore, node v₅ is not a member of the detected community.

There are four pseudo-code of LCDPC displaying in Algorithm 1, Algorithm 2, Algorithm 3, and Algorithm 4. The flow chart of each process is shown in Figure 5. The details of each procedure are shown in the following text.

FIGURE 5

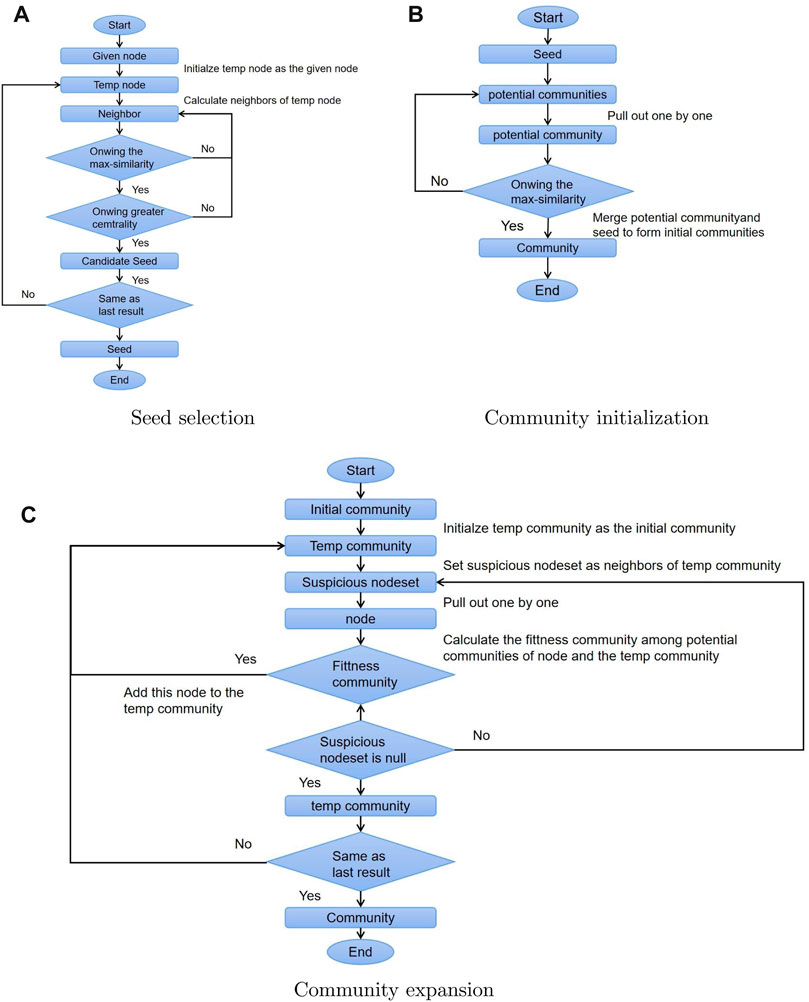
FIGURE 5. The flow chart of LCDPCs. (A) The flow chart of seed selection process. (B) The flow chart of community initialization process. (C) The flow chart of community expansion process.

Potential community exploration. Line three initializes a community P to the empty set to store the potential community. Line four initializes a list to store the nodes that make up the potential community. Then the first node from list is pulled out and v_temp is initialized as this node (Line 6). Lines eight to nine search for node sets that are linked in the common neighbors between the neighbors of v’ and the neighbors of v_temp and store these nodes in P and list, respectively. Lines 5–10 repeat the algorithm until there are no nodes in list. Saving a potential community P obtained above to Ps (Line 11). Lines 2–12 repeat the algorithm until each node v_i neighbors v. Line 13 returns all the potential communities Ps.

Seed selection. The seed selection procedure aims to search for the most suitable node as the seed of the target community where the given node is located. In the process of seed selection, LCDPC searches the node that meets the following two conditions: first, the degree of the node is greater than that of the given node; second, the node similarity between this node and the given node is the highest among neighboring nodes of the given node. In Algorithm 2, Line one initializes a community to the empty set to store the result community after the community expansion procedure. Line two calculates the degree of each node in the graph, which is the measurement of node similarity. Line seven calculates the neighboring nodes N (v_temp). Line 10 calculates the similarity between the seed and each node in the neighboring nodes of the seed. Lines 8–17 search the seed based on the two conditions among N (v_temp). The seed will be replaced iteratively by the node searched by the program above until no node meets the conditions (Lines 5–18)).

Community initialization. The community initialization procedure generates an initial community based on the seed. The initial community consists of the seed and the potential community of the seed that has the highest similarity to the seed. In Algorithm 3, Line three calculates the potential community sets P(v_seed) of the seed based on Definition.5. Line five calculates the similarity between the seed and each potential community in P(v_seed). The seed and the potential community with the highest similarity to the seed form the initial community (Lines 4–10).

Community expansion. The community expansion procedure adds eligible suspicious nodes to the initial community to form the resulting community. The eligible suspicious nodes should satisfy the condition that the fittest community of the node is the detected community expanded from the initial community. In Algorithm 4, the initial community generated by the community initialization procedure is assigned to the temporary community (Line 1). Line two initializes a list of suspicious nodes to the empty set. Line five obtains the community neighbors N(C_temp) of community C_temp based on Definition.3. Line one assigns N(C_temp) to the list of suspicious nodes. For each node in the list of suspicious nodes, LCDPC gets the potential community set (Line 9) and calculates the fittest community (Line 10). If the fittest community is the detected community, the node will be added to the detected community (Lines 11–12), and Line 13 adds the neighboring nodes that are outside the detected community to the list of suspicious nodes. The program stops when there is no suspicious node meeting the condition, which means that the community does not change anymore (Line 16).

Algorithm 1. Potential communities exploration.

Input: Graph G = {V, E}, link set E, node set V, node v.

Output: Potential communities Ps.

Process:

1: Calculate neighboring nodes N(v) of v based on Definition.1;

2: for all v_i ∈ N(v) do

3: Initialize P = ø

4: Initialize list = v_i

5: do

6: Initialize v_temp = pull out the first node from list

7: Calculate neighboring nodes N (v_temp) of v_temp based on Definition.1;

8: P = P ∪ (N(v) ∩ N (v_temp))

9: list = list ∪ (N(v) ∩ N (v_temp))

10: while list = = ø

11: Add P to Ps

12: end for

13: return Ps

Algorithm 2. Seed selection.

Input: Graph G = {V, E}, link set E, node set V, seed node v_seed.

Output: candidate seed v_seed.

Process:

1: Initialize a community C, C = ø;

2: Calculate the degree $d_{v_i}$ of each node v_i ∈ V;

3: Set v_temp = v_seed;

4: Set max _similarity = 0;

5: do

6: v_seed = v_temp;

7: Calculate neighboring nodes N (v_temp) of v_temp based on Definition.1;

8: for all v_i ∈ N (v_temp) do

9: if $d_{v_i}>d_{v_{\mathit{temp}}}$ then

10: Calculate the node similarity NS(v_i, v_temp) between v_i and

11: v_temp based on Definition.6;

12: if NS(v_i, v_temp) > max _similarity then

13: v_temp = v_i;

14: max _similarity = NS(v_i, v_temp);

15: end if

16: end if

17: end for

18: while v_temp ≠ v_seed

19: return v_seed

Algorithm 3. Community initialization.

Input: Graph G = {V, E}, link set E, node set V, seed node v_seed.

Output: Initial Community C_initial.

Process:

1: Set similarity_max = 0;

2: Calculate the neighboring community N (v_seed) of v_seed based on Definition.2;

3: Calculate the potential community set P (v_seed) based on Definition.5;

4: for all $P{(v_{\mathit{seed}})}_i\in \mathbf{P}(v_{\mathit{seed}})$ do

5: Calculate the node community similarity $NCS(v_{\mathit{seed}},P{(v_{\mathit{seed}})}_i)$ between $P{(v_{\mathit{seed}})}_i$ and v_seed based on Definition.6;

6: if $NCS(v_{\mathit{seed}},P{(v_{\mathit{seed}})}_i)>similarity\text{\_}max$ then

7: $C_{\mathit{initial}}=P\left.{(v_{\mathit{seed}})}_i\right)\cup v_{\mathit{seed}}$;

8: $similarity\text{\_}max=NCS(v_{\mathit{seed}},P{(v_{\mathit{seed}})}_i)$;

9: end if

10: end for

11: return C_initial

Algorithm 4. Community expansion.

Input: Graph G = {V, E}, link set E, node set V, Initial Community C_initial.

Output: Community C.

Process:

1: Set C_temp = C_initial;

2: Set suspicious_list = ø;

3: do

4: C = C_temp;

5: Get the community neighbors N(C_temp) of community C_temp based on Definition.3

6: suspicious_list = N(C_temp);

7: while suspicious_list ≠ ø do

8: Pull v_i from suspicious_list;

9: Get the potential community set P(v_i) based on Definition.5

10: Calculate the fittest community FC(v_i) of v_i based on Definition.8

11: if FC(v_i) = C_temp then

12: Add node v_i to C_temp;

13: update suspicious_list = N(v_i) − C_temp;

14: end if

15: end while

16: while C ≠ C_temp

17: return C

3.4.1 Time complexity analysis

We analyze the time complexity of LCDPC on a network G with an average degree of $\bar{d}$ in the following. The analysis is performed in three steps of our algorithm.

The first step is to execute the Algorithm 2 to find candidate core members of the seed node; this step requires $O({\bar{d}}^4)$ [18]. In the second step, we initialize the detected community based on the output of Algorithm 2, as shown in the first phase of Algorithm 3. Detecting all suspicious nodes requires $O(\bar{s})$ where $\bar{s}$ is the mean size of the potential community. Then Algorithm 4 is executed to identify each suspicious node; this algorithm takes $O({\bar{d}}^3)$. Accordingly, the time complexity of step 2 is $O(\bar{s}{\bar{d}}^3)$. The last step is to expand the community from the initial community. This requires $O(r\bar{s}{\bar{d}}^3)$ where r is the maximum length of the path from the seed node to the community fringe. Finally, the overall time complexity of our method is $O({\bar{d}}^4+r\bar{s}{\bar{d}}^3)$.

4 Experiments and analyses

All the proposed algorithms and the comparison algorithms in this paper are written in JAVA and run on a computer with Intel (R) Core (TM) i5-4590 CPU, 3.3 GHz, and 16 GB RAM.

4.1 Evaluation criteria

To verify the performance of the proposed algorithms, we use the following two common evaluation criteria of community detection: NMI [44] (the normalized mutual information) and the F-measure [45].

4.1.1 Normalized mutual information

Danon et al. proposed normal mutual information (NMI) measure [44] based on information entropy to measure the similarity between real-world communities and detected communities. This measure defines a confusion matrix N with the rows denoting real-world communities and the columns denoting detected communities. Element N_ij in matrix N represent the numbers of nodes that exist in both community i and community j [44]. The formula of NMI is:

$NMI\left(A,B\right)=\frac{-2{\sum }_{i=1}^{c_A}{\sum }_{j=1}^{c_B}{N}_{ij}\log \left(N_{ij}N/N_{i.}{N}_{.j}\right)}{{\sum }_{i=1}^{c_A}{N}_{i.}\log \left(N_{i.}/N\right)+{\sum }_{j=1}^{c_B}{N}_{.j}\log \left(N_{.j}/N\right)}(7)$

where c_A denotes the number of real-world communities and c_B denotes the number of detected communities. N_i. and N_.j denote the sum of elements in row i and column j respectively [44].

NMI is used to assess the performance of algorithms in dividing communities. A good partition means a great NMI value. The extreme case is NMI value is one when the partition is correct absolutely.

4.1.2 F-measure

F-Measure is a widely used evaluation criterion to assess the performance of community detection algorithms. F-Measure is defined as:

$F=2\times \frac{\text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}(8)$

The recall and precision are as follows:

$Recall=\frac{\left|C_G\cap C_D\right|}{|C_G}(9)$

$Precision=\frac{\left|C_G\cap C_D\right|}{|C_D}(10)$

where C_G denotes the real-world community and C_D denotes the detected community,

F − Measure is the weighted harmonic average of Recall and Precision.

4.2 Datasets

4.2.1 Artificial networks

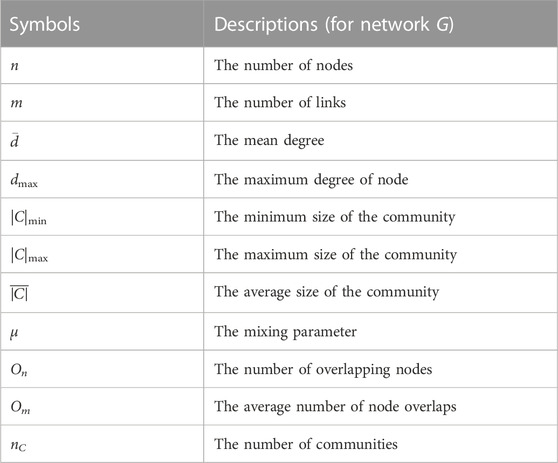
We used a set of artificial networks generated by LFR [46] (Lancichinetti Fortunato Radicchi) benchmark networks to test the performance of the proposed algorithms. LFR is a common method to generate artificial networks that have the properties of real-world networks. The topology of the generated artificial networks is controlled by the following parameters: μ is a mixing parameter that is used to control the difficulty of revealing the community structure; |C|_min is the minimum size of the community, and |C|_max is the maximum size of the community; $\bar{d}$ is the mean node degree and d_max is the maximum node degree O_n is the number of overlapping nodes and O_m is the average number of node overlaps. The parameter settings of LFR benchmark networks are listed in Table 2, where the expression [a: b: c] means the value of the parameter ranges from a to c with a span of b. As displayed in Table 2, we generate three groups of benchmark networks: LFR-μ, LFR-α_size, LFR-α_degree. LFR-μ aims to examine the performance of the algorithm with the change in community identifiability. LFR-α_size aims to examine the performance of the algorithm with the change of community size. LFR-α_degree aims to examine the performance of the algorithm with the change in node degree. To ensure the accuracy of the experiments, we generated 10 artificial networks for each group of parameters and took the average value as the result.

TABLE 2

TABLE 2. The parameter settings of LFR benchmark networks.

The symbols mentioned in this section and their descriptions are displayed in Table 3.

TABLE 3

TABLE 3. Symbols and descriptions.

4.2.2 Real-world networks

Table 4 displays the characteristics of six widely used real-world networks involved in this paper. Karate is a network of a karate club [42]. The nodes of the network represent members of the club and the links between two nodes denote a friendship between the two members. Dolphins is a network of bottlenose dolphins living in New Zealand [47]. Each node represents a bottlenose dolphin and if two dolphins are in frequent contact, there will be a link between the nodes representing them. Books is a network of political books [48]. The nodes represent political books on the Amazon website, and there is a link between the nodes representing two books if they are often bought together. Football is a network of college football teams in America [6]. Each node of the network represents a college and the links indicate that two football teams which have played against each other. Amazon is a network of products on the Amazon website [33]. LastFM is a social network of music website users, where the nodes of the network denote users of LastFM and links denote mutual follower relationships between them [49].

TABLE 4

TABLE 4. The characteristics of real-world networks.

4.3 Experimental settings

We name the proposed algorithm that performs the process of potential community exploration to be LCDPC1 and the one that does not perform the process as LCDPC2. To verify the performance of the proposed algorithm, we compared it to eight state-of-the-art local community detection algorithms: RTLCD (a Robust Two-stage Local Community Detection algorithm) [18], Clauset [50], LWP (Luo, Wang, and Promislow) [51], Chen [52], LS (Link Similarity) [53], VI (Vertex Influence) [54], LCD (Local Community Detection based on Maximum Cliques) [55] and LCDDCE (Local Community Detection method on line graph through Degree Centrality and Expansion) [56].

Ding et al. [18] proposed a robust community detection algorithm RTLCD that consists of two stages: seed selection stage and community expansion stage. RTLCD searches the core member of the community where the given node is located in the seed selection stage, which solves the seed-dependent problem. RTLCD expands from the core member to the local community based on the relationship strength between nodes and communities in the community expansion stage, which solves the seed-invalid problem.

Based on the concept of Newman’s [57] modularity, Clauset et al. [50] introduced a local community quality function ΔR, which can be expressed as the ratio of the links within the community to the links with one or more endpoints outside the community. The Clauset algorithm adds nodes that cause the maximum increment of the quality function ΔR to the community.

Based on the Clauset algorithm, LWP et al. [51] proposed an improved quality function M, which can be expressed as the edges within the community divided by the number of edges between communities. The LWP algorithm expands the community by adding nodes that cause the maximum increment of M to the community and deletes nodes that cause the maximum increment of M but are separated from the community. Different from Clauset, LWP has definite termination criteria.

Chen et al. [52] introduced a novel quality function L, which takes the connection among nodes in the community and the connection between communities into consideration. To solve the outliers problem, the Chen algorithm checks for the changes in the quality function of the community after removing nodes.

Wu et al. [53] proposed a link similarity algorithm (LS) that can be defined as the intersection of a node’s neighbors and the nodes and neighborhoods of the community. First, greedy optimization of link similarity is performed, which adds nodes with the largest similarity to the community. Second, whether the nodes on the boundary should continue to remain in the community is checked. Third, nodes that have more neighbors in the boundary than in the community are removed.

Fanrong et al. [55] took advantage of the maximum clique expansion and proposed the LCD algorithm, which takes the maximum clique as the seeds. LCD detects all the maximum cliques in the network as seeds and expands the community from these seeds according to greedy optimization until all the maximum cliques are assigned to communities.

Yao et al. [54] proposed a variable influence local community detection algorithm (VI) based on a mechanism of influence attenuation, which is capable of detecting communities with variable scale according to the demands.

Wang et al. [56] introduced a line graph model to local community detection, and proposed an algorithm based on node centrality and PageRank. First, edges are transferred into nodes based on the line graph model. Second, nodes are ranked by a novel node similarity and PageRank and seeds are determined by this ranking. Third, the community is expanded by a fitness function.

In our experiments, all the algorithms were run in six real-world networks and three groups of LFR artificial networks, and the average of the experimental results was recorded. α in LCDDCE is set to 1.5. Note that all the algorithms that ran for more than 24 h were terminated. We take each node in the network as a given node and execute the algorithm with this given node. Finally, the results of all nodes are averaged as the performance of the algorithm on this network.

4.4 Experimental results on artificial networks

4.4.1 Experimental results on LFR-μ

The purpose of LFR-μ is to examine the performance of algorithms with the change in community identifiability. Figures 6A, B display the NMI and F-Measure metrics for the proposed algorithms and the comparison algorithms on LFR-μ. From the pictures, we can observe that the trend of all results is downward with the increase of mix parameter μ. The reason for this phenomenon is as follows. The definition of parameter μ is the sharing ratio between the node and nodes in other communities; in other words, the parameter μ represents the ratio between links outside the community and all links of the node. Therefore, as the parameter μ increases, the community structure becomes more difficult to detect.

FIGURE 6

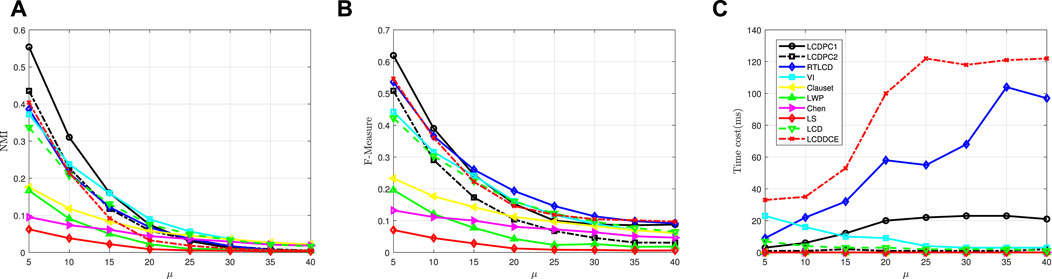
FIGURE 6. The performance of algorithms on LFR-μ. (A) NMI on LFR-μ. (B) F-measure on LFR-μ. (C) Time cost on LFR-μ.

5As shown in Figures 6A, B, when μ ≤ 0.5, except for Chen and LS, the results show a significant downward trend, and the performance of LCDPC has always been at a high level. Although the NMI and F-Measure metrics of Chen and LS are stable, they are always at a low level. When μ > 0.5, the results of all algorithms are stable at a low level, because the mixed parameter μ is so great that the community structure is very complex, and all algorithms cannot effectively detect the community structure.

In addition, the performance of LCDPC1 is better than that of LCDPC2 on each value of parameter μ. As the parameter μ increases, the difference between LCDPC1 and LCDPC2 in performance decreases. The reason for this outcome is as follows. With the increase in the parameter μ, the links between the node and the other communities increase. In this condition, it is easy for external adjacent nodes of the node to form the potential community. The scale of the external community formed by LCDPC1 and LCDPC2 is almost the same, which leads to a decrease in the gain effect of the application of potential community exploration. Therefore, the exploration of potential communities plays a better role in community detection in simple networks than in complex networks.

Figure 6C shows the time cost index of all the algorithms. We can observe that the majority of results remain stable at a low. RTLCD shows a significant upward trend with the growth of μ. VI reaches a peak at μ = 0.1 and decreases gradually. LCDPC1 increases slightly and remains stable at μ = 0.4.

4.4.2 Experimental results on LFR-α_size

The purpose of LFR-α_size is to examine the performance of algorithms with the change of community size. Figures 7A, B display the NMI and F-Measure metrics for the proposed algorithms and the comparison algorithms on LFR-α_size. The top and bottom x − label in the graph represent the maximum and minimum community sizes, respectively. As seen from the figures above, the results of algorithms on LFR-α_size decrease with the increase in α_size. This is because communities in the network become more diverse with the increase of parameter α_size, which makes the boundaries of the community more difficult to identify.

FIGURE 7

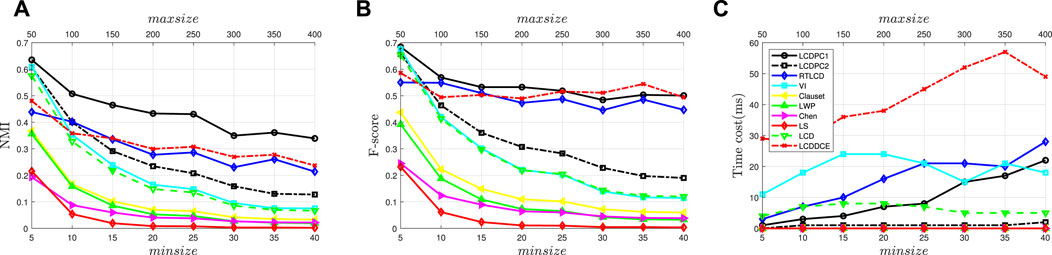
FIGURE 7. The performance of algorithms on LFR-α_size. (A) NMI on LFR-α_size. (B) F-measure on LFR-α_size. (C) Time cost on LFR-α_size.

From Figures 6A, B, we can observe that LCDPC1 outperforms the other algorithms on LFR-α_size and shows a smooth declining trend. When minc = 5, LCDPC2, VI and LCD perform as well as LCDPC1. However, when minc > 5, the performance of LCDPC2, VI and LCD decrease sharply. The reason for this result is as follows. As mentioned above, the community of the network becomes more diverse with the increase in the parameter α_size. Therefore, the similarity between a neighboring community to a node becomes diverse. The application of potential community exploration helps LCDPC1 subdivide the similarity from a neighboring community to a node. The detailed similarity division makes LCDPC1 have a better effect than other algorithms. This explanation is confirmed in Figures 7A, B, where the results gap between LCDPC1 and LCDPC2 becomes wider with the increase of the parameter α_size.

4.4.3 Experimental results on LFR-α_degree

The purpose of LFR-α_degree is to demonstrate the performance of algorithms with the change of node degrees. Figures 8A, B display the NMI and F-Measure metrics for the proposed algorithms and the comparison algorithms on LFR-α_degree. The top and bottom x − label in the graph represent the maximum and mean values of node degree, respectively. From the figures above, we find that the efficiency in community detection of algorithms on LFR-α_size improves with the increase of parameter α_size. The reason for this outcome is as follows. In the LFR network, the parameter α_degree represents the node diversity. As the parameter α_degree increases, the richer node diversity can bring more node information, which makes it easier for the algorithm to identify nodes.

FIGURE 8

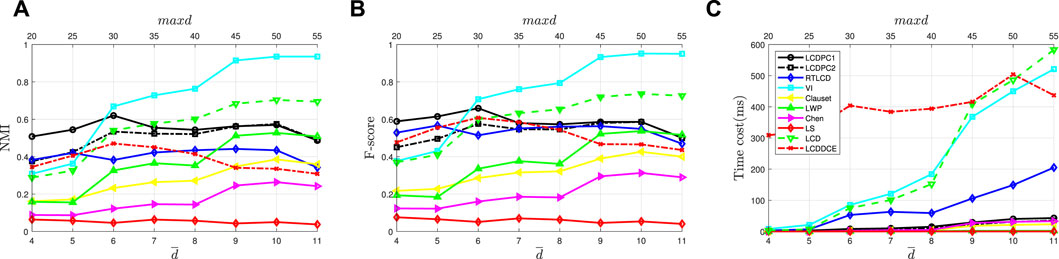
FIGURE 8. The performance of algorithms on LFR-α_degree. (A) NMI on LFR-α_degree. (B) F-measure on LFR-α_degree. (C) Time cost on LFR-α_degree.

From Figures 8A, B, we find that the performance of VI, LCD improves significantly with increasing α_degree. However, as shown in Figure 8C, these algorithms consume much more time on node information processing with the increase of α_degree. Furthermore, the difference between LCDPC1 and LCDPC2 in terms of the gain effect of potential community application, decreases with the increase in the parameter α_degree. As mentioned above, with the increase of parameter α_degree, nodes are easier to identify, which weakens the gain effect of potential communities application. Therefore, the application of potential communities is effective in identifying nodes with poor degrees.

4.5 Experimental results on real-world networks

Table 5 displays NMI, Recall, Precision, F-Measure and Time metrics of the proposed algorithms with other comparison algorithms on five real-world networks. Table 6 lists the performance differences between LCDPC1 and LCDPC2 in terms of NMI, Recall, Precision and F-Measure metrics. From Table 5, we find that LCDPC1 shows better average performance in detecting communities of real networks than the other comparison algorithms. This result shows that the proposed algorithm outperforms state-of-the-art local community detection algorithms in community identification.

TABLE 5

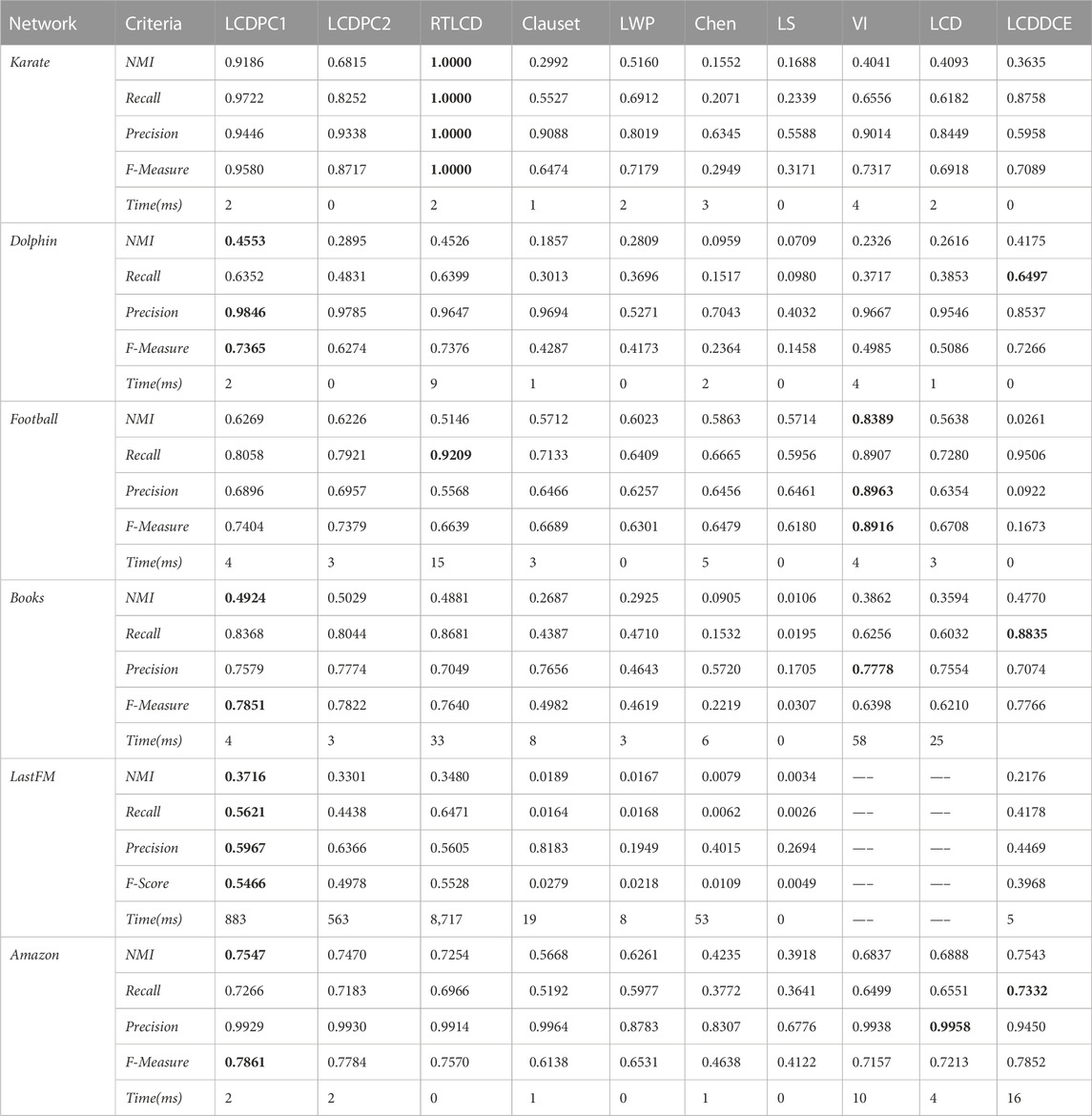
TABLE 5. The algorithm results on real-world networks. The maximum value in a criterion is marked in bold.

TABLE 6

TABLE 6. The difference between LCDPC1 and LCDPC2.

From Table 6, we can observe that LCDPC1 has improved in terms of NMI, Recall, Precision and F-Measure metrics compared to LCDPC2. This outcome verifies the effectiveness of the potential community application in community identification. Especially for the Karate and Dolphins networks, LCDPC1 has significant improvement compared to LCDPC2 in community identification. The common characteristic of the Karate and Dolphins networks is that they all have low mean degree values. Furthermore, we find that LCDPC1 has limited improvement compared to LCDPC2 in identifying communities on the Football and Books networks. Both the Football and Books networks have high mean degree values. These findings indicate that the potential community application has a more significant improvement in the efficiency of community identification on the network with a high mean node degree than that with a low mean node degree. In addition, LCDPC1 has good improvement on the LastFM network and has limited improvement on the Amazon network compared to LCDPC2. The LastFM and Amazon networks have the same low mean node degree, but the difference is that the LastFM has a great average community size and the Amazon network is poor. This outcome verifies that the potential community application has a more significant improvement in identifying communities on the network with a greater average community size than those with a lesser average community size.

5 Conclusion

Local community detection is efficient in detecting local community structures based on seeds. However, the existing algorithms ignore the effect of community structure in undetected networks.

This paper introduces the abstract concept of the potential community into the local community detection algorithm to help determine the membership of suspicious nodes. We propose a three-stage algorithm based on potential community exploration, which performs seed selection, community initialization, and community expansion in order. First, the seed selection searches for a suitable seed to replace the given node. Second, the community initialization process forms the initial community by combining the seed and its suitable potential community. Finally, the community expansion process adds eligible nodes to the initial community for community expansion.

The proposed algorithm is compared to eight state-of-the-art local community detection algorithms on artificial networks and real-world networks. The experimental results show the following conclusions. First, the potential community application can improve the efficiency of community identification. Second, the improvement in potential community application on community identification is related to the parameters μ, α_size, and α_degree. The improvement of potential community application increases with increasing α_size and decreases with increasing μ and α_degree.

However, the experimental results show that the potential community application is not obviously better for some networks, especially networks with a low mean node degree. Therefore, in future work, we will improve the algorithm to expand the role of potential community applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material further inquiries can be directed to the corresponding authors.

Author contributions

SW write and revise the manuscript. JY, XD, JZ, and MZ contributed to paper ideas amd data curation, analysis. All authors approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Newman M. Networks: An introduction. Oxford, UK: Oxford University Press (2010).

Google Scholar

2. Fortunato S. Community detection in graphs. Phys Rep (2009) 486(3-5):75–174.

Google Scholar

3. Newman MEJ. Fast algorithm for detecting community structure in networks. Phys Rev E (2004) 69(6):066133. doi:10.1103/physreve.69.066133

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pizzuti C. Evolutionary computation for community detection in networks: A review. IEEE Trans Evol Comput (2018) 22(3):464–83. doi:10.1109/tevc.2017.2737600

CrossRef Full Text | Google Scholar

5. Xie J, Kelley S, Szymanski BK. Overlapping community detection in networks: The state-of-the-art and comparative study. Acm Comput Surv (2013) 45(4):1–35. doi:10.1145/2501654.2501657

CrossRef Full Text | Google Scholar

6. Girvan M, Newman MEJ. Community structure in social and biological networks. Proc Natl Acad Sci United States America (2002) 99(12):7821–6. doi:10.1073/pnas.122653799

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhu J, Chen B, Zeng Y. Community detection based on modularity and k-plexes. Inf Sci (2020) 513:127–42. doi:10.1016/j.ins.2019.10.076

CrossRef Full Text | Google Scholar

8. Ma L, Chiew K, Huang H, He Q. Evaluation of local community metrics: From an experimental perspective. J Intell Inf Syst (2018) 51(1):1–22. doi:10.1007/s10844-017-0480-5

CrossRef Full Text | Google Scholar

9. Luo W, Zhang D, Jiang H, Ni L, Hu Y. Local community detection with the dynamic membership function. IEEE Trans Fuzzy Syst (2018) 26(5):3136–50. doi:10.1109/tfuzz.2018.2812148

CrossRef Full Text | Google Scholar

10. Luo W, Lu N, Ni L, Zhu W, Ding W. Local community detection by the nearest nodes with greater centrality. Inf Sci (2020) 517:377–92. doi:10.1016/j.ins.2020.01.001

CrossRef Full Text | Google Scholar

11. Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure in complex networks. New J Phys (2009) 11(3):033015. doi:10.1088/1367-2630/11/3/033015

CrossRef Full Text | Google Scholar

12. Baumes J, Goldberg MK, Krishnamoorthy MS, Magdon-Ismail M, Preston N. Finding communities by clustering a graph into overlapping subgraphs. In: AC 2005, Proceedings of the IADIS International Conference on Applied Computing; February 22-25, 2005; Algarve, Portugal (2005). p. 97–104.

Google Scholar

13. Lee C, Reid F, McDaid A, Hurley N. Detecting highly overlapping community structure by greedy clique expansion. In: Proceedings of the 4th SNAKDD Workshop (2010). p. 33–42.

Google Scholar

14. Whang JJ, Gleich DF, Dhillon IS. Overlapping community detection using neighborhood-inflated seed expansion. IEEE Trans Knowledge Data Eng (2016) 28(5):1272–84. doi:10.1109/tkde.2016.2518687

CrossRef Full Text | Google Scholar

15. Li J, Wang X, Cui Y. Uncovering the overlapping community structure of complex networks by maximal cliques. Physica A: Stat Mech Its Appl (2014) 415:398–406. doi:10.1016/j.physa.2014.08.025

CrossRef Full Text | Google Scholar

16. Li J, Wang X, Eustace J. Detecting overlapping communities by seed community in weighted complex networks. Physica A: Stat Mech Its Appl (2013) 392(23):6125–34. doi:10.1016/j.physa.2013.07.066

CrossRef Full Text | Google Scholar

17. Ahmad Z, Amir S. A hierarchical approach for influential node ranking in complex social networks. Expert Syst Appl (2017) 93:200. doi:10.1016/j.eswa.2017.10.018

CrossRef Full Text | Google Scholar

18. Ding X, Zhang J, Yang J. A robust two-stage algorithm for local community detection. Knowledge-Based Syst (2018) 152:188–99. doi:10.1016/j.knosys.2018.04.018

CrossRef Full Text | Google Scholar

19. Mohammadi M, Moradi P, Jalili M. Sce: Subspace-based core expansion method for community detection in complex networks. Physica A: Stat Mech its Appl (2019) 527:121084. doi:10.1016/j.physa.2019.121084

CrossRef Full Text | Google Scholar

20. Cheng J, Zhang W, Yang H, Su X, Ma T, Chen X. A seed-expanding method based on TOPSIS for community detection in complex networks. Complexity (2020) 2020(1):1–14. doi:10.1155/2020/9017239

CrossRef Full Text | Google Scholar

21. Rezaei AA, Munoz J, Jalili M, Khayyam H. Vital node identification in complex networks using a machine learning-based approach (2022). arXiv:2202.06229.

Google Scholar

22. Kanawati R. Empirical evaluation of applying ensemble methods to ego-centred community identification in complex networks. Neurocomputing (2015) 150(PB):417–27. doi:10.1016/j.neucom.2014.09.042

CrossRef Full Text | Google Scholar

23. Zhang R, Li L, Bao C, Zhou L, Kong B. The community detection algorithm based on the node clustering coefficient and the edge clustering coefficient. In: Proceedings of the World Congress on Intelligent Control and Automation (WCICA); 05 March 2015. Shenyang: IEEE (2015). p. 3240–5. doi:10.1109/WCICA.2014.7053250

CrossRef Full Text | Google Scholar

24. Wang P, Liu J. A multi-agent genetic algorithm for local community detection by extending the tightest nodes. In: 2016 IEEE Congress on Evolutionary Computation (CEC); 24-29 July 2016. Vancouver, BC, Canada: IEEE (2016). p. 3215–21. doi:10.1109/CEC.2016.7744196

CrossRef Full Text | Google Scholar

25. Delis A, Ntoulas A, Liakos P. Scalable link community detection: A local dispersion-aware approach. In: Proceedings - 2016 IEEE International Conference on Big Data (Big Data); 05-08 December 2016. Washington, DC, USA: IEEE (2016). p. 716–25. doi:10.1109/BigData.2016.7840664

CrossRef Full Text | Google Scholar

26. Zhu J, Chen B, Zeng Y. Community detection based on modularity and k-plexes. Inf Sci (2020) 513:127–42. doi:10.1016/j.ins.2019.10.076

CrossRef Full Text | Google Scholar

27. Kloster K, Gleich DF. Heat kernel based community detection. In: Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (2014). p. 1386–95.

CrossRef Full Text | Google Scholar

28. Hu Y, Yang B, Wong HS. A weighted local view method based on observation over ground truth for community detection. Inf Sci (2016) 355-356:37–57. doi:10.1016/j.ins.2016.03.028

CrossRef Full Text | Google Scholar

29. He K, Sun Y, Bindel D, Hopcroft J, Li Y. Detecting overlapping communities from local spectral subspaces. In: Proceedings - IEEE International Conference on Data Mining, ICDM; 07 January 2016. Atlantic City, NJ, USA: IEEE (2016). p. 769–74. doi:10.1109/ICDM.2015.89

CrossRef Full Text | Google Scholar

30. Yao Y, Wu W, Lei M, Zhang X. Community detection based on variable vertex influence. In: 2016 IEEE First International Conference on Data Science in Cyberspace (DSC); 02 March 2017. Changsha, China: IEEE (2017). p. 418–23. doi:10.1109/DSC.2016.99

CrossRef Full Text | Google Scholar

31. You X, Ma Y, Liu Z. A three-stage algorithm on community detection in social networks. Knowl Based Syst (2020) 187:104822. doi:10.1016/j.knosys.2019.06.030

CrossRef Full Text | Google Scholar

32. Zhang J, Ding X, Yang J. Revealing the role of node similarity and community merging in community detection. Knowl Based Syst (2019) 165:407–19. doi:10.1016/j.knosys.2018.12.009

CrossRef Full Text | Google Scholar

33. Yang J, Leskovec J. Defining and evaluating network communities based on ground-truth. Knowledge Inf Syst (2015) 42(1):181–213. doi:10.1007/s10115-013-0693-z

CrossRef Full Text | Google Scholar

34. Raghavan UN, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks. Phys Rev E Stat Nonlinear Soft Matter Phys (2007) 76(3):036106. doi:10.1103/physreve.76.036106

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gregory S. Finding overlapping communities in networks by label propagation. New J Phys (2010) 12(10):103018. doi:10.1088/1367-2630/12/10/103018

CrossRef Full Text | Google Scholar

36. Tang M, Liu Q, Ma T, Cao J, Tian Y, Al-Dhelaan A, et al. $\mathcal{K}$ -Lowest-Influence overlapping nodes based community detection in complex networks. IEEE Access (2019) 7:109646–61.

CrossRef Full Text | Google Scholar

37. Tao W, Yin L, Wang X. A community detection method based on local similarity and degree clustering information. Physica A Stat Mech Its Appl (2017) 490:1344. doi:10.1016/j.physa.2017.08.090

CrossRef Full Text | Google Scholar

38. Li Y, He K, Kloster K, Bindel D, Hopcroft JE. Local spectral clustering for overlapping community detection. ACM Trans Knowl Discov Data (2018) 12(2):1:27–17:27. doi:10.1145/3106370

CrossRef Full Text | Google Scholar

39. Okuda M, Satoh S, Sato Y, Kidawara Y. Community detection using restrained random-walk similarity. IEEE Trans pattern Anal machine intelligence (2019) 43(1):89. doi:10.1109/TPAMI.2019.2926033

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Luo W, Lu N, Ni L, Zhu W, Ding W. Local community detection by the nearest nodes with greater centrality. Inf Sci (2020) 517:377–92. doi:10.1016/j.ins.2020.01.001

CrossRef Full Text | Google Scholar

41. Bahadori S, Zare H, Moradi P. Podcd: Probabilistic overlapping dynamic community detection. Expert Syst Appl (2021) 174:114650. doi:10.1016/j.eswa.2021.114650

CrossRef Full Text | Google Scholar

42. Zachary WW. An information flow model for conflict and fission in small groups. J Anthropological Res (1977) 33(4):452–73. doi:10.1086/jar.33.4.3629752

CrossRef Full Text | Google Scholar

43. Jaccard P. Etude comparative de la distribution florale dans une portion des alpes et des jura. Bulletin Del La Societe Vaudoise Des Sciences Naturelles (1901) 37(142):547–79.

Google Scholar

44. Danon L, Díaz-Guilera A, Duch J, Arenas A. Comparing community structure identification. J Stat Mech Theor Exp (2005) 2005(9):P09008–228. doi:10.1088/1742-5468/2005/09/p09008

CrossRef Full Text | Google Scholar

45. Li J, Wang X, Wu P. Review on community detection methods based on local optimization. J Stat Mech Theor Exp (2015) 30(2):238–47.

Google Scholar

46. Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms. Phys Rev E Stat Nonlinear Soft Matter Phys (2008) 78(4):046110. doi:10.1103/physreve.78.046110

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lusseau D, Schneider K, Boisseau OJ, Haase P, Slooten E, Dawson SM. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations: Can geographic isolation explain this unique trait. Behav Ecol Sociobiol (2003) 54(4):396–405. doi:10.1007/s00265-003-0651-y

CrossRef Full Text | Google Scholar

48. Krebs V. Social network of political books (2004). Available from: www.visualcomplexity.com.

Google Scholar

49. Rozemberczki B, Sarkar R. Characteristic functions on graphs: Birds of a feather, from statistical descriptors to parametric models. In: Proceedings of the 29th ACM International Conference on Information and Knowledge Management (CIKM ’20), ACM (2020). p. 1325–34. doi:10.1145/3340531.3411866

CrossRef Full Text | Google Scholar

50. Clauset A. Finding local community structure in networks. Phys Rev E (2005) 72(2):026132–6. doi:10.1103/physreve.72.026132

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Luo F, Wang JZ, Promislow E. Exploring local community structures in large networks. Web Intelligence Agent Syst (2008) 6(4):387–400. doi:10.3233/wia-2008-0147

CrossRef Full Text | Google Scholar

52. Chen J, Zaïane O, Goebel R. Local community identification in social networks. In: 2009 International Conference on Advances in Social Network Analysis and Mining; 04 September 2009. Athens, Greece: IEEE (2009). p. 237–42. doi:10.1109/ASONAM.2009.14

CrossRef Full Text | Google Scholar

53. Wu Y, Huang H, Hao Z, Chen F. Local community detection using link similarity. J Comput Sci Technol (2012) 27(6):1261–8. doi:10.1007/s11390-012-1302-4

CrossRef Full Text | Google Scholar

54. Yao Y, Wu W, Lei M, Zhang X. Community detection based on variable vertex influence. In: 2016 IEEE First International Conference on Data Science in Cyberspace (DSC); 02 March 2017. Changsha, China: IEEE (2017). p. 418–23. doi:10.1109/DSC.2016.99

CrossRef Full Text | Google Scholar

55. Fanrong M, Mu Z, Yong Z, Ranran Z. Local community detection in complex networks based on maximum cliques extension. Math Probl Eng (2014) 2014:653670. doi:10.1155/2014/653670

CrossRef Full Text | Google Scholar

56. Wang G, Wang K, Wang H, Lu H, Zhou X, Feng Y. Uncovering local community structure on line graph through degree centrality and expansion. Int J Mod Phys B (2021) 35:2150120. doi:10.1142/s0217979221501204

CrossRef Full Text | Google Scholar

57. Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2004) 66(2):026113. doi:10.1103/physreve.69.026113

PubMed Abstract | CrossRef Full Text | Google Scholar