- 1Tata Institute of Fundamental Research, Hyderabad, India
- 2Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm, Sweden
We present direct numerical simulations (DNS) study of confined buoyancy-driven bubbly flows in a Hele-Shaw setup. We investigate the spectral properties of the flow and make comparisons with experiments. The energy spectrum obtained from the gap-averaged velocity field shows E(k) ∼ k for k < kd, E(k) ∼ k−5 for k > kd, and an intermediate scaling range with E(k) ∼ k−3 around k ∼ kd. We perform an energy budget analysis to understand the dominant balances and explain the observed scaling behavior. For k < kd, energy injection balances dissipation due to drag, whereas for k > kd, the net injection balances net dissipation. We also show that the Navier-Stokes equation with a linear drag can be used to approximate large scale flow properties of bubbly Hele-Shaw flow.
1 Introduction
Flows generated by dilute bubble suspensions (bubbly flows) are relevant in many natural and industrial processes [1]. As the bubbles rise due to buoyancy and stir the fluid, they generate complex spatiotemporal flow structures “pseudo-turbulence” [2–6]. The underlying physical mechanisms responsible for the flow are the interaction between wakes caused by individual bubbles and the interaction of bubbles with the flow generated by their neighbors [3,5].
Early experiments characterized pseudo-turbulence in bubbly flows at a low-volume fraction by measuring the energy spectrum E(k) ∼ k−3 (where k is the wave number). They argued that the power-law scaling appears due to a balance of energy production with viscous dissipation [2]. Subsequent experimental studies have verified the power-law scaling in the energy spectrum [5,7–9].
Only recent numerical studies have started investigating pseudo-turbulence at experimentally relevant parameter ranges [6,10,11]. A scale-by-scale energy budget analysis has unraveled the details of the energy transfer mechanism. Buoyancy injects energy at scales comparable to the bubble diameter; it is then transferred to smaller scales by non-linear fluxes due to surface tension and kinetic energy, where it gets dissipated by viscosity. Quite remarkably, these studies also reveal that the statistics of the velocity fluctuations do not depend either on the viscosity or density contrast [6,11,12].
How does the physics of bubbly flows altered in the presence of confinement? Earlier studies have investigated this question in a Hele-Shaw setup with bubbles whose unconfined diameter is larger than the confinement width [13–15]. Numerical simulations and experiments [1,16–18] on an isolated rising bubble show that, compared to an unconfined bubble, the wake flow of the confined bubble is severely attenuated. Nevertheless, the experiments on bubbly flows in the Hele-Shaw setup still observe the power-law scaling of pseudo-turbulence between scales comparable to the bubble diameter and twenty times the bubble diameter.
In this paper, we perform a numerical investigation of buoyancy-driven bubbly flow in a Hele-Shaw setup. To make a comparison with experiments, we choose moderate volume fractions ϕ = 5–10%. We investigate the energy spectrum of the gap-averaged velocity field and, consistent with experiments, observe an interediate power-law scaling in the energy spectrum E(k) ∼ k−3. Using a scale-by-scale energy budget analysis, we show that confinement dramatically alters the energy budget compared to the unbounded bubbly flows. The viscous drag due to the confining walls balances energy injected by buoyancy at large scales. Non-linear transfer mechanisms due to surface tension and kinetic energy are negligible. Finally, we show that two-dimensional Navier-Stokes equations with an added drag term can be used as a model to study large scale flow properties.
The rest of the paper is organised as follows. In Section 2, we discuss the governing equations and the details of the numerical method used. In Section 3, we present results for bubbly flows in the Hele-Shaw setup and study the energy budget. We then show that the two-dimensional Navier-Stokes equations with a linear drag is a good model to study large scale properties of bubbly flows under confinement. Finally, in Section 4, we present our conclusion.
2 Equations and numerical methods
We study the dynamics of bubbly flows in a vertical Hele-Shaw cell (see Figure 1) by solving the Navier-Stokes equations with surface tension force acting at the interface,
Here, ∇* ≡ (∂x, ∂y, ∂z), C is an indicator function whose value is 0 inside the bubble phase and 1 in the fluid phase,
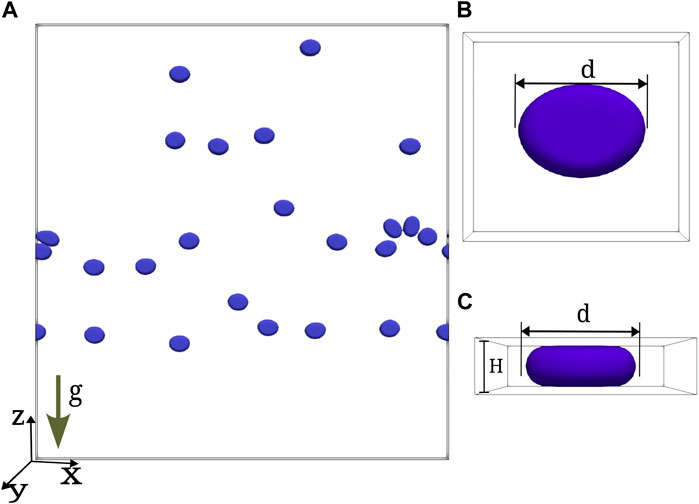
FIGURE 1. (A) Representative plot showing bubbles of diameter d in a Hele-Shaw setup. The length along x −and z −directions is L, and the gap width in y −direction is H; (B) Top view of a bubble (zoomed view); (C) Front view of the bubble (zoomed view).
The non-dimensional numbers that characterize the flow are the Galilei number
2.1 Gap width averaged equations
Experiments often use gap width averaged velocities to study statistical properties of the flow. Following the procedure outlined in [20,21] and assuming density ϱ to be constant along wall-normal direction, and starting from the NSHS equations, we get the following equations for the gap averaged indicator function c and horizontal components of the velocity2:
Here,
2.2 Numerical method
We use a second-order finite-volume solver PARIS [22] to simulate NSHS (1). For bubble tracking and updating the indicator function PARIS employs a front-tracking method, and the time marching is performed using the first order Euler method.
2.3 Initial conditions and parameters
We consider a cuboid of breadth Ly = H, and with equal length and height (Lx = Lz = L) [see Figure 1]. The simulation domain (Lx, Ly, Lz) is discretized with (Nx, Ny, Nz) equispaced collocation points. We use periodic boundary conditions in the x and z directions, and impose no-slip velocity boundary U = 0 at the walls (y = 0 and y = H) [23]. We place Nb bubbles in random positions and initialize each one as an ellipsoid of volume V = 4.73 × 103 (mono-disperse suspension). The front tracking module of the PARIS solver [22] employs a symmetry boundary condition for the surface tension force at the walls such that the net force at the wall would be tangent to the wall. This ensures a thin layer of fluid (approximately O(0.13)δy, where δy = H/Ny) between the bubble and the wall. Our grid resolution is comparable (or higher) to a previous numerical study on Hele-Shaw with bubbles [23]. The bubbles are allowed to relax in the absence of gravity until they achieve the equilibrium pan-cake-like configuration [23] with diameter d = 2H.
In Table 1 we summarize the parameters used in our simulations. We choose parameters such that the dimensionless numbers (Ga, Bo, H/d, and ϕ) are comparable to experiments [15,17,18]. We simulate low At = 0.08 and high At = 0.9, and verify that the spectral properties are insensitive to density contrast [6,11,12].

TABLE 1. Parameters used in our simulations. We fix L =512, H = 12, Nx = Nz, and d =24 for all the runs.
3 Results
In this section, we present the results of our numerical investigations. We obtain the density ϱ and the velocity U fields by performing the DNS of NSHS Eq. 1, and from them, we get the corresponding gap averaged fields. We monitor the time evolution of the gap averaged energy and investigate the flow properties in a statistically steady state. The plot in Figure 2 shows a typical snapshot of the bubble configuration along with the flow streamlines in the steady-state. Similar to the experiments [15], we observe that the flow disturbances are mostly localized in the bubble vicinity. Furthermore, the horizontal alignment of bubbles is also observed in experiments [15] as well as numerical simulation of stratified bubbly flows in a Hele-Shaw setup [23]. As is conventional in the experiments [14,15], we investigate the spectral properties of the gap-averaged velocity field (2).
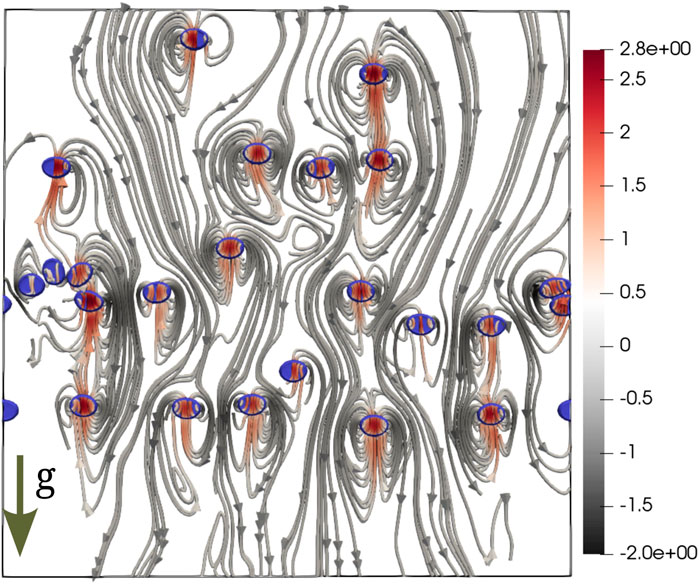
FIGURE 2. Instantaneous bubble configuration superimposed with flow streamlines in the steady-state (run
3.1 Time evolution
From (2), we obtain the following balance equation for the gap-averaged kinetic energy E
where ϵμ is the gap-averaged viscous energy dissipation, ϵd is the dissipation due to drag, ϵinj is the gap-averaged energy injected due to buoyancy, ϵσ is the contribution due to the surface tension, and the angular brackets denote spatial averaging.
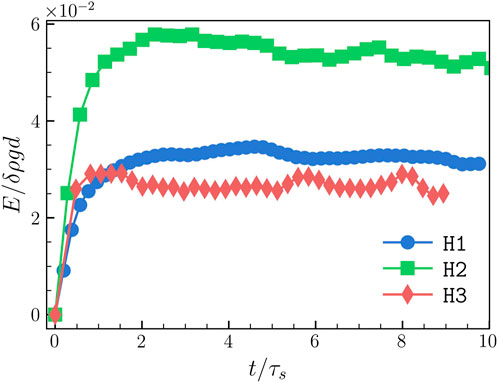
In Figure 3, we plot the time-evolution of the kinetic energy E and observe that a statistically steady state is achieved for t > 0.8τs. Furthermore, in Table 2 we show that the energy injected by buoyancy is primarily balanced by the dissipation due to drag in the steady state (∂tE ≈ 0).
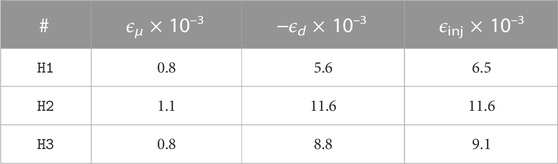
TABLE 2. Time-averaged values of the energy injection ϵinj, viscous dissipation ϵμ, and dissipation due to drag ϵd in the statistically steady state.
3.2 Energy spectra and scale-by-scale energy budget
The energy spectrum and co-spectra for the gap-averaged velocity field are defined as:
Here,
In Figure 4, we plot the energy spectra E(k) and cospectra Eρu(k) for our simulations
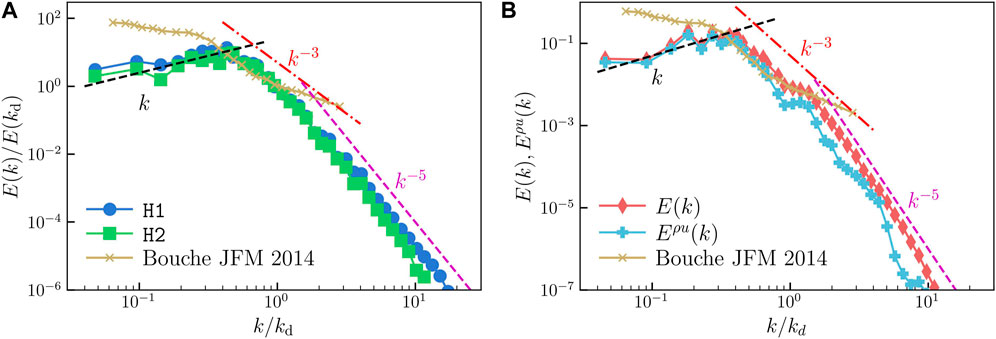
FIGURE 4. (A) Log-log of the energy spectra [E(k) versus k] for low At runs
The k−3 scaling range observed in our simulaiton is consistent with earlier experiments that also observe an intermediate k−3 scaling subrange for 0.2⪅k/kd⪅1 [15]. We verify this by overlaying the energy spectrum obtained in [15] over our data in Figure 4.
Risso [24] argues that the k−3 scaling could be modelled as a signal consisting of a sum of localized random bursts. Although this explanation is consistent with Figure 2, it does not highlight the underlying mechanisms that generate the observed scaling. Lance and Bataille [2] take an alternate viewpoint and argue that the balance of energy production and viscous dissipation leads to the k−3 scaling.
The scaling of the energy spectrum we observe differs from earlier studies on two-dimensional unbounded flows [10,12] at comparable Ga. They find an inverse energy cascade with E(k) ∼ k−5/3 for k < kd and a E(k) ∼ k−3 scaling for k > kd due to the balance of energy injected by surface tension with viscous dissipation.
In what follows, we present an energy budget analysis to explain the observed scaling of the energy spectrum.
3.2.1 Energy budget
Since the scaling behaviour observed in our simulations
where D(k) is the viscous dissipation,
The plot in Figure 5A shows the different contributions to the budget. Clearly for k < kd, the energy injected by buoyancy is balanced by the drag
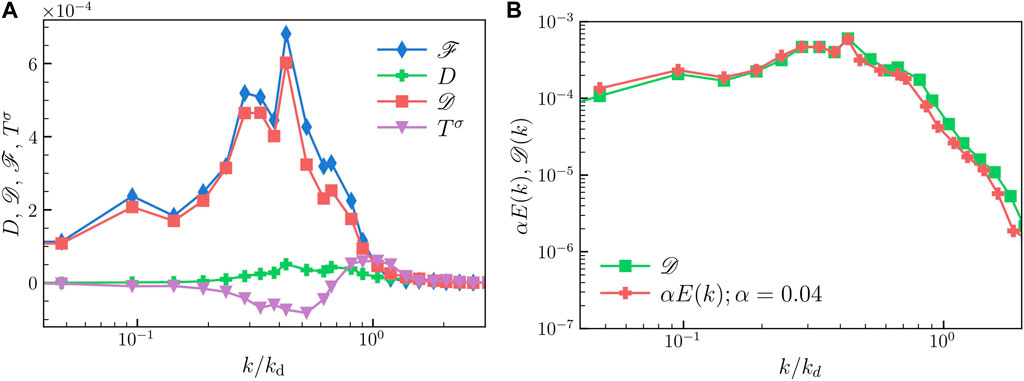
FIGURE 5. (A) Lin-log plot of the different contributions to the spectral energy budget (4) obtained from run
The situation is more complicated for k > kd. The zoomed-in plot of the energy balance (see Figure 6A) reveals that both buoyancy and the surface tension inject energy that gets dissipated by the viscous forces
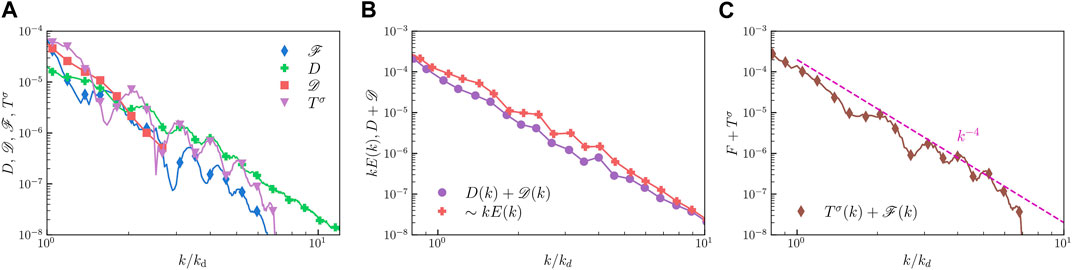
FIGURE 6. (A) Zoomed in plot showing contributions to the spectral energy budget for k > kd. (B) Log-log plot showing comparison of the scaled dissipation spectrum ∼ kE(K) and the net dissipation
Given the limited cross-over scaling range E(k) ∼ k−3 in Figure 4, we are unable to argue about the underlying mechanisms. Thus the plausible explanation for the −3 scaling is the argument by Risso [24] that we have discussed in the previous section.
3.3 Two-dimensional Navier-Stokes equations with a linear drag (NSD)
In this section we investigate whether two-dimensional Navier-Stokes equations with a linear drag coefficient (5) are able to model the confined bubbly flows In the following, we assume all the fields are two-dimensional and for comparison with the gap-averaged quantities, we choose the same symbols.
Earlier studies [13,17,18,28] have used NSD Eq. 5 to investigate the dynamics of an isolated bubble in a Hele-Shaw setup with H/d ≤ 0.5 and found the results to be consistent with the experiments. In the following, we use NSD equations to study bubbly flows.
We perform direct numerical simulation of NSD equations on a square domain of area L2 and discretize it with 20482 equi-spaced points. The bubbles are initialized as circles of diameter d = 24 and all the parameters of the simulation are identical to our run
In Figure 7A, we plot the bubble configuration and the flow streamlines. Clearly the large scale flow properties resemble those observed for the NSHS simulation. The flow disturbances are localized in the vicinity of the bubbles and we also observe horizontal alignment of bubbles.
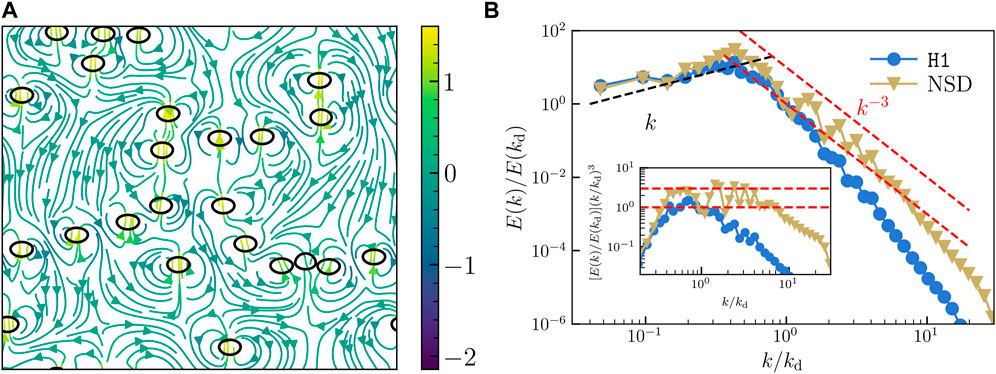
FIGURE 7. (A) Snapshot of the bubble positions overlaid with flow streamlines. (B) Comparison of the gap-averaged energy spectra for our NSHS run
The plot in Figure 7B shows a comparison of the gap-averaged energy spectrum E(k) obtained from the NSHS equation with that obtained from NSD Eq. 5. We find that the energy spectrum are nearly identical for k < kd, E(k) ∼ k. However, discrepancies are observed for k > kd, in contrast to E(k) ∼ k−5 for the NSHS simulations we find E(k) ∼ k−3 for the NSD simulations. As pointed out in earlier section, the oscillation in the energy spectrum appear with a period kd.
Using (5), and ignoring the inertial contributions, we obtain the following energy balance
In Figure 8, we plot the contribution of different terms in (6) towards energy balance. For k < kd, similar to NSHS, we observe that energy injected by buoyancy is balanced by the linear drag. However, a different balance appears for k > kd. In contrast to NSHS, a dominant balance is observed in the NSD equations. The energy transfer by surface tension to small scales balances viscous dissipation leading to the observed E(k) ∼ k−3 scaling in the energy spectrum. Similar small-scale balance has also been reported in earlier two-dimensional unbounded bubbly flow simulations [12]. Therefore, we conclude that although the NSD model captures the large scale dynamics of the Hele-Shaw flow (NSHS), it is unable to correctly capture the small scale physics.
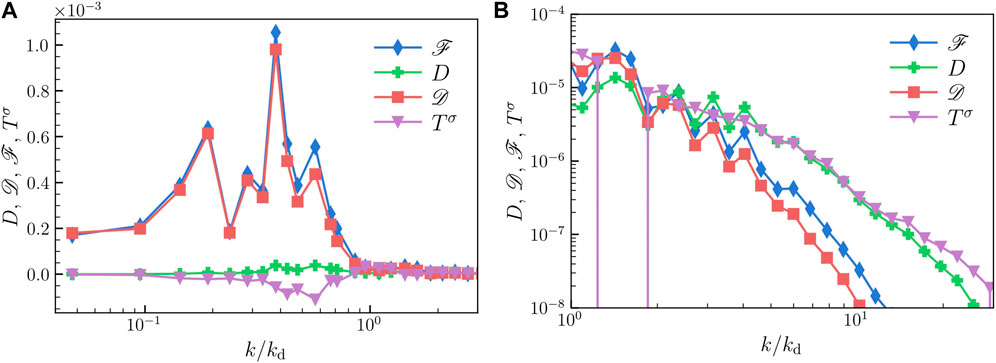
FIGURE 8. Different contributions towards the energy budget for (A) k < kd and (B) k > kd obtained from NSD simulation.
4 Conclusion
We have investigated the spectral properties of the two-dimensional bubbly flows under confinement in a Hele-Shaw setup for experimentally relevant Ga and ϕ. The flow visualization in the steady state is similar to earlier experimental observations [15]. The energy spectrum obtained from the gap-averaged velocity field shows E(k) ∼ k for k < kd and E(k) ∼ k−5 for k > kd. We also observe an intermediate scaling range with E(k) ∼ k−3 around k ∼ kd. A scale-by-scale energy budget analysis reveals the dominant balances. For k < kd, energy injection balances dissipation due to drag, whereas for k > kd, the net injection balances net dissipation. Finally, we show that the Navier-Stokes equation with a linear drag can be used to approximate large scale flow properties of bubbly Hele-Shaw flow but it fails to correctly capture energy balance at scales smaller than the bubble diameter.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
PP contributed to conception and design of the study. RR and VP contributed equally. RR performed initial NSHS and NSD simulations. VP performed NSHS simulations. VP and PP performed the analysis and wrote the manuscript. All authors read, and approved the submitted version.
Funding
We acknowledge support from the Department of Atomic Energy (DAE), India under Project Identification No. RTI 4007, and DST (India) Project Nos. ECR/2018/001135, MTR/2022/000867, and DST/NSM/R&D_HPC_Applications/2021/29.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1112304/full#supplementary-material
Footnotes
1Alternatively referred to as the Archimedes number.
2See Supplementary Material for a detailed derivation.
3As the density contrast is negligible for the low At, we do not plot the co-spectra for
References
2. Lance M, Bataille J. Turbulence in the liquid phase of a uniform bubbly air–water flow. J Fluid Mech (1991) 222:95–118. doi:10.1017/s0022112091001015
3. Risso F. Agitation, mixing, and transfers induced by bubbles. Annu Rev Fluid Mech (2018) 50:25–48. doi:10.1146/annurev-fluid-122316-045003
4. Mudde RF. Gravity-driven bubbly flows. Annu Rev Fluid Mech (2005) 37:393–423. doi:10.1146/annurev.fluid.37.061903.175803
5. Mathai V, Lohse D, Sun C. Bubbly and buoyant particle–laden turbulent flows. Annu Rev Condens Matter Phys (2020) 11:529–59. doi:10.1146/annurev-conmatphys-031119-050637
6. Pandey V, Ramadugu R, Perlekar P. Liquid velocity fluctuations and energy spectra in three-dimensional buoyancy-driven bubbly flows. J Fluid Mech (2020) 884:R6. doi:10.1017/jfm.2019.991
7. Riboux G, Risso F, Legendre D. Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J Fluid Mech (2010) 643:509–39. doi:10.1017/s0022112009992084
8. Prakash VN, Mercado JM, Wijngaarden LV, Mancilla E, Tagawa Y, Lohse D, et al. Energy spectra in turbulent bubbly flows. J Fluid Mech (2016) 791:174–90. doi:10.1017/jfm.2016.49
9. Mendez-Diaz S, Serrano-Garcia JC, Zenit R, Hernández-Cordero JA. Power spectral distributions of pseudo-turbulent bubbly flows. Phys Fluids (2013) 25:043303. doi:10.1063/1.4800782
10. Innocenti A, Jaccod A, Popinet S, Chibbaro S. Direct numerical simulation of bubble-induced turbulence. J Fluid Mech (2021) 918:A23. doi:10.1017/jfm.2021.288
11. Pandey V, Mitra D, Perlekar P. Turbulence modulation in buoyancy-driven bubbly flows. J Fluid Mech (2022) 932:A19. doi:10.1017/jfm.2021.942
12. Ramadugu R, Pandey V, Perlekar P. Pseudo-turbulence in two-dimensional buoyancy-driven bubbly flows: A dns study. Eur Phys J E (2020) 43:73–8. doi:10.1140/epje/i2020-11997-0
13. Roig V, Roudet M, Risso F, Billet A-M. Dynamics of a high-Reynolds-number bubble rising within a thin gap. J Fluid Mech (2012) 707:444–66. doi:10.1017/jfm.2012.289
14. Bouche E, Roig V, Risso F, Billet A. Homogeneous swarm of high-Reynolds-number bubbles rising within a thin gap. Part-1. Bubble dynamics. J Fluid Mech (2012) 704:211–31. doi:10.1017/jfm.2012.233
15. Bouche E, Roig V, Risso F, Billet A. Homogeneous swarm of high-Reynolds-number bubbles rising within a thin gap. Part-2. Liquid dynamics. J Fluid Mech (2014) 758:508–21. doi:10.1017/jfm.2014.544
16. Kelley E, Wu M. Path instabilities of rising air bubbles in a Hele-Shaw cell. Phys Rev Lett (1997) 79:1265–8. doi:10.1103/physrevlett.79.1265
17. Wang X, Klaasen B, Degrève J, Blanpain B, Verhaeghe F. Experimental and numerical study of buoyancy-driven single bubble dynamics in a vertical Hele-Shaw cell. Phys Fluids (2014) 26:123303. doi:10.1063/1.4903488
18. Filella A, Patricia E, Roig V. Oscillatory motion and wake of a bubble rising in a thin-gap cell. J Fluid Mech (2015) 778:60–88. doi:10.1017/jfm.2015.355
19. Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. J Comput Phys (1992) 100:335–54. doi:10.1016/0021-9991(92)90240-y
20. Gondret P, Rabaud M. Shear instability of two-fluid parallel flow in a Hele–Shaw cell. Phys Fluids (1997) 9:3267–74. doi:10.1063/1.869441
21. Alexakis A, Biferale L. Cascades and transitions in turbulent flows. Phys Rep (2018) 767:1–101. doi:10.1016/j.physrep.2018.08.001
22. Aniszewski W, Arrufat T, Crialesi-Esposito M, Dabiri S, Fuster D, Ling Y, et al. Parallel, robust, interface simulator (Paris). Comp Phys Commun (2021) 263:107849. doi:10.1016/j.cpc.2021.107849
23. Ganesh M, Kim S, Dabiri S. Induced mixing in stratified fluids by rising bubbles in a thin gap. Phys Rev Fluids (2020) 5:043601. doi:10.1103/physrevfluids.5.043601
24. Risso F. Theoretical model for k−3 spectra in dispersed multiphase flows. Phys Fluids (2011) 23:011701. doi:10.1063/1.3530438
25. Mitchell M, Muftakhidinov B, Tobias W (2023). Engauge digitizer software. markummitchell. Available at: github.io/engauge-digitize
28. Wang X, Klaasen B, Degrève J, Mahulkar A, Heynderickx G, Reyniers M-F, et al. Volume-of-fluid simulations of bubble dynamics in a vertical Hele-Shaw cell. Phys Fluids (2016) 28:053304. doi:10.1063/1.4948931
29. Bretherton F. The motion of long bubbles in tubes. J Fluid Mech (1961) 10:166–88. doi:10.1017/s0022112061000160
Keywords: buoyancy driven bubbly flows, Hele-Shaw setup, energy budget analysis, turbulence, pseudo-turbulence
Citation: Ramadugu R, Pandey V and Perlekar P (2023) Energy spectra of buoyancy-driven bubbly flow in a vertical Hele-Shaw cell. Front. Phys. 11:1112304. doi: 10.3389/fphy.2023.1112304
Received: 30 November 2022; Accepted: 21 March 2023;
Published: 06 April 2023.
Edited by:
Federico Toschi, Eindhoven University of Technology, NetherlandsReviewed by:
Arash G. Nouri, University of Pittsburgh, United StatesFederico Municchi, Colorado School of Mines, United States
Andrea Scagliarini, Institute for Calculation Applications Mauro Picone, National Research Council (CNR), Italy
Copyright © 2023 Ramadugu, Pandey and Perlekar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Prasad Perlekar, cGVybGVrYXJAdGlmcmgucmVzLmlu
†These authors have contributed equally to this work and share first authorship
 Rashmi Ramadugu
Rashmi Ramadugu Vikash Pandey2†
Vikash Pandey2† Prasad Perlekar
Prasad Perlekar