Processes at lithium-hydride/deuteride surfaces upon low energy impact of H/D

Sputtering, reflection, and retention processes at amorphous and crystalline lithium hydride surfaces due to impact of low energy (1–100 eV) hydrogen and deuterium atoms over the range of 0^o −85^o angle of incidence at 300 K surface temperature were investigated by atomistic computational methods. Classical molecular dynamics simulations were performed with improved reactive bond-order force field (ReaxFF) potentials that include long-range polarization effects. In addition to probabilities of surface processes, the energy and angular spectra of ejected particles were obtained. Comparison of these results with those previously obtained on pristine lithium surfaces indicates the importance of saturation of the Li surface and near-surface region with hydrogen. We show that such saturation, which is typical in both laboratory and fusion device experiments with lithium coating of the plasma-facing surfaces, significantly changes the surface processes with hydrogen irradiation in the understudied low-energy region of impact energies.

1 Introduction

Conditioning of plasma-facing components (PFCs) is a key issue in tokamak operations [1]. Li evaporation and conditioning have been used in different machines to improve plasma performance [2, 3]. In NSTX, Li conditioning decreased the H-mode access power threshold, increased the stored energy, and allowed longer plasma discharges when compared with plasma discharges with no Li conditioning [3]. These improvements have been associated with the reduction of fuel recycling. While the plasma performance is strongly influenced by the PFCs, the PFCs are modified with each exposure to the plasma. This requires extensive experimental and computational studies of LiH-coated PFCs upon low-energy H and D ion irradiation to properly explain the relationship between Li PFCs and plasma performance and determine reasons for the improved tokamak operating conditions [4–7]. Understanding Li-based plasma-material interaction (PMI) is of particular importance for the Lithium Tokamak eXperiment-β (LTX-β), whose low recycling regime is enabled by Li-coated plasma-facing surfaces [2, 8]. Although most of the plasma-facing wall in LTX-β is coated with Li, the surface is rapidly saturated by H bombardment in the presence of plasma, up to a Li:H ratio of 1:1 [9], implying that knowledge of the effects of H and D irradiation on pristine Li (amorphous and crystalline) [10, 11] is not enough to reveal the properties of a complex material formed by accumulation of H or D in pure Li. In fact, wall surfaces and target surfaces in experiments might be even more complex than LiH due to additional reactions of Li and LiH with water in the background residual gases [6], resulting in a mixture of LiH, Li₂O, and LiOH. Pure Li can exist only as an initial transition phase as a tokamak PFC material. Accumulation of hydrogen in Li changes the physical and chemical properties of the irradiated material. In this paper we show the changes of the reflection, retention, and sputtering processes in fully hydrogen-saturated, mainly in amorphous, but also in crystalline lithium hydride material under the bombardment of low-energy hydrogen and deuterium atoms (1–100 eV). This contributes to studies of chemical and physical erosion and H recycling of Li PFCs under hydrogen-saturated conditions.

The computational and experimental data for dynamical processes at LiH surfaces at impact energies below 100 eV are scarce, and often inadequate. For example, popular codes based on the Binary Collision Approximation (BCA) (TRIM/SRIM family of codes [12]) assume only close-encounter collision between an impact atom and atoms of a target surface. This approach, being applicable at high-impact energies, usually undervalues the probabilities of the processes studied in this paper. Herein, sputtering, reflection, and retention processes are studied in detail, obtaining probabilities at various impact energies and angles and isotopic composition of incident particles, as well as related effects, as are energy and angular spectra, and composition of ejected particles. Classical molecular dynamics (CMD), with proper bond-order potentials, is a suitable atomistic approach to these processes if taken with special care. Namely, the low electronegativity of lithium (0.98) in comparison to hydrogen (2.2) [13, 14] implies some ionic character (30%) in addition to the strong covalent character of Li-H bonding, creating a polarization environment for the impact hydrogen atoms and their consequential partial charging. As discussed in [10, 11], this long-term polarization effect can be considered in CMD by the Electronegativity Equalization Method (EEM) [15, 16], in combination with reactive bond-order (BO) potentials (ReaxFF [17, 18]), implemented in the Large Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code [19]. Interestingly, the applications of ReaxFF combined with EEM [20–22] have shown good agreement with results of quantum-classical molecular dynamics [23] using tight-binding DFT [24–26], as well as with experimental results [27].

Section 2 describes the computational approach used to obtain the results as well as development of improved ReaxFF potentials for LiH. The calculated data we show and discuss in Section 3. Our conclusions are given in Section 4.

2 Materials and methods

2.1 Preparation of the surface. Calculation

We prepared crystalline (FCC, lattice constant 4.007Å) and amorphous LiH slabs with dimensions of 4.9 × 4.9 × 10.6 nm³ consisting of 14,730 Li and 14,499 H atoms with an average mass density of 0.762 g/cm³, which is within 3% of the commonly reported LiH crystal density [28] of 0.78 g/cm³ (Figure 1). The crystal structure was geometry optimized to minimize its energy, and the amorphization of LiH was achieved by subjecting the FCC LiH crystal to a repeated heating and cooling regime, as described in [10]. The periodic boundary conditions were removed from the z-direction (Figure 1), and the system was further equilibrated at 300 K to allow the relaxation of the surface atoms. The irradiation simulations were performed under the NVE ensemble with a timestep (Δt) of 0.1 fs for energies of impact particle E greater than 50 eV and Δt = 0.35 fs otherwise. The incident particles were emitted toward and from approximately 1 nm above the surface, varying their x and y coordinates. Each particle in the process was labeled during the calculations, clearly distinguishing the origin (reflected or sputtered) of ejected particles. A statistical average of N = 1,022 trajectories were taken to calculate the reflection, retention, and sputtering probabilities. We only considered the number of successful, completed trajectories (N_s ≤ N), which were fully evolved for the given number of time steps. The probability p) of an impact outcome is calculated as n/N_s, where n is the sample size of the impact outcome (reflection (P_R), retention (P_ret), and sputtering (P_s)). The maximal standard error (MSE) [29], which is shown as an error bar in the probability graphs (Section 3), was calculated as p/√n. A more detailed discussion of such computational methodology can be found elsewhere [10, 11, 20].

FIGURE 1

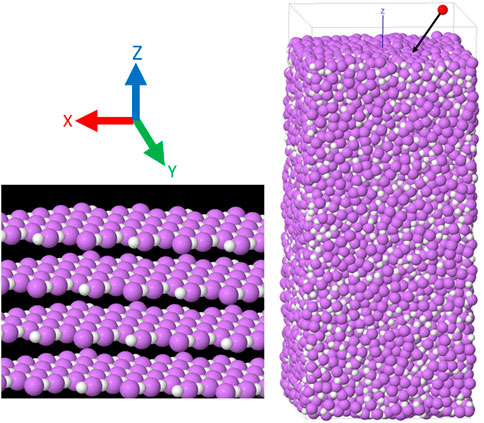
FIGURE 1. An incident particle and LiH surface system. The crystalline LiH structure (left) was transformed by heating and annealing into an amorphous Li + H structure (right), which was bombarded by H and D atoms, varying their point of origin, energy, and angle of incidence at the surface.

2.2 Development of the Li-H potential

As discussed in the Introduction, our atomistic simulations are based on classical molecular dynamics, using ReaxFF potentials in the LAMMPS code. The ReaxFF method is chosen for its capability to model dynamics of breaking and forming chemical bonds [17, 18] and use of the EEM is to calculate the dynamic changes of atomic charges in the system. The latter is particularly important in the presence of polarizable atoms like lithium mixed with atoms of significantly different electronegativity.

Shin et al. [30] recently published Li/Al/Ti/P/O/H ReaxFF parameters for solid electrolyte systems. This force field was extensively trained for Li atoms and Li-O bond parameters. However, the Li-Li and Li-H bond parameters were not trained in that work and were treated as dummy bonds. Also, the H-H bond parameters were not trained for short-range interactions. To develop the Li/H ReaxFF force field parameters for the present PMI systems, we trained the Li-Li and Li-H bond parameters of this force field to reproduce Li and Li-H equations of states, their heats of formation, and Li-Li and Li-H binary interactions. As a reasonable initial guess, we started with the Li-Li and Li-H parameters previously published by Raju et al. [31]. The H-H parameters were merged into the force field, previously developed and published [32, 33]. Figures 2A–C show potential energy curves calculated by DFT and ReaxFF potentials for the various lattice configurations used for the training. These curves represent the functional relationship between the internal energy and the lattice constant (also known as the equation of states), where the energy of the optimized lattice (DFT) is defined as zero energy.

FIGURE 2

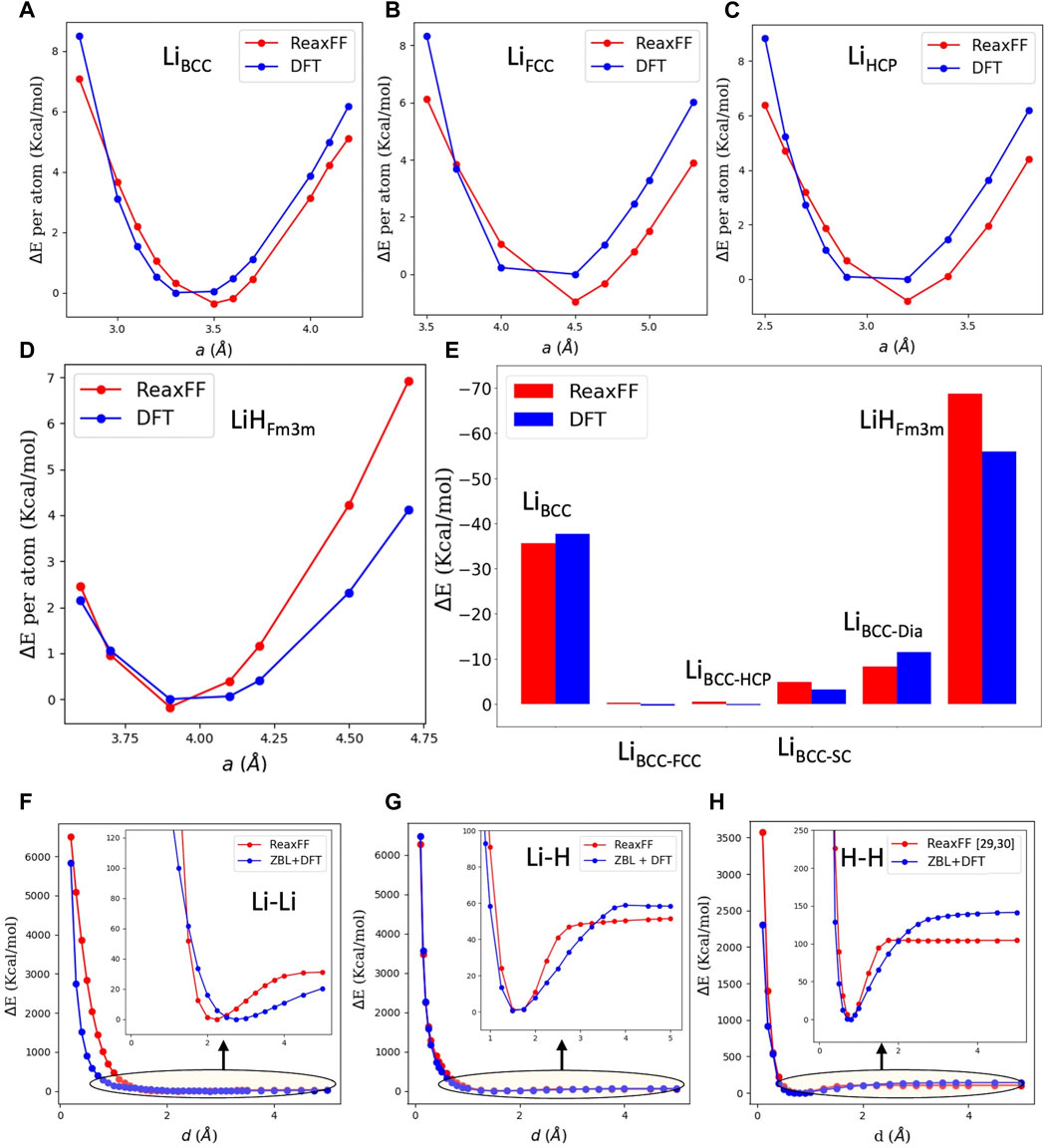
FIGURE 2. Comparison between DFT and ReaxFF force field used in present study. (A–D) Potential energy curves for Li metal lattices, i.e., BCC, FCC, HCP, and for the LiH Fm3m-lattice, obtained by DFT calculations and by ReaxFF. (E) Cohesive energy of the Li BCC lattice, formation energy of the LiH Fm3m-lattice, and relative stability of the Li BCC-lattice to the Li FCC, HCP, SC, and Dia-lattices. (F–H) Li-Li, L-H, and H-H diatomic potentials. In (A–D) and (F–H), the minimum energy from the DFT calculation is chosen as zero energy, hence ∆E = Energy–min(E_DFT).

ReaxFF is in good agreement with the DFT energies (within 1 kcal/mol per atom) for ±20% variation in lattice constant. Figure 2E shows ReaxFF and DFT comparison for cohesive energy of the Li BCC-lattice, the heat of formation of the Li-H Fm3m-lattice, and heats of formation of the Li-FCC, Li-HCP, Li–Diamond (Dia), and Li-SC lattices relative to the Li BCC-lattice. The Diamond and SC lattices are high-energy phases for Li; subsequently we do not give high weight to these phases in training the present force field. In this work, energetic H/D particles impact a Li-H/D surface; hence the short-range repulsive interactions are important, especially for H-H and H-Li. We use a combination of DFT (PBE functional) and ZBL (Ziegler–Biersack–Littmark [34]) energies to train the Li-Li, Li-H, and H-H short-range interactions. The ZBL energies are used for short distances (<0.6 Å), and DFT (PBE) energies are used elsewhere. For Li-H, we train the close-range encounters up to the repulsive energy of ∼6,000 kcal/mol (∼260 eV), which is sufficiently larger than the maximum energy of impact particles in the present study (100 eV). Figures 2F–H compare ReaxFF and ZBL + DFT energies for an atomic pair of Li-Li, Li-H, and H-H. We ensure a good agreement for the Li-H and H-H interaction potential (Figures 2G,H) for modeling high-energy H/D particle impact on a Li-H/D slab.

3 Results and discussion

In this section, we show the results for the reflection, sputtering, and retention of the H and D impacts for LiH and LiD amorphous surfaces, respectively, with a focus on the comparison and differences of the results with the impacts at pristine lithium surfaces. As discussed in the Introduction, such comparison is of importance for understanding the processes in both experimental fusion devices, like LTX-β, and in laboratory experiments. Namely, any lithium surface exposed to the H(D) irradiation will saturate with impact particles in a short time. In addition, it is generally understood that any solid surface of a PFC, exposed to huge particle fluxes in a fusion device, will be amorphized. Thus, the results of irradiation of amorphous LiH are more relevant for practical application than those for crystalline or amorphous pristine lithium surfaces. Furthermore, both lithium and hydrogen in the surfaces of both wall coatings in fusion devices and targets in experimental measurements may interact with oxygen from water in the background residual gases creating more complex compounds, and the resulting surface will likely be a mixture of LiH, Li₂O, and LiOH. Only the response of hydrogen irradiation of the LiH component is investigated in the present study.

We note that a:M and c:M notations mean “amorphous M″ and “crystalline M″ respectively. Material M is LiH or LiD but could also be pristine Li. For energy and angle of incidence of impact particles we will use E and θ, respectively. This notation will be used in the remaining text.

We first discuss the probabilities of reflection, p_R. The retention probabilities are defined by the particle conservation principle, P_ret = 1-P_R.

3.1 Probabilities of the particle ejection

3.1.1 Reflection

The calculated P_R of incident H and D on a:LiH and a:LiD, respectively, at a variety of impact energies and angles of incidence are shown in Figure 3. The presence of H in a:LiH decreases the reflection probability in comparison to the one from a:Li, in spite of the fact that the mass density of LiH is larger than that of Li. This is because H atoms in a:LiH are less efficient targets for reflection of H due to the high transfer of kinetic energy in the collision of two H atoms. Thus, for H impact at θ = 0^o (Figure 3A) and impact energy E = 100 eV, we get P_R = 0.25 from a:Li, which is 2.8 times larger than P_R = 0.089 from a:LiH. By lowering the impact energy, this ratio decreases to 2.0 at E = 25 eV, while at E = 5 eV it reduces to P_R (Li)/P_R (LiH) = 0.198/0.138 = 1.4. With an increase in incident angle, the ratio of the reflection probabilities from a:LiH and a:Li decrease, and for almost grazing angles these trends reverse. Thus, for θ = 85^o, the ratio of reflection probabilities from a:Li and a:LiH are 0.763/0.853 = 0.89 at 100 eV, and 0.383/0.400 = 0.96 at 5 eV. The same trend is also obtained for D reflection from a:LiD (Figure 3B). Thus, for impacts at 0^o, the ratios are P_R (Li)/P_R (LiD) = 0.129/0.0528 = 2.4, 0.134/0.081 = 1.6, and 0.069/0.074 = 0.9 at 100, 25, and 5 eV, respectively.

FIGURE 3

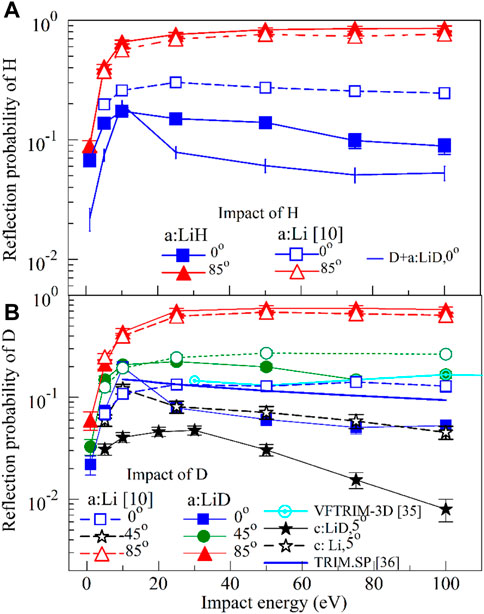
FIGURE 3. The probabilities of reflection per impact (P_R) of H and D at amorphous surfaces at 300 K, for impact energies in the range 1–100 eV, and for various incident angles. (A) Comparison of P_R for H impacts at (A)LiH surfaces for the impact of H at 0° and 85°. The P_R for impact of H at the (A)Li surface [10], as well as for D+a:LiD at 0^o for isotope effects, are also shown for comparison. (B) Comparison of P_R for D impacts at (A) LiD and (A)Li surfaces for the impact of D at 0°, 45^o, and 85° and at crystalline (C)LiD and (C)Li surfaces at a 5^o incident angle. Shown probabilities are averages over all successful trajectories, with error bars being maximal standard errors. The VFTRIM-3D data for the reflection of D from an amorphous LiD surface at an incident angle of 45^o [35], and TRIM.SP [36] data for D+a:Li at 0^o are also shown.

For impacts at 45^o, the corresponding ratios are 0.265/0.167 = 1.6, 0.245/0.224 = 1.1, and 0.126/0.150 = 0.84. Finally, at 85^o, P_R (Li) and P_R (LiD) are close in value, with a slight dominance of P_R (LiD), like in the case of P_R (LiH). The VFTRIM-3D data [35] for D+a:LiD at 45^o are in good agreement with our data for E ≥ 75 eV, while at lower energies this data underestimates, typical for a BCA. The TRIM.SP data [36] for the D+a:Li system, are also shown in Figure 3B. These data are almost a factor of two larger than our data for the D+a:LiD system though these show reasonable agreement with our data for the D+a:Li system [10]. One can draw the following conclusions from the above discussion: 1) The reflection probabilities in the considered impact energy range are significantly bigger from the a:Li surface than from a:LiH and a:LiD surfaces at low angles of incidence; and 2) Concerning isotope effects, reflection for the D+a:LiD system is, for most impact energies, 2–3 times smaller than for the H+a:LiH system. A comparison of the crystalline surfaces, c:Li and c:LiD, shows even larger dominance of the reflection from the c:Li. At E = 100 eV the ratio is P_R (c:Li)/P_R (c:LiD) = 0.045/0.008 ≈ 5.6, which drops to a value of about 2 at 25 eV and 5 eV impact energies.

It is important to stress that since reflection is smaller at LiH surfaces than at pristine lithium surfaces, the retention P_ret = 1-P_R of the impact particles is larger. At θ = 0^o and E = 100 eV, the probability of retention of H at a:LiH is 0.93, while for a:Li it is 0.75. For D impact at a:LiD this number is 0.95, while at a:Li it is 0.87. Retention drastically drops with increasing angle of incidence, and for almost grazing incidence (θ = 85^o) at H impact of E = 100 eV, it is 0.24 for a:Li but 0.14 for a:LiH, with similar values for D at a:Li and a:LiD.

3.1.2 Sputtering

The sputtering probability per incident atom, at given angle of incidence and impact energy, is calculated as a ratio of the number of trajectories of sputtered atoms A $\left(n_{sp}^A\right)$ and the total number of completed trajectories (N_s), i.e., $P_{sp}^A=n_{sp}^A/N_s$. A completed or successful trajectory is a line that follows consecutive positions of an impact particle either for the full input number of time steps or until exiting the predefined computational box size. The sputtering probability is calculated for Li and H separately. Li is sputtered in the form of Li atoms or LiH and Li₂ molecules. Whether Li and H are sputtered in the form of atoms or molecules, the sputtering probability of each of them is calculated by counting total number of corresponding atoms.

To compare the current data for sputtering probabilities from a:LiH with those from a:Li [10], it is necessary to consider sputtering probabilities P_s of Li and H separately, which are shown for various energies E and angles θ in Figure 4. Not surprisingly, sputtering of H is more effective than sputtering of Li at lower incident H energies, and this difference is reduced with an increase in θ and E. While the probability of the dominant sputtering product, H, is nearly constant for impact energies in range 25–100 eV, the Li sputtering probability increases with increasing incident energy over the same range, for θ of 45^o and 85^o. For an incident angle of 0^o, the Li sputtering probability decreases for energies E larger than 75 eV. For incident H atoms at 100 eV at θ = 0^o, mainly H atoms are ejected, while at θ = 85^o sputtering probabilities of H and Li have similar values. Interestingly, sputtering of Li from a:LiH and a:Li are close to each other, especially at larger energies. Still, the total sputtering probability from a:LiH is significantly larger than from a:Li due to the large contribution of H sputtering.

FIGURE 4

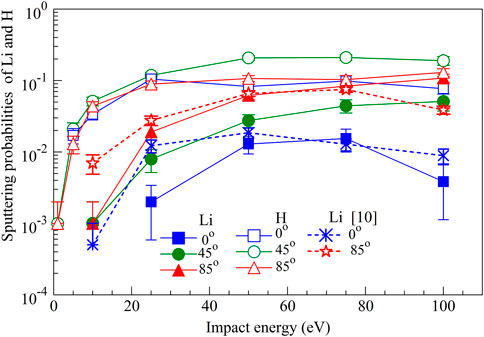
FIGURE 4. Sputtering probabilities of Li and H atoms per impact of H in the range of impact energies 1–100 eV, for various angles of incidence θ on an a:LiH surface at 300 K. Results are also shown for Li sputtering from an a:Li surface upon the impact of H at various θ [9].

Although the prime interest for the LTX-β device is hydrogenated (using H atoms) Li surfaces, we also calculated the sputtering from LiD surfaces to compare with existing experiments and computational results, available at incident angles of 45^o [35]. As shown in Figure 5, our calculations of sputtering probabilities by D impacts at θ = 45^o for the a:LiD surface compare well with previous experimental (Ion Surface Interaction Experiment, IIAX) and VFTRIM-3D data for Li sputtering from Li saturated by D. The TRIM.SP sputtering probabilities for D+a:Li [36, 37], shown in Figure 5.

FIGURE 5

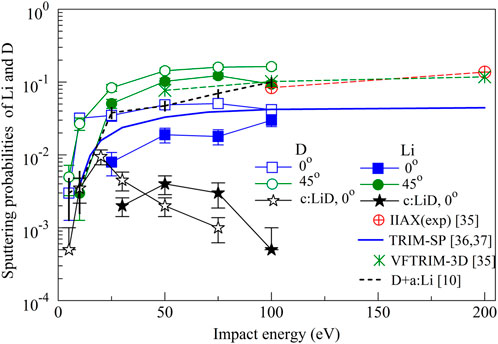
FIGURE 5. Sputtering probabilities of Li and D atoms per impact of D atom, for several impact angles, as functions of incident energy of D impact at a:LiD surface at 300 K. Comparison with available experimental and computational data from Refs. [35, 36] are also shown. The data in [35] are for Li sputtering by D impact at 45^o at lithium saturated by D. TRIM.SP data of [36, 37] are for D on a monoatomic Li target.

Are also smaller than our published data [10] for D+a:Li, but in most of the considered energy range are larger than our current data for Li sputtering for the D+a:LiD system. We note that detailed TRIM.SP studies of sputtering at Li and other metal targets by D and T in a wide energy range are available from Eckstein’s work [36–39].

As in the case of sputtering from a:LiH by incident H atoms, the sputtering of D dominates the sputtering from a:LiD, though to a smaller extent. However, sputtering from c:LiD due to incident D atoms is smaller from a:LiD, and sputtering of Li dominates sputtering from c:LiD at impact energies larger than about 50 eV.

3.2 Initial depth of ejected particles

Distributions of the deepest reach of incident atoms inside the surface before reflection, called the reflection depth (RD) [10], are of importance for defining an active thickness of the surface slab. Thus, if an experiment is performed with a LiH layer on a substrate whose thickness is smaller than the reflection depth, both measured reflection and sputtering [10] are highly influenced by the substrate, rather than describing only the LiH surface effects. In addition, the sputtering process is largely enabled by the reflected atoms, as shown in [10], indicating that sputtered particles cannot originate from the depths in the surface larger than the RD. Figure 6A presents the cumulative.

FIGURE 6

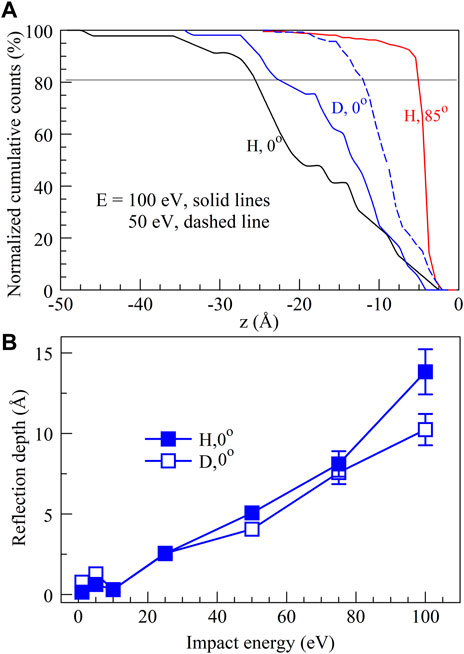
FIGURE 6. (A) Normalized cumulative counts of reflection depths of incident H and D atoms inside (A)LiH and (A)LiD surfaces, respectively, for several impact energies and angles. (B) Average reflection depths of H and D in (A)LiH and (A)LiD, respectively, for a range of impact energies at 0^o angle of incidence.

Normalized distributions of the RDs for various impact energies and angles. From this plot, one can conclude that 95% of H impacts at 100 eV have a RD less than 3.4 nm for θ = 0^o, but only 0.9 nm for

θ = 85^o. However, for impact of D at 0^o, the RD is smaller, and the 95% limit in Figure 6A is reached at 2.6 nm for E = 100 eV and 1.5 nm for E = 50 eV. These values for the RD in a:LiH are 2.5–3 times smaller than those of an a:Li surface. This difference is partially caused by the larger mass density of a:LiH than a:Li, but also by larger kinetic energy loss of impact atoms in lithium-hydride due to the larger energy transfer in the collision of impact H with H atoms in a:LiH. Thus, for the amorphous Li slab, for E = 100 eV at 0^o, the 95% limit of RD is reached at 7.8 nm for H and 6.1 nm for D, which is in both cases 2.3 times larger than for a:LiH and a:LiD, respectively. For θ = 85^o, the RD is 3.6 times larger for a:Li than for a:LiH.

A good estimate of the RDs are their average values over all trajectories for a given impact energy and angle. As shown in Figure 6B, the change of the mean RD for H impacts at θ = 0^o over a range of impact energies on a:LiH is 0.15 Å/eV, while for D impacts at the same conditions on a:LiD this value is 0.11 Å/eV, calculated as the average slope of the curves at Figure 6B. Note that the average values capture less than 50% of reflected atom distributions. Therefore, values of the RDs for various energies in Figure 6A can be approximately obtained by multiplying the values of the average reflection depths by factor of two.

Distributions of the depth of origination of the sputtered particles, so called “initial sputtering depth” (ISD) [10] were calculated for Li and H atoms ejected from an a:LiH slab; Figure 7A shows the normalized cumulative distributions of ISDs of sputtered Li and H atoms with respect to the a:LiH-vacuum interface (defined to be 0-nm depth) resulting from incident H or D impact at 0^o and 85° angle of incidence, for two impact energies. From the figure, 95% of the sputtered Li atoms upon impact of H at E = 100 eV and θ = 0^o at an a:LiH surface are from depths smaller than 1.3 nm, while sputtered H atoms originate from depths smaller than 0.9 nm. For impact of H atoms at 50 eV, sputtered Li atoms originate at depths smaller than 1 nm and sputtered H atoms originate at depths smaller than 0.7 nm. For impacts of H of E = 100 eV at θ = 85^o, both Li and H atoms originate at depths ≤0.4 nm. D impacts on a:LiD cause ejection of Li and D from depths similar to those on a:LiH.

FIGURE 7

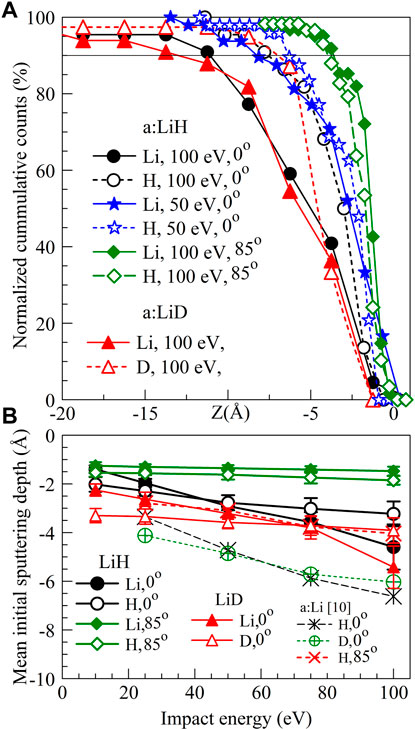
FIGURE 7. Initial sputtering depth of Li and H or D atoms were calculated in an (A)LiH or (A)LiD slab target at 300 K, due to H and D impacts. (A) Distribution of the initial sputtering depths as function of impact energy at incident angles of 0°or 85°. (B) Impact energy dependence of the mean initial sputtering depths, defined by Eq. 2, of Li and H or D atoms in an (A)LiH or (A)LiD slab target for various cases of incident H or D atoms.

Following [10], we calculate the mean initial sputtering depth $\overline{d}$ (MISD) of a distribution using counts of the sputtered particles C_i in an interval of 2 Å centered at the sputtering depth (d_i)

$\overline{d}=\frac{\sum d_i{C}_i}{\sum C_i}(1)$

The MISDs in Figure 7B are shown as functions of incident energy for incident angles of 0° and 85° for H, and of 0° for D, at a:LiH and a:LiD target slabs. Like in case of the Li target, the MISD increases with impact energy, and are for Li not larger than 0.45 nm for H impact at a:LiH and not larger than 0.55 nm for D impact at a:LiD for E = 100 eV and θ = 0°. The corresponding values of MISD in case of a:Li target [10] are larger than 0.6 nm. For H impacts at θ = 85° at a:LiH, the MISD stays below 0.2 nm for both sputtered Li and H. On the other hand, the mean initial sputtering depths of H and D are smaller than 0.4 nm from a:LiH, a:LiD and a:Li. Similar conclusions hold also for a crystalline Li target (not shown here).

It is important to stress that the MISD for incident H atoms on a pristine a:Li surface is about 50% larger for sputtered Li than in the case on a:LiH. This is likely the result of the combined effects of the higher density of a:LiH compared to a:Li, and a more efficient energy transfer of the incident H with H atoms in a:LiH. We showed in [10] that the dominant mechanism of Li sputtering in a:Li systems is by incident H that has already reflected off of Li that is deeper in the bulk of the slab. This means that the reflection depth of H in a:LiH is a relevant parameter for the MISD of Li. As shown above, the reflection depth of H in a:LiH is 2.5–3 times smaller than in a:Li, which can also explain the disparity in the initial sputtering depths for a:LiH and a:Li surfaces.

3.3 Spectra of ejected particles

3.3.1 Energy spectra

As shown in Figure 8, the energies of reflected H and D atoms from a:LiH and a:LiD surfaces, respectively, averaged over all trajectories show similar trends and values to the energies of reflected H and D atoms from a pristine a:Li surface [10], i.e., a linear dependence of E_av on impact energy, with slopes that strongly increase with the impact angle θ. For instance, H atoms reflected from a:LiH with an incident angle of 85° will have an average reflected energy of 90% of the impact energy, while those with an incident angle of 0° will have an average reflected energy of 33% of the impact energy. Also, the slopes are larger for impact of H at a:LiH than for D at a:LiD surfaces.

FIGURE 8

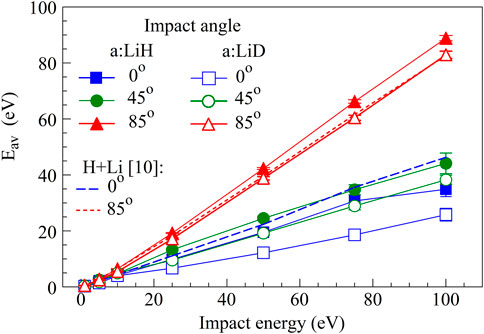
FIGURE 8. Average energies (Eav) of the reflected atoms H and D from amorphous LiH and LiD surfaces, respectively, shown as a function of the incident energy for various angles of incidence. For comparison, the data for Eav of H incident at an a:Li surface [10] are shown as dashed lines.

Figure 9A shows average kinetic energies (E_sp) of the sputtered atoms, H and Li, as a function of incident energy. The averaging was done over all completed trajectories (N_s ≈ 1,000) at each incident energy and angle. For H impacts at 100 eV and 0^o angle of incidence, the E_sp values of sputtered Li atoms are smaller by nearly an order of magnitude than those of sputtered H atoms, while these two E_sp values approach each other for θ = 85^o. Previously reported energies of sputtered Li from a:Li [10] are significantly smaller than the presently calculated values from a:LiH. As seen in Figure 9A, the initial sputtering depth for H in a:LiH is significantly smaller than the one for H in a:Li. This causes Li sputtered by a:LiH to have a smaller number of collisions on the way out and, thus, higher sputtered energies.

FIGURE 9

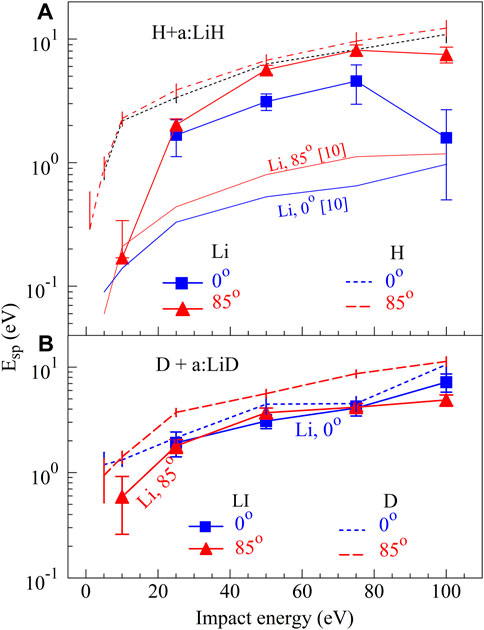
FIGURE 9. (A) Average kinetic energies (E_sp) of the Li and H atoms, sputtered from an (A)LiH surface over a range of impact energy (E) of incident H atoms at two angles of incidence (θ). Averaging is done for each E and θ over all sputtering trajectories. (B) Similar plots as in (A), but for D atoms incident at an (A)LiD surface.

The energies of sputtered hydrogen species are weak functions of the incident angle. This is also a case with sputtered Li by D atoms incident on an a:LiD surface, as shown in Figure 9B, but not for sputtered Li by H atoms incident on an a:LiH surface in Figure 8A. Although the transfer of energy to Li atoms is more efficient by incident D than by H, the average energies of sputtered Li are not systematically larger in Figure 9B than in Figure 9A. The reason for this can be seen in Figure 8, showing that the kinetic energies of reflected H are larger than energies of reflected D. Having in mind that majority of the sputtered particles are kicked out of the surface by the reflected impact particles, the energy of the sputtered particles is tied to the energy of the reflected particles.

3.3.2 Angular distributions

For incident atoms reflected from a surface, the angular distributions (dN/dΩ) are calculated [27–29] from the number of reflected particles $N\left(\theta ,\delta \theta \right)$ into interval $\delta \theta$ around $\theta$, as in [10], by

$\frac{dN}{d\Omega }=C\frac{N\left(\theta ,\delta \theta \right)}{2\pi \delta \theta \sin \theta }(2)$

where C is a normalization constant, and θ is here the angle of the velocity of the reflected particle with respect to the surface normal. In Figure 10, we show the angular distributions of the reflected H atoms incident at an a:LiH surface with an impact energy of 50 eV. The distributions are normalized to the maximum value at each incident angle (0^o, 45^o, and 85^o) shown by the arrows.

FIGURE 10

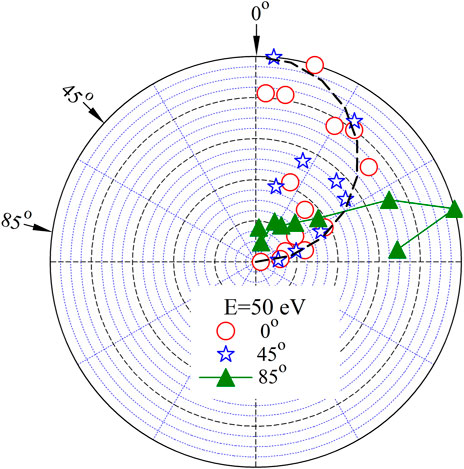
FIGURE 10. Angular distributions of reflected H atoms for incident H at an impact energy of 50 eV, from an a:LiH surface at 300 K for various angles of incidence. The distributions are shown in the form of a polar diagram with the reflected particle curves normalized to unity at their maximum values for each angle of incidence. Lambert’s cosine law is shown by a dashed line.

Incident H atoms at 0° and 45° show diffuse-type angular distributions, while incident H atoms at 85° exibit a pronounced specular peak. As in the case of reflection from an a:Li surface [10], these observations are consistent with the trend of an increase of the average reflection energy with an angle of incidence, especially at larger angles in Figure 8. Namely, the reflection energy gets closer to the impact energy with an increase of incident angle, which signifies less inelastic scattering and thus, more specular reflection.

Eq. 2 is also used to calculate the angular distributions of sputtered Li and H atoms shown in Figure 11, as was done for the reflected particles. The distributions are of the diffuse type, though there is a trend of sputtered Li atoms toward specular directions with increase of incident angles (Figure 10A). These tendencies were also seen for reflection and sputtering from a:Li targets [10].

FIGURE 11

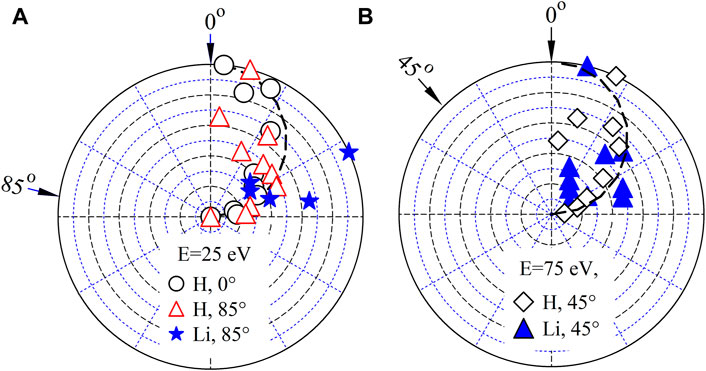
FIGURE 11. Angular distributions of H and Li particles sputtered by impact of H atoms from an (A) LiH surface at 300 K, with impact energies of (A) 25 eV and (B) 75 eV. The dN/dΩ values in the polar diagrams are normalized to their respective maximum values at each impact energy. Lambert’s cosine law is shown by a dashed line.

3.4 Depth distributions of retained particles

The information on the maximal thickness needed for the a:LiH and a:LiD targets is contained in the information on the distributions of the retained particles. Due to the ps time scale in obtaining the distributions, these can also be used as initial conditions for calculation of the diffusion of the accumulated hydrogen upon impact. The maximum reflection depth limits, as discussed for Figure 6, do not exceed 4 nm in a:LiH for impacts with E = 100 eV and θ = 0^o. This means that that a 10-nm thick Li slab in this work is sufficient for studying the reflection and sputtering from a LiH surface for E up to 100 eV. The distributions of the retained particles (Figure 12) were studied in the a:LiH slab described in Section 2 and used for all calculations in this paper. While all energies and angles result in maximums of distributions at about or less than 3-nm depth, their widths and heights differ significantly. The normalized cumulative counts of retained atoms show that 90% of impacting H atoms at 100 eV and 0^o angle of incidence are retained at depths less than about 7 nm, while this depth for impacting D is less than 5 nm (Figure 12A). Also, 90% of impacting H atoms at E = 50 eV and θ = 0° are retained at depths less than 3.5 nm (Figure 12B). The tails of the distributions extend to no more than 10 nm. For incidence at 85° and E = 100 eV, 90% of retained H atoms in a:LiH are at depths smaller than 6 nm (Figure 12B). As a comparison, for an a:Li surface, 90% of impacting H atoms at 100 eV and 0° angle of incidence are retained at depths less than about 15 nm with the tail of the distribution extending to 22 nm, while 90% of impacting D atoms are retained at depths less than about 12.5 nm with the tail of the distribution extending to 20 nm [10]. These significantly smaller depths reached by the retained atoms in LiH and LiD are partially a consequence of the higher mass density of LiH (0.78 g/cm3) and LiD (0.87 g/cm3) in comparison to that of Li of ≈0.5 g/cm3, but also because of an efficient energy transfer of kinetic energy of impact atoms when colliding with H atoms in the LiH slab, causing larger energy loss of impact particles.

FIGURE 12

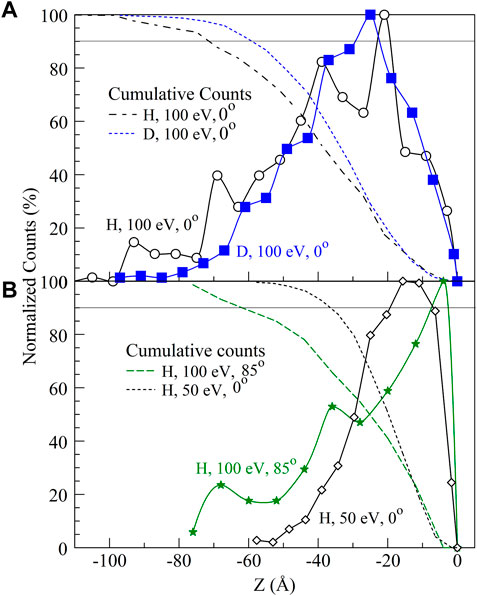
FIGURE 12. Distributions of impacting H and D atoms retained in a:LiH and a:LiD targets at 300 K (solid lines with symbols), respectively, and normalized cumulative counts (in %) of the retained atoms (dashed lines). All distributions are scaled to its maximum value for each incident data.

Indicative of the dependence of the penetration depth on the impact energy are the almost linear curves in Figure 13, which differ in slope for the various systems. We find that D+a:LiD and H+a:LiH data have only slightly different slopes. However, D+a:Li and H+a:Li data are well distinguished from each other and from the D+a:LiD curve. Finally, the penetration depth and its slope for the D+a:Li system obtained by TRIM.SP [36] differ significantly from the data obtained by MD reported herein, and mostly agrees with the H+a:Li curve. We note that the values in Figure 13 are calculated by averaging of all trajectories at each energy and are at least a factor of two smaller than 90% of distributions of the penetration depths shown in Figure 12.

FIGURE 13

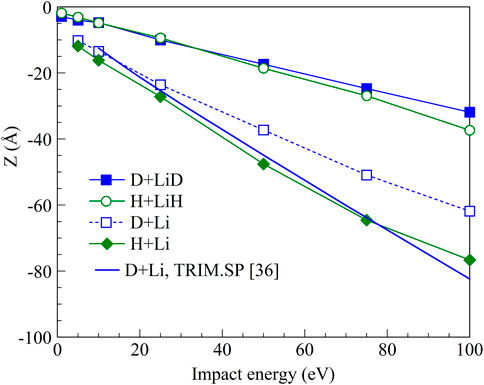
FIGURE 13. Energy dependence of the mean penetration depths of impacting H and D atoms that are incident at 0^o.

4 Conclusion

Due to a fast accumulation of H in Li (up to ratio 1:1), a pure Li surface exists as an initial transient in a tokamak PFC material at low temperatures. The accumulation of hydrogen in Li changes the physical and chemical properties of the irradiated material, and the information obtained from the studies of a pristine lithium surface irradiated by hydrogen are not sufficient to reveal the properties of a complex material formed by accumulation of H or D in pure Li. Molecular dynamics calculations with advanced and improved, bond order ReaxFF potentials, combined with EEM, were used to study the reflection, retention, and sputtering processes by H and D atoms incident at amorphous and crystalline lithium hydride and lithium deuteride surfaces. The range of particle impact energies of 1–100 eV and angles of incidence of 0°–85°, where 0° is perpendicular to the surface, were investigated. These ranges of impact parameters have been poorly described in literature, both experimentally and computationally. The MD parameters, such as the time steps, preparation of the surface slab, the slab size, and the number of particle trajectories, were carefully chosen by the relevant computational experiments. The amorphous structure of the surface target as well as its temperature were selected to mimic the laboratory experiments related to LTX-β. Notably, all atoms in the system were labelled, enabling clear distinction of the origin of ejected species, obtaining reflection, retention, and sputtering probabilities “on the same footing” for any given set of conditions. The probabilities and their uncertainties were acquired by scanning the surface at different points using independent impacts. These were calculated as average values per impact atom and reported with maximal standard error values. Since retention and reflection probabilities must sum together to be unity, we found it sufficient to discuss only the reflection and sputtering results in detail.

The important outcome of the present study is comparison of the data from the Li surface saturated by H with that from pristine Li. There is a number of interesting effects that distinguish the processes at a:LiH and a:Li surfaces. The probability of reflection of impacting atoms is smaller from a:LiH than from a:Li, which means that retention of H in a:LiH is larger than in a:Li. For H, Li impacts atoms in the surface are the main “reflectors”. Although the density of Li atoms in a:Li and a:LiH are not much different, the impacting H loses a lot of its energy in scattering off surface H’s in a:LiH, which doesn’t happen in a:Li. For the same reason, the penetration of H in a:LiH is smaller than in a:Li, leading to both smaller reflection depths and shallower distributions of retained atoms in a:LiH. Also, the energies of reflected atoms from a:LiH are smaller than those from a:Li, causing smaller initial sputtering depths. In effect, sputtered Li atoms have a smaller number of collisions on the way out, leading to higher energies of Li atoms sputtered from a:LiH. All these conclusions are valid for both H+a:LiH and D+a:LiD when compared with processes at a:Li.

Comparing the processes by incident H at a:LiH and incident D at a:LiD, the main differences come from more efficient kinetic energy transfer from D to Li, than from H to Li, and thus deeper penetration of H in a:LiH than D into a:LiD. The probabilities of reflection of H from a:LiH are systematically larger than those of D from a:LiD, as could be expected from the smaller mass difference of D and its main “reflector”, Li. Similarly, the energy of the ejected H from a:LiH is systematically higher than that of ejected D from a:LiD, which has a consequence that the energy of sputtered Li is higher by H than by D, in spite of the higher efficiency of energy transfer to Li from incident D than from incident H. However, the Li sputtering probabilities by incident D at a:LiD are somewhat larger than those for incident H at a:LiH, likely due to the more efficient transfer of energy in collisions of D and Li.

The mentioned differences are largely diminished or lost at almost glancing incidence of impact atoms, for both H vs D, and a:LiH vs a:Li. At near glancing incidence, characteristics of the reflected H, and consequently sputtered Li atoms, are the dominance of specular ejection of both reflected H and sputtered Li atoms. This is not a case for the sputtered H or D atoms, which follow a diffuse, cos-like Lambert law.

Due to the presence of water in the background residual gases in the vacuum chambers of fusion devices or in experiments with more controlled conditions, the surface might evolve as a mixture of Li, H, and O, which could create LiH, Li₂O, and LiOH compounds. However, investigations of such an evolution of three atomic components and their complex chemistry is beyond the scope of this paper. In addition, the long-time evolution of such a system would need to include large-scale diffusion and transitions within a complex mixture, which would happen at much longer time scales than the ps-ns scale feasible for our molecular dynamics calculations at the present time. We point out that a study of the multicomponent surface evolution upon H/D impact in the presence of oxygen is planned in our future work.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

PK did the conceptualization, developed computational method and analysis software, did computation, analysis, validation, and visualization and curation of the data, provided some of the computational resources, wrote original draft. EO, AM and AS took part in writing - review and editing, visualization, validation, and data curation. SD and AvanD developed and verified advanced ReaxFF potentials for Li-H. BK supervised the work, did review and editing of the manuscript, performed project administration, funding acquisition, provided resources and validation.

Funding

This work is supported by the U.S. Department of Energy, Office of Science/Fusion Energy Sciences under Award Number DE-SC0019308 to Princeton University. SD and AvanD were supported by DE-SC0022013 to Pennsylvania State University for development of the Li-H potentials.

Acknowledgments

PK is grateful to Princeton University for using the Stellar HPC cluster, to Stony Brook University for access to the SeaWulf HPC, and to XSEDE for access to the SDSC Expanse HPC through grant TG-DMR110037.

Conflict of interest

Author PSK is employed by TheoretiK.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Winter J. Wall conditioning in fusion devices and its influence on plasma performance. Plasma Phys Control Fusion (1996) 38:1503–42. doi:10.1088/0741-3335/38/9/001

CrossRef Full Text | Google Scholar

2. Lucia M, Kaita R, Majeski R, Bedoya F, Allain JP, Abrams T, et al. Dependence of LTX plasma performance on surface conditions as determined by in situ analysis of plasma facing components. J Nucl Mater (2015) 463:907–10. doi:10.1016/j.jnucmat.2014.11.006

CrossRef Full Text | Google Scholar

3. Kugel H, Mansfield D, Maingi R, Bell MG, Bell RE, Allain JP, et al. Evaporated lithium surface coatings in NSTX. J Nucl Mater (2009) 390:1000–4. doi:10.1016/j.jnucmat.2009.01.262

CrossRef Full Text | Google Scholar

4. Allain JP, Ruzic DN, Hendricks MR. Measurements and modeling of D, He and Li sputtering of liquid lithium. J Nucl Mater (2001) 290:180–4. doi:10.1016/S0022-3115(00)00508-0

CrossRef Full Text | Google Scholar

5. Allain JP, Brooks JN, Alman DA, Gonzalez LE. Model development and analysis of temperature-dependent lithium sputtering and sputtered Li+ transport for tokamak plasma-facing applications. J Nucl Mater (2005) 337:94–8. doi:10.1016/j.jnucmat.2004.10.144

CrossRef Full Text | Google Scholar

6. Skinner CH, Sullenberger R, Koel BE, Jaworski MA, Kugel HW. Plasma facing surface composition during NSTX Li experiments. J Nucl Mater (2013) 438:S647–50. doi:10.1016/j.jnucmat.2013.01.136

CrossRef Full Text | Google Scholar

7. Buzi L, Nelson AO, Yang Y, Kaita R, Krstić PS, Koel BE. Sputtering of lithium and lithium compound films under deuterium and helium ion bombardment. Nucl Mater Energ (2019) 19:411–5. doi:10.1016/j.nme.2019.02.037

CrossRef Full Text | Google Scholar

8. Majeski R, Bell RE, Boyle DP, Kaita R, Kozub T, LeBlanc BP, et al. Compatibility of lithium plasma-facing surfaces with high edge temperatures in the Lithium Tokamak Experiment. Phys Plasmas (2017) 24(1-6):056110. doi:10.1063/1.4977916

CrossRef Full Text | Google Scholar

9. Baldwin MJ, Doerner RJ, Luckhardt SC, Conn RW. Deuterium retention in liquid lithium. Nucl Fusion (2002) 42:1318–23. doi:10.1088/0029-5515/42/11/305

CrossRef Full Text | Google Scholar

10. Krstic PS, Ostrowski ET, Dominguez-Gutierrez FJ, Abe S, Koel BE. Sputtering and reflection processes from amorphous lithium surfaces by low-energy impacts of H and D atoms and D2 molecules. J Nucl Mater (2022) 568(1-16):153848. doi:10.1016/j.jnucmat.2022.153848

CrossRef Full Text | Google Scholar

11. Krstic PS, Abe S, Schiltz-Rouse E, Ostrowski ET, Koel BE. Energy, angle, and temperature dependencies of the sticking of D atoms on Li surfaces. J Appl Phys (2022) 131(1-6):243304. doi:10.1063/5.0096816

CrossRef Full Text | Google Scholar

12. Stoller RE, Toloczko MB, Was GS, Certain AG, Dwaraknath S, Garner F. On the use of SRIM for computing radiation damage exposure. Nucl Instr Meth Phys Res B (2013) 310:75–80. doi:10.1016/j.nimb.2013.05.008

CrossRef Full Text | Google Scholar

13. Pauling L. The nature of the chemical bond. IV. The energy of single bonds and the relative electronegativity of atoms. J Am Chem Soc (1932) 54:3570–82. doi:10.1021/ja01348a011

CrossRef Full Text | Google Scholar

14. Allen LC. Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms. J Am Chem Soc (1989) 111:9003–14. doi:10.1021/ja00207a003

CrossRef Full Text | Google Scholar

15. Mortier WJ, Ghosh SK, Shankar S. Electronegativity-equalization method for the calculation of atomic charges in molecules. J Am Chem Soc (1986) 108:4315–20. doi:10.1021/ja00275a013

CrossRef Full Text | Google Scholar

16. Bultinck P, Langenaeker W, Lahorte P, De Proft F, Geerlings P, Waroquier M, et al. The electronegativity equalization method I: Parametrization and validation for atomic charge calculations. J Phys Chem A (2002) 106:7887–94. doi:10.1021/jp0205463

CrossRef Full Text | Google Scholar

17. van Duin ACT, Dasgupta S, Lorant F, Goddard WA. ReaxFF: A reactive force field for hydrocarbons. J Phys Chem A (2001) 105:9396–409. doi:10.1021/jp004368u

CrossRef Full Text | Google Scholar

18. Han SS, van Duin ACT, Goddard WA, Mo H. Optimization and application of lithium parameters for the reactive force field, ReaxFF. Reaxff J Phys Chem A (2005) 109:4575–82. doi:10.1021/jp051450m

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys (1005) 117:1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

20. Domínguez-Gutiérrez FJ, Krstic PS, Allain JP, Bedoya F, Islam MM, Lofti R, et al. Deuterium uptake and sputtering of simultaneous lithiated, boronized, and oxidized carbon surfaces irradiated by low-energy deuterium. J Appl Phys (2018) 123(1-10):195901. doi:10.1063/1.5026415

CrossRef Full Text | Google Scholar

21. Lele A, Krstic P, van Duin ACT. ReaxFF force field development for gas-phase hBN nanostructure synthesis. J Chem Phys A (2022) 126:568–82. doi:10.1021/acs.jpca.1c09648

CrossRef Full Text | Google Scholar

22. Dominguez-Gutierrez FJ, Bedoya F, Krstic PS, Allain JP, Irle S, Skinner CH, et al. Unraveling the plasma-material interface with real time diagnosis of dynamic boron conditioning in extreme tokamak plasmas. Nucl Fusion (2017) 57(1-7):086050. doi:10.1088/1741-4326/aa7b17

CrossRef Full Text | Google Scholar

23. Krstić PS, Harrison RJ, Sumpter BG. Excited state quantum-classical molecular dynamics. Phys Scr (2006) T124:101–7. doi:10.1088/0031-8949/2006/T124/020

CrossRef Full Text | Google Scholar

24. Elstner M, Porezag D, Jungnickel G, Elsner J, Haughk M, Frauenheim TH, et al. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys Rev B (1998) 58:7260–8. doi:10.1103/PhysRevB.58.7260

CrossRef Full Text | Google Scholar

25. Krstic PS, Allain JP, Allouche A, Jakowski J, Dadras J, Taylor CN, et al. Dynamics of deuterium retention and sputtering of Li–C–O surfaces. Fusion Eng Des. (2012) 87:1732–6. doi:10.1016/j.fusengdes.2011.07.009

CrossRef Full Text | Google Scholar

26. Krstic PS, Allain JP, Taylor CN, Dadras J, Maeda S, Morokuma K, et al. Deuterium uptake in magnetic-fusion devices with lithium-conditioned carbon walls. Phys Rev Lett (2013) 110(1-5):105001. doi:10.1103/PhysRevLett.110.105001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Buzi L, Yang Y, Dominguez-Gutierrez FJ, Nelson AO, Hofman M, Krstic PS, et al. Hydrogen retention in lithium and lithium oxide films. J Nucl Mater (2018) 502:161–8. doi:10.1016/j.jnucmat.2018.02.010

CrossRef Full Text | Google Scholar

28.DR Lide, editor. CRC handbook of chemistry and Physics. 86th ed. Boca Raton, FL: CRC Press (2005). p. 4.70. ISBN 0-8493-0486-5.

Google Scholar

29. Krstic PS, Reinhold CO, Stuart SJ. Chemical sputtering by impact of excited molecules. Europhysics Lett (2007) 77(1-6):33002. doi:10.1209/0295-5075/77/33002

CrossRef Full Text | Google Scholar

30. Shin YK, Sengul MY, Jonayat ASM, Lee W, Gomez ED, Randall CA, et al. Development of a ReaxFF reactive force field for lithium ion conducting solid electrolyte Li_1+xAl_xTi_2−x(PO₄)₃ (LATP). Phys Chem Chem Phys (2018) 20:22134–47. doi:10.1039/c8cp03586e

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Raju M, Ganesh KPRC, van Duin ACT. Reactive force field study of Li/C systems for electrical energy storage. J Comput Theor Chem (2015) 11:2156–66. doi:10.1021/ct501027v

CrossRef Full Text | Google Scholar

32. van Duin ACT, Zou C, Joshi K, Bryantsev V, Goddard WA. A ReaxFF reactive force field for proton transfer reactions in bulk water and its applications to heterogeneous catalysis, Computational Analysis. Cambridge: Royal Society of Chemistry (2014). Chapter 6.

Google Scholar

33. Fedkin MV, Shin YK, Dasgupta N, Yeon J, Zhang W, van Duin ACT, et al. Development of the ReaxFF methodology for electrolyte–water systems. J Phys Chem A (2019) 123:2125–41. doi:10.1021/acs.jpca.8b10453

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ziegler JF, Biersack JP, Littmark U. The stopping and range of ions in matter, Vol. 1. New York, NY: Pergamon (1985).

Google Scholar

35. Allain JP, Ruzic DN. Measurements and modelling of solid phase lithium sputtering. Nucl Fusion (2002) 42:202–10. doi:10.1088/0029-5515/42/2/312

CrossRef Full Text | Google Scholar

36. Eckstein W. Calculated sputtering, reflection and range values (IPP 9/132). Munich: Garching: Max-Planck-Institute für Plasmaphysik (2002).

Google Scholar

37. Eckstein W, Garcia-Rosales C, Roth J, Ottenberger W. Sputtering data (IPP 9/82). Munich: Garching: Max-Planck-Institute für Plasmaphysik (1993).

Google Scholar

38. Eckstein W. Sputtering, reflection and range values for plasma edge codes (IPP 9/117). Munich: Garching: Max-Planck-Institute für Plasmaphysik (1998).

Google Scholar

39. Eckstein W. Sputtering yields. In: R Behrisch, and W Eckstein, editors. Sputtering by particle bombardments. Berlin: Springer (2007).

Google Scholar