Highly charged ion (HCI) clocks: Frontier candidates for testing variation of fine-structure constant

Attempts are made to unify gravity with the other three fundamental forces of nature. As suggested by higher dimensional models, this unification may require space and time variation of some of the dimensionless fundamental constants. In this scenario, probing temporal variation of the electromagnetic fine structure constant $(\alpha =\frac{e^2}{\hslash c})$ in a low energy regime at the cosmological time scale is of immense interest. Atomic clocks are ideal candidates for probing α variation because their transition frequencies are measured with ultra-high precision. Since atomic transition frequency is a function of α, measurement of a clock frequency at different temporal and spatial locations can yield signatures to ascertain variation of α. Highly charged ions (HCIs) are very sensitive to variation of α and are least affected by external perturbations, making them excellent platforms for searching for temporal variation of α. In this work, we overview HCIs suitable for building atomic clocks because of their spectroscopic features and sensitivity to variation of α. The selection of HCI clock candidates is outlined based on two general rules—by analyzing trends in fine structure splitting and level-crossing patterns along a series of isoelectronic atomic systems of the periodic table. Two variants of relativistic many-body methods in the configuration interaction and coupled-cluster theory frameworks are employed to determine the properties of HCIs proposed for atomic clocks. These methods treat electronic correlation and relativistic effects under the frame of the Dirac-Coulomb Hamiltonian rigorously, while other higher-order relativistic effects are included approximately. Typical systematic effects of the HCI clock frequency measurements are discussed using the calculated atomic properties. This review will help understand limits and potentials of the proposed HCIs as the prospective atomic clock candidates and guide future HCI clock experiments.

1 Introduction

Atomic clocks, used for frequency standards, help us define the unit of time with very high precision so that they lose only one second over the age of our universe. These clocks are based on either neutral atoms or singly charged atomic ions. With the advent of recent laser cooling and trapping techniques of atomic systems, modern optical clock frequencies have been measured with uncertainties that are much lower than the present 10⁻¹⁶ level caesium microwave-based primary atomic clock [1–3]. Uncertainty of optical lattice clock based on ¹⁷¹Yb atoms has reached an uncertainty of 1.4 × 10⁻¹⁸ [4, 5] whereas ⁸⁷Sr optical lattice clocks offer uncertainty of around 2.0 × 10⁻¹⁸ [6, 7]. Similarly, uncertainties of ¹⁷¹Yb⁺ and ⁴⁰Ca⁺ ion clocks have both reached an accuracy of 3 × 10⁻¹⁸ [8, 9]. There have been continuous efforts to reduce uncertainties in the clock frequency measurements and miniaturize the atomic clocks, intending to utilize them in many sophisticated instruments and space science research.

Among various scientific applications of atomic clocks, see the review by Safronova et al [10] for more details, atomic clocks serve as an important tool to probe temporal and spatial variation of the fine-structure constant (α). Atomic energy levels are functions of α. Thus any variation in the α value will result in changes in the energy levels over time and space. Since optical clocks can measure atomic transition frequencies to ultra-high precision, they are the most suitable instruments for detecting any drift in the α value. The clock transitions have different sensitivity to variation of α. The sensitivity of an energy level to α variation is gauged through a relativistic sensitivity coefficient q by defining it as

${\omega }_t={\omega }_0+qx,(1)$

where ω₀ is the angular frequency of the transition for the present-day value of the fine-structure constant α(0) and ω_t is the angular frequency of the transition corresponding to another value of α(t) at time t such that x = (α(t)/α(0))² − 1 ≈ 2(α(t) − α(0))/α(0). Sometimes it is convenient to introduce a dimensionless sensitivity coefficient K_α by defining it as K_α = q/ω₀. Here, q and K_α are often referred to as a frequency’s absolute and relative sensitivity factor to variation of α.

Table 1 summarizes the currently prevailing clock frequencies with regard to their sensitivity to variation of α. Some of them has low sensitivities to α variation, like the clock transition in Al⁺, Ca⁺, Sr and Yb, while the 4f¹⁴6s ²S_1/2 − 4f¹³6s ²F°_7/2 transition in Yb⁺ and the 5d¹⁰6s ²S_1/2 − 5d⁹6s^{2 2}D_5/2 transition in Hg⁺ have relatively higher sensitivity coefficients to variation of α. Such contrast sensitivities to variation of α suggest different accuracy requirements in the frequency measurements if they are used for testing variation of α. Assuming the time variation rate of α per year is around 10⁻¹⁶ level, to detect such a small variation rate of α within a year time, minimum requirements of fractional uncertainties of the Sr, Yb, and Hg atomic clock frequencies would be about 8 × 10⁻¹⁷, 5 × 10⁻¹⁷ and 2 × 10⁻¹⁸, respectively, by considering their sensitivity coefficients to α variation. Thus, for any further constraining to the temporal variation of α lower than 10⁻¹⁶, the aimed uncertainty level in the clock frequency measurement has to be less than 10⁻¹⁸ if an a-year-around experiment is planned. On the one hand, researchers endeavour to push for minimizing uncertainty levels further down in the clock frequency measurements to meet the requirement for inferring any signature of α variation from the measurements, and on the other hand, selecting a suitable pair of clock transitions having very different sensitivity to variation of α is a good option. To be specific, when a measurement of the frequency of an optical clock at the frequency f₁ relative to another optical clock at the frequency f₂ is conducted (the two optical clocks have different sensitivities to α variation), the time-variation of the ratio f₁/f₂ can be expressed as

$\frac{\partial }{\partial t}\ln \frac{f_1}{f_2}=\frac{\partial }{\partial t}\ln R=\ln \dot{R}=\left[K_{\alpha }\left(1\right)-K_{\alpha }\left(2\right)\right]\frac{\partial }{\partial t}\ln \alpha ,(2)$

where $R=\frac{f_1}{f_2}$ is the frequency ratio, K_α(1) and K_α(2) are the sensitivity factors of the respective clock frequency. For example, the ¹⁹⁹Hg⁺ and ²⁷Al⁺ optical frequency standards have a big difference in K_α as K_α(Al⁺)-K_α(Hg⁺) = 2.95, and their frequency ratio of $f_{{\text{Al}}^{+}}/f_{{\text{Hg}}^{+}}$ has been measured over a timescale of about 1 year, yielding a drift rate of $f_{{\text{Al}}^{+}}/f_{{\text{Hg}}^{+}}=(-0.53\pm 0.79)\times 10^{-16}$ and constrained the temporal variation of α as $\dot{\alpha }/\alpha =(-1.6\pm 2.3)\times 10^{-17}$ [12]. Similarly, Lange in PTB compared two optical clocks based on the E2 and E3 transitions of ¹⁷¹Yb⁺ that have the difference in K_α as K_α(E3)-K_α(E2) = −6.95. The frequency ratio f_E3/f_E2 was measured over 1,500 days, which determined $\dot{R}/R=-6.8(7.5)\times 10^{-18}$ per year and yield $\dot{\alpha }/\alpha =(1.0\pm 1.1)\times 10^{-18}$ per year.

TABLE 1

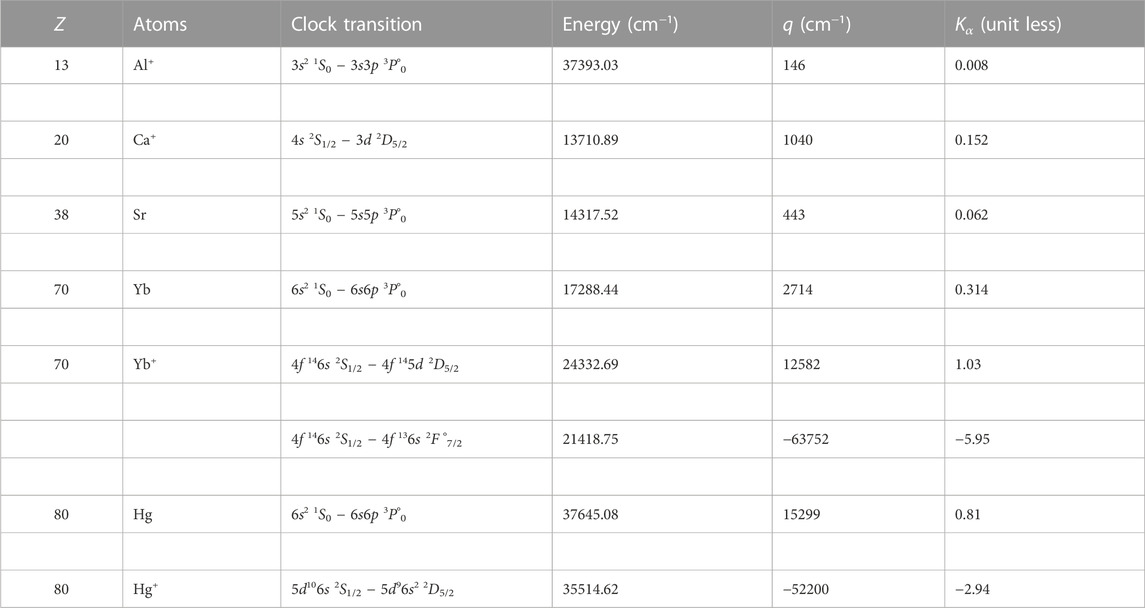
TABLE 1. A summary of the sensitivity coefficients, q and K_α, of the clock transition frequency to variation of α, with definition given in text and the data source is taken from Ref. [11].

In the aim of ultimately observing the variation of α, it is necessary to improve the clock frequency measurements consistently. In this sense, even improving the limit on the constraint of α variation over time is meaningful. One way of proceeding with this task is to work hard to find ways to minimize uncertainties in the existing atomic clocks. Alternatively, we can look for other suitable candidates least influenced by stray electromagnetic fields. One such possibility is to use nuclear transitions for the clock frequency measurements. The presence of a low-lying metastable state in ^229mTh with excitation energy around 8 eV is identified to be the perfect choice for this purpose [14, 15]. Many efforts are already gone into directly detecting nuclear transition by measuring the isomeric state energy of ^229mTh precisely for achieving nuclear clock [16–19]. This transition has also been explored for testing variation of fundamental constants by different groups [20–23]. The other novel thought has been put into exploring highly charged ions (HCIs) for making atomic clocks [24]. Investigation of spectral properties of HCIs has a very long history, which is immensely interesting for identifying abundant elements in the solar corona and other astrophysical objects, describing exotic phenomena in the nuclear reactions, diagnosing plasma processes, etc. [25–28]. However, HCIs are recognized as potential candidates for making ultra-precise atomic clocks, developing tools for quantum information, and probing possible variations of α. Following the pioneering works by Berengut et al., which suggested enhanced sensitivity to variation of α in the HCIs [29–34], a long list of HCIs are being proposed [35–52] to select appropriate HCIs for consideration for the clock experiments. All these proposed HCI candidates appear promising for building atomic clocks and probing α variation, but there could be slight differences in setting up their experiments. Since the HCIs possess very compacted electron orbitals than their isoelectronic neutral atoms or singly charged ions, they can be strongly immune to external perturbations. Apart from this, it would be relatively easier to detect a signature of α variation in HCIs at the same level of accuracy in the clock frequency measurements with respect to optical lattice clocks or singly charged ion clocks owing to their enhanced sensitivity α coefficients.

In this brief review, we shortlist the HCIs that can be prospective candidates for optical atomic clocks other than those previously listed in a review by Safronova et al. [10]. Most of these HCIs have large α varying sensitivity coefficients for the clock transitions, which implies that they are excellent platforms for searching of temporal variation of α. Selection of HCIs for atomic clocks is further addressed based on the forbidden transitions within fine-structure splitting and those among interconfigurations that undergo orbital energy crossings. Relativistic many-body methods employed to calculate HCI properties are described briefly. Finally, prominent systematic effects of the HCI clock frequency measurements due to stray electromagnetic fields are discussed before summarizing the work.

2 Importance of α-variation studies

Actual values of many of the dimensionless physical constants need to be verified experimentally as their magnitudes are predicted differently by different models with strong scientific arguments. Though there has yet to be strong evidence to show that their values are not constant, there is also no strong scientific argument justifying that they have to be constants over time or space. Thus, any plausible signature in the temporal or spatial variation of fundamental physical constants would answer either of these questions. If slight temporal or spatial variation in the fundamental constants is possible, it will support some of the phenomena beyond the Standard Model of particle physics. This is why probing temporal and spatial variation of α is of immense interest to the research community [10, 28, 53, 54]. One of the biggest consequences of investigating the temporal and spatial variation of α is to support multidimensional theories that try to unify all four fundamental interactions [55–62]. Such theories also predict violation of Einstein’s equivalence principle. Thus, any signature of variation in the α value can also imply violation of Einstein’s equivalence principle.

In astronomy, observation of absorption spectral lines from distant astronomical objects such as quasars with large red shift constant (z) can be used directly for probing variation of α. Observations using the Kerk telescope suggest that the fractional drift in α is smaller by an amount Δα/α=(α_z − α₀)/α₀=(0.543 ± 0.116) × 10^–5 around 10¹⁰ years ago over the range 0.2 < z < 4.2 [63, 64]. Observations of spectral lines from quasar J1120 + 0641 in the redshift range 5.5–7.1 using the Very Large Telescope (VLT) is used to search for variation of α. It is worth mentioning that observations at z = 7.1 correspond to the Universe about 0.8 billion years old. These observations reported the result as Δα/α=(−2.18 ± 7.27) × 10^–5, which is consistent with null temporal variation [65]. Very recently, Murphy et al. observed HE 0515–4414 by the VLT with the redshift range of 0.6–2.4. They combined their observed spectral lines data with 28 measurements from other spectrographs to mitigate the wavelength calibration errors and reported a weighted mean of Δα/α= (−0.5 ± 0.5_stat ± 0.4_sys) parts-per-million (ppm). Webb et al. proposed a theory of spatial dipole of α by analyzing observed data from both the Keck and VLT telescopes [28]. It does not seem to have strong evidence in favour of this theory as data from both the Keck and VLT observations used for this analysis had significant systematic effects [66, 67].

Another class of data is inferred from the geophysical data analysis from the Oklo natural fission reactor and cosmological observations, which correspond to a slightly smaller time scale than the astrophysical observations. The signature of temporal variation of α can be easily detected from events that correspond to the early epoch of the Universe. The data from the Oklo nuclear reactor offers a limit as Δα/α <1.1\times 10⁻⁸ over a time span of 2 Gyr [68].

Laboratory-based atomic clocks provide measurements of the time variation of α in the present-day time scale. Table 2 summarizes the current most stringent limit to $(\mathrm{\Delta }\alpha /\mathrm{\Delta }t)/\alpha =\dot{\alpha }/\alpha$ per year, which is determined by the laboratory measurement of the ratio of two clock frequencies over a reasonably long time. It includes measurements of the clock frequency ratio of the Hg⁺ and Al⁺ optical clocks over the course of a year (Δt = 1yr), which yields as $\dot{\alpha }/\alpha =(-1.6\pm 2.3)\times 10^{-17}$ [12]. The other one is the ratio deduced from the electric quadrupole (E2) and electric octupole (E3) clock frequency measurements in Yb⁺ over around 4 years (Δt = 4yr), which suggests $\dot{\alpha }/\alpha =(1.0\pm 1.1)\times 10^{-18}$ per year [13], agreeing with the previous finding of null variation. Similar interpretations on the time variation of α have been made from the other clock frequency measurements found from Refs. [69–75].

TABLE 2

TABLE 2. Time-varying frequency ratio R measurements using different combinations of optical atomic clocks (A₁ and A₂), and their corresponding α varying sensitivity coefficients from two separate works. The inferred limits on the time drift of α are also given from these works.

Findings of variation of Δα from different studies have been reviewed in Refs. [11, 33, 53, 76, 77]. Table 3 compares limits to the temporal variation in α from various sources. The interpretation of the astrophysical observations and geophysical data, principally the Oklo phenomenon, are highly dependent on many assumptions. Limits derived from the laboratory studies by comparing frequencies of the atomic clocks in that sense can be much less unambiguous. However, these results can only restricted to the present day phenomena and to the region of space of the earth’s orbit. The time drift of the ratio of two atomic frequencies can also depend on the proton-to-electron mass ratio via μ_N/μ_B = 1/μ when at least one of the atomic clock frequencies is based on the hyperfine transition like the Rb and Cs microwave clocks [13, 71, 73, 74]. Together this quantity with α variation can tell us about possible variation of a strong-interaction parameter X_q, that denotes the ratio between the average quark mass and the quantum chromodynamic scale Λ_QCD. Therefore, comparison of two optical clock frequencies is quite important in order to infer directly signatures of the variation of the fundamental constants.

TABLE 3

TABLE 3. Comparison of various limits to variation in α with its absolute value (Δα/α) obtained from different types of works over a time interval Δt. The corresponding limits in annual fractional rate of change $(\dot{\alpha }/\alpha )$, with a crude assumption of a linear change in time, are also given for the purpose of comparing them with the values given in Ref. [76] if one wishes to do so.

3 Potential candidates of HCI clocks

In the past decade, many HCIs have been proposed for making atomic clocks. A list of these ions and their proposed clock transitions are mentioned in Table 4. Transition energies and their sensitivity coefficients q and K are also given in the same table. The first optical HCI clock, based on the Ar¹³⁺ ions, has been demonstrated at the uncertainty level 2.2 × 10⁻¹⁷. It used sympathetic cooling techniques to decrease temperature to milli-kelvin to cool the ions produced using the electron beam ion trap (EBIT). The accuracy of this HCI based optical clock is already comparable to that of many optical clocks in its first attempt itself [78, 79]. The clock transition in the Ar¹³⁺ ion was proposed by Yudin et al [37] in 2014, along with many other HCIs having magnetic-dipole (M1) transitions between the np ²P_1/2 − ²P_3/2 and among the np^{2 3}P_0,1 fine structure splitting of many monovalent and divalent HCIs respectively. Later, we analyzed major systematics theoretically of clock transitions in the monovalent B-like, Al-like, and Ga-like ions [44, 46].

TABLE 4

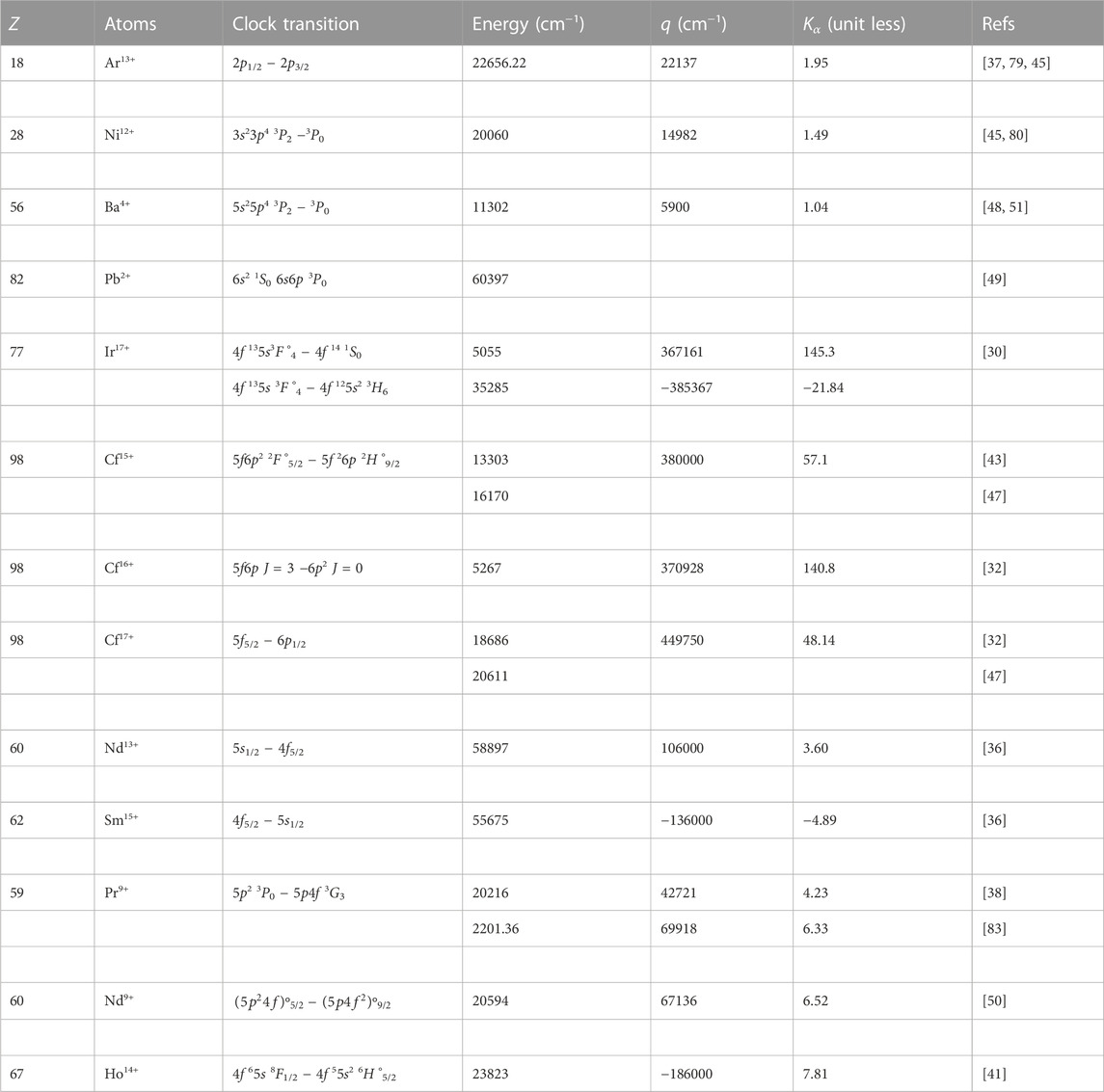
TABLE 4. A summary of the HCIs proposed for making optical clocks. The definition of q and K_α is given in text.

Based on the electric quadrupole (E2) transition between the np^{4 3}P_0,2 fine structure splitting, the Ni¹²⁺ ion along with the other three HCIs, Cu¹³⁺, Pd¹²⁺ and Ag¹³⁺, were proposed as promising candidates for making high-accuracy optical clocks [45]. The transition rate of the E2 transition is usually far slower than that of the M1 transition. Therefore the advantage of considering the E2 transitions in these ions for clocks is that they all possess larger quality factors than the M1 transitions between the (np)²P_1/2,3/2 fine structure splittings. The spectroscopy lines of the Ni¹²⁺ ion in the EBIT has been identified by Liang et al. very recently [80]. Ba⁴⁺ with 5s²5p⁴ configuration was proposed by Beloy [48] as the mediumly ionized clock. The α varying sensitivity coefficients in the Ar¹³⁺, Ni¹²⁺ and Ba⁴⁺ ions are found to be much larger than most of the available singly charged ion and neutral atomic clocks except Hg⁺ and Yb⁺ clocks.

Among all the proposed HCIs, Ir¹⁷⁺ shows having the largest sensitivity to variation of α [30]. The double-hole configuration of Ir¹⁷⁺ offers several transitions in the optical range. Two of them, 4f¹³5s ³F°₄ − 4f^{14 1}S₀ and 4f¹³5s ³F°₄ − 4f¹²5s^{2 3}H₆, are claimed to be suitable as clock transitions [30]. The optical lines in Ir¹⁷⁺ along with other Nd-like W, Re, Os, and Pt ions, have been identified by Winderger el al [81]. Their inferred transition energy of the 4f¹³5s ³F°₄ − 4f¹²5s^{2 3}H₆ transition lies between 4.0392 and 4.6397 eV. However, this value disagrees with the theoretical values that predict 3.7623 eV [82] and 3.003 eV [81]. Similarly, the 4f¹³5s ³F°₄ − 4f^{14 1}S₀ transition that has been identified to have the largest q and K values are not observed experimentally, while transition energies from different theoretical results show about 20% difference [81, 82]. The Cf¹⁶⁺ and Cf¹⁷⁺ ions proposed by Berengut et al. [32] and the Cf¹⁵⁺ ion proposed by Dzuba [43] for atomic clocks also have relatively large q and K values. Porsev et al. have also explored the possibility of developing optical clocks using the Cf¹⁵⁺ and Cf¹⁷⁺ ions [47].

The ultra-narrow 5s_1/2 − 5f_5/2 optical transitions in Nd¹³⁺ and Sm¹⁵⁺ were proposed for the construction of the HCI clocks and search for variation of the fine-structure constant [36]. These lines have relatively large q and K values, but their transition wavelengths are about 170 and 180 nm, which are out of the accessible range of the currently available lasers. Safronova et al. searched for the visible lines in a series of the Ag-like, Cd-like, In-like, and Sn-like HCIs for the development of frequency standards and to probe variation of the fine-structure constant [38–40]. Among these ten HCIs recommended by them, the Pr⁹⁺ ion seems to be the more attractive, which has an optical transition 5p^{2 3}P₀ − 5p4f ³ G₃ between the ground and the first excited states. The lifetime of the excited clock state was estimated to be 10¹⁴ s, and it has a wavelength at 475 nm, which can be accessed by the currently available. Bekker et al. present the EBIT measurements of the spectra of Pr⁹⁺, which refines the energy levels of such proposed nHz-wide clock line and demonstrates about Pr⁹⁺ having very large sensitivity coefficient to variation of α and variation of local Lorentz invariance probing coefficient [83]. The Sb-like Nd⁹⁺ ion was proposed by Yu et al. [50] as a possible HCI clock. The Nd⁹⁺ ion has the ground state configuration as ${(5p^{2}4f)°}_{5/2}$ and the first excited state configuration as ${(5p4f^2)°}_{9/2}$. The E2 transition of ${(5p^{2}4f)°}_{5/2}-{(5p4f^2)°}_{9/2}$ shows large q and K values and feasibility of making a high accuracy atomic clock.

Dzuba et al. studied the I-like Ho¹⁴⁺ ion as a possible candidate for an extremely accurate and stable optical clock which has q and K slightly larger than Pr⁹⁺ and Nd⁹⁺. The Ho¹⁴⁺ ion has all the desired features, including relatively strong optical electric-dipole (E1) and M1 transitions can be used for cooling and detection. The electronic configuration of the ground state of this ion has seven valence electrons in the open s and f shells, which gives rise to a large number of fine structure splitting. Nakajima et al. have observed the visible spectra of the above ion using a compact electron beam ion trap [84]. They found that the ground state configuration of Ho¹⁴⁺ is [Kr]4f⁶5s with 577 fine structure levels spreading over an energy range of about 40 eV, and the electronic configuration of the first-excited configuration of this ion [Kr]4f⁵5s², with 200 fine structure levels spreading over the similar energy range. Their results show a huge number of emissions in the Ho¹⁴⁺ visible spectra, whereas these lines are challenging to distinguish while experimenting as they all have similar transition probabilities.

4 General directions for identifying HCI clock candidates

The HCIs have very compact sizes and wave functions compared with their counter neutral atoms and singly charged ions, which are accompanied with the scaling laws for energies and transition matrix elements with increasing the charge number Z_ion in an isoelectronic sequence [26, 85]. In order to understand the enhancement of q in the HCIs, Berengut et al suggested a simple analytical expression as [29, 85].

$q_n\approx -I_n\frac{{\left(Z\alpha \right)}^2}{\nu \left(j+1/2\right)}(3)$

and

$I_n=-E_n=\frac{Z_a^2}{2n^2}=\frac{{\left(Z_{\mathit{ion}}+1\right)}^2}{2{\nu }^2},(4)$

where Z is the atomic number, j is the total angular momentum of the orbital, I_n = −E_n represents the positive ionization potential energy of the electron in the electronic orbital, and n is the integer principal quantum number. The equality in Eq. (4) relates I_n to E_n by using an effective principle quantum number ν and an effective charge Z_a that the electron sees at larger distances, considering the screening in a multi-electron system. Eqs 3, 4 explain how enhancement of q increases with I_n, i.e., with larger Z_ion. Besides, q is related to j, which indicates that the excitation among orbitals with larger j differences can have bigger q. Appearance of Z means a heavy element is preferred, usually offering larger relativistic effects. Besides, the hole state in an otherwise filled external shell will have the highest q for particular values of Z and Z_a.

The energy scaling with Z_ion indicates that transitions in HCIs are frequently in the XUV and x-ray range unsuitable for making atomic clocks. However, we can realize that on occasions where HCIs have forbidden transitions can be in the optical region, as has been pointed out by the previous studies. Firstly, the energy interval between the fine structure and the hyperfine structure energy levels increase greatly with the charge number Z_ion in the HCI isoelectronic sequences, which leads to widening these level splitting. It causes transition lines to change from the microwave, as seen in the neutral atoms and singly charged ions, to the optical in HCIs. The other possible approach can be adopted to find suitable HCIs for clocks by analyzing the orbital energy crossings in the isoelectronic sequences of atomic systems. Near level crossings, frequencies of transitions involving the orbital sequence switching can be much smaller than the ionization potentials. This helps to distinguish suitable transitions that can be in the optical range in a prudent manner.

In the following, we overview two basic rules for selecting HCIs as candidates for making atomic clocks. In fact, from a general observation point of view of all the previously proposed HCI candidates for clocks, can be classified into two categories: HCIs with the M1 and E2 clock transitions among the fine structure splitting and HCIs with the forbidden transitions among the electronic configurations whose candidatures can be understood using orbital energy crossing scheme. Thus, we proceed further to investigate more HCIs along the same lines of thoughts to search for other suitable candidates for HCI clocks.

4.1 Forbidden transitions within fine-structure splitting

Studies of spectroscopic properties of forbidden lines are attractive for quite a long time in the fields of astronomical and laboratory research since they are frequently observed in astrophysical observations, e.g., in the solar corona and in solar flares, and high-temperature fusion plasma, where these forbidden lines are often used as diagnostic tools to find out temperature, constituents and ion densities [86–91]. The M1 transition lines occur amongst the fine-structure splitting of the HCI isoelectronic sequences and are usually found in the optical range. They are easier to observe in contrast to the resonant lines that appear in the far ultraviolet region. Biemont and coworkers have carried out comprehensive studies on many radiative properties of transition lines in HCIs having ground state configurations as 3p^k, 4p^k, 5p^k, and 6p^k [92–102] with k = 1, 2, 3, ⋯ number of valence electrons.

Recently, many optical forbidden transitions between the fine-structure splitting in the HCIs are considered as clock transitions, and many of them are listed in Table 5. As can be seen from the above table, many proposals have considered the forbidden M1 transitions between the fine-structure splitting ²P_1/2 −²P_3/2 in HCIs having single p-valence orbital and between the fine -structure splitting ³P₀ −³P₁ in HCIs having two p valence electrons for making ultra-precise atomic clocks. Yu et al. have investigated B-, Al-, and Ga-like HCIs for making atomic clocks that have fine-structure splitting as 2p_1/2,3/2, 3p_1/2,3/2 and 4p_1/2,3/2 respectively. It was found in this work that the M1 transitions between these fine structure splitting have appropriate wavelengths and quality factors as well as relatively smaller systematics (at the 10^–19 level). Therefore, these ions are appeared to be excellent candidates to be considered for making atomic clocks [44, 45]. One can presume from these analyses that HCIs with np^k ground state configurations with n ≥ 5 can have similar transition properties and be suitable for atomic clocks.

TABLE 5

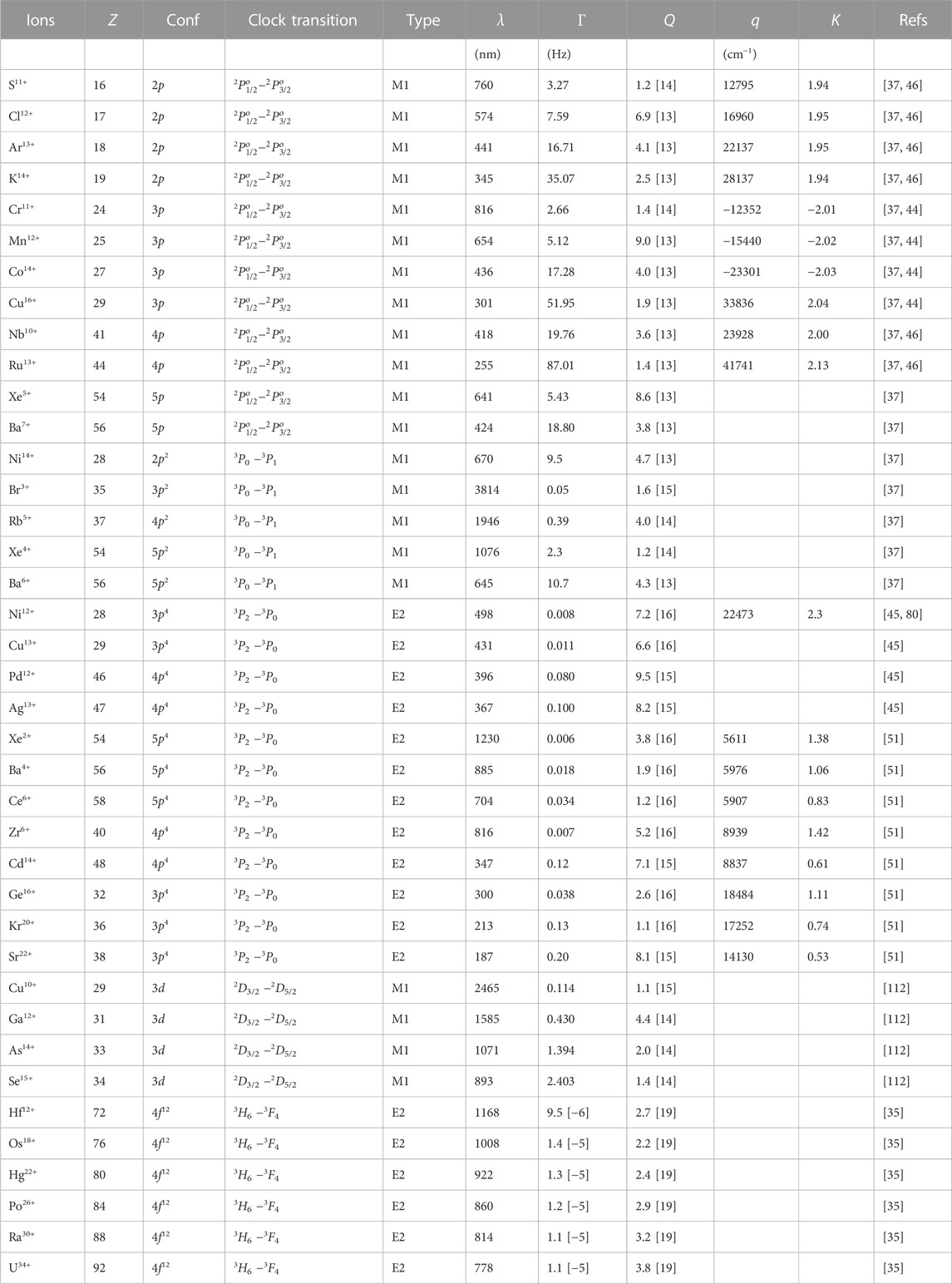
TABLE 5. Summary of selected M1 and E2 HCI transitions of fine-structure splittings. a [b] should be read as a × 10^b.

Compared with M1 transitions, wherever E2 transitions play important roles in deciding the lifetimes of an upper state, they can offer larger quality factors if considered as clock transitions. Yu et al. have proposed the S-like Ni¹²⁺ and Cu¹³⁺ ions having the 3p⁴ ground-state configurations, and the Se-like Pd¹²⁺ and Ag¹³⁺ ions having the 4p⁴ ground-state configurations as potential candidates for making an ultra-precise atomic clock, as listed in Table 5. The ³P₂ −³P₀ transitions in the ⁵⁸Ni¹²⁺ and ¹⁰⁶Pd¹²⁺ ions with nuclear spin I = 0 and the |³P₂, F = 1/2⟩ − |³P₀, F = 3/2⟩ transition in ⁶³Cu¹³⁺ with I = 3/2, and the |³P₂, F = 3/2⟩ − |³P₀, F = 1/2⟩ transition in ¹⁰⁷Ag¹³⁺ with I = 1/2 can also be suitable for clock transitions, which can offer clock transitions with fractional uncertainties below 10^–19 level. These HCIs have simple atomic energy level structures to carry out spectroscopic measurements, and the quality factors of the respective clock transitions are of the order 10¹⁵–10¹⁶. Allehabi et al. have identified ³P₂ −³P₀ transitions from HCIs of group-16 elements that are governed by E2 channel and are in the optical region as possible high-accuracy optical clocks, including the S−, Se−, and Te-like systems, which have 3p⁴, 4p⁴, and 5p⁴ ground configurations [51] as listed in Table 5.

The forbidden transitions among the fine-structure splitting in HCIs possessing nd^k configuration in their ground state are more complicated to study than the HCIs having np^k configurations in the ground state. The reason is d-orbitals have many subshells bestowing strong open-shell problems. As a result, it is challenging to study transition properties among the fine-structure splitting of these HCIs, even using the available sophisticated atomic many-body methods. Some of these transitions are found to be useful in the production processes 13.5-nm-wavelength extreme ultraviolet (EUV) radiation for nanolithographic applications [103]. They also give rise EUV spectra between 10 and 25 nm in the tungsten HCIs from the 3d open-shell configurations as listed in the NIST database [104]. It is natural to anticipate that some of these transitions could be considered for atomic clocks. Theoretical studies carried out in Refs. [105–111] support this idea. A wide range of calculations on the M1 and E2 transition probabilities among the fine-structure splitting of the 3d ²D_3/2 − −3d ²D_5/2 transitions are performed in the K-like sequence HCIs to find out their feasibility for using optical clocks [112]. Some of them are listed in Table 5.

Now we turn to the transitions involving fine-structure partners of open 4f shells. For the reason mentioned above in the case of the nd^k configurations, theoretical studies of these transitions are even more complicated than the open p- and d-shells. Electrons from the open-shell 4f orbitals usually show strong correlation effects with the inner s, p, and d shells. Historically, the forbidden transitions among the fine structures of the open f-shell configurations are widely investigated for various applications such as carrying out temperature and density diagnostics of plasma, and astronomical spectral identifications [113–117]. A series of HCIs from Hf¹²⁺ to U³⁴⁺ that have 4f¹² valence shells were proposed to be excellent candidates for building exceptionally accurate atomic clocks by Derevianko et al. [35, 118]. Some of them are listed in Table 5. In addition to the highly forbidden laser-accessible transitions within the 4f¹² ground-state configurations that can be used to be the clock transitions, these ions also have additional M1 and E2 transitions along with the M1 clock transitions that can be used for cooling ions during the measurement.

In Table 5, we compare the q and K values for the proposed candidates of the HCI clocks when they are reported earlier. Most of them have larger q and K values than their isoelectronic neutral atoms and singly charged ions, however, are still less than the singly charged ions Hg⁺ and Yb⁺. It indicates that q and K are not significantly prominent in the M1 and E2 transitions between the fine-structure splittings.

4.2 Orbital energy crossings in complex HCIs

Generally, the ordering of energy levels in neutral atoms follows the n + l and n orbital filling scheme (often referred to as Madelung rule [119]), where n and l are the principles and angular quantum numbers. According to this rule, we can assume that the order of the atomic orbital filling in the neutral and singly charged ions would be 1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p → 5s → 4d → 5p → 6s → 4f → 5d → 6p → 7s → 5f → 6d → 7p⋯. However, this rule is violated in the hydrogen-like ions, in which the filling order of the orbitals complies with the Coulombic ordering. That is, orbitals with smaller n are filled first, and for equal n, the orbitals with smaller l are filled. If we follow this ordering, then nd orbitals are filled first instead of (n + 1)s orbitals after the np orbitals. Similarly, nf orbitals are filled first instead of (n + 1)s orbitals after the nd. The phenomenon of the orbital energy of nd and nf diving down while (n + 1)s and also (n + 1)p rising up as the Z and Z_ion increasing in an isoelectronic sequence is referred to as the orbital energy crossing, which is first investigated by Berengut, et al., [34]. They exterminated all the energy crossing in the periodical table. The previously proposed HCIs for making atomic clocks are mostly concentrated on the nd − (n + 1)s crossing and the 4f − 5s crossing.

4.2.1 The nd − (n + 1)s level crossings

Table 6 summarizes the 3d − 4s energy level-crossing occurring in the K-like and Ca-like isoelectronic sequences and the isoelectronic sequences of the elements belonging to the 3d metals. The ground state configurations of the singly charged ions belonging to these elements are generally 3d^x−14s, while the ground state configuration of their double charged ions happens to be 3d^x with x denoting the number of the valence electrons that is one (x = 1) for the K-like isoelectronic sequence, two (x = 2) for the Ca-like isoelectronic sequences, and so on till x = 10 for the Ni-like isoelectronic sequences. So one would anticipate that the 3d − 4s energy level crossing can occur in these isoelectronic sequences when the charges of the ions increase further. However, there have been several exceptions seen where no 3d − 4s level-crossings have occurred in these isoelectronic sequences, such as HCIs belonging to the Ti-like and V-like isoelectronic sequences which have the number of the valence electrons close to half-filling and to the Fe-, Co-, and Ni-like isoelectronic sequences that are close to full-filling. In these cases, the ground state configuration is preferred to be 3d^x. Table 7 summarizes the 4d − 5s energy level-crossings that occur in a series of isoelectronic sequences of elements from the fifth row of the periodic table. The 4d − 5s energy level-crossings are observed in the Rb-, Sr-, and Y-like isoelectronic sequences with x = 1–3 and in the Mo-like isoelectronic sequence with x = 6. However, no such energy level crossings are seen in the isoelectronic sequences with the number of valence electrons close to half- or fully-filled. i.e., for x = 4, 5, 7, 8, 9, 10. For the elements belonging to the sixth row of the periodic table, the 5d − 6s energy level crossings are observed in some isoelectronic sequences, shown in Table 8, such as in the Tm-, Yb-, Lu-, Ta-, W-, and Ir-like isoelectronic sequences.

TABLE 6

TABLE 6. The energy levels of some ions in the K-like (N = 19), Ca-like (N = 20), and the forth row transition metals from Sc-to Ni-like (N = 21 − 28) isoelectronic sequence HCIs, where N is the number of the electron, Z is the atomic number, and x is the number of valence electrons. The closed-shell configuration is [Ar] ≡ 1s²2s²2p⁶3s²3p⁶. The data are taken from the NIST database [120], and units are in cm⁻¹.

TABLE 7

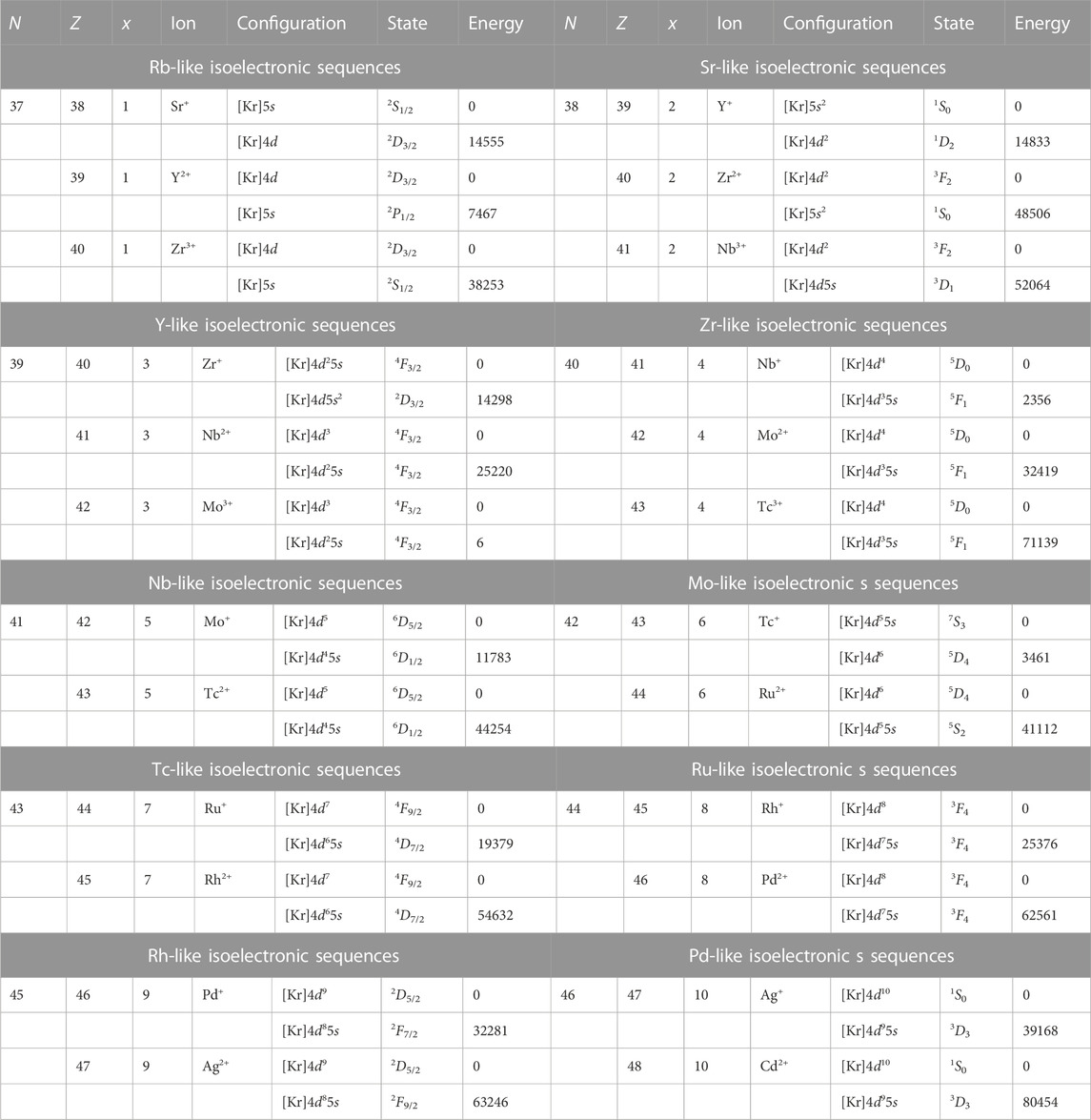
TABLE 7. The energy level of some ions in the Rb-like (N = 37), Sr-like (N = 38), and the fifth row transition metals from Y- to Pd-like (N = 39 − 46) isoelectronic sequence HCIs, where N is the number of the electron, Z is the atomic number, and x is the number of valence electron. [Kr] ≡ 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶. The data are from the NIST database [120] and in cm⁻¹.

TABLE 8

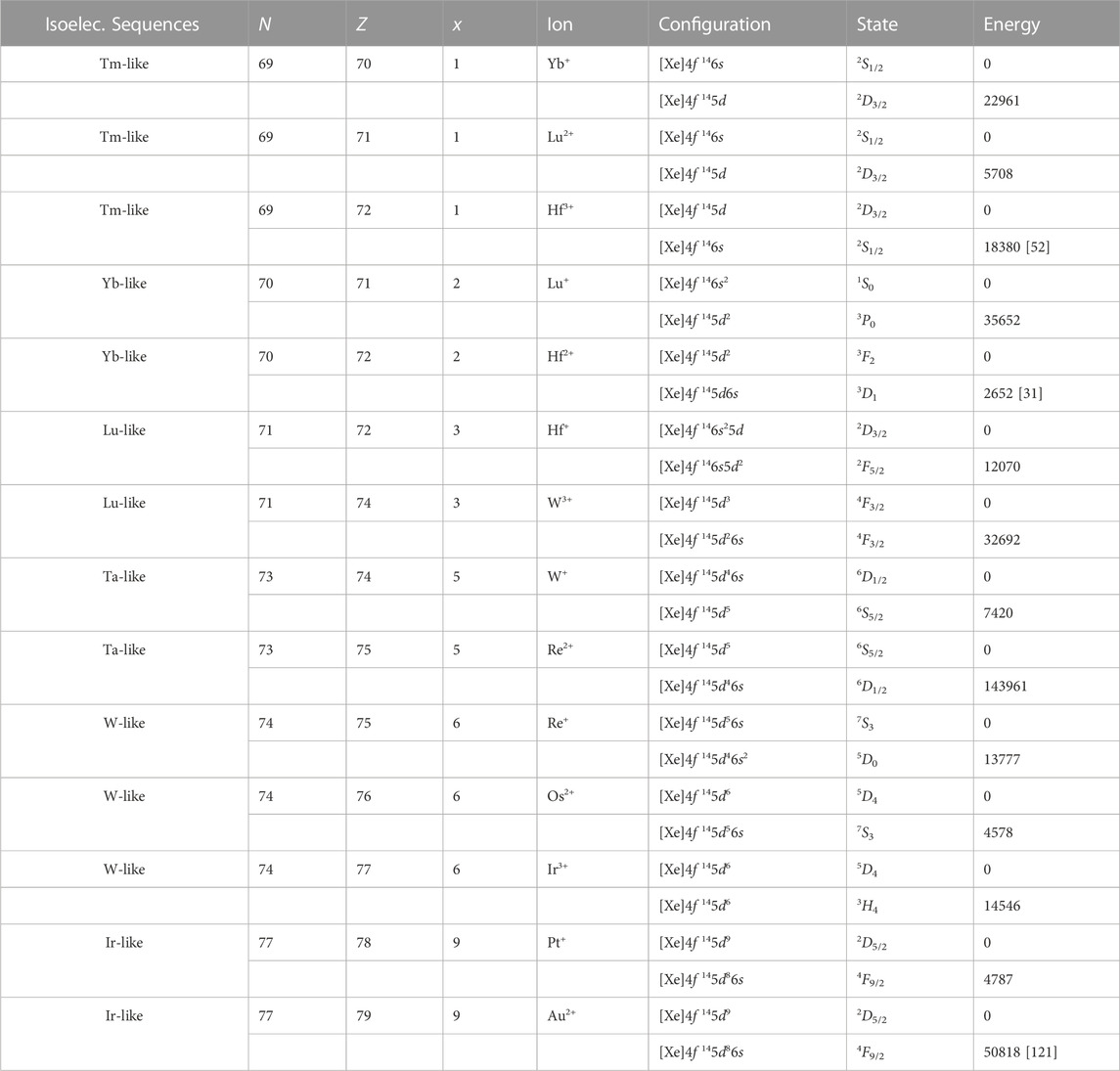
TABLE 8. The energy levels of some ions in the isoelectronic (Isoelec.) sequences of several sixth row transition metals, where N is the number of the electron, Z is the atomic number, and x is the number of valence electron. [Xe] ≡ 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰5s²5p⁶. The data is taken from the NIST database unless cited others. Units for all the values are in cm⁻¹.

As shown in Tables 6, Tables 7, Tables 8, the nd − (n + 1) s energy level-crossings happen often in the doubly-charged ions. In these doubly-charged ions, transition wavelengths between their ground and first excited states in these ions are within the optical range. Such transitions are accompanied by changes in the electronic angular momenta from the s to d orbitals. Thus, considering these HCIs as atomic clocks would offer substantial relativistic sensitivity coefficients to probe α variation. For example, The Ac²⁺, Zr²⁺, Hf²⁺, and Hg²⁺ has been suggested as suitable candidate for laboratory searches of space-time variation of α [31]. We find that many double charged HCI ions have similar transitions, such as the 3d² − 3d4s transition in Ti²⁺, the 3d³ − 3d²4s transition in V²⁺, the 4d³ − 4d²5s transition in Nb²⁺, the 5d⁵ − 5d⁴6s transition in Re²⁺, the 5d⁶ − 5d⁵6s transition in Os²⁺, and the 5d⁹ − 5d⁸6s transition in Au²⁺, which could be the promising HCIs for the study of possible temporal variation of α. The singly and triply charged ions also have some new interesting optical transitions, for example, Allehabi, et al. have demonstrated that the metastable excited state in Hf⁺ and Hf³⁺ may be good clock states having sufficiently long-lived upper states, insensitive to the external perturbations, and additional E1 cooling line available [52].

4.2.2 The 4f − 5s and 4f − 5p level crossings

The 4f − 5s orbital energy crossing frequently occurs in the isoelectronic sequences of the electronic configuration containing open-shelled 5s and 4f orbital. Table 9 lists some HCIs in such kinds of isoelectronic sequences. This type of HCIs usually has the large number of charge, larger than 10 in most cases. The Ag-, Cd-, In-, Sn-like HCIs containing one, two, three, and four valence electrons have been investigated by Safronova, et al [38–40]. When valence electrons are larger than 4, the electronic configuration becomes far more complicated. Therefore there is little data available for such kind of HCIs. Dzuba has investigated the energy levels of the I-like Ho¹⁴⁺ and Xe-like Er¹⁵⁺ with x = 6 and 7, which are proposed as candidates for an extremely accurate and stable optical atomic clock which is found to have large values of q and K suitable for the study of time variation of α. When x ≥ 12, there observed some HCIs having the 4f − 5s crossing in the hole states of the 5s and 4f shells, as listed in Table 9. For example, the Ir¹⁷⁺ ion has been proposed for the search of variation of α, and its hole state of 5s4f¹⁴ has extremely high values of q and K, indicating the hole states can dramatically enhance the sensitivity to α variation [30]. Nandy and Sahoo have also investigated the W¹³⁺, Ir¹⁶⁺ and Pt¹⁷⁺ HCIs with ground state configurations 4f¹³ as promising optical clock candidates to probe variation of α [124].

TABLE 9

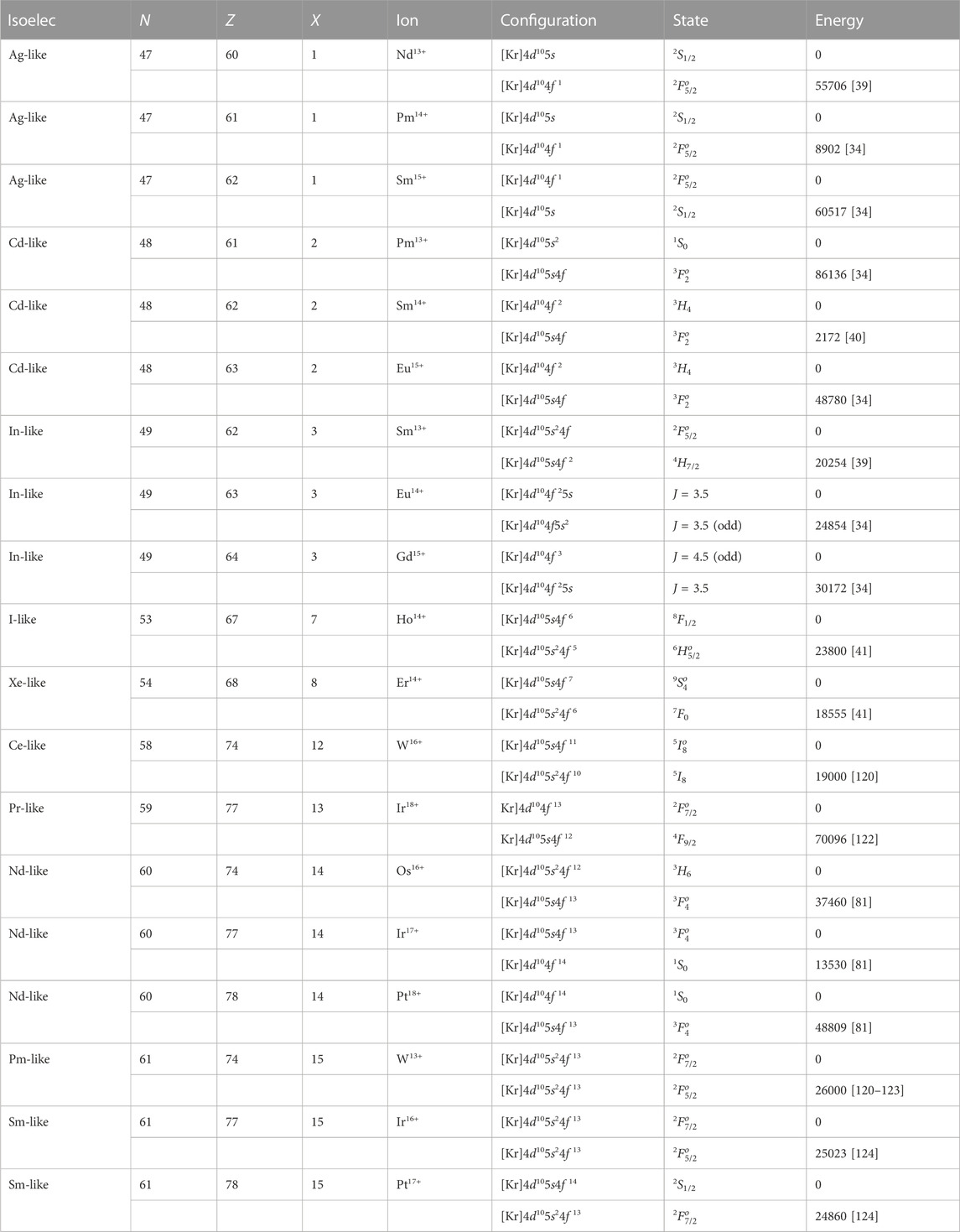
TABLE 9. The energy level of HCIs in the isoelectronic sequences containing the different number of 5s and 4f valence electrons x, where N is the number of the electron, Z is the atomic number. [Kr] ≡ 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶. Units for values are in cm⁻¹.

The 4f − 5p energy level-crossing occurs in the isoelectronic sequences containing the open-shelled 5p and 4f configurations, and this type of HCIs usually have mediated number of charge, around ten or lower. Table 10 lists some of these kinds of HCIs. Safronova et al. have proposed In-like Pr¹⁰⁺ and Sn-like Pr⁹⁺ and Nd¹⁰⁺ as the potential candidates for atomic clocks [38–40]. Berengnut et al. have also proposed Sn-like Pr⁹⁺ as a promising candidate for developing an extremely accurate atomic clock for the measurement of sensitivity to variation of α. Yu et al. have calculated the atomic energy levels of Sb-like Nd⁹⁺ and suggested Nd⁹⁺ as a potential candidate for making an atomic clock [50]. The In-, Sn-, and Sb-like HCIs with mediated number of charge contain one, two, and three valence electrons distributing on the 5p and 4f shells. However, accurate calculation of such systems also needs to take into two inner occupied 5s electrons, which makes multi-valent systems containing three to five valence electrons distributing on 11 orbitals of 5s, 5p, and 4f. Their complex electronic configurations make studying spectroscopic properties from theoretical and experimental viewpoints challenging. Due to the scarcity of data on energy level, isoelectronic sequences with x larger than 3 are not in Table 10. When x ≥ 14, there observed the hole state of 4f shell in some HCIs, for example W^(8–13)+ ions, as listed in 10. Their 4f- or 5p − excitation causes a lot of transitions with energies in the optical range. There has been greatly renewed interest in the spectral emission of tungsten from high-temperature plasma [116, 126, 128–132].

TABLE10

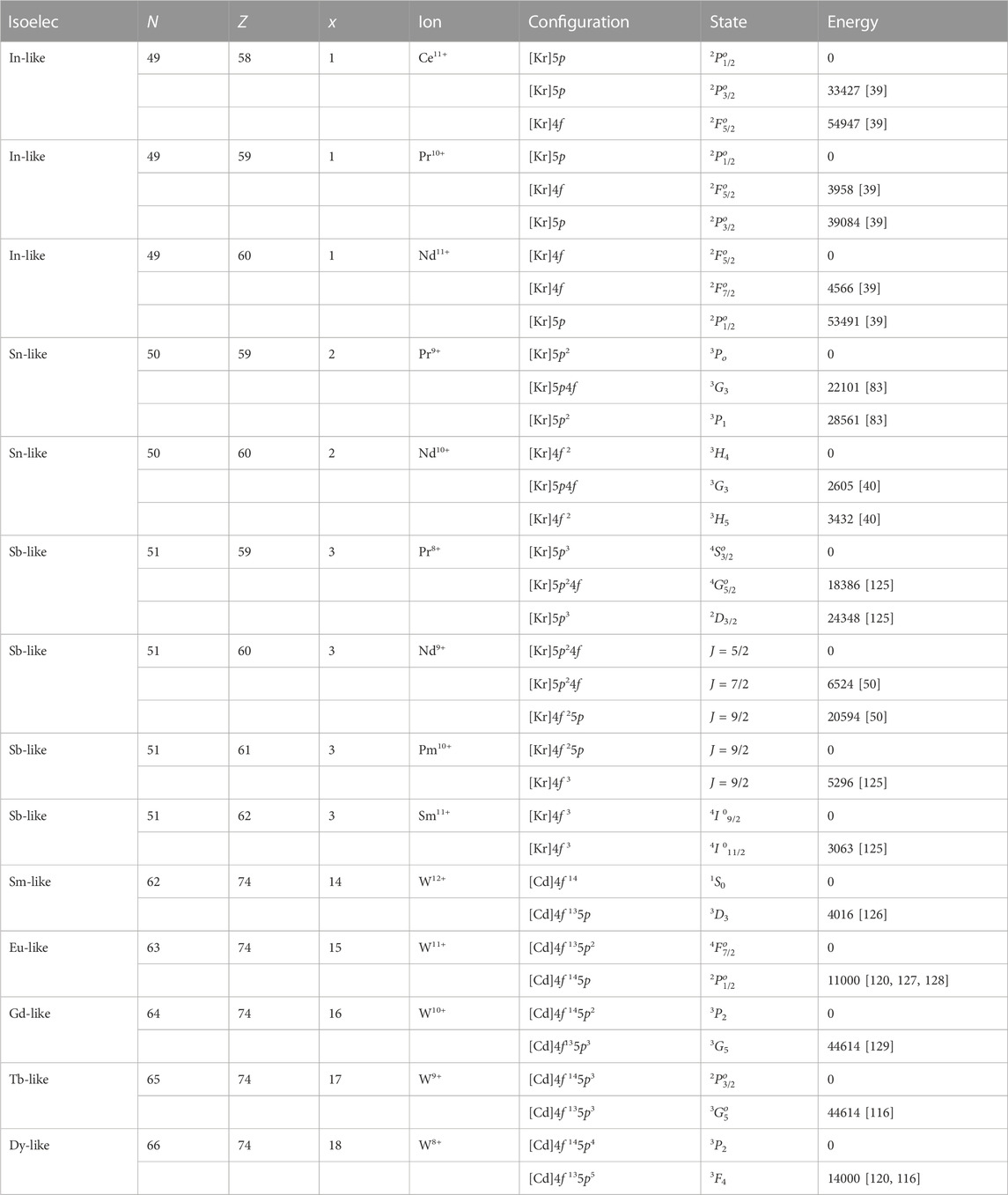
TABLE10. The energy level of HCIs in the isoelectronic sequences containing the different number of 5p and 4f valence electrons x, where N is the number of the electron, Z is the atomic number. [Kr] ≡ 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶ and [Cd] ≡ 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰5s². Units of all values are in cm⁻¹.

Tables 6, Tables 7, Tables 8, Tables 9, Tables 10 compile a series of HCIs that underline the orbital energy-crossings in their electronic configurations. Many of these HCIs show optical transitions between the ground and low-lying excited states. Although the exact values of q and K for these transitions are mostly absent in the literature, their values can be conjectured to be very large from the characterstics of the s − f and p − f inter-configuration transitions. Such features in atomic clocks are useful for probing α variation. It is, therefore, necessary to estimate energies and other spectroscopic properties of these relevant for estimating systematic errors if they are undertaken for atomic clocks.

5 Relativistic many-body methods

There is a great need to determine the energies and radiative properties of the HCIs to determine their suitability for atomic clocks. Again, their high-accuracy estimations are also essential for gauging the atomic clocks’ systematic effects. The required atomic data include energy level structures, atomic polarizabilities, hyperfine structure constants, Landé g_J factors, quadrupole moments, etc., which are unknown for many HCIs. For theoretical evaluation of these quantities, it is necessary to employ methods that can reliably estimate them. Though relativistic contributions from the Breit and quantum electrodynamics (QED) effects would be significant in the HCIs, Coulomb interactions still play decisive roles in accurately determining properties of the interested HCIs for finding their aptness to make atomic clocks. Thus, we adopt relativistic many-body methods that can estimate atomic properties with reasonable accuracy in HCIs, and corrections from the higher-order relativistic effects are estimated approximately wherever required. Again, it is impossible to employ a single many-body method to all the HCIs undertaken here for investigation due to their multi-valence electronic configurations. We choose a method that can be applied aptly in HCIs with a particular electronic configuration class. In this view, we have considered methods like the configuration interaction (CI) method, general active space configuration interaction (GASCI) method and Fock-space relativistic coupled-cluster (FS-RCC) theory in the present work. In all the methods, wave functions obtained using the Dirac-Hartree-Fock (DHF) method are considered the starting point. Correlation effects due to the residual Coulomb interactions are included through the many-body approaches.

5.1 Approximations in the Hamiltonian

To take into account the major relativistic effects and electron correlation effects in the HCIs, we first consider the Dirac-Coulomb (DC) Hamiltonian in our calculations which in atomic units (a.u.) is given by

$\begin{array}{ll}\hfill H^{DC}& =\sum _i\left[c{\mathit{\alpha }}_i\cdot {\mathbf{p}}_i+\left({\beta }_i-1\right)c^2+V_{\mathit{nuc}}\left(r_i\right)\right]+\sum _{i,j>i}\frac{1}{r_{ij}}\hfill \\ \hfill & =\sum _i{h}_i+\sum _{i,j>i}{g}_{ij},\hfill \end{array}(5)$

where the rest mass energies of the electrons are subtracted. In this expression c is the speed of light, V_nuc(r) is the nuclear potential and α = (α_x, α_y, α_z) and β are the 4 × 4 Dirac matrices with the components

${\alpha }_x=\left(\begin{array}{cc}\hfill 0_2\hfill & \hfill {\sigma }_x\hfill \\ \hfill {\sigma }_x\hfill & \hfill 0_2\hfill \end{array}\right),{\alpha }_y=\left(\begin{array}{cc}\hfill 0_2\hfill & \hfill {\sigma }_y\hfill \\ \hfill {\sigma }_y\hfill & \hfill 0_2\hfill \end{array}\right),{\alpha }_z=\left(\begin{array}{cc}\hfill 0_2\hfill & \hfill {\sigma }_z\hfill \\ \hfill {\sigma }_z\hfill & \hfill 0_2\hfill \end{array}\right)\text{and}\beta =\left(\begin{array}{cc}\hfill I\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I\hfill \end{array}\right),(6)$

for the identity matrix I and the Pauli spin matrices

${\sigma }_x=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),{\sigma }_y=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -i\hfill \\ \hfill i\hfill & \hfill 0\hfill \end{array}\right)\text{and}{\sigma }_z=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right).(7)$

In our calculations, we adopt either the Gaussian or Fermi nuclear charge distribution [133] to obtain the nuclear potentials of the heavier HCIs. The Gaussian nuclear charge distribution is defined by

$\rho \left(r\right)={\left(\frac{\eta }{\pi }\right)}^{\frac{3}{2}}{e}^{-\eta r^2}(8)$

with $\eta =\frac{3}{2}{R}_{\mathit{rms}}^{-2}$, where R_rms is the root mean square (rms) nuclear charge radius of the atomic nucleus. This leads to the expression for nuclear potential observed by an electron as

$V_{\mathit{nuc}}\left(r\right)=-\frac{Z}{r}erf\left(\sqrt{\eta }r\right).(9)$

In the Fermi nuclear charge distribution, it is given as

$\rho \left(r\right)=\frac{{\rho }_0}{1+e^{\left(r-b\right)/a}},(10)$

where ρ₀ is the normalization constant, b is the half-charge radius and a = 2.3/4 ln 3 is known as the skin thickness. We obtain the b value using the relation

$b=\sqrt{\frac{5}{3}{R}_{\mathit{rms}}^2-\frac{7}{3}{a}^2{\pi }^2}(11)$

and rms charge radius of a given nucleus with atomic mass A is estimated in fm by

$R_{\mathit{rms}}=0.836A^{1/3}+0.570.(12)$

The above expression gives the nuclear potential expression as

$V_{\mathit{nuc}}\left(r\right)=-\frac{Z}{\mathcal{N}r}\left\{\begin{array}{cc}\hfill \frac{1}{b}\left(\frac{3}{2}+\frac{a^2{\pi }^2}{2b^2}-\frac{r^2}{2b^2}+\frac{3a^2}{b^2}{P}_2^{+}\frac{6a^3}{b^{2}r}\left(S_3-P_3^{+}\right)\right)& \mathrm{f}\mathrm{o}\mathrm{r}{r}_i\le b\hfill \\ \hfill \frac{1}{r_i}\left(1+\frac{a62{\pi }^2}{b^2}-\frac{3a^{2}r}{b^3}{P}_2^{-}+\frac{6a^3}{b^3}\left(S_3-P_3^{-}\right)\right)& \mathrm{f}\mathrm{o}\mathrm{r}{r}_i>b,\hfill \end{array}\right.(13)$

where the factors are

$\mathcal{N}=1+\frac{a^2{\pi }^2}{b^2}+\frac{6a^3}{b^3}{S}_3\text{with}{S}_k=\sum _{l=1}^{\infty }\frac{{\left(-1\right)}^{l-1}}{l^k}{e}^{-lb/a}\text{and}{P}_k^{\pm }=\sum _{l=1}^{\infty }\frac{{\left(-1\right)}^{l-1}}{l^k}{e}^{\pm l\left(r-b\right)/a}.(14)$

Whenever necessary, we add the potential (V^B) due to the Breit interaction to the DC Hamiltonian to take into account the contribution from this higher-order relativistic effect and is given by

$V^B=-\sum _{j>i}\frac{\left[{\mathit{\alpha }}_i\cdot {\mathit{\alpha }}_j+\left({\mathit{\alpha }}_i\cdot {\widehat{\mathit{r}}}_{\mathbf{ij}}\right)\left({\mathit{\alpha }}_j\cdot {\widehat{\mathit{r}}}_{\mathbf{ij}}\right)\right]}{2r_{ij}},(15)$

where ${\widehat{\mathit{r}}}_{\mathbf{ij}}$ is the unit vector along the inter-electronic distance r_ij.

Similarly, contributions from the QED effects are estimated approximately by considering the lower-order vacuum polarization (VP) interaction (V_VP) and the self-energy (SE) interactions (V_SE) through the model potentials. We account for V_VP through the Uehling and Wichmann-Kroll potentials (V_VP = V^Uehl + V^WK), given by

$V^{\mathit{Uehl}}=-\frac{2}{3}\sum _i\frac{{\alpha }^2}{r_i}{\int }_0^{\infty }dxx{\rho }_n\left(x\right){\int }_1^{\infty }dt\sqrt{t^2-1}\left(\frac{1}{t^3}+\frac{1}{2t^5}\right)\left[e^{-2ct|r_i-x|}-e^{-2ct\left(r_i+x\right)}\right](16)$

and

$V^{WK}=\sum _i\frac{0.368Z^2}{9\pi c^3\left(1+{\left(1.62c{r}_i\right)}^4\right)}\rho \left(r_i\right),(17)$

respectively. The SE contribution V_SE is estimated by including two parts as

$V_{\mathrm{SE}}^{ef}=A_l\sum _i\frac{2\pi Z{\alpha }^3}{r_i}{I}_1^{ef}\left(r_i\right)-B_l\sum _i\frac{\alpha }{r_i}{I}_2^{ef}\left(r_i\right)(18)$

known as effective electric form factor part and

$\begin{array}{ll}\hfill V_{\mathrm{SE}}^{mg}& =-\sum _k\frac{i{\alpha }^3}{4}\mathit{\gamma }\cdot {\mathbf{\nabla }}_k\frac{1}{r_k}{\int }_0^{\infty }dxx{\rho }_n\left(x\right){\int }_1^{\infty }dt\frac{1}{t^3\sqrt{t^2-1}}\hfill \\ \hfill & \times \left[e^{-2ct|r_k-x|}-e^{-2ct\left(r_k+x\right)}-2ct\left(r_k+x-|r_k-x|\right)\right],\hfill \end{array}(19)$

known as the effective magnetic form factor part. In the above expressions, we use

$A_l=\left\{\begin{array}{c}0.074+0.35Z\alpha \text{for}l=\mathrm{0,1}\hfill \\ 0.056+0.05Z\alpha +0.195Z^2{\alpha }^2\text{for}l=2,\hfill \end{array}\right.(20)$

and

$B_l=\left\{\begin{array}{c}1.071-1.97x^2-2.128x^3+0.169x^4\text{for}l=\mathrm{0,1}\hfill \\ 0\text{for}l\ge 2.\hfill \end{array}\right.(21)$

The integrals are given by

$I_1^{ef}\left(r\right)={\int }_0^{\infty }dxx{\rho }_n\left(x\right)\left[\left(Z|r-x|+1\right)e^{-Z|r-x|}-\left(Z\left(r+x\right)+1\right)e^{-2ct\left(r+x\right)}\right](22)$

and

$\begin{array}{ll}{I}_2^{ef}\left(r\right)\hfill & ={\int }_0^{\infty }dxx{\rho }_n\left(x\right){\int }_1^{\infty }dt\frac{1}{\sqrt{t^2-1}}\left\{\left(1-\frac{1}{2t^2}\right)\left[\ln \left(t^2-1\right)+4\ln \left(\frac{1}{Z\alpha }+\frac{1}{2}\right)\right]-\frac{3}{2}+\frac{1}{t^2}\right\}\hfill \\ \hfill & \left\{\frac{\alpha }{t}\left[e^{-2ct|r-x|}-e^{-2ct\left(r+x\right)}\right]+2r_A{e}^{2r_{A}ct}\left[E_1\left(2ct\left(|r-x|+r_A\right)\right)-E_1\left(2ct\left(r+x+r_A\right)\right)\right]\right\}\hfill \end{array}(23)$

with the orbital quantum number l of the system, x = (Z − 80)α, r_A = 0.07Z²α³, and the exponential integral $E_1(r)={\int }_r^{\infty }ds{e}^{-s}/s$.

The atomic Hamiltonian given by Eq. 5 can be expressed in the second-quantization formalism as

$H^{DC}=\sum _{pq}{h}_q^p{a}_p^{+}{a}_q+\frac{1}{4}\sum _{\mathit{pqrs}}{V}_{qs}^{pr}{a}_p^{+}{a}_r^{+}{a}_s{a}_q,(24)$

where $h_q^p=⟨p|\widehat{h}|q⟩$ and $V_{qs}^{pr}=⟨pr|\widehat{g}|qs⟩-⟨pr|\widehat{g}|sq⟩$ with the indices {p, q, r, s} denote atomic orbitals. Due to the presence of two-body Coulomb (and also Breit and QED) interactions, it is not possible to obtain atomic wave functions of multi-electron systems exactly. In practice, it is dealt with by dividing the atomic Hamiltonian into an effective one-body term and residual interactions; i.e. H = H₀ + V_es. As mentioned earlier, the one-body part H₀ is constructed using the DHF method in this work while correlation contributions from V_es are included at different levels of approximations through various methods that are outlined briefly below.

5.2 CI and GASCI methods

The DHF method is a good starting point to construct the exact atomic wave functions in a many-electron system. The complete spectrum of single-particle solutions obtained from the DHF procedure constitutes a one-particle basis from which one may construct determinants that approximate the wave function for an atomic closed-shell system through an anti-symmetric Hartree-product (Slater determinant) of four-spinors

$\mathrm{\Phi }\left({\mathbf{r}}_{\mathbf{1}},{\mathbf{r}}_{\mathbf{2}},\dots ,{\mathbf{r}}_{\mathbf{N}}\right)=\mathbf{A}\left({\psi }_1\left({\mathbf{r}}_{\mathbf{1}}\right),{\psi }_2\left({\mathbf{r}}_{\mathbf{1}}\right),\dots ,{\psi }_N\left({\mathbf{r}}_{\mathbf{N}}\right)\right).(25)$

In the CI method, the exact wave function |Ψ⟩ of an atomic state (known as atomic state function (ASF)) is constructed by expressing it as a linear sum of all possible singly, doubly up to N-tuple excited Slater determinants (referred as configuration state functions (CSFs)) with respect to the DHF wave function (|Φ₀⟩). i.e.

$|\mathrm{\Psi }\rangle =C_0|{\mathrm{\Phi }}_0\rangle +\sum _I{C}_I|{\mathrm{\Phi }}_I\rangle +\sum _{II}|{\mathrm{\Phi }}_{II}\rangle +\cdots ,(26)$

where C_n with n = 0, I, II, ⋯ are the CSF mixing coefficients for the respective CSFs |Φ_n⟩. In the second-quantization form, we can express as [134].

$|\mathrm{\Psi }\rangle =\left(C_0+\sum _{ai}{c}_i^a{a}_a^{+}{a}_i+\sum _{a>b,i>j}{c}_{ij}^{ab}{a}_a^{+}{a}_b^{+}{a}_i{a}_j+\cdots \right)|{\mathrm{\Phi }}_0\rangle .(27)$

The second and the third terms within the brackets are the single and double excitations, respectively, expressed in terms of creation (a⁺) and annihilation (a) operators. The coefficients of Eq. 27 are obtained by solving

$\mathbf{H}\mathbf{C}=E_{\mathbf{CI}}\mathbf{C},(28)$

where H is the matrix of the atomic Hamiltonian and C is the matrix of the expansion coefficients. The diagonalization of the Hamiltonian H matrix gives the spectrum of exact eigenvalues E_CI for the system for a given basis set.

In practice, carrying out a full CI is impossible, so we have to choose only a small subset of determinants that carries most of the correlation energies. This is generally done by truncating the CI expansion. Usually, the singly and doubly excited configurations are retained and this truncated CI method is referred to as CISD, where ‘S’ and ‘D’ stand for the single and double excitations, respectively. Correlation energy that arises from the excitations from the single reference DHF determinant is often referred to as dynamic correlation energy. In many situations, multi-reference determinant states are considered to take into account static correlation effects by simultaneously exciting electrons from all the determinants [135]. In the CI approach, such a selection of reference is referred to as multi-reference CI (MRCI) method. This is more effective, and the diagonalization of Eq. 28 can converge faster.

A restricted active space CI (RASCI) method has been developed to account for both the dynamics and static correlations rigorously [136]. In the RASCI, the active orbital space is divided into three subspace: RAS1, RAS2, and RAS3. RAS1 is the occupied space in which at the most two electron holes are created; RAS3 is the unoccupied space that receives at most two electrons from RAS1 and eventually from RAS2; RAS2 is the current active space in which all the possible excitations are considered is formed by both the occupied and unoccupied orbitals. Better choice of reference wave functions can be made through the GASCI method [137–139]. The GASCI can be considered as the complete generalization of the RASCI method. In this method, the number of subspaces and the number of excited electrons can be arbitrary in contrast to the restriction on the number of the subspace and the number of the excited electrons having two in the RASCI method. So the approximation made to the wave function in the CI method can be improved through the inclusion of more core-valence and core-core correlation space.

To illustrate the application of the GASCI method, we take an example of the Ni¹²⁺ HCI and demonstrate how the CSFs are decided. We may consider its valence configuration 3p⁴ with the core occupation 1s²2s²2p⁶3s². The scheme of the GASCI employed for Ni¹²⁺ is shown in Table 11. Here, the correlated orbitals are divided into five subsets I-V, which correspond to the core (1s, 2s, 2p, and 3s), the valence (3p), and the rest (virtual) orbitals, receptively. The ‘minimal’ (min) and ‘maximal’ (max) number of electrons (min, max) in the I, II, and III types of space are (2, 4), (6, 8), and (10, 12), respectively. That is to say, only single and double excitations are allowed in core orbitals. When the valance orbitals 3p (space IV) are included, at most three electrons are allowed to excite out of the total core + valance space. According to this GASCI scheme, the possible excitations are 1) single or double excitations from the core with no excitation from the valence space; 2) single excitations from the core and single excitations from the valance space; 3) single excitations from the core and double excitations from the valance space; 4) double excitations from the core and single excitations from the valance space; and 5) no excitation from the core but singles, doubles and/or triple excitations from the valance space. Combining all of those possible occupations from the core, valence and virtual orbitals forms a CI space with about 7 × 10⁹ determinants in Ni¹²⁺, which includes the most dominant core-core, core-valence, and valence-valance correlations. This means that the GASCI scheme can design a complete and near-complete core and valence spaces based on the multi-reference configurations of CI method.

TABLE 11

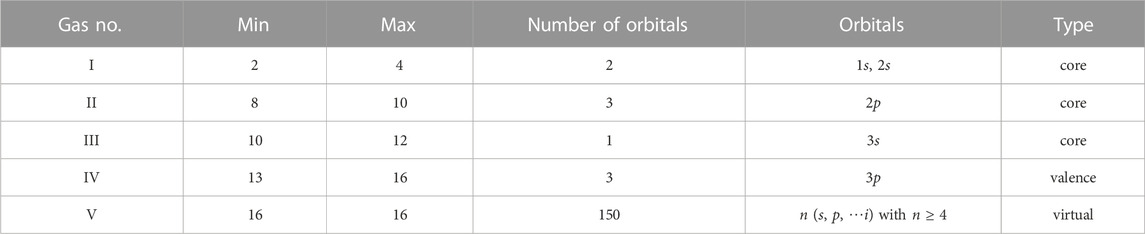
TABLE 11. Demonstration of GASCI scheme for Ni¹²⁺, where ‘min’ and ‘max’ denote the minimal and maximal number of accumulated electrons occupied in the respective core, valence, and virtual orbitals.

The GASCI method is well suited to apply to the multi-valence atomic systems having open-shell configurations in the p, d, and f shells. This method is also apt to employ to the HCIs exhibiting strong degeneracy among the energy levels due to level-crossings [50]. The GASCI can be employed using the relativistic quantum chemistry code package DIRAC [140, 141]. This method has been applied to calculate atomic properties of the Sb-like Nd⁹⁺ ion.

5.3 FS-RCC method

The FS-RCC method is an all-order perturbative method, and different contributions arising through the FS-RCC calculations can be understood through perturbative analysis. To understand this point, we start with the basic formulation of many-body perturbation theory to derive the expression for the ASF in the FS-RCC method. The FS-RCC method are well adaptive to the study of the single-particle or hole system, for example the B-, Al-, and Ga-like HCIs of one p valence and the W¹³⁺, Ir¹⁶⁺, and Pt¹⁸⁺ ions of one 4f hole.

The ASF |Ψ_v⟩ of an atomic system with a closed-core and a valence orbital v can be expressed by

$|{\mathrm{\Psi }}_v\rangle ={\mathrm{\Omega }}_v|{\mathrm{\Phi }}_v\rangle ,(29)$

where Ω_v and |Φ_v⟩ are referred to as the wave operator and the reference state respectively. For the computational simplicity we choose the working reference state as the DHF wave function |Φ_c⟩ for the closed core, then the actual reference state is constructed from it as $|{\mathrm{\Phi }}_v\rangle =a_v^{†}|{\mathrm{\Phi }}_c\rangle$ for the respective state with the valence orbital v.

Following the form of the reference states in our approach, Ω_v can now be divided as

${\mathrm{\Omega }}_v=1+{\chi }_c+{\chi }_v,(30)$

where χ_c and χ_v are responsible for carrying out the excitations from |Φ_c⟩ and |Φ_v⟩, respectively, due to the residual interaction V_r = H − H₀ for the DHF Hamiltonian H₀. In a perturbative series expansion, we can express as

${\chi }_c=\sum _k{\chi }_c^{\left(k\right)}\text{and}{\chi }_v=\sum _k{\chi }_v^{\left(k\right)},(31)$

where the superscript k refers to the number of times V_r is considered. The kth order amplitudes for the χ_c and χ_v operators are obtained by solving the equations

$\left[{\chi }_c^{\left(k\right)},H_0\right]P=Q{V}_r\left(1+{\chi }_c^{\left(k-1\right)}\right)P(32)$

and

$\begin{array}{ll}\hfill \left[{\chi }_v^{\left(k\right)},H_0\right]P& =Q{V}_r\left(1+{\chi }_c^{\left(k-1\right)}+{\chi }_v^{\left(k-1\right)}\right)P-\sum _{m=1}^{k-1}{\chi }_v^{\left(k-m\right)}\hfill \\ \hfill & \times P{V}_r\left(1+{\chi }_c^{\left(m-1\right)}+{\chi }_v^{\left(m-1\right)}\right)P,\hfill \end{array}(33)$

where the projection operators P = |Φ_c⟩⟨Φ_c| and Q = 1 − P describe the model space and the orthogonal space of the DHF Hamiltonian H₀ respectively. The energy of the state |Ψ_v⟩ is evaluated by using an effective Hamiltonian

$H_v^{\mathit{eff}}=P{a}_{v}H{\mathrm{\Omega }}_v{a}_v^{†}P.(34)$

Using the normal order Hamiltonian H_N = H − PHP in place of H in the above expression, the attachment energy of a state with the valence orbital v is evaluated.

The above formulation is generalized to all-orders in the FS-RCC method as

$|{\mathrm{\Psi }}_v\rangle \equiv {\mathrm{\Omega }}_v|{\mathrm{\Phi }}_v\rangle =e^T\left\{1+S_v\right\}|{\mathrm{\Phi }}_v\rangle (35)$

with χ_c = e^T − 1 and χ_v = e^TS_v − 1, where T and S_v are the CC excitation operators that excite electrons from the core and core along with the valence orbitals to the virtual space respectively. In the singles and doubles approximation (RCCSD method), it is given as

$T=T_1+T_2\text{and}{S}_v=S_{1v}+S_{2v}.(36)$

The amplitudes of these operators are evaluated using the equations

$⟨{\mathrm{\Phi }}_c^{\ast }|{\bar{H}}_N|{\mathrm{\Phi }}_c⟩=0(37)$

and

$\langle {\mathrm{\Phi }}_v^{*}|\left({\bar{H}}_N-\mathrm{\Delta }{E}_v\right)S_v|{\mathrm{\Phi }}_v\rangle =-\langle {\mathrm{\Phi }}_v^{*}|{\bar{H}}_N|{\mathrm{\Phi }}_v\rangle ,(38)$

where $|{\mathrm{\Phi }}_c^{*}\rangle$ and $|{\mathrm{\Phi }}_v^{*}\rangle$ is the excited state configurations for the DHF states |Φ_c⟩ and |Φ_v⟩ respectively and ${\bar{H}}_N={\left(H_N{e}^T\right)}_l$ with subscript l represents for the linked terms only. Here $\mathrm{\Delta }{E}_v=H_v^{\mathit{eff}}-H_c^{\mathit{eff}}$ is the attachment energy of the electron in the valence orbital v with $H_c^{\mathit{eff}}=PH\left(1+{\chi }_c\right)P$. Following Eq. 34, expression for ΔE_v is given by

$\mathrm{\Delta }{E}_v=⟨{\mathrm{\Phi }}_v|{\bar{H}}_N\left\{1+S_v\right\}|{\mathrm{\Phi }}_v⟩.(39)$

Contributions from important triply excited configurations can be included at the cost of RCCSD method computation by defining perturbative operators as

$T_3^{\mathit{pert}}=\frac{1}{6}\sum _{\mathit{abc,pqr}}\frac{{\left(H_N{T}_2\right)}_{\mathit{abc}}^{\mathit{pqr}}}{{ϵ}_a+{ϵ}_b+{ϵ}_c-{ϵ}_p-{ϵ}_q-{ϵ}_r},(40)$

and

$S_{3v}^{\mathit{pert}}=\frac{1}{4}\sum _{ab,pqr}\frac{{\left(H_N{T}_2+H_N{S}_{2v}\right)}_{\mathit{abv}}^{\mathit{pqr}}}{{ϵ}_a+{ϵ}_b+{ϵ}_v-{ϵ}_p-{ϵ}_q-{ϵ}_r},(41)$

where {a, b, c} and {p, q, r} represent the occupied and virtual orbitals, respectively, and ϵs are their corresponding DHF orbital energies.

The transition matrix element and the expectation value of any operator O between the fine-structure states |Ψ_i⟩ and |Ψ_f⟩ are calculated in terms of the expression

$\frac{\langle {\mathrm{\Psi }}_f|O|{\mathrm{\Psi }}_i\rangle }{\sqrt{\langle {\mathrm{\Psi }}_i|{\mathrm{\Psi }}_i\rangle \langle {\mathrm{\Psi }}_f|{\mathrm{\Psi }}_f\rangle }}=\frac{\langle {\mathrm{\Phi }}_f|{\tilde{O}}_{fi}|{\mathrm{\Phi }}_i\rangle }{\sqrt{\langle {\mathrm{\Phi }}_i|{\tilde{N}}_i|{\mathrm{\Phi }}_i\rangle \langle {\mathrm{\Phi }}_f|{\tilde{N}}_f|{\mathrm{\Phi }}_f\rangle }}(42)$

where ${\tilde{O}}_{fi}=\{1+S_f^{†}\}{e}^{T^{+}}O{e}^T\{1+S_i\}$ and ${\tilde{N}}_{k=f,i}=\{1+S_k^{+}\}{e}^{T^{+}}{e}^T\{1+S_k\}$. In the expectation value evaluation, it turns out to be |Ψ_i⟩ = |Ψ_f⟩. We adopt iterative procedures [142, 143] to account for contributions from both the non-terminating series $e^{T^{+}}O{e}^T$ and $e^{T^{+}}{e}^T$ that appear in Eq. 42.

6 Systematics of HCI clocks

One of the most important aspects of modern atomic clocks is to achieve very high-precision measurements such that they can be applied for probing fundamental physics, including the variation of α. Thus, systematic effects observed in an experiment play essential roles in deciding whether a transition frequency measurement in an atomic system is suitable for undertaking the task. From this point of view, it is imperative to determine the significance of some of the noted systematics that needs to be analyzed in atomic systems before considering them in the experiments. The major systematics responsible for deciding an HCI clock’s accuracy is Stark shifts due to lasers, BBR shifts, thermal radiation shifts, magnetic field shifts, motion-induced shifts, micromotion shifts, collisional shifts, etc., to cite a few. These systematics are also commonly seen in the neutral atom and singly charged ion-based atomic clocks. Determining each of these effects would require performing separate experiments. However, as discussed earlier, they can be estimated quite accurately by employing potential relativistic many-body methods. In fact, prior theoretical studies can also guide the experimental to decide about the conditions like the ac and dc electric field strengths, gradient, orientation, and polarization of the quantized field, etc., in an atomic clock experiment. Though the general perception is that HCIs can have small systematics on the ground that their orbitals are very much contracted, in some cases, one of the systematics can be too large due to either degeneracy of the states or other factors. Therefore, it is essential to analyze the above systematics a prior by employing reliable many-body methods before a HCI is undertaken in the experiment to achieve clock frequency measurement below 10⁻¹⁹ level. Here we discuss the formulations of some of the aforementioned systems and how they are determined theoretically. Other systematics, such as the motional and collisional shifts, are non-trivial to estimate theoretically and depend on environmental conditions and are not discussed here. Still, they can be controlled well by utilizing currently available well-advanced ion trap techniques [12, 144–147].

6.1 Electric quadrupole shift

One of the most important and dominating systematic shifts in an atomic clock experiment is the electric quadrupole shift caused due to the gradient of the electric field (∇E) experienced by the atomic states of the clock transition during the measurement. This can be estimated by calculating the expectation value of the corresponding interaction Hamiltonian H_Q = −∇E ⋅Θ(γ, K) as

$\mathrm{\Delta }{E}_{\mathit{Quad}}=⟨\gamma K,M_K=K|H_Q|\gamma K,M_K=K⟩,(43)$

where K is the angular momentum of the state with its component M_K, γ represents for other quantum numbers such as parity and Θ(γ, K) is known as quadrupole moment, which is the expectation value of the electric quadrupole operator $\mathrm{\Theta }=\frac{e}{2}(3z^2-r^2)$, of the state. Using the Wigner-Eckart theorem. The electric quadrupole moment can be written as

$\begin{array}{ll}\hfill \mathbf{\Theta }\left(\gamma ,K\right)& =\langle \gamma KK|\mathrm{\Theta }|\gamma KK\rangle \hfill \\ \hfill & =\left(\begin{array}{ccc}\hfill K\hfill & \hfill 2\hfill & \hfill K\hfill \\ \hfill -K\hfill & \hfill 0\hfill & \hfill K\hfill \end{array}\right)\langle \gamma K\Vert \mathbf{\Theta }\Vert \gamma K\rangle .\hfill \end{array}(44)$

For the hyperfine level, K ≡ F, the quadrupole shift can be expressed as

$E_{\mathit{Quad}}\left(\gamma JF{M}_F\right)=-K_1{K}_2\mathrm{\Theta }\left(\gamma ,J\right),(45)$

where

$K_1=\frac{2A_E\left[3M_F^2-F\left(F+1\right)\right]}{\sqrt{\left(2F+3\right)\left(2F+2\right)\left(2F+1\right)2F\left(2F-1\right)}}(46)$

and

$K_2={\left(-1\right)}^{I+J+F}\left(2F+1\right)\left\{\begin{array}{ccc}\hfill J\hfill & \hfill 2\hfill & \hfill J\hfill \\ \hfill F\hfill & \hfill I\hfill & \hfill F\hfill \end{array}\right\}{\left(\begin{array}{ccc}\hfill J\hfill & \hfill 2\hfill & \hfill J\hfill \\ \hfill -J\hfill & \hfill 0\hfill & \hfill J\hfill \end{array}\right)}^{-1},(47)$

for A_E representing the strength of the gradient of the applied electric field. According to the angular momentum selection rules for the above expression, ΔE_Quad will be zero for the states with J = 1/2 and J = 0. The expression in Eq. 47 ensures that quadrupole shifts in any of the hyperfine levels of the J = 1/2, 0 state is zero. However, a finite electric quadrupole shift still exists for those states of J with values other than 0 and 1/2. In such cases, it is possible to design experimental schemes to cancel out the electric quadrupole shift by choosing appropriate hyperfine levels or averaging out the measurements. For those ions that do not have a proper combination of F and M_F values for the zero quadrupole shift, experimental techniques can be adopted like averaging the clock frequencies measured in the three orthogonal directions of the quantizing external field to suppress the electric quadrupole shift down to the limit below 10⁻¹⁹ level [148, 149].

6.2 Quadratic stark shift

The quadratic Stark shift of a level level (γ, J, F, M_F) with component M_F can be evaluated by

$\begin{array}{ll}\hfill E_{\mathit{Stark}}\left(\gamma ,J,F,M_F\right)& =-\frac{1}{2}\alpha \left(\gamma ,J,F\right){\mathcal{E}}^2\hfill \\ \hfill & =-\frac{1}{2}{\alpha }^{\left(0\right)}\left(\gamma ,J,F\right){\mathcal{E}}_z^2-\frac{1}{4}{\alpha }^{\left(2\right)}\left(\gamma ,J,F\right)\frac{\left[3M_F^2-F\left(F+1\right)\right]}{F\left(2F-1\right)}\left(3{\mathcal{E}}_z^2-{\mathcal{E}}^2\right),\hfill \end{array}(48)$

where $\mathcal{E}$ and ${\mathcal{E}}_z$ are the total strength and strength in the z-direction of the applied electric field, α⁽⁰⁾(γ, J, F) and α⁽²⁾(γ, J, F) are the scalar and tensor components of the total polarizability α(γ, J, F) of the hyperfine level. These quantities can be related to their corresponding values in the atomic state as [148].

${\alpha }^{\left(0\right)}\left(\gamma ,J,F\right)={\alpha }^{\left(0\right)}\left(\gamma ,J\right)(49)$

and

$\begin{array}{ll}\hfill {\alpha }^{\left(2\right)}\left(\gamma ,J,F\right)& ={\left(-1\right)}^{I+J+F}\left\{\begin{array}{ccc}\hfill F\hfill & \hfill J\hfill & \hfill I\hfill \\ \hfill J\hfill & \hfill F\hfill & \hfill 2\hfill \end{array}\right\}{\alpha }^{\left(2\right)}\left(\gamma ,J\right)\hfill \\ \hfill & \times {\left[\frac{F\left(2F-1\right)\left(2F+1\right)\left(2J+3\right)\left(2J+1\right)\left(J+1\right)}{\left(2F+3\right)\left(F+1\right)J\left(2J-1\right)}\right]}^{1/2}.\hfill \end{array}(50)$

The differential values of α⁽⁰⁾ and α⁽²⁾ in clock transitions of HCIs are usually very small compared to the typical values obtained in the neutral atom or singly charged ion clocks. For example, for a typical value of electric field strength E = 10 V/m, the differential Stark shift for most previously proposed HCIs can be estimated using the above relation to be far below 10⁻¹⁹ level.

6.3 BBR shift

The BBR shift of hyperfine F level can be estimated using the expression

$\begin{array}{ll}\hfill E_{\mathit{BBR}}^{E1}& =-\frac{1}{2}{\left(831.9V/m\right)}^2{\left[\frac{T\left(K\right)}{300}\right]}^4{\alpha }^{\left(0\right)}\left(\gamma ,J,F\right)\hfill \\ \hfill & =-\frac{1}{2}{\left(831.9V/m\right)}^2{\left[\frac{T\left(K\right)}{300}\right]}^4{\alpha }^{\left(0\right)}\left(\gamma ,J\right),\hfill \end{array}(51)$

where T in K is the temperature at which the experiment is to be conducted. Using the scalar polarizabilities of the interesting clock states, the BBR shift can be estimated. It can be noticed that BBR shifts for atomic states and their hyperfine levels are the same. The environmental temperature in the HCI clock is generally far below the room temperature. In this situation, the BBR shifts are not the major limiting factors for the HCI clocks.

6.4 Zeeman shift

The linear Zeeman shifts in the clock transitions can be avoided by selecting F = 0 hyperfine levels wherever possible, else M_F = 0 sublevels of finite F hyperfine levels. For the finite F levels with non-zero M_F sublevel, the linear Zeeman shift can also be removed technically by alternating π-polarized transitions with extreme angular momentum states with two opposite sublevels (e.g. M_F = ±2) during the measurements [12]. However, it is not possible to get rid-off the second-order Zeeman shifts in such situations and they would provide the dominant uncertainties due to the Zeeman effects. The second-order Zeeman shift of a hyperfine level F with sublevel M_F due to magnetic field strength $\mathcal{B}$ is given by [150].

$E_{\mathit{Zeem}}^2={\beta }_{\mathit{Zeem}}\left(\gamma ,J,F,M_F\right){\mathcal{B}}^2,(52)$

where

${\beta }_{\mathit{Zeem}}\left(\gamma ,J,F,M_F\right)=-\frac{{\left({\mu }_B{g}_J\right)}^2}{\hslash }\sum _{F^{\prime }}\frac{|⟨F^{\prime }{M}_F|J_z|F{M}_F⟩{|}^2}{E_{F^{\prime }}-E_F},(53)$

with J_z denoting the z-component of J, E_F is the hyperfine energy level and F′ corresponds to all possible intermediate hyperfine levels. The hyperfine energy level is given by [151].

$E_F=\frac{1}{2}{A}_{\mathit{hyf}}C+B_{\mathit{hyf}}\frac{\frac{3}{2}C\left(C+1\right)-2I\left(I+1\right)J\left(J+1\right)}{2I\left(2I-1\right)2J\left(2J-1\right)},(54)$

where C = F(F + 1) − I(I + 1) − J (J + 1). The E_F values can be determined using the hyperfine structure constants A_hyf and B_hyf. The angular momentum matrix element is given by

$|⟨F^{\prime }{M}_{F^{\prime }}|J_z|F{M}_F⟩{|}^2=J\left(J+1\right)\left(2J+1\right)\left(2F+1\right)\left(2F^{\prime }+1\right){\left(\begin{array}{ccc}\hfill F\hfill & \hfill 1\hfill & \hfill F^{\prime }\hfill \\ \hfill -M_F\hfill & \hfill 0\hfill & \hfill M_F\hfill \end{array}\right)}^2{\left\{\begin{array}{ccc}\hfill J\hfill & \hfill F\hfill & \hfill I\hfill \\ \hfill F^{\prime }\hfill & \hfill J\hfill & \hfill 1\hfill \end{array}\right\}}^2.(55)$

Thus, β_Zeem (γ, J, F, M_F) of a hyperfine level can be determined if Landé g_J factor of the atomic state is known. For a given typical experimental condition, $\mathcal{B}$ value can be decided suitably to estimate the second-order Zeeman shift. It is, in principle, possible to control the strength of the magnetic field in experiments to reduce uncertainties due to the Zeeman shifts to achieve the clock frequency measurements to the intended level of precision.

7 Summary

A new generation of atomic clocks that would provide ultra-precise clock frequency measurements is highly required to probe many subtle effects supporting physics beyond the Standard Model of particle physics. Atomic clocks based on highly charged ions, having a high sensitivity to variation of α and extremely low sensitivity to external perturbations, are understood to possess such potentials.

In the past decade, many HCIs have been proposed as candidates for making an ultra-precise atomic clock, which has highly stable laser-accessible clock transition, enhanced sensitivity to variation of α, and advantageous atomic properties to inhibit external perturbations. Based on two basic rules that outline the M1 and E2 forbidden transition in fine-structure splittings and the higher order forbidden transition in complex configuration accompanied with orbital crossing, a shortlist of HCI clock candidates are summarized, which includes Ar¹³⁺, Ni¹²⁺, Ba⁴⁺, Pb²⁺, Ir¹⁷⁺, Cf¹⁵⁻¹⁷⁺, Nd¹³, Sm¹⁵⁺, Pr⁹⁺, Nd⁹⁺, Ho¹⁴⁺, etc., The first atomic clock based on Ar¹³⁺ has been realized now and reached 10⁻¹⁷ frequency uncertainty at the moment. The other ions aside from Ar¹³⁺ can offer better frequency stability and higher sensitivity to variation of α, indicating a new possibility for making atomic clocks. These discussions would help understand the merits and dis-merits of those HCIs and also guide seeking new highly charged ions candidates for clock and applications in searching for the variation of α.

Knowledge of spectroscopic data essential to analyze the feasibility of considering a highly charged ion for an atomic clock experiment is currently limited. In order to realize those proposed HCI clocks, more efforts are needed, including more accurate data prediction for energies that help identify clock transition lines and various atomic properties needed for a full assessment of the systematic shifts. High-accuracy relativistic many-body methods are employed to fulfil such tasks by using variants of relativistic configuration and coupled-cluster methods. The challenges are the complete treatment of the complex electron correlation often met in strongly open 4f-shelled configurations mixed with the 5s and 5p valence electrons. Rigorous treatment contributions from QED in fine structure splitting require accurate determination of energies and transition probabilities.

The proposed HCIs are the prospective candidates who offer the most precise frequency standards. With theoretical and experimental progress, the atomic clock based on new HCI candidates will lead to ideal platforms to probe temporal variation of α. Upon the fruitful accomplishment of such clocks, they can promote other high-precision experiments and invoke new exciting avenues for researching fundamental physics.

Author contributions

Y-MY and BS contribute equally to this work and share the first authorship. B-bS contributed to the part contents of the CI method as well as the relativistic effects and level-crossings in HCIs.

Funding

This work is supported by The National Key Research and Development Program of China (2021YFA1402104), the National Natural Science Foundation of China under Grant No. 11874064, and Project supported by the Space Application System of China Manned Space Program.

Acknowledgments

BS would like to acknowledge use of Vikram-100 HPC of Physical Research Laboratory (PRL), Ahmedabad.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lodewyck J, Bilicki S, Bookjans E, Robyr JL, Shi CY, Vallet G, et al. Optical to microwave clock frequency ratios with a nearly continuous strontium optical lattice clock. Metrologia (2016) 53(4):1123–30. doi:10.1088/0026-1394/53/4/1123

CrossRef Full Text | Google Scholar

2. Riehle F, Gill P, Arias F, Robertsson L. The CIPM list of recommended frequency standard values: Guidelines and procedures. Metrologia (2018) 55(2):188–200. doi:10.1088/1681-7575/aaa302

CrossRef Full Text | Google Scholar

3.Boulder Atomic Clock Optical Network (BACON) Collaboration. Frequency ratio measurements at 18-digit accuracy using an optical clock network. Nature (2021) 591(7851):564–9. doi:10.1038/s41586-021-03253-4

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Schioppo M, Brown RC, McGrew WF, Hinkley N, Fasano RJ, Beloy K, et al. Ultrastable optical clock with two cold-atom ensembles. Nat Photon (2016) 11(1):48–52. doi:10.1038/nphoton.2016.231

CrossRef Full Text | Google Scholar

5. McGrew WF, Zhang X, Fasano RJ, Schaffer SA, Beloy K, Nicolodi D, et al. Atomic clock performance enabling geodesy below the centimetre level Atomic clock performance enabling geodesy below the centimetre level. Nature (2018) 564(7734):87–90. doi:10.1038/s41586-018-0738-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Takano T, Takamoto M, Ushijima I, Ohmae N, Akatsuka T, Yamaguchi A, et al. Geopotential measurements with synchronously linked optical lattice clocks. Nat Photon (2016) 10(10):662–6. doi:10.1038/nphoton.2016.159

CrossRef Full Text | Google Scholar

7. Oelker E, Hutson RB, Kennedy CJ, Sonderhouse L, Bothwell T, Goban A, et al. Demonstration of 4.8 × 10¹⁷ stability at 1s for two independent optical clocks. Nat Photon (2019) 13(10):714–9. doi:10.1038/s41566-019-0493-4

CrossRef Full Text | Google Scholar

8. Huntemann N, Sanner C, Lipphardt B, Tamm C, Peik E. Single-ion atomic clock with 3 × 10⁻¹⁸ systematic uncertainty. Phys Rev Lett (2016) 116(6):063001. doi:10.1103/physrevlett.116.063001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Huang Y, Zhang BL, Zeng MY, Hao YM, Ma ZX, Zhang HQ, et al. Liquid-nitrogen-cooled Ca⁺ optical clock with systematic uncertainty of 3 × 10⁻¹⁸. Phys Rev Appl (2022) 17(3):034041. doi:10.1103/physrevapplied.17.034041

CrossRef Full Text | Google Scholar

10. Safronova MS, Budker D, DeMille D, Kimball DFJ, Derevianko A, Clark CW. Search for new physics with atoms and molecules. Rev Mod Phys (2018) 90(2):025008. doi:10.1103/revmodphys.90.025008

CrossRef Full Text | Google Scholar

11. Flambaum VV, Dzuba VA. Search for variation of the fundamental constants in atomic, molecular, and nuclear spectra. Can J Phys (2009) 87(1):25–33. doi:10.1139/p08-072

CrossRef Full Text | Google Scholar

12. Rosenband T, Hume DB, Schmidt PO, Chou CW, Brusch A, Lorini L, et al. Frequency ratio of Al⁺ and Hg⁺ single-ion optical clocks metrology at the 17th decimal place. Science (2008) 319(5871):1808–12. doi:10.1126/science.1154622

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lange R, Huntemann N, Rahm JM, Sanner C, Shao H, Lipphardt B, et al. Improved limits for violations of local position invariance from atomic clock comparisons. Phys Rev Lett (2021) 126(1):011102. doi:10.1103/physrevlett.126.011102

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Peik E, Zimmermann K, Okhapkin M, Tamm C. Prospects for a nuclear optical frequency standard based on thorium-229. In: L Maleki, editor. Proceedings of the seventh symposium on frequency standards and metrology. Singapore: World Scientific (2009). p. 532–8.

CrossRef Full Text | Google Scholar

15. Campbell CJ, Radnaev AG, Kuzmich A, Dzuba VA, Flambaum VV, Derevianko A. Single-ion nuclear clock for metrology at the 19th decimal place. Phys Rev Lett (2012) 108:120802. doi:10.1103/physrevlett.108.120802

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wense L, Seiferle B, Laatiaoui M, Neumayr JB, Maier H, Wirth H, et al. Direct detection of the ²²⁹Th nuclear clock transition. Nature (2016) 553:47–51. doi:10.1038/nature17669

CrossRef Full Text | Google Scholar

17. Seiferle B, Wense L, Bilous PV, Amersdorffer I, Lemell C, Libisch F, et al. Energy of the ²²⁹Th nuclear clock transition. Nature (2019) 573:243–6. doi:10.1038/s41586-019-1533-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sikorsky T, Geist J, Hengstler D, Kempf S, Gastaldo L, Enss C, et al. Measurement of the ²²⁹Th isomer energy with a magnetic microcalorimeter. Phys Rev Lett (2020) 125:142503. doi:10.1103/physrevlett.125.142503

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Beeks K, Sikorsky T, Schumm T, Thielking J, Okhapkin MV, Peik E. The thorium-229 low-energy isomer and the nuclear clock. Nat Rev (2021) 3(238):238–48. doi:10.1038/s42254-021-00286-6

CrossRef Full Text | Google Scholar

20. Flambaum VV. Enhanced effect of temporal variation of the fine structure constant and the strong interaction in ²²⁹Th. Phys Rev Lett (2006) 97:092502. doi:10.1103/physrevlett.97.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Berengut JC, Dzuba VA, Flambaum VV, Porsev SG. Proposed experimental method to determine α sensitivity of splitting between ground and 7.6 ev isomeric states in ²²⁹Th. Phys Rev Lett (2009) 102:210801. doi:10.1103/physrevlett.102.210801

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fadeev P, Berengut JC, Flambaum VV. Sensitivity of ²²⁹Th nuclear clock transition to variation of the fine-structure constant. Phys Rev A (2020) 102:052833. doi:10.1103/physreva.102.052833

CrossRef Full Text | Google Scholar

23. Fadeev P, Berengut JC, Flambaum VV. Effects of variation of the fine structure constant α and quark mass m_q in Mössbauer nuclear transitions. Phys Rev C (2022) 105:L051303. doi:10.1103/physrevc.105.l051303

CrossRef Full Text | Google Scholar

24. Kozlov MG, Safronova MS, Crespo López-Urrutia JR, Schmidt PO. Highly charged ions: Optical clocks and applications in fundamental physics. Rev Mod Phys (2018) 90(4):045005. doi:10.1103/RevModPhys.90.045005

CrossRef Full Text | Google Scholar

25. Raymond JC. Highly charged ions in astrophysics. MA: Physics of Highly-Ionized Atoms (1989).

Google Scholar

26. Gillaspy JD. Highly charged ions. J Phys B: Mol Opt Phys (2001) 34(19):R93–R130. doi:10.1088/0953-4075/34/19/201

CrossRef Full Text | Google Scholar

27. Prochaska JX, Howk JC, Wolfe AM. The elemental abundance pattern in a galaxy at z=2.626. Nature (2003) 423(6935):57–9. doi:10.1038/nature01524

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Webb JK, King JA, Murphy MT, Flambaum VV, Carswell RF, Bainbridge MB. Indications of a spatial variation of the fine structure constant. Phys Rev Lett (2011) 107(19):191101. doi:10.1103/physrevlett.107.191101

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Berengut JC, Dzuba VA, Flambaum VV. Enhanced laboratory sensitivity to variation of the fine-structure constant using highly charged ions. Phys Rev Lett (2010) 105(12):120801. doi:10.1103/physrevlett.105.120801

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Berengut JC, Dzuba VA, Flambaum VV, Ong A. Electron-hole transitions in multiply charged ions for precision laser spectroscopy and searching for variations in α. Phys Rev Lett (2011) 106(21):210802. doi:10.1103/physrevlett.106.210802

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Berengut JC, Dzuba VA, Flambaum VV. Transitions in Zr, Hf, Ta, W, Re, Hg, Ac, and U ions with high sensitivity to variation of the fine-structure constant. Phys Rev A (2011) 84(5):054501. doi:10.1103/physreva.84.054501

CrossRef Full Text | Google Scholar

32. Berengut JC, Dzuba VA, Flambaum VV, Ong A. Optical transitions in highly charged californium ions with high sensitivity to variation of the fine-structure constant. Phys Rev Lett (2012) 109(7):070802. doi:10.1103/physrevlett.109.070802

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Berengut JC, Flambaum VV. Manifestations of a spatial variation of fundamental constants in atomic and nuclear clocks, Oklo, meteorites, and cosmological phenomena. Euro Lett (2000) 97(2):20006. doi:10.1209/0295-5075/97/20006

CrossRef Full Text | Google Scholar

34. Berengut JC, Dzuba VA, Flambaum VV, Ong A. Highly charged ions withE1,M1, andE2 transitions within laser range. Phys Rev A (2012) 86(2):022517. doi:10.1103/physreva.86.022517

CrossRef Full Text | Google Scholar

35. Dzuba VA, Derevianko A, Flambaum VV. High-precision atomic clocks with highly charged ions: Nuclear-spin-zero f¹²-shell ions. Phys Rev A (2012) 86(5):054501. doi:10.1103/physreva.86.054501

CrossRef Full Text | Google Scholar

36. Dzuba VA, Derenvianko A, Flambaum VV. Ion clock and search for the variation of the fine-structure constant using optical transitions in Nd¹³⁺ and Sm¹⁵⁺. Phys Rev A (2012) 86(2):054502. doi:10.1103/physreva.86.054502

CrossRef Full Text | Google Scholar

37. Yudin VI, Taichenachev AV, Derevianko A. Magnetic-dipole transitions in highly charged ions as a basis of ultraprecise optical clocks. Phys Rev Lett (2014) 113(23):233003. doi:10.1103/physrevlett.113.233003

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Safronova MS, Dzuba VA, Flambaum VV, Safronova UI, Porsev SG, Kozlov MG. Highly charged ions for atomic clocks and quantum information, and search for α variation. Phys Rev Lett (2014) 113(3):030801. doi:10.1103/physrevlett.113.030801

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Safronova MS, Dzuba VA, Flambaum VV, Safronova UI, Porsev SG, Kozlov MG. Highly charged Ag-like and In-like ions for the development of atomic clocks and the search for α variation. Phys Rev A (2014) 90(4):042513. doi:10.1103/physreva.90.042513

CrossRef Full Text | Google Scholar

40. Safronova MS, Dzuba VA, Flambaum VV, Safronova UI, Porsev SG, Kozlov MG. Atomic properties of Cd-like and Sn-like ions for the development of frequency standards and search for the variation of the fine-structure constant. Phys Rev A (2014) 90(5):052509. doi:10.1103/physreva.90.052509

CrossRef Full Text | Google Scholar

41. Dzuba VA, Flambaum VV, Katori H. Optical clock sensitive to variations of the fine-structure constant based on the Ho¹⁴⁺ ion. Phys Rev A (2015) 91(2):022119. doi:10.1103/physreva.91.022119

CrossRef Full Text | Google Scholar

42. Dzuba VA, Flambaum VV. Highly charged ions for atomic clocks and search for variation of the fine structure constant. Hyperfine Interact (2015) 79–86. doi:10.1007/s10751-015-1166-4

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Dzuba VA, Safronova MS, Safronova UI, Flambaum VV. Actinide ions for testing the spatial α-variation hypothesis. Phys Rev A (2015) 92:060502. doi:10.1103/physreva.92.060502

CrossRef Full Text | Google Scholar

44. Yu YM, Sahoo BK. Scrutinizing Al-like ⁵¹V¹⁰⁺, ⁵³Cr¹¹⁺, ⁵⁵Mn¹²⁺, ⁵⁷Fe¹³⁺, ⁵⁹Co¹⁴⁺, ⁶¹Ni¹⁵⁺, and ⁶³Cu¹⁶⁺ ions for atomic clocks with uncertainties below the 10⁻¹⁹ level. Phys Rev A (2016) 94(6):062502. doi:10.1103/PhysRevA.94.062502

CrossRef Full Text | Google Scholar

45. Yu YM, Sahoo BK. Selected highly charged ions as prospective candidates for optical clocks with quality factors larger than 10¹⁵. Phys Rev A (2018) 97:041403. doi:10.1103/physreva.97.041403

CrossRef Full Text | Google Scholar

46. Yu YM, Sahoo BK. Investigating ground-state fine-structure properties to explore suitability of boronlike S¹¹⁺-K¹⁴⁺ and galliumlike Nb¹⁰⁺-Ru¹³⁺ ions as possible atomic clocks. Phys Rev A (2019) 99(2):022513. doi:10.1103/physreva.99.022513

CrossRef Full Text | Google Scholar

47. Porsev SG, Safronova UI, Safronova MS, Schmidt PO, Bondarev AI, Kozlov MG, et al. Optical clocks based on the Cf¹⁵⁺ and Cf¹⁷⁺ ions. Phys Rev A (2020) 102:012802. doi:10.1103/physreva.102.012802

CrossRef Full Text | Google Scholar

48. Beloy K, Dzuba VA, Brewer SM. Quadruply ionized barium as a candidate for a high-accuracy optical clock. Phys Rev Lett (2020) 125:173002. doi:10.1103/physrevlett.125.173002

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Beloy K. Prospects of a Pb²⁺ ion clock. Phys Rev Lett (2021) 127(1):013201. doi:10.1103/physrevlett.127.013201

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Yu YM, Pan D, Chen SL, Arora B, Guan H, Gao K, et al. Atomic structure of Nd⁹⁺ for highly charged ion clocks. Atoms (2022) 10(4):123. doi:10.3390/atoms10040123

CrossRef Full Text | Google Scholar

51. Allehabi SO, Brewer SM, Dzuba VA, Flambaum VV, Beloy K. High-accuracy optical clocks based on group-16-like highly charged ions. Phys Rev A (2022) 106:043101. doi:10.1103/physreva.106.043101

CrossRef Full Text | Google Scholar

52. Allehabi SO, Dzuba VA, Flambaum VV. Atomic clocks highly sensitive to the variation of the fine-structure constant based on Hf II, Hf IV, and W VI ions. Phys Rev A (2022) 106:032807. doi:10.1103/physreva.106.032807

CrossRef Full Text | Google Scholar

53. Uzan JP. The fundamental constants and their variation: Observational and theoretical status. Rev Mod Phys (2003) 75(2):403–55. doi:10.1103/revmodphys.75.403

CrossRef Full Text | Google Scholar

54. Srianand R, Chand H, Petitjean P, Aracil B. Limits on the time variation of the electromagnetic fine-structure constant in the low energy limit from absorption lines in the spectra of distant quasars. Phys Rev Lett (2004) 92(12):121302. doi:10.1103/physrevlett.92.121302

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Patrignani C, others (Particle Data Group). Review of particle physics. Chin Phys C (2016) 90:100001. doi:10.1088/1674-1137/40/10/100001

CrossRef Full Text | Google Scholar

56. Tanabashi M, (Particle data group). Review of particle physics. Phys Rev D (2018) 98(3):030001.

Google Scholar

57. Zyla PA, others (Particle Data Group). Review of particle physics. Prog Theor Exp Phys (2020)(8) 083C01.

Google Scholar

58. Overduin JM, Wesson PS. Kaluza-klein gravity. Phys Rep (1997) 283(5-6):303–78. doi:10.1016/s0370-1573(96)00046-4

CrossRef Full Text | Google Scholar

59. Salam A, Strathdee J. On kaluza-klein theory. Ann Phys (1982) 141(2):316–52. doi:10.1016/0003-4916(82)90291-3

CrossRef Full Text | Google Scholar

60. Chodos A, Jaffe RL, Johnson K, Thorn CB, Weisskopf VF. New extended model of hadrons. Phys Rev D (1974) 9(12):3471–95. doi:10.1103/physrevd.9.3471

CrossRef Full Text | Google Scholar

61. Marciano W, Pagels H. Quantum chromodynamics. Phys Rep (1978) 36(3):137–276. doi:10.1016/0370-1573(78)90208-9

CrossRef Full Text | Google Scholar

62. Bronnikov KA. Scalar-tensor theory and scalar charge. Acta Phys Pol B (1973) B4.

Google Scholar

63. Webb JK, Murphy MT, Flambaum VV, Dzuba VA, Barrow JD, Churchill CW, et al. Further evidence for cosmological evolution of the fine structure constant. Phys Rev Lett (2001) 87(9):091301. doi:10.1103/physrevlett.87.091301

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Murphy MT, Webb JK, Flambaum VV. Further evidence for a variable fine-structure constant from Keck/HIRES QSO absorption spectra. Mon Not R Astron Soc (2003) 345(2):609–38. doi:10.1046/j.1365-8711.2003.06970.x

CrossRef Full Text | Google Scholar

65. Wilczynska MR, Webb JK, Bainbridge M, Barrow JD, Bosman SEI, Carswell RF, et al. Four direct measurements of the fine-structure constant 13 billion years ago. Sci Adv (2020) 6(17):eaay9672. doi:10.1126/sciadv.aay9672

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Whitmore JB, Murphy MT. Impact of instrumental systematic errors on fine-structure constant measurements with quasar spectra. Mon Not R Astron Soc (2015) 447:446–62. doi:10.1093/mnras/stu2420

CrossRef Full Text | Google Scholar

67. Dumont V, Webb JK. Modelling long-range wavelength distortions in quasar absorption echelle spectra. Mon Not R Astron Soc (2017) 468:1568–74. doi:10.1093/mnras/stx381

CrossRef Full Text | Google Scholar

68. David Davis E. The oklo natural fission reactors and improved limits on the variation in the fine structure constant. AIP Conf Proc (2019) 2160(1):070012. doi:10.1063/1.5127735

CrossRef Full Text | Google Scholar

69. Peik E, Lipphardt B, Schnatz H, Schneider T, Tamm C, Karshenboim SG. Limit on the present temporal variation of the fine structure constant. Phys Rev Lett (2004) 93:170801. doi:10.1103/physrevlett.93.170801

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Fortier TM, Ashby N, Bergquist JC, Delaney MJ, Diddams SA, Heavner TP, et al. Precision atomic spectroscopy for improved limits on variation of the fine structure constant and local position invariance. Phys Rev Lett (2007) 98:070801. doi:10.1103/physrevlett.98.070801

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Guéna J, Abgrall M, Rovera D, Rosenbusch P, Tobar ME, Laurent P, et al. Improved tests of local position invariance using ⁸⁷Rb and ¹³³Cs fountains. Phys Rev Lett (2012) 98:080801. doi:10.1103/physrevlett.109.080801

CrossRef Full Text | Google Scholar

72. Leefer N, Weber CTM, Cingöz A, Torgerson JR, Budker D. New limits on variation of the fine-structure constant using atomic dysprosium. Phys Rev Lett (2013) 111:060801. doi:10.1103/physrevlett.111.060801

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Godun RM, Nisbet-Jones PBR, Jones JM, King SA, Johnson LAM, Margoli HS, et al. Frequency ratio of two optical clock transitions in ¹⁷¹Yb and constraints on the time variation of fundamental constants. Phys Rev Lett (2014) 113:210801. doi:10.1103/physrevlett.113.210801

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Huntemann N, Lipphardt B, Chr T, Gerginov V, Weyers S, Peik E. Improved limit on a temporal variation of m_p/m_e from comparisons of Yb⁺ and Cs atomic clocks. Phys Rev Lett (2014) 113:210802. doi:10.1103/physrevlett.113.210802

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Ashby N, Parker TE, Patla BR. A null test of general relativity based on a long-term comparison of atomic transition frequencies. Nat Phys (2018) 14:822–6. doi:10.1038/s41567-018-0156-2

CrossRef Full Text | Google Scholar

76. Lea SN. Limits to time variation of fundamental constants from comparisons of atomic frequency standards. Rep Prog Phys (2007) 70(9):1473–523. doi:10.1088/0034-4885/70/9/r01

CrossRef Full Text | Google Scholar

77. Karshenboim SG. Some possibilities for laboratory searches for variations of fundamental constants. Can J Phys (2000) 78(7):639–78. doi:10.1139/p00-045

CrossRef Full Text | Google Scholar

78. Micke P, Leopold T, King SA, Benkler E, Spieβ LJ, Schmoger L, et al. Coherent laser spectroscopy of highly charged ions using quantum logic Coherent laser spectroscopy of highly charged ions using quantum logic. Nature (2020) 578:60–5. doi:10.1038/s41586-020-1959-8

PubMed Abstract | CrossRef Full Text | Google Scholar

79. King SA, Spieβ LJ, Micke P, Wilzewski A, Leopold T, Benkler E, et al. An optical atomic clock based on a highly charged ion. Nature (2022) 611:43–7. doi:10.1038/s41586-022-05245-4

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Liang SY, Zhang TX, Guan H, Lu QF, Xiao J, Chen SL, et al. Probing multiple electric-dipole-forbidden optical transitions in highly charged nickel ions. Phys Rev A (2021) 103:022804. doi:10.1103/physreva.103.022804

CrossRef Full Text | Google Scholar

81. Windberger A, Crespo López-Urrutia JR, Bekker H, Oreshkina NS, Berengut JC, Bock V, et al. Identification of the predicted 5s-4f level crossing optical lines with applications to metrology and searches for the variation of fundamental constants. Phys Rev Lett (2015) 114:150801. doi:10.1103/PhysRevLett.114.150801

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Cheung C, Safronova MS, Porsev SG, Kozlov MG, Tupitsyn , Bondarev AI. Accurate prediction of clock transitions in a highly charged ion with complex electronic structure. Phys Rev Lett (2020) 124:163001. doi:10.1103/physrevlett.124.163001

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Bekker H, Borschevsky A, Harman Z, Keitel CH, Pfeifer T, Schmidt PO, et al. Detection of the 5p − 4f orbital crossing and its optical clock transition in Pr⁹⁺. Nat Commun (2019) 10(1):5651–7. doi:10.1038/s41467-019-13406-9

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Nakajima T, Okada K, Wada M, Dzuba VA, Safronova MS, Safronova UI, et al. Visible spectra of highly charged holmium ions observed with a compact electron beam ion trap. Nucl Instrum Meth B (2017) 408:118–21. doi:10.1016/j.nimb.2017.03.135

CrossRef Full Text | Google Scholar

85. Berengut JC, Flambaum VV, Ong A. Testing spatial alpha-variation with optical atomic clocks based on highly charged ions. EPJ Web of Conferences (2013) 57:02001. doi:10.1051/epjconf/20135702001

CrossRef Full Text | Google Scholar

86. Davidson K, Netzer K. The emission lines of quasars and similar objects. Rev Mod Phys (1979) 51(4):715–66. doi:10.1103/revmodphys.51.715

CrossRef Full Text | Google Scholar

87. Tsamis YG, Barlow MJ, Liu XW, Danziger IJ, Storey PJ. A deep survey of heavy element lines in planetary nebulae - I. Observations and forbidden-line densities, temperatures and abundances. Mon Not R Astron Soc (2003) 345(1):186–220. doi:10.1046/j.1365-8711.2003.06972.x

CrossRef Full Text | Google Scholar

88. Träbert E, Beiersdorfer P, Utter SB, Brown GV, Chen H, Harris CL, et al. Experimental M1 transition rates of coronal lines from Ar X, Ar XIV, and Ar XV. ApJS (2000) 541(1):506–11. doi:10.1086/309427

CrossRef Full Text | Google Scholar

89. Träbert E, Beiersdorfer P, Brickhouse NS, Golub L. High-resolution laboratory spectra on the λ¹³¹ channel of the aia instrument on board the solar dynamics observatory. ApJS (2014) 211(1):14. doi:10.1088/0067-0049/211/1/14

CrossRef Full Text | Google Scholar

90. Brewer JM, Fischer DA, Valenti JA, Piskunov N. Spectral properties of cool stars: Extended abundance analysis of 1617 planet-search stars. ApJS (2016) 225(2):32. doi:10.3847/0067-0049/225/2/32

CrossRef Full Text | Google Scholar

91. Wahlgren GM, Nielsen KE, Leckrone DS. High-resolution spectroscopy of the hot Am star HR 3383. Mon Not R Astron Soc (2021) 500(2):2451–60. doi:10.1093/mnras/staa3323

CrossRef Full Text | Google Scholar

92. Bie E, Bromage GF. Transition probabilities for forbidden lines: The silicon isoelectronic sequence from S III in to Sn XXXVII. Mon Not R Astron Soc (1983) 205(4):1085–96. doi:10.1093/mnras/205.4.1085

CrossRef Full Text | Google Scholar

93. Biemont E, Hansen JE. Forbidden transitions in 3p⁴ and 4p⁴ configurations. Phys Scr (1986) 34(2):116–30. doi:10.1088/0031-8949/34/2/005

CrossRef Full Text | Google Scholar

94. Biemont E, Hansen JE. Calculations of transition probabilities for forbidden lines in 3pⁿ and 4pⁿ configurations. Nucl Instrum Meth B (1987) 23(1-2):274–7. doi:10.1016/0168-583x(87)90460-5

CrossRef Full Text | Google Scholar

95. Biemont E, Cowan RD, Hansen JE. Transition probabilities for forbidden lines in the ground-state configuration of the bromine isoelectronic sequence. Phys Scr (1988) 37(6):850–4. doi:10.1088/0031-8949/37/6/002

CrossRef Full Text | Google Scholar

96. Biemont E. and Quinet P. Forbidden lines in 6p^k (k = 1 − 5) configurations. Phys Scr (1996) 54(1):36–43. doi:10.1088/0031-8949/54/1/006

CrossRef Full Text | Google Scholar

97. Sugar J, Musgrove A. Energy levels of copper, Cu I through Cu XXIX. J Phys Chem Ref D (1990) 19(3):527–616. doi:10.1063/1.555855

CrossRef Full Text | Google Scholar

98. Shirai T, Nakagaki T, Nakai Y, Sugar J, Ishii K, Mori K. Spectral data and grotrian diagrams for highly ionized copper, Cu X-Cu XXIX. J Phys Chem Ref Data (1991) 20(1):1–81. doi:10.1063/1.555885

CrossRef Full Text | Google Scholar

99. Chou HS, Chan JY, Chang YH, Huang KN. Energy-level scheme and transition probabilities of S-like ions. Data Nucl Data Tables (1996) 62(1):77–145. doi:10.1006/adnd.1996.0003

CrossRef Full Text | Google Scholar

100. Bhatia AK, Doschek GA. Atomic data and spectral line intensities for Ni XIII. Data Nucl Data Tables (1998) 68(1):49–90. doi:10.1006/adnd.1997.0757

CrossRef Full Text | Google Scholar

101. Träbert E, Saathoff G, Wolf A. Ground configuration level lifetimes in S-like Ni and Cu ions (Ni XIII and Cu XIV) measured at a heavy-ion storage ring. EPJ D (2004) 30(3):297–302. doi:10.1140/epjd/e2004-00099-9

CrossRef Full Text | Google Scholar

102. Träbert E, Hoffmann J, Krantz C, Wolf A, Ishikawa Y, Santana JA. Atomic lifetime measurements on forbidden transitions of Al-Si-P- and S-like ions at a heavy-ion storage ring. J Phys B: Mol Opt (2008) 42(2):025002. doi:10.1088/0953-4075/42/2/025002

CrossRef Full Text | Google Scholar

103. Torretti F, Windberger A, Ryabtsev A, Dobrodey S, Bekker H, Ubachs W, et al. Optical spectroscopy of complex open-4d-shell ions Sn⁷⁺-Sn¹⁰⁺. Phys Rev A (2017) 95(4):042503. doi:10.1103/physreva.95.042503

CrossRef Full Text | Google Scholar

104. Ralchenko Y, Draganic IN, Osin D, Gillaspy JD, and Reader J. Spectroscopy of diagnostically important magnetic-dipole lines in highly charged 3dⁿ ions of tungsten. Phys Rev A (2011) 83(3):032517. doi:10.1103/physreva.83.032517

CrossRef Full Text | Google Scholar

105. Safronova MS, Safronova UI, Porsev SG, Kozlov MG, Ralchenko Y. Relativistic all-order many-body calculation of energies, wavelengths, and M1 and E2 transition rates for the 3dⁿ configurations in tungsten ions. Phys Rev A (2018) 97(1):012502. doi:10.1103/physreva.97.012502

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Si R, Guo XL, Brage T, Chen CY, Hutton R, Fischer CF. Breit and qed effects on the 3d⁹²D_3/2 → ²D_5/2 transition energy in Co-like ions. Phys Rev A (2018) 98(1):012504. doi:10.1103/physreva.98.012504

CrossRef Full Text | Google Scholar

107. Biemont E, Hansen JE. Energy levels and transition probabilities in 3d and 3d⁹ configurations. Phys Scr (1989) 39(3):308–13. doi:10.1088/0031-8949/39/3/005

CrossRef Full Text | Google Scholar

108. Ali MA, Kim YK. Electric quadrupole and magnetic dipole transition probabilities in the potassium isoelectronic sequence. Phys Rev A (1988) 38(8):3992–7. doi:10.1103/physreva.38.3992

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Charro E. Curiel Z, and Martacute in I. Atomic data for M1 and E2 emission lines in the potassium isoelectronic sequence. A&A (2002) 387(3):1146–52. doi:10.1051/0004-6361:20020288

CrossRef Full Text | Google Scholar

110. Träbert , E, Beiersdorfer P, Brown GV, Chen H, Thorn DB, and Bimont E. Experimental M1 transition rates in highly charged Kr ions. Phys Rev A (2001) 64(4):042511. doi:10.1103/physreva.64.042511

CrossRef Full Text | Google Scholar

111. Guise ND, Tan JN, Brewer SM, Fischer CF, Jonsson P. Measurement of the Kr XVIII 3d²D_5/2 lifetime at low energy in a unitary penning trap. Phys Rev A (2014) 89(4):040502. doi:10.1103/physreva.89.040502

CrossRef Full Text | Google Scholar

112. Liu JP, Li CB, Zhou HX. Theoretical investigation on forbidden transition properties of fine-structure splitting in ²D state for K-like ions with 26⩽Z⩽36. Chin Phys B (2017) 26(2):103201. doi:10.1088/1674-1056/26/10/103201

CrossRef Full Text | Google Scholar

113. Biémont E, Quinet P. Recent advances in the study of lanthanide atoms and ions. Phys Scr (2003) T10538.

Google Scholar

114. Radžiūtė L, Gaigalas G, Kato D, Jönsson P, Rynkun P, Kučas S, et al. Energy level structure of Er³⁺. J Quant Spectrosc RA (2015) 152:94–106. doi:10.1016/j.jqsrt.2014.11.007

CrossRef Full Text | Google Scholar

115. Clementson J, Beiersdorfer P, Magee EW, McLean HS, Wood RD. Tungsten spectroscopy relevant to the diagnostics of ITER divertor plasmas. J Phys B: Mol Opt Phys (2010) 43(14):144009. doi:10.1088/0953-4075/43/14/144009

CrossRef Full Text | Google Scholar

116. Mita PM, Kato D, Murakami I, Sakaue HA, Nakamura N. Identification of visible lines from multiply charged W⁸⁺ and W⁹⁺ ions. Phys Rev A (2020) 102(4):042818. doi:10.1103/physreva.102.042818

CrossRef Full Text | Google Scholar

117. Radžiūtė L, Gaigalas G, Kato D, Rynkun P, Tanaka M. Extended calculations of energy levels and transition rates for singly ionized lanthanide elements. II. Tb-Yb. ApJS (2021) 257(2):29. doi:10.3847/1538-4365/ac1ad2

CrossRef Full Text | Google Scholar

118. Derevianko A, Dzuba VA, Flambaum VV. Highly charged ions as a basis of optical atomic clockwork of exceptional accuracy. Phys Rev Lett (2012) 109(18):180801. doi:10.1103/physrevlett.109.180801

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Madelung EE. Die mathematischen hilfsmittel der Physikers. Berlin: Springer (1936).

Google Scholar

120. Kramida A, Ralchenko Y, Reader JNIST ASD Team. NIST atomic spectra database (2020). ver. 5.8.

Google Scholar

121. Zainab A, Tauheed A. Revised and extended analysis of doubly ionized gold: Au III. J Quant Spectrosc RA (2019) 237:106614. doi:10.1016/j.jqsrt.2019.106614

CrossRef Full Text | Google Scholar

122. Safronova UI, Flambaum VV, Safronova MS. Transitions between the 4f-core-excited states in Ir¹⁶⁺, Ir¹⁷⁺, and Ir¹⁸⁺ ions for clock applications. Phys Rev A (2015) 92:022501. doi:10.1103/physreva.92.022501

CrossRef Full Text | Google Scholar

123. Liu YL, Wu CQ, Ding XB, Zhang FL, Zhang L, Yao K, et al. The M1 transitions and visible spectra of W¹³⁺ ion. Phys Lett A (2022) 454:128500. doi:10.1016/j.physleta.2022.128500

CrossRef Full Text | Google Scholar

124. Nandy DK, Sahoo BK. Highly charged W¹³⁺, Ir¹⁶⁺, and Pt¹⁷⁺ ions as promising optical clock candidates for probing variations of the fine-structure constant. Phys Rev A (2016) 94(3):032504. doi:10.1103/physreva.94.032504

CrossRef Full Text | Google Scholar

125. Huo X, Jiang G, Li X. Atomic properties and transition parameters of highly charged Sb-like isoelectronic ions. Can J Phys (2017) 95:590–4. doi:10.1139/cjp-2016-0740

CrossRef Full Text | Google Scholar

126. Lu Q, Fu N, Yan CL, Qu FH, Yang Y, Wang K, et al. Experimental and theoretical investigations of visible spectra of W¹²⁺. J Quant Spectrosc RA (2022) 279:108064. doi:10.1016/j.jqsrt.2022.108064

CrossRef Full Text | Google Scholar

127. Singh N, Aggarwal S, Mohan M. Extended atomic structure calculations for W¹¹⁺ and W¹³⁺. Atoms (2020) 8:92. doi:10.3390/atoms8040092

CrossRef Full Text | Google Scholar

128. Fu N, Lu Q, Yan CL, Xu GQ, Wang K. Re-investigation and line identifications for W¹¹⁺ in the visible range. J Phys B (2022).

CrossRef Full Text | Google Scholar

129. Lu Q, Yan CL, Fu N, Yang Y, Chen CY, Xiao J, et al. Measurement and identification of visible lines from W¹⁰⁺. J Quant Spectrosc RA (2021) 262:107533. doi:10.1016/j.jqsrt.2021.107533

CrossRef Full Text | Google Scholar

130. Safronova UI, Safronova MS. Correlation and relativistic effects for the 4f − nl and 5p − nl multipole transitions in er-like tungsten. Phys Rev A (2011) 84:012511. doi:10.1103/physreva.84.012511

CrossRef Full Text | Google Scholar

131. Lu Q, Yan CL, Meng J, Xu GQ, Yang Y, Chen CY, et al. Visible spectra of W⁸⁺ in an electron-beam ion trap. Phys Rev A (2021) 103:022808. doi:10.1103/physreva.103.022808

CrossRef Full Text | Google Scholar

132. Kozio K, Rzadkiewicz J. Theoretical level energies, radiative lifetimes and transitions in W IX. Data Nucl Data Tables (2021) 137:101372. doi:10.1016/j.adt.2020.101372

CrossRef Full Text | Google Scholar

133. Visscher L, Dyall KG. Dirac-fock atomic electronic structure calculations using different nuclear charge distributions. Data Nucl Data Tables (1997) 67(2):207–24. doi:10.1006/adnd.1997.0751

CrossRef Full Text | Google Scholar

134. Helgaker T, Jrgensen P, Olsen J. Molecular electronic structure theory. Chichester: Wiley (2000).

Google Scholar

135. Dykstra CE. Theory and applications of computational chemistry: The first forty years. Netherlands: Elsevier (2005).

Google Scholar

136. Olsen J, Roos B, Jorgensen P, Jensen HJA. Determinant based configuration interaction algorithms for complete and restricted configuration interaction spaces. J Chem Phys (1988) 89(4):2185–92. doi:10.1063/1.455063

CrossRef Full Text | Google Scholar

137. Fleig T, Olsen J, Marian CM. The generalized active space concept for the relativistic treatment of electron correlation. I. kramers-restricted two-component configuration interaction. J Chem Phys (2001) 114(11):4775–90. doi:10.1063/1.1349076

CrossRef Full Text | Google Scholar

138. Fleig T, Olsen J, Visscher L. The generalized active space concept for the relativistic treatment of electron correlation. II. large-scale configuration interaction implementation based on relativistic 2- and 4-spinors and its application. J Chem Phys (2003) 119(6):2963–71. doi:10.1063/1.1590636

CrossRef Full Text | Google Scholar

139. Fleig T, Jensen HJA, Olsen J, Visscher L. The generalized active space concept for the relativistic treatment of electron correlation. III. large-scale configuration interaction and multiconfiguration self-consistent-field fourcomponent methods with application to UO₂. J Chem Phys (2006) 124(10):104106. doi:10.1063/1.2176609

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Jensen HJA, Bast R, Gomes ASP, Saue T., Visscher L, Aucar IA, et al. A relativistic ab initio electronic structure program, Release DIRAC22 (2022). doi:10.5281/zenodo.6010450

CrossRef Full Text | Google Scholar

141. Saue T, Bast R, Gomes ASP, Jensen HJA, Visscher L, Aucar IA, et al. The Dirac code for relativistic molecular calculations. J Chem Phys (2020) 152:204104. doi:10.1063/5.0004844

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Sahoo BK, Das BP. Relativistic normal coupled-cluster theory for accurate determination of electric dipole moments of atoms: First application to the ¹⁹⁹Hg atom. Phys Rev Lett (2018) 120(20):203001. doi:10.1103/physrevlett.120.203001

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Li CB, Yu YM, Sahoo BK. Relativistic coupled-cluster-theory analysis of energies and hyperfine-structure constants and and dipole polarizabilities of Cd⁺. Phys Rev A (2018) 97(2):022512. doi:10.1103/physreva.97.022512

CrossRef Full Text | Google Scholar

144. Berkel DJ, Miller JD, Bergquist JC, Itano WM, Wineland DJ. Minimization of ion micromotion in a Paul trap. J Appl Phys (1998) 83(10):5025–33. doi:10.1063/1.367318

CrossRef Full Text | Google Scholar

145. Keller J, Partner HL, Burgermeister T, Mehlstäubler TE. Precise determination of micromotion for trapped-ion optical clocks. J Appl Phys (2015) 118(10):104501. doi:10.1063/1.4930037

CrossRef Full Text | Google Scholar

146. Dubé P, Madej AA, Tibbo M, Bernard JE. High-accuracy measurement of the differential scalar polarizability of a ⁸⁸Sr⁺ clock using the time-dilation effect. Phys Rev Lett (2014) 112(17):173002. doi:10.1103/physrevlett.112.173002

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Huang Y, Guan H, Bian W, Ma L, Liang K, Li T, et al. A comparison of two ⁴⁰Ca single-ion optical frequency standards at the 5 × 10¹⁷ level and an evaluation of systematic shifts. Appl Phys B (2017) 123(5):1–18. doi:10.1007/s00340-017-6731-x

CrossRef Full Text | Google Scholar

148. Itano WM. External-field shifts of the ¹⁹⁹Hg⁺ optical frequency standard. J Res Nat Inst Stan (2000) 105(6):829. doi:10.6028/jres.105.065

CrossRef Full Text | Google Scholar

149. Dubé P, Madej AA, Bernard JE, Marmet L, Boulanger JS, Cundy S. Electric quadrupole shift cancellation in single-ion optical frequency standards. Phys Rev Lett (2005) 95(3):033001. doi:10.1103/physrevlett.95.033001

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Sobelman . Atomic spectra and radiative transitions. New York: Springer Science & Business Media (2012).

Google Scholar

151. Sahoo BK. Nuclear quadrupole moment of ⁴³Ca a and hyperfine-structure studies of its singly charged ion. Phys Rev A (2009) 80(1):012515. doi:10.1103/physreva.80.012515

CrossRef Full Text | Google Scholar