- 1Keya Medical, Shenzhen, China
- 2Keya Medical, Seattle, WA, United States
- 3University at Buffalo, State University at New York, Buffalo, NY, United States
- 4UNC Charlotte, Charlotte, NC, United States
- 5Carnegie Mellon University, Pittsburgh, PA, United States
Modeling sequential information for image sequences is a vital step of various vision tasks and convolutional long short-term memory (ConvLSTM) has demonstrated its superb performance in such spatiotemporal problems. Nevertheless, the hierarchical data structures (e.g., human body parts and vessel/airway tree in biomedical images) in various tasks cannot be properly modeled by sequential models. Thus, ConvLSTM is not suitable for analyzing tree-structured image data that has a rich relation among its elements. In order to address this limitation, we present a tree-structured ConvLSTM model for tree-structured image analysis which can be trained end-to-end. To demonstrate its effectiveness, we first evaluate the proposed tree-structured ConvLSTM model on a synthetic Tree-Moving-MNIST dataset for tree-structured modeling. Experimental results demonstrate the superiority of the tree-structured ConvLSTM model for tree-structured image analysis compared with other alternatives. Additionally, we present a tree-structured segmentation framework which consists of a tree-structured ConvLSTM layer and an attention fully convolutional network (FCN) model. The proposed framework is validated on four large-scale coronary artery datasets. The results demonstrate the effectiveness and efficiency of the proposed method, showing its potential use cases in the analysis of tree-structured image data.
1 Introduction
Various real-world applications involve high dimensional data with rich structures. Owing to their abilities to process sequences with arbitrary length, convolutional long short-term memory (ConvLSTM) models Shi et al. [1] and their variants Shi et al. [2]; Patraucean et al. [3] have achieved state-of-the-art results on many tasks related to spatiotemporal predictions. Examples include precipitation nowcasting Shi et al. [1], action classification Li et al. [4], 3D biomedical image segmentation Jinzheng et al. [5], and object motion prediction William et al. [6]. One major difference between ConvLSTM and the traditional long short-term memory (LSTM) is that the vector multiplication is replaced by the more efficient convolutional operations. By this means, ConvLSTM preserves the spatial topology of the inputs. Additionally, it introduces sparsity and locality to the LSTM units to reduce model over-parameterization and overfitting Ballas et al. [7].
Albeit its effectiveness, ConvLSTM assumes that the input data is sequential. However, in many practical problems, the input data has intrinsic non-linear structures so that it is difficult to be modeled sequentially but can be better represented by more complex structures, such as trees or graphs. For instance, in action recognition Baccouche et al. [8], human body parts are naturally represented in a tree structure. Based on the geometric interactions of the nodes in the tree, the action label is determined. Tree-like structure is also commonly observed in medical imaging applications, such as human airways, blood vessels (e.g., arteries, veins, and capillaries) and nervous structures, in which the anatomical structures are recursively split into branches. Sequential ConvLSTM is conceptually and practically insufficient to model such tree-structured data.
Attempts have been made by adopting traditional LSTM based models to handle tree-structured input data. The part-aware LSTM used an individual cell for each body joint and a shared output gate for all body joints for 3D action recognition Shahroudy et al. [9]. Nevertheless, simply aggregating the outputs from all the cells cannot yield satisfactory solutions since it neglects the complex hierarchically spatial relationships of body parts.
Recently, tree-structured LSTM is proposed for learning syntactic representations in language processing problems Tai et al. [10]. Graph neural networks are also introduced for data that could be organized into complex graph structures Hamilton et al. [11]. However, these approaches are not suitable for image analysis since their input-to-state and state-to-state transitions are both formulated with fully-connected operations and the spatial correlations are not taken into consideration Tai et al. [10]; Nam Khanh and Weiwei [12]; David and Tommi [13]. In this work, inspired by the sequential ConvLSTM Shi et al. [1], we develop a tree-structured convolutional recurrent model, i.e., tree-structured ConvLSTM, for leveraging the rich topology of trees. The proposed tree-structured ConvLSTM is not only able to efficiently capture discriminative features from each node in a tree but also capable of taking the inter-node correlations in the tree into considerations. Furthermore, we propose a new deep learning architecture combining the attention FCN and tree-structured ConvLSTM and apply it to automated coronary artery segmentation from 3D cardiac computed tomography angiography (CTA). The attention FCN extracts hierarchical multi-scale features from each node, and the tree-structured ConvLSTM efficiently captures the appearance evolution in tree structures. As our framework effectively models the inter-node correlations, the generated segmentation results are more accurate as well as anatomically reasonable. The main contributions of this work can be summarized as follows:
• Inspired by sequential ConvLSTM, we propose tree-structured ConvLSTM so that convolution operations can be applied to high dimensional data understanding such as tree structures. The superiority over a sequential ConvLSTM is demonstrated on an image classification task with tree-structured data (i.e., synthetic Tree-Moving-MNIST dataset).
• The proposed tree-structured ConvLSTM is a unified model and is capable of propagating information among the entire tree. Thus, it avoids applying the sequential ConvLSTM locally to each branch of a tree-structured data, which is suboptimal.
• We present a framework composed of a tree-structured ConvLSTM and an attention FCN model. The proposed framework is general and can be easily extended to other tree-structured image segmentation tasks. In this work, it is extensively validated on four coronary artery segmentation datasets. Without extensive tuning, it outperforms other state-of-the-art baseline models by a large margin.
2 Related work
Recurrent neural networks (RNNs) have been proven to be efficient tools for sequence learning. Their recursive formulations naturally allow the handling of variable-length sequences problem. Nevertheless, the notorious vanishing or exploding gradients problem Pascanu et al. [14] during the training phase (i.e., back-propagation through time) prevents RNNs from achieving satisfying results in applications requiring long-term dependencies. This problem is alleviated by the LSTM Gers et al. [15] which incorporates long-term stable memory over time using a series of gating functions. LSTM has been widely used, achieving state-of-the-art results in numerous sequence learning applications, such as such as COVID-19 detection Hassan et al. [16]; Li et al. [17], video sequence processing Kong et al. [18]; Donahue et al. [19], cancer metastasis detection Kong et al. [20], and time series analysis Du et al. [21]. However, the traditional LSTM is not suitable for image sequence analysis since it uses fully-connected structure during both the input-to-state and state-to-state transitions, neglecting the spatial information. Different from traditional LSTM, ConvLSTM Shi et al. [1] takes image sequence as input and the vector multiplications in traditional LSTM are replaced by convolutional operations. By this means, ConvLSTM preserves the spatial topology of the inputs and introduces sparsity and locality to LSTM units to reduce over-parameterization and overfitting. Thus, ConvLSTM models are more suitable for spatiotemporal prediction problems. However, sequential ConvLSTM is not capable of dealing with tree-structured data.
Recently, applying deep learning to graph and tree-like data that has complex structures are becoming a hot topic Wang et al. [22,23]. It has been explored in various problem settings, ranging from supervised, unsupervised to reinforcement learning. Graph neural network is first presented in Scarselli et al. [24] to process data organized in graph structures. Following this line of work, various types of graph convolution networks Zhang et al. [25] are proposed. We briefly classify them into two main categories: spectral and non-spectral approaches. Spectral approaches take input the spectral representations of the graph. One of the seminal work is the spectral network Bruna et al. [26], in which the eigendecomposition of the graph Laplacian is computed by the convolution operation. However, this operation is computationally intensive. To address this problem, Henaff et al. [27] introduce a parameterization with smooth coefficients to spatially localize the filters. Nevertheless, the spectral methods are dependent on the graph Laplacian (the structure of the graph). As a result, a trained model can hardly generalize to graphs that have different structures from the training data. Non-spectral approaches directly apply convolution operations to spatially close nodes. For instance, GraphSAGE Hamilton et al. [11] directly generates embeddings for graphs from each node’s neighboring nodes. A special subset of graphs can be organized as hierarchical structures, i.e., trees. Attempts have also been made to extend sequential LSTM and gated recurrent unit (GRU) Cho et al. [28] to trees to eliminate their limitations. For instance, tree-structured LSTM Tai et al. [10] has been proposed for language processing. Nevertheless, as the vector multiplication was used in both graph and tree-structured networks, they are not suitable for image analysis. In contrast, our tree-structured ConvLSTM model considers both spatial information and inter-node dependencies in the tree structure. In this work, the data can be naturally organized as tree structure. Thus, we decide to investigate the capability of tree-structured models. We also plan to investigate the applications in which the image data can be organized as graphs.
Numerous works have been dedicated to the segmentation of 3D tree-like structures. One kind of approaches rely on local or voxel-level information (e.g., prior knowledge of the intensity distribution in tree structures). For example, Schneider et al. Schneider et al. [29] extract local steerable features from the 3D data, which are further used by the random forests to conduct voxel-wise classification. However, voxel-wise approaches are especially prone to errors (causing noisy contours, holes, breaks, etc.). Tracking-based methods, instead, better leverage the anatomical structure of the tree. For instance, Macedo et al. Macedo et al. [30] present a technique for tracking centerlines by building bifurcation detectors based on 2D features. Nevertheless, the final segmentation results are highly dependent on the initial seeding of trees. Geometry and topology of the tree have been proven to be beneficial for tree segmentation De Bruijne et al. [31]; De Bruijne et al. [32]. However, these priors typically require domain-specific knowledge of a certain task, and the enforced priors also restrict these approaches and make it difficult to be extended to other similar tasks. The above methods attempt to directly segment objects organized in tree structures, which is extremely difficult. To address this issue, the state-of-the-art approaches Bauer et al. [33] often adopt a two-stage framework for the segmentation of complex tree-structured image data. For instance, in Jin et al. [34]; Bauer et al. [33], tree-structured tubular structures are first identified to provide preliminary topology information. Afterward, the segmentation algorithms are conducted on the initial tree-structured structures. In Jin et al. [34], a 3D FCN network is first utilized to preliminarily segment the airway. Then, a graph-based based method utilizing the tree-like topology of the airway is performed to considerably boost the segmentation result. These works demonstrate that topology information in tree-structured image data is crucial for object segmentation in tree-structured image data.
3 Tree-structured convolutional LSTM
We develop a tree-structured convolutional recurrent model, referred to tree-structured ConvLSTM, for image analysis with tree-structured data. We first review the LSTM/ConvLSTM algorithms and then introduce the proposed tree-structured ConvLSTM model.
3.1 Revisiting LSTM/ConvLSTM algorithms
In the LSTM model, each unit maintains a memory cell ct. A typical LSTM unit includes three gates: input gate it, forget gate ft, and output gate ot. These gates are essentially non-linear functions which control the information flow at each time step t, listed as follows:
where σ is the sigmoid function, xt is the input at the current time step t. ⊙ denotes Hadamard product, and Wi, Ui, Wf, Uf, Wo, Uo, Wm, and Um are the weight matrices for each unit1.
LSTM applies vector multiplications on the input elements. While image sequences are composed of spatial as well as temporal components, the standard LSTM treats the input as vectors by vectorizing the input feature map. As no spatial information is considered, the results are suboptimal for image sequence analysis. In order to preserve the spatiotemporal information, the fully connected multiplicative operations of the input-to-state and state-to-state transitions are replaced by convolutions in ConvLSTM Shi et al. [1], formally,
where * denotes convolutional operation,
3.2 Tree-structured ConvLSTM
As in the standard sequential ConvLSTM, each tree-structured ConvLSTM unit j consists of an input gate ij, an output gate oj, a memory cell
The workflow of the tree-structured ConvLSTM is illustrated in Figure 1. The gating mechanism of our tree-structured ConvLSTM is similar to LSTM, with two distinct differences. First, the gating signals in tree-structured ConvLSTM is 2D feature maps, instead of feature vectors in the standard LSTM. Second, tree-structured ConvLSTM has to consider the scenarios with more than one child. As the current node j has two children, l1 and l2, two forget gates (i.e.,
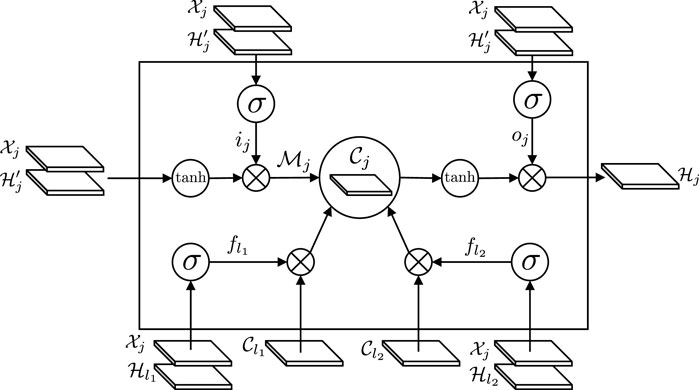
FIGURE 1. The workflow of the tree-structured ConvLSTM. The gating mechanism of our tree-structured ConvLSTM is similar to LSTM, with two distinct differences. First, the gating signals in tree-structured ConvLSTM is 2D feature maps, instead of feature vectors in the standard LSTM. Second, tree-structured ConvLSTM has to consider the scenarios with more than one child. As the current node j has two children, l1 and l2, two forget gates (i.e.,
4 Framework for tree-structured image segmentation
We formulate the coronary artery segmentation as a machine learning problem over tree structures, in which the learning occurs over a collection of trees and the prediction is generated at the node level. In this formulation, each node j is associated with an input image
In this section, we present a segmentation framework that applies the tree-structured ConvLSTM model described above to a image segmentation task with tree-structured data. The input nodes (green circles) are organized as a tree structure. All the nodes in the input tree are fed into an encoder, yielding high dimensional feature maps for the tree nodes. Afterward, a tree-structured ConvLSTM layer takes the feature maps as input. Note the information flow (red arrow line) in the hidden states of the tree-structured ConvLSTM. Benefited from the ability of the tree-structured ConvLSTM to learn the inter-node dependencies in tree structures, the feature maps are more anatomically reasonable. Finally, the decoder generates the output tree, or the final segmentation results (yellow circles).
4.1 Encoding-decoding structure
The backbone network of the proposed segmentation framework is an attention FCN Kong et al. [35], which is based on the U-Net Ronneberger et al. [36]. It consists of two phases: encoding and decoding. In the encoding stage, 3 × 3 convolutional operation followed by a rectified linear unit (ReLU) and 2 × 2 pooling operation with stride 2 for downsampling are progressively applied to the input of tree node. In this way, multi-scale high dimensional image representations are generated from each node
Then, a tree-structured ConvLSTM layer is used to propagate the context information among the units in the tree. More specifically, we apply the tree-structured ConvLSTM layers to the image representations generated in the encoding phase of the attention FCN. Thanks to the tree-structured ConvLSTM layer, the spatial information is preserved for each tree node and the topological information is merged into the image representations. Finally, in the decoding stage, the high dimensional representations are progressively rescaled to the same dimension as the original input.
In each rescaling operation, the image representations are upsampled with a deconvolution layer, followed by a concatenation with the corresponding feature maps generated in the encoding phase, and convolutional layers of kernel size 3 × 3 and ReLU layers. The tree-structured ConvLSTM layer is followed by an attention block with three convolutional layers and Conv3_2 layer is followed by an attention block of four convolutional layers. To reduce the computational cost, we do not apply attention operation to Conv4_2 layer. By stacking attention FCN and tree-structured ConvLSTM layer together and forming an encoding-decoding structure, we are able to build a network model for the general tree-structured segmentation problems.
4.2 Attention component for salient region detection
Attention mechanism has demonstrated its effectiveness in various vision-related tasks, e.g., image captioning Xu et al. [37], representation learning Fan et al. [38], and visual question answering Lu et al. [39]. In this work, we propose a novel attention block to guide our network to attend to objects of interest. Integrating the attention mechanism into our framework brings at least two advantages: 1) Attention can help highlight the foreground regions, thereby avoiding distractions of some non-salient background regions. In the example of the coronary artery segmentation task, attention guides the network to focus on the coronary artery when there are some other tissues with similar intensity distributions around the coronary artery. 2) By filtering out unrelated regions, the subsequent layers can focus on more challenging regions, e.g., the coronary artery boundaries.
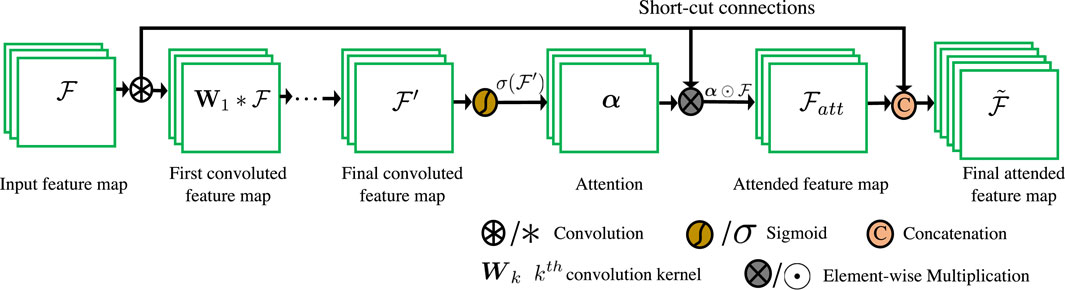
We also illustrate its detailed structure in feature maps in Figure 2. Given the convolutional feature map
Specifically, several convolutional layers of 3 × 3 (for computational efficiency) are first deployed after the feature map
where k is the number of convolutional layers in the attention block. Wk is the convolution kernel of the kth convolutional layer.
Finally, Fan et al. Fan and Zhou [41] demonstrate that the sigmoid function dilutes the gradients during backpropagation. To mitigate this problem, we concatenate the original feature map with the generated attended context feature to yield the final feature map
5 Experiments and results
In this section, extensive experiments are carried out to evaluate the proposed methods. In Section 5.1, we first compare the multi-label classification error of the proposed tree-structured ConvLSTM with that of other methods on a synthetic Tree-Moving-MNIST dataset. Relatively simple dataset allows us thoroughly analyze the capability of our approach for tree-structured learning. Then, we evaluate the proposed segmentation framework on four challenging 3D cardiac CTA datasets to demonstrate its effectiveness on the segmentation tasks with tree-structured data in Section 5.2.
5.1 Multi-label classification for tree-moving-MNIST dataset
5.1.1 Dataset and evaluation metrics
We generate a synthetic Three-Moving-MNIST dataset using a process similar to Srivastava et al. [42], which is illustrated in Figure 3. All data instances in the dataset are tree-structured and each node contains handwritten digits bouncing inside a 64 × 64 patch. For each data instance, the digits keep moving from leaf nodes to the root node. For every three steps, the digits merge with another moving digit. Finally, the root node contains all the digits from the leaf nodes. In all the instances, the leaf nodes are randomly chosen from 0 to 9 in the MNIST dataset. The starting position and velocity direction are chosen uniformly at random and the velocity amplitude is randomly chosen in
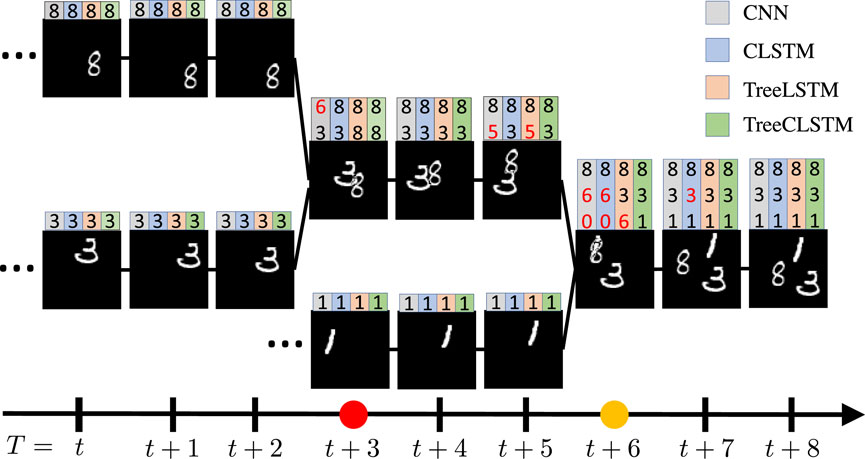
FIGURE 3. One example from Tree-Moving-MNIST with three digits bounding inside a 64×64 patch from time T = t to T = t +8. On the top of each node shows the prediction results of CNN in gray color, sequential ConvLSTM (CLSTM) in blue color, fully connected tree-structured LSTM (TreeLSTM) in orange color, and tree-structured ConvLSTM (TreeCLSTM) in green color, respectively. The digits in red color denote wrong predictions. Note that all methods, except TreeCLSTM, has false predictions to certain extent. The red and yellow dots on the time axis (bottom) denote the timestep that the digits merge with others. Note that CNN, CLSTM, TreeLSTM, and TreeCLSTM tend to make false predictions at these timesteps because of their weak capabilities to model the inter-node dependencies among the tree nodes.
We keep tracking of the whole evolving process, as illustrated in Figure 3. In this example, all the input nodes
5.1.2 Results
We consider the following baselines: 1) A normal CNN architecture (CNN), i.e., LeNet LeCun et al. [43], 2) LeNet with sequential ConvLSTM (CLSTM), 3) LeNet with tree-structured LSTM (TreeLSTM), 4) LeNet with tree-structured ConvLSTM (TreeCLSTM).
More specifically, each tree node
In experiments, CNN is applied to each tree node independently. For CLSTM, TreeLSTM, and TreeCLSTM, the LSTM layers are inserted into LeNet before the first fully connected layer. For CLSTM, we divide the tree into five cells (each cell has three nodes) according to the merging points and the CLSTM is applied to each cell. As illustrated in Table 1, TreeCLSTM achieves the lowest overall classification error, 13.5%, outperforming the other methods. Figure 3 shows the predictions of these methods on a randomly chosen example. Note that all methods, except TreeCLSTM, has false predictions (red digits on top of each tree node) to a certain extent. The red and yellow dots on the time axis (bottom) denote the timestep that the digits merge with others. Note that CNN, CLSTM, TreeLSTM, and TreeCLSTM tend to make false predictions at these timesteps because of their weak capabilities to model the inter-node dependencies among the tree nodes.

TABLE 1. Overall classification error comparison of different networks on the Tree-Moving-MNIST dataset.
We also break down the total classification error into three parts, corresponding to the classification errors on the nodes containing 1, 2, and 3 digits, respectively. As is shown in Figure 4, for all the methods, the nodes with only one digit has the lowest classification error as it does not need the inter-node information. By contrast, classifying the nodes with three digits is the most difficult as more digits may occlude each other. TreeCLSTM has the lowest misclassification rates on the nodes with 2 and three digits due to its ability to efficiently leverage the inter-node information in the tree. TreeLSTM shows higher misclassification due to vectorized hidden states. CNN and CLSTM have lower classification error on the nodes with only one digit because they focus on learning local patterns. However, they perform poorly on nodes that need inter-node information because they are not able to leverage the full inter-node context of the tree structure.
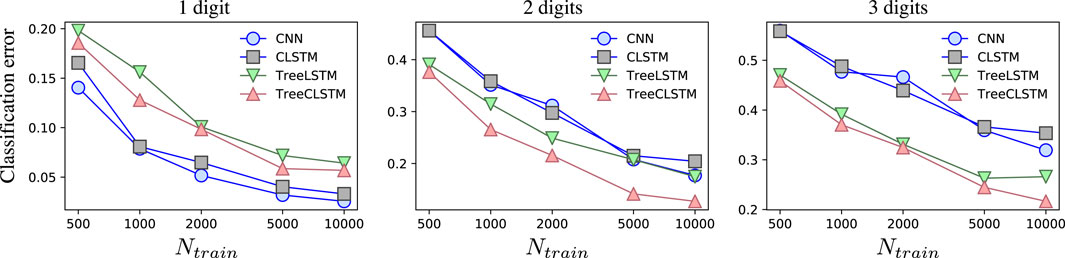
FIGURE 4. Average classification error using different methods as a function of the number of the training examples. From the left to right panes, the plots are corresponding to the classification errors on the nodes containing 1, 2, and 3 digits, respectively.
In summary, these experiments demonstrate the effectiveness of the proposed tree-structured ConvLSTM for tree-structured learning.
5.2 Coronary artery tree segmentation
Next, we evaluate the performance of the proposed tree segmentation framework using 3D cardiac CTA datasets to further demonstrate the advantages of tree-structured ConvLSTM on the segmentation tasks.
5.2.1 Dataset and evaluation metrics
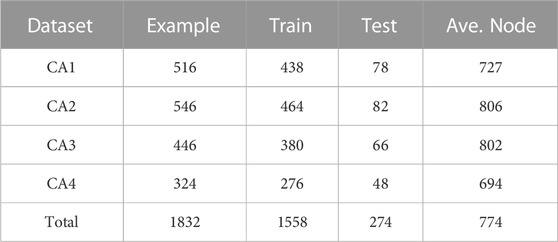
Four 3D cardiac CTA datasets (CA1, CA2, CA3, and CA4) are collected from four hospitals to validate the proposed method. The ground truth coronary artery regions of these datasets were delineated by the experts from our collaborative hospitals. A summary of these datasets is listed in Table 2. To the best of our knowledge, these datasets are the largest reported in the field. Each dataset is randomly split into three parts: 80% for training, 5% for validation, and 15% for testing.
Figure 5 illustrates our workflow for coronary artery segmentation. The first step is centerline extraction. In this step, a 3D U-Net Çiçek et al. [44] is first employed to generate the preliminary coronary artery tree segmentation. The coronary arteries are elongated and thin structures with complex topologies. Thus, solely using this step is extremely difficult to generate a satisfactory segmentation results. We then use the centerline extraction approach (minimal path extraction filter) that is similar to Mueller [45] to generate the centerlines for the 3D cardiac CTA datasets.

FIGURE 5. Coronary artery segmentation pipeline. The first step is centerline extraction. In this step, We first utilize a pretrained 3D U-Net Çiçek et al. [44] to generate the preliminary coronary artery. The coronary arteries are with complex topologies. Thus, solely using this step is extremely difficult to generate a satisfactory segmentation results. We then use the centerline extraction approach that is similar to Mueller [45] to generate the centerlines for the 3D cardiac CTA datasets. Then, we crop a image patch of size 41×41 around each centerline point that is perpendicular to the centerline. We organize the nodes into a tree structure according to the topological structures of the centerline. Finally, We feed the cardiac image tree into the trained tree-structured segmentation network, yielding the final predicted coronary artery.
Then, we crop a image patch of size 41 × 41 (35 is the largest diameter of the coronary artery in our dataset) around each centerline point that is perpendicular to the centerline. Afterward, we normalize each image patch with the mean value of the aorta to increase the contrast of the coronary artery regions and the empirical thresholding value of the calcification regions 1,000 to highlight the calcification regions, which are further concatenated with the preliminary coronary artery segmentation result, yielding a three-channel image for each centerline point. We organize them into a tree structure according to the topological structures of the centerline, with each node being the generated three-channel image.
Finally, We feed the cardiac image tree into the trained tree-structured segmentation network, yielding the final predicted coronary artery. We then compare the predicted coronary arteries generated by our tree-structured segmentation framework with the ground truth to evaluate the proposed method. As the focus of this paper is to demonstrate the effectiveness of the proposed tree-structured ConvLSTM for modeling inter-node dependencies in tree-structures, we only compare our framework with other approaches for generating the final coronary arteries from the cardiac images that are organized as tree structures.
The segmentation results were evaluated by the average dice score coefficient (Ave. D) of the tree nodes:
where J denotes the number of tree nodes.
Dice tends to underestimate the difference between two masks as they focus on the whole segmentation instead of the local discrepancies, which is essential in guaranteeing a topologically accurate segmentation and error-free downstream tasks, such as computational hemodynamics. We also evaluate the result with two additional metrics: 95% Hausdorff distance and 95% radius difference. The 95% Hausdorff distance first sort the distances between the predicted mask and the ground truth. Then the 95 percentile is selected as the distance to alleviate the noises in the masks. 95% radius difference is defined as the 95 percentile of the radius difference between the predicted and the ground truth masks. These two metrics highlight the difference between two masks that are not visually differentiable.
5.2.2 Implementation details
All the models were trained using PyTorch Paszke et al. [46] framework and all the experiments were conducted on a workstation equipped with an NVIDIA Tesla P40 GPU. The networks were trained with Adam optimizer Kingma and Ba [47] using an initial learning rate of 0.001 and a weight decay of 0.0005 and a momentum of 0.9. We randomly initialized the weights of all the convolutional layers according to Gaussian distribution with a mean of 0 and a standard deviation of 0.02. For the tree-structured ConvLSTM layers, we clipped the gradient norm of the weights by 50. These models were trained with early-stopping on Ave. D.
5.2.3 Results
For fair comparison, we compare our tree-structured ConvLSTM (Tree CLSTM) with two baselines: 1) a small 3D densely-connected volumetric convnets (DenseVoxNet) Yu et al. [48], which achieved state-of-the-art performance on complex vascular-like segmentation tasks, 2) sequential ConvLSTM (CLSTM). For DenseVoxNet, we crop a volume along the coronary artery centerline with a size of 41 × 41 × 20. For CLSTM, we propagate the information from the root to each leaf node.
As illustrated in Table 3, the proposed TreeCLSTM compares favorably with these two baselines in all the datasets, outperforming DenseVoxNet by 1.02%, 0.91%, 0.90%, 0.88% on CA1, CA2, CA3, CA4, respectively, and surpassing CLSTM by 0.79%, 0.80%, 1.22%, 0.77% on CA1, CA2, CA3, CA4, respectively. We also evaluate these methods on the aggregated dataset (Total) of CA1, CA2, CA3, and CA4 to demonstrate the capacity of our network for a large-scale dataset. TreeCLSTM still outperforms DenseVoxNet and CLSTM by 1.6% and 0.87%, respectively. Additionally, the 95% Hausdorff and 95% Radius Diff. of TreeCLSTM outperform significatnly over DenseVoxNet, CLSTM. These results demonstrate the effectiveness of our methods in dealing with the tree-structured segmentation problems.In the multi-label classification for Tree-Moving-MNIST, we demonstrated that classification error is highest on those nodes that have multiple digits. In the coronary artery segmentation problem, however, we guess that segmentation around bifurcation nodes is much more challenging because dynamics in these nodes are much more difficult to model than the normal nodes. To confirm this point, we conduct an additional experiment on the aggregated dataset (Total), in which we compare the methods above around the bifurcation nodes (nodes within four nodes’ distance from the bifurcation nodes) in the trees. As is illustrated in Table 4, TreeCLSTM surpasses DenseVoxNet and CLSTM by a large margin in terms of Ave. D (6.85% and 3.71%, respectively). Additionally, attention further improves the final accuracy (0.53%). All in all, our approach outperforms other methods, especially around bifurcation nodes.
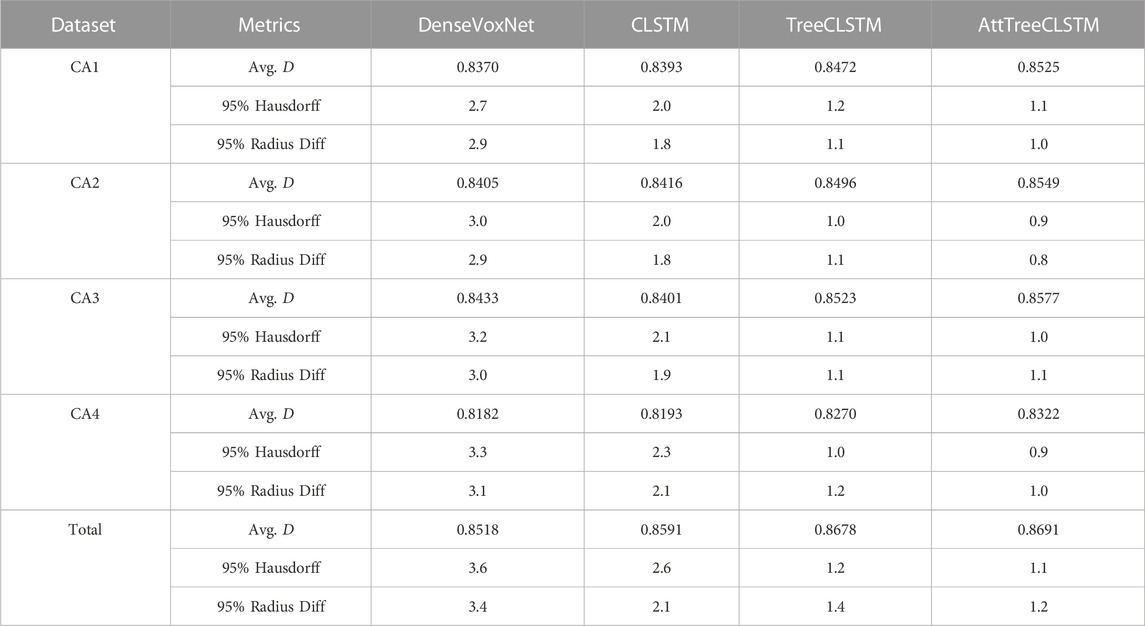
TABLE 3. Comparison of 3D densely-connected volumetric convnets (DenseVoxNet) Yu et al. [48], sequential ConvLSTM (CLSTM) Shi et al. [1], tree-structured ConvLSTM (TreeCLSTM), and tree-structured ConvLSTM with attention (AttTreeCLSTM) in terms of Ave. D, 95% Hausdorff, and 95% Radius Difference.

TABLE 4. Comparison of DenseVoxNet Yu et al. [48], CLSTM Shi et al. [1], TreeCLSTM, and AttTreeCLSTM around bifurcation nodes (with two or more children nodes) in terms of Ave. D.
5.2.4 Evaluation of the robustness to initial segmentation
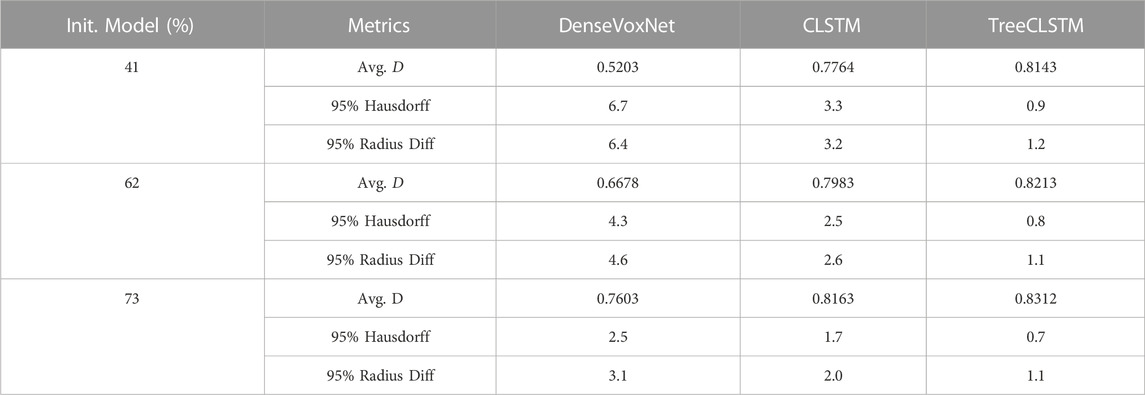
In this application, the proposed segmentation framework depends on a 3D U-Net network for the initial segmentation and centerline extraction. It is natural to question the proposed framework’s dependence on the initial segmentation result. To answer this question, we used three different 3D U-Net models to generate the initial segmentation for the testing dataset. These models have the same network architecture but with different initial segmentation performance (41%, 62%, and 73% respectively). The inital segmentation is used for centerline extraction and then used as the input for the proposed AttTreeCLSTM model. Table 5 show the comparison results. According to the result, the initial segmentation results nearly have no impact on the final segmentation result. The Avg. D, 95% Hausdorff, and 5% Radius Diff. of TreeCLSTM slightly improve from 0.8143, 0.9, and 1.2 to 0.8312, 0.7, and 1.1. On the contrary, the performance of DenseVoxNet severely degrades as the performance of the initial segmentation get worse. The performance degradation of CLSTM is between these two methods.
This phenomenon can be explained by the fact that the centerline extraction is less sensitive to the initial segmentation result. Although the initial segmentation gets really bad when the Avg. D approaches 41%, it still captures the whole structure of the coronary artery and the proposed framework can utilize the structured information to refine the coronary artery segmentation. On the contrary, DenseVoxNet and CLSTM doesn’t or only partially utilize the structured information.
Additionally, we also test if the proposed method is robust to random perturbations of the initial segmentation result and the extracted centerline. The following experiments are conducted: 1) randomly dilate the initial segmentation by a maximum of four voxels; 2) randomly erode the initial segmentation by a maximum of four voxels; 3) randomly choose one of the leaf nodes as the root and set the root node as leaf node. 4) randomly perturb the centerline points by a maximum of four voxles. Note that four voxels are considered a large perturbation as the image patch size is only 41 × 41. Table 6 summarizes the final segmentation result. The results suggest that the proposed model is relatively robust to the perturbations to the initial segmentation (random dilation and erosion) and the centerline (random centerline perturbation). Randomly choosing one of the leaf node has a higher impact on the segmentation result. The performance degradation maybe result from the fact that we are not fully using the prior knowledge.

TABLE 6. Performance of the proposed model with different perturbation schemes applied to the initial segmentation and the centerline.
5.2.5 Evaluation of the proposed attention model
To demonstrate the effectiveness of the proposed attention mechanism in our tree-structured ConvLSTM, we compare attention TreeCLSTM (AttTreeCLSTM) with the non-attention implementation (TreeCLSTM). With attention, the Ave. D of TreeCLSTM increased by 0.53%, 0.53%, 0.54%, 0.52%, 0.13% on CA1, CA2, CA3, CA4, and total, respectively. Figure 6 shows some examples of the generated attention maps (3rd, 6th, and 9th columns) and the corresponding ground truths (2nd, 5th, and 8th columns) alongside with the original input subvolumes (1st, 4th, and 7th columns). The results demonstrate that the proposed attention component can attend to the coronary arteries. With the proposed attention module, AttTreeCLSTM outperforms TreeCLSTM and obviously generates better results than other methods.
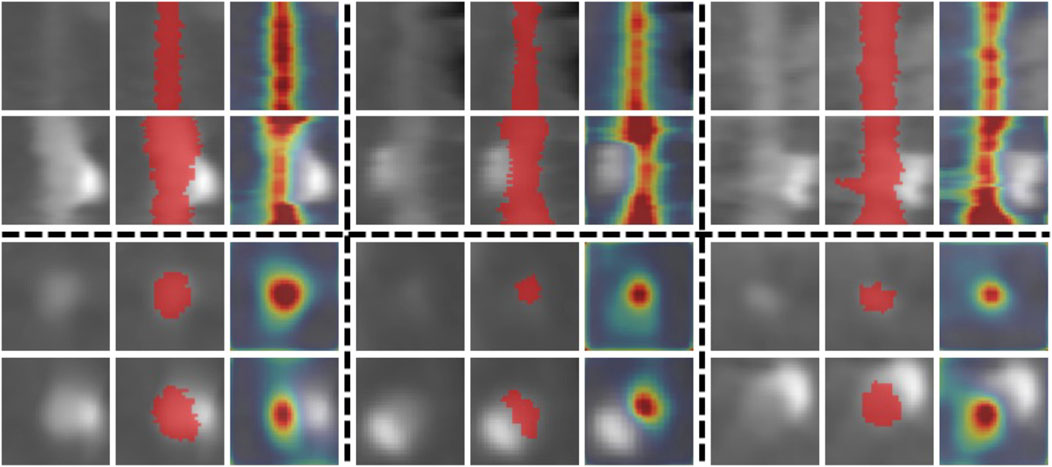
FIGURE 6. Attention examples. The 1st, 4th, and 7th columns show input subvolumes. The 2nd, 5th, and 8th columns show the corresponding ground truths (red) overlaid on the original subvolumes. The 3rd, 6th, and 9th columns show the generated attention maps overlaid on the subvolumes. The top two rows show some examples viewed along the coronary artery. The bottom two rows show samples viewed in the cross-section direction.
5.2.6 Evaluation of the locations of tree-structured ConvLSTM
As the feature maps contain all the encoded high dimensional features in the decoding stage, the tree-structured ConvLSTM layer can be inserted into different layers of the decoding stage in the segmentation framework. Thus, we evaluate the performance of our framework when the tree-structured ConvLSTM is inserted into different layers of the decoding network. As illustrated in Table 7, we compare our formulation (tree-structured ConvLSTM before the decoding network) with the tree-structured ConvLSTM. Results in Table 7 suggest that inserting tree-structured ConvLSTM into initial (lower) layers of the decoding network leads to better performance and our formulation achieves the best overall performance. This may be attributed to the fact that upper layers contain local features that are specific to the current tree node. As a result, combing local specific features from other tree nodes does not help the segmentation.
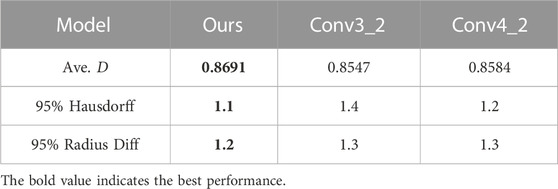
TABLE 7. Ave. D obtained when tree-structured ConvLSTM is inserted after different layers in the decoding stage.
5.3 Comparisons of computational costs
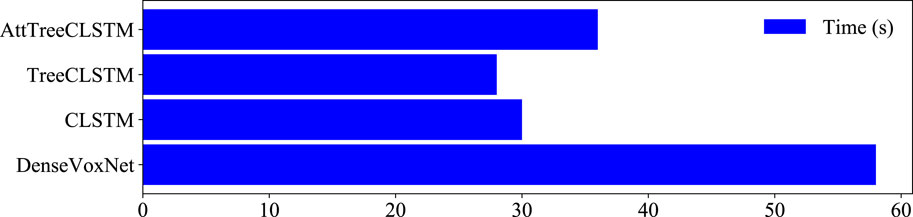
Figure 7 shows the computational costs for the above methods. Among all these methods, DenseVoxNet takes the longest time: 58 s. CLSTM and TreeCLSTM take 28 s and 30 s, which are 2.1 and 1.9 times faster than DenseVoxNet, respectively. Finally, AttTreeCLSTM takes slightly more time than CLSTM: AttCLSTM takes 8s more time than tree-structured ConvLSTM. Considering that 11 s is required to preprocess a data example and 1s is required to load the data examples to memory in average, the average model inference time is 46 s, 16 s, 18 s, and 24 s respectively for DenseVox, CLSTM, TreeCLSTM, and AttTreeCLSTM. The results demonstrate that the proposed tree-structured ConvLSTM significantly speed up the inference. Additionally, the attention mechanism can further boost the performance while marginally increase the computational cost.
5.4 Discussions
We compared our tree-structured ConvLSTM based segmentation framework (TreeConvLSTM) with ConvLSTM and DenseVox on four large scale datasets. According to Table 3, the performance of TreeConvLSTM consistently outperforms other methods. Additionally, we evaluated their performance on the aggregated dataset to test their scalability. TreeConvLSTM also beats ConvLSTM and DenseVox. Additionally, we noticed that annotators spend considerably more time around bifurcation nodes. Thus, comparing the performance around the bifurcation nodes is also important. In Table 4, we compared their performance around the bifurcation nodes. According to Table 4, TreeConvLSTM considerably outperforms ConvLSTM and DenseVox. Thus, it is safe to say that our tree-structured ConvLSTM based segmentation framework consistently outperforms ConvLSTM and DenseVox in this task, especially around bifurcation nodes.
Furthermore, in our coronary artery segmentation task, the coronary artery tree is relatively rigid, which is already determined by the anatomical structure of the coronary artery. However, we observe that our coronary tree does not have a natural order, which means that the information can be propagated either from the root to the leaves of the tree or from the leaves to the root. Thus, we tested the performance of these two different propagation orders. The experiment demonstrates that the order is not important (the performance difference is within 0.04%). Thus, we conclude that our method is relatively insensitive to the order of information propagation. In addition, Table 3 offers additional insights. CA1, CA2, CA3, and CA4 are collected from four different hospitals. As a result, the coronary arteries in these four datasets have totally variant anatomical structures. According to Table 4, the performance difference is within 2% for these four datasets, even without considering other variations such as intensity and appearance.
Finally, we offer some additional insights for using our tree-structured LSTM. First, we noticed that some objects can be naturally represented by tree structures, such as human body parts Oliveira et al. [49], human pose Newell et al. [50], and blood vessel Liskowski and Krawiec [51]. Our method is especially applicable to these applications. Second, there exist a lot of tasks requiring considering the correlation among landmarks such as face landmark Liu et al. [52]; Alexandre et al. [53]; Jeon et al. [54] and clothing keypoints Liu et al. [55]. Considering the abundance of these structures, we believe our method can be potentially be leveraged to benefit a wide range of applications.
As the proposed framework is general and not specific to any specific application. We believe it can be a good candidate for solving tree/hierarchical-structured problem. More specifically, it can be used for human body part/keypoint detection, pose recognition in images and videos, and facial keypoint hierarchical detection and tracking.
6 Conclusion
In this work, we explicitly consider the tree structures in classification and segmentation tasks by presenting tree-structured ConvLSTM model. The multi-label classification results on the synthetic Tree-Moving-MNIST dataset clearly show the superiority of the proposed tree-structured ConvLSTM model in tree-structured learning. To demonstrate the effectiveness of the proposed tree-structured ConvLSTM model on more complex vision tasks, we propose an end-to-end tree-structured segmentation framework which consists of an attention FCN subnet and a tree-structured ConvLSTM subnet. More specifically, the attention FCN subnet extracts multi-scale high dimensional image representations from each tree node while reducing the distractions from non-salient regions, and tree-structured ConvLSTM integrates the inter-node dependencies in the tree. The proposed approach has been successfully applied to the challenging coronary artery segmentation problem, which so far has not benefited from the advanced hierarchical machine learning approaches. We believe that our tree-structured ConvLSTM structure is general enough to be applicable to other tree-structured vision tasks. For the future work, we will investigate the feasibility to apply the tree-structured ConvLSTM to other tree-structured image analysis problems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by Shenzhen Science and Technology Program (Grant No. KQTD2016 112809330877).
Conflict of interest
YL, KC, YY and XW were employed by Keya Medical, Shenzhen, China. BK and FG were employed by the Keya Medical, Seattle, United States.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1We assume zero biases in Eq. 1 in this paper for simplicity.
2Tree-Moving-MNIST dataset and the code for multi-label classification will be released soon.
References
1. Shi X, Chen Z, Wang H, Yeung D-Y, Wong W-K, Woo W. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In: Advances in Neural Information Processing Systems; December 7-12, 2015; Canada (2015).
2. Shi X, Gao Z, Lausen L, Wang H, Yeung D-Y, Wong W-k., et al. Deep learning for precipitation nowcasting: A benchmark and a new model. In: Advances in Neural Information Processing Systems; December 4-9, 2017; USA (2017).
3. Patraucean V, Handa A, Cipolla R. Spatio-temporal video autoencoder with differentiable memory. In: International Conference on Learning Representations, Workshop; May 2-4, 2016; San Juan (2016).
4. Li Z, Gavrilyuk K, Gavves E, Jain M, Snoek CG. Videolstm convolves, attends and flows for action recognition. Computer Vis Image Understanding (2018) 166:41–50. doi:10.1016/j.cviu.2017.10.011
5. Jinzheng C, Lu L, Yuanpu X, Fuyong X, Lin Y. Improving deep pancreas segmentation in ct and mri images via recurrent neural contextual learning and direct loss function. In: Medical Image Computing and Computer-Assisted Intervention; September 11-13, 2017; Canada (2017).
6. William L, Gabriel K, Davi d. DC. Deep predictive coding networks for video prediction and unsupervised learning. In: International Conferenceon Learning Representations; April 24-26, 2017; France (2017).
7. Ballas N, Yao L, Pal C, Courville A. Delving deeper into convolutional networks for learning video representations. In: International Conference on Learning Representations; May 7-9, 2015; USA (2015).
8. Baccouche M, Mamalet F, Wolf C, Garcia C, Baskurt A. Sequential deep learning for human action recognition. In: International workshop on human behavior understanding. Germany: Springer (2011).
9. Shahroudy A, Liu J, Ng T-T, Wang G. Ntu rgb+ d: A large scale dataset for 3d human activity analysis. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 27-30 June 2016; USA (2016).
10. Tai KS, Socher R, Manning CD. Improved semantic representations from tree-structured long short-term memory networks. Proc 53rd Annu Meet Assoc Comput Linguistics 7th Int Jt Conf Nat Lang Process (2015) 1:1556–66. doi:10.3115/v1/P15-2
11. Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs. In: Advances in neural information processing systems. US: MIT Press (2017).
12. Nam Khanh T, Weiwei C. Multiplicative tree-structured long short-term memory networks for semantic representations. In: Proceedings of the Seventh Joint Conference on Lexical and Computational Semantics; June 5-6, 2018; USA (2018).
13. David A-M, Tommi SJ. Tree-structured decoding with doubly-recurrent neural networks. In: International Conferenceon Learning Representations; April 24 - 26, 2017; France (2017).
14. Pascanu R, Mikolov T, Bengio Y. On the difficulty of training recurrent neural networks. In: International Conference on Machine Learning; June 21, 2013; USA (2013).
15. Gers FA, Schmidhuber J, Cummins F. Learning to forget: Continual prediction with lstm. Neural Comput (2000) 12:2451–71. doi:10.1162/089976600300015015
16. Hassan A, Shahin I, Alsabek MB. Covid-19 detection system using recurrent neural networks. In: 2020 International Conference on Communications, Computing, Cybersecurity, and Informatics (CCCI); 03-05 November 2020; Sharjah (2020).
17. Li L, Qin L, Xu Z, Yin Y, Wang X, Kong B, et al. Using artificial intelligence to detect Covid-19 and community-acquired pneumonia based on pulmonary ct: Evaluation of the diagnostic accuracy. Radiology (2020) 296:E65–E71. doi:10.1148/radiol.2020200905
18. Kong B, Zhan Y, Shin M, Denny T, Zhang S. Recognizing end-diastole and end-systole frames via deep temporal regression network. In: International Conference on Medical Image Computing and Computer-assisted Intervention; October 17-21, 2016; Greece (2016).
19. Donahue J, Anne Hendricks L, Guadarrama S, Rohrbach M, Venugopalan S, Saenko K, et al. Long-term recurrent convolutional networks for visual recognition and description. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 07-12 June 2015; USA (2015).
20. Kong B, Wang X, Li Z, Song Q, Zhang S. Cancer metastasis detection via spatially structured deep network. In: International Conference on Information Processing in Medical Imaging; June 25-30, 2017; USA (2017).
21. Du W, Côté D, Liu Y. Saits: Self-attention-based imputation for time series. Expert Syst Appl (2023) 219:119619. doi:10.1016/j.eswa.2023.119619
22. Wang X, Youbing Y, Bai J, Song Q, Cao K, Lu Y, et al. Method and system for disease quantification modeling of anatomical tree structure (Google Patents). US Patent (2022) 11(462):326.
23. Wang X, Yin Y, Cao K, Bai J, Lu Y, Ouyang B, et al. Method and system for anatomical tree structure analysis. US Patent App (2023) 17/971:038.
24. Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G. The graph neural network model. IEEE Trans Neural Networks (2009) 20:61–80. doi:10.1109/tnn.2008.2005605
25. Zhang Q, Chang J, Meng G, Xu S, Xiang S, Pan C. Learning graph structure via graph convolutional networks. Pattern Recognition (2019) 95:308–18. doi:10.1016/j.patcog.2019.06.012
26. Bruna J, Zaremba W, Szlam A, LeCun Y. Spectral networks and locally connected networks on graphs. arXiv preprint arXiv:1312.6203 (2013).
27. Henaff M, Bruna J, LeCun Y. Deep convolutional networks on graph-structured data. arXiv preprint arXiv:1506.05163 (2015).
28. Cho K, Van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, et al. Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078 (2014).
29. Schneider M, Hirsch S, Weber B, Székely G, Menze BH. Joint 3-d vessel segmentation and centerline extraction using oblique hough forests with steerable filters. Med Image Anal (2015) 19:220–49. doi:10.1016/j.media.2014.09.007
30. Macedo MM, Galarreta-Valverde MA, Mekkaoui C, Jackowski MP. A centerline-based estimator of vessel bifurcations in angiography images. In: Medical imaging 2013: Computer-aided diagnosis. Washington: International Society for Optics and Photonics (2013).
31. De Bruijne M, van Ginneken B, Viergever MA, Niessen WJ. Adapting active shape models for 3d segmentation of tubular structures in medical images. In: Biennial International Conference on Information Processing in Medical Imaging; July 20-25, 2003; UK (2003).
32. De Bruijne M, Van Ginneken B, Niessen WJ, Loog M, Viergever MA. Model-based segmentation of abdominal aortic aneurysms in cta images. In: Medical imaging 2003: Image processing. USA: International Society for Optics and Photonics (2003).
33. Bauer C, Eberlein M, Beichel RR. Graph-based airway tree reconstruction from chest ct scans: Evaluation of different features on five cohorts. IEEE Trans Med Imaging (2015) 34:1063–76. doi:10.1109/tmi.2014.2374615
34. Jin D, Xu Z, Harrison AP, George K, Mollura DJ. 3d convolutional neural networks with graph refinement for airway segmentation using incomplete data labels. In: International Workshop on Machine Learning in Medical Imaging; September 10, 2017; Canada (2017).
35. Kong B, Sun S, Wang X, Song Q, Zhang S. Invasive cancer detection utilizing compressed convolutional neural network and transfer learning. In: International Conference on Medical Image Computing and Computer-Assisted Intervention; September 16-20, 2018; Spain (2018).
36. Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention; October 5-9, 2015; Germany (2015).
37. Xu K, Ba J, Kiros R, Cho K, Courville A, Salakhudinov R, et al. Show, attend and tell: Neural image caption generation with visual attention. In: International Conference on Machine Learning; July 11, 2015; France (2015).
38. Fan X, Gong M, Xie Y, Jiang F, Li H. Structured self-attention architecture for graph-level representation learning. Pattern Recognition (2019) 100:107084. doi:10.1016/j.patcog.2019.107084
39. Lu J, Yang J, Batra D, Parikh D. Hierarchical question-image co-attention for visual question answering. In: Advances in Neural Information Processing Systems; December 5-10, 2016; Barcelona, Spain (2016).
40. Liu N, Han J, Yang M-H. Picanet: Learning pixel-wise contextual attention for saliency detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 18-23 June 2018; USA (2018).
41. Fan H, Zhou J. Stacked latent attention for multimodal reasoning. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; June 23 2018; Salt Lake City (2018).
42. Srivastava N, Mansimov E, Salakhudinov R. Unsupervised learning of video representations using lstms. In: Proceedings of the International Conference on International Conference on Machine Learning; June 25 - 29, 2006; USA (2015).
43. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE (1998) 86:2278–324. doi:10.1109/5.726791
44. Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3d u-net: Learning dense volumetric segmentation from sparse annotation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention; October 17-21, 2016; Greece (2016).
46. Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, et al. Automatic differentiation in pytorch (2017).
47. Kingma DP, Ba J. A method for stochastic optimization. In: International Conference on Learning Representations; May 7-9, 2015; USA (2015).
48. Yu L, Cheng J-Z, Dou Q, Yang X, Chen H, Qin J, et al. Automatic 3d cardiovascular mr segmentation with densely-connected volumetric convnets. In: International Conference on Medical Image Computing and Computer-Assisted Intervention; September 11-13, 2017; Canada (2017).
49. Oliveira GL, Valada A, Bollen C, Burgard W, Brox T. Deep learning for human part discovery in images. In: IEEE International Conference on Robotics and Automation; 16-21 May 2016; Sweden (2016).
50. Newell A, Yang K, Deng J. Stacked hourglass networks for human pose estimation. In: European conference on computer vision. Germany: Springer (2016).
51. Liskowski P, Krawiec K. Segmenting retinal blood vessels with deep neural networks. IEEE Trans Med Imaging (2016) 35:2369–80. doi:10.1109/tmi.2016.2546227
52. Liu Z, Zhu X, Hu G, Guo H, Tang M, Lei Z, et al. Semantic alignment: Finding semantically consistent ground-truth for facial landmark detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; June 20 2019; CA, USA (2019).
53. Alexandre GR, Soares JM, Thé GAP. Systematic review of 3d facial expression recognition methods. Pattern Recognition (2019) 100:107108. doi:10.1016/j.patcog.2019.107108
54. Jeon B, Jang Y, Shim H, Chang H-J. Identification of coronary arteries in ct images by bayesian analysis of geometric relations among anatomical landmarks. Pattern Recognition (2019) 96:106958. doi:10.1016/j.patcog.2019.07.003
Keywords: tree-structured ConvLSTM, vessel segementation, attention, hierarchical data structures, deep learning
Citation: Lu Y, Kong B, Gao F, Cao K, Lyu S, Zhang S, Hu S, Yin Y and Wang X (2023) Attention-driven tree-structured convolutional LSTM for high dimensional data understanding. Front. Phys. 11:1095277. doi: 10.3389/fphy.2023.1095277
Received: 11 November 2022; Accepted: 24 February 2023;
Published: 27 March 2023.
Edited by:
Zhifan Gao, Sun Yat-sen University, ChinaReviewed by:
Zhihui Guo, Microsoft Research, United StatesYuanzhang Tang, University of Washington, United States
Copyright © 2023 Lu, Kong, Gao, Cao, Lyu, Zhang, Hu, Yin and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xin Wang, eGlud0BrZXlhbWVkbmEuY29t
†These authors contributed equally to this work and share first authorship
 Yi Lu1†
Yi Lu1† Xin Wang
Xin Wang