- 1Department of Physics, The Hong Kong University of Science and Technology, Hong Kong, China
- 2Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States
We determine a constitutive equation for developed three-dimensional granular flows based on a series of discrete element method simulations. In order to capture non-local phenomena, normal stress differences, and secondary flows, we extend a previously proposed granular temperature-sensitive rheological model by considering Rivlin-Ericksen tensors up to second order. Three model parameters are calibrated with the inertial number and a dimensionless granular temperature. We validate our model by running finite difference method simulations of inclined chute flows. The model successfully predicts the velocity and stress fields in this geometry, including secondary vortical flows that previous first-order models could not predict and slow creeping zones that local models miss. It simultaneously captures the non-trivial variation among diagonal components of the stress tensor throughout the domain.
1 Introduction
Granular materials (sand, gravel, coal, salt, rice, wheat, pills, etc.) are essential to our lives and used in diverse scientific fields and industries. Although the microscopic interactions between grains are simple, the macroscopic mechanical properties of granular flows arising from these simple interactions are surprisingly complex and still subject to debate.
One hypothetical way to write the constitutive equation for granular flows is to assume that the deviatoric stress is codirectional to the strain rate tensor D:
where σ is the stress tensor, P is the pressure,
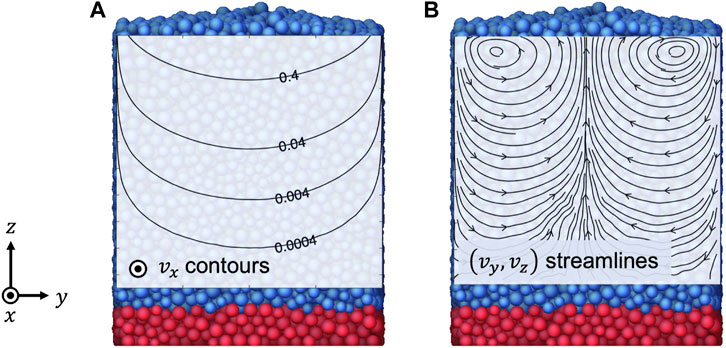
FIGURE 1. Snapshot from DEM simulation of granular flow in a chute with an inclination angle of tan−1(0.50). Contour plot in (A) shows downstream velocity vx which decreases exponentially with depth (creeping flow). The unit is
To describe this non-locality, several first-order models have introduced a diffusing scalar field that fluidizes (softens) the material. The definition of the diffusing field depends on the model. Some models have utilized the population of shear transformation zones [9–11]. The partial fluidization theory proposed by Aranson and Tsimring [12, 13]; [14] uses the average ratio of “solid contacts” as the diffusing scalar field. Inspired by a plastic flow model for soft glassy materials [15, 16], Kamrin and colleagues [17–19] have proposed the non-local granular fluidity (NGF) model that accurately describes many different inhomogeneous flows. In the NGF model, the diffusing parameter or “fluidity” is defined as the shear rate-to-μ ratio
Based on the fact that the fluidity is related to the velocity fluctuations, Kim and Kamrin [25] have recently proposed a first-order non-local model removing rheological dependence on ϕ. Using discrete element method (DEM) simulations in steady-state planar shear flows, a simpler constitutive relation between μ, I, and a dimensionless granular temperature Θ ≡ ρsT/P has been identified:
where the exponent p is approximately 1/6 for spheres in 3D and f(I) is a monotonically increasing function of I and its details depends on the material properties such as surface friction. This μ(I, Θ) relation has successfully explained the non-locality of granular flows, bridging the softening effect of granular temperature in the kinetic theory and the fluidity field in the NGF model.
However, the first-order model lacks the ability to explain a group of phenomena in granular flows. One example is a bulging surface of a channel flow. When a granular material is released steadily down an inclined plane with rough side walls, the surface of the flowing region becomes convex upward [26–29]. Another phenomenon that the first-order model cannot predict is the secondary flow. In the cylindrical Couette geometry under gravity, non-zero velocities in the radial and the gravity directions (transverse directions) have been observed and named “secondary flow” in the sense that this flow is relatively slow and perpendicular to the primary flow direction [30–33]. The right streamline plot in Figure 1 illustrates an example of the secondary flow: an inclined chute flow has non-zero transverse velocities perpendicular to the downstream direction. The anomalous shear stress observed in the plane of the secondary flows [30, 34] also cannot be accounted for in the first-order model. These phenomena occur in the presence of broken codirectionality, where the deviatoric stress and strain rate tensors are not proportional. Many other studies have also found that granular flows exhibit broken codirectionality in the form on non-zero normal stress differences [35–45] or broken coaxiality where the principal axes of the stress and strain rate tensors are not aligned [45–47]. Therefore, the constitutive equation needs to be corrected beyond the codirectionality hypothesis (Eq. 1) to achieve higher accuracy.
In the present study, we propose a non-local second-order fluid model to cover both non-locality and broken codirectionality of three-dimensional granular flows. As previous researchers have suggested [29, 45, 48], we assume steadily flowing granular fluids are incompressible non-Newtonian fluids and adopt the tensor form of the second-order fluid, also known as the Rivlin-Ericksen fluid of second grade, as the constitutive equation. In this second-order model, three functions should be calibrated. The major difference from the previous second-order models is that we take into account the dimensionless granular temperature Θ as well as I in the calibration because we know that the first-order model’s μ depends both on I and Θ. For the calibration, planar shear flows of frictional spheres are simulated using the discrete element method (DEM). We separately measure the three normal stresses, which are required to calculate the model parameters for the quadratic terms. It also allows us to examine the first and second normal stress differences.
Furthermore, we validate our non-local second-order model in a more complex geometry. Using the functions calibrated from the planar shear tests, we run the finite difference method (FDM) simulations of rough-walled inclined chute flow (Figure 1) with four different slope angles. We compare the FDM predictions to the DEM data to demonstrate that our second-order model can correctly predict the secondary flows and the stress fields as well as the primary creeping flows.
2 Model calibration: Planar shear flows
2.1 Second-order model
Following previous studies [29, 45, 48], we assume that a flowing granular material behaves like a second-order fluid where the stress tensor is of the form:
where An are called the nth order Rivlin-Ericksen tensors and an are scalar parameters. The Rivlin-Ericksen tensors are given by the recurrence relation
where L = ∇v is the velocity gradient tensor. In steady state, this relation yields A1 = 2D and A2 = 4D2 + 2(DW − WD) where D = (L + LT)/2 is the strain rate tensor and W = (L − LT)/2 is the spin tensor. Therefore, we can rewrite Eq. 3 as
where the scalar parameters μ1, μ2, and μ3 play the same role as those in Srivastava et al. [45]. Since all but the identity tensor in the above expression are deviatoric, the pressure P represents the hydrostatic pressure P ≡ − tr σ/3. Our definition of the shear rate
In Srivastava et al. [45], μ1, μ2, and μ3 were assumed to depend only on I. However, the previous non-local first-order model by Kim and Kamrin [25], which is equivalent to the case of μ2 = μ3 = 0, suggests that μ1 depends on both I and Θ. It suggests that μ2 and μ3 may also be affected by Θ in inhomogeneous flows. In this work, we run various planar shear flows using DEM simulations to find the expressions for μ1, μ2, and μ3 in terms of I and Θ. Using our calibrated parameters, we check the predictive capability of our model in chute flows with different inclination angles.
2.2 Methods
2.2.1 DEM simulation settings for planar shear flows
In order to identify the parameters in the second-order model, we use LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator), which implements the discrete element method (DEM), to simulate many different homogeneous and inhomogeneous planar shear flows of 3D frictional spheres. The grain diameter di is set to be uniformly distributed from 0.8d to 1.2d to prevent crystallization. When we calculate I, the local average diameter is used. The mass of the grains is determined as
As in Kim and Kamrin [25], we test simple shear flows (Figure 2A), shear flows under gravity (Figure 2B), flows in vertical and tilted chutes (θ = 90° and 60° in Figure 2C), and “concave flows” (Figure 2D). The concave flow is named so because the plot of the shear rate against height becomes concave upward due to the outward body force
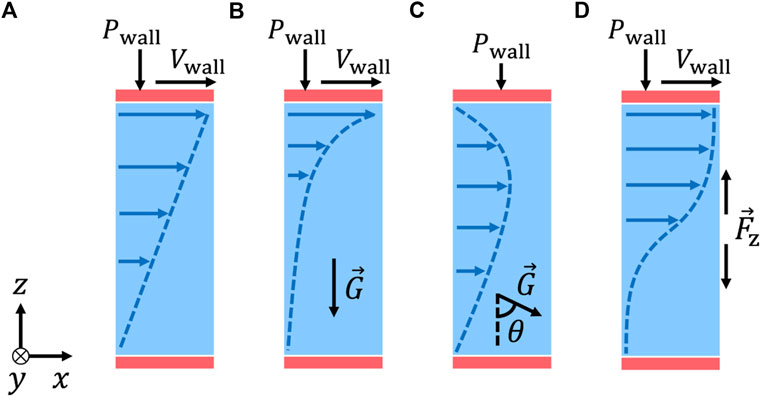
FIGURE 2. Schematic diagrams of planar shear flows used for model calibration in Section 2: (A) simple shear, (B) shear with gravity, (C) chute flows (θ = 60° and 90°), and (D) concave flows. Red rectangles represent wall particles whose velocities are set to form rigid walls. Dashed lines indicate velocity profiles. x is the flow direction, y is the vorticity direction, and z is the velocity gradient direction.
The continuum variables at each height are obtained by coarse graining, in the same way as [25]. The instantaneous packing fraction at time t can be calculated as
where A is the area of the horizontal plane and Aki is the cross-sectional area between the ith particle and the plane of z = zk. We kept the interval of zk less than 0.5d. The macroscopic velocity field can be calculated as
where
where
where σi is the contact stress of the ith particle, and σK = −ρsϕ T is the kinetic stress [43]. The specific formula for σi is
where Vi is the volume of the ith particle,
2.2.2 Calculation of model parameters in planar shear flows
The second-order model parameters μ1, μ2, and μ3 can be calculated from the measured stress tensor and velocity gradient tensor in the DEM planar shear flows (Figure 2). By symmetry, both homogeneous and inhomogeneous flows have negligible mean vy and vz and the mean vx changes only in the z-direction. Therefore, the velocity gradient tensor has only one non-zero component:
respectively. Using
and
we can express the stress tensor (Eq. 5) as
Because
with the assumption that the flow follows the second-order fluid equation (Eq. 5).
2.3 Model calibration results from DEM planar shear flows
2.3.1 Normal stress ratio measurement
The ratios between the coarse-grained normal stresses from the planar shear tests are plotted in Figure 3. Figure 3A shows that the normal stress in the flow direction σxx is nearly the same as the normal stress in the velocity gradient direction σzz for the low I regime (I < 0.1). As I increases beyond 0.1, the magnitude of σxx becomes larger than the magnitude of σzz and their ratio σxx/σzz keeps increasing. This behavior is similar to previous findings in 2D and 3D granular systems [35, 36, 38–40, 43, 45]. On the other hand, the normal stress in the vorticity direction σyy is spread between 85% and 95% of σzz for I < 0.1. As I increases beyond 0.1, the ratio becomes even smaller as shown in Figure 3B. This is in line with previous observations [37, 43, 45].
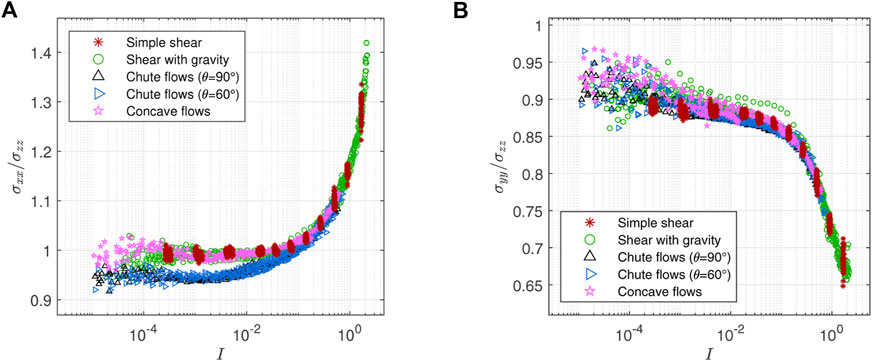
FIGURE 3. Normal stress ratios in planar shear tests: (A) σxx/σzz is near 1 for I < 0.1 and increases rapidly as I increases for I > 0.1. (B) σyy/σzz is spread between 0.85 and 0.95 for I < 0.1 and becomes even smaller as I increases for I > 0.1.
2.3.2 μ1 measurement
In the planar shear tests with one velocity component, the coefficient of the first-order derivative in the second-order model μ1 can be calculated as |σxz|/P (Eq. 15). Previously, Kim and Kamrin [25] have examined μ = |σxz/σzz| assuming P = −σzz and identified that μΘp data collapse into a master curve f(I) when p ≈ 1/6. The second-order model, however, does not assume the normal stress isotropy and the DEM stress data actually exhibits significant anisotropy. Therefore, we measure μ1 = |σxz|/P with P = −(σxx + σyy + σzz)/3 and recalibrate the master curve that μ1Θ1/6 data collapse into.
The scattered μ1 data in the μ1 vs. I plot in Figure 4A can be gathered to a single line by multiplying by
where f1(I) can be fitted by a form
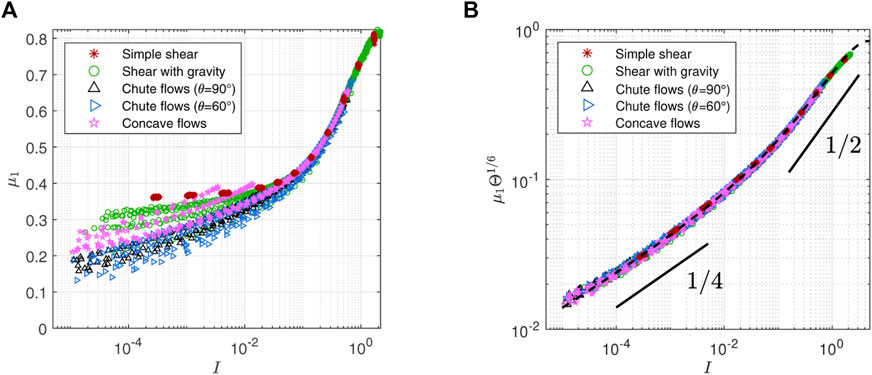
FIGURE 4. (A) Shear stress to pressure ratio μ1 = |σxz|/P vs. inertial number I. Scattered data indicate μ1 is not a function of I alone. (B) Rescaling μ1 by the dimensionless temperature to the power of 1/6 makes scattered points collapse into a master curve: μ1Θ1/6 = f1(I). Dashed trend line is f1(I) used for the FDM simulations in Section 3.
2.3.3 μ2 measurement
The coefficient of the
where f2(I) can be fitted by
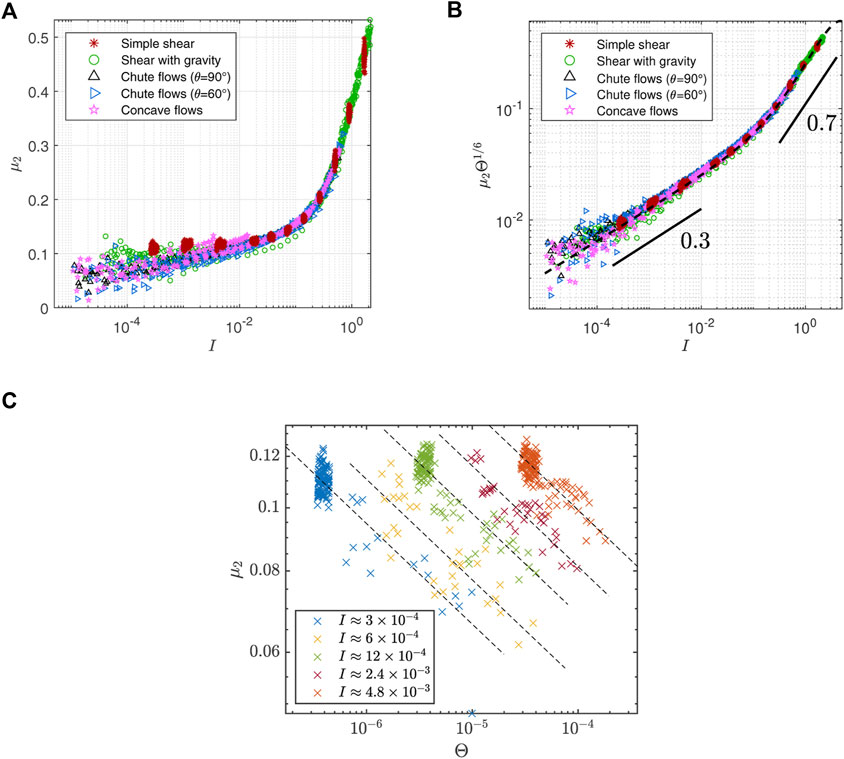
FIGURE 5. (A) μ2 vs. I in DEM simulations of planar shear flows. Scattered data indicate μ2 is not a function of I alone. (B) Rescaling μ2 by
As in [25], we plot μ2 vs. Θ at many fixed choices of I to see the functional dependence more clearly. We choose five panels of data in 0.9I* < I < 1.1I* for I* = {3 × 10–4, 6 × 10–4, 1.2 × 10–3, 2.4 × 10–3, 4.8 × 10–3}. The dashed lines in Figure 5C illustrate the best-fit lines of a multivariate linear regression whose slope is measured as −0.154 ± 0.014 which equals −p2. The actual error could be larger than this standard error measured only from the chosen data. Since p2 seems not so different from 1/6 which is the exponent of μ1 and the data collapse is strong with 1/6 in Figure 5B, we assume both μ1 and μ2 scale with the same 1/6 power of Θ for the continuum simulations in Section 3. It remains for further research to identify the exponents and the master curves more accurately.
2.3.4 μ3 measurement
The coefficient of the DW − WD term, μ3, can be calculated as (σxx − σzz)/(4P) according to Eq. 15. It represents a measure of the difference between the normal stresses in the flow direction and the velocity gradient direction; Figure 6A shows that μ3 is near or slightly above zero for I < 0.1. The only exception is the data from the chute flow geometries, which go up to 0.02. This behavior is significantly different from the non-local effect of granular temperature observed in Figure 4A because the data from the other inhomogeneous flows (the shear with gravity and the concave flows) follow the same curve as the homogeneous flow data, which means flows with different Θ can have the same μ3 for a given I. Θ is not enough to explain this deviation and there must be other factors that affect the μ3 measurement in the chute flows. We discuss another possible μ3 calibration to resolve this issue in the next section. Here, we choose to exclude the problematic chute flow data in calibrating μ3. Figure 6B shows that, as I increases, μ3 becomes negative and decreases almost linearly:
where f3(I) ≈ − 0.045I (dashed line) for μp = 0.4. For a fixed I, f3(I) would decrease (increase in magnitude) with μp as [45] has shown for homogeneous flows.
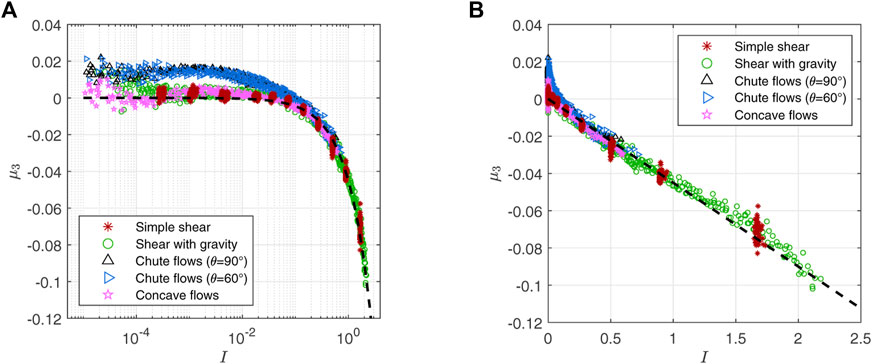
FIGURE 6. (A) μ3 = (σxx − σzz)/(4P) vs. I plot using a logarithmic scale on the I-axis. μ3 is near zero for I < 0.1 except for chute flow data which go up to 0.02. (B) As I increases, μ3 becomes negative and decreases almost linearly. Dashed trend lines in both plots indicate f3(I) = −0.045I.
2.3.5 Alternative μ3 calibration using temperature anisotropy
The chute flows’ peculiar μ3 behavior in Figure 6A may be attributed to the anisotropy of the granular temperature. This possibility suggests an alternative way to calibrate μ3 which could be implemented in future work. Let us denote the dimensionless granular temperature tensor as
where Tij is the (i, j)th element of the granular temperature tensor introduced in Eq. 8. The difference between normal elements in the flow direction and the vorticity direction, Θxx − Θyy, behaves similarly to μ3 in that the chute flow data diverge from the other data as I decreases as shown in Figure 7A. The anisotropy of the granular temperature tensor may cause the peculiar behavior of μ3, or there is another unknown macroscopic variable that affects both Θxx − Θyy and μ3 in a similar pattern. In any case, we can calibrate μ3 using this correlation. For example, adding an arbitrary function
as shown in Figure 7B. This collapse only shows the correlation between μ3 and Θxx − Θyy in our DEM data. The actual (more accurate) expression for μ3 may differ from Eq. 20. More diverse Θxx − Θyy vs. I curves are needed to clearly verify the data collapse as our current flow geometries have generated only two different branches as can be seen in Figure 7A. Also, it is not obvious how to define Θxx and Θyy in a general flow. Therefore, we leave this problem for future research and choose to use the simpler μ3 expression, Eq. 18, for the continuum simulations in Section 3.
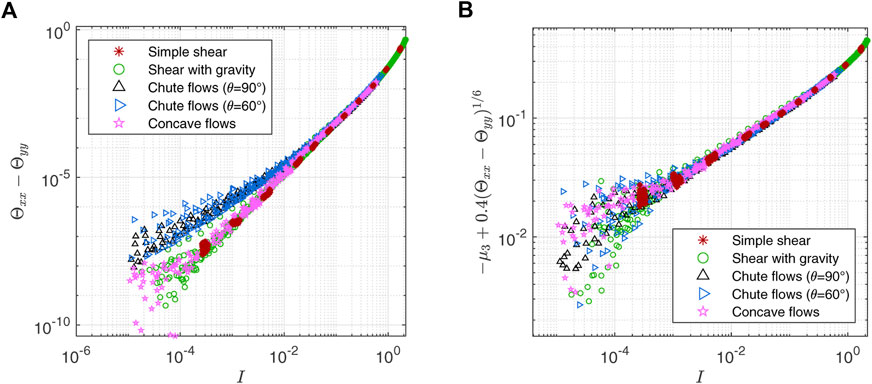
FIGURE 7. (A) Difference between two diagonal elements of dimensionless granular temperature tensor (Θxx − Θyy). Chute flow data diverge from the other data as I decreases, which is similar to the μ3 behavior in Figure 6A. (B) Adding
2.3.6 Normal stress differences
In this section, we examine the first and second normal stress differences as they are commonly measured quantities to represent the normal stress anisotropy of a material, even though we do not utilize them explicitly in our continuum model. The first normal stress difference is defined as N1 = σxx − σzz which is the same as 4μ3P (Eq. 15). Figure 8A shows that N1/P is almost zero for I < 10–1 and grows negative as I increases above 10–1. It means that, as I increases, the magnitude of stress in the flow direction |σxx| becomes larger than that in the gradient direction |σzz|. This is consistent with previous observations in 2D and 3D granular systems [35, 36, 38–40, 43, 45]. The peculiar chute data do not collapse into a single line even if the horizontal axis is changed to |σxz/σzz| as can be seen in Figure 8B.
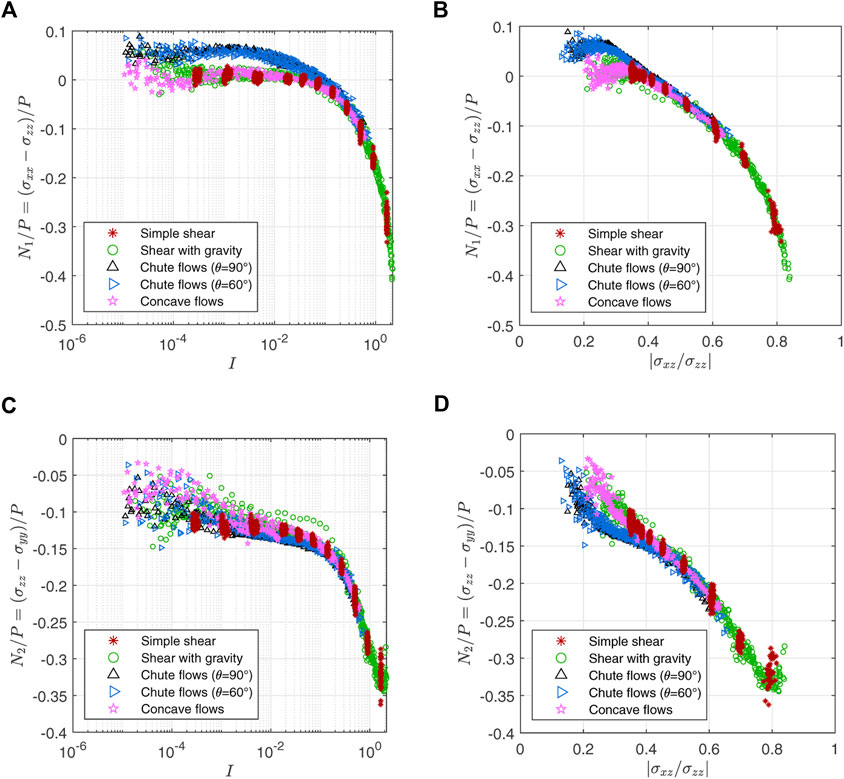
FIGURE 8. Variation of the first (N1) and second (N2) normal stress differences divided by pressure: The first row is N1/P = (σxx − σzz)/P plotted against (A) I and (B) |σxz/σzz|. N1/P is close to zero for I < 10–1 and grows negative as I increases above 10–1. The second row is N2/P = (σzz − σyy)/P plotted against (C) I and (D) |σxz/σzz|. N2 is always negative for a non-zero I
On the other hand, the second normal stress difference N2 = σzz − σyy represents normal stress anisotropy in the plane formed by the velocity gradient and the vorticity directions. N2 can be written as −(μ2 + 2μ3)P (Eq. 15). Figure 8C displays that N2/P behaves like μ1 and μ2 in that the inhomogeneous flow data are scattered and the simple shear data do not converge to zero in the quasi-static regime. However, the chute flow data are still a bit out of the trend. This peculiarity is more noticeable when the horizontal axis is |σxz/σzz| as shown in Figure 8D. All the other N2/P data seem to form a single line while the chute data with |σxz/σzz| < 0.4 have lower N2/P values. Another important feature of Figure 8C is that N2 is always negative for a non-zero I, which is in line with previous observations [37, 43, 45]. It has been known that a negative N2 makes the free surface convex up in a channel flow with no surface tension [29, 54–57]. This convex surface is also observed in our inclined chute flow simulations in Section 3.
If we look closely at Figures 8B, D where the horizontal axes are |σxz/σzz|, the chute flow data go higher than the other data in Figure 8B and lower in Figure 8D. Because the peculiar chute deviations have opposite signs in N1 and N2, we are intrigued to observe their sum N1 + N2. This variable is actually another normal stress difference σxx − σyy. Interestingly, (N1 + N2)/P exhibits a collapsed line when the horizontal axis is |σxz/σzz| canceling the above deviations as displayed in Figure 9B. Meanwhile; Figure 9A demonstrates that (N1 + N2)/P vs. I plot does not form a collapsed line and its pattern is similar to vertically flipped μ1 vs. I plot (Figure 4A). Therefore, (N1 + N2)/P may depend only on |σxz/σzz| or μ1.
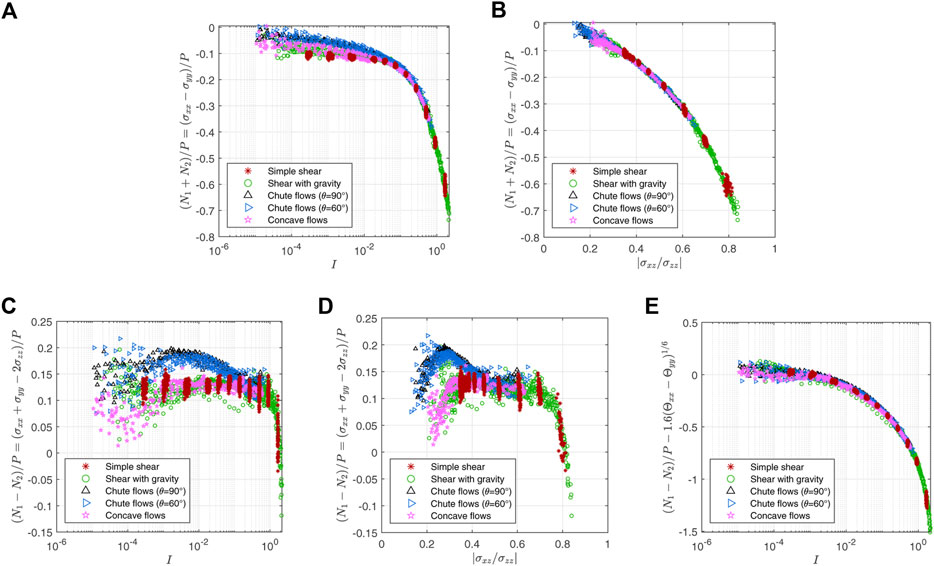
FIGURE 9. Sum and difference of the first (N1) and second (N2) normal stress differences divided by pressure: (N1 + N2)/P = (σxx − σyy)/P exhibits non-locality when plotted against I (A), but it forms a collapsed line when plotted against |σxz/σzz| (B). Plotting (N1 − N2)/P = (σxx + σyy −2σzz)/P against (C) I or (D) |σxz/σzz| does not form a data collapse. (E) Subtracting an arbitrary function
If (N1 + N2)/P is indeed a function of |σxz/σzz| or μ1, we need one more equation to represent N1 and N2 separately. (N1 − N2)/P may provide that equation. However, Figures 9C, D show that (N1 − N2)/P plots whose horizontal axis is I or |σxz/σzz| do not have a well-collected collapse in contrast to the collapse seen in Figure 9B. (N1 − N2)/P is almost a constant between 0.1 and 0.15 except for the chute data which go up to 0.2. It seems as if the peculiarity of the chute data is canceled in the (N1 + N2)/P plot and pushed into the (N1 − N2)/P plot to become more conspicuous. Although (N1 − N2)/P cannot be written as a function of a single dimensionless variable, we can still utilize Θxx − Θyy in Figure 7A. For example, Figure 9E demonstrates that subtracting
Using (N1 + N2)/P and (N1 − N2)/P data collapses, we may solve for μ2 and μ3 in terms of I, Θ and Θxx − Θyy. However, as mentioned above, Θxx − Θyy in a more complex flow geometry is not simple to define. Also, the data collapse in 9E is not yet clear because it is achieved only for two big branches of (N1 − N2)/P while adding an arbitrary function with two fitting parameters. Thus, further research is needed to build a more general rheological model that incorporates the temperature anisotropy and its impact on (N1 − N2)/P.
3 Model validation: Inclined chute flows
In this section, we show how our second-order non-local model can be applied to a more complex flow geometry with less symmetry. For that, we use data from DEM simulations of rough-walled inclined chute flows (Figure 10A) gathered in [25]. Unlike the planar shear flows used in calibration where the time-averaged macroscopic quantities depend only on the height (z), in this inclined chute geometry, the mean fields depend on two spatial coordinates (y and z). Moreover, the mean velocity fields have three non-zero components forming a secondary flow. The expression for stress becomes more complicated than Eq. 14 because the velocity gradient tensor now has six non-zero terms (the derivatives with respect to the downstream coordinate (x) are still negligible due to symmetry). We demonstrate that our model calibrated from the simple tests can be applied to this complex case. We run finite difference method (FDM) simulations of the full partial differential equation (PDE) system of the model, including Eq. 5 and continuum momentum balance to compare with DEM results. Unlike [25], the current model is able to describe the transverse secondary flow which is perpendicular to the downstream direction and could not be predicted by the first-order model.
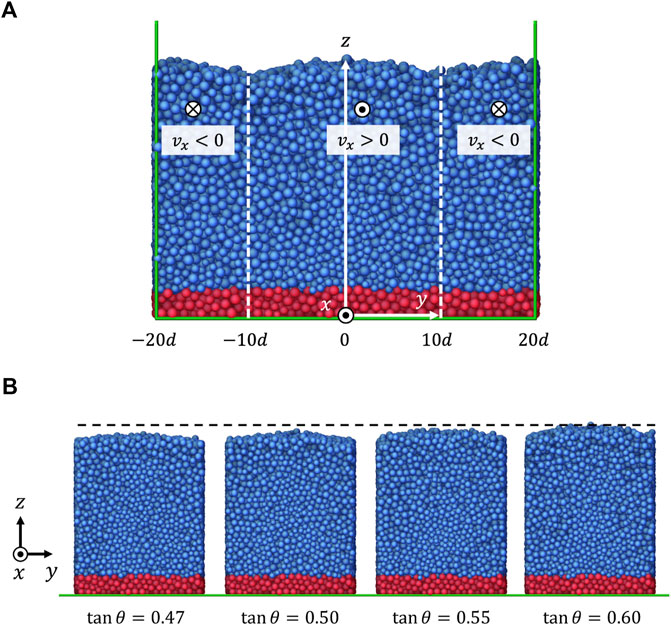
FIGURE 10. (A) DEM simulation of inclined chute flow with θ = tan−1(0.60). Green lines are boundaries of the DEM simulation domain which is periodic in x and y directions. vx is positive in the middle zone (−10d < y <10d) where gravity is
3.1 DEM simulation settings for inclined chute flows
Using the same granular material used in the planar shear tests, we run the inclined chute flow simulations for four inclination angles: θ = tan−1(0.47), tan−1(0.50), tan−1(0.55), and tan−1(0.60). Figure 10A shows a snapshot of the θ = tan−1(0.60) case. The size of the system is Lx = 120d, Ly = 40d. The simulation domain (green lines) is periodic in the x and y-directions. A total of 131,566 particles are simulated. For a rough frictional bottom, the particles whose center height is lower than z = 3d (colored red in Figure 10A) are frozen; their translational and rotational velocities are fixed to zero. Except for these fixed particles, there are 115,619 mobile particles (colored blue in Figure 10A). Gravity is applied differently in the middle zone (−10d < y < 10d) and the outer zone (y < − 10d or y > 10d). In the middle zone, gravity is tilted in the x-direction
At steady state, we measure the continuum fields
Figure 10B illustrates snapshots of the simulations with different inclination angles viewed from the positive x-axis. It shows that the maximum height of the material increases as the inclination angle increases. This volume increase can be explained by the ϕ(μ) relation found in [25], which claims that the volume density decreases as μ increases at steady state. As discussed previously, it is also observed that the shape of the top surface is convex such that the grains in the middle of the surface keep falling to the side boundaries where the surface is lower. This convex surface is formed possibly because the second normal stress difference N2 is negative.
3.2 Continuum simulation methods
In this section, stress and velocity fields in inclined chute flows are predicted by the second-order non-local model using an explicit FDM scheme. We compute the stress field σ using Eq. 5 combined with Eqs. 16-18.
To predict the flow, we numerically solve the Cauchy momentum equation given by
where
We use the projection method which is an efficient algorithm for solving the time-dependent Navier-Stokes equations in incompressible flows [58]. It needs to be modified a little from Chorin’s original projection method because our fluid is not incompressible. This algorithm allows us to calculate the pressure field easily by decoupling the pressure and the velocity fields. We decompose the stress into σ′ = σ + PI and −PI which results in two differential equations connected by an intermediate velocity v*. The first step of the projection method algorithm is to update v* from the current velocity vn through
where Δt is the FDM time step. The next step of the algorithm is to correct v* to obtain the velocity in the next step vn+1:
where the pressure in the next step Pn+1 can be obtained by solving a Poisson-type equation. We multiply Eq. 23 by ρ and take the divergence. We assume ∇ ⋅ (ρvn+1) = 0 because we are interested in steady state where the (Eulerian-frame) density field does not change in time
The pressure should be symmetrically distributed across the side boundaries due to the specificity of the geometry. The bottom pressure should satisfy
Using MATLAB, we numerically solve the decomposed momentum equations, Eqs 22, 23, on a 20 × 40 stress grid. We use the local density measured in the DEM simulations. Since we do not know how to predict Θ, we simply insert the DEM data of Θ into μ1(I, Θ) and μ2(I, Θ) calibrated as Eqs 16, 17 respectively to obtain the stress tensor defined in Eq. 5. The granular temperature should follow a separate PDE, “fluctuation energy balance” in the kinetic theory [21, 22, 59], but its form is still under debate in the dense limit. To predict Θ, this PDE should be clarified in the future. The general form of the fluctuation energy balance is in Supplementary Material. We use Eq. 18 for μ3(I). Pressure is obtained from the Poisson equation, Eq. 24. We input the traction force extracted from the DEM data at the top of the FDM domain because our FDM grid is rectangular and does not conform to the bulged shape of the free surface. The velocity is updated until the system’s average velocity reaches a steady state.
3.3 Analysis of model predictions
We compare the results of the DEM simulations and the continuum simulations varying the inclination angle from θ = tan−1(0.47) to tan−1(0.60). Figure 11 illustrates the transverse velocity fields (vy, vz) from the DEM data (upper row) and the FDM solutions to the second-order model (lower row). The predicted transverse velocity fields show remarkable similarity to the DEM velocity data especially for the faster flows with larger inclination angles. We can see that the vortex location (center of the rotational flow) and the magnitude of transverse velocity (length of the arrows) are successfully predicted. The second-order model’s ability to predict these transverse flows is a huge improvement from the first-order model.
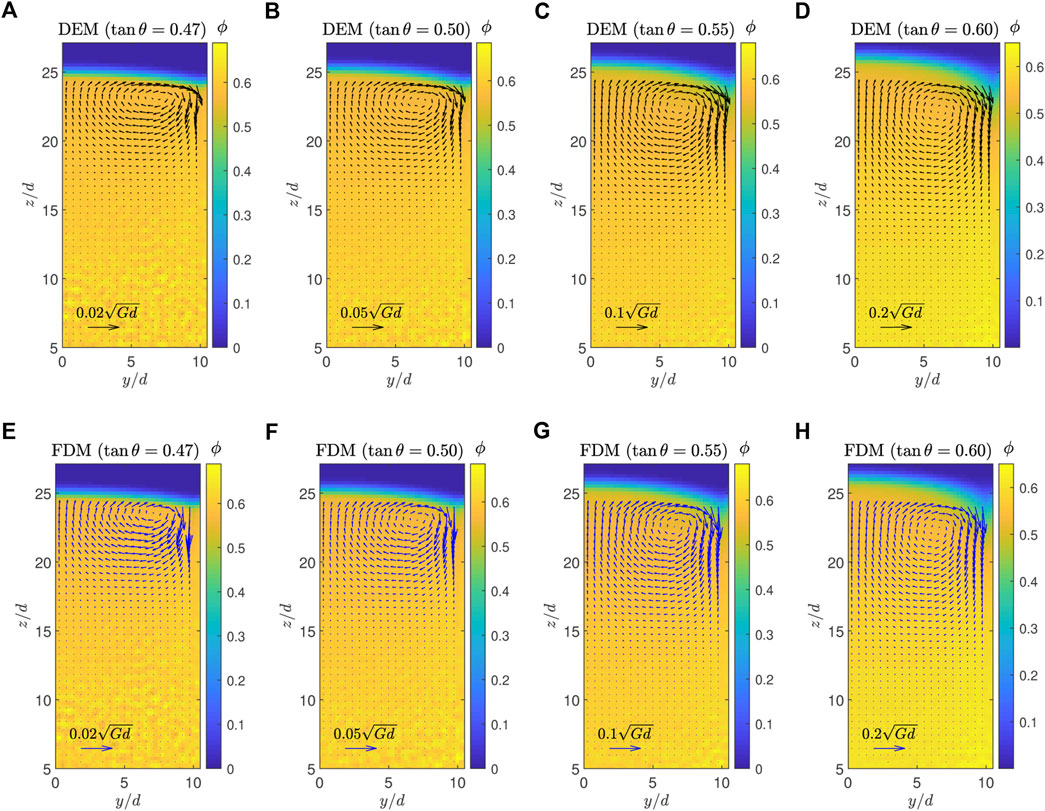
FIGURE 11. Transverse velocity comparison between the DEM simulations (A–D) and the FDM simulations using the second-order model (E–H): (A) DEM with tan θ = 0.47, (E) FDM with tan θ = 0.47, (B) DEM with tan θ = 0.50, (F) FDM with tan θ = 0.50, (C) DEM with tan θ = 0.55, (G) FDM with tan θ = 0.55, (D) DEM with tan θ = 0.60, and (H) FDM with tan θ = 0.60. Arrows indicate (vy, vz) and their length scales are displayed at the bottom of the figures. Packing fraction is shown as color in the background.
This predictive power mostly comes from μ2 in our geometry. μ3 has a relatively smaller impact on the results. If we keep μ3 and set μ2 to zero, the prediction becomes totally different from DEM. However, if we keep μ2 and set μ3 to zero, the FDM simulation still generates similar secondary flows even though the results are not as accurate as the full second-order model’s. These results are shown in Supplementary Material.
The solution of the first-order model must have zero transverse velocities for a free surface flow (no surface traction). Without μ2 and μ3, v = (vx(y, z), 0, 0) can satisfy the momentum balance (Eq. 21), which is discussed in Supplementary Material. If an external traction is applied, the first-order model can have non-zero vy and vz. In this case, σyz is no longer zero and transverse velocities are generated to match this stress. However, we have checked that the first-order models’ FDM solutions to the transverse velocities are completely different from the DEM data. The results can be found in Supplementary Material.
Figure 11E indicates that the transverse velocity prediction slightly mismatches the DEM data for tan θ = 0.47. That is, possibly because the transverse velocity is too small compared to the error of the model calibration, or the highest grid points are too close to the material surface where the packing fraction drops rapidly and the granular temperature anisotropy is strong. We could not lower the highest grid points as the vortex location is about 2d below the surface for tan θ = 0.47. This issue may be resolved by a more accurate modeling including the whole granular temperature tensor and a deformable grid to effectively exclude areas where ϕ drops rapidly.
The downstream velocity vx is accurately predicted by our model as the first-order non-local model did in [25]. This is expected because the shear stress associated with D is determined by a function μ1(I, Θ) which is almost identical to the previous μ(I, Θ) while the other higher-order terms have little impact on vx. Figures 12A–D illustrates the contours of
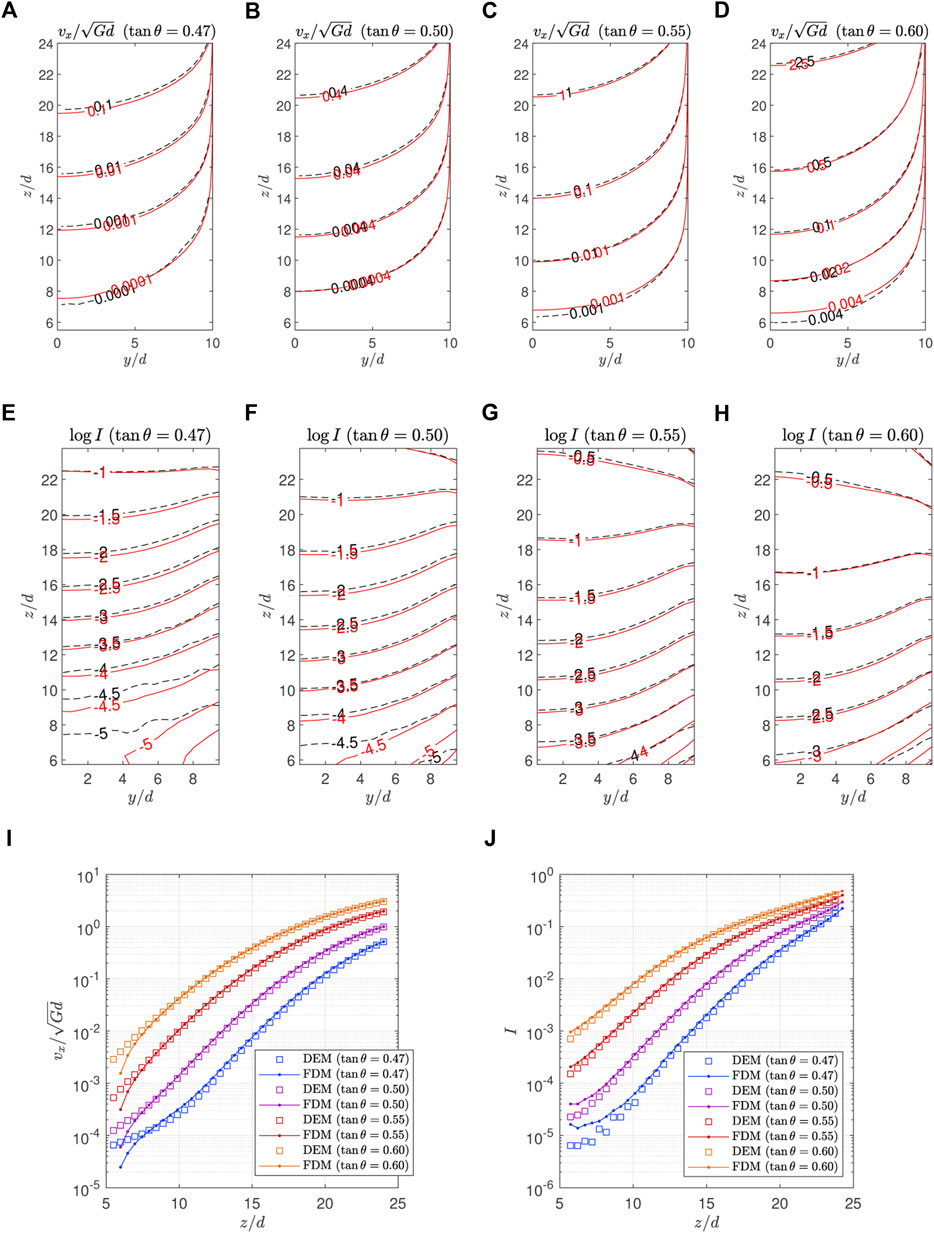
FIGURE 12. Comparison of (A–D)
The second-order model’s pressure P is obtained by solving the Poisson equation, Eq. 24, with the boundary conditions described in Section 3.2. Figure 13A visualizes the results for tan θ = 0.60. If the granular material is static and its density is uniform, the pressure increases linearly in proportion to the depth H − z where H is the surface height. However, the pressure in the inclined chute flow slightly deviates from this lithostatic pressure because the surface becomes not flat due to the normal stress anisotropy. To make this subtle deviation stand out, we subtract a linear function
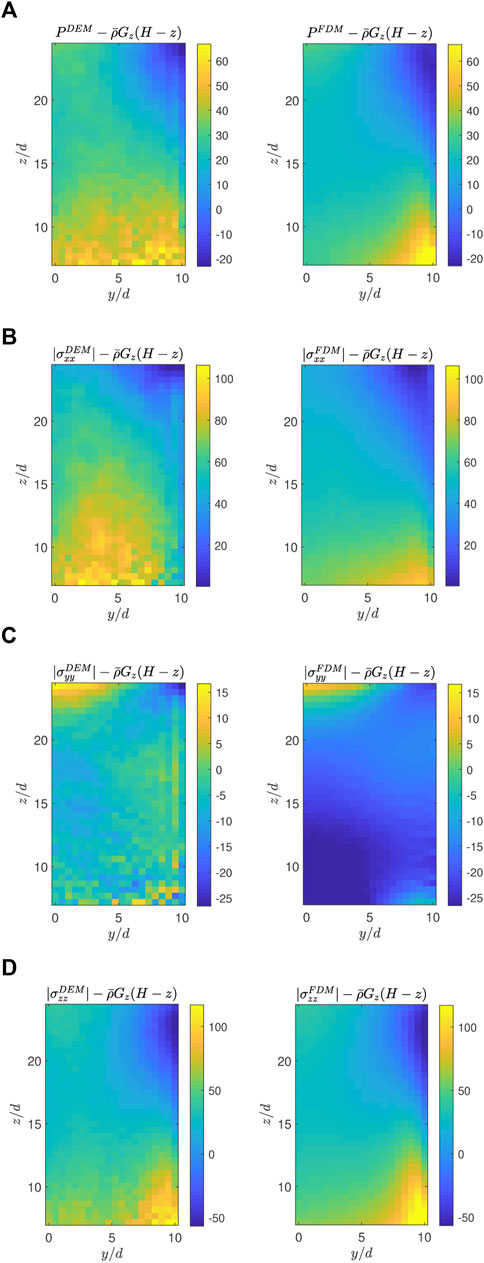
FIGURE 13. Comparison of pressure and normal stress maps between the DEM simulation (left) and the FDM simulation using the second-order model (right) with tan θ = 0.60: (A)
From the pressure, the granular temperature, and the velocity field, the stress tensor is computed through Eq. 5. Overall, the predictions of the second-order model on stress are well matched with the DEM results. Figure 13 illustrates the differences between the normal stresses and the linear reference pressure for tan θ = 0.60. The second-order model successfully predicts the large deviations of σxx and σzz from the linear reference pressure as shown in Figures 13B, D. Figure 13C demonstrates that σyy is flatter than the other components, which is also well captured by the FDM simulation. The patterns of σyy seem different in Figure 13C, but the actual error is insignificant considering that the colorbar range is narrower than the other plots.
The off-diagonal elements of the stress tensor are also well predicted by the second-order model. Figure 14 shows that the model predicts the gradual variations of σxy/P, σxz/P, and σyz/P accurately in the inclined chute flow with tan θ = 0.60. In particular, it is interesting to see the model’s ability to estimate σyz in Figure 14C while having accurate velocity fields because this component is much smaller than the other stresses and predicted to be zero in the first-order model. The first-order model may produce similar σxy, σxz and pressure patterns. However, it cannot predict the normal stress differences and σyz because it predicts zero transverse velocities and a flat surface, which results in an isotropic pressure and zero σyz.
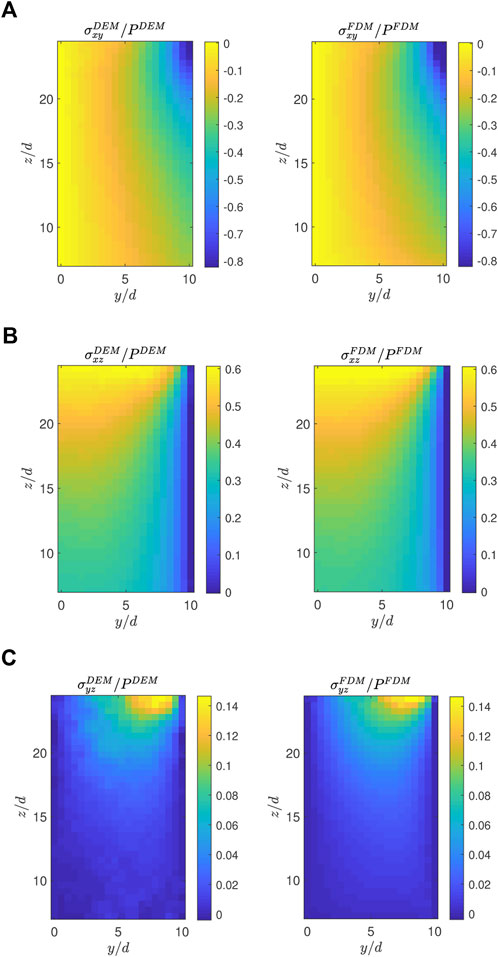
FIGURE 14. Comparison of off-diagonal stress maps between the DEM simulation (left) and the FDM simulation using the second-order model (right) with tan θ =0.60: (A) σxy/P, (B) σxz/P, and (C) σyz/P.
4 Conclusion
Combining the μ(I, Θ) model and the second-order fluid model, we have proposed a second-order temperature-dependent model for three-dimensional granular flows that can describe both non-local phenomena (arising from the diffusion implicit in the temperature field) and broken codirectionality. From DEM data of planar shear tests, we have identified the model parameters μ1, μ2, and μ3 as functions of I and Θ. As in the μ(I, Θ) model, μ1 multiplied by
In addition, we have examined the first and second normal stress differences N1 and N2 in the same geometry. N2/P is negative and decreases as I increases, exhibiting Θ dependence similar to μ1 and μ2. By adding N1/P and N2/P together, a clear data collapse has been achieved forming a function of the shear-to-normal stress ratio. We have also seen the possibility that (N1 − N2)/P is a function of I and Θxx − Θyy, but more rigorous verification is needed in the future.
Using the model parameters calibrated from the planar shear flows, we have validated the second-order model in the rough-walled inclined chute geometry, which is more complex due to less symmetry. We have run FDM simulations using the projection method inputting DEM traction at the upper boundary and DEM Θ for the whole domain. Our second-order model successfully describes the the flow field including the transverse secondary flows which the first-order models fail to capture. The location, size, and shape of the flow vortex in the secondary flow is well matched by the FDM simulations including how the vortex changes with the inclination angle. We have also found that μ2 plays a more important role than μ3 in predicting the transverse velocities even if μ2 and μ3 together have better predictions. The second-order model, like the μ(I, Θ) model, has also accurately predicted the downstream velocity fields including the quasi-static creeping regime. Moreover, the second-order model has generated almost identical pressure and normal stress patterns as the DEM data.
Although we have made significant progress towards more accurate granular rheology by combining the μ(I, Θ) relation and a second-order fluid model to describe non-locality and broken codirectionality, there are still puzzles to be solved. For example, the governing equation of the granular temperature should be precisely identified to complete the model. While the current model utilizes a scalar temperature, the aforementioned potential role of temperature tensor anisotropy suggests a tensorial heat equation may be needed to go beyond the accuracy level of the model shown herein. Also, the constitutive relation could be further intertwined with the granular temperature tensor and the strain rate tensor. Solving these problems will refine our model, enabling even more accurate and universal prediction of granular flows.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
SK and KK contributed to the conception of the study and the design of tests. SK performed all numerical simulations, conducted the data analysis, and wrote the first draft. KK contributed to draft revisions. SK and KK approved the submitted work.
Funding
SK and KK acknowledge funding from Army Research Office grant W911NF-19-1-0431.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1092233/full#supplementary-material
References
1.GDR MiDi. On dense granular flows. The Eur Phys J E (2004) 14:341–65. doi:10.1140/epje/i2003-10153-0
2. da Cruz F, Emam S, Prochnow M, Roux JN, Chevoir F. Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys Rev E (2005) 72:021309. doi:10.1103/PhysRevE.72.021309
3. Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature (2006) 441:727–30. doi:10.1038/nature04801
4. Jop P, Forterre Y, Pouliquen O. Initiation of granular surface flows in a narrow channel. Phys Fluids (2007) 19:088102. doi:10.1063/1.2753111
5. Koval G, Roux JN, Corfdir A, Chevoir F. Annular shear of cohesionless granular materials: from the inertial to quasistatic regime. Phys Rev E (2009) 79:021306. doi:10.1103/PhysRevE.79.021306
6. Komatsu TS, Inagaki S, Nakagawa N, Nasuno S. Creep motion in a granular pile exhibiting steady surface flow. Phys Rev Lett (2001) 86:1757–60. doi:10.1103/PhysRevLett.86.1757
7. Martinez E, Gonzalez-Lezcano A, Batista-Leyva AJ, Altshuler E. Exponential velocity profile of granular flows down a confined heap. Phys Rev E (2016) 93:062906. doi:10.1103/PhysRevE.93.062906
8. Tang Z, Brzinski TA, Shearer M, Daniels KE. Nonlocal rheology of dense granular flow in annular shear experiments. Soft Matter (2018) 14:3040–8. doi:10.1039/C8SM00047F
9. Falk ML, Langer JS. Dynamics of viscoplastic deformation in amorphous solids. Phys Rev E (1998) 57:7192–205. doi:10.1103/PhysRevE.57.7192
10. Lemaître A. Rearrangements and dilatancy for sheared dense materials. Phys Rev Lett (2002) 89:195503. doi:10.1103/PhysRevLett.89.195503
11. Lois G, Lemaître A, Carlson JM. Numerical tests of constitutive laws for dense granular flows. Phys Rev E (2005) 72:051303. doi:10.1103/PhysRevE.72.051303
12. Aranson IS, Tsimring LS. Continuum description of avalanches in granular media. Phys Rev E (2001) 64:020301. doi:10.1103/PhysRevE.64.020301
13. Aranson IS, Tsimring LS. Continuum theory of partially fluidized granular flows. Phys Rev E (2002) 65:061303. doi:10.1103/PhysRevE.65.061303
14. Volfson D, Tsimring LS, Aranson IS. Order parameter description of stationary partially fluidized shear granular flows. Phys Rev Lett (2003) 90:254301. doi:10.1103/PhysRevLett.90.254301
15. Goyon J, Colin A, Ovarlez G, Ajdari A, Bocquet L. Spatial cooperativity in soft glassy flows. Nature (2008) 454:84–7. doi:10.1038/nature07026
16. Bocquet L, Colin A, Ajdari A. Kinetic theory of plastic flow in soft glassy materials. Phys Rev Lett (2009) 103:036001. doi:10.1103/PhysRevLett.103.036001
17. Kamrin K, Koval G. Nonlocal constitutive relation for steady granular flow. Phys Rev Lett (2012) 108:178301. doi:10.1103/PhysRevLett.108.178301
18. Henann DL, Kamrin K. A predictive, size-dependent continuum model for dense granular flows. Proc Natl Acad Sci U S A (2013) 110:6730–5. doi:10.1073/pnas.1219153110
19. Kamrin K, Henann DL. Nonlocal modeling of granular flows down inclines. Soft Matter (2015) 11:179–85. doi:10.1039/c4sm01838a
20. Zhang Q, Kamrin K. Microscopic description of the granular fluidity field in nonlocal flow modeling. Phys Rev Lett (2017) 118:058001. doi:10.1103/PhysRevLett.118.058001
21. Jenkins JT, Savage SB. A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J Fluid Mech (1983) 130:187–202. doi:10.1017/S0022112083001044
22. Lun CKK, Savage SB, Jeffrey DJ, Chepurniy N. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J Fluid Mech (1984) 140:223–56. doi:10.1017/S0022112084000586
23. Garzó V, Dufty JW. Dense fluid transport for inelastic hard spheres. Phys Rev E (1999) 59:5895–911. doi:10.1103/PhysRevE.59.5895
24. Jenkins JT, Berzi D. Dense inclined flows of inelastic spheres: Tests of an extension of kinetic theory. Granular Matter (2010) 12:151–8. doi:10.1007/s10035-010-0169-8
25. Kim S, Kamrin K. Power-law scaling in granular rheology across flow geometries. Phys Rev Lett (2020) 125:088002. doi:10.1103/PhysRevLett.125.088002
26. Félix G, Thomas N. Relation between dry granular flow regimes and morphology of deposits: formation of levées in pyroclastic deposits. Earth Planet Sci Lett (2004) 221:197–213. doi:10.1016/S0012-821X(04)00111-6
27. Deboeuf S, Lajeunesse E, Dauchot O, Andreotti B. Flow rule, self-channelization, and levees in unconfined granular flows. Phys Rev Lett (2006) 97:158303. doi:10.1103/PhysRevLett.97.158303
28. Takagi D, McElwaine JN, Huppert HE. Shallow granular flows. Phys Rev E (2011) 83:031306. doi:10.1103/PhysRevE.83.031306
29. McElwaine JN, Takagi D, Huppert HE. Surface curvature of steady granular flows. Granular Matter (2012) 14:229–34. doi:10.1007/s10035-012-0339-y
30. Gutam KJ, Mehandia V, Nott PR. Rheometry of granular materials in cylindrical Couette cells: Anomalous stress caused by gravity and shear. Phys Fluids (2013) 25:070602. doi:10.1063/1.4812800
31. Fischer D, Börzsönyi T, Nasato DS, Pöschel T, Stannarius R. Heaping and secondary flows in sheared granular materials. New J Phys (2016) 18:113006. doi:10.1088/1367-2630/18/11/113006
32. Krishnaraj KP, Nott PR. A dilation-driven vortex flow in sheared granular materials explains a rheometric anomaly. Nat Commun (2016) 7:10630. doi:10.1038/ncomms10630
33. Dsouza PV, Nott PR. Dilatancy-driven secondary flows in dense granular materials. J Fluid Mech (2021) 914:A36. doi:10.1017/jfm.2020.1029
34. Mehandia V, Gutam KJ, Nott PR. Anomalous stress profile in a sheared granular column. Phys Rev Lett (2012) 109:128002. doi:10.1103/PhysRevLett.109.128002
35. Walton OR, Braun RL. Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. J Rheology (1986) 30:949–80. doi:10.1122/1.549893
36. Campbell CS. The stress tensor for simple shear flows of a granular material. J Fluid Mech (1989) 203:449–73. doi:10.1017/S0022112089001540
37. Silbert LE, Ertaş D, Grest GS, Halsey TC, Levine D, Plimpton SJ. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys Rev E (2001) 64:051302. doi:10.1103/PhysRevE.64.051302
38. Alam M, Luding S. Rheology of bidisperse granular mixtures via event-driven simulations. J Fluid Mech (2003) 476:69–103. doi:10.1017/S002211200200263X
39. Alam M, Luding S. First normal stress difference and crystallization in a dense sheared granular fluid. Phys Fluids (2003) 15:2298–312. doi:10.1063/1.1587723
40. Alam M, Luding S. Non-newtonian granular fluid: simulation and theory. In: R Garcia-Rojo, HJ Herrmann, and S McNamara, editors. Powders and grains (2005). 1141–4.
41. Depken M, Lechman JB, Hecke MV, Saarloos WV, Grest GS. Stresses in smooth flows of dense granular media. Europhysics Lett (Epl) (2007) 78:58001. doi:10.1209/0295-5075/78/58001
42. Sun JIN, Sundaresan S. A constitutive model with microstructure evolution for flow of rate-independent granular materials. J Fluid Mech (2011) 682:590–616. doi:10.1017/jfm.2011.251
43. Weinhart T, Hartkamp R, Thornton AR, Luding S. Coarse-grained local and objective continuum description of three-dimensional granular flows down an inclined surface. Phys Fluids (2013) 25:070605. doi:10.1063/1.4812809
44. Saha S, Alam M. Normal stress differences, their origin and constitutive relations for a sheared granular fluid. J Fluid Mech (2016) 795:549–80. doi:10.1017/jfm.2016.237
45. Srivastava I, Silbert LE, Grest GS, Lechman JB. Viscometric flow of dense granular materials under controlled pressure and shear stress. J Fluid Mech (2021) 907:A18. doi:10.1017/jfm.2020.811
46. Rycroft CH, Kamrin K, Bazant MZ. Assessing continuum postulates in simulations of granular flow. J Mech Phys Sol (2009) 57:828–39. doi:10.1016/j.jmps.2009.01.009
47. Bhateja A, Khakhar DV. Rheology of dense granular flows in two dimensions: Comparison of fully two-dimensional flows to unidirectional shear flow. Phys Rev Fluids (2018) 3:062301. doi:10.1103/PhysRevFluids.3.062301
48. Wu WT, Aubry N, Antaki JF, Massoudi M. Normal stress effects in the gravity driven flow of granular materials. Int J Non-Linear Mech (2017) 92:84–91. doi:10.1016/j.ijnonlinmec.2017.03.016
49. Cundall PA, Strack ODL. A discrete numerical model for granular assemblies. Géotechnique (1979) 29:47–65. doi:10.1680/geot.1979.29.1.47
50. Kamrin K, Koval G. Effect of particle surface friction on nonlocal constitutive behavior of flowing granular media. Comput Part Mech (2014) 1:169–76. doi:10.1007/s40571-014-0018-3
51. Liu D, Henann DL. Size-dependence of the flow threshold in dense granular materials. Soft Matter (2018) 14:5294–305. doi:10.1039/c8sm00843d
52. Gaume J, Chambon G, Naaim M. Quasistatic to inertial transition in granular materials and the role of fluctuations. Phys Rev E (2011) 84:051304. doi:10.1103/PhysRevE.84.051304
53. Christoffersen J, Mehrabadi M, Nemat-Nasser S. A micromechanical description of granular material behavior. J Appl Mech (1981) 48:339–44. doi:10.1115/1.3157619
54. Wineman AS, Pipkin A. Slow viscoelastic flow in tilted troughs. Acta Mech (1966) 2:104–15. doi:10.1007/bf01176732
55. Tanner RI. Some methods for estimating the normal stress functions in viscometric flows. Trans Soc Rheol (1970) 14:483–507. doi:10.1122/1.549175
56. Kuo Y, Tanner R. On the use of open-channel flows to measure the second normal stress difference. Rheol Acta (1974) 13:443–56. doi:10.1007/bf01521740
57. Couturier E, Boyer F, Pouliquen O, Guazzelli E. Suspensions in a tilted trough: second normal stress difference. J Fluid Mech (2011) 686:26–39. doi:10.1017/jfm.2011.315
58. Chorin AJ. Numerical solution of the navier-stokes equations. Math Comput (1968) 22:745–62. doi:10.1090/s0025-5718-1968-0242392-2
Keywords: granular materials, soft matter, granular flows, rheology, fluid dynamics, continuum mechanics, non-newtonian fluid, discrete element method
Citation: Kim S and Kamrin K (2023) A second-order non-local model for granular flows. Front. Phys. 11:1092233. doi: 10.3389/fphy.2023.1092233
Received: 07 November 2022; Accepted: 04 January 2023;
Published: 17 January 2023.
Edited by:
Joshua Albert Dijksman, Wageningen University and Research, NetherlandsReviewed by:
Hisao Hayakawa, Kyoto University, JapanAbram H Clark, Naval Postgraduate School, United States
János Török, Budapest University of Technology and Economics, Hungary
Raúl Cruz Hidalgo, University of Navarra, Spain
Copyright © 2023 Kim and Kamrin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ken Kamrin, a2thbXJpbkBtaXQuZWR1
 Seongmin Kim
Seongmin Kim Ken Kamrin
Ken Kamrin