
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 02 February 2023
Sec. Atomic and Molecular Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1086980
This article is part of the Research TopicEditor’s Challenge in Atomic and Molecular Physics: Applications and Advances in Fundamental PhysicsView all 4 articles
Theories that extend the Standard Model of particle physics often introduce new interactions that violate charge-parity (CP) symmetry. Charge-parity-violating effects within an atomic nucleus can be probed by measuring its nuclear magnetic quadrupole moment (MQM). The sensitivity of such a measurement is enhanced when using a heavy polar molecule containing a nucleus with quadrupole deformation. We determine how the energy levels of a molecule are shifted by the magnetic quadrupole moment and how those shifts can be measured. The measurement scheme requires molecules in a superposition of magnetic sub-levels that differ by many units of angular momentum. We develop a generic scheme for preparing these states. Finally, we consider the sensitivity that can be reached, showing that this method can reduce the current uncertainties on several charge-parity-violating parameters.
The observed baryon asymmetry in the Universe is one of the important unsolved problems in cosmology. Possible models that can lead to this asymmetry are discussed in Refs. [1, 2]. One such model is due to Sakharov, where the asymmetry can arise under conditions of baryon number violation, C and CP-violation, and thermal non-equilibrium [3]. The Standard Model cannot account for the observed asymmetry [4], motivating theories beyond the Standard Model to introduce new sources of CP-violation [5]. Equivalently, since these theories respect CPT symmetry [6], they introduce new sources of T-violation. An elementary particle with a permanent electric dipole moment (EDM) violates both P and T symmetries [7, 8], and measurements of these EDMs have been exceptionally fruitful in testing physics beyond the Standard Model. Paramagnetic molecules such as 174YbF [9], 232ThO [10] and 180HfF+ [11] are excellent probes of P,T-violating physics. These molecules are primarily sensitive to the electron EDM, de, and the scalar P,T-violating electron-nucleon interaction, CS. The most precise measurement thus far, in ThO, constrains new CP-violating interactions to mass scales above 30 TeV in some models and above 3 TeV in most [10].
These electron EDM measurements use paramagnetic molecules with a heavy atom of zero nuclear spin, I = 0. As a result, they are not sensitive to P,T-violating nuclear moments1. Instead, one can use isotopes with nuclear spin to probe CP-violating effects within the nucleus. The lowest-order P,T-violating nuclear moment is the EDM (which requires I ≥ 1/2), but that is effectively screened by the outer electrons [13]. The screening is incomplete due to the finite size of the nucleus [12], but in paramagnetic atoms and molecules the remaining effect (the nuclear Schiff moment) is negligible compared to the contribution from the electron EDM. Conversely, in diamagnetic atoms and molecules the contribution from the electron EDM is small and the Schiff moment can be probed. At present, the most stringent limits on the size of nucleon EDMs and P,T-violating nucleon-nucleon interactions come from a measurement of the nuclear Schiff moment of 199Hg [14], a diamagnetic atom with I = 1/2. An experiment is being constructed that aims to improve on these constraints by measuring the Schiff moment of 205Tl in a beam of TlF molecules, taking advantage of the strong polarisation in an electric field due to the small splitting between opposite parity rotational states [15]. Since the Schiff moment is a screened effect, it is interesting to consider the effect of higher-order moments. The next-order nuclear moment of interest is the magnetic quadrupole moment (MQM) (requires I ≥ 1), which is not screened and can contribute significantly to the P,T-violating energy shifts of atoms and molecules.
A spherical nucleus can acquire an MQM from the EDM of its valence proton or neutron [16], or from P,T-odd nucleon-nucleon interactions involving the valence nucleon [17]. If we denote the total nuclear MQM as M and the contribution to the MQM from a single proton or neutron as
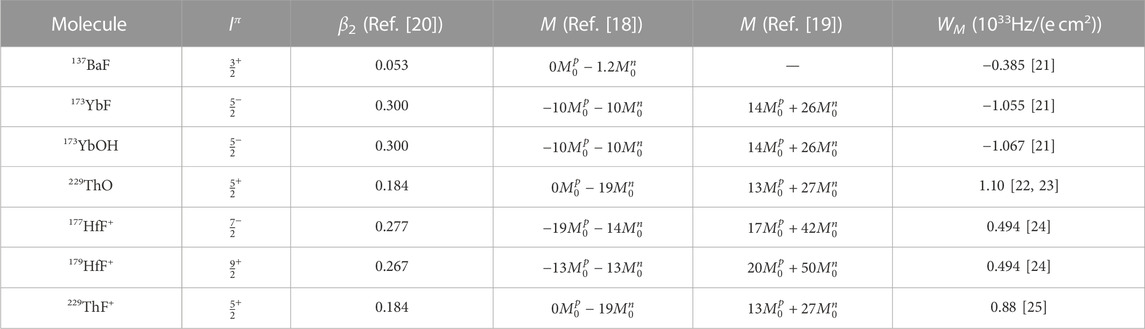
TABLE 1. Properties of certain molecules relevant for a nuclear MQM measurement. The selected molecules are ones currently being used or explored for electron EDM measurements. The P,T-violating energy shift due to a nuclear MQM, M, is proportional to WMM, where WM is the interaction strength. We list the nuclear spin, parity, quadrupole deformation (β2), M, and WM. The collective enhancement of M due to the deformation of the nucleus was calculated in [18, 19] using different nuclear orbitals, and expressed in terms of the single-nucleon contributions to the MQM,
In this paper, we consider how to make a measurement of nuclear MQMs using heavy, polar molecules. We first calculate the size of energy shifts in various states of a molecule due to the nuclear MQM. We then describe a procedure for preparing the molecules in the states most sensitive to the MQM. In particular, we introduce a generic state preparation and readout method which utilises the large tensor Stark shifts in molecules to induce a high-order coupling between the two states used for the measurement. Finally, we assess the sensitivity of such an experiment to CP-violating parameters in the hadronic sector, and compare this to other experiments such as Schiff moment or neutron EDM measurements. Our analysis applies to a wide range of molecules, though we will often use 173YbF as a specific example. The nuclear spin of 173Yb is 5/2, while that of 19F is 1/2. We note that the advantages of polyatomic molecules for measuring MQMs and other CP-violating effects are outlined in Ref. [26].
We consider a molecule in a 2Σ state with electron spin S and rotational angular momentum N. The nucleus of interest has spin I. The molecule is in an electric field
where Hrot = BN2 is the rotational energy,
where n is a unit vector along the internuclear axis and
where T(1)(S, I(2)) is a rank-1 tensor constructed from S and I(2); the latter is a rank-2 tensor constructed from the nuclear spin I. We see that the MQM interaction has been simplified to a vector Q that acts along the symmetry axis of the molecule, z′.
To keep the calculation simple, we first neglect Hhyp. Its effects are considered later. We find it advantageous to use a basis where the rotational and spin wavefunctions are separated, so we choose the basis set denoted by |G, MG; N, MN⟩, where G = S + I is the total spin and MG and MN are the projections of G and N on the laboratory z-axis. Hrot + HStark is diagonal in G, MG and MN, but the electric field mixes states of different N. After diagonalizing Hrot + HStark we obtain the eigenfunctions
The energy shift due to HM is
In this equation, ζ depends only on the electron and nuclear spins and is evaluated in Appendix A, whereas η is independent of the spins and expresses the degree of alignment between the internuclear axis of the molecule and the laboratory z-axis, often known as the polarization factor. It is given by
where μmol is the dipole moment along the internuclear axis. Figure 1 shows the evaluation of ζ for a few selected values of S and I. In all the examples given in Figure 1, the largest MQM energy shift is found for the states |G, MG = ±G⟩, where G does not take its maximum possible value. It is interesting that the configuration where the electron and nuclear spins are parallel is not the one most sensitive to the nuclear MQM. We find this to be true for larger values of S and I as well.

FIGURE 1. Values of ζ in hyperfine states |G, MG⟩, for (A) S = 1/2, I = 1; (B) S = 1/2, I = 3/2; (C) S = 1, I = 1. These are calculated using Eq. A6.
Now we consider the effect of Hhyp, which includes the spin-rotation interaction, the magnetic dipole hyperfine interaction and the electric quadrupole hyperfine interaction [28]. To handle this, we introduce the spin of the second nucleus I2, an intermediate angular momentum F1 = G + N and the total angular momentum F = F1 + I2. Using the field-free coupled basis, |N, G, F1, F, MF⟩, we diagonalize Hrot + HStark + Hhyp to find the new eigenstates
The matrix elements needed to calculate ΔEM are given in Appendix A.
Although Eq. 6 will be more accurate than Eq. 4, we expect the latter to work well for most 2Σ molecules since they have no spin-orbit coupling and the largest spin-rotation coupling is typically much smaller than the hyperfine and rotational energies. As a concrete example, for the 2Σ ground state of 173YbF, the electron-spin-rotation coupling strength is γ = −13 MHz, the hyperfine Fermi contact strength between the electron and Yb nuclear spins is bF(Yb) = −1.98 GHz, and the rotational constant is B = 7.24 GHz [28, 29]. The fluorine nucleus has spin I2 = 1/2 but this gives rise to a much smaller hyperfine splitting than that of the Yb nucleus (bF(F) = 0.17 GHz). Consequently, the decoupled basis
Table 2 lists the MQM energy shifts of all states that correlate to the lowest rotational level of ground state 173YbF, in a static electric field of 18 kV/cm. At this field, the polarization factor is η = 0.676. We have given both ΔEM calculated using Eq. 6 and the approximate result
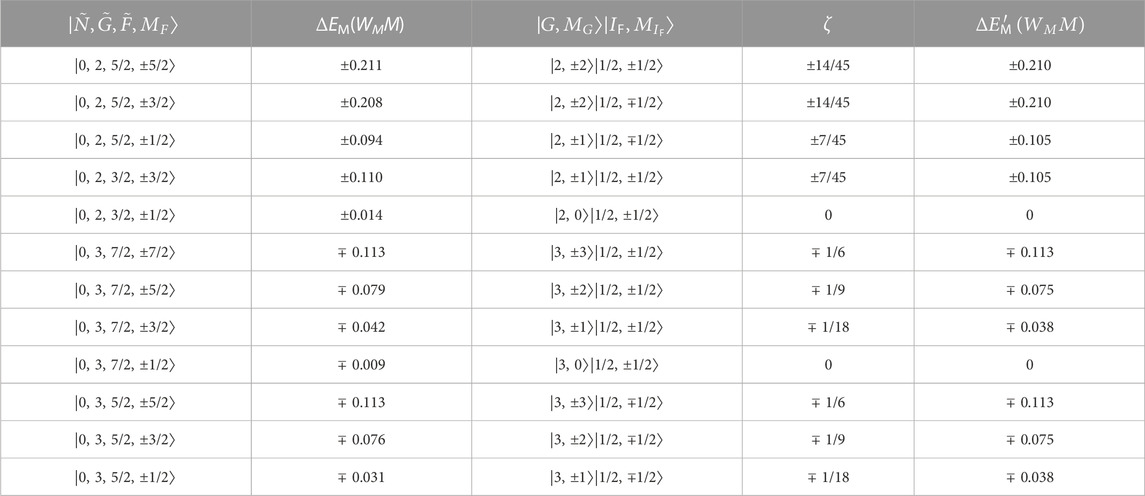
TABLE 2. MQM energy shifts for states correlating to the lowest rotational level of 173YbF, in an electric field of 18 kV/cm. We have dropped
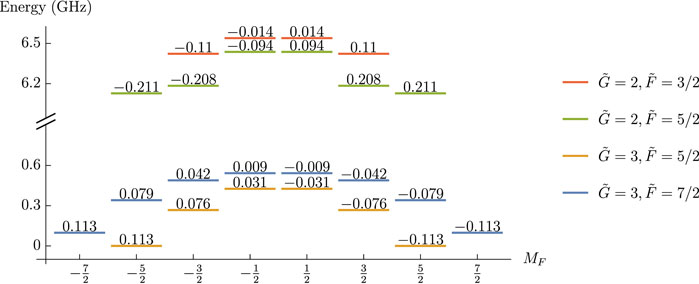
FIGURE 2. MQM energy shifts in the ground rotational state manifold of 173YbF. The shifts are calculated at
An MQM measurement can be done in a similar way to measurements of the electron EDM or the nuclear Schiff moment [10, 15, 30]. Using the notation2 |F, MF⟩, let us define states |0⟩ = |F, F⟩ and
A particular challenge in this measurement scheme, which does not typically arise in related experiments, is the preparation of a superposition of ±MF states where MF and −MF differ by several units. For example, consider the levels of 173YbF shown in Figure 2. The states most sensitive to the MQM have
We first describe how the molecules can be optically pumped into a single quantum state. This is done at zero electric field. We choose the state |0⟩ = |F, MF = F⟩, where F is the target angular momentum for the MQM measurement. A small magnetic field defines the z-axis. It should be small enough that Zeeman splittings are small compared to the linewidth of the relevant optical transitions, but large enough to ensure that MF is preserved. Then, using circularly polarized light with k-vector along z, we drive an optical transition where the excited state angular momentum is F′ = F. The light drives only σ+ transitions so the target state is a dark state and the population will be pumped into this state. There will be decay channels to other hyperfine and rotational states that are not resonant with the optical pumping light. Additional lasers need to be used to drive population out of these states. These extra lasers should have their polarizations modulated at a rate that is close to the Rabi frequency, to ensure that there are no other dark states in the system.
Figure 3 shows an example of this procedure for 173YbF molecules. Within the ground state X2Σ+, each rotational manifold (labelled by N) is split into states G = 2 and G = 3 by the Yb hyperfine interaction. Each of these is then further split by spin-rotation and F hyperfine interactions. As an example, the inset shows the hyperfine structure of the N = 2, G = 3 manifold, spanning roughly 1 GHz. The figure also shows the lowest rotational manifold of the electronically excited state, A2Π1/2 (J′ = 1/2). This is split into states of opposite parity by the Λ-doubling interaction, then by the Yb hyperfine interaction yielding states labelled by
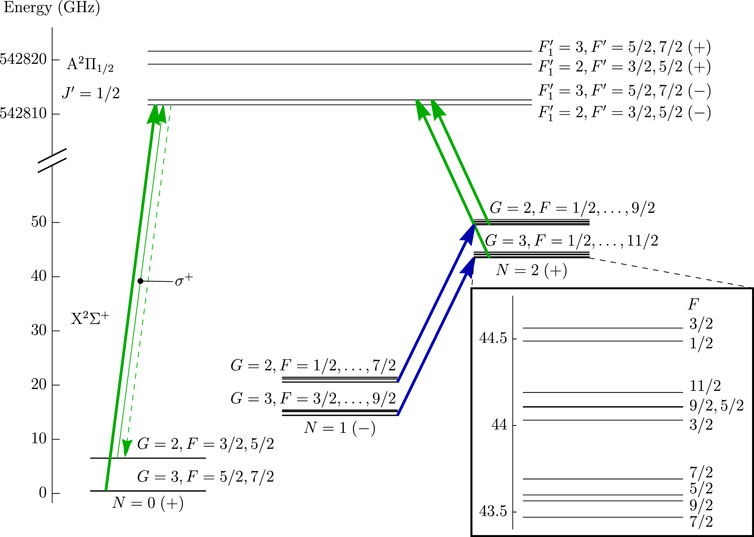
FIGURE 3. Optical pumping scheme for 173YbF molecules. Thick green arrows denote transitions driven using polarization-modulated light. The thin green arrow denotes light that drives only σ+ transitions from the G = 2 manifold of N = 0. The target state, |N = 0, G = 2, F = 5/2, MF = 5/2⟩, is the only dark state. Microwave transitions (blue arrows) can also be driven in order to bring population from N = 1 to the target state. The inset shows the hyperfine structure within N = 2, G = 3.
Next, we show how to drive effective Rabi oscillations between the initial state |F, MF = F⟩ and the superposition state
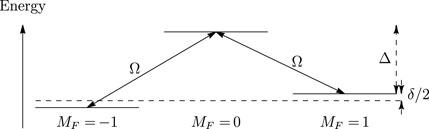
FIGURE 4. An F = 1 system with tensor Stark splitting Δ and couplings Ω between the MF = 0 sublevel and MF = ±1 sublevels. The MF = ±1 states have a splitting δ between them.
The Hamiltonian describing this system, in the basis {MF = −1, MF = 0, MF = 1}, is
This is the same Hamiltonian as for a two-photon Raman transition after transforming to the rotating frame. In that situation, Ω is the Rabi frequency, Δ is the one-photon detuning and δ is the two-photon or Raman detuning. Motivated by this, we consider the situation where Δ ≫Ω, δ and the initial state is one of the MF = ±1 states. Then, adiabatic elimination of the MF = 0 state reduces the dynamics to that of an effective two-level system:
This system undergoes Rabi oscillations between the MF = ±1 states at the effective generalised Rabi frequency,
This approach can be generalised to states of higher angular momentum. For example, consider the F = 5/2 system illustrated in Figure 5. Here we have two different tensor Stark splittings Δ1,2, and three couplings between adjacent levels Ω1,2,3. As before, these couplings can be generated by a magnetic field orthogonal to the electric field. For simplicity, we have made states of equal MF degenerate. The Hamiltonian for this six-level system is
We adiabatically eliminate all states except for |MF = ±5/2⟩ to derive the effective two-level Hamiltonian
The derivation is given in Appendix B. We have assumed that the shifts Δ1,2 are much greater than the couplings Ω1,2,3. The effective Rabi frequency is
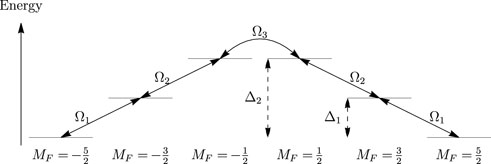
FIGURE 5. An F = 5/2 system with tensor Stark splittings Δ1 and Δ2, and couplings Ω1, Ω2, Ω3 between states of adjacent MF.
Figure 6A compares the numerical solution of the Schrödinger equation using Eq. 9 to the effective two-level dynamics described by Eq. 10. We see excellent agreement between the effective model and the complete solution. We also find that two-level Rabi flopping dynamics are obtained whenever Δ1 ≫Ω1, without needing to constrain Δ2, Ω2, Ω3. The first condition ensures that the amplitudes of all intermediate states remain small, even when Ω2 and Ω3 are large. This greatly increases the effective Rabi frequency, producing a rapid coupling between the stretched states even though this is a high-order process mediated through many intermediate states. Note that in this case the effective Rabi frequency is no longer given by Eq. 11. Figure 6B compares the numerical solution to the two-level model in the case where the coupling between the states is similar to Δ2. The numerical solution shows almost perfect Rabi oscillations between the stretched states, with negligible population in any of the other states. The Rabi frequency is larger than given by Eq. 11.
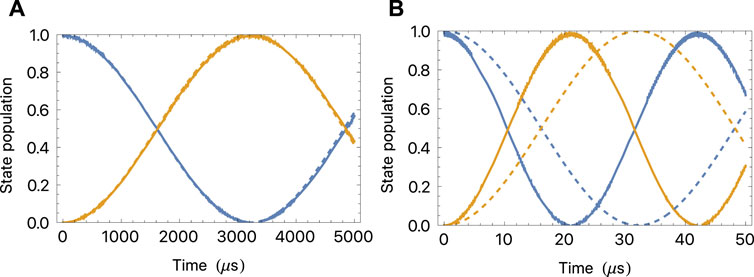
FIGURE 6. Dynamics of the six-level system shown in Figure 5. Populations of the states MF = 5/2 (blue) and MF = −5/2 (orange). Solid lines: solutions of the Schrödinger equation for the Hamiltonian given in Eq. 9. Dashed lines: effective two-level model, Eq. 10. Parameters are: (A) Ω1 = Ω2 = Ω3 = 2π × 6 MHz, Δ1 = Δ2 = 2π × 100 MHz. (B) Same as (A) except Δ2 = 2π × 10 MHz.
Let us consider again the specific example of the G = 2 manifold of 173YbF. The upper half of Figure 2 shows the level structure of this manifold of 10 states in an electric field
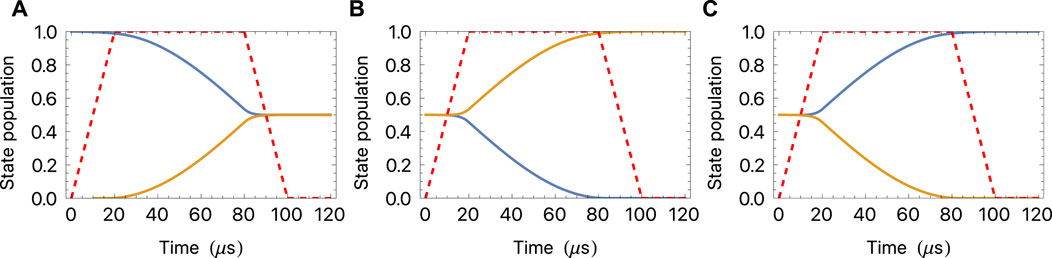
FIGURE 7. Dynamics within the G = 2 manifold of 173YbF induced by a pulse of magnetic field orthogonal to the electric field, calculated by numerical solution of the Schrödinger equation for all 10 levels shown in the upper half of Figure 2. Populations of the states MF = 5/2 (blue) and MF = −5/2 (orange) as Bx is ramped on and off for a total time of 100 µs. The maximum value of the field is 5.9 mT and its amplitude relative to this maximum is shown by the dashed red line. (A) Initial state is |5/2, 5/2⟩; final state is | + ⟩. (B) Initial state is | + ⟩; final state is |5/2, −5/2⟩. (C) Initial state is | − ⟩; final state is |5/2, 5/2⟩.
Finally, we consider the sensitivity of a molecular MQM experiment to hadronic CP-violating parameters, and compare related experiments. Again, we use 173YbF as a prototypical example. The parameters of the experiment are the coherence time τ and the number of molecules measured N. At the shot-noise limit, the statistical uncertainty of an ideal frequency measurement will be
If we assume that the CP-violating energy splitting in 173YbF is due only to the MQM of the Yb nucleus, 2ΔCP = 0.42WMM, then the uncertainty is equivalent to a 2σ-sensitivity on the MQM of 4.5 × 10−13 e fm2. From this, we can calculate the expected level to which we can measure various CP-violating parameters, using the parameter sensitivities compiled in Table 3. We compare these to the experimental constraints set by the Schiff moment measurement of 199Hg [14] and the projected sensitivities of the proposed Schiff moment measurement of 205Tl from a TlF beam experiment [15]. The former is S (199
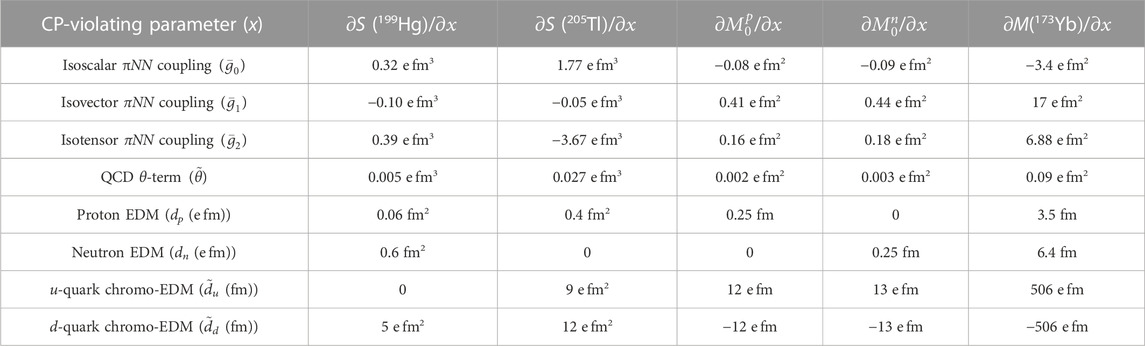
TABLE 3. The dependence of the Schiff moments of 199Hg and 205Tl [36], nucleon MQMs and the MQM of 173Yb [19] on CP-violating parameters. The dependence of M(173Yb) is calculated from the enhancement of nucleon MQMs as given in Table 1. Throughout, we take the strong π-meson nucleon-nucleon interaction constant to be g = 13.6 [18].
Table 4 shows the 95% confidence limit constraints on CP-violating parameters set by the 199Hg experiment, as well as projected 2σ-sensitivities for experiments using TlF and YbF, given the uncertainties quoted above. We find that a measurement of the MQM of 173Yb using YbF molecules can make large improvements relative to the current limits on CP-violating parameters obtained from the Hg experiment. The measurement also gives greater sensitivities than obtainable from the proposed TlF experiment, even though the projected frequency uncertainty of the TlF experiment is 20 times smaller.
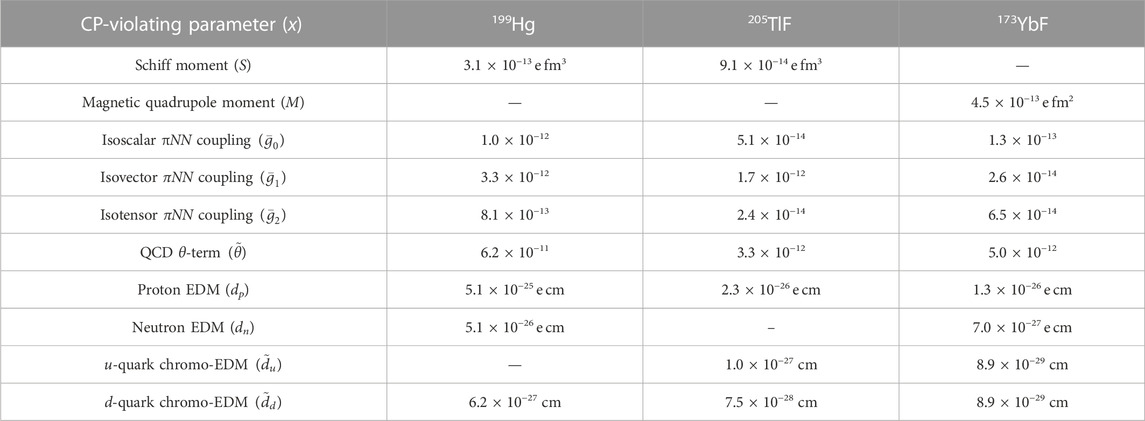
TABLE 4. Constraints (95% CL) on CP-violating parameters set experimentally by 199Hg [14], and projected 2σ-sensitivities from proposals to measure these in 205TlF [15] and 173YbF (this paper). For 199Hg, the constraints given here differ from those given in [14] because we use the coefficients from [36].
Measurements of nuclear MQMs in isotopologues of heavy, paramagnetic molecules have the potential to probe hadronic CP-violating physics at a level well beyond current limits. We have calculated the molecular energy shifts to be expected, showing which states should be used. We find that measurements will require molecules prepared in a superposition of magnetic sub-levels that differ by many units of angular momentum, and we have described a general method for preparing these states. These experiments would benefit from the recent advances in laser cooling applied to molecules [38]. The nuclear spin of the heavy atom in the molecule leads to large hyperfine intervals and a more complex hyperfine structure which makes the laser cooling more difficult than for the isotopologues cooled so far. Nevertheless, a recent study [39] shows how cooling of the required molecules can be done with relatively small additions to existing experiments.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
CH performed the calculations and analyses and prepared the first draft of the manuscript. JL contributed to the concepts and ideas presented. BS conceived the study, contributed to the concepts and supervised the work. MT contributed to the state preparation method, checked the calculations, revised the manuscript and supervised the work. All authors discussed the work regularly, contributed to manuscript revision, read and approved the submitted version.
This work was supported by funding in part from the Science and Technology Facilities Council (grants ST/S000011/1 and ST/V00428X/1); the Sloan Foundation (grant G-2019-12505); and the Gordon and Betty Moore Foundation (grant 8864). The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of these funding bodies.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1The light atom in the molecule often has nuclear spin but its contribution to any P,T-violating signal scales approximately as Z2, where Z is the atomic number [12], so is much smaller than that of the heavy atom. For example, in YbF, the contribution from the F atom is about 60 times smaller than that of Yb.
2Here, for notational convenience, we have dropped the tildes and the other quantum numbers.
3This calculation comes from ΔCP = ηWSS, where the polarisation factor η = 0.547 and WS = 40 539 au = 1.8 × 106 Hz/(e fm3) [37].
1. Dolgov AD, Zeldovich YB. Cosmology and elementary particles. Rev Mod Phys (1981) 53:1–41. doi:10.1103/revmodphys.53.1
3. Sakharov AD. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. Sov Phys Usp (1991) 34:392–3. doi:10.1070/pu1991v034n05abeh002497
4. Canetti L, Drewes M, Shaposhnikov M. Matter and antimatter in the universe. New J Phys (2012) 14:095012. doi:10.1088/1367-2630/14/9/095012
5. Bödeker D, Buchmüller W. Baryogenesis from the weak scale to the grand unification scale. Rev Mod Phys (2021) 93:035004.
7. Purcell EM, Ramsey NF. On the possibility of electric dipole moments for elementary particles and nuclei. Phys Rev (1950) 78:807. doi:10.1103/physrev.78.807
8. Landau L. On the conservation laws for weak interactions. Nucl Phys (1957) 3:127–31. doi:10.1016/0029-5582(57)90061-5
9. Hudson JJ, Kara DM, Smallman IJ, Sauer BE, Tarbutt MR, Hinds EA. Improved measurement of the shape of the electron. Nature (2011) 473:493–6. doi:10.1038/nature10104
10. Andreev V, Ang DG, DeMille D, Doyle JM, Gabrielse G, Haefner J, et al. Improved limit on the electric dipole moment of the electron. Nature (2018) 562:355. doi:10.1038/s41586-018-0599-8
11. Cairncross WB, Gresh DN, Grau M, Cossel KC, Roussy TS, Ni Y, et al. Precision measurement of the electron's electric dipole moment using trapped molecular ions. Phys Rev Lett (2017) 119:153001. doi:10.1103/physrevlett.119.153001
12. Hinds EA. Testing time reversal symmetry using molecules. Phys Scr (1997) T70:34–41. doi:10.1088/0031-8949/1997/t70/005
13. Schiff LI. Measurability of nuclear electric dipole moments. Phys Rev (1963) 132:2194–200. doi:10.1103/physrev.132.2194
14. Graner B, Chen Y, Lindahl EG, Heckel BR. Reduced limit on the permanent electric dipole moment of Hg199. Phys Rev Lett (2016) 116:161601. doi:10.1103/physrevlett.116.161601
15. Grasdijk O, Timgren O, Kastelic J, Wright T, Lamoreaux S, DeMille D, et al. CeNTREX: A new search for time-reversal symmetry violation in the 205Tl nucleus. Quan Sci. Technol. (2021) 6:044007. doi:10.1088/2058-9565/abdca3
18. Flambaum VV, DeMille D, Kozlov MG. Time-Reversal symmetry violation in molecules induced by nuclear magnetic quadrupole moments. Phys Rev Lett (2014) 113:103003. doi:10.1103/physrevlett.113.103003
19. Lackenby BGC, Flambaum VV. Time reversal violating magnetic quadrupole moment in heavy deformed nuclei. Phys Rev D (2018) 98:115019. doi:10.1103/physrevd.98.115019
20. Möller P, Sierk AJ, Ichikawa T, Sagawa H. Nuclear ground-state masses and deformations: FRDM(2012). At Data Nucl Data Tables (2016) 109-110:1–204. doi:10.1016/j.adt.2015.10.002
21. Denis M, Hao Y, Eliav E, Hutzler NR, Nayak MK, Timmermans RGE, et al. Enhanced P,T-violating nuclear magnetic quadrupole moment effects in laser-coolable molecules. J Chem Phys (2020) 152:084303. doi:10.1063/1.5141065
22. Skripnikov LV, Petrov AN, Titov AV, Flambaum VV. CP-violating effect of the Th nuclear magnetic quadrupole moment: Accurate many-body study of ThO. Phys Rev Lett (2014) 113:263006. doi:10.1103/physrevlett.113.263006
23. Skripnikov LV, Petrov AN, Titov AV, Flambaum VV. Erratum:CP-Violating effect of the Th nuclear magnetic quadrupole moment: Accurate many-body study of ThO [phys. Rev. Lett.113, 263006 (2014)]. Phys Rev Lett (2015) 115:259901. doi:10.1103/physrevlett.115.259901
24. Skripnikov LV, Titov AV, Flambaum VV. Enhanced effect of CP-violating nuclear magnetic quadrupole moment in a HfF+ molecule. Phys Rev A (2017) 95:022512. doi:10.1103/physreva.95.022512
25. Skripnikov LV, Titov AV. Theoretical study of ThF+ in the search for T, P-violation effects: Effective state of a Th atom in ThF+ and ThO compounds. Phys Rev A (2015) 91:042504. doi:10.1103/PhysRevA.91.042504
26. Hutzler NR. Polyatomic molecules as quantum sensors for fundamental physics. Quan Sci. Technol. (2020) 5:044011. doi:10.1088/2058-9565/abb9c5
27. Brown J, Carrington A. Rotational spectroscopy of diatomic molecules. Cambridge: Cambridge University Press (2003).
28. Steimle TC, Ma T, Linton C. The hyperfine interaction in the AΠ1∕22 and XΣ+2 states of ytterbium monofluoride. J Chem Phys (2007) 127:234316. doi:10.1063/1.2820788
29. Wang H, Le AT, Steimle TC, Koskelo EAC, Aufderheide G, Mawhorter R, et al. Fine and hyperfine interaction in 173YbF. Phys Rev A (2019) 100:022516. doi:10.1103/physreva.100.022516
30. Ho CJ, Devlin JA, Rabey IM, Yzombard P, Lim J, Wright SC, et al. New techniques for a measurement of the electron's electric dipole moment. New J Phys (2020) 22:043031. doi:10.1088/1367-2630/ab83d2
31. Yashchuk VV, Budker D, Gawlik W, Kimball DF, Malakyan YP, Rochester SM. Selective addressing of high-rank atomic polarization moments. Phys Rev Lett (2003) 90:253001. doi:10.1103/physrevlett.90.253001
32. Rochester SM, Szymanski K, Raizen M, Pustelny S, Auzinsh M, Budker D. Efficient polarization of high-angular-momentum systems. Phys Rev A (2016) 94:043416. doi:10.1103/physreva.94.043416
33. Alauze X, Lim J, Trigatzis M, Swarbrick S, Collings FJ, Fitch NJ, et al. An ultracold molecular beam for testing fundamental physics. Quan Sci. Technol. (2021) 6:044005. doi:10.1088/2058-9565/ac107e
34. Fitch NJ, Lim J, Hinds EA, Sauer BE, Tarbutt MR. Methods for measuring the electron's electric dipole moment using ultracold YbF molecules. Quan Sci. Technol. (2021) 6:014006. doi:10.1088/2058-9565/abc931
35. Augenbraun BL, Lasner ZD, Frenett A, Sawaoka H, Miller C, Steimle TC, et al. Laser-cooled polyatomic molecules for improved electron electric dipole moment searches. New J Phys (2020) 22:022003. doi:10.1088/1367-2630/ab687b
36. Flambaum VV, Dzuba VA. Electric dipole moments of atoms and molecules produced by enhanced nuclear Schiff moments. Phys Rev A (2020) 101:042504. doi:10.1103/physreva.101.042504
37. Flambaum VV, Dzuba VA, Tran Tan HB. Time- and parity-violating effects of the nuclear Schiff moment in molecules and solids. Phys Rev A (2020) 101:042501. doi:10.1103/physreva.101.042501
38. Fitch NJ, Tarbutt MR. Laser-cooled molecules. Adv Mol Opt Phys (2021) 70:157–262. doi:10.1016/bs.aamop.2021.04.003
In Section 2, we considered the energy level shifts of a 2Σ molecule due to the nuclear MQM interaction. Here, we provide more details of the calculation. As described in Section 2, the Hamiltonian is
In the field-free basis, the matrix elements of Hrot are
We can write
Neglecting the hyperfine interaction, the energy shift due to HM is
This factorizes as
The first factor depends only on electron and nuclear spins and evaluates to
The second factor is
and that
Thus, we see that
which is straightforward to calculate once the eigenvalues
When we include the hyperfine interaction and the spin of the second nucleus, we use the field-free basis |N, G, F1, F, MF⟩ as discussed in Section 2. The matrix elements of Hhyp depend on the terms included in the hyperfine interaction and can all be found in [27]. The eigenstates of Hrot + HStark + Hhyp are denoted
This can be evaluated with the help of the matrix element
The time-dependent Schrödinger equation for the Hamiltonian given in Eq. 9 can be written as (setting ℏ = 1):
where the amplitudes {a(t), b(t), c(t), d(t), e(t), f(t)} correspond to those of MF = −5/2, −3/2, −1/2, 1/2, 3/2, 5/2 respectively. Consider the initial condition where f (0) = 1 and all other amplitudes are zero at t = 0, and the assumption that Δ1, Δ2 ≫Ω1, Ω2, Ω3. Then, we can approximate
We now substitute the expression for e(t) into d(t) to get
Since the tensor shifts are much greater than the direct couplings between MF states, the LHS is approximately d(t). Next, we substitute this expression into the equation for c(t) above and repeat the process. Eventually, we substitute an expression for b(t) into the first differential equation involving a(t) to get
Similarly, we find for f(t),
which together give the effective two-level Hamiltonian in Eq. 10.
Keywords: nuclear magnetic quadrupole moment, CP-violation experiment, low energy tests of fundamental physics, beyond standard model, fundamental physics with molecules
Citation: Ho CJ, Lim J, Sauer BE and Tarbutt MR (2023) Measuring the nuclear magnetic quadrupole moment in heavy polar molecules. Front. Phys. 11:1086980. doi: 10.3389/fphy.2023.1086980
Received: 01 November 2022; Accepted: 19 January 2023;
Published: 02 February 2023.
Edited by:
Michael Charlton, Swansea University, United KingdomReviewed by:
Klaus Jungmann, University of Groningen, NetherlandsCopyright © 2023 Ho, Lim, Sauer and Tarbutt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. R. Tarbutt, bS50YXJidXR0QGltcGVyaWFsLmFjLnVr
†Present address: C. J. Ho,Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.