The nucleon-induced deuteron breakup process as a laboratory for chiral dynamics

The nucleon-induced deuteron breakup reaction is studied within the Faddeev approach at incoming nucleon laboratory energies of 135 and 200 MeV. The chiral semilocal momentum-space (SMS) potential developed up to N⁴LO⁺, supplemented by the N²LO three-nucleon interaction, is used. Our investigation is focused on the determination of theoretical uncertainties in a predicted cross section related to its dependence on the value of the cutoff parameter of the regulator. We also compare predictions based on the complete N²LO potential with those based on the two-nucleon force upgraded to the N⁴LO⁺ order and augmented with the N²LO three-nucleon force. In addition, we study the three-nucleon force effects predicted by this model of interaction. Our systematic study covers the entire kinematically allowed phase space; however, our main results are obtained when additional restrictions on energies and cross section values are imposed. In such a case, we observe that the dependence of the differential cross sections on the regulator cutoff is moderate at 135 MeV and much stronger at 200 MeV. For the latter energy, it can amount to up to 45% in specific kinematic configurations. Taking into account terms beyond, N²LO in a two-body interaction changes the cross section up to 20% (27%) at E = 135(200) MeV. The inclusion of the three-nucleon force leads to effects of approximately 27% at both energies. We illustrate these dependencies with a few examples of the exclusive cross section as a function of the arc length of the S-curve.

1 Introduction

The precise determination of the nature of interactions between nucleons is a long-standing problem of nuclear physics. H. Yukawa’s meson exchange theory in 1935 was the catalyst for the first attempts to solve this problem [1]. Over time, it was understood that nuclear forces are residual interactions stemming from those between quarks and gluons, and therefore, the theory of nuclear forces, dealing with nucleons and mesons, should have an effective character. This idea was further developed by S. Weinberg, who in seminal papers [2, 3] showed how to derive nuclear interactions from the effective chiral Lagrangian. This gave a new impetus to the development of the modern theory of nuclear forces and current operators. Soon after the pioneering work by S. Weinberg, C. Ordóñez, et al. presented the first applications of the proposed formalism to nucleon–nucleon scattering using time-ordered perturbation theory [4]. These important steps laid the foundations on which D. R. Entem and R. Machleidt [5], and later E. Epelbaum, W. Glöckle, and Ulf-G. Meißner [6–8] built the chiral effective field theory (EFT) of nuclear forces, developing the first generation of the chiral two-nucleon (NN) interactions up to N³LO. The N³LO NN potential of [8] provided a good description of the NN data, but it was clear that to obtain results of quality that surpass the predictions of non-chiral phenomenological models, such as the AV18 [9] or CD-Bonn [10] potentials, it was necessary to take into account contributions from higher orders in the chiral expansion.

A number of attempts have been made to improve various aspects of these chiral interactions, resulting in the development of new potentials by several groups, for example, [11–14]. These interactions differ from the first generation of chiral NN potentials and each other in many ways, including but not limited to different regularization approaches, fitting strategies, values of the pion-nucleon low-energy constants (LECs), and treatment of the Δ(1232) degrees of freedom. In [12, 14, 15], the chiral EFT expansion for NN potentials was pushed to the fifth order of the chiral expansion (N⁴LO). The N⁴LO potentials of [12, 14] benefit from using the most reliable determination of the pion-nucleon LECs by matching the chiral perturbation theory to the solution of the Roy–Steiner equation at the subthreshold kinematic point [16]. The latest version of the potentials developed by the Bochum group [12] employs semi-local momentum-space (SMS) regularization, which reduces the amount of cutoff artifacts. At the highest order considered, N⁴LO⁺, the four N⁵LO contact interactions in F-waves are taken into account. These additional contact terms are needed from a partial wave analysis point of view to describe certain very precise proton–proton scattering data at intermediate and higher energies. The same N⁵LO contact interactions are also included in the N⁴LO version of the non-locally regularized potentials in [14]. Finally, the SMS potentials of [12] have been updated in [17] to take into account isospin-breaking interactions up to N⁴LO.

The leading contributions of the three-nucleon force (3NF) at N²LO were derived using the chiral EFT [18, 19]. In [20–22], the sub-leading 3NF contributions were worked out using dimensional regularization in the calculation of loop integrals. The first application of the leading chiral 3NF to Nd scattering is shown in [19], while the first results for the triton using the non-locally regularized N³LO 3NF are presented in [23], based on the previous generation of NN chiral potentials [8]. An efficient algorithm for performing partial wave decomposition of the 3NF was developed in [24]. Notably, while the expressions for the 3NF are available for N⁴LO [20, 21, 25–28] (except for one topology), their application to few- and many-nucleon systems requires additional effort. Specifically, it was shown that the use of dimensional regularization in the derivation of the 3NF in combination with cutoff regulators in the Schrödinger equation leads to inconsistent results that violate chiral symmetry [29, 30]. Consequently, the 3NF and current operators beyond N²LO need to be rederived using a symmetry-preserving cutoff regularization consistent with the SMS NN potentials of [12, 17].

In the meantime, exploratory studies on the role of higher-order short-range 3NF terms in the 3N continuum have been carried out [31–33], showing very promising results. These terms were, in particular, found to be important for solving the nucleon-analyzing power puzzle at low energies [31, 33]. However, complete calculations beyond the NN system are currently only available at N²LO. In particular, the application of the SMS NN force along with the N²LO 3NF regularized in the same way to 3N scattering observables and high- and medium-mass nuclei has been carried out [34]. For more details on the aforementioned applications and related topics, see the review articles [29, 30, 35, 36] and the references therein. In [37], the discussion of a simultaneous determination of the free parameters entering the NN and 3N forces can be found.

The functional form of the regulator and the choice of the cutoff values have attracted considerable attention in the community, both in connection with conceptual issues related to a proper renormalization of the Schrödinger equation in chiral EFT and in the context of an efficient treatment of the nuclear many-body problem. For a collection of different views on these and related topics, see [38] and the references therein. The most recent SMS potentials developed by the Bochum group in [12, 17] are available for the cutoff values in the range of Λ = 400 − 550 MeV, with Λ = 450 MeV giving the best description of the NN data. Smaller cutoff values were shown in [12] to introduce significant cutoff artifacts and degrade the description of NN scattering data. On the other hand, cutoff values larger than Λ = 550 MeV were found to lead to spurious deeply bound states, resulting in strongly non-perturbative interactions that are difficult to apply beyond the NN system. Clearly, the calculated observables show some residual dependence on the regulator value, which can be used to perform a posteriori consistency checks by confronting it with the estimated truncation uncertainty [39–41] (see [32, 34, 42] for some examples).

While in [43] we showed examples of our predictions for differential cross sections, for the nucleon analyzing power A_Y(N), and for the deuteron analyzing power A_XX at a few chosen kinematic configurations, in this work we present more systematic studies. Therefore, we performed a search over the whole kinematically available phase space at two reaction energies: E = 135 MeV and E = 200 MeV. This phase space is spanned by five independent kinematic variables, which can be chosen as four angles defining the directions of the momenta of two outgoing nucleons and the energy of one of the nucleons. Our study allows us to identify regions where predictions based on different cutoff values differ substantially.

This approach can also be applied to other features of the potential. In the following, in addition to the cutoff dependence, we also examine how the predictions change with the chiral order and discuss the role played by the three-nucleon force. Performing calculations at two energies (135 and 200 MeV) gives additional information on how the quality of predictions based on the chiral SMS potential depends on the reaction energy. This, in turn, allows us to specify the applicability range of the chiral expansion.

Of particular interest is the possible existence of kinematic configurations for which the observables show an enhanced dependence on the chiral order or the sensitivity to the value of the regulator. Such configurations provide an opportunity to test the theory by comparing theoretical predictions with experimental data and validating the estimated truncation uncertainties. Thus, in this work, we not only show the uncertainties associated with the cutoff values and the chiral order but also give details of the most interesting configurations. This establishes a guide for experimental groups interested in the nucleon-induced deuteron breakup process.

Our article is organized as follows. In the next section, we discuss the formalism used to obtain the breakup observables. Section 3 covers the results for the differential cross section, first for E = 200 MeV and then for E = 135 MeV. We summarize the aforementioned results in Section 4.

2 Formalism

The framework of the Faddeev equation has proven to be a precise method for solving the 3N problem with all realistic interactions, including the chiral ones. Since we are working in momentum space, the SMS interaction can be immediately incorporated into our codes. In the following, we provide the most fundamental steps of our approach (for details, see, e.g., [44–46]).

In this approach, the Faddeev equation for an auxiliary state, T|ψ⟩, plays a key role. It reads

$T|\psi \rangle =tP|\psi \rangle +tP{G}_{0}T|\psi \rangle +\left(1+t{G}_0\right)V_4^{\left(1\right)}\left(1+P\right)|\psi \rangle +\left(1+t{G}_0\right)V_4^{\left(1\right)}\left(1+P\right)T|\psi \rangle ,(1)$

where the initial state |ψ⟩consists of a deuteron and the relative momentum eigenstate of the projectile neutron, $V_4^{(1)}$ is part of a 3N force that is symmetric under an exchange of particles 2 and 3, P is a permutation operator that takes into account the identity of the nucleons, and G₀ is the free 3N propagator. The 2N t-matrix is, for a given 2N interaction V, a solution of the Lippmann–Schwinger equation,

$t=V+V{\tilde{G}}_{0}t,(2)$

where ${\tilde{G}}_0$ is the 2N free propagator. Once Eq. 1 is solved, the transition amplitude U₀ to the final three-body scattering state |ψ′⟩ is calculated as

$\langle {\psi }^{\prime }|U_0|\psi \rangle =\langle {\psi }^{\prime }|\left(1+P\right)T|\psi \rangle (3)$

and used to find observables [45].

We solve Eq. 1 in the momentum space partial wave scheme. We work with the |p, q, α⟩ states, with $p=|\vec{p}|$ and $q=|\vec{q}|$ being the magnitudes of the relative Jacobi momenta $\vec{p}$ and $\vec{q}$. Furthermore, α represents a set of discrete quantum numbers for the 3N system in the jI-coupling

$\alpha =\left(\left(l,s\right)j;\left(\lambda ,\frac{1}{2}\right)I;\left(j,I\right)J{M}_J;\left(t\frac{1}{2}\right)T{M}_T\right).(4)$

Here, l, s, j, and t denote the orbital angular momentum, total spin, total angular momentum, and total isospin of the 2–3 subsystem, respectively. Furthermore, λ and I are the orbital and total angular momenta of spectator nucleon 1, with respect to the center of mass of the 2–3 subsystem. Finally, J, M_J, T, and M_T are the total angular momentum of the 3N system, its projection on the quantization axis, the total 3N isospin, and its projection, respectively.

We solve Eq. 1 by generating its Neumann series and summing it up by using the Pade method [45]. For the results presented here, we use all partial waves with j ≤ 5 and $J\le \frac{25}{2}$, including the three-nucleon interaction up to $J=\frac{7}{2}$. More details about our numerical performance are shown in [45].

The unambiguous definition of the kinematic configuration of three free nucleons requires a priori knowledge of nine kinematic variables, which can be reduced to five using the conservation laws. We follow a common choice and use four angular variables: θ₁, ϕ₁, θ₂, and ϕ₂ to define the directions of the momenta of nucleons 1 and 2. As the fifth variable, we chose the position on the S-curve, that is, curves located in the E₁–E₂ plane and defined by kinematically allowed (E₁ and E₂) pairs. The possible positions of the S-curve in the E₁–E₂ plane and a convention for the location of its starting point (S = 0) are discussed, e.g., in [45]. Some points on the curve correspond to particularly interesting kinematic configurations. The final-state interaction (FSI) configuration is the one in which the momenta of two nucleons are equal, leading to vanishing relative energy. This makes the cross section for this configuration sensitive to the ¹S₀ interaction, which results in an enhancement of the cross section referred to as the FSI peaks. The QFS configuration, in which one of the nucleons serves as a spectator particle, is also noteworthy. The quasi-free scattering mechanism also increases the cross section; however, here different partial waves contribute.

In the following section, we show the results of our search over the entire kinematically available phase space for the nucleon-deuteron breakup process. We use the same grid for θ₁, θ₂, and ϕ₂ values taken in the range [2.5°, 177.5°] and with a step of 5°, assuming that ϕ₁ = 0 since the unpolarized observables only depend on ϕ₁₂ = ϕ₁ − ϕ₂. For the energies studied here, the S-curve length is typically in the range of 50–200 MeV. We have checked that the observables are accurately described when we use a step of 0.5 MeV along each S-curve.

3 Results for the differential cross section

3.1 E = 200 MeV: Cutoff dependence

To study the dependence of our predictions on the regulator value Λ, we choose the five-fold differential cross sections ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}$ and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}$ obtained with Λ = 400 MeV and Λ = 550 MeV, respectively. Having them at our disposal, we construct (ϕ₁ = 0°)

${\delta }^{400-550}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right)\equiv \frac{{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{400}-{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{550}}{\frac{1}{2}\left({\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{400}+{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{550}\right)}(5)$

and then, for given θ₁ and θ₂, we find its maximum over the remaining variables

${\mathrm{\Delta }}^{400-550}\equiv {\mathrm{\Delta }}^{400-550}\left({\theta }_1,{\theta }_2\right)\equiv \underset{\left\{{\varphi }_2,S\right\}}{\max }{\delta }^{400-550}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right).(6)$

Here and in the following, the calculations are performed with the NN interaction at the highest available order, that is, at N⁴LO⁺, supplemented by the 3NF at N²LO.

The resulting Δ^400−550 at E = 200 MeV is shown in Figure 1A. The white area shows the kinematically forbidden region. The symmetry with respect to the diagonal, as shown in Figure 1, reflects the fact that two nucleons (1 and 2) are indistinguishable. Some small deviations from symmetry seen in the figure are due to the finite grid of points on the S-curves used in the calculations. When interpreting the results obtained for Δ^400−550, it is important to keep in mind that the differences have already been maximized with respect to the not explicitly shown kinematic variables ϕ₂ and S. This implies that the actual residual cutoff dependence of the calculated cross sections, encoded in the quantity δ^400−550, is on average much smaller than the deviations shown in Figure 1 for Δ^400−550. The same comment applies to the results shown for the dependence on the chiral order and the effects of the 3NF.

FIGURE 1

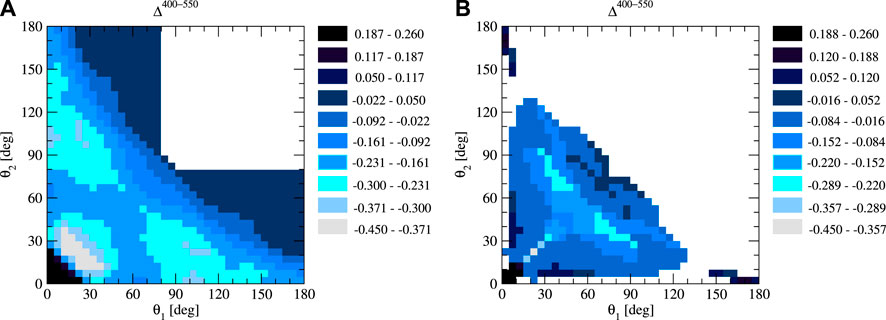
FIGURE 1. Δ^400−550 in the incoming nucleon lab. Kinetic energy E_lab = 200 MeV. (A) shows predictions based on all the configurations studied, while for (B), additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV and E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>$0.01 [mb sr⁻² MeV⁻¹].

We observe that Δ^400−550 is spread over the range (−0.440, 0.260), so the two regulator values can yield predictions that diverge by more than 30%. In the majority of the available area in the (θ₁ and θ₂) subspace Δ^400−550 ∈ (−30% − 5%), the maximal Δ^400−550 values are concentrated at small θ₁ and θ₂ angles. It is interesting to note that the lowest Δ^400−550 values also occur at relatively small polar angles. The particular configurations with extreme Δ^400−550 in these regions are related to the FSI.

Among the configurations leading to Δ^400−550 shown in Figure 1A, there are very likely some with very small cross sections, which can result in large Δ^400−550. Such configurations are not of interest when planning feasible measurements. Thus, in Figure 1B, we show the same Δ^400−550 but after imposing additional conditions on the cross sections: ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>0.01$ [mb sr⁻² MeV⁻¹] and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>0.01$ [mb sr⁻² MeV⁻¹] and on the energies: E₁ > 10 MeV and E₂ > 10 MeV. Notably, these conditions remove many configurations, producing more white space in the graph, and Δ^400−550 decreases on average. While the spread of the Δ^400−550 variation remains nearly unchanged, the distribution of the Δ^400−550 values changes, resulting in, on average, smaller in magnitude values of Δ^400−550. In particular, the configurations with |Δ^400−550| ≥ 0.289 occupy less than 1% of the θ₁–θ₂ phase space shown.

To display the full information on the specific configurations leading to the Δ^400−550 values shown in Figure 1B, Figure 2 shows the corresponding energy E₁ and the relative azimuthal angle ϕ₁₂, which by our choice of ϕ₁ = 0° is equivalent to ϕ₂, as functions of the polar angles θ₁ and θ₂. The analogous figure not shown for E₂ is a mirror image of that for E₁ with respect to the diagonal θ₁ = θ₂. In most cases, E₁ takes on small (below approximately 30 MeV) or large (above approximately 160 MeV) values, and only in about a quarter of configurations, do the largest Δ^400−550 occur at intermediate E₁ energies. The ϕ₁₂ angles corresponding to the most pronounced Δ^400−550 are usually above approximately 130°; however, for some combinations (θ₁ and θ₂), the smallest ϕ₁₂ is preferred.

FIGURE 2

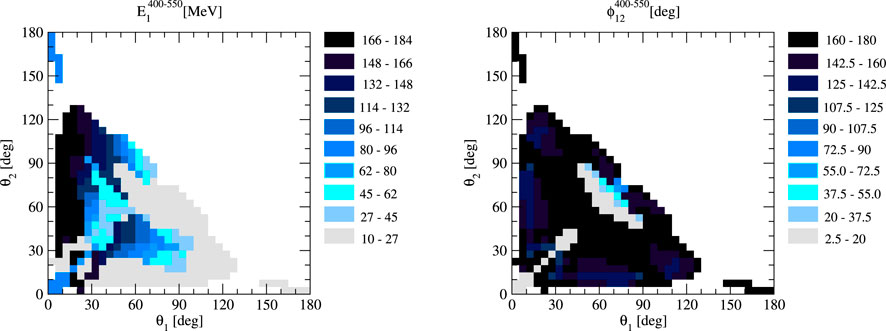
FIGURE 2. Values of nucleon 1 energy E₁ (left) and the azimuthal angle ϕ₂ (right) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 1.

Figure 3 shows the differential cross section $\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}$ as a function of the arc-length S for three configurations that maximize Δ^400−550 at one S point. The left panel shows a configuration where both θ_i are small (θ₁ = 12.5° and θ₂ = 7.5°), while the central panel shows the case where θ₁ = θ₂ = 27.5°. For the first configuration, the maximal δ^400−550(θ₁, θ₂, ϕ₂, S) occurs in the maximum of the FSI peak at S ≈ 134 MeV. In this case, the softer interaction yields a larger cross section. On the contrary, in the case of the configuration shown in Figure 3B, predictions based on the SMS potential with Λ = 400 MeV are smaller around S = 111 MeV than those with the cutoff Λ = 550 MeV. Finally, in Figure 3C, we give an example of the configuration from a different position in the θ₁ − θ₂ plane, namely, for large θ₁ and small θ₂. Here, again, the cross section resulting from the interaction at Λ = 400 MeV exceeds the one obtained at Λ = 550 MeV, leading to δ^400−550(172.5°, 2.5°, 177.5°, 92 MeV) = 0.128.

FIGURE 3

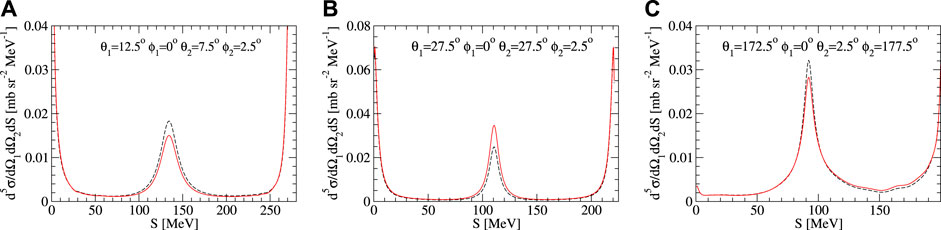
FIGURE 3. Differential cross sections maximizing Δ^400−550 at three selected kinematic configurations defined by (A) θ₁ = 12.5°, θ₂ = 7.5°, ϕ₁₂ = 2.5°, (B) θ₁ = 27.5°, θ₂ = 27.5°, ϕ₁₂ = 2.5°, and (C) θ₁ = 172.5°, θ₂ = 2.5°, ϕ₁₂ = 177.5°. The dashed black (solid red) curve represents the N⁴LO⁺ results at Λ = 400(550) MeV.

3.2 E = 200 MeV: Changes with the chiral order

Similar to the previously defined Δ^400−550, we also studied

${\mathrm{\Delta }}^{\mathit{N2LO-N4LO+}}\equiv {\mathrm{\Delta }}^{\mathit{N2LO-N4LO+}}\left({\theta }_1,{\theta }_2\right)\equiv \underset{\left\{{\varphi }_2,S\right\}}{\max }{\delta }^{\mathit{N2LO-N4LO+}}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right)(7)$

with

${\delta }^{\mathit{N2LO-N4LO+}}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right)\equiv \frac{{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{\mathit{N2LO}}-{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{\mathit{N4LO+}}}{\frac{1}{2}\left.\left({\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{\mathit{N2LO}}+{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{\mathit{N4LO+}}\right)\right)}(8)$

and where ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N2LO}}\left({(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N4LO+}}\right)$ are the differential cross sections obtained with the NN force at N²LO (N⁴LO⁺) supplemented in both cases by the 3NF at N²LO. The regulator value Λ = 450 MeV is used. The free parameters of the 3NF, c_D and c_E, were determined separately when the 3NF was combined with the N²LO or N⁴LO⁺ NN force, in such a way that the ³H binding energy [47] and the differential cross section for the neutron-deuteron elastic scattering data [48] are properly described. The definition (8) shows that both δ^N2LO−N4LO+(θ₁, θ₂, ϕ₂, E₁) and subsequently Δ^N2LO−N4LO+ carry partial information about the convergence of the results to the chiral order.

Figure 4A shows that there are big differences between the predictions based on both combinations of two- and three-nucleon forces in the whole available kinematic area when no additional constraints are imposed on the cross sections and nucleon energies. Δ^N2LO−N4LO+ varies in the range (−200%, 200%). The picture is not as symmetric as in Figure 1A. This shows that in many cases, the magnitude of Δ^N2LO−N4LO+ depends on a very precise position on the S-curve, which is understandable when we deal with small values of the cross sections. In fact, once the additional conditions on the cross sections and energies are applied, the symmetry is restored, as shown in Figure 4B. The values of Δ^N2LO−N4LO+ are now substantially smaller and range approximately from −30%, 30%. The inclusion of the higher chiral order contributions in the NN interaction decreases the breakup cross section, which leads to positive Δ^N2LO−N4LO+, in configurations where one of the θ_i is small (below 20°) and the second θ_j takes intermediate values in the range θ_i ∈ (60°, 120°). In the other parts of the allowed θ₁ and θ₂ space, the negative Δ^N2LO−N4LO+ values prevail. Specifically, for one of the θ_i in the range (30°, 60°) and another one in the range (30°, 90°), Δ^N2LO−N4LO+ takes the smallest values corresponding to ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N4LO+}}>{(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N2LO}}$.

FIGURE 4

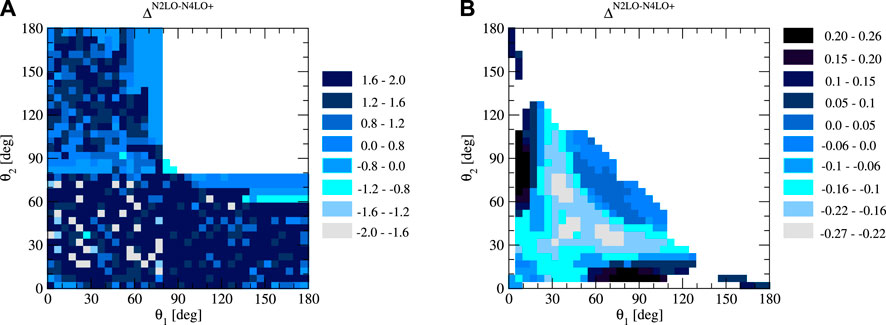
FIGURE 4. Δ^N2LO−N4LO+ in the incoming nucleon lab. Kinetic energy E_lab = 200 MeV. (A) shows predictions based on all the configurations studied, while for (B), additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV, E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N2LO}}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{\mathit{N4LO+}}>$0.01 [mb sr⁻² MeV⁻¹].

Figure 5 shows E₁ and ϕ₁₂ for configurations maximizing Δ^N2LO−N4LO+ for given θ₁ and θ₂. The picture is similar to that of Figure 2—again, the energy of the first nucleon takes the largest possible values, while the energy of the second nucleon remains small. ϕ₁₂ is above 150° for most of the configurations; however, there are also configurations, clustered around the diagonal or around a straight line intersecting the diagonal at θ₁ = θ₂ = 60° with ϕ₁₂ below 20°.

FIGURE 5

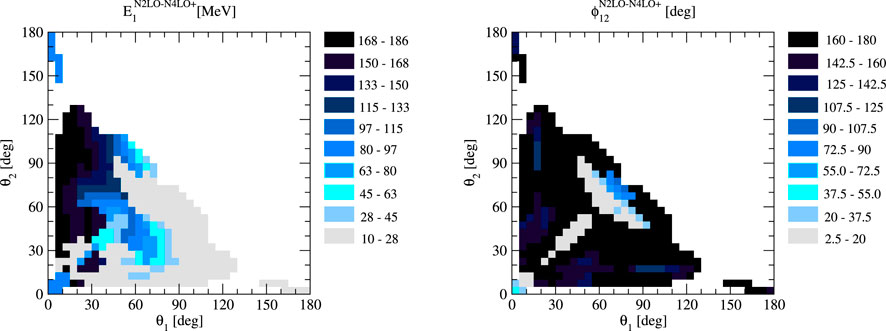
FIGURE 5. Values of nucleon 1 energy E₁ (left) and the azimuthal angle ϕ₂ (right) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 4.

A few examples of $\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}$ with large |Δ^N2LO−N4LO+| are shown in Figure 6. In all the cases, a clear difference between N²LO + N²LO and N⁴LO⁺+N²LO predictions is observed in one of the maxima of the cross section; however, for the configuration shown in the central panel, the largest (negative) δ^N2LO−N4LO+(θ₁, θ₂, ϕ₂, S) occurs at the slope of the cross section around S = 160 MeV. A relatively large spread of cross sections and the angles defining this configuration make it, in our opinion, an encouraging case for experimental efforts. In the future, it would be interesting to investigate the origin of the enhanced sensitivity of these configurations to the details of the nuclear Hamiltonian and to study the effects of the isospin-breaking corrections to the NN force considered in ref. [17].

FIGURE 6

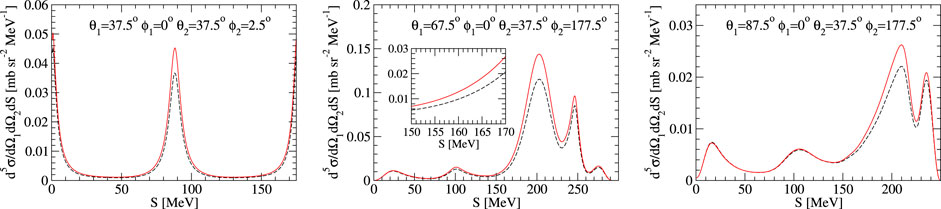
FIGURE 6. Differential cross sections at three selected kinematic configurations with maximal Δ^N2LO−N4LO+ values. The dashed black (solid red) curve represents predictions based on the N²LO (N⁴LO⁺) NN force supplemented in both cases by the N²LO 3NF. Λ = 450 MeV was used.

3.3 E = 200 MeV: 3NF effects

Finally, for the predictions at Λ = 450 MeV, we define accordingly

${\delta }^{\mathit{3NF}}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right)\equiv \frac{{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{NN}-{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{NN+3NF}}{\frac{1}{2}\left.\left({\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{NN}+{\left(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS}\right)}^{NN+3NF}\right)\right)}(9)$

and

${\mathrm{\Delta }}^{\mathit{3NF}}\equiv {\mathrm{\Delta }}^{\mathit{3NF}}\left({\theta }_1,{\theta }_2\right)\equiv \underset{\left\{{\varphi }_2,S\right\}}{\max }{\delta }^{\mathit{3NF}}\left({\theta }_1,{\theta }_2,{\varphi }_2,S\right).(10)$

In Eq. 9, the two cross sections are obtained at Λ = 450 MeV, with the N⁴LO⁺ NN force alone or combined with the N²LO 3NF.

Our results for Δ^3NF are shown in Figures 7, 8. The Δ^3NF values are in the range (−0.378, 0.386) without constraints on the cross sections and energies and in the range (−0.270, 0.386) when these restrictions are taken into account. Initially, in most of the θ₁ − θ₂ regions, Δ^3NF is negative or close to zero. For almost half of the θ₁ − θ₂ combinations, we observe the importance of the 3NF as Δ^3NF is in the range (−0.378, − 0.150). Only for both polar angles below $\approx 25°{\mathrm{\Delta }}^{\mathit{3NF}}$ becomes positive. If configurations with small cross sections and energies are neglected, we find in the most typical case −0.14 < Δ^3NF < − 0.07. The largest positive Δ^3NF value occurs either when both polar angles are small or when one of them is small and the other one is very large. The distribution of nucleon energies in the configurations contributing to Figure 7B reveals that the largest |Δ^3NF| is observed when one of the observed nucleons absorbs nearly all of the kinetic energy, while the energy of the remaining observed nucleon becomes close to the imposed threshold of 10 MeV. For most of the configurations, ϕ₁₂ is large, and only for configurations close to this diagonal θ₁ = θ₂ or close to the line perpendicular to that diagonal at θ₁ = 60°small relative azimuthal angles are preferred.

FIGURE 7

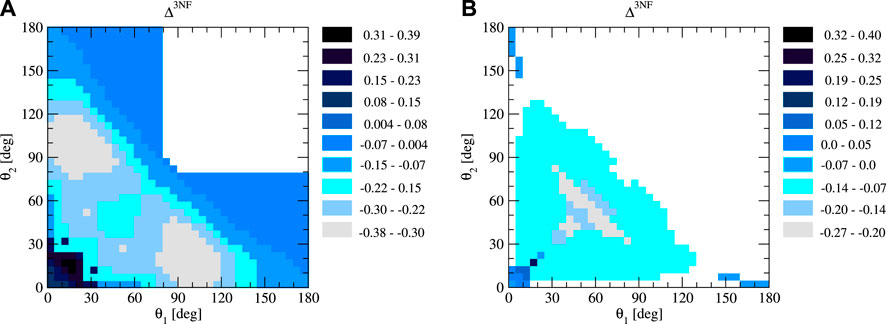
FIGURE 7. Δ^3NF in the incoming nucleon lab. Kinetic energy E_lab = 200 MeV. (A) shows predictions based on all the configurations studied, while for (B), additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV, E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>$0.01 [mb sr⁻² MeV⁻¹].

FIGURE 8

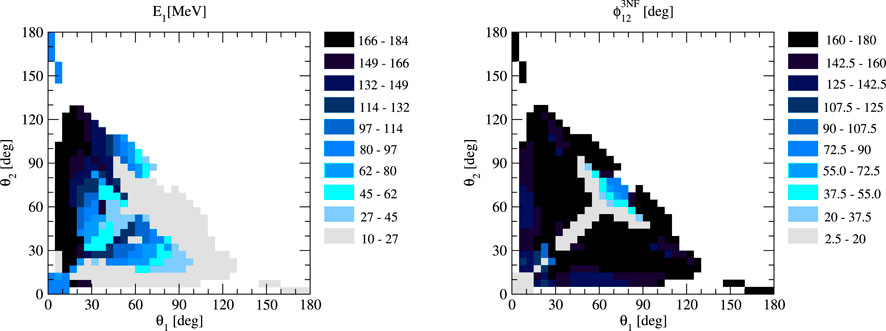
FIGURE 8. Values of nucleon 1 energy E₁ (left) and the azimuthal angle ϕ₂ (right) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 7.

Figure 9 shows the differential cross section at three configurations selected from those that maximize Δ^3NF. Figure 9A shows a case where 3NF lowers the cross section by about 39% at S = 128 MeV. In the two remaining configurations, 3NF increases the cross section by 22% at S = 71 MeV (Figure 9B) and by 23% at S = 187.5 MeV (Figure 9C).

FIGURE 9

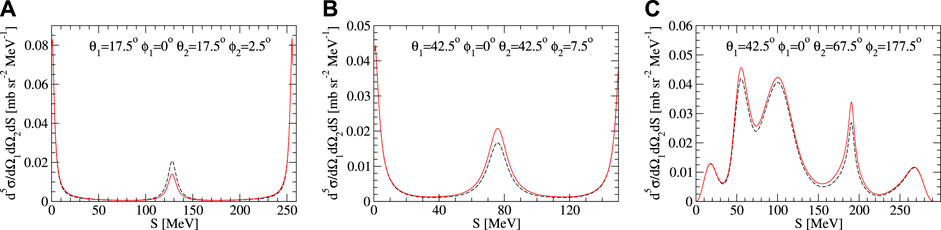
FIGURE 9. Differential cross sections maximizing Δ^3NF at three selected kinematic configurations defined by (A) θ₁ = 17.5°, θ₂ = 17.5°, ϕ₁₂ = 2.5°, (B) θ₁ = 42.5°, θ₂ = 42.5°, ϕ₁₂ = 7.5°, and (C) θ₁ = 42.5°, θ₂ = 67.5°, ϕ₁₂ = 177.5°. The dashed black curve represents predictions based on the N⁴LO⁺ NN force only. The red solid curve stands for predictions based on the N⁴LO⁺ NN force supplemented by the N²LO 3NF. Λ = 450 MeV was used.

This concludes our discussion of the cross section at E = 200 MeV, and in the remaining part of Section 3, we present similar maps as above, but for the deuteron breakup reaction induced by nucleons with a lower kinetic energy of E = 135 MeV.

3.4 E = 135 MeV: Cutoff dependence

Figure 10 shows Δ^400−550, both before and after implementing the cutoff conditions on the energies E₁ and E₂ and the exclusive cross sections, obtained with Λ = 400 MeV or Λ = 550 MeV. As in the case of E = 200 MeV, the N⁴LO⁺ NN interaction is used, complemented by the N²LO 3NF. We also maintain the same thresholds for energies and the same cross sections as were used at E = 200 MeV.

FIGURE 10

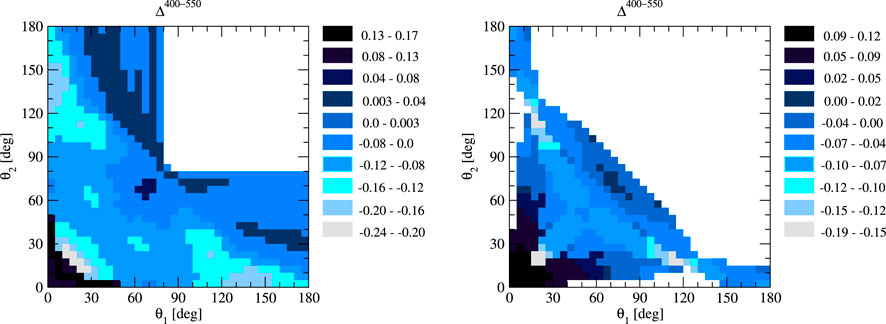
FIGURE 10. Δ^400−550 in the incoming nucleon lab. Kinetic energy E_lab = 135 MeV. The left panel shows predictions based on all the configurations studied, while for the right panel, additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV, E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>$0.01 [mb sr⁻² MeV⁻¹].

Initially, Δ^400−550 varies between −24%, 17% but most often remains in the (−12%, 4%) intervals. The interesting configurations with Δ^400−550 < −20% are typically those with one of the θ_i below at approximately 30° and another θ_i in the (45°, 100°) range. The maximal positive Δ^400−550 occurs only in the part of the θ₁ − θ₂ plane where both θ_i are small. After reducing the number of allowed configurations by applying the threshold conditions, Δ^400−550 is found in the (−19%, 12%) range. Maximal values, around Δ^400−550 = 10%, survive at both θ_i small. On the contrary, regions with large negative Δ^400−550 are significantly shrunk. In most of the phase space, Δ^400−550 belongs to (−10%, 0%). Comparing the resulting picture and numbers with those at E = 200 MeV, there is a significant increase in the magnitude of Δ^400−550 when moving to higher energies, on average by a factor of two. This is, of course, perfectly in line with the expectations based on the fact that the truncation uncertainty of the chiral EFT grows with energy.

The pattern of E₁ for configurations leading to maximal Δ^400−550 at E = 135 MeV is similar to that at E = 200 MeV, as shown in Figure 11. Of course, the lower reaction energy results in lower final state nucleon energies, but again, in some θ₁ − θ₂ regions, we obtain combinations of small E₁ and medium or large E₂ values, or vice versa, or both energies are about half of the maximal available energy. The pattern for ϕ₁₂ is even more similar to that for E = 200 MeV—large relative angles dominate the picture, and only for θ₁ ≈ θ₂⪅60° ϕ₁₂ is small. These similarities and the similar patterns shown in Figures 4B, 12B suggest that the considered observables at these two energies may exhibit sizeable correlations.

FIGURE 11

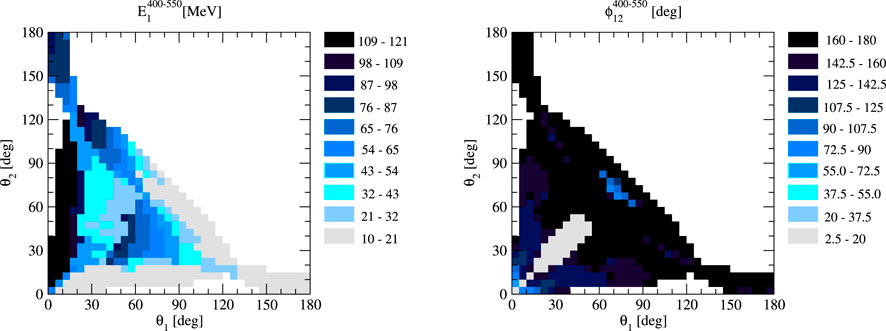
FIGURE 11. Values of the nucleon 1 energy E₁ (left) and the azimuthal angle ϕ₂ (right) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 10.

FIGURE 12

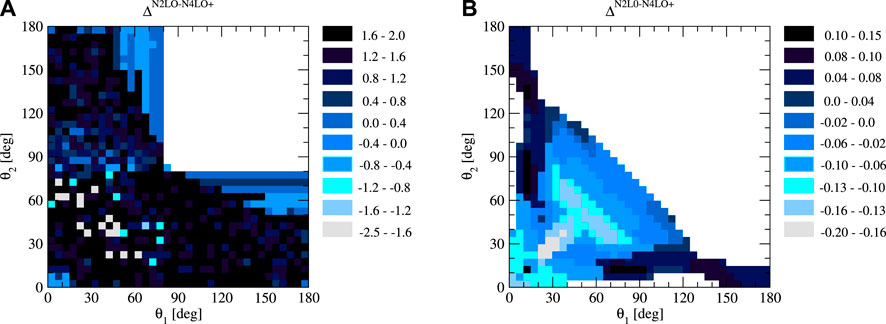
FIGURE 12. Δ^N2LO−N4LO+ in the incoming nucleon lab. Kinetic energy E_lab = 135 MeV. (A) shows predictions based on all studied configurations, while for (B), additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV, E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>$0.01 [mb sr⁻² MeV⁻¹].

3.5 E = 135 MeV: Changes with the chiral order

Next, Figures 12, 13 show the analysis of Δ^N2LO−N4LO+ and the corresponding kinematic configurations maximizing it. Similar to the case of E = 200 MeV, Δ^N2LO−N4LO+ is huge: Δ^N2LO−N4LO+ ∈ (−2.5, 2) for E = 135 MeV if no additional conditions are imposed on the energies and the cross sections. For most of θ₁ − θ₂ pairs, we find configurations where Δ^N2LO−N4LO+ takes values above 80%. Imposing the threshold conditions used here, which limits the possible number of configurations, leads to a much smaller Δ^N2LO−N4LO+ between −20% and +15%. For a significant part of the phase space, the N⁴LO⁺ NN force increases the cross sections, which results in negative Δ^N2LO−N4LO+. Similar to the results at E = 200 MeV, the highest values of Δ^N2LO−N4LO+ appear at one of the small azimuthal angles, below approximately 20°, and another one in the range of (70°, 180°). Configurations with the largest negative Δ^N2LO−N4LO+ have at E = 135 MeV a slightly different distribution than observed in Figure 4B—in addition to the previously observed patterns, now also configurations with θ₁ = θ₂ ∈ (20°, 30°) contribute. The full range for Δ^N2LO−N4LO+ at E = 135 MeV is slightly narrower than that at E = 200 MeV.

FIGURE 13

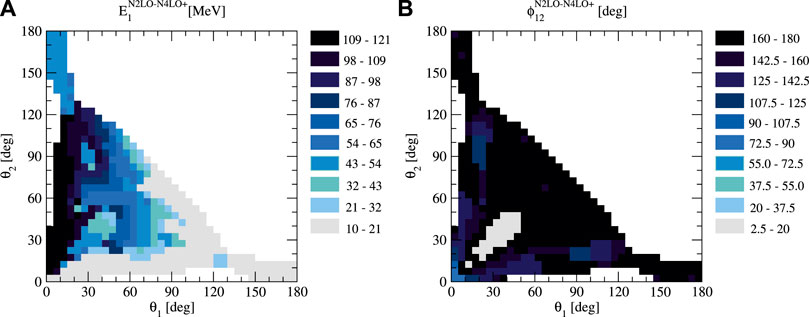
FIGURE 13. Values of nucleon 1 energy E₁ (A) and the azimuthal angle ϕ₂ (B) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 12.

The distribution of nucleon energies at E = 135 MeV is again reminiscent of that observed at E = 200 MeV, taking into account a different absolute energy scale. More deviations are observed for ϕ₁₂, as shown in Figure 13B. At E = 135 MeV, the smallest ϕ₁₂ survives only in one of the two large regions observed for higher energies in Figure 5. Also, for the smallest θ₁ and θ₂ medium values of ϕ₁₂ are now preferred instead of small ϕ₁₂.

3.6 E = 135 MeV: 3NF effects

The effects of the 3N interaction at E = 135 MeV are shown in Figure 14. With no additional constraints on energies and cross sections, we find |Δ^3NF| up to 30%. Actions of the 3NF are possible in both directions —there are configurations where the three-body potential decreases the cross section (positive Δ^3NF) or where the cross section is increased (negative Δ^3NF). The first configurations are those with θ₁ and θ₂ below $\approx 30°$ but above 5°. In the other dominant part of the θ₁ − θ₂ plane, Δ^3NF is negative and in many cases remains below −10%. This does not change much when only cross sections above 0.01 [mb sr⁻² MeV⁻¹] and energies above 10 MeV are considered. Nearly, for all the allowed configurations contributing to Figure 14 Δ^3NF < − 5%. The largest 3NF effects are clustered around the line parallel to the diagonal in θ₁ = θ₂ ≈ 60°. Δ^3NF above +10% requires both θ_i small. Comparing the results in Figure 14 with those in Figure 7, we observe that the maximal 3NF effects change slightly between E = 135 MeV and E = 200 MeV but are on average larger at higher energies.

FIGURE 14

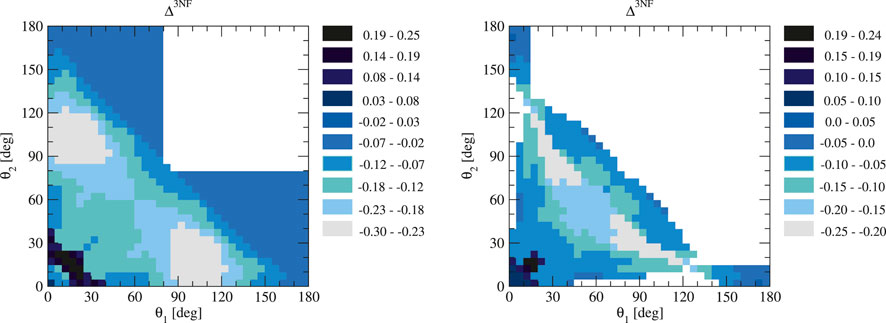
FIGURE 14. Δ^3NF at the incoming nucleon lab. Kinetic energy E_lab = 135 MeV. The left panel shows predictions based on all the configurations studied, while for the right panel, additional thresholds for the energies of the detected neutrons and the magnitude of the cross sections have been imposed: E₁ > 10 MeV, E₂ > 10 MeV, ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{400}>$0.01 [mb sr⁻² MeV⁻¹], and ${(\frac{d^5\sigma }{d{\mathrm{\Omega }}_{1}d{\mathrm{\Omega }}_{2}dS})}^{550}>$0.01 [mb sr⁻² MeV⁻¹].

The pattern of nucleon energies at which Δ^3NF is minimized shows that two detected nucleons have intermediate energies in the approximate range of 30 − 70 MeV, as shown in Figure 15. The large ϕ₁₂ dominates almost all the configurations examined. The only exceptions are some of the configurations on the diagonal θ₁ = θ₂ including those yielding the largest positive Δ^3NF. The medium nucleon’s energies and large relative azimuthal angles again provide good opportunities for measurements.

FIGURE 15

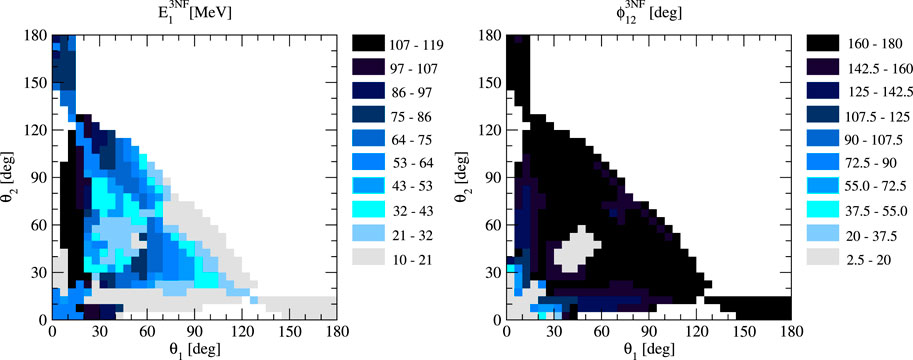
FIGURE 15. Values of nucleon 1 energy E₁ (left) and the azimuthal angle ϕ₂ (right) in the θ₁–θ₂ plane corresponding to the kinematic configurations from the right panel of Figure 14.

4 Conclusions

Recent progress in the derivation of nuclear forces from the chiral effective field theory has reduced substantially uncertainties in model predictions. The inclusion of higher-order terms of the chiral expansion in the NN interaction significantly improves the description of the NN data and extends the energy range in which chiral forces can be reliably applied. However, some questions remain. In this article, we address the problem of the regulator’s dependence on nucleon-deuteron predictions. More precisely, we use the SMS interaction [12] up to N⁴LO⁺ and supplement it with the N²LO three-nucleon interaction [34], which is fully consistent with the SMS NN force up to this order. Within this interaction model, we study the exclusive cross section for the nucleon-deuteron breakup process at two energies of the incoming nucleon: E = 135 MeV and E = 200 MeV. We do not restrict ourselves to selected final kinematic configurations, but perform a systematic search over the whole kinematically allowed phase space, defining dense grids of momenta directions and energies of two outgoing nucleons. This yields a total of 36³ = 46656 combinations of (θ₁, θ₂, and ϕ₁₂), and for each of them, we have on average approximately 100 grid points on the S-curve; thus, the total number of studied configurations amounts to five million. Having such a rich set of predictions, we present them in the form of maps in θ₁ − θ₂ planes, identifying the configurations for which there are the largest differences between cross sections based on different cutoff values. Keeping in mind that such maps can serve as a guide for experimental studies, we impose additional conditions on the magnitudes of the cross sections and energies of the detected nucleons. We find that at E = 200(135) MeV, the cutoff dependence can spread the resulting predictions significantly. The most significant effects appear for configurations that appear to be relatively easily accessible experimentally. The maps included in the article allow one to unambiguously read out all the details of such configurations. The observed cutoff variations should be tamed by adding 3NFs of order N⁴LO. It is well known that additional 3N contact interactions appear in this order [25, 26]. The configurations with the largest cutoff dependence will be good candidates to determine the corresponding low energy constants.

A similar approach allowed us to investigate the sensitivity of the cross sections to upgrading the two-body interaction from N²LO to N⁴LO⁺. We observed that the inclusion of higher-order terms in the NN interaction is necessary at the relatively high energies studied here, as it changes the cross section by up to approximately 20% (27%) at E = 135(200) MeV. Finally, we observed that the inclusion of the three-nucleon interaction leads to effects of up to 27% at both energies studied.

The present work focuses on the configurations that show the highest sensitivity to different features of the nuclear Hamiltonian. The differences between the predictions we have found exceed typical experimental uncertainties achievable today. Thus, measurements of the cross section in the configurations discussed here may help to further constrain the chiral nuclear forces. It would also be interesting to confront the observed residual dependence of the breakup observables on the cutoff values and the EFT expansion order with the estimated truncation errors.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

RS—conceptualization of the work, coding, performing computations, analyzing results, preparing figures, and writing the manuscript; JG—writing code, analyzing results, and writing the manuscript; HW—writing code, analyzing results, and writing the manuscript; VC—writing code, performing computations, analyzing results, and preparing figures; EE—writing code, analyzing results, and writing the manuscript; AN—writing code, computing 3NF matrix elements, analyzing results, and writing the manuscript; VS—writing code, performing computations, and preparing figures.

Funding

This work was supported in part by the BMBF (grant no. 05P21PCFP4), by the DFG, and the NSFC through funds provided to the Sino-German CRC 110 “Symmetries and the Emergence of Structure in QCD” (NSFC grant no. 12070131001, project-ID 196253076—TRR 110), and by the ERC Nuclear Theory (grant no. 885150), by the MKW NRW under funding code NW21-024-A, and by the EU Horizon 2020 research and innovation program (STRONG-2020, GA 824093).

Acknowledgments

The numerical calculations were performed on the JURECA and the JURECA Booster at the Jülich Supercomputing Center in Jülich, Germany. We are grateful to the members of the LENPIC collaboration for sharing their insights into the considered topics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yukawa H. On the interaction of elementary particles. i. Proc Physico-Mathematical Soc Jpn (1935) 17:48. 3rd Series. doi:10.11429/ppmsj1919.17.0_48

CrossRef Full Text | Google Scholar

2. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B (1990) 251:288–92. doi:10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

3. Weinberg S. Effective chiral Lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B (1991) 363:3–18. doi:10.1016/0550-3213(91)90231-L

CrossRef Full Text | Google Scholar

4. Ordóñez C, Ray L, van Kolck U. Two-nucleon potential from chiral Lagrangians. Phys Rev C (1996) 53:2086–105. doi:10.1103/PhysRevC.53.2086

CrossRef Full Text | Google Scholar

5. Entem DR, Machleidt R. Accurate charge dependent nucleon potential at fourth order of chiral perturbation theory. Phys Rev C (2003) 68:041001. doi:10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

6. Epelbaoum E, Glöckle W, Meißner U-G. Nuclear forces from chiral Lagrangians using the method of unitary transformation (i): Formalism. Nucl Phys A (1998) 637:107–34. doi:10.1016/S0375-9474(98)00220-6

CrossRef Full Text | Google Scholar

7. Epelbaum E, Glöckle W, Meißner U-G. Nuclear forces from chiral Lagrangians using the method of unitary transformation ii: The two-nucleon system. Nucl Phys A (2000) 671:295–331. doi:10.1016/S0375-9474(99)00821-0

CrossRef Full Text | Google Scholar

8. Epelbaum E, Glöckle W, Meißner U-G. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl Phys A (2005) 747:362–424. doi:10.1016/j.nuclphysa.2004.09.107

CrossRef Full Text | Google Scholar

9. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C (1995) 51:38–51. doi:10.1103/PhysRevC.51.38

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Machleidt R. High-precision, charge-dependent bonn nucleon-nucleon potential. Phys Rev C (2001) 63:024001. doi:10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

11. Ekström A, Baardsen G, Forssén C, Hagen G, Hjorth-Jensen M, Jansen GR, et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys Rev Lett (2013) 110:192502. doi:10.1103/PhysRevLett.110.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Reinert P, Krebs H, Epelbaum E, Krebs H. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A (2018) 54:86. doi:10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

13. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C (2016) 94:054007. doi:10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

14. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C (2017) 96:024004. doi:10.1103/PhysRevC.96.024004

CrossRef Full Text | Google Scholar

15. Epelbaum E, Krebs H, Meißner U-G. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett (2015) 115:122301. doi:10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner U-G. Matching pion-nucleon roy-steiner equations to chiral perturbation theory. Phys Rev Lett (2015) 115:192301. doi:10.1103/PhysRevLett.115.192301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Reinert P, Krebs H, Epelbaum E. Precision determination of pion-nucleon coupling constants using effective field theory. Phys Rev Lett (2021) 126:092501. doi:10.1103/PhysRevLett.126.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

18. van Kolck U. Few-nucleon forces from chiral Lagrangians. Phys Rev C (1994) 49:2932–41. doi:10.1103/PhysRevC.49.2932

CrossRef Full Text | Google Scholar

19. Epelbaum E, Nogga A, Glöckle W, Kamada H, Meißner U-G, Witała H. Three-nucleon forces from chiral effective field theory. Phys Rev C (2002) 66:064001. doi:10.1103/PhysRevC.66.064001

CrossRef Full Text | Google Scholar

20. Bernard V, Epelbaum E, Krebs H, Meißner U-G. Subleading contributions to the chiral three-nucleon force: Long-range terms. Phys Rev C (2008) 77:064004. doi:10.1103/PhysRevC.77.064004

CrossRef Full Text | Google Scholar

21. Bernard V, Epelbaum E, Krebs H, Meißner U-G. Subleading contributions to the chiral three-nucleon force. ii. short-range terms and relativistic corrections. Phys Rev C (2011) 84:054001. doi:10.1103/PhysRevC.84.054001

CrossRef Full Text | Google Scholar

22. Ishikawa S, Robilotta MR. Two-pion exchange three-nucleon potential: O(q**4) chiral expansion. Phys Rev C (2007) 76:014006. doi:10.1103/PhysRevC.76.014006

CrossRef Full Text | Google Scholar

23. Skibiński R, Golak J, Topolnicki K, Witała H, Epelbaum E, Glöckle W, et al. Triton with long-range chiral n³lo three-nucleon forces. Phys Rev C (2011) 84:054005. doi:10.1103/PhysRevC.84.054005

CrossRef Full Text | Google Scholar

24. Hebeler K, Krebs H, Epelbaum E, Golak J, Skibiński R. Efficient calculation of chiral three-nucleon forces up to n³LO for ab initio studies. Phys Rev C (2015) 91:044001. doi:10.1103/PhysRevC.91.044001

CrossRef Full Text | Google Scholar

25. Girlanda L, Kievsky A, Viviani M. Subleading contributions to the three-nucleon contact interaction. Phys Rev C (2011) 84:014001. doi:10.1103/PhysRevC.84.014001

CrossRef Full Text | Google Scholar

26. Girlanda L, Kievsky A, Viviani M. Erratum: Subleading contributions to the three-nucleon contact interaction. Phys Rev C (2020) 102:019903. doi:10.1103/PhysRevC.102.019903

CrossRef Full Text | Google Scholar

27. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at n⁴lo: Longest-range contributions. Phys Rev C (2012) 85:054006. doi:10.1103/PhysRevC.85.054006

CrossRef Full Text | Google Scholar

28. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at n⁴lo. ii. intermediate-range contributions. Phys Rev C (2013) 87:054007. doi:10.1103/PhysRevC.87.054007

CrossRef Full Text | Google Scholar

29. Epelbaum E, Krebs H, Reinert P. High-precision nuclear forces from chiral EFT: State-of-the-art, challenges and outlook. Front Phys (2020) 8:98. doi:10.3389/fphy.2020.00098

CrossRef Full Text | Google Scholar

30. Epelbaum E, Krebs H, Reinert P. Semi-local nuclear forces from chiral eft: State-of-the-art & challenges. In: Tanihata I, Toki H, Kajino T, editors. Handbook of nuclear Physics. Singapore: Springer (2022). p. 0000.

Google Scholar

31. Girlanda L, Kievsky A, Viviani M, Marcucci LE. Short-range three-nucleon interaction from a = 3 data and its hierarchical structure. Phys Rev C (2019) 99:054003. doi:10.1103/PhysRevC.99.054003

CrossRef Full Text | Google Scholar

32. Epelbaum E, Golak J, Hebeler K, Kamada H, Krebs H, Meißner U-G, et al. Towards high-order calculations of three-nucleon scattering in chiral effective field theory. Eur Phys J A (2020) 56:92. doi:10.1140/epja/s10050-020-00102-2

CrossRef Full Text | Google Scholar

33. Witała H, Golak J, Skibiński R. Significance of chiral three-nucleon force contact terms for understanding of elastic nucleon-deuteron scattering. Phys Rev C (2022) 105:054004. doi:10.1103/PhysRevC.105.054004

CrossRef Full Text | Google Scholar

34. Maris P, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, Hüther T, et al. Light nuclei with semilocal momentum-space regularized chiral interactions up to third order. Phys Rev C (2021) 103:054001. doi:10.1103/PhysRevC.103.054001

CrossRef Full Text | Google Scholar

35. Epelbaum E, Hammer H-W, Meissner U-G. Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

36. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept (2011) 503:1–75. doi:10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

37. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C (2015) 91:051301. doi:10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

38. Tews I, Davoudi Z, Ekström A, Holt JD, Becker K, Briceño R, et al. Nuclear forces for precision nuclear Physics: A collection of perspectives. Few Body Syst (2022) 63:67. doi:10.1007/s00601-022-01749-x

CrossRef Full Text | Google Scholar

39. Epelbaum E, Krebs H, Meißner U-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A (2015) 51:53. doi:10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

40. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev C (2015) 92:024005. doi:10.1103/PhysRevC.92.024005

CrossRef Full Text | Google Scholar

41. Melendez JA, Furnstahl RJ, Phillips DR, Pratola MT, Wesolowski S. Quantifying correlated truncation errors in effective field theory. Phys Rev C (2019) 100:044001. doi:10.1103/PhysRevC.100.044001

CrossRef Full Text | Google Scholar

42. Filin AA, Baru V, Epelbaum E, Krebs H, Möller D, Reinert P. Extraction of the neutron charge radius from a precision calculation of the deuteron structure radius. Phys Rev Lett (2020) 124:082501. doi:10.1103/PhysRevLett.124.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Maris P, Roth R, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Nuclear properties with semilocal momentum-space regularized chiral interactions beyond N²LO. Phys Rev C (2022) 106:064002. doi:10.48550/ARXIV.2206.13303

CrossRef Full Text | Google Scholar

44. Glöckle W. The quantum mechanical few-body problem. Berlin Heidelberg New York Tokyo: Springer-Verlag (1983).

Google Scholar

45. Glöckle W, Witaɬa H, Hüber D, Kamada H, Golak J. The three-nucleon continuum: Achievements, challenges and applications. Phys Rep (1996) 274:107–285. doi:10.1016/0370-1573(95)00085-2

CrossRef Full Text | Google Scholar

46. Witała H, Glöckle W, Golak J, Nogga A, Kamada H, Skibiński R, et al. Nd elastic scattering as a tool to probe properties of 3n forces. Phys Rev C (2001) 63:024007. doi:10.1103/PhysRevC.63.024007

CrossRef Full Text | Google Scholar

47. Wang M, Audi G, Kondev FG, Huang W, Naimi S, Xu X. The AME2016 atomic mass evaluation (II). tables, graphs and references. Chin Phys C (2017) 41:030003. doi:10.1088/1674-1137/41/3/030003

CrossRef Full Text | Google Scholar

48. Sekiguchi K, Sakai H, Witała H, Glöckle W, Golak J, Hatano M, et al. Complete set of precise deuteron analyzing powers at intermediate energies: Comparison with modern nuclear force predictions. Phys Rev C (2002) 65:034003. doi:10.1103/PhysRevC.65.034003

CrossRef Full Text | Google Scholar