In vivo measurement of attenuation coefficient of blood in a dorsal hand vein in a frequency range of 10–45 MHz: A preliminary study

In this study, the attenuation coefficient of blood was measured in vivo in the frequency range of 10–45 MHz. A procedure to correct the distribution of sound pressure in the measurements was discussed. Further, in vivo measurements were applied on the dorsal hand vein of four healthy subjects at rest and during avascularization. As a preliminary result, less variation of the measured attenuation coefficients was achieved by the proposed method. The comparable results of the inclination of the attenuation coefficients were obtained at rest and during avascularization. Furthermore, the attenuation coefficients during avascularization were markedly higher than those at rest, reflecting the degree of red blood cell aggregation promoted by avascularization. This method may aid in the non-invasive evaluation of blood properties reflecting the degree of red blood cell aggregation.

1 Introduction

Cardiovascular diseases (CVD) are one of the leading causes of death worldwide, and atherosclerosis is the primary factor for CVD development [1] and is closely related to the physical and chemical properties of blood [2]. Therefore, evaluating blood properties is crucial for early diagnosis of arteriosclerosis.

The elevation of lipid concentration not only increases the viscosity in blood but also promotes the progression of atheroma formation [3]. Notably, blood viscosity values are highly correlated with blood pressure and are higher in patients with hypertension [4] as well as dyslipidemia and diabetes. By focusing on the propagation of ultrasonic waves in viscoelastic media, the higher the viscosity, the greater the attenuation coefficient [5]. Therefore, in vivo non-invasive measurements of the attenuation coefficient of blood are expected to be effective for screening atherosclerosis.

The attenuation coefficient of human blood has been measured by several researchers [6–18]. However, most of these coefficient values were obtained from sampled blood [6–12, 15, 16, 18]. Moreover, the attenuation coefficients were measured below 10 MHz [6–11, 15], and the measurements were not conducted around the human body temperature [10, 11, 15], or the measurement temperature was not provided [6, 8, 12, 16]. Secomski et al. measured the attenuation coefficient of blood in vivo [13, 14, 17]. They measured the depth dependence of the power of a Doppler signal backscattered in a blood vessel. However, as the objective of their study was to determine the level of hematocrit, the measurement results at 16 and 20 MHz [13] or only 20 MHz [14, 17] were used considering the sensitivity of their experimental system to the hematocrit level of blood. Therefore, the frequency dependence of the attenuation coefficient of blood in vivo was not discussed.

We have been studying methods for evaluating the size of red blood cell (RBC) aggregates by analyzing the scattering power spectrum obtained via ultrasonic backscattering measurements of RBCs [19–24]. Notably, the backscattering power obtained from a single sphere significantly depends on the frequency for each aggregate size [25], and the larger the diameter of a sphere, the smaller the slope of the frequency dependence of the power spectrum. The size of RBC aggregates is estimated by fitting the slope of the measured power spectrum to that of a single scattering sphere’s theoretically obtained scattering characteristics. To extract the scattering property from RBC aggregates, the power spectrum obtained from the vascular lumen is normalized by that obtained from the posterior wall of a blood vessel [20–23] or compared with the reference scattering spectrum [24]. To estimate the size of RBC aggregates with greater accuracy, the attenuation coefficients of the skin and blood must be measured, and the attenuation property differences between the two power spectra must be corrected [22–24]. To measure the attenuation coefficient, power spectra at only two different depths were used. Then, there was a problem that the variation of the measured attenuation coefficients was large.

In the present study, first, a procedure to correct the distribution of sound pressure in the measurements was discussed. Furthermore, as a preliminary study, we non-invasively measured the attenuation coefficient of blood in a dorsal hand vein in the frequency range of 10–45 MHz at rest and during avascularization for four subjects to show the possibility for an evaluation method of the blood property. A procedure to robustly measure the attenuation coefficient of blood was experimentally discussed.

2 Methods

2.1 Principle

The experimental setup for measuring the attenuation coefficient using a high-frequency ultrasonic probe is depicted in Figure 1. The method in the present study is based on the spectral log difference method [26, 27]. However, it is difficult to prepare a reference phantom with a known attenuation coefficient in the frequency range in the present study. Therefore, the sound pressure property difference between different depths was corrected by measuring reflection spectra from the flat plate in water [24]. Ultrasonic waves transmitted from the ultrasound probe propagated through water in the membrane and skin and then irradiated the vascular lumen. Waves scattered from the RBCs in the vascular lumen were received using the same ultrasonic probe. The power spectrum $P_{\mathrm{s}}\left(f,d_i\right)$ of the scattering wave from the vascular lumen at a depth $d_i$ is described as

$\begin{array}{c}{P}_{\mathrm{s}}\left(f,d_i\right)={\left|S\left(f\right)X\left(f\right)G\left(f\right)H\left(f,d_i\right)A\left(f,{0:d}_i\right)\right|}^2,\end{array}(1)$

where $S\left(f\right)$ denotes the backscattering property of RBCs, $X\left(f\right)$ denotes the frequency characteristic of the applied signal, $G\left(f\right)$ denotes the transmitting and receiving characteristics of the ultrasound probe, $H\left(f,d_i\right)$ denotes the sound pressure property of the ultrasound probe at a depth $d_i$, $A\left(f,{0:d}_i\right)$ denotes the attenuation property of the round-trip propagation path between the probe ($d=0$) and a point at depth $d_i$, and $f$ denotes the frequency. $H\left(f,d_i\right)$ also includes the transmission losses at the boundaries between water and the skin and between the skin and the blood vessel. $A\left(f,{0:d}_i\right)$ is caused by scattering and absorption.

FIGURE 1

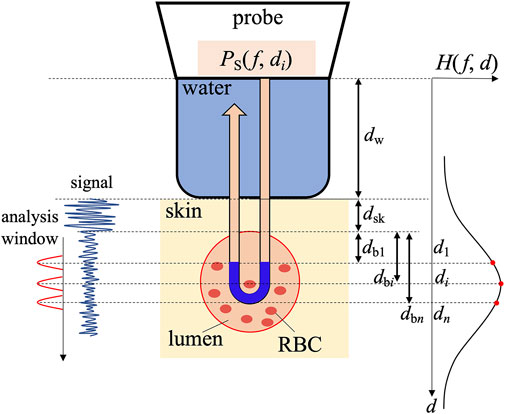
FIGURE 1. Experimental arrangement for the measurement of the attenuation coefficient of blood. $H\left(f,d\right)$ denotes the sound pressure property of the ultrasound probe. $d_i$ is the depth from the probe surface. $d_{\mathrm{w}}$, $d_{\mathrm{s}\mathrm{k}}$, and $d_{\mathrm{b}i}$ are the length of water, skin, and blood, respectively.

In our experiment, we set two points along an ultrasonic beam at depths $d_i$ and $d_{\mathrm{s}}$ in the lumen of a blood vessel to obtain the attenuation property of blood between the two points, where $d_{\mathrm{s}}$ was set as the starting point. By assuming that $S\left(f\right)$, $X\left(f\right)$, and $G\left(f\right)$ do not depend on the depth $d_i$ or $d_{\mathrm{s}}$, the following relationship holds:

$\begin{array}{c}\frac{P_{\mathrm{s}}\left(f,d_i\right)}{P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)}=\frac{{\left|H\left(f,d_i\right)\right|}^2}{{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2}\bullet \frac{{\left|A\left(f,{0:d}_i\right)\right|}^2}{{\left|A\left(f,0:d_{\mathrm{s}}\right)\right|}^2}.\end{array}(2)$

As illustrated in Figure 1, because the acoustic path is approximately divided into a path in water with a propagation length $d_{\mathrm{w}}$, a path in the skin with a propagation length $d_{\mathrm{s}\mathrm{k}}$, and a path in the blood in a vessel, the attenuation property $\left|A\left(f,{0:d}_i\right)\right|$ is expressed as the product of that in water $\left|A_{\mathrm{w}}\left(f,{0:d}_{\mathrm{w}}\right)\right|$, that in skin $\left|A_{\mathrm{s}\mathrm{k}}\left(\left.f,{d_{\mathrm{w}}:(d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}\right)\right)\right|$, and that in blood $\left|A_{\mathrm{b}}\left(f,{\left({d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}\right){:(d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}+d}_{\mathrm{b}i}\right)\right|$, as follows:

$\begin{array}{c}\left|A\left(f,d_i\right)\right|=\left|A_{\mathrm{w}}\left(f,{0:d}_{\mathrm{w}}\right)\bullet A_{\mathrm{s}\mathrm{k}}\left(\left.f,{d_{\mathrm{w}}:(d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}\right)\right)\bullet A_{\mathrm{b}}\left(\left.f,{\left({d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}\right){:(d_{\mathrm{w}}+d}_{\mathrm{s}\mathrm{k}}+d}_{\mathrm{b}i}\right)\right)\right|,\end{array}(3)$

where $d_{\mathrm{b}i}$ denotes the distance from the anterior wall to the depth $d_i$ in the blood vessel.

Let us assume that the attenuation property ${\left|A\left(f,{0:d}_i\right)\right|}^2$ can be modeled using the attenuation coefficient of the medium, $\alpha \left(f\right)$, as follows:

$\begin{array}{c}{\left|A\left(f,{0:d}_i\right)\right|}^2=e^{-4d_i\alpha \left(f\right)}.\end{array}(4)$

By applying Eq. 4 to Eq. 3, the following equation can be derived:

$\begin{array}{c}{\left|A\left(f,{0:d}_i\right)\right|}^2=e^{-4d_{\mathrm{w}}{\alpha }_{\mathrm{w}}\left(f\right)-4d_{\mathrm{s}\mathrm{k}}{\alpha }_{\mathrm{s}\mathrm{k}}\left(f\right)-4d_{\mathrm{b}i}{\alpha }_{\mathrm{b}}\left(f\right)},\end{array}(5)$

where ${\alpha }_{\mathrm{w}}\left(f\right)$, ${\alpha }_{\mathrm{s}\mathrm{k}}\left(f\right)$, and ${\alpha }_{\mathrm{b}}\left(f\right)$ denote the attenuation coefficients of water, skin, and blood, respectively. When $d_i$ is close to $d_{\mathrm{s}}$ and they include the same transmission losses, by substituting Eq. 5 into Eq. 2, the following relationship can be derived because the attenuation properties in water and skin are canceled:

$\begin{array}{c}\frac{P_{\mathrm{s}}\left(f,d_i\right)}{P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)}=\frac{{\left|H\left(f,d_i\right)\right|}^2}{{\left|H\left(f,d_{\mathrm{r}}\right)\right|}^2}\bullet \exp \left(-4{\alpha }_{\mathrm{b}}\left(f\right)\left(d_{\mathrm{b}i}-d_{\mathrm{b}\mathrm{s}}\right)\right)\\ =\frac{{\left|H\left(f,d_i\right)\right|}^2}{{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2}\bullet \exp \left(-4{\alpha }_{\mathrm{b}}\left(f\right)∆d\right),\end{array}(6)$

where $∆d={d_{\mathrm{b}i}-d_{\mathrm{b}s}=d}_i-d_{\mathrm{s}}$, that is, the distance between the depth $d_i$ and depth $d_{\mathrm{s}}$ of the starting point, where $d_i$ is the different depth with $d_{\mathrm{s}}$. Based on Eq. 6, the attenuation coefficient ${\alpha }_{\mathrm{b}}\left(f\right)$ of blood can be derived as follows:

$\begin{array}{c}{\alpha }_{\mathrm{b}}\left(f\right)=\frac{1}{4∆d}\left[\ln \left(\frac{P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{s}}\left(f,d_i\right)}\right)-\ln \frac{{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2}{{\left|H\left(f,d_i\right)\right|}^2}\right].\end{array}(7)$

Thus, to determine ${\alpha }_{\mathrm{b}}\left(f\right)$, we must eliminate the second term on the right-hand side of Eq. 7, that is, the ratio of the sound pressure property up to the depth $d_i$ to that up to $d_{\mathrm{s}}$, ${\left|H\left(f,d_i\right)\right|}^2/{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2$. In our analysis, the term ${\left|H\left(f,d_i\right)\right|}^2/{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2$ was determined in advance using the power spectra $P_{\mathrm{R}}\left(f,d_i\right)$ and $P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)$ of the waves reflected from the surface of a flat plate set at different depths $d_i$ and $d_{\mathrm{s}}$ in water, respectively [24].

As well as Eq. 1, the power spectrum $P_{\mathrm{R}}\left(f,d\right)$ at depth $d$ in water can be expressed as follows:

$\begin{array}{c}{P}_{\mathrm{R}}\left(f,d\right)={\left|RX\left(f\right)G\left(f\right)H\left(f,d\right)A_{\mathrm{w}}\left(f,0:d\right)\right|}^2,\end{array}(8)$

where $R$ denotes the reflection coefficient from water to the flat plate, and we can assume that it does not depend on the frequency. Similar to Eq. 2, by assuming that $R$, $X\left(f\right)$, and $G\left(f\right)$ do not depend on the depth $d_i$ or $d_{\mathrm{s}}$, the following relationship holds:

$\begin{array}{c}\frac{{\left|H\left(f,d_i\right)\right|}^2}{{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2}\cong \left(\frac{P_{\mathrm{R}}\left(f,d_i\right)}{P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)}\right)\frac{1}{{\left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2},\end{array}(9)$

where ${∆A}_{\mathrm{w}}\left(f,∆d\right)$ denote the attenuation properties in water at a distance $∆d{=d}_i-d_{\mathrm{s}}$. Using Eq. 4, ${∆A}_{\mathrm{w}}\left(f,∆d\right)$ can be calculated as follows:

$\begin{array}{c}{\left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2=e^{-4∆d{\alpha }_{\mathrm{w}}\left(f\right)},\end{array}(10)$

where ${\alpha }_{\mathrm{w}}\left(f\right)$ can be determined in advance based on published data [28].

By substituting Eqs 9, 10 into Eq. 7, we can obtain the attenuation coefficient ${\alpha }_{\mathrm{b}}\left(f\right)$ by correcting the effect of the ratio of the sound pressure properties ${\left|H\left(f,d_i\right)\right|}^2/{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2,$ as follows:

$\begin{array}{c}\widehat{{\alpha }_{\mathrm{b}}}\left(f\right)=\frac{1}{4∆d}\left[\ln \left(\frac{P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{s}}\left(f,d_i\right)}\right)-\ln \left(\left(\frac{P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{R}}\left(f,d_i\right)}\right){\left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2\right)\right]\\ =\frac{1}{4∆d}\ln \left(\frac{P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{s}}^{\prime }\left(f,d_i\right)}\right),\end{array}(11)$

where $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ is defined by

$\begin{array}{c}{P}_{\mathrm{s}}^{\prime }\left(f,d_i\right)=P_{\mathrm{s}}\left(f,d_i\right)\bullet \left(\frac{P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{R}}\left(f,d_i\right)}\right){\bullet \left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2\\ =P_{\mathrm{s}}\left(f,d_i\right)\bullet \left(\frac{P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)}{P_{\mathrm{R}}\left(f,d_i\right)}\right)\bullet e^{-4∆d{\alpha }_{\mathrm{w}}\left(f\right)}.\end{array}(12)$

This denotes the power spectrum whose sound property $H\left(f,d_i\right)$ is corrected by the sound pressure property $H\left(f,d_{\mathrm{s}}\right)$ at the starting depth $d_{\mathrm{s}}$ based on the attenuation property difference in water ${\left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2$. Thus, the corrected power spectrum $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ is different from $P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)$ only by the attenuation property difference in blood ${\left|{∆A}_{\mathrm{b}}\left(f,∆d\right)\right|}^2$, which is caused by the difference $∆d$ in depth.

Therefore, the procedure for estimating the attenuation coefficient ${\alpha }_{\mathrm{b}}\left(f\right)$ is as follows: In advance, the power spectra $P_{\mathrm{R}}\left(f,d_i\right)$ and $P_{\mathrm{R}}\left(f,d_{\mathrm{s}}\right)$ are obtained by measuring the radiofrequency (RF) signals reflected from the surface of a flat plate set at two depths $d_i$ and $d_{\mathrm{s}}$ in water, respectively. Following this, for in vivo measurements, the power spectra $P_{\mathrm{s}}\left(f,d_i\right)$ and $P_{\mathrm{s}}\left(f,d_{\mathrm{s}}\right)$ are obtained by measuring the RF signals scattered from blood at depths $d_i$ and $d_{\mathrm{s}}$ in the vascular lumen, respectively. The attenuation property in water ${\left|{∆A}_{\mathrm{w}}\left(f,∆d\right)\right|}^2$ is determined based on Eq. 10. By substituting these values into Eq. 12, the corrected power spectrum $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ can be determined, and the attenuation coefficient of blood, ${\alpha }_{\mathrm{b}}\left(f\right)$, given in Eq. 11, is estimated.

The robustness of the attenuation coefficient $\widehat{{\alpha }_{\mathrm{b}}}\left(f\right)$ given in Eq. 11 is confirmed by measuring the power spectra at multiple sets $\left\{d_i,d_{\mathrm{s}}\right\}$ of different depths.

2.2 In vivo experiments

A high-frequency ultrasound system (Tomey UD-8000) was used for subsequent in vivo experiments. The sampling frequency was 240 MHz. A mechanical scanning linear probe comprising a concave transducer with an operating central frequency of 30 MHz (frequency range: 19–40 MHz) was connected to the ultrasound system. The focal length of the probe $d_F$ was 8.75 mm.

Prior to the in vivo measurement, the sound pressure ${\left|H\left(f,d\right)\right|}^2$ of the ultrasound probe was measured by setting a flat silicone rubber plate at depth $d$; this was perpendicular to the beam direction of the ultrasound probe in water. The RF signals reflected from the flat plate were measured by changing the depth $d$ of the plate with a 0.1 mm interval around the focal depth $d_F$ of the probe.

As a preliminary study, in vivo measurements were applied on the dorsal hand vein of four healthy subjects A, B, C, and D for 20 s. The diameters of the dorsal hand vein (approximately 2–3 mm) were much larger than the wavelength (51 μm at 30 MHz). These measurements were approved by the Ethics Committee of the Graduate School of Engineering, Tohoku University, and all the participants agreed to participate in the present study. RF signals scattered from the lumen were obtained using ultrasonic short-axis measurements [29]. The focal depth $d_F$ of the probe was set at the center of the lumen. In addition to the measurements conducted at rest, RF signals were acquired after avascularization of the dorsal hand vein using crucible scissors [24]. By pressing two points on the fingertip and heart sides, the blood flow was stopped upstream, and the backflow of blood was avoided downstream. Notably, RBC aggregation is more likely to occur in the lumen between the two points under low shear rates.

Data for five frames were acquired every 10 s for control from 0 s to 60 s, avascularization was applied immediately after the measurement at 60 s, and data for 13 frames were acquired for 70–190 s every 10 s. RF data along 15 beams passing through the center of the vascular lumen were used in each frame. The power spectrum was obtained by windowing the RF signals using a Hanning window with a length of 0.15 μs at each depth $d_i$; following this, the power spectra obtained for the 15 beams for five frames were averaged to obtain the power spectrum $P_{\mathrm{s}}\left(f,d_i\right)$ at each time instant for each depth $d_i$. Here, $d_{\mathrm{s}}$ was set at 8.7 mm around a focal depth of 8.75 mm. Seven power spectra $P_{\mathrm{s}}\left(f,d_i\right)$ were averaged from 0 to 60 s for the control, and seven power spectra $P_{\mathrm{s}}\left(f,d_i\right)$ were averaged from 130 to 190 s for the data acquired during avascularization because the aggregation state stabilized within 1 min after avascularization [30].

3 Results

Figures 2A, B depict ultrasonic short-axis B-mode images of the vascular lumen in the dorsal hand vein at rest and during avascularization for subject A, respectively. The lumen brightness in Figure 2B appears higher than that in Figure 2A owing to the increased scattering power caused by RBC aggregation. As illustrated in each B-mode image, the central depths $\left\{d_i\right\}$ of the analysis windows of the RF signals were set from 8.1 mm to 8.9 mm at 0.1 mm intervals.

FIGURE 2

FIGURE 2. B-mode images of the dorsal hand vein (A) at rest and (B) during avascularization.

Figures 3A, B present the corrected power spectra $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ obtained from Eq. 12. The corrected power spectra $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ during avascularization (Figure 3B) were larger than those at rest (Figure 3A). Figures 3C, D depict the depth dependence of the corrected received power $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ for signals scattered from the blood vessel at 20, 30, and 40 MHz at rest and during avascularization, respectively. The corrected received power $P_{\mathrm{s}}^{\prime }\left(f,d_i\right)$ decreased almost linearly as the depth $d$ increased, and the power change increased with the frequency $f$.

FIGURE 3

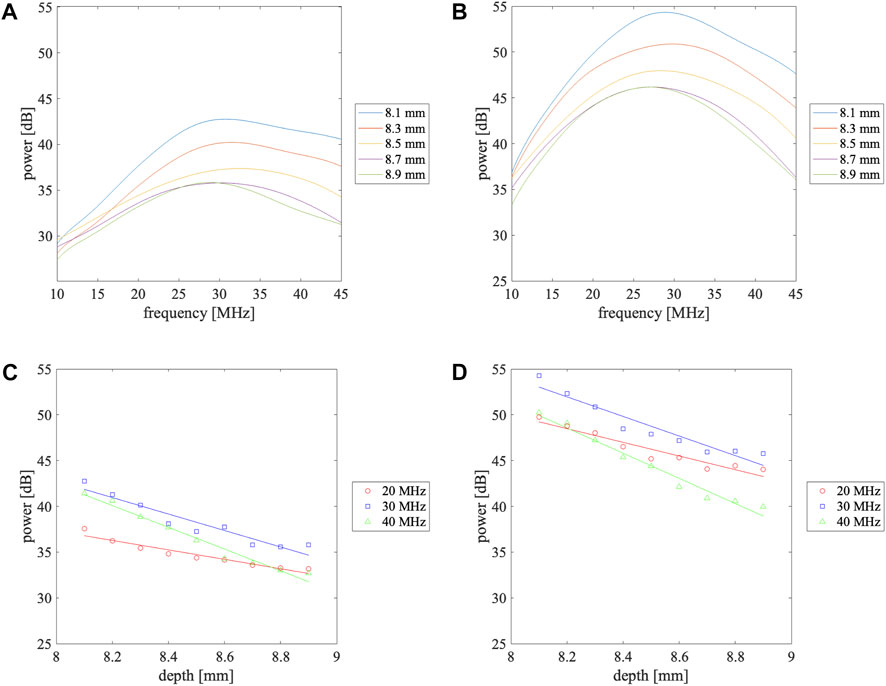
FIGURE 3. Power spectra measured at different depths in the vascular lumen (A) at rest and (B) during avascularization and depth dependence of the power received from the vascular lumen at 20, 30, and 40 MHz (C) at rest and (D) during avascularization. The solid lines in (C) and (D) are the linearly approximated line.

Using Eq. 11, the attenuation coefficient $\mathrm{\alpha }\left(f\right)$ of blood was estimated with the data obtained from 8.1 mm to 8.9 mm at 0.1 mm intervals at rest and during avascularization, and the results for subject A are presented in Figure 4A. The attenuation coefficients $\mathrm{\alpha }\left(f\right)$ both at rest and during avascularization increased almost linearly in the frequency range of 10–45 MHz. The attenuation coefficients at rest, ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$, and during avascularization, ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)$, were ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)=0.178f\left[\mathrm{M}\mathrm{H}\mathrm{z}\right]-1.04$ [dB/mm] and ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)=0.158f\left[\mathrm{M}\mathrm{H}\mathrm{z}\right]+0.56$ [dB/mm] at 10–45 MHz, respectively. Thus, ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)$ is greater than ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$ by approximately 1.1 dB. The scattering power increased owing to avascularization, as depicted in Figure 2 [19–24]. Using the method proposed in the present study, we could non-invasively observe that the increase in the backscattering component reduced the propagation component as the increase of attenuation coefficient. We obtained the attenuation coefficients from the power spectra at the following pairs of two depths {8.1 mm and 8.9 mm}, {8.2 mm and 8.8 mm}, and {8.3 mm and 8.7 mm}. The results are shown in Figures 4B, C with the data obtained from 8.1 mm to 8.9 mm at 0.1 mm intervals at rest and during avascularization, respectively. The root-mean-square errors in fitting a linear line to the measured attenuation coefficients were 0.21 (dB/mm) and 0.14 (dB/mm) for {8.1 mm and 8.9 mm}, 0.28 (dB/mm) and 0.26 (dB/mm) for {8.2 mm and 8.8 mm}, and 0.54 (dB/mm) and 0.32 (dB/mm) for {8.3 mm and 8.7 mm}, at rest and during avascularization, respectively. In contrast, those were 0.17 (dB/mm) and 0.13 (dB/mm) for the data obtained from 8.1 mm to 8.9 mm at 0.1 mm intervals, at rest and during avascularization, respectively. By setting many analysis points, the variations of the measured attenuation coefficients to the linear line were reduced. Next, we obtained the attenuation coefficient from the power spectrum with each frame from 0 to 60 s and from 130 to 190 s from 8.1 mm to 8.9 mm at 0.1 mm intervals. The results are shown in Figures 4D, E at rest and during avascularization, respectively. Averaging seven frames reduced the variations, and it clarified the difference in attenuation coefficients between at rest and during avascularization. From Figures 4B–E, the improvement of the robustness in the attenuation coefficient measurement was confirmed. Figure 4F shows the attenuation coefficients for four subjects A, B, C, and D. The attenuation coefficients were different for each subject. However, the attenuation coefficients during avascularization, ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)$, were larger than those at rest, ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$ for all subjects.

FIGURE 4

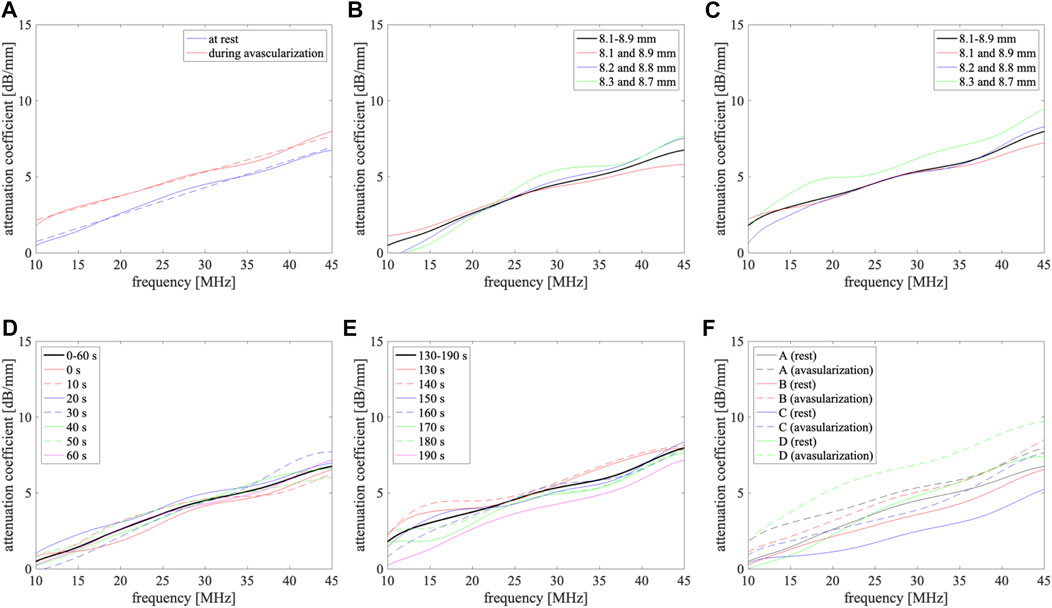
FIGURE 4. Attenuation coefficients of blood at rest and during avascularization. (A) Subject A, solid lines: measured results using power spectra from 8.1 mm to 8.9 mm at 0.1 mm intervals, dashed lines: linearly approximated lines; (B,C) at rest and during avascularization for subject A, respectively, black line: obtained using power spectra from 8.1 mm to 8.9 mm at 0.1 mm intervals, red, blue, and green lines: obtained from power spectra at two depths {8.1 mm and 8.9 mm}, {8.2 mm and 8.8 mm}, and {8.3 mm and 8.7 mm}, respectively; (D,E) at rest and during avascularization for subject A, respectively, black line: obtained using seven frames, the other lines: obtained from power spectra with each frame from 0 to 60 s and from 130 to 190 s; (F) subjects A (black), B (red), C (blue), and D (green), solid lines: at rest, dashed lines: during avascularization.

4 Discussion

As shown in Figures 4B, C, the improvement of the robustness of the measured attenuation coefficients was confirmed by setting plural analysis depths. In this study, the analysis points were set from 8.1 to 8.9 mm at 0.1-mm intervals. It is difficult to expand the analysis region because of the signal-to-noise ratio of the received signals and the size of the blood vessel. To increase the analysis points, it is necessary to shorten the interval. In contrast, measured attenuation coefficients differed at each frame from Figures 4D, E. Therefore, the discussion of the relationship between measurement accuracy and the number of analysis points is necessary for our future work.

The attenuation coefficients for four subjects A-D were 2.5–4.8 dB/mm at rest and 3.9–5.3 dB/mm during avascularization at 30 MHz. The attenuation coefficients in blood strongly depend on the hematocrit level [17]. Therefore, the attenuation coefficient differences among subjects could be caused by the differences in blood properties. The relationship between the attenuation coefficients and blood properties will be investigated in the future.

The average attenuation coefficients at rest, ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$, for four subjects were 2.0 dB/mm at 20 MHz and 3.8 dB/mm at 30 MHz. Previous literature reports these values to be 1.6 dB/mm [12] and 1.2 dB/mm [18] at 30 MHz for sampled blood, and 0.6–0.9 dB/mm at 20 MHz based on in vivo measurements depending on hematocrit levels of 32.0%–49.3% [17]. The attenuation coefficient measured herein is larger than that reported in the literature. This increase could be caused by the incomplete correction of the ratio of sound pressure properties ${\left|H\left(f,d_i\right)\right|}^2/{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2$ because the propagation media differed between water in the flat plate measurement and blood and skin in the in vivo measurement.

There is blood flow in vivo. Laminar flow is assumed in the dorsal hand vein. Then, the blood velocities are the highest in the center of the blood vessel and the lowest near the anterior and posterior walls in the depth direction. The lowest velocity might cause red blood cell aggregation as well as during avascularization because of the low shear rate. In the present study, the focal point of the probe ($d_{\mathrm{F}}$ = 8.75 mm) was set at the center of the lumen. Therefore, the slight scattering property distribution might occur, that is, larger scattering in the shallower position, and it decreased as a larger depth around the focal point. Then, it might cause an apparent larger attenuation coefficient. Therefore, it might also be one of the reasons that the measured attenuation coefficient became larger than those in the Refs. [12, 17, 18]. In contrast, there is no blood flow during avascularization, and there is no effect on the attenuation coefficient by the blood flow. Therefore, the effect of the blood flow did not change the magnitude relationship of the attenuation coefficients at rest and during avascularization.

In contrast, ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)$ were markedly greater than ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$ for four subjects, as presented in Figure 4D. The relative relationship between them is correct even if the ratio of the sound pressure properties ${\left|H\left(f,d_i\right)\right|}^2/{\left|H\left(f,d_{\mathrm{s}}\right)\right|}^2$ has an error because the same ratio is employed for the correction as the analysis range is the same at rest and during avascularization. Therefore, the proposed method demonstrates the potential to non-invasively evaluate blood properties, reflecting the degree of RBC aggregation.

To correct the ratio of the sound pressure properties, a flat plate was used as a reflector. The analysis was based on the plane wave model. In contrast, a mechanical scanning linear probe comprising a concave transducer was used. Therefore, aberration could also affect the result. The effect will be discussed in the future by a simulation experiment or an experimental investigation using a reference phantom whose attenuation coefficient is measured by the pulse transmission method.

5 Conclusion

In this study, the attenuation coefficient of blood was measured in vivo at 10–45 MHz at rest and during avascularization. For this, the differences in sound pressure properties among several measurement points were measured using a flat plate placed in water in advance, and the values were used for correction. In vivo measurements were applied in the dorsal hand vein of four healthy subjects. As a preliminary result, less variation of the measured attenuation coefficients was achieved by the proposed method. The comparable results of the inclination of the attenuation coefficients were obtained at rest and during avascularization. Furthermore, the attenuation coefficient during avascularization ${\mathrm{\alpha }}_{\mathrm{a}\mathrm{v}\mathrm{a}}\left(f\right)$ was found to be markedly greater than that at rest ${\mathrm{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(f\right)$, primarily owing to RBC aggregation. Thus, the usefulness of this measurement method was successfully demonstrated.

Hereafter, we aim to improve our evaluation of sound properties, including the effect of different media, and we aim to include other subjects, such as arteriosclerosis patients, to demonstrate the usefulness of the non-invasive method for evaluating blood properties.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving human participants were reviewed and approved by Ethics committee concerning medical research involving humans Graduate School of Engineering, Tohoku University. The patients/participants provided their written informed consent to participate in this study.

Author contributions

Study design, data processing, interpretation of data, and manuscript writing, MA; experimental work and data processing, KH; study support and interpretation of data, SM; study support, SY; study support and manuscript review, YI; study design, interpretation of data, and manuscript review, HK. All Authors have read the manuscript and agreed to the published version of the manuscript.

Funding

This work was partially supported by JSPS KAKENHI 21H03835.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ross R. Atherosclerosis – An inflammatory disease. N Engl J Med (1999) 340:115–26. Available at: https://www.nejm.org/doi/full/10.1056/NEJM199901143400207 (Accessed January 31, 2023).

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fossum E, Høieggen A, Moan A, Nordby G, Velund TL, Kjeldsen SE. Whole blood viscosity, blood pressure and cardiovascular risk factors in healthy blood donors. Blood Press (1997) 6:161–5. doi:10.3109/08037059709061932

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Rasyid A, Harris S, Kurniawan M, Mesiano T, Hidayat R. Fibrinogen and LDL influence on blood viscosity and outcome of acute ischemic stroke patients in Indonesia. Ann Neurosci (2019) 26:30–4. doi:10.1177/0972753119900630

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Letcher RL, Chien S, Pickering TG, Sealey JE, Laragh JH. Direct relationship between blood pressure and blood viscosity in normal and hypertensive subjects: Role of fibrinogen and concentration. Am J Med (1981) 70:1195–202. doi:10.1016/0002-9343(81)90827-5

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Auld BA. Acoustic fields and waves in solids. New York: John Wiley & Sons (1973). p. 86–97.

Google Scholar

6. Carstensen EL, Li K, Schwan HP. Determination of the acoustic properties of blood and its components. J Acoust Soc Am (1953) 25:286–9. doi:10.1121/1.1907033

CrossRef Full Text | Google Scholar

7. Carstensen EL, Schwan HP. Acoustic properties of hemoglobin solutions. J Acoust Soc Am (1959) 31:305–11. doi:10.1121/1.1907716

CrossRef Full Text | Google Scholar

8. Woodcock JP. Ultrasonic absorption – a new technique. Ultrasonics (1970) 8:213–5. doi:10.1016/0041-624X(70)91036-X

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kikuchi Y, Okuyama D, Kasai C, Yoshida Y. Measurements on the sound velocity and the absorption of human blood in 1-10 MHz frequency range (In Japanese). Rec Semin Tohoku Univ (1972) 41:152–9.

Google Scholar

10. Shung KK, Reid JM. The acoustical properties of deoxygenated sickle cell blood and hemoglobin S solution. Ann Biomed Eng (1977) 5:150–6. doi:10.1007/BF02364015

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Narayana PA, Ophir J, Maklad NF. The attenuation of ultrasound in biological fluids. J Acoust Soc Am (1984) 76:1–4. doi:10.1121/1.391097

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lockwood GR, Ryan LK, Hunt JW, Foster FS. Measurement of the ultrasonic properties of vascular tissues and blood from 35–65 MHz. Ultrasound Med Biol (1991) 17:653–66. doi:10.1016/0301-5629(91)90096-F

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Secomski W, Nowicki A, Tortoli P. Estimation of hematocrit by means of attenuation measurement of ultrasonic wave in human blood. Proc IEEE Ultrason Symp (2001) 1277–80. doi:10.1109/ULTSYM.2001.991953

CrossRef Full Text | Google Scholar

14. Secomski W, Nowicki A, Guidi F, Tortoli P, Lewin PA. Noninvasive in vivo measurements of hematocrit. J Ultrasound Med (2003) 22:375–84. doi:10.7863/jum.2003.22.4.375

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Stride E, Saffari N. Theoretical and experimental investigation of the behaviour of ultrasound contrast agent particles in whole blood. Ultrasound Med Biol (2004) 30:1495–509. doi:10.1016/j.ultrasmedbio.2004.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dukhin AS, Goetz PJ, van de Ven TGM. Ultrasonic characterization of proteins and blood cells. Colloids Surf B Biointerfaces (2006) 53:121–6. doi:10.1016/j.colsurfb.2006.08.011

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Secomski W, Nowicki A, Tortoli P, Olszewski R. Multigate Doppler measurements of ultrasonic attenuation and blood hematocrit in human arteries. Ultrasound Med Biol (2009) 35:230–6. doi:10.1016/j.ultrasmedbio.2008.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Treeby BE, Zhang EZ, Thomas AS, Cox BT. Measurement of the ultrasound attenuation and dispersion in whole human blood and its components from 0-70 MHz. Ultrasound Med Biol (2011) 37:289–300. doi:10.1016/j.ultrasmedbio.2010.10.020

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Saitoh N, Hasegawa H, Kanai H. Estimation of scatterer diameter using ultrasonic backscattering property for assessment of red blood cell aggregation. Jpn J Appl Phys (2009) 48:07GJ08. doi:10.1143/JJAP.48.07GJ08

CrossRef Full Text | Google Scholar

20. Fukushima T, Hasegawa H, Kanai H. Estimation of scatterer diameter by normalized power spectrum of high-frequency ultrasonic RF echo for assessment of red blood cell aggregation. Jpn J Appl Phys (2011) 50:07HF02. doi:10.1143/JJAP.50.07HF02

CrossRef Full Text | Google Scholar

21. Kurokawa Y, Taki H, Yashiro S, Nagasawa K, Ishigaki Y, Kanai H. Estimation of size of red blood cell aggregates using backscattering property of high frequency ultrasound: In vivo evaluation. Jpn J Appl Phys (2016) 55:07KF12. doi:10.7567/JJAP.55.07KF12

CrossRef Full Text | Google Scholar

22. Arakawa M, Nagasawa K, Fukase A, Higashiyama K, Mori S, Yashiro S, et al. Basic study for size estimation of red blood cell aggregates by analyzing ultrasonic backscattering properties considering ultrasonic propagation attenuation. Proc IEEE Ultrason Symp (2020) 1–4. doi:10.1109/IUS46767.2020.9251333

CrossRef Full Text | Google Scholar

23. Nagasawa K, Fukase A, Mori S, Arakawa M, Yashiro S, Ishigaki Y, et al. Evaluation method of the degree of red blood cell aggregation considering ultrasonic propagation attenuation by analyzing ultrasonic backscattering properties. J Med Ultrason (2021) 48:3–12. doi:10.1007/s10396-020-01065-z

CrossRef Full Text | Google Scholar

24. Higashiyama K, Mori S, Arakawa M, Yashiro S, Ishigaki Y, Kanai H. Estimation of aggregate size of red blood cell by introducing reference power spectrum measured for hemispherical ultrafine wire. Jpn J Appl Phys (2022) 61:SG1046. doi:10.35848/1347-4065/ac4683

CrossRef Full Text | Google Scholar

25. Morse PM, Feshbach H. Methods of theoretical physics. New York: McGraw-Hill (1953).

Google Scholar

26. Kuc R, Schwartz M. Estimating the acoustic attenuation coefficient slope for liver from reflected ultrasound signals. IEEE Trans Son Ultrason (1979) 26:353–61. doi:10.1109/T-SU.1979.31116

CrossRef Full Text | Google Scholar

27. Labyed Y, Bigelow TA. A theoretical comparison of attenuation measurement techniques from backscattered ultrasound echoes. J Acoust Soc Am (2011) 129:2316–24. doi:10.1121/1.3559677

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hashimoto Y, Akashi N, Kushibiki J. Measurements of ultrasonic attenuation coefficients of water in VHF/UHF range (In Japanese). Tech Rep IEICE (1997) 97:37–42.

Google Scholar

29. Fukase A, Higashiyama K, Mori S, Arakawa M, Yashiro S, Ishigaki Y, et al. Stabilization of red blood cell aggregation evaluation using short-axis view of vein of ultrasound. Jpn J Appl Phys (2021) 60:SDDE08. doi:10.35848/1347-4065/abf3d5

CrossRef Full Text | Google Scholar

30. Chayer B, Allard L, Qin Z, Garcia-Duitama J, Roger L, Destrempes F, et al. Pilot clinical study of quantitative ultrasound spectroscopy measurements of erythrocyte aggregation within superficial veins. Clini Hemorheol Microcirc (2020) 74:109–26. doi:10.3233/CH-180541

PubMed Abstract | CrossRef Full Text | Google Scholar