
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 16 March 2023
Sec. Space Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1076346
Satellite signal threat is an important kind of satellite signal anomaly, which will lead to ranging biases of user receiver. BOC modulation is used more and more widely in the field of satellite navigation system. In the existing literature, there is a shortage that the non-ideal characteristics of the channel are not taken into account in the ranging biases analysis of BOC signal threat. The non-ideal characteristic of the receiving channel is one of the main bias sources of navigation signal reception. In the process of receiving navigation signal, due to the jitter caused by channel noise and the non-ideal phase of the channel, ranging biases will be introduced. To solve this problem, this paper proposes the analysis model of ranging biases of BOC signal threat based on non-ideal channel characteristics, and analyzes the non-ideal group delay characteristics of BOC (1,1) signal incoherent ranging mode. From the analysis results of ranging biases under multiple threated signals, it can be seen that the non-ideal group delay characteristics will worsen the ranging biases of BOC signal threat in most cases. In the sense of minimum ranging biases caused by BOC signal threat, 0.3chip∼0.35chip is the recommended parameter for non-coherent reception of BOC (1,1) early late code.
Satellite signal threat is one of the faults of the satellite system that results in abnormal integrity. In history, GPS signals have been detected abnormal for many times [1–4]. The study of the effect of satellite signal threat is an important content of the study on integrity of satellite navigation system. After the signal threat of GPS PRN 19 satellite in 1993 [1], the International Civil Aviation Organization (ICAO) used the second-order step threat model to describe the threat characteristics of BPSK signal [5–7]. The second-order step threat model of BPSK signal is also called ICAO threat model. Although the modeling of ICAO threat model is derived from the approximation of GPS PRN 19 satellite signal threat characteristics, it describes the general impact on signal characteristics when the general digital and analog devices in the satellite signal generation unit are abnormal. Therefore, as the basic model of BPSK signal integrity research, this model has extensive research significance and application value.
With the wide application of BOC modulation in GPS modernization program, European Galileo system and Beidou system in China [8–10], experts at home and abroad have made in-depth research on parameter design of BOC signal and user reception algorithm [10–15] but the research on the integrity of BOC signal has just started [16, 17]. At present, the main research on the integrity of BOC signal is that the BOC signal threat results in the receiver ranging biases. Phelts et al. extended the ICAO threat model of BPSK signal to the BOC signal and expanded the ranging of threat parameters. The ranging biases of BOC threat signal to ideal infinite bandwidth receiver in the form of early late code incoherent tracking were simulated and analyzed [16]. Fontanella et al. extended the threat parameter ranging of ICAO model to a greater extent to describe the threat model of BOC signal, and finally simulated and analyzed the ranging biases of BOC threat signal to the ideal low-pass filter receiver [17]. Xiao et al. compared the differences of phase discriminator functions of several typical BOC tracking modes and gave suggestions on the design of receiver front-end filter bandwidth and correlator interval, but did not analyze the ranging biases performance of BOC threat signals through non-ideal receiving channels and different receiver algorithms [18, 19]. The influence of waveform threat on ranging performance was analyzed by He et al. The signal used was BPSK signal, which did not involve the analysis of IBOC signal [20–23]. Gabriel Wong et al. introduced the threat of different satellite signals and the ranging biases under different code intervals [24]. M. Jean Baptiste Pagot et al. established signal threat models for new GNSS signals such as Galileo E1C, E5a, GPS L5, and compared the effect of different front-end bandwidth on signal reception [3]. Therefore, the current research on receiver ranging biases caused by BOC signal threat does not take into account the non-ideal characteristics of the channel.
Channel is an important part of the signal link of navigation receiver. Its non-ideal group delay characteristics can lead to threat of signal correlation peak, which affects the receiver’s ranging performance [25]. Chen et al analyzed the influence of receiver group delay on QMBOC signal correlation peak, but did not involve signal threat and final ranging biases [26]. Li et al have done a lot of research on channel characteristics of navigation signals, which can provide theoretical reference for channel model in this paper [27–35]. In order to reduce the influence of group delay on signal ranging performance in actual receiver channel design, it is necessary to study the effect of channel characteristics on ranging performance to guide receiver design.
This paper focuses on the influence analysis of receiver ranging biases caused by BOC signal threat. This paper reviews ICAO threat model and its extension on BOC signal, and establishes a theoretical analysis model of BOC signal threat ranging biases considering channel non-ideal characteristics. Considering the non-ideal characteristics of channel group delay, the relationship between the BOC(1,1) signal threat ranging biases and the design parameters such as the receiver’s early late code interval is analyzed, and useful conclusions for the design of BOC receiver are obtained.
Starting from the actual satellite signal generation process, the International Civil Aviation Organization (ICAO) uses a second-order step threat model to describe the BPSK signal threat. The traditional BPSK signal threat model can be extended to the BOC signal threat. In Figure 1, satellite signal generation components include digital devices and analog devices in two categories [5, 36–38]. The second-order step threat model is divided into three basic models based on the failure condition of each type of device: digital threat (Threat Model A, TM A), analog threat (Threat Model B, TM B), digital-analog threat (Threat Model C, TM C). Digital threat model corresponds to some digital faults such as satellite navigation data processing unit, analog threat model corresponds to some analog processing unit faults in the satellite signal generation process, and digital-analog threat model corresponds to the faults in the whole satellite signal generation process [2, 8].
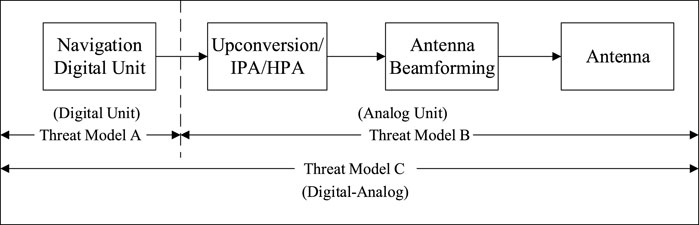
FIGURE 1. Corresponding relationship between signal threat model and fault of satellite signal generator.
The digital threat signal is caused by faults of the digital device (navigation data unit) in the satellite signal generation unit, which shows that the falling edge of the pseudo code is ahead of or behind the normal falling edge. The falling edge of pseudo code is represented by
Analog threat signal is caused by faults of analog devices in the satellite signal generation unit, which exhibits a second-order damped oscillation in amplitude. The analog threat signal can be equivalent to the response of a normal pseudo code signal after passing through a second-order filter, which is mathematically described as the unit-step response:
where
Digital-analog threat signals is caused by faults of digital and analog device in the satellite signal generation unit. The signal amplitude exhibits a second-order damped oscillation, and the pseudo code falling edge is ahead or behind the normal falling edge. The ranging of each threat parameter is
The top of the correlation peak between the receiver’s local pseudo code signal and the digital-analog threat signal is flat and the whole correlation peak is threated. Figure 2 A1, B1 show digital threat signal and the correlation peak for the BOC(1,1) signal; Figure 2 A2, B2 show analog threat signal and the correlation peak for the BOC(1,1) signal; Figure 2 A3, B3 show digital-analog threat signal and the correlation peak for the BOC(1,1) signal:
From the perspective of the complete processing flow from generation to reception of BOC signal, BOC signal will go through the process of satellite generation, space propagation, ground user reception and measurement. The analysis of space propagation characteristics is relatively complex, including the influence of troposphere, ionosphere, multipath and interference, among which the troposphere propagation characteristics are mainly represented by the propagation delay independent of carrier frequency. If various factors such as multipath and interference are considered in the actual environment, the complete signal flow of BOC signal will be very complex. In order to simplify the analysis of the problem, this section temporarily does not consider factors such as multipath and interference, but mainly considers the influence of non-ideal channels such as signal generation filter, ionospheric propagation characteristics and receiver equivalent filter on BOC signal threat. Therefore, the BOC signal processing flow is simplified as shown in Figure 3.
The threat of the BOC signal is mainly manifested in the threat of the correlation peak function, which leads to the biases of the receiver when tracking the BOC signal and measuring the pseudo range. The factors that cause the threat of correlation peak function include: threat of BOC signal, non-ideal characteristics of satellite signal generation filter (including non-ideal amplitude frequency response and non-ideal group delay), ionospheric propagation characteristics and non-ideal characteristics of receiver equivalent filter. In order to simplify the analysis, the non-ideal characteristics of satellite signal generation filter, ionospheric propagation characteristics and receiver equivalent filter are collectively referred to as channel non-ideal. It is worth pointing out that the threat of BOC signal correlation peak leads to the biases of receiver measurement (mean shift of measurement biases), which is independent of noise [27, 28]. Therefore, the influence of thermal noise is not considered in the analysis of ranging biases of BOC signal threat.
In this way, if the channel is not ideal, the equivalent analysis model of ranging biases of BOC signal threat is shown in Figure 4.

FIGURE 4. Equivalent analysis model of ranging biases of BOC signal threat based on non-ideal channel.
The original BOC signal generated on the satellite is set as
According to the conversion relationship between the time domain cross correlation function and the frequency domain cross power spectrum of the two signals, we can get:
Where,
The definition of ideal low-pass filtering can be written as:
Where,
The definition of the channel non-ideal equivalent filter can be written as:
Where,
The equivalent analysis model in Figure 4 can be used to analyze the BOC signal threat ranging biases based on the non-ideal group delay characteristics. The non-ideal group delay characteristics are the typical non-ideal channel effect [27, 28]. This section analyzes the influence of BOC signal threat under the non-ideal group delay characteristics. Let
Assuming that
Where
BOC signal tracking adopts the structure of Bump-jump early late code non-coherent tracking. In the Bump jump method, the correlation function of energy can be obtained by computing the square sum (
Figure 5 shows the correlation by BOC(1,1) Bump-jump method under ideal condition
The ranging biases of BOC (1,1) signal under three threat models of digital threat (TM A), analog threat (TM B) and digital-analog threat (TM C) are analyzed.
Under the digital threat model (TM A) of
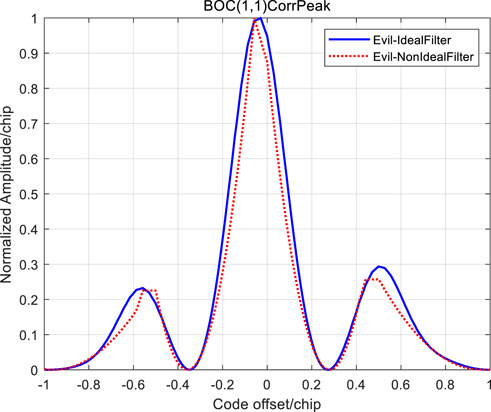
FIGURE 6. Correlation function of Bump-jump tracking method for BOC (1,1) signal TMA with non-ideal channel.
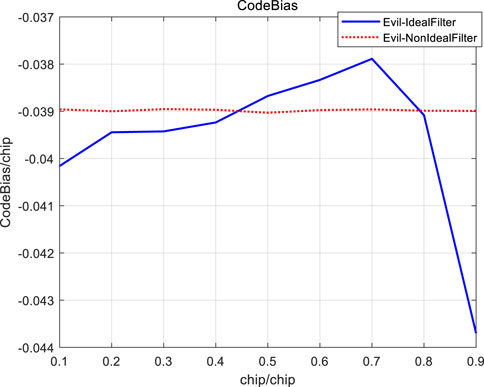
FIGURE 7. Ranging biases of Bump-jump tracking method for BOC (1,1) Signal TMA with non-ideal Channels.
Under the analog threat model (TM B) of
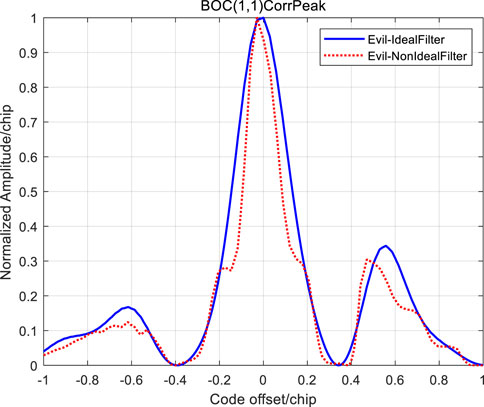
FIGURE 8. Correlation function of Bump-jump tracking method for BOC (1,1) signal TMB with non-ideal channel.
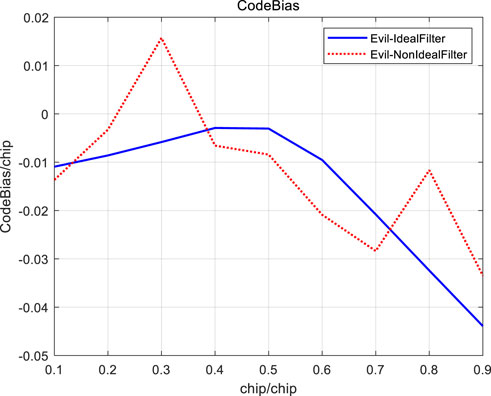
FIGURE 9. Ranging biases of Bump-jump tracking method for BOC (1,1) signal TMB with non-ideal channels.
Under the digital-analog threat model (TM C) of
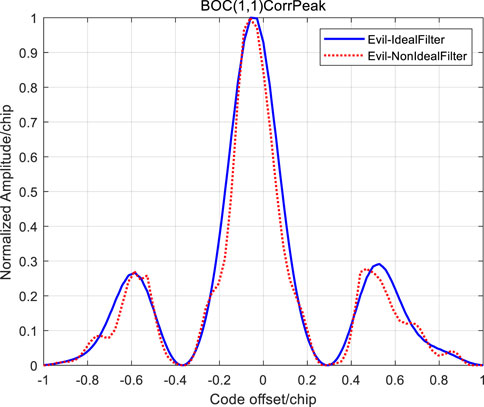
FIGURE 10. Correlation function of Bump-jump tracking method for BOC (1,1) signal TMC with non-ideal channel.
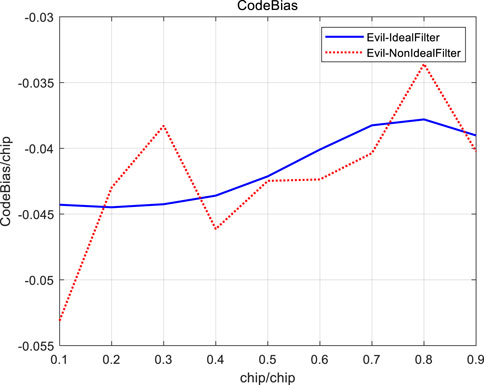
FIGURE 11. Ranging biases of Bump-jump tracking method for BOC (1,1) signal TMC with non-ideal channels.
Based on the above results, the following conclusions can be drawn: when the group delay characteristics of the channel are not ideal, the correlation peak shape of BOC signal threat will be further deteriorated under most of the early late code interval parameters, which will greatly increase the code tracking biases of BOC (1,1) signal. In addition, it is not difficult to find out from the above data results that, from the perspective of minimizing the ranging biases caused by signal threat, for the design of non-coherent reception of BOC (1,1) signal early late codes, if the early late code interval is selected between 0.3 chip and 0.35 chip, the ranging biases of BOC signal caused by the above three threat models under the ideal low-pass filter and non-ideal quadratic group delay channel characteristics are minimal or relatively small.
The non-ideal characteristics of channel group delay are not considered in the analysis of BOC signal distortion ranging deviation in the existing literature. This paper proposes an equivalent analysis model which is based on the assumption that the Bump-jump tracking method is used. And the range deviation of BOC (1,1) signal distortion under the time delay of the quadratic curve group is analyzed. The analysis results show that, the correlation peak of the BOC signal received through the non-ideal channel is deformed more than that of the BOC signal received through the ideal channel, and the ranging biases fluctuates significantly under different early late code intervals. Therefore, the characteristics of the non-ideal channel will worsen the ranging biases of the BOC signal threat in most cases. For the receiver, the early late code interval that is closer to the ranging biases of the ideal filter should be selected. It can be seen from the analysis results of ranging biases under multiple threated signals that in the sense of minimum ranging biases caused by BOC signal threat, 0.3 chip∼0.35 chip is the recommended parameter for BOC (1,1) incoherent reception of early late codes. The analysis model in this paper can also be used to analyze the ranging biases of other higher-order BOC signals under different channel non-ideal characteristics when they are threated.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Conceptualization: LW and XW; methodology and validation: XW and YEX; formal analysis and investigation: LW and QM; resources: LZ; writing—original draft preparation: LW; writing—review and editing: LX and YAX.
This research was funded by the National Natural Science Foundation of China (U20A0193&62003354).
The authors would like to thank the College of Electronic Sciences for providing the test platform.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Edgar C, Czopek F, Barker LB. A Co-operative Anomaly resolution on PRN-19. In: Proceedings of the 12th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1999); September 1999; Nashville, TN (1999). p. 2269–71.
2. Barker B, Huser SJ. Protect yourself navigation payload anomalies and the importance of adhering to ICD-GPS-200. In: Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998); September 1998; Nashville, TN (1998). p. 1843–54.
3. Jean-Baptiste P. Modeling and monitoring of new GNSS signal distortions in the context of civil aviation. Chromepet, Chennai: MITT (2016). p. 1–16.
4. Shallberg KW, Ericson SD, Phelts E. Catalog and description of GPS and WAAS L1 C/A signal deformation events. In: Proceedings of the 2017 International Technical Meeting of The Institute of Navigation; January 2017; Monterey, California (2017). p. 508–20. doi:10.33012/2017.14877
5. Phelts RE. Multicorrelator techniques for robust mitigation of threats to GPS signal quality. Stanford, CA: Stanford University PHD (2001). p. 1–17.
6. Eric P R, Karl S, Todd W. WAAS signal deformation monitor performance: Beyond the ICAO threat model. In: Proceedings of the ION 2017 Pacific PNT Meeting; May 2017; Honolulu, Hawaii (2017). p. 1–3. doi:10.33012/2017.15103
7.International Civil Aviation Organization. ICAO international standards and recommended practices. Annex 10 to the convention on international civil aviation. Volume I radio navigation aids seventh edition: ISBN 978-92-9258-504-4[S]. Montreal, Canada: International Civil Aviation Organization (2018).
8. Betz JW. Binary offset carrier modulations for radionavigation. Navigation, J Inst Navigation (2002) 48(4):227–46. doi:10.1002/j.2161-4296.2001.tb00247.x
9. Fine P, Wilson W. Tracking algorithm for GPS offset carrier signals[C]. In: Proceedings of U.S. Institute of Navigation NTM Conference; San Diego, CA (1999). p. 671–6.
10. Julien O, Cannon ME. A new unambiguous BOC(n,n) signal tracking technique. In: Proceedings of the European Navigation Conference; Rotterdam (2004). p. 1–3.
11. Ferrara NG, Bhuiyan MZ, Söderholm S, Ruotsalainen L, Kuusniemi H. A new implementation of narrowband interference detection, characterization, and mitigation technique for a software-defined multi-GNSS receiver. GPS Solutions (2018) 22(4):106. doi:10.1007/s10291-018-0769-z
12. Sun X, Zhou Q, Ji Y, Fu Q, Miao Q, Wu S. An unambiguous acquisition algorithm for BOC (n, n) signal based on sub-correlation combination. Wireless Personal Commun (2019) 106(3):1609–28. doi:10.1007/s11277-019-06232-1
13. Sun C, Zhao HB, Zhuang C, Feng W. The IFFT-based SQM method against digital distortion in GNSS signals. GPS Solutions (2017) 21(4):1457–68. doi:10.1007/s10291-017-0622-9
14. Guo Y, Wang X, Lu X, Rao Y, He C. Algorithm research on high-precision tracking of beidou-3 B1C signal. In: Sun J, Yang C, Yang Y, editors. China satellite navigation conference (CSNC) 2019 proceedings. CSNC 2019. Lecture notes in electrical engineering, vol 562. Singapore: Springer (2019). p. 1–4. doi:10.1007/978-981-13-7751-8_45
15. Lu M, Li W, Ya Z, Cui X. Overview of BDS III new signals. Navigation (2019) 66(1):19–35. doi:10.1002/navi.296
16. Phelts RE, Akos DM. Effects of signal deformations on modernized GNSS signals. J Glob Positioning Syst (2006) 5:2–10. doi:10.5081/jgps.5.1.2
17. Fontanella D, Paonni M, Eissfeller B. A novel evil waveforms threat model for new generation GNSS signals theoretical analysis and performance. In: 2010 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC). Noordwijk, Netherlands: IEEE (2010). doi:10.1109/NAVITEC.2010.5708037
18. Xiao W, Liu W, Sun G. Modernization milestone: BeiDou M2-S initial signal analysis. GPS Solutions (2016) 20(1):125–33. doi:10.1007/s10291-015-0496-7
19. Han Q, Liu W, Xiao W. Equalization algorithm for GNSS receiver channel by FIR filters. In: 2017 Eighth International Conference on Intelligent Control and Information Processing (ICICIP). Hangzhou, China: IEEE (2017). p. 319–24.
20. He C, Guo J, Lu X, Wang X, Rao Y, Kang L, et al. A new evil waveforms evaluating method for new BDS navigation signals. GPS Solutions (2018) 22(2):37–13. doi:10.1007/s10291-018-0698-x
21. He C, Guo J, Lu X, Wang X, Liu F. The impact of carrier leakage and spectral asymmetry distortions on the performance of navigation signals. China Satellite Navigation Conf (2012) 161:147–60. doi:10.1007/978-3-642-29193-7_13
22. He C, Lu X, Guo J, Su C, Wang W, Wang M. Initial analysis for characterizing and mitigating the pseudo-range biases of BeiDou Navigation Satellite System. Satellite Navigation (2020) 1(1):3–10. doi:10.1186/s43020-019-0003-3
23. He C, Guo J, Lu X, Wang X. Measurements and offline analysis of bei dou GEO signal. In: ION 2013 (2013). p. 28–30.
24. Gabriel W. Impact of nominal signal deformations on satellite navigation systems. Stanford, CA: Standford University (2014).
25. Coco DS, Clayton C, Dahlke S, Clynch J. Variability of GPS satellite differential group delay biases. IEEE Trans Aerosp Electron Syst (1991) 27(6):931–8. doi:10.1109/7.104264
26. Chen L, Zhao W, Xu Q, Zhang L. The Effect Analysis of Filter group delay on QMBOC signal correlation peak. Bacolod: CSNC (2022).
27. Li P, Huang Y, Zhou B, Ou G. Research on all-pass network for wideband satellite receiver’s RF front-end group delay equalization. Virginia, USA: ION GNSS (2012).
28. Zhu X, Li Y, Yong S, Zhuang Z. A novel definition and measurement method of group delay and its application. IEEE Trans Instrumentation Meas (2009) 56(1):229–33. doi:10.1109/TIM.2008.927197
29. Lu Z, Chen F, Xie Y, Sun Y, Cai H. High precision pseudo-range measurement in GNSS anti-jamming antenna array processing. Electronics (2020) 9(3):412. doi:10.3390/electronics9030412
30. Song J, Lu Z, Xiao Z, Li B, Sun G. Optimal order of time-domain adaptive filter for anti-jamming navigation receiver. Remote Sensing (2021) 14(1):48. doi:10.3390/rs14010048
31. Wang F, Li P, Zhong S, Ni S. A fitting method of RF Channel Group delay characteristics for high precision navigation. In: IEEE 10th International Conference on Electronics Information and Emergency Communication (ICEIEC). Beijing, China: IEEE (2020). p. 26–30. doi:10.1109/ICEIEC49280.2020.9152281
32. Lu Z, Song J, Huang L, Ren C, Xiao Z, Li B. Distortionless 1/2 overlap windowing in frequency domain anti-jamming of satellite navigation receivers. Remote Sensing (2022) 14(8):1801. doi:10.3390/RS14081801
33. Wang F, Li P, Mou W, Zhong S, Ni S. Piecewise fitting technology of group delay difference based on fourier decomposition. In: IEEE 3rdInternational Conference on Information Communication and Signal Processing(ICICSP). Shanghai, China: IEEE (2020). p. 353–8. doi:10.1109/ICICSP50920.2020.9232113
34. Lu Z, Chen H, Chen F, Nie J, Ou G. Blind adaptive channel mismatch equalisation method for GNSS antenna arrays. IET Radar, Sonar & Navigation (2018) 12(4):383–9. doi:10.1049/iet-rsn.2017.0416
35. Lu Z, Nie J, Chen F, Chen H, Ou G. Adaptive time taps of STAP under channel mismatch for GNSS antenna arrays. IEEE Trans Instrumentation Meas (2017) 66(11):2813–24. doi:10.1109/TIM.2017.2728420
36. Liu WS, Xiao W. Performance analysis of GNSS signal distortions detection based on multi-correlators processing. CSNC (2022) 1:5. doi:10.26914/c.cnkihy.2022.000858
37. Phelts RE, Mitelman A, Pullen S. Transient performance analysis of a multicorrelator signal quality monitor. Beaumont, TX, USA: ION GPS (2001).
Keywords: GNSS signal threat, binary offset carrier (BOC) signal, ranging biases, non-ideal channel, group delay characteristics
Citation: Wenxiang L, Wei X, Xiaozhou Y, Manli Q, Zukun L, Xiangjun L and Xin Y (2023) Analysis of ranging biases of BOC signal threat based on non-ideal channel group delay characteristics. Front. Phys. 11:1076346. doi: 10.3389/fphy.2023.1076346
Received: 21 October 2022; Accepted: 06 March 2023;
Published: 16 March 2023.
Edited by:
Olga V. Khabarova, Tel Aviv University, IsraelReviewed by:
Zhaowen Yan, Beihang University, ChinaCopyright © 2023 Wenxiang, Wei, Xiaozhou, Manli, Zukun, Xiangjun and Xin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiao Wei, eGlhb3dlaTEyQG51ZHQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.