A stochastic reaction–diffusion modeling investigation of FLASH ultra-high dose rate response in different tissues

Purpose: The aim of the study was to propose a theory based on topology and geometry of diffusion channels in tissue to contribute to the mechanistic understanding of normal tissue sparing at ultra-high dose rates (UHDRs) and explore an interplay between intra- and inter-track radical recombination through a reaction–diffusion mechanism.

Methods: We calculate the time evolution of particle track structures using a system of coupled reaction–diffusion equations on a random network designed for molecular transport in porous and disordered media. The network is representative of the intra- and inter-cellular diffusion channels in tissues. Spatial cellular heterogeneities over the scale of track spacing are constructed by incorporating random fluctuations in the connectivity between network sites, resembling molecular mass and charge heterogeneities at the cellular level.

Results: We demonstrate the occurrence of phase separation among the tracks as the complexity in intra- and inter-cellular structure increases. At the strong limit of structural disorder, tracks evolve individually like isolated islands with negligible inter-track as they propagate like localized waves in space, analogous to the Anderson localization in quantum mechanics. In contrast, at the limit of weak disorder in a homogeneous medium, such as water, the neighboring tracks melt into each other and form a percolated network of non-reactive species. Thus, the spatiotemporal correlation among chemically active domains vanishes as the inter-cellular complexity of the tissue increases from normal tissue structure to fractal-type malignancy.

Conclusion: Differential FLASH normal tissue sparing may result from the interplay of the proximity of tracks over the intra- and inter-cellular landscape, a transition in the spatial distribution of chemical reactivity, and molecular crowding. In this context, insensitivities in the radiobiological responses of the tumors to FLASH-UHDR are interpreted via a lack of geometrical correlation among isolated tracks. The structural and geometrical complexities of cancerous cells prevent the clustering of tracks over a timescale, in which inter-track chemical reactivities presumably prevail in normal tissues. A series of systematic experiments on radiolysis-induced diffusivity and reactivity in actual normal and cancerous tissues must be performed to classify the tissues potentially spared by FLASH-UHDRs and verify our theory.

1 Introduction

The unique normal tissue sparing of FLASH ultra-high dose rates (UHDRs), which is 40 Gy/s and higher, has recently attracted considerable attention [1–18]. Preclinical studies have shown that FLASH-UHDR delivery reduces the toxic effects of radiation on DNA and cells in normal tissues compared to conventional dose rates (CDRs), whereas tumor tissues seem to be equally responsive to either dose rate modality ([17] and references therein). However, the interpretation of the experimental data and the underlying microscopic mechanism is under intensive investigation and debate among researchers in the field of radiation therapy.

Among the theories proposed for the interpretation of the experimental data [1–6, 8, 9, 11], the authors of the present work hypothesized a transition between intra- and inter-track reactions as the major physical mechanism for differential biological responses of CDR vs. FLASH-UHDR [10, 13, 14]. In these models, the time evolution of radiolysis products is assumed to propagate in homogeneous and uniform media, equivalent to water, regardless of the tissue type. Thus, the presented models lack differentiation with respect to tissue types upon exposure at FLASH-UHDRs.

A series of systematic experiments was recently conducted and published [15] on measurements of chemical yields of 7-hydroxy-coumarin-3-carboxylic acid in solutions irradiated by proton- and carbon-ion beams at UHDRs. These experimental studies have revealed evidence in favor of the inter-track coupling hypothesis, originally predicted by performing molecular dynamics simulations of track–track chemical interactions. The results of these simulations, presented in [10], have led to the interpretation of molecular crowding in populations of reactive oxygen species (ROS) and the formation of agglomerates in the form of non-reactive oxygen species (NROS), consistent with recent observations reported in [15].

In this work, we extend our model calculation on the same physical grounds as in [10, 13, 14] and consider the cellular structure of normal and cancerous tissues at a coarse-grained scale. We develop a mathematical description of tissue structure complexity to examine the interplay between the rates of radical diffusion and recombination as a function of this structural complexity. We predict the occurrence of intra- to inter-track transitions as the structural complexity decreases from, for example, tumor to normal tissue.

1.1 Terminology

In a nutshell, the passage of a high-energy particle (electron, proton, or heavier charged particles) through matter leaves a linear dynamical footprint of a cylindrically symmetric (isotropic) exchange of energy with the electrons and nuclei constituting molecular structures. This linear structure and its branches are known as a particle track.

A single track is a random collection of a sharp spatiotemporal distribution of non-ionized and ionized excitations with a varying nanometer-scale diameter, which depends on the particle’s kinetic energy that determines the magnitude of energy exchange. Due to the quantum electrodynamic nature of energy exchange, the excitations are created within attoseconds after the passage of the particle.

Immediately after their creation, molecular excitations and ions undergo decay processes. The relaxation time associated with the decay of excitations (including recombination of mobile ions into various types of stable products and chemical species) is much longer than their generation time. Because the excited molecules and ions are mobile in cellular structures, they decay at the same time as they diffuse away from the center of the track.

The presence of high concentrations of localized excitonic energy of molecules surrounding mobilized ions induces an explosive irreversible flow of thermal energy to ion species, which, in turn, theoretically significantly enhances the effective diffusion constant of these ions. The core temperature of a track depends on the particle type and its linear energy loss per unit length (linear energy transfer, LET). It can go up to several thousands of Kelvin for heavy charged particles [13]. Ions move randomly along the radial direction away from the hot core of the tracks with a thermally boosted kinetic energy that generates shock waves [13, 44–46]. They asymptotically lose their kinetic energy and fall into cold diffusion at a thermal equilibrium condition because of collisions and energy exchange with the molecules in the environment. Eventually, ions rest at room temperature with a transformed chemical composition.

It should be noted that such physical and chemical phenomena are not included in standard MC models based on homogenous and uniform water medium. Nonetheless, these phenomena may have significant effects on the measured endpoint of MC simulations, such as radical yields. Throughout this process, biological damage to the host’s cellular structure occurs as ions interact chemically with bio-molecules, such as DNA and lipids in membranes.

A typical radiotherapy beam of particles forms a random distribution of expanding and decaying tracks in targeted (tumors) and untargeted (normal tissues) volumes. Initially, as pointed out previously, the tracks expand individually via a time-dependent diffusion mechanism as they decay due to deexcitation and ion-recombination processes. The time evolution of such an ensemble of individually evolving tracks can be reduced to that of a single track if the geometrical overlap among tracks is negligible. We refer to this limit as an “independent track structure”. Conversely, the “strongly correlated track structure” can be anticipated at a limit in which the process of inter-track ion exchanges, chemical transformation, and recombination occurs simultaneously due to the destructive interference of sufficiently close tracks, a molecular-crowding phenomenon. Therefore, we refer to these two distinguishable classes of chemical exchange mechanisms as intra- and inter-track states.

The transition between intra- and inter-track recombination depends on the dose and dose rate. More precisely, the higher the beam flux (the number of particles entering a unit area per unit of time), the higher the compactness of particles in a given time interval hitting the target. In this limit, the probability of overlap among the tracks before their annihilation becomes significant. Thus, under certain conditions, a transition from the intra-track to inter-track reaction can be predicted. In our recent publications [10, 13, 14], the latter has been hypothesized to be a physical mechanism for FLASH-UHDRs.

2 Materials and methods

This model aims to describe the effects of intra- and inter-track diffusion and interaction as a function of the structural complexity of the target medium. To this end, we develop a reaction–diffusion model of spatially and temporally separated particle tracks and calculate the interaction of OH radicals from the tracks to form H₂O₂. Importantly, the model utilizes a spatially varying diffusion constant, whereby the solutions to the reaction–diffusion system are calculated numerically by stochastic variation of the diffusion constant. Subsequently, this reaction–diffusion system is related to an analogous percolation model of diffusing ions in order to define the target structural heterogeneity with a measure from percolation theory, the site occupation probability p, and relate this to the diffusion constant.

2.1 Reaction–diffusion model

In this model, the radiation-induced chemicals are concentrated in a core of a cylindrically symmetric body/cloud of track structure. As a track structure is nothing but a cloud of ROS and NROS, the expansion of the track can be interchangeably considered for the description of the time evolution of the system of coupled ROS and NROS (i.e., their diffusion and reaction processes). In particular, we performed the track structure calculation by conventional MC methods in a homogenous water medium where the location of ionization and molecular excitation points were identified. After the construction of a cylindrical cloud of ROS and NROS, we further considered reaction–diffusion solutions in an inhomogeneous and rough cellular medium. This kind of matching between MC and the coarse-grained reaction–diffusion model is inevitable unless atomistic (not volumetric) cellular structures and molecular inhomogeneities are added in the next generations of MC codes.

The mathematical details of our model calculation with analytical solutions for the time evolution of a single track are given in the Supplementary Appendix. We used the analytical formulas given in the Supplementary Appendix to cross-check our numerical solutions obtained from discretizing the space and time in a finite difference approach employed to calculate the solutions of the coupled reaction–diffusion partial differential equations of multi-track structures:

$\begin{array}{ccc}\hfill \frac{\partial u}{\partial t}& =\hfill & G+\vec{\nabla }\cdot \left(D_f\left(\vec{r}\right)\vec{\nabla }u\right)-k_{1}u+k_{2}v-2k_3{u}^2-k_{12}uv,\hfill \\ \hfill & \hfill & \hfill \end{array}(1)$

$\frac{\partial v}{\partial t}=k_{1}u-k_{2}v+k_3{u}^2.(2)$

Here, $u(\vec{r},t)$ and $v(\vec{r},t)$ represent ROS and NROS densities, respectively, for example, u = [^•OH] and v = [H₂O₂] at spatial coordinate, $\vec{r}$, and time, t. $G(\vec{r},t)$ and $D_f(\vec{r})$ represent the ROS production yield, proportional to the dose rate, and diffusion constant of the fast-moving species (neglecting the diffusion of slow-moving species), and k₁, k₂, k₃, k₁₂ are reaction rate constants. k₁ represents the scavenging rate of ROS. The dependence of the diffusion constant on cellular or tissue inhomogeneities has been accounted for in Eq. 1 by $D_f(\vec{r})$.

In the limit of ideal diffusion, where D_f is a constant, independent of the position of ROS in space, and in the absence of all reaction rates, k₁ = k₂ = k₃ = k₁₂ = 0, the time evolution of a single track, created initially at time t = 0, far from the initial nano-scale dimension of the track, represented by radius w, asymptotically approaches a Gaussian distribution function modulus, a factor proportional to the initial number of chemical species, c₀:

$u\left(\vec{r},t\right)=\frac{c_0}{4\pi D_{f}t}\exp \left(-\frac{r^2}{4D_{f}t}\right),(3)$

where c₀ = πw²u₀ and u₀ is the initial density of ROS, integrated over a unit length along the trajectory of the primary particle. Note that the Gaussian function is the exact solution of the diffusion equation, ∂u/∂t = D_f∇²u, with a spike-like initial and boundary condition.

As a representative of ROS that causes damage to DNA and/or lipids in membranes, we consider ^•OH-radicals for u. ^•OH-radicals are known to diffuse through cellular space and react with biomolecules, including DNA, proteins inside and outside the cells, and lipids in cell membranes. Denoting k₁, an average decay (scavenging) rate of a population of ^•OH in the track (resulting in DNA, proteins, lipids, or, in general, biomolecular (BM) hydrogen abstraction as described in [30] in which [DNA^•] and [BM^•] partially contribute to v, e.g., v = [H₂O₂] + [DNA^•] + [BM^•]) introduces an exponential decay in solutions of u, in Eq. 3:

$u\left(\vec{r},t\right)=\frac{c_0}{4\pi D_{f}t}\exp \left(-\frac{r^2}{4D_{f}t}-k_{1}t\right).(4)$

If cells were uniform and homogeneous, like in liquid water, the diffusion of ions induced by radiation must have occurred like in an ordered medium, as described in Eq. 4. However, the current models in radiobiology do not consider intra- and inter-cellular inhomogeneities in the diffusion of radiolysis products due to a lack of experimental data and theoretical models.

To fill the gaps in our understanding of diffusion channels at the microscopic levels, we performed a series of molecular dynamics simulations to investigate the diffusion of ^•OH-radicals [43]. To visualize some of these effects in real time, we uploaded samples of our simulations in the form of videos available on YouTube [26, 27]. The simulations have clearly shown that variability in the molecular mass and charge distribution and, in general, chemical, physical, and mechanical composition of the micro-environment of cells may dramatically alter the diffusion of ^•OH-radicals. Therefore, it is a natural generalization to consider spatial fluctuations in the diffusion constant $D_f(\vec{r})$ because of an abundance of such molecular heterogeneities in cellular tissue. To incorporate the randomness at a coarse-grained level, we performed a Monte Carlo sampling on D_f and solved numerical solutions of the stochastic reaction–diffusion partial differential equations for various realizations of $D_f(\vec{r})$ after discretizing the space and time coordinates.

2.2 Random walk percolation model

As a complementary model to the reaction–diffusion model given in Eqs 1, 2, we cross-validated the numerical results against the solutions of random walk or Brownian motion on the same random network throughout the percolation theory [40–42]. More details on the description of the modeling of the diffusion constant can be found in Supplementary Section SE.

In this context, a regular lattice is a lattice with no disorder. It is an ordered lattice with all diffusion links connected to neighboring sites throughout the lattice points. In a classical disorder model, the diffusion from an occupied site to a neighboring occupied site can be simulated through the random walk. In this model, the diffusion can be parameterized in terms of a single site occupation probability p and the random walk probability q = 1/2d, where d is the embedding dimension of the square lattice and 2d is the geometrical coordination number of any site on the lattice. In other words, on a realization of a random lattice, p and 1 − p are the fraction of occupied and unoccupied sites, a parameter that determines the average size of the clusters on the lattice. In this model, the diffusion constant, D_f, is an increasing function of p. It continuously increases with p above a critical value (a percolation threshold, p_c) and reaches a maximum value at p = 1, where all lattice sites are occupied, corresponding to a regular lattice with no disorder.

In a random walk, on a regular lattice with p = 1, at every trial or simulation time step, the diffusing ion randomly selects one of its nearest neighbor sites with probability q and moves to that selected site. On a random lattice with p < 1, we first check if the site is occupied with probability p, then the move to that site occurs with probability q, and the ion moves one step. Otherwise, the ion stays on the initial site with probability 1 − p, and the search for another move to another occupied neighboring site continues in the next random walk trial unless no occupied neighboring sites are available.

The diffusion constant of such a Brownian particle can be calculated by the Einstein relation, ⟨r²⟩ = 2D_ft. Here, $\vec{r}$ is the Euclidean distance that measures how far the particle has moved randomly away from the center of the coordinates where it was created. Above the network percolation threshold (p > p_c), the Brownian motion can find at least one trajectory to cross the entire system, and D_f = ⟨⟨r²⟩⟩/2t represents the mean diffusion constant of the entire network. Otherwise, if all clusters are found to be isolated, D_f = 0 (including at the percolation point, p = p_c). In the latter case, although diffusion through the entire network is not possible, a limited diffusion confined within a cluster can still occur. In this case, the diffusion length is limited to the cluster size.

One may expect a finite number of tracks passing through a single cluster to interact and recombine (the red tracks in Figure 1) because diffusion among them is possible. Note that $⟨⟨\vec{r}⟩⟩=0$ because of the unbiased random walk considered in these simulations. For a given p, ⟨⟨⋯ ⟩⟩ represents double averaging, that is, random walk averaging subjected to a specific network configuration, followed by ensemble averaging over a large number of random network configurations. Thus, $D_f=⟨⟨r^2⟩⟩/2t=\frac{1}{2N_c}{\sum }_{i=1}^{N_c}{⟨r^2⟩}_i/t_i$, where i is an index going over different realizations of the N_c random configurations subjected to a given p. Using the same simulation time for all N_c random configurations, $t_1=t_2=\dots =t_{N_c}=t$ simplifies the expression to $D_f=\frac{1}{2t{N}_c}{\sum }_{i=1}^{N_c}{⟨r^2⟩}_i$. An alternative approach on ensemble average over various clusters connecting the opposite boundaries of the lattice is given in Supplementary Section SE.

FIGURE 1

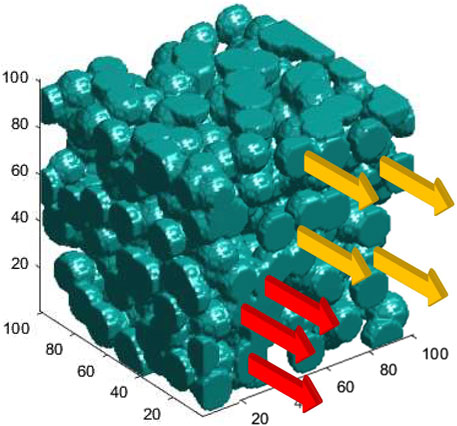
FIGURE 1. Schematic sketch of tracks passing through a porous media, representative of heterogeneities in cells and tissues. Clusters through which diffusion is allowed are shown in blue. In contrast, diffusion is forbidden in the void space among the clusters. Red arrows represent interacting (mediated by diffusion) tracks as they pass through a single cluster; hence, they are connected tracks. Orange arrows passing through isolated islands represent non-interacting tracks.

For a perfect network (a network with no disorder, such as a homogeneous medium in normal cells), where p = 1, D_f is at its maximum. It decays continuously to lower diffusion values for p_c ≤ p ≤ 1, vanishes at p = p_c, and remains zero within p ≤ p_c. Note that close to p = p_c (from above), the clusters in the network form a self-similar fractal-type structure in short distances with a Hausdorff dimension that is a measure of the tissue/cell roughness or, more specifically, their fractal dimension [40, 41].

Interested readers may refer to [40–42] for a discussion on the concepts of percolation and fractal dimensionality of a porous network embedded in three-dimensional space. The mathematical techniques introduced in [40–42] are relevant to the present applications, where we consider the porous space of malignant cells in which diffusion of radiolysis products is unlikely to occur in the voids among the clusters.

As a first step in proof-of-principle and to demonstrate the effects of cellular structures and textures on the interpretation of the tissue-sparing of FLASH-UHDR, we consider two types of media to study the transport of chemical species in typical normal and tumor cells/tissues. Because of substantial differences in intra- and inter-cellular structure and chemical compositions of tumor versus normal cells, we solve reaction–diffusion equations in a homogenous and isotropic medium, similar to liquid water, as a representative of normal cells/tissues and in a heterogenous fractal-type porous and disordered medium for tumors [31, 32].

At the limit of strong disorder, the entire cellular structure can be divided into clusters or isolated islands. Consider an object in 3D as sketched in Figure 1, for example, a cell or a tissue segment. A cluster is a set of connected points on that object, disconnected from the rest of the points via diffusion due to structural heterogeneities. Thus, each cluster consists of connected sites, among which the diffusion of radiolysis products occurs normally. Hence, diffusion is forbidden in the space among the clusters. In Figure 1, tracks with different color codes are designated based on their classifications as interacting (red) and non-interacting (orange). The underlying porous media, representing the topology of diffusion channels in tumor cell/tissue, is depicted in blue, where diffusion can be performed. The blobs represent the topography of a spongy structure. The clusters are separated by clear voids, the space where diffusion is forbidden. They represent highly dense chemical heterogeneities at the molecular level that slow down or even block diffusion. Tumor calcification with the density in primary or metastatic lesions, such as metastatic lymph nodes, with a CT value above 60 Hounsfield Unit, represents such voids.

The structure in Figure 1 can be considered at the level of single cells or cell agglomerates in tissues, depending on the scale of the structure at hand. The topology of random diffusion channels, sketched in Figure 1, was constructed mathematically within a single cell and scaled up to the structure of tissues, assuming self-similarity and scale invariance of fractal structures, one of the characteristics of the disorder patterns. At the single-cell level, the rationale behind such a construction is the diffusion of ^•OH radicals through molecular heterogeneities.

The porous structure depicted in Figure 1 was created using a MATLAB code with a random number generator drawn from a uniform distribution to introduce blobs with specific radii at random locations in a 3D cube. The radius was chosen to be slightly larger than half the distance of a pair of nearest neighbor sites to illustrate the overlap between the two nearest neighbor blobs.

At UHDR, where the possibility of finding closely spaced tracks is likely, the ratio of the cellular diffusion correlation length ξ and the mean track spacing determines the domain of intra- and inter-track dominance. ξ is a measure of the size of the isolated islands in a single cell, that is, the mean diameter of the blue blobs in Figure 1.

Note that in our approach, the details of cellular structures, such as the exact locations of various organelles, are averaged out due to the random distribution of cells with respect to the random distribution of tracks, which is equivalent to a compound distribution as considered in the formulation of the theory of dual radiation action (TDRA) [33, 34]. TDRA considers the energy transfer in ionizations and regards the deposited energy proportional to the DNA double-strand breaks and the number of cellular sublethal lesions.

3 Results

3.1 Track interaction in the reaction–diffusion model

3.1.1 Interaction in an ordered medium

Figures 2, 3 present the time evolution of two tracks, simultaneously starting from two cylindrically symmetric clouds of ionization with radius w. The real-time motion of these tracks is available online.

FIGURE 2

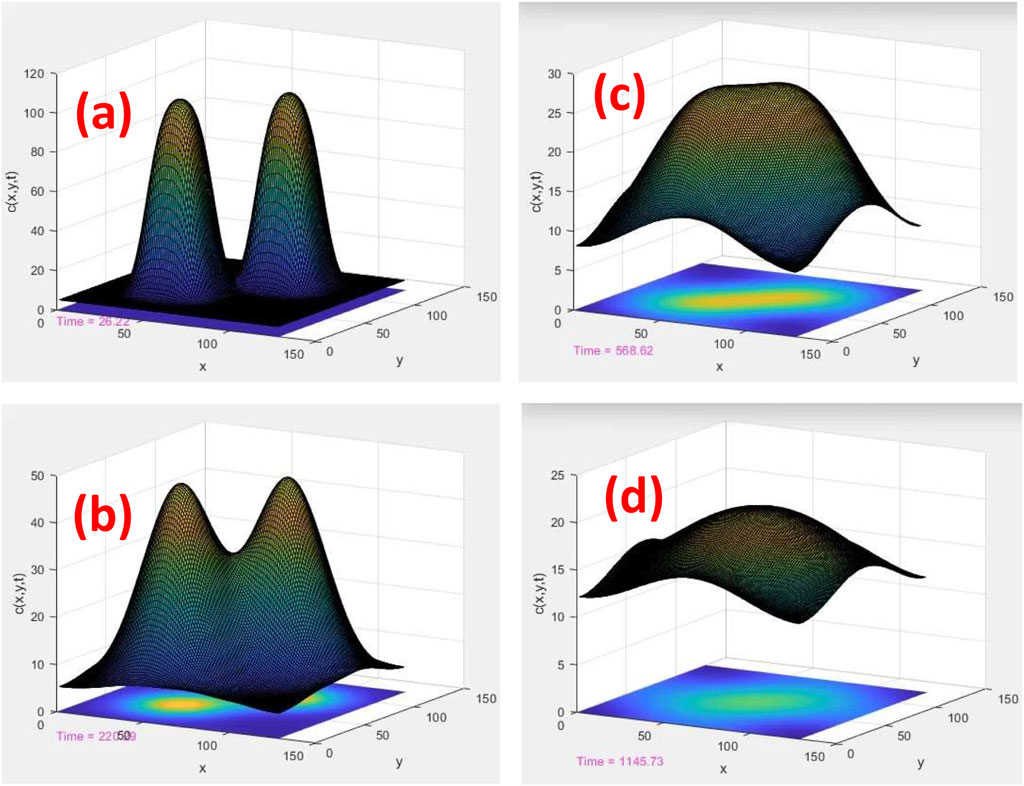
FIGURE 2. Time evolution of two tracks, u_i (x, y) and u_j (x, y), in a homogeneous and uniform medium. c (x, y) = u_i (x, y) + u_j (x, y) is the total density of ROS calculated by the superposition of individual ROSs. (x, y) are the planner coordinates of the plane perpendicular to the axis of cylindrical tracks. The length scales are displayed in nm, and the time scales are 26, 220, 569, and 1,146 ps for (A–D), respectively

FIGURE 3

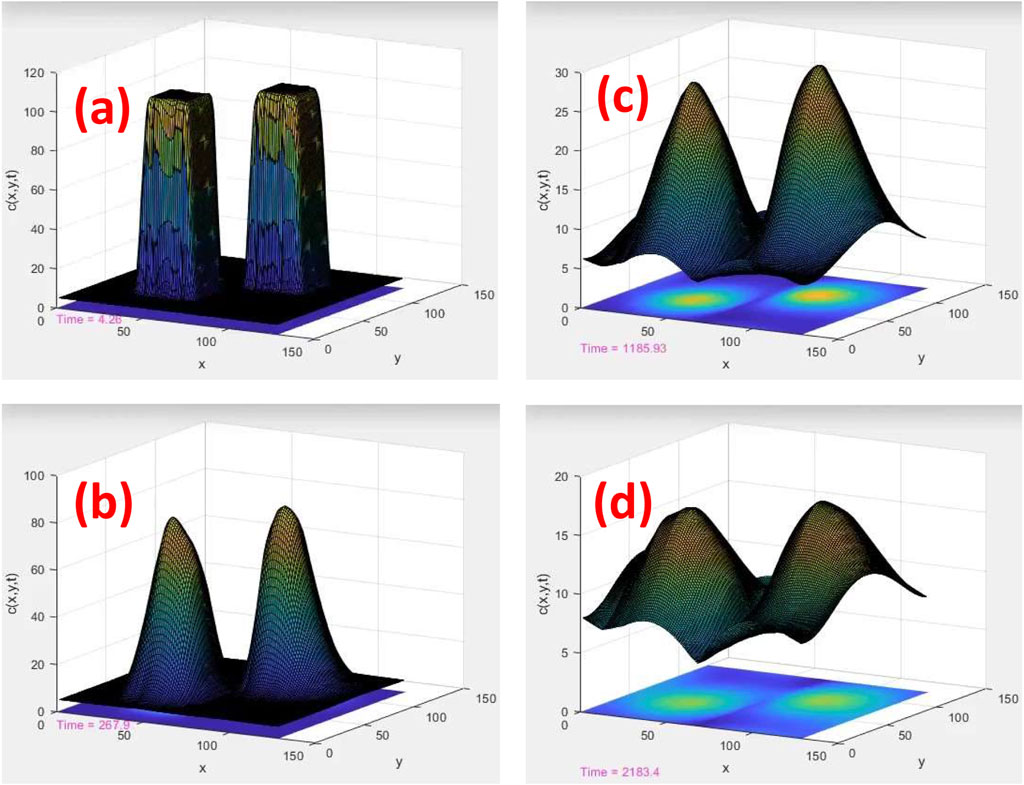
FIGURE 3. Time evolution of two tracks in a porous medium with random connectivity among the diffusion sites. Similar to Figure 2, c (x, y) = u_i (x, y) + u_j (x, y). The length scales are displayed in nm, and the time scales are 4, 268, 1,186, and 2,183 ps for (A–D), respectively

In Figures 2A–D, a solution of the aforementioned 2D reaction–diffusion equation as a function of time was calculated in a homogenous and uniform medium, such as water. As shown, two cylindrical tracks evolve initially into two uncorrelated Gaussian probability distribution functions (PDFs) with centers located at ${\vec{r}}_i$ and ${\vec{r}}_j$ before they collapse together, where

$u_i\left(\vec{r},t\right)=c_0\frac{e^{-\frac{|\vec{r}-{\vec{r}}_i{|}^2}{4D_f\left(t-t_i\right)}-k_1\left(t-t_i\right)}}{4\pi D_f\left(t-t_i\right)},(5)$

and

$u_j\left(\vec{r},t\right)=c_0\frac{e^{-\frac{|\vec{r}-{\vec{r}}_j{|}^2}{4D_f\left(t-t_j\right)}-k_1\left(t-t_j\right)}}{4\pi D_f\left(t-t_j\right)}.(6)$

Here, D_f and k₁ are the diffusion constant and reaction rates, respectively. Our approach to numerical calculation of the time-dependent solutions of the diffusion equation subjected to a cylindrically symmetric initial condition and fitting to Gaussian functions at distances away from the cylinder can be found in Supplementary Appendix SD. To clarify the notations, i and j in these equations are the indices of tracks. In a discrete space-time version of reaction–diffusion equations, $\vec{r}=(x,y,z)$ is expressed by (n_xΔ_x, n_yΔ_y, n_zΔ_z), where n_x, n_y, n_z = {0, ±1, ±2, … } are integer numbers and (Δ_x, Δ_y, Δ_z) are the elements of the space grids along (x, y, z) directions. Similarly, t = n_tΔ_t, where n_t = 0, 1, 2, … and Δ_t denotes the time intervals.

Without loss of generality, to illustrate the effects of tissue types, we considered the creation time of tracks t_i = t_j in these simulations. This condition approximately fulfills the time sequence of the track inductions at UHDR. Note that, in general, the temporal distribution of the tracks, hence their relative time elapse, depends on the dose rate. However, at UHDR, and only for the sake of simplicity of illustration on the effects of random diffusion on the time evolution of the tracks and the track–track recombination, we have intentionally neglected the time elapse among the tracks in comparison with other time scales involved in the present reaction–diffusion model.

As the simulation time proceeds in Figures 2A–D, two Gaussians merge together and form an elongated single PDF. The geometrical overlap of two Gaussians can be calculated analytically:

$\begin{array}{ccc}\hfill ⟨u_i|u_j⟩\left(t\right)& =\hfill & \int d\vec{r}{u}_i\left(\vec{r},t\right)u_j\left(\vec{r},t\right)\hfill \\ \hfill & =\hfill & c_0^2\frac{e^{-\frac{|{\vec{r}}_i-{\vec{r}}_j{|}^2}{8D_{f}t}-2k_{1}t}}{8\pi D_{f}t}.\hfill \end{array}(7)$

As the two Gaussians combine, like melting two droplets into a single droplet, diffusion slows down in the overlap area. Instead, the diffusion is performed with a rate calculated by Eq. 7 from the periphery of combined Gaussians to the outside. In this model, intra-track interaction is parameterized by the rate constants k₁, k₂, k₃, k₁₂, and inter-track interaction is the geometrical overlap of the tracks, as given in Eq. 7.

Note that the Gaussian functions in Eqs 5, 6 are the analytical solutions of a single track in a uniform system. These solutions demonstrate the calculation of overlap integral analytically in a uniform system, as given in Eq. 7.

3.1.2 Interaction in a disordered medium

In a system of multi-tracks, as in Figure 2, or even a single track in a disordered medium, such as in Figure 3, the analytical solutions are not available, and the overlap integral should be calculated numerically by discretizing space and time. In such situations, we used analytical forms of solutions derived in the Supplementary Appendix to compare with the numerical solutions and check the accuracy of our finite difference method.

As shown in Figures 3A–D, we calculated a solution of a reaction–diffusion equation with an identical initial condition as in Figures 2A–D, except that the calculation was performed on a network with random connectivity between the neighboring sites to mimic the geometrical disorder of tumor cells with strong inhomogeneity and/or fractal-type porosity.

A series of connectivity probabilities p was drawn from a uniform distribution within the interval of zero and one and subsequently convoluted to the diffusion constant D_f for each diffusion site in the network. Although the reaction rate k₁ can be considered another random variable, we kept it constant at the same value as in the simulation shown in Figure 2 to isolate the effects of diffusion. Note that a special case of p = 1 describes the transport of ions on a homogeneous network with uniform connectivity that links nearest neighbor sites, corresponding to the kinetics of ions among normal cells, with the results depicted in Figure 2.

The time and length scales in Figures 2, 3 were chosen based on the conventional values of the diffusion constants. To simulate the expansion of a track of ^•OH-radicals at thermal equilibrium with the environment at room temperature and by using an empirical value $D_f=4.3\times 10^{-9}{m}^2/s=0.43{\mathring{A}}^2/ps$ [13], we divide the square sides of the computational boxes into steps with 0.1 nm length. In these calculations, the time advances via 0.1 ps intervals to fulfill the Courant–Friedrichs–Lewy condition or the Nyquist sampling theorem in signal processing, in which the simulation time steps are required to be half or less of the period of the quickest dynamics. Accordingly, such length scales set the lateral sides of the computational boxes in Figures 2, 3 to 13 nm, larger than six folds of the width of a DNA double-stranded helix that is approximately 2 nm. The running times of these simulations were terminated at 0.5 μs with no significant differences from the times corresponding to Figures 2D, 3D. This condition simply allows the simulation to run until the numerical solutions converge to a satisfactory value. By monitoring the overlap integral between two tracks as a function of time, the numerical results do not change significantly beyond a time value, reported as a cutoff time. Once this condition has been fulfilled numerically, we terminate the simulation.

3.2 Relation to the percolation model

The overlap between two adjacent tracks is expected to happen at time scale t = ℓ²/2D_f if the relevant length scale for diffusion (i.e., the diffusion length), ${⟨⟨r^2⟩⟩}^{1/2}$, becomes comparable to inter-track spacings ℓ. Even below the percolation limit, p < p_c, where clusters do not connect from one side of the tissue to the other, tracks can overlap through intra-cluster diffusion channels if two or more tracks pass through a single cluster.

Another interesting combination of a system of tracks and isolated clusters can be represented by two neighboring tracks that pass through two separated and disconnected clusters with no diffusion channel between them, corresponding to a non-interacting track configuration as shown in Figure 1, where our construction of the structure and topology of random diffusion channels is illustrated schematically.

A collection of configurations of a system of tracks and tissue clusters under the condition, p < p_c, some with finite D_f, combined with vanishing D_f, leads to a system of tracks with lower effective interaction compared with tissues under the condition p > p_c, where all clusters are connected. The former represents tumors, and the latter represents normal tissues. Thus, the problem is interesting from a mathematical point of view as it describes the time evolution of percolating tracks mediated through diffusion channels subjected to percolation of the underlying medium, cellular structures, and tissues (i.e., a compound percolation system).

At FLASH-UHDR conditions, if the correlation length in the network connectivity, ξ, (i.e., a measure of cluster size) is smaller than the mean inter-track distances, diffusion effectively does not occur to the extent of track spacings; thus, the response of the tissue falls into the class of isolated/single track states. This is a scenario the percolation theory predicts for typical tumor cells/tissues irradiated by a source of FLASH-UHDR.

As can be seen clearly from these two simulations, the effect of randomness in connectivity among the diffusion channels is to localize the tracks such that the cell/tissue responses exhibit insensitivity to the time-elapse among the tracks simply because of negligible inter-track overlaps. Hence, the cells and tissues with strong porosities and disorder in their diffusion channels (either normal or cancerous) under radiation must exhibit insensitivity to the dose rate, the same phenomenon observed empirically from the tumors under FLASH-UHDR.

To illustrate the ideas proposed in this work in the clinical setting, Figures 4A, B present schematic sketches of two tracks generated by two beamlets before and after entering the patient’s body, respectively. The diffusive expansion of the beamlet tracks in normal tissues, depicted by the thicker arrows, and in tumor (prostate), depicted by thinner arrows, are seen. At a given time after the beamlets enter, they expand more rapidly in normal tissues because of higher diffusivity compared to the two isolated beamlets in tumors. A larger expansion of tracks in normal tissues yields higher overlaps.

FIGURE 4

FIGURE 4. Schematic sketch of the diffusion expansion of two-particle tracks in the air before (A) and after (B) entering the patient body. The width of the arrows in normal tissues (thicker arrows) and the tumor (thinner arrows in the prostate) demonstrates the extent of inter-track overlaps in different tissue types. In normal tissues, the expanded tracks allow inter-track overlaps, whereas, in tumor tissues, the localized tracks yield negligible inter-track overlaps. At a given dose where the number of tracks (shown by arrows) is given, the lack of inter-track overlaps justifies insensitivities of radiobiological responses to dose rates.

We note that the two-track calculation presented in these figures, with the use of a periodic boundary condition, an equivalent of the repetitive configurations, has been presented only to illustrate the effects of disorders. The readers must be aware that this calculation is in no way a substitute for the quantification of the dosimetry aspects of the beams. The latter must be done by a MC toolkit, such as TOPAS [47], with an extension and inclusion of the disorders in the simulation of reaction and diffusion of the chemical species.

4 Discussion

Understanding the chemical processes of reaction–diffusion processes of radiation-induced chemical species in cells is crucial to the proper modeling of FLASH UHDRs. Current approaches to this modeling neglect a) the effect of thermal spikes in the cores of particle tracks on the diffusion of the resultant chemical species and b) the influence of spatial heterogeneities within tissue on their diffusion. In recent years, several techniques have been developed to measure molecular diffusion in cellular environments [31, 32, 35–38]. In general, the diffusion constant substantially depends on the size of molecules, the roughness of the inter- and intra-cellular structures, and the chemical composition, such as calcification at the metastatic lesions and texture of the cells. The cellular texture may range from uniform and homogeneous to strongly disordered, exhibiting fractal geometries as in tumor cells [31, 32]. The latter mechanism bounds the range of molecular random walks and blocks the Brownian motion of chemical pathways below the percolation limit of the diffusion at p = p_c associated with the underlying fractal dimensionality and self-similarity of the cellular structure. Despite these reports and observations, there is no study in the radio-biological literature to address the effects of cell types on the diffusion of ion species.

This study aims to qualitatively highlight the tissue heterogeneities in modeling inter-track coupling at FLASH-UHDR, particularly as all models neglect the differences in heterogeneities among tissues and consider all cell types to be equivalent to uniform and homogenous liquid water.

More sophisticated models, such as molecular dynamics simulations, require the incorporation of cellular internal and external structures in the calculation of D_f. Our recently performed simulations [43] revealed the sensitivity of D_f on local chemical, physical, and mechanical molecular compositions of the environment of ^•OH-radicals, including the density of water molecules. The details of these simulations are beyond the scope of this work; however, the results clearly support the hypothesis of the present study (e.g., the diffusion processes of ROS and NROS in the following real-time simulations [26, 27]).

Along this line of thoughts, we remark that the reported abnormal growth of the tumor cell membrane [31, 32] and its fractal-type interface may lead us to suggest a correlation with the growth of internal heterogeneities in the physico-chemical and molecular composition in the bulky texture of the cell that influences the Brownian motion and the spatial distribution of small radiolysis molecules including ^•OH radicals. To the best of our knowledge, there is no experimental evidence in favor or against such correlations; however, we provide plausible justifications below in favor of the existence of the disordered internal molecular structures of cancerous cells.

In our model, diffusion through a disordered system and a porous media, as in a single cell, has been described by random walks through fractal-type structures embedded in three-dimensional space regardless of the roughness of the cellular surface, in which it controls inter-cellular diffusion through the cell membranes. In this model, a combination of these two types of diffusive channels determines the overall intra- and inter-track recombination of chemical species.

Although diffusion and reaction within a single cell and to the cell nucleus are considered a source of DNA damage, there are recent studies related to non-DNA damage through lipids [18] and cell membranes [28] through Ferroptosis pathways [29]. The intra- and inter-cellular diffusion mechanism introduced in this theoretical study correlates the DNA and lipid damage throughout cell nuclei and membranes to the hypothetical intra- and inter-track FLASH mechanisms.

At the level of a single cell, in the absence of any experimental data, one may propose a reasonable assumption that the bulk properties of tumor cells resemble their fractal-type surface morphology unless there was an annealing or relaxation process that allowed repositioning of the atoms and molecules to reside at their equilibrium locations, like in a controlled process of crystal growth of materials. For example, such a process may occur in liquid or more advanced techniques, such as in vapor deposition or epitaxy, where crystal defects and imperfections can be eliminated by controlling environmental and external parameters, such as pressure and temperature.

Under in vivo or in vitro conditions, the rapid doubling time in the growth process of the wild-type cancerous cells means that such annealing that requires a slower processing timescale is unlikely to occur. Unlike controlled manufacturing conditions in the growth processing of artificial materials, the internal physical structure of tumor cells under uncontrolled growth may face alteration of the stored mechanical energy and tension due to out-of-equilibrium rearrangement of the molecules. Thus, it is expected that the internal structure of tumor cells exhibits roughness in their mechanical properties, heterogeneity in their mass densities, and disorder in their diffusion channels, behaviors observed in growth conditions far from equilibrium.

Snowflakes with internal defects similar to colloidal aggregates in their crystalline structure are another example of natural systems exhibiting bulky heterogeneities with a correlation to their fractal-type surface interface. Similar to our hypothetical malignant cells, they belong to states of matter that exhibit topologically distinct classes of porosity in their mass density. Thus, the systems form under ballistic growth conditions [48]. Metallic glass alloys are yet another example of a glassy or disordered phase of materials that form under a rapid decrease in temperature (i.e., quenching conditions). Closer to our hypothetical heterogeneities in tumor cells, we may enumerate abnormalities, such as grain boundaries, crystalline defects, and dislocations that affect stored mechanical energies and local diffusion channels in normal metallic alloys.

The underlying physical processes of tissue response to radiation dose rate, including differential biological responses of various tissues, either normal or malignant, can be formulated through inter-track overlap. In this model, the tissue’s biological responses are categorized based on the geometrical correlation and collective evolution of the tracks. In a single fraction, tracks with negligible overlaps do not lead to a physico-chemical response sensitive to the dose rate. Thus, the typical tumor responses fit into topologically distinct classes of uncorrelated and evolutionary single tracks: dominant intra-track recombination. In contrast, normal tissue responses can fall into another class of collective chemical crowding of the correlated tracks, where inter-track recombination is dominant. The transition between inter- and intra-track reaction–diffusion processes is responsible for these two seemingly distinguished behaviors among tissue types.

As illustrative examples of structural disorders, we presented time evolutions of the solutions of the coupled partial differential equations of two separate tracks, initially created at two locations, in Figures 2, 3. An underlying network among the reaction–diffusion sites is considered to model the diffusion channels in tissues. In this model, a tissue is represented by a network with random connectivity among the sites. In Figure 2, a network with uniform and homogeneous connectivity has been considered to represent normal tissues. In Figure 3, a random network defined by a random represents cancerous cells or tissues identified to behave like self-similar fractals at the percolation threshold, p = p_c, the point where the diffusion channels are blocked due to the emergence of isolated islands.

The results shown in Figure 2 illustrate the role of tissue texture in forming overlaps among tracks as a function of time. In Figure 3, randomness in diffusion channels, which is unique to transport through porous and disordered structures, limits the diffusion range. Thus, the tracks evolve individually like isolated islands with negligible overlap. This is consistent with the scaling theory of percolation and localization of thermal waves/Schrödinger equation.

Note that lowering the diffusion constant without incorporating the randomness in the network connectivity does not lead to the localization of Gaussian PDFs, as the absolute value of the diffusion constant does not change the overall effect in inter-track evolution and their overlap. More precisely, the time evolution of the diffusion equation is invariant under the scaling of the diffusion constant. A simultaneous scaling of diffusion length and time gives a similar trend in the tracks’ geometrical overlaps. However, with constant intra- and inter-track reaction rates, this scaling rule breaks down unless we scale them simultaneously.

Finally, for the interested readers, we remark that track localization observed in these simulations that is consistent with the percolation theory of diffusion on porous and disordered media was extensively studied in the context of semiconductor physics. The phenomenon known as Anderson localization [49] was extensively studied quantum mechanically to describe the metal-insulator transitions in condensed matter and solid-state physics. Here, we map the normal and tumor tissues problem to a similar transition between metals (where conduction electrons are in the extended states) and insulators (where conduction electrons form pockets of localized states). We suggest that the mechanism modeled in these computer simulations interprets the empirically observed differential tissue-sparing of FLASH-UHDR. The interplay of this hypothesis and that of differential antioxidant or oxygen concentrations is currently under investigation.

The relevance of inter-track interaction has recently been examined in [22] by MC simulation of interacting proton tracks, where no significant changes in ^•OH-radicals or H₂O₂ yields were found at clinically relevant doses. This claim is also supported by other simplistic geometric track overlap models. A similar assessment was given for clinical beams of carbon [21].

These theoretical results contrast the experimental evidence of [23], which measured lower H₂O₂ yields at UHDR compared to CDR. Furthermore, references [4, 24] observed a similar decrease in H₂O₂ yields at UHDR with electrons. This discrepancy and the observation that MC simulations tend to measure an increase in H₂O₂ yields as the dose rate increases as opposed to the experimentally measured decrease in H₂O₂ yields suggests that the theoretical models and MC simulations do not provide an adequate representation of the interdependent chemical reactions occurring in the irradiation of oxygenated water. This may have to do with limitations of the MC simulations, such as the lack of any simulated dissolved oxygen or the neglect of physical effects, such as thermal spikes. In either case, the chemical impact of inter-track interactions at UHDR continues to demand further studies for a complete understanding but remains outside of the scope of the present manuscript, which instead examines the effect of structural heterogeneity in biological tissue on inter-track interaction.

5 Conclusion

This theoretical study aims to present a model calculation based on the reaction–diffusion of reactive species induced by ionizing radiation and points to possible transitions in the molecular crowding of the track structures. This transition is dependent on the structural heterogeneity of the target tissue. As described in the model, higher heterogeneity results in limited diffusion of reactive species, decreasing the probability of inter-track overlap. Tracks with negligible overlaps do not lead to a physico-chemical response sensitive to radiation dose rate. A significant difference in this structural heterogeneity between normal and tumor tissue is hypothesized to result in the observed differential sparing of the FLASH effect. A systematic experimental cell/tissue database must be generated to validate the hypothesis presented in this work.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author contributions

RA wrote the main manuscript, prepared figures performed mathematical derivations and computational steps. The rest of the authors (AB, AF, SB, and ES) scientifically exchanged the hypothesis and contributed to writing the manuscript. RM contributed to the scientific proposal and supervised the project.

Funding

AF is funded through the Sêr Cymru II 80761-BU-103 project by Welsh European Funding Office (WEFO) under the European Development Fund (ERDF).

Acknowledgments

The authors would like to acknowledge useful discussion and scientific exchanges with Drs. Niayesh Afshordi and Sohrab Rahvar. The first author dedicates this work to Mahsa Amini, who lost her life fighting for women’s rights, and would like to acknowledge Drs. Muhammad Sahimi, Nasser Nafari, and Steve Girvin for the percolation theory and the topological aspects of condensed matter physics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1060910/full#supplementary-material

References

1. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med (2014) 6:245ra93. doi:10.1126/scitranslmed.3008973

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Montay-Gruel P, Bouchet A, Jaccard M, Patin D, Serduc R, Aim W, et al. X-rays can trigger the FLASH effect: Ultra-high dose-rate synchrotron light source prevents normal brain injury after whole brain irradiation in mice. Radiother Oncol (2018) 129(3):582–8. doi:10.1016/j.radonc.2018.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Vozenin MC, De Fornel P, Petersson K, Favaudon V, Jaccard M, Germond JF, et al. The advantage of FLASH radiotherapy confirmed in mini-pig and catcancer patients. Clin Cancer Res (2019) 25(1):35–42. doi:10.1158/1078-0432.ccr-17-3375

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Montay-Gruel P, Acharya MM, Petersson K, Alikhani L, Yakkala C, Allen BD, et al. Long-term neurocognitive benefits of FLASH radiotherapy driven by reduced reactive oxygen species. Proc Natl Acad Sci USA (2019) 116(22):10943–51. doi:10.1073/pnas.1901777116

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Buonanno M, Grilj V, Brenner DJ. Biological effects in normal cells exposed to FLASH dose rate protons. Radiother Oncol (2019) 139:51–5. doi:10.1016/j.radonc.2019.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Vozenin MC, Baumann M, Coppes RP, Bourhis J. FLASH radiotherapy international workshop. Radiother Oncol (2019) 139:1–3. doi:10.1016/j.radonc.2019.07.020

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Darafsheh A, Hao Y, Zwart T, Wagner M, Catanzano D, Williamson JF, et al. Feasibility of proton FLASH irradiation using a synchrocyclotron for preclinical studies. Med Phys (2020) 47:4348–55. doi:10.1002/mp.14253

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Spitz DR, Buettner GR, Petronek MS, St-Aubin JJ, Flynn RT, Waldron TJ, et al. An integrated physico-chemical approach for explaining the differential impact of FLASH versus conventional dose rate irradiation on cancer and normal tissue responses. Radiother Oncol (2019) 139:23–7. doi:10.1016/j.radonc.2019.03.028

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Koch CJ. Re: Differential impact of FLASH versus conventional dose rate irradiation: Spitz et al., Radiother Oncol (2019) 139:62–3. doi:10.1016/j.radonc.2019.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Abolfath R, Grosshans D, Mohan R. Oxygen depletion in FLASH ultra-high-dose-rate radiotherapy: A molecular dynamics simulation. Med Phys (2020) 47:6551–61. doi:10.1002/mp.14548

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lai Y, Jia X, Chi Y. Modeling the effect of oxygen on the chemical stage of water radiolysis using GPU-based microscopic Monte Carlo simulations, with an application in FLASH radiotherapy. Phys Med Biol (2021) 66:025004. doi:10.1088/1361-6560/abc93b

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jansen J, Knoll J, Beyreuther E, Pawelke J, Skuza R, Hanley R, et al. Does FLASH deplete oxygen? Experimental evaluation for photons, protons, and carbon ions. Med Phys (2021) 48:3982–90. doi:10.1002/mp.14917

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Abolfath R, Baikalov A, Bartzsch S, Afshordi N, Mohan R. The effect of non-ionizing excitations on the diffusion of ion species and inter-track correlations in flash ultra-high dose rate radiotherapy. Phys Med Biol (2022) 67:105005. doi:10.1088/1361-6560/ac69a6

CrossRef Full Text | Google Scholar

14. Baikalov A, Abolfath R, Mohan R, Schüler E, Wilkens JJ, Bartzsch1 S. An analytical model of intertrack interaction at ultra-high dose rates and its relevance to the FLASH effect. submitted to Med. Phys (2022).

Google Scholar

15. Kusumoto T, Inaniwa T, Mizushima K, Sato S, Hojo S, Kitamura H, et al. Radiation chemical yields of 7-hydroxy-coumarin-3-carboxylic acid for proton- and carbon-ion beams at ultra-high dose rates: Potential roles in FLASH effects. Radiat Res (2022) 198:255–262. doi:10.1667/rade-21-00.230.1

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Van den Heuvel F, Vella A, Fiorini F, Brooke M, Hill M, Ryan A, et al. Using oxygen dose histograms to quantify voxelised ultra-high dose rate (FLASH) effects in multiple radiation modalities. Phys Med Biol (2022) 67:125001. doi:10.1088/1361-6560/ac71ef

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Vozenin M-C, Bourhis J, Durante M. Towards clinical translation of FLASH radiotherapy. Nat Rev Clin Oncol (2022) 19:791–803. doi:10.1038/s41571-022-00697-z

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Froidevaux P, Grilj V, Bailat C, Reiner Geyer W, Bochud F, Vozenin M-C. FLASH irradiation does not induce lipid peroxidation in lipids micelles and liposomes. Radiat Phys Chem (2023) 205:110733. doi:10.1016/j.radphyschem.2022.110733

CrossRef Full Text | Google Scholar

21. Weber UA, Scifoni E, Durante M. FLASH radiotherapy with carbon ion beams. Med Phys (2022) 49:1974–92. doi:10.1002/mp.15135

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Thompson S, Prise K, McMahon S. Investigating the potential contribution of inter-track interactions within ultra-high dose-rate proton therapy. Phys Med Biol (2023) 68:055006. doi:10.1088/1361-6560/acb88a

CrossRef Full Text | Google Scholar

23. Blain G, Vandenborre J, Villoing D, Fiegel V, Fois GR, Haddad F, et al. Proton irradiations at ultra-high dose rate vs. Conventional dose rate: Strong impact on hydrogen peroxide yield. Radiat Res (2022) 198:318–324. doi:10.1667/rade-22-00021.1

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kacem H, Almeida A, Cherbuin N, Vozenin M-C. Understanding the FLASH effect to unravel the potential of ultra-high dose rate irradiation. Int J Radiat Biol (2022) 98:506–16. doi:10.1080/09553002.2021.2004328

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Abolfath R, Fraile A. Lipid Bilayer destruction by ionizing radiation, thermal spikes and shock waves (2023). Available at: https://www.youtube.com/watch?v=0GYgT8sIpUk (Accessed March 13, 2023).

Google Scholar

27. Abolfath R, Fraile A. Nano-bubbles/cavities induced by charged particles simulated by MD-ReaxFF with ≈ 150,000 water molecules. The running time up to 2 ps shows the cavity expands up to 10 nm in diameter (2023). The video is available at: https://www.youtube.com/watch?v=Sh_6s34WzNE (Accessed March 13, 2023).

Google Scholar

28. Kale RK, Sitasawad SL. Radiation induced lipid peroxidation in liposomes. Phys Chem (1990) 36:361–4. doi:10.1016/1359-0197(90)90019-e

CrossRef Full Text | Google Scholar

29. Tang Z, Huang Z, Huang Y, Chen Y, Huang M, Liu H, et al. Ferroptosis: The silver lining of cancer therapy. Front Cel Dev. Biol. (2021) 9:765859. doi:10.3389/fcell.2021.765859

CrossRef Full Text | Google Scholar

30. Abolfath RM, van Duin ACT, Brabec T. Reactive molecular dynamics study on the first steps of DNA damage by free hydroxyl radicals. J Phys Chem A (2011) 115:11045–9. See the real-time simulations and movies at: http://qmsimulator.wordpress.com/. doi:10.1021/jp204894m

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Klein K, Maier T, Hirschfeld-Warneken VC, Spatz JP. Marker-free phenotyping of tumor cells by fractal analysis of reflection interference contrast microscopy images. Nano Lett (2013) 13:5474–9. doi:10.1021/nl4030402

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Thiagarajah JR, Kim JK, Magzoub M, Verkman AS. Slowed diffusion in tumors revealed by microfiberoptic epifluorescence photobleaching. Nat Methods (2006) 3:275–80. doi:10.1038/nmeth863

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kellerer AM, Rossi HH. A generalized formulation of dual radiation action. Radiat Res (2012) 178:AV204–13. doi:10.1667/rrav17.1

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Abolfath R, Helo Y, Bronk L, Carabe A, Grosshans D, Mohan R. Renormalization of radiobiological response functions by energy loss fluctuations and complexities in chromosome aberration induction: Deactivation theory for proton therapy from cells to tumor control. Eur Phys J D (2019) 73:64. doi:10.1140/epjd/e2019-90263-5

CrossRef Full Text | Google Scholar

35. Dix JA, Verkman AS. Crowding effects on diffusion in solutions and cells. Annu Rev Biophys (2008) 37:247–63. doi:10.1146/annurev.biophys.37.032807.125824

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Mourao MA, Hakim JB, Schnell S. Connecting the dots: The effects of macromolecular crowding on cell physiology. Biophysical J (2014) 107:2761–6. doi:10.1016/j.bpj.2014.10.051

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Cross SE, Jin Y-S, Rao J, Gimzewski JK. Nanomechanical analysis of cells from cancer patients. Nat Nanotechnology (2007) 2:780–3. doi:10.1038/nnano.2007.388

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zink D, Fischer AH, Nickerson JA. Nuclear structure in cancer cells. Nat Rev Cancer (2004) 4:677–87. doi:10.1038/nrc1430

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Stauffer D, Aharony A. Introduction to percolation theory. 2nd ed. Oxfordshire: Taylor and Francis (2003).

Google Scholar

41. Sahimi M. Applications of percolation theory. Boca Raton: CRC Press (2003). Springer-2023 2nd Edition.

Google Scholar

42. Li M, Liu R-R, Lü L, Hua M-B, Xu S, Zhang Y-C. Percolation on complex networks: Theory and application. Phys Rep (2021) 907:1–68. doi:10.1016/j.physrep.2020.12.003

CrossRef Full Text | Google Scholar

43. Abolfath RM, Biswas PK, Rajnarayanam R, Brabec T, Kodym R, Papiez L. Multiscale QM/MM molecular dynamics study on the first steps of guanine-damage by free hydroxyl radicals in solution. J Phys Chem A (2012) 116:3940–5. doi:10.1021/jp300258n

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Friis I, Verkhovtsev AV, Solov’yov IA, Solov’yov AV. Lethal DNA damage caused by ion-induced shock waves in cells. Phys Rev E (2021) 104:054408. doi:10.1103/physreve.104.054408

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Friis I, Verkhovtsev A, Solov’yov IA, Solov’yov AV. Modeling the effect of ion-induced shock waves and DNA breakage with the reactive CHARMM force field. J Comp Chem (2020) 41:2429–39. doi:10.1002/jcc.26399

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Fraile A, Smyth M, Kohanoff J, Solov’yov AV. First principles simulation of damage to solvated nucleotides due to shock waves. J Chem Phys (2019) 150:015101. doi:10.1063/1.5028451

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Schuemann J, McNamara AL, Ramos-Mendez J, Perl J, Held KD, Paganetti H, et al. TOPAS-nBio: An extension to the TOPAS simulation toolkit for cellular and sub-cellular radiobiology. Radiat Res (2019) 191:125–138. doi:10.1667/rr15226.1

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Barabasi A-L, Stanley HE. Fractal concepts in surface growth. Cambridge: Cambridge University Press (1994).

Google Scholar

49. Lee PA, Ramakrishnan TV. Disordered electronic systems. Rev Mod Phys (1985) 57:287–337. doi:10.1103/revmodphys.57.287

CrossRef Full Text | Google Scholar

50. Carslaw HS, Jaeger JC. The Laplace transformation: Problems on the cylinder and sphere. Composite cylindrical regions. In: Conduction of heat in solids. New York: Oxford University Press (1959). p. 345–347.

Google Scholar

51. Abramowitz M, Stegun IA. Handbook of mathematical functions. Mineola: Dover publisher (1964).

Google Scholar

52. Arfken GB, Weber HJ. Mathematical methods for physicists. 4th ed. Cambridge: Academic Press (1995).

Google Scholar