A low phase noise high power Er-fiber frequency comb synchronized to the hydrogen maser clock by harmonic phase locking

We demonstrate a low phase noise all polarization-maintaining (PM) Er-fiber optical frequency comb (OFC) with low phase noise, which is synchronized to the hydrogen maser clock (HMC) using the 18th harmonic of the repetition rate for tight phase locking. The instability of the locked carrier envelope offset frequency is 1.24 × 10⁻¹⁸@1 s, the phase noise of the OFC is −96 dBc/Hz at 1 Hz offset, and the corresponding RMS timing jitter of the repetition rate is 62 fs (1 Hz–1 MHz). The residual frequency instability of the repetition rate (200 MHz) is 1.46 × 10⁻¹⁴@1 s, and the residual phase noise of the OFC normalized to 10 MHz is −138 dBc/Hz at 1 Hz offset and declines to about −160 dBc/Hz at the far-end, much lower than that of the HMC (−122 dBc/Hz at 1 Hz and −156 dBc/Hz at the far-end).

1 Introduction

In recent years, optical frequency combs (OFCs) have attracted increasing research attention [1–3] owning to their promising applications in scientific research and engineering, including precise time and frequency metrology [4–6], ultra-stable microwave generation [7, 8], attosecond pulse generation [9, 10], optical time/frequency transfer [11, 12], etc. These applications are all based on the comb-like spectral distribution, enabling them to achieve the conversion of optical and microwave frequencies. The frequency of any longitudinal mode can be defined as f_n = nf_r + f_ceo, where n is the number of comb lines, f_r is the repetition rate correlated with the cavity length, and f_ceo is the carrier-envelope offset (CEO) frequency induced by the group velocity dispersion. OFCs can be stabilized by simultaneously locking a comb line (with an optical reference) and f_ceo or locking fr (with a microwave-domain reference) and f_ceo. The frequency instability of the OFC under the above two referencing schemes can reach a magnitude of 10⁻¹⁸ (optical referencing) and 10⁻¹²–10⁻¹³ (microwave-referencing), respectively [13–16]. Different referencing schemes possess their distinctive advantages and application fields. For instance, optical-referencing OFCs own ultralow instability, enabling them to be extensively employed in two-way optical time and frequency transfer [17, 18], and the comparison of the optical atomic clock [19–21]. On the other hand, microwave-referencing OFCs have accurate repetition rates, computable longitudinal mode frequency, and low maintenance costs, which benefits them to be utilized in microwave frequency transfer [22, 23], optical frequency metrology [24–26], and ultralow noise frequency synthesis [27, 28], etc.

These broad application prospects further promote the sustainable development of the OFC. With the development of laser technology, the types of OFCs are also becoming increasingly diverse, ranging from the earliest Ti:sapphire OFCs [29, 30] to fiber OFCs [31, 32] to on-chip integrated OFCs [27, 33], among which fiber OFCs are the most widely used because of their high cost performance, small size, and favorable heat dissipation properties. In recent years, as the increasing of the PM fibers’ maturity, PM OFCs have received more and more attention due to its lower environmental sensitivity and higher robustness, especially the PM Er-fiber OFCs, of which the wavelengths are in the telecommunication C band, enabling low-loss transmission of the OFC pulses through optical fibers [34–37]. The locking point of the microwave-referencing OFC is usually at the repetition rate, which is generally 100 MHz–250 MHz for the Er-fiber OFC. The phase noise of these microwave-referencing Er-fiber OFCs is generally between −60 dBc/Hz and −80 dBc/Hz at 1 Hz offset, it is difficult to further reduce this noise level [38, 39].

The metric for the stability performance of the OFC can be indicated by the fractional frequency stability δν/ν, where δν and ν are the noise equivalent and carrier frequency of the comb mode [40], respectively. When the carrier frequency increases from radio frequency to optical frequency, the stability of the OFC will be substantially improved. That is why the instability of optical referencing OFCs is much lower than that of microwave-referencing OFCs. Inspired by this, we propose a scheme to suppress the phase noise of microwave-referencing OFCs by changing the reference frequency from the repetition rate of the laser to its high harmonic. Assuming that the performance of the phase-locking loop remains unchanged, and ignoring the residual phase noise introduced by the reference frequency conversion, when the reference frequency increases by N times, the fractional frequency instability decreases to δν/Nν, and the phase noise power spectral density will be decreased by a factor of N² [3]. In this paper, we use a 3.6-GHz reference signal to stabilize a comb with 200 MHz repetition rate to reduce the phase noise and improve the stability of the OFC. In addition, some applications require high output power, such as two-way optical time and frequency transfer and terahertz-wave generation [41–45], etc. Hence, we further present a method of in-loop optical amplification to amplify the output power of the OFC, and compress the output pulse duration to reduce the time jitter. Compared to the out-of-loop amplification, this design can decrease the phase noise induced by the optical amplification of the OFC.

2 Experiment setup and results

The schematic diagram of the OFC is presented in Figure 1. The OFC consists of an oscillator (part a), an optical power amplification unit (part b), an f_ceo generation and detection unit (part c), and an electronic control unit (part d).

FIGURE 1

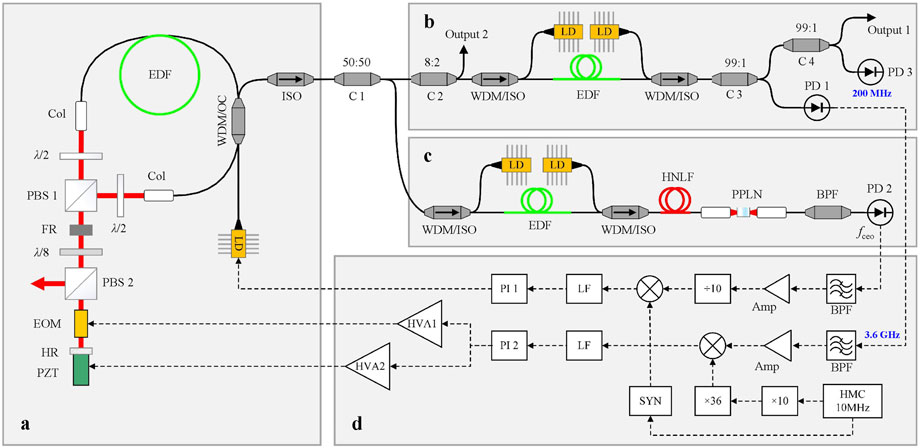
FIGURE 1. The schematic diagram of the optical frequency comb. (a–d) are the oscillator (a), the optical power amplification unit (b), the f_ceo generation and detection unit (c), and an electronic control unit (d), respectively. LD, laser diode; WDM, 980 nm/1,550 nm wavelength division multiplexer; Col, fiber collimator; EDF, Er-doped fiber; λ/2, half-wave plate; λ/8, eighth-wave plate; FR, Faraday rotator; PBS, polarizing beam splitter cube; EOM, electro-optic modulator; HR, high reflector; PZT, piezoelectric actuator; ISO, isolator; C1-C4, coupler; HNLF, high-nonlinear fiber; PD, photodetector; BPF, band pass filter; AMP, amplifier; SYN: synthesizer; PI, proportional integral controller; HVA, high voltage amplifier; LF, loop filter.

2.1 Oscillator

The oscillator is an all polarization-maintaining femtosecond fiber laser based on the non-linear amplified loop mirror (NALM) mechanism, with an electro-optic modulator (EOM) and a PZT in the cavity for feedback control of the repetition rate. Compared with the non-linear polarization rotation mechanism, the laser based on NALM is more robust, since it can be fabricated by a polarization-maintaining (PM) fiber that is capable of protecting the polarization state of light from environmental perturbations. The repetition rate of the laser is 200 MHz. To achieve such a high repetition rate, the oscillator adopts a highly doped erbium-doped fiber with a 40 cm length as the gain medium (the absorption coefficient is 80 dB/m@1530 nm), and the fiber coupler in the NALM is replaced by a polarizing beam splitter (PBS) cube to reduce the cavity length. The net dispersion of the cavity is about 4,944 fs². The oscillator is pumped by two 980 nm laser diodes with a combined output power of 1.2 W. The output spectrum of the laser is shown in Figure 2A. The 3-dB bandwidth of the spectrum is 34 nm, and the pulse duration is 0.84 ps (sech² fitting), as shown in Figure 2B. The relative intensity noise (RIN) of the pump LD and the free-running laser is illustrated in Figure 2C. It can be seen that the RIN of the pump LD is −75 dBc/Hz at the frequency of 1 Hz, and decreases to about −120 dBc/Hz at 100 Hz, and remains unchanged when the frequency is larger than 100 Hz. The RIN of the laser is −107 dBc/Hz at the frequency of 1 Hz and −137 dBc/Hz at the frequency of 100 kHz. For accurate frequency control, the temperature of the oscillator is stabilized to 28°C by two thermoelectric coolers (TEC), of which the control accuracy is below 0.002°C.

FIGURE 2

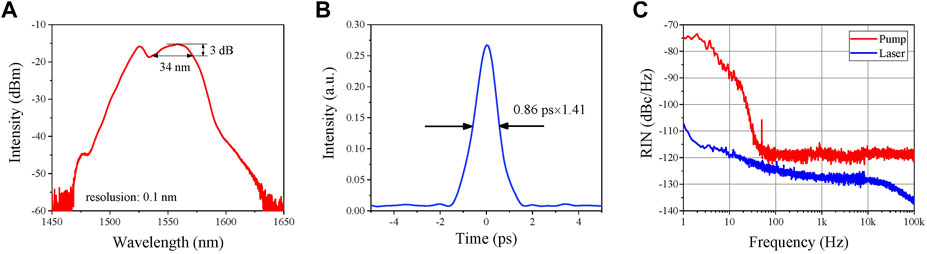
FIGURE 2. Spectrum (A), autocorrelation curve (B), and relative intensity noise (C) of the oscillator.

2.2 Optical power amplification

The output power of the oscillator is 11 mW. The output beam is split into two branches by a 50:50 fiber coupler, one for f_ceo detection and the other for optical power amplification and f_r detection. The output power of the OFC is amplified to 280 mW by chirped pulse amplification, and the pulse duration of the OFC is compressed to 67 fs before f_r detection to achieve low inherent noise. Figures 3A, B show the optical spectrum and autocorrelation function of the high-power pulses. In order to reduce the amplification of spontaneous emission (ASE) noise, the detection of the locked signal is implemented at the end of the amplifier.

FIGURE 3

FIGURE 3. (A) Spectrum and (B) autocorrelation curve of the OFC.

2.3 Detection and phase locking of f_ceo

The f_ceo is detected by collinear f-2f interference. First, the seed laser of the branch is amplified to 280 mW through chirped pulse amplification, with the pulse duration compressed to about 50 fs(sech² fitting). Afterward, the high-energy pulse train is injected into a PM highly non-linear optical fiber to generate a one-octave spanning supercontinuum (SC). The spectrum of the SC is shown in Figure 4A, where the power density at 1,050 nm and 2,100 nm is 0.73 mW/nm and 0.16 mW/nm, respectively. Subsequently, the octave spanning SC is coupled to a PM f-2f fiber interferometer for f_ceo detection. The interferometer is a self-developed all-PM fiber system, which consists of a1550-nm input PM fiber focuser, a 3-mm PPLN crystal with a period of 31.93 μm, a 1064-nm output PM fiber focuser, and a 1,050 nm band pass filter with bandwidth of 10 nm. The tail fiber length of the input focuser is 12 cm for the dispersion compensation of the SC. The RF spectrum of the f_ceo beat note is shown in Figure 4B. The signal-to-noise ratio (SNR) of the detected f_ceo reaches 50 dB at a resolution bandwidth (RBW) of 300 kHz.

FIGURE 4

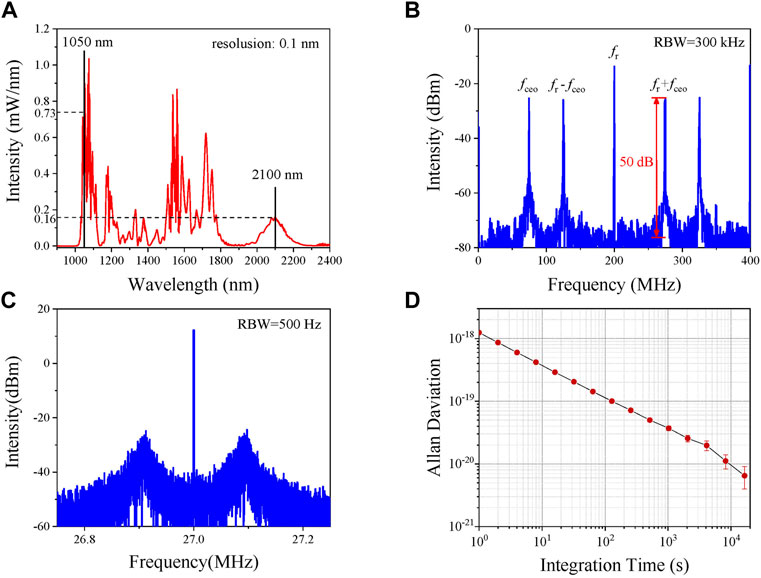
FIGURE 4. (A) Supercontinuum over an octave span for f_ceo detection; (B) f_ceo spectrum; (C) the fractional phase locked f_ceo + f_r; (D) the instability of the locked f_ceo.

The phase locked loop (PLL) electronics system is shown in Figure 1. The f_ceo is locked using the f_ceo + f_r beat signal, shown in Figure 4B. It is fractional phase locked on a 27 MHz reference signal by feedback control of the driven current of the pump LD. Figure 4C shows the spectrum of the fractional phase locked f_ceo + f_r, which reveals that the control bandwidth of the loop is about 100 kHz. Figure 4D shows the instability of the locked f_ceo, which is 1.24 × 10⁻¹⁸@1 s with a slope of τ^−1/2. This instability is mainly due to the deadtime of the frequency counter.

2.4 Harmonically phase locking of f_r

In order to improve the stability and decrease the phase noise of the comb, f_r is locked using a higher harmonic. As mentioned above, irrespective of the residual phase noise introduced by the reference frequency conversion, phase locking based on the higher harmonic can improve the stability and reduces the phase noise of OFCs. Here, we chose the 3.6 GHz harmonic for the phase locking, because 3.6 GHz is a critical point. When the locking point higher than 3.6 GHz, the phase locking requires two levels of amplification, which will increase the residual phase noise of the OFC. Meanwhile, to improve the quality of the high-frequency harmonic signal, an ultrafast photodetector (PD1) with a bandwidth of 25 GHz is utilized for harmonic detection. The radio-frequency (RF) spectrum of PD1 is shown in Figure 5A, where the intensity of the 3.6 GHz harmonic is −26.27 dBm. Then the 3.6-GHz harmonic is filtered, amplified, and mixed with the reference to obtain an error signal. This error signal is fed back to the modulation voltage applied on the EOM and the PZT in the cavity through a PI controller (as shown in Figure 1) to achieve the phase locking of f_r. To minimize the residual phase noise, the 3.6 GHz reference signal is directly converted by the 10-MHz HMC through two stages of frequency multiplying, and in this process, ultralow noise ×10 and ×36 frequency multipliers are used successively. The phase noise of the HMC is shown in Figure 5B, where the power spectral density is −122 dBc/Hz at 1 Hz offset and below −156 dBc/Hz at the far-end. The black line in Figure 5B represents the residual phase noise of the 3.6 GHz reference, which is normalized to 10 MHz. The residual phase noise measurement diagram of the 3.6-GHz reference is shown in Figure 6A. The 3.6-GHz reference is divided to 360 MHz and compared with the 10 MHz HMC by Symmetricom 5125A. The residual phase noise describes the phase noise added by the frequency multiplication link, which is −139 dBc/Hz at 1 Hz offset, much lower than that of the HMC. This indicates that the 3.6 GHz reference well inherits the frequency stability of the HMC.

FIGURE 5

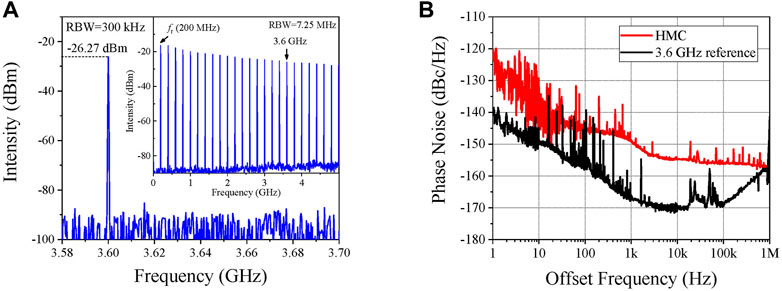
FIGURE 5. (A) Radio-frequency spectrum of PD1; (B) phase noise of hydrogen maser clock (HMC) and the 3.6-GHz reference.

FIGURE 6

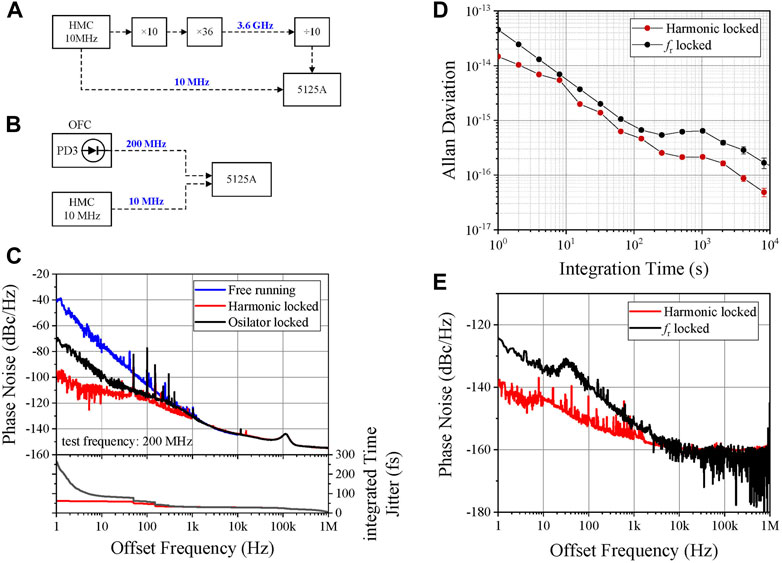
FIGURE 6. (A) Residual phase noise measurement diagram of the 3.6-GHz reference; (B) residual phase noise/instability measurement diagram; (C) frequency instability of the OFC; (D) phase noise of the free running OFC, harmonic locked OFC and out-of-loop amplified (oscillator locked) OFC; (E) residual phase noise of the OFC.

Figure 6C shows the residual frequency instability of the OFC, measured by Symmetricom 5125A and with the HMC as the reference. The measurement diagram of the residual frequency instability is shown in Figure 6B. The residual frequency instability excludes the instability caused by the reference HMC, and directly reflects the stability of the phase locking system. The Allan deviation is 1.46 × 10⁻¹⁴ at an average time of 1 s and decreases to 4.85 × 10⁻¹⁷ at about 8,000 s. The black points in Figure 6C represent the residual frequency instability of the OFC phase locked by the 200-MHz reference. This reference is generated by an HMC-based frequency synthesizer. The Allan deviation of the locked OFC is 4.54 × 10⁻¹⁴ at an average time of 1 s, and decreases to 1.67 × 10⁻¹⁶ at about 8,000 s. Compared with the 200 MHz locked OFC, the 3.6 GHz phase locking method improves the stability of the OFC evidently.

Figure 6D shows the phase noise of the OFC under the free running and the phase locked conditions, measured by an R&S FSWP phase noise analyzer. The test signal is the 200-MHz repetition frequency detected by PD3. Using the harmonic phase locking method, the phase noise of the OFC is well suppressed, which declines from −43 dBc/Hz to −96 dBc/Hz at 1 Hz offset. The corresponding absolute RMS timing jitter of the repetition rate is 62 fs from 1 Hz to 1 MHz. Moreover, we also test the phase noise and the absolute RMS timing jitter of the out-of-loop optical power amplification. The results are shown with the black lines in Figure 6D. The phase noise of the OFC with the out-of-loop EDFA is −70 dBc/Hz at 1 Hz offset, and the absolute RMS timing jitter is 264 fs from 1 Hz to 1 MHz, which is much higher than the in-loop design. This indicates that in-loop optical power amplification can well suppress the phase noise caused by the EDFA.

Figure 6E shows the residual phase noise of the OFC, normalized to 10 MHz, with the HMC as the reference. The red line and the black line represent the residual phase noise of the OFC, locking on the 200-MHz and 3.6-GHz reference, respectively. The measurement system of the residual frequency instability is the same as that of the residual frequency instability, as shown in Figure 6A. The power spectral density of the 3.6 GHz locked OFC is −138 dBc/Hz at 1 Hz offset and declines to about −160 dBc/Hz at the far-end, much lower than the phase noise of the HMC. This manifests that the OFC inherits the stability of the HMC very well. Compared with the 200 MHz locked OFC, of which the residual phase noise is −124 dBc/Hz at 1 Hz offset, the 3.6 GHz locked OFC has much lower residual phase noise, indicating that the harmonic phase locking method can significantly improve the OFC performance. At a lower offset, the residual phase noise slope is ultimately limited by the frequency multiplier, which is used to generate the 3.6-GHz reference. This means that if the phase noise of the frequency multiplier can be decreased, the residual phase noise of the PLL can be further improved.

3 Conclusion

To conclude, we demonstrate an all PM Er-fiber OFC with low phase noise and high power, which is synchronized to the HMC using the 18th harmonic of the repetition rate for tight phase locking. By using a 3.6-GHz reference signal to stabilize a comb with a repetition rate of 200 MHz, the residual frequency instability of the OFC could reach 1.46 × 10⁻¹⁴@1 s, and the residual phase noise of the OFC normalized to 10 MHz could be as low as −138 dBc/Hz at 1 Hz offset and declines to about −160 dBc/Hz at the far-end. Meanwhile, we present an in-loop optical amplification method to amplify the output power of the OFC to reduce the phase noise and time jitter. The phase noise of the OFC could reach −96 dBc/Hz at 1 Hz offset, and the corresponding RMS timing jitter of the repetition rate could be reduced to 62 fs(1 Hz–1 MHz). Compared to the repetition rate phase locking method, harmonic phase locking for the frequency stabilization of OFC could distinctively decrease the phase noise and improve the stability of the OFC. Our proposals can be widely applied in optical frequency measurement and microwave frequency transfer.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conception and design of study: YZ, PZ, and LY. ML; acquisition of data: ML, XY, and BR; analysis and/or interpretation of data: ML, XY, YZ. PZ, RY, and XC; Drafting the manuscript: ML; revising the manuscript critically for important intellectual content: TL, YZ, and PZ. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB35030101), the Quantum Control and Quantum Information of the National Key Research and Development Program of China (Grant No. 2020YFA0309800), National Natural Science Foundation of China (Grant No. 12103060), the West Light Foundation of the Chinese Academy of Sciences (XAB2019B19), and the Nature Foundation of Shaanxi (Grant No. 2021JQ-320).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kim J, Song Y. Ultralow-noise mode-locked fiber lasers and frequency combs: Principles, status, and applications. Adv Opt Photon (2016) 8(3):465. doi:10.1364/aop.8.000465

CrossRef Full Text | Google Scholar

2. Diddams SA. The evolving optical frequency comb [invited]. J Opt Soc America B (2010) 27(11):B51. doi:10.1364/josab.27.000b51

CrossRef Full Text | Google Scholar

3. Fortier T, Baumann E. 20 Years of developments in optical frequency comb technology and applications. Commun Phys (2019) 2(1):153–16. doi:10.1038/s42005-019-0249-y

CrossRef Full Text | Google Scholar

4. Picqué N, Hänsch TW. Frequency comb spectroscopy. Nat Photon (2019) 13(3):146–57. doi:10.1038/s41566-018-0347-5

CrossRef Full Text | Google Scholar

5. Rao B-J, Zhang Y-Y, Yan L-L, Wu Y-L, Zhang P, Fan S-T, et al. Er: Fiber femtosecond optical frequency comb aimed at measurement of frequency of D1 line in Li atoms. Acta Photonica Sinica (2019) 48(1):114003. doi:10.3788/gzxb20194801.0114003

CrossRef Full Text | Google Scholar

6. Zheng X, Sun Y, Chen J-J, Jiang W, Pachucki K, Hu S-M. Measurement of the frequency of the 2 ³S − 2 ³P transition of ⁴ He. Phys Rev Lett (2017) 119(26):263002. doi:10.1103/PhysRevLett.119.263002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bahmanian M, Scheytt JC. A 2–20-ghz ultralow phase noise signal source using a microwave oscillator locked to a mode-locked laser. IEEE Trans Microwave Theor Tech (2021) 69(3):1635–45. doi:10.1109/tmtt.2020.3047647

CrossRef Full Text | Google Scholar

8. Yan L, Zhao W, Zhang Y, Zhang P, Zhao C, Zhang X, et al. Ultra-stable microwave signal generation with Er: Fiber-based optical frequency comb. In: 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC); 14-18 April 2019; Orlando, FL, USA. IEEE (2019).

CrossRef Full Text | Google Scholar

9. Pupeza I, Zhang C, Högner M, Ye J. Extreme-ultraviolet frequency combs for precision metrology and attosecond science. Nat Photon (2021) 15(3):175–86. doi:10.1038/s41566-020-00741-3

CrossRef Full Text | Google Scholar

10. Agostini P, DiMauro LF. The Physics of attosecond light pulses. Rep Prog Phys (2004) 67(6):1563. doi:10.1088/0034-4885/67/8/c01

CrossRef Full Text | Google Scholar

11. Lu H, Li Z, Wang J, Meng H, Zhao J. Two-way optical time and frequency transfer over a 20-km fiber link based on optical frequency combs. IEEE Photon J (2019) 11(1):1–7. doi:10.1109/jphot.2019.2896639

CrossRef Full Text | Google Scholar

12. Shen Q, Guan J-Y, Zeng T, Lu Q-M, Huang L, Cao Y, et al. Experimental simulation of time and frequency transfer via an optical satellite–ground link at 10^-18 instability. Optica (2021) 8(4):471–6. doi:10.1364/optica.413114

CrossRef Full Text | Google Scholar

13. Leopardi H, Davila-Rodriguez J, Quinlan F, Olson J, Sherman JA, Diddams SA, et al. Single-branch Er: Fiber frequency comb for precision optical metrology with 10^-18 fractional instability. Optica (2017) 4(8):879–85. doi:10.1364/optica.4.000879

CrossRef Full Text | Google Scholar

14. Ning K, Hou L, Fan S-T, Yan L-L, Zhang Y-Y, Rao B-J, et al. An all-polarization-maintaining multi-branch optical frequency comb for highly sensitive cavity ring-down spectroscopy. Chin Phys Lett (2020) 37(6):064202. doi:10.1088/0256-307X/37/6/064202

CrossRef Full Text | Google Scholar

15. Pang L, Han H, Zhao Z, Liu W, Wei Z. Ultra-stability Yb-doped fiber optical frequency comb with 2×10^-18/S stability in-loop. Opt Express (2016) 24(25):28993–9000. doi:10.1364/oe.24.028993

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bing-Jie R, Pan Z, Ming-Kun L, Xi-Guang Y, Lu-Lu Y, Xin C, et al. Multi-branch erbium fiber-based femtosecond optical frequency comb for measurement of cavity ring-down spectroscopy. Acta Physica Sinica (2022) 71(8):084203. doi:10.7498/aps.71.20212162

CrossRef Full Text | Google Scholar

17. Giorgetta FR, Swann WC, Sinclair LC, Baumann E, Coddington I, Newbury NR. Optical two-way time and frequency transfer over free space. Nat Photon (2013) 7(6):434–8. doi:10.1038/nphoton.2013.69

CrossRef Full Text | Google Scholar

18. Sinclair LC, Bergeron H, Swann WC, Khader I, Cossel KC, Cermak M, et al. Femtosecond optical two-way time-frequency transfer in the presence of motion. Phys Rev A (2019) 99(2):023844. doi:10.1103/PhysRevA.99.023844

CrossRef Full Text | Google Scholar

19. Nemitz N, Ohkubo T, Takamoto M, Ushijima I, Das M, Ohmae N, et al. Frequency ratio of Yb and Sr clocks with 5 × 10−17 uncertainty at 150 seconds averaging time. Nat Photon (2016) 10(4):258–61. doi:10.1038/nphoton.2016.20

CrossRef Full Text | Google Scholar

20. Kim ME, McGrew WF, Nardelli NV, Clements ER, Hassan YS, Zhang X, et al. Improved interspecies optical clock comparisons through differential spectroscopy. Nat Phys (2022). doi:10.1038/s41567-022-01794-7

CrossRef Full Text | Google Scholar

21. Campbell GK, Ludlow AD, Blatt S, Thomsen JW, Martin MJ, de Miranda MHG, et al. The absolute frequency of the ⁸⁷ Sr optical clock transition. Metrologia (2008) 45(5):539–48. doi:10.1088/0026-1394/45/5/008

CrossRef Full Text | Google Scholar

22. Marra G, Margolis HS, Lea SN, Gill P. High-stability microwave frequency transfer by propagation of an optical frequency comb over 50 Km of optical fiber. Opt Lett (2010) 35(7):1025–7. doi:10.1364/OL.35.001025

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Jung K, Shin J, Kang J, Hunziker S, Min C-K, Kim J. Frequency comb-based microwave transfer over fiber with 7x10^-19 instability using fiber-loop optical-microwave phase detectors. Opt Lett (2014) 39(6):1577–80. doi:10.1364/OL.39.001577

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Lin H, Yang L, Feng XJ, Zhang JT. Discovery of new lines in the R9 multiplet of the 2v₃ band of ¹² C H₄. Phys Rev Lett (2019) 122(1):013002. doi:10.1103/PhysRevLett.122.013002

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Margolis HS, Huang G, Barwood GP, Lea SN, Klein HA, Rowley WRC, et al. Absolute frequency measurement of the 674-nm ⁸⁸ Sr⁺ clock transition using a femtosecond optical frequency comb. Phys Rev A (2003) 67(3):032501. doi:10.1103/PhysRevA.67.032501

CrossRef Full Text | Google Scholar

26. Madej AA, Bernard JE, Dubé P, Marmet L, Windeler RS. Absolute frequency of the ⁸⁸ Sr⁺5s²S_{1 ∕ 2}-4d²D_{5 ∕ 2} reference transition at 445 T hz and evaluation of systematic shifts. Phys Rev A (2004) 70(1):012507. doi:10.1103/PhysRevA.70.012507

CrossRef Full Text | Google Scholar

27. Spencer DT, Drake T, Briles TC, Stone J, Sinclair LC, Fredrick C, et al. An optical-frequency synthesizer using integrated photonics. Nature (2018) 557(7703):81–5. doi:10.1038/s41586-018-0065-7

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lucas E, Brochard P, Bouchand R, Schilt S, Südmeyer T, Kippenberg TJ. Ultralow-noise photonic microwave synthesis using a soliton microcomb-based transfer oscillator. Nat Commun (2020) 11(1):374. doi:10.1038/s41467-019-14059-4

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Jones DJ, Diddams SA, Ranka JK, Stentz A, Windeler RS, Hall JL, et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science (2000) 288(5466):635–9. doi:10.1126/science.288.5466.635

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ramond T, Diddams SA, Hollberg L, Bartels A. Phase-coherent link from optical to microwave frequencies by means of the broadband continuum from a 1-ghz Ti: Sapphire femtosecond oscillator. Opt Lett (2002) 27(20):1842–4. doi:10.1364/ol.27.001842

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Washburn BR, Diddams SA, Newbury NR, Nicholson JW, Yan MF, Jørgensen CG. Phase-locked, erbium-fiber-laser-based frequency comb in the near infrared. Opt Lett (2004) 29(3):250–2. doi:10.1364/ol.29.000250

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhang Y-Y, Yan L-L, Zhao W-Y, Meng S, Fan S-T, Zhang L, et al. A long-term frequency-stabilized erbium-fiber-laser-based optical frequency comb with an intra-cavity electro-optic modulator. Chin Phys B (2015) 24(6):064209. doi:10.1088/1674-1056/24/6/064209

CrossRef Full Text | Google Scholar

33. Zhang M, Buscaino B, Wang C, Shams-Ansari A, Reimer C, Zhu R, et al. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature (2019) 568(7752):373–7. doi:10.1038/s41586-019-1008-7

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhang P, Zhang Y-Y, Li M-K, Rao B-J, Yan L-L, Chen F-X, et al. All polarization-maintaining Er: Fiber-based optical frequency comb for frequency comparison of optical clocks. Chin Phys B (2022) 31(5):054210. doi:10.1088/1674-1056/ac40f6

CrossRef Full Text | Google Scholar

35. Kuse N, Lee CC, Jiang J, Mohr C, Schibli TR, Fermann ME. Ultra-low noise all polarization-maintaining Er fiber-based optical frequency combs facilitated with a graphene modulator. Opt Express (2015) 23(19):24342–50. doi:10.1364/OE.23.024342

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kuse N, Jiang J, Lee CC, Schibli TR, Fermann ME. All polarization-maintaining Er fiber-based optical frequency combs with nonlinear amplifying loop mirror. Opt Express (2016) 24(3):3095–102. doi:10.1364/OE.24.003095

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Ohmae N, Kuse N, Fermann ME, Katori H. All-polarization-maintaining, single-port Er:fiber comb for high-stability comparison of optical lattice clocks. Appl Phys Express (2017) 10(6):062503. doi:10.7567/APEX.10.062503

CrossRef Full Text | Google Scholar

38. Zhu Z, Liu Y, Luo D, Gu C, Zhou L, Xie G, et al. Tunable optical frequency comb from a compact and robust Er: Fiber laser. High Power Laser Sci Eng (2020) 8:e17. doi:10.1017/hpl.2020.17

CrossRef Full Text | Google Scholar

39. Yan L-L, Zhang Y-Y, Zhang L, Fan S-T, Zhang X-F, Guo W-G, et al. Attosecond-resolution Er: Fiber-based optical frequency comb. Chin Phys Lett (2015) 32(10):104207. doi:10.1088/0256-307x/32/10/104207

CrossRef Full Text | Google Scholar

40. Di Domenico G, Schilt S, Thomann P. Simple approach to the relation between laser frequency noise and laser line shape. Appl Opt (2010) 49(25):4801–7. doi:10.1364/ao.49.004801

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Shams H, Balakier K, Fice MJ, Ponnampalam L, Graham C, Renaud CC, et al. Coherent frequency tuneable thz wireless signal generation using an optical phase lock loop system. In: 2017 International Topical Meeting on Microwave Photonics (MWP); 23-26 October 2017; Beijing, China. IEEE (2017).

CrossRef Full Text | Google Scholar

42. Gollapalli RP, Duan L. Atmospheric timing transfer using a femtosecond frequency comb. IEEE Photon J (2010) 2(6):904–10. doi:10.1109/jphot.2010.2080315

CrossRef Full Text | Google Scholar

43. Hasanuzzaman G, Shams H, Renaud CC, Mitchell J, Seeds AJ, Iezekiel S. Tunable thz signal generation and radio-over-fiber link based on an optoelectronic oscillator-driven optical frequency comb. J Lightwave Technol (2019) 38(19):5240–7. doi:10.1109/jlt.2019.2953070

CrossRef Full Text | Google Scholar

44. Kang HJ, Yang J, Chun BJ, Jang H, Kim BS, Kim Y-J, et al. Free-space transfer of comb-rooted optical frequencies over an 18 Km open-air link. Nat Commun (2019) 10(1):4438–8. doi:10.1038/s41467-019-12443-8

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Shen Q, Guan J-Y, Ren J-G, Zeng T, Hou L, Li M, et al. Free-space dissemination of time and frequency with 10⁻¹⁹ instability over 113 km. Nature (2022) 610:661–6. doi:10.1038/s41586-022-05228-5

PubMed Abstract | CrossRef Full Text | Google Scholar