Hypomagnetic field effects as a potential avenue for testing the radical pair mechanism in biology

1 Introduction

Weak magnetic field effects are widespread in biology [1]. The strength of the magnetic field in such phenomena can go below the magnitude of the geomagnetic field. Hypomagnetic fields, which are near-zero fields and can be produced by shielding the Earth’s magnetic field, are also known to impact biological functions [2–9], such as plants’ growth, development, and evolution [2, 3, 8–10], reactive oxygen species [5], circadian rhythm [7], learning and memory [11] and so on. Such effects, which are also often referred to as low field effects (LFEs), have been observed in genetics, developmental processes, the circadian clock, neurons and the brain, and so forth. It has also been suggested that extinction events on Earth [12] may be related to the changes in geomagnetic field [13]. Early studies, motivated by the concerns around the health of astronauts in outer space, concluded that exposure to hypomagnetic fields had adverse effects on human health [14–17]. Apart from hypomagnetic field effects on animal and human cells and tissues, deprivation in the geomagnetic field can influence the development of plants as well [8, 9]. It, therefore, seems pertinent to conclude that the geomagnetic field may play essential roles in living organisms, and diminishing it or making it disappear could result in adverse consequences.

Earth’s magnetic field, depending on latitude, ranges from ∼24 to ∼66 μT [18], which is hundreds of times smaller than the strength of a typical refrigerator magnet. Remarkably, the scale of energies corresponding to the geomagnetic field is about a million times smaller than thermal energies, k_BT (k_B and T are the Boltzmann constant and temperature, respectively), at biologically relevant temperatures. This makes any classical interpretation of hypomagnetic field effects in biology highly challenging. Thus far, the mechanisms behind such effects remain elusive [19, 20]. It must also be noted that classical models based on stochastic resonance [21], ion channels [22], and magnetic induction [23] have also been proposed for weak magnetic field effects in biology. However, for instance, in Ref. [24], the authors show that the experimental observation supports the radical pair mechanism based on cryptochrome for avian magnetoreception.

It is known that applied magnetic fields can influence reaction rates and yields in certain chemical reactions [25–28]. The key elements in these processes are pairs of radicals–transient molecules with an odd number of electrons in their outer shell–that carry quantum spins. Electrons possess spins of $S=\frac{1}{2}$. Spin also has a magnetic feature, meaning that any other spins and magnetic field around can influence the particle’s spin state (radical). A pair of radicals can be formed by electron transfer between two molecules or by breaking a chemical bond. A radical pair can be in a singlet or triplet state, depending on the donor and acceptor molecule’s spin configuration [29]. Spin is usually a conserved quantity in reactions involving organic molecules, which is essential for magnetic field effects in biochemical reactions involving radical pairs [30]. In other words, depending on the spin state of the radical pair, the chemical process will take either singlet or triplet paths, resulting in different chemical yields.

It has been proposed that the radical pair mechanism underlies many magnetic field effects across biology [1]. Radical pair models have been proposed for LFEs [28], including avian magnetoreception [31, 32], isotope effects on xenon anesthesia [33] and lithium effects on mania [34], and magnetic field effects on the circadian clock [35]. In recent studies, it is also suggested that radical pairs may explain hypomagnetic field effects on hippocampal neurogenesis [36] and microtubule reorganization [37]. The LFEs on radical pair reactions have been extensively studied experimentally and theoretically [38–43]. Here, based on the radical pair mechanism, we show that changing the magnetic field experienced by a biological system from the geomagnetic field to near zero can, under certain conditions, lead to stronger effects than changing it from the geomagnetic field to a much stronger field (Figure 2). We hence suggest that hypomagnetic field effects are an interesting way of testing radical pair models.

2 Results

2.1 Spin dynamics

Starting from a singlet state, the initial spin density matrix for the radical pair reads as follows:

$\widehat{\rho }\left(0\right)=\frac{1}{M}{\widehat{P}}^S,(1)$

and for triplet initial state:

$\widehat{\rho }\left(0\right)=\frac{1}{3M}{\widehat{P}}^T,(2)$

where

${\widehat{P}}^S=\left|S\right.⟩\otimes \left.⟨S\right|\otimes {\widehat{\mathbb{1}}}_M,(3)$

${\widehat{P}}^T=\left\{\left|T_{+}\right.⟩\otimes \left.⟨T_{+}\right|+\left|T_0\right.⟩\otimes \left.⟨T_0\right|+\left|T_{-}\right.⟩\otimes \left.⟨T_{-}\right|\right\}\otimes {\widehat{\mathbb{1}}}_M,(4)$

${\widehat{P}}^S+{\widehat{P}}^T={\widehat{\mathbb{1}}}_{4M},(5)$

$M=\prod _i^n\left(2I_i+1\right).(6)$

Here ${\widehat{P}}^S$ and ${\widehat{P}}^T$ are the singlet and triplet projection operators, respectively, M is the nuclear spin multiplicity, I_i is the spin angular momentum of i-th nucleus, and ${\widehat{\mathbb{1}}}_n$ is the n × n identity matrix.

For studying the spin dynamics of the radical pairs, it is essential to consider the interactions between the unpaired electron spins on each radical with each other, surrounding nuclear spins, and external magnetic fields. All these interactions can be included in the Hamiltonian of the system, $\widehat{H}$. The next step is solving the density matrix equation:

$\frac{d\widehat{\rho }\left(t\right)}{dt}=-\frac{i}{\hslash }\left[\widehat{H},\widehat{\rho }\left(t\right)\right],(7)$

where $\widehat{\rho }(t)$ and $\widehat{H}$ are the spin density and Hamiltonian operators, respectively, i is the imaginary unit and ℏ is the reduced Planck constant. [⋅, ⋅ ] denotes the commutator.

For simplicity, let us consider only the isotropic hyperfine $({\widehat{H}}_{\mathit{HFI}})$ and Zeeman $({\widehat{H}}_Z)$ interactions. We neglect dipolar and exchange interactions; it should be noted that including these terms in the model can reduce the magnetic field sensitivity [36, 44]. However, this may be compensated by potential amplification effects in the biological systems [35, 45]. Of note, the anisotropic components of the hyperfine interactions are only relevant when the radicals are aligned and immobilised [46]. The Hamiltonian for this system reads as follows:

$\widehat{H}={\widehat{H}}_Z+{\widehat{H}}_{\mathit{HFI}}=-{\gamma }_{e}h\left({\widehat{\mathbf{S}}}_A+{\widehat{\mathbf{S}}}_B\right)\cdot \mathbf{B}+\sum _i^{N_A}{a}_{iA}{\widehat{\mathbf{S}}}_A{\widehat{\mathbf{I}}}_{iA}+\sum _i^{N_B}{a}_{iB}{\widehat{\mathbf{S}}}_B\cdot {\mathbf{I}}_{iB},(8)$

where γ_e, h, ${\widehat{\mathbf{S}}}_{A/B}$, B, a_iA/B, ${\widehat{\mathbf{I}}}_{iA/B}$, and N_A/B are the electron magnetogyric ratio, the Planck constant, the spin operators of electron A/B, the magnetic field, the isotropic hyperfine coupling constants for electron A/B, nuclear spin of i-th nucleus for electron A/B, and the number of nuclear spins coupled to electron A/B, respectively.

Let us consider a minimal model comprising two electron spins, A and B, where A is coupled to a spin-1/2 nucleus, ${\widehat{\mathbf{S}}}_A\otimes {\widehat{\mathbf{I}}}_A\otimes {\widehat{\mathbf{S}}}_B$, and the magnetic field has only z component, B_z. In this case, the Hamiltonian has the following form:

$\widehat{H}=\left[\begin{array}{cccccccc}\hfill \frac{a}{4}+B_z\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{a}{4}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{a}{4}+B_z\hfill & \hfill 0\hfill & \hfill \frac{a}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a}{4}-B_z\hfill & \hfill 0\hfill & \hfill \frac{a}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a}{2}\hfill & \hfill 0\hfill & \hfill -\frac{a}{4}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a}{2}\hfill & \hfill 0\hfill & \hfill -\frac{a}{4}-B_z\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a}{4}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a}{4}-B_z\hfill \end{array}\right](9)$

where a is the hyperfine coupling constant. The normalized eigenstates of this system, ψ_i, are the following:

$\begin{array}{cc}\hfill {\psi }_1& ={\left|\uparrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B,\hfill \\ \hfill {\psi }_2& ={\left|\uparrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B,\hfill \\ \hfill {\psi }_3& =\frac{\alpha }{\xi }{\left|\uparrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B+\frac{2a}{\delta }{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B,\hfill \\ \hfill {\psi }_4& =\frac{-1}{\sqrt{5}}{\left|\uparrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B-\frac{2\mathrm{s}\mathrm{g}\mathrm{n}\left(\alpha \right)}{\sqrt{5}}{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B,\hfill \\ \hfill {\psi }_5& =\frac{a}{2\xi }{\left|\uparrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B-\frac{4\alpha }{\delta }{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B,\hfill \\ \hfill {\psi }_6& =\frac{2}{\sqrt{5}}{\left|\uparrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B-\frac{\mathrm{s}\mathrm{g}\mathrm{n}\left(\eta \right)}{\sqrt{5}}{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B,\hfill \\ \hfill {\psi }_7& ={\left|\downarrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B,\hfill \\ \hfill {\psi }_8& ={\left|\downarrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B.\hfill \end{array}(10)$

where $\alpha =B-\frac{a}{4}$, $\xi =\sqrt{|\alpha {|}^2+\frac{a^2}{4}}$, $\delta =\sqrt{{\alpha }^2+4a^2}$, and η = 4B − 3a.

In this simple model, we assume the radical pairs are initially in a singlet state and the nuclear spin is up. In the rest of this paper and the expression for the singlet yield in this section, the initial nuclear states are averaged over:

$\frac{1}{\sqrt{2}}\left({\left|\uparrow \right.⟩}_A\otimes {\left|\downarrow \right.⟩}_B-{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_B\right)\otimes {\left|\uparrow \right.⟩}_N=\frac{1}{\sqrt{2}}\left({\left|\uparrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\downarrow \right.⟩}_B-{\left|\downarrow \right.⟩}_A\otimes {\left|\uparrow \right.⟩}_N\otimes {\left|\uparrow \right.⟩}_B\right).(11)$

This initial state overlaps with three out of eight eigenstates of the system, ψ₂, ψ₃, and ψ₅. At extremely low fields, two of these three states are degenerate. The third one is split from the other two by the hyperfine interaction, as shown in Figure 1. Due to this, even in hypomagnetic conditions, this energy difference results in S-T mixing.

FIGURE 1

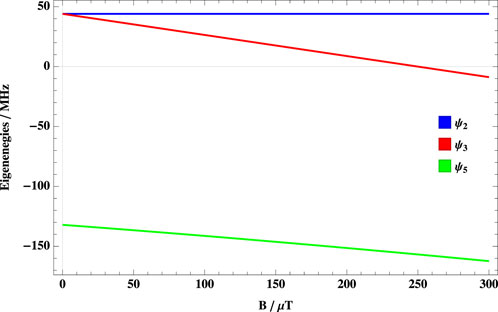
FIGURE 1. Dependence of the eigenenergies on B. Eigenenergies of three states that overlap with the singlet initial state as a function of the applied magnetic field with a hyperfine coupling constant of 1,000 μT.

Following the work of Timmel et al. [28, 43], the chemical fate of the radical pair can be modelled by separating spin-selective reactions of the singlet and triplet pairs. For simplicity, it is assumed that k = k_S = k_T, where k_S and k_T are the singlet and triplet reaction rates, respectively. The final singlet yield, Φ^S(S), for periods much greater than the radical pair lifetime reads as follows:

${\mathrm{\Phi }}^{S\left(S\right)}=k{\int }_0^{\infty }⟨{\widehat{P}}^S⟩\left(t\right)e^{-kt}dt=\frac{1}{4}-\frac{k}{4\left(k+r\right)}+\frac{1}{M}\sum _m^{4M}\sum _n^{4M}{\left|\left.⟨m\right|{\widehat{P}}^S\left|n\right.⟩\right|}^2\frac{k\left(k+r\right)}{{\left(k+r\right)}^2+{\left({\omega }_m-{\omega }_n\right)}^2},(12)$

where the fractional triplet yield can be calculated as Φ^T(S) = 1 − Φ^S(S). Similarly, if the radical pairs start off in triplet states, the singlet yield fraction reads as follows:

${\mathrm{\Phi }}^{S\left(T\right)}=\frac{1}{4}+\frac{k}{12\left(k+r\right)}-\frac{1}{3M}\sum _m^{4M}\sum _n^{4M}{\left|\left.⟨m\right|{\widehat{P}}^S\left|n\right.⟩\right|}^2\frac{k\left(k+r\right)}{{\left(k+r\right)}^2+{\left({\omega }_m-{\omega }_n\right)}^2}.(13)$

Applied magnetic fields can alter the fractional singlet/triplet yield. Figure 2 shows the dependence of the fractional singlet yield for singlet-born radical pairs for different sets of relaxation rate, r, reaction rate, k, and one isotropic hyperfine coupling constant. It is clear that there is a peak in the hypomagnetic field range for most values of k and r. It is noteworthy that the peak diminishes when the reaction rate is slower than the spin relaxation rate. One can also see that there is a dip at intermediate field values, then a rise at higher fields, but this rise is not as high as the peak for the hypomagnetic field range. In the considered parameter range, the radical pair mechanism thus predicts quite significant hypomagnetic field effects. It should also be noted that the case of triplet-born and singlet-born radical pairs have the same behavior, but with peaks and dips exchanged.

FIGURE 2

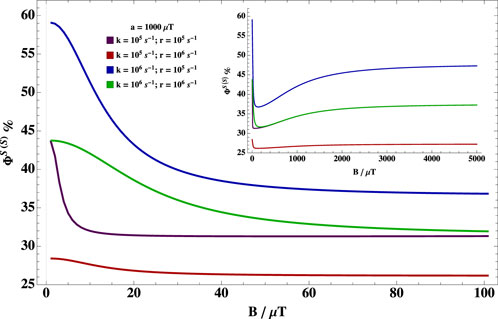
FIGURE 2. Dependence of the fractional singlet yield on B. Dependence of the fractional singlet yield for (a) singlet-born (Φ^S(S)) radical pair on the external magnetic field B with one isotropic hyperfine coupling of 1,000 μT for different relaxation rate, r, and reaction rates, k. There is a peak in the hypomagnetic field range for most values of k and r. The peak diminishes when the reaction rate is slower than the spin relaxation rate. One can also see that there is a dip at intermediate field values, then a rise at higher fields, but this rise is not as high as the peak for the hypomagnetic field range (see the inset).

2.2 Hypomagnetic field effect

One can define hypomagnetic field effects, ΔΘ_HMF↔GMF (similar to previous works on LFEs, e.g., Ref. [28]), as the absolute value of the ratio of the difference between the singlet (triplet) yield at near zero magnetic fields (1 μT) and at the geomagnetic field range (50 μT) over the singlet yield at near-zero magnetic field:

$\mathrm{\Delta }{\mathrm{\Theta }}_{HMF\leftrightarrow GMF}^{i\left(j\right)}=\left|\frac{{\mathrm{\Phi }}_{\mathit{HMF}}^{i\left(j\right)}-{\mathrm{\Phi }}_{\mathit{GMF}}^{i\left(j\right)}}{{\mathrm{\Phi }}_{\mathit{HMF}}^{i\left(j\right)}}\right|,(14)$

where i, j = {S, T}.

We numerically explore the hypomagnetic field effects for the radical pair model using Eq. 14. This is particularly relevant for experiments based on screening the geomagnetic field (of which there are quite many) [1].

Figure 3 shows the dependence of the hypomagnetic field effect on the hyperfine coupling constant for different sets of relaxation and reaction rates. It is worth noting that the hypomagnetic field effects are more evident when the hyperfine coupling is larger than the spin relaxation and reaction rates. This is even more pronounced when the spin relaxation is slower than the reaction rate. It is also worth mentioning that if the hyperfine coupling constant is much larger than the reaction and spin relaxation rate, the hypomagnetic field effects can reach considerable values (say $>10\%$) for a < 20,000 μT. For too high values of the hyperfine coupling constant, there are no hypomagnetic field effects. This is due to the fact that, for all different rates, at far too large hyperfine couplings, the hyperfine interaction dominates the Zeeman interaction, and hence there are no quantum beats.

FIGURE 3

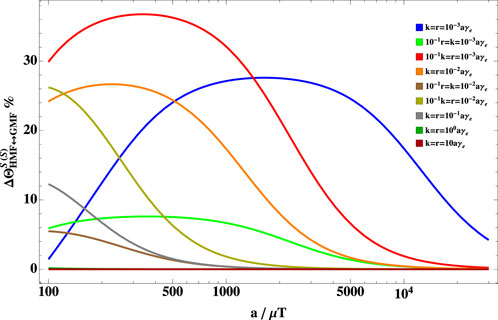
FIGURE 3. Dependence of $\mathrm{\Delta }{\mathrm{\Theta }}_{HMF\leftrightarrow GMF}^{S(S)}$ on a, r, k. One of the radicals is coupled to a nucleus with $\frac{1}{2}$-spin and the other one with no hyperfine interaction. The hypomagnetic field effects are more evident when the hyperfine coupling is larger than the spin relaxation and reaction rates. This is even more pronounced when the spin relaxation is slower than the reaction rate. If the hyperfine coupling constant is much larger than the reaction and spin relaxation rate, the hypomagnetic field effects can reach considerable values (say $>10\%$) for a < 20,000 μT (e.g., Blue curve). γ_e = 1.76 × 10¹¹ s⁻¹ T⁻¹ is the electron magnetogyric ratio. Due to the dominance of the hyperfine interaction over the Zeeman interaction, for too high values of the hyperfine coupling constant, there are no hypomagnetic field effects; this depends on the relaxation and reaction rates.

Figure 4 shows the hypomagnetic field effects based on the singlet yield ratio with singlet initial states, Φ^S(S), where that one of the radicals is coupled to one nuclear spin-$\frac{1}{2}$ with a hyperfine coupling of 1,000 μT. The effect is higher than 10% when k ∈ [10⁵–10⁷] s⁻¹ and r < 10⁶ s⁻¹. The maximum value for hypomagnetic field effects for singlet-born radical pairs reaches ∼40%.

FIGURE 4

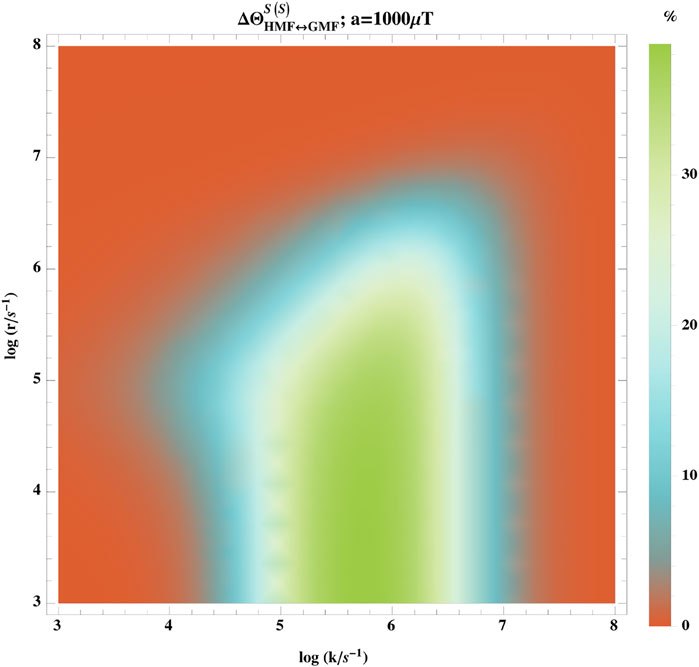
FIGURE 4. Dependence of $\mathrm{\Delta }{\mathrm{\Theta }}_{HMF\leftrightarrow GMF}^{S(S)}$ on k and r. The hypomagnetic field effect is based on the singlet yield ratio of 1 μT (HMF) over 50 μT (GMF) with singlet initial states. In this model, one of the radicals has no hyperfine interaction, and the other one is coupled to one nucleus with an isotropic hyperfine coupling constant of a = 1,000 μT. The hypomagnetic field effects are significant when r < 10⁶ s⁻¹, k ∈ [10^4.5, 10^6.5] s⁻¹, and k < r.

Most organic radicals possess several nuclei carrying spin with positive or negative isotropic hyperfine coupling constant. Figure 5 shows the dependence of the hypomagnetic field effect on spin relaxation rate and reaction rate for these sets of isotropic hyperfine coupling constants: a_iso = { + 500, + 500}μT, a_iso = { + 500, − 500}μT, and $a_{\mathit{eiso}}=500\sqrt{2}\mu$T. The signs of the hyperfine couplings have a minor impact on the fractional yield for the hypomagnetic field effects. Here, one of the radicals is coupled to two nuclei, and the other radical has no hyperfine interaction. a_eiso is the effective hyperfine coupling constant:

$a_{\mathit{eiso}}=\sqrt{\frac{4}{3}\sum _i^N{a}_i^2{I}_i\left(I_i+1\right)}.(15)$

FIGURE 5

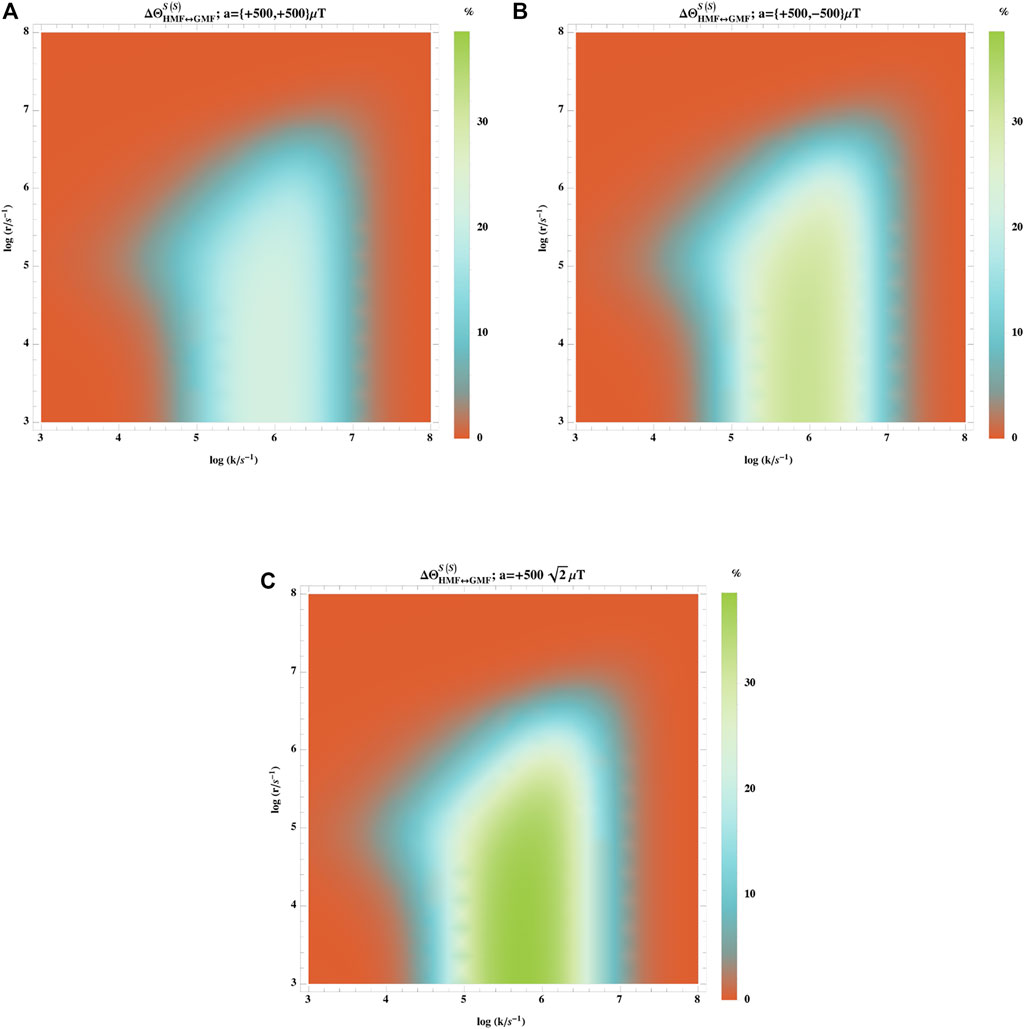
FIGURE 5. Comparing different signs for the hyperfine couplings in the case of multiple nuclei. Dependence of $\mathrm{\Delta }{\mathrm{\Theta }}_{HMF\leftrightarrow GMF}^{S(S)}$ on k, r, and signs of the hyperfine coupling constants. The hypomagnetic field effect is based on the singlet yield ratio of 1 μT (HMF) over μT (GMF) with initial singlet states. In this model, one of the radicals has no hyperfine interaction and the other one is coupled to two nuclei with these isotropic hyperfine coupling constants: (A) a_iso = { + 500, + 500}μT, (B) a_iso = { + 500, − 500}μT, (C) $a_{\mathit{eiso}}=500\sqrt{2}\mu$T. The signs of the hyperfine couplings have a negligible impact on the fractional yield for the hypomagnetic field effects. The effective coupling constant has a stronger effect than the other coupling constants.

The effect is higher than 10% when k ∈ [10⁵–10⁷] s⁻¹ and r < 10⁶ s⁻¹. In this range of parameters, the effective hyperfine coupling constant shows stronger effects relative to the other sets of couplings.

In the present work, the second nuclear spin was considered to be on the same radical as the first one, and the other radical had no hyperfine interaction. It should also be noted that when the second nucleus is not in the same radical as the first one, the hypomagnetic field effect should be extremely small [28].

We also investigate how the initial state of the radical pairs (singlet or triplet) impacts the hypomagnetic field effects. Figure 6 shows the hypomagnetic field effects based on singlet/triplet yield with singlet/triplet initial states. The effect is evident when k ∈ [10⁵–10⁷] s⁻¹ and r < 10⁶ s⁻¹. However, the effect is more pronounced when it is based on singlet (triplet) yield with triplet (singlet) initial states, Φ^S(T) (Φ^T(S)), whereas the effect based on triplet yield with triplet initial states, Φ^T(T), is less than 10%.

FIGURE 6

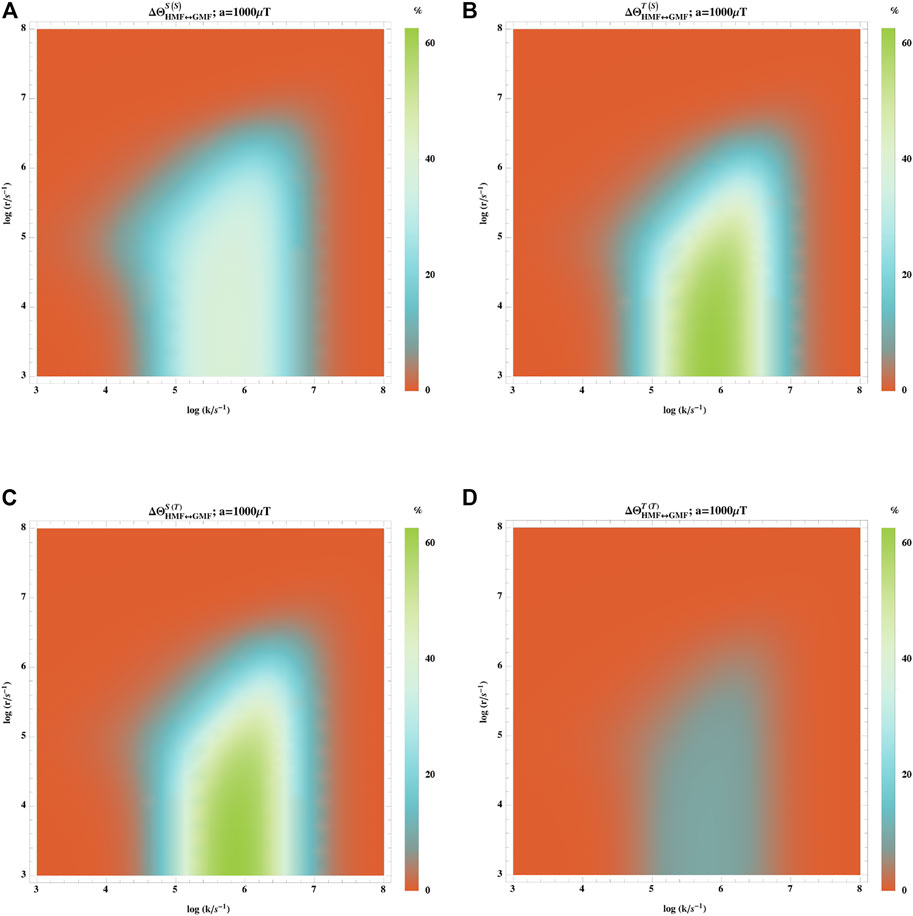
FIGURE 6. Impact of the initial state of the radical pairs (singlet or triplet) on the hypomagnetic field effects. The hypomagnetic field effect is based on the singlet yield ratio with initial singlet states (A), the triplet yield ratio with initial singlet states (B), the singlet yield ratio with initial triplet states (C), and the triplet yield ratio with initial triplet states (D). In this model, one of the radicals has no hyperfine interaction, and the other one is coupled to an isotropic hyperfine coupling constant of a_eiso = 1,000 μT. The effect is evident when k ∈ [10⁵–10⁷] s⁻¹ and r < 10⁶ s⁻¹. However, the effect is more pronounced when is based on singlet (triplet) yield with triplet (singlet) initial states, Φ^S(T) (Φ^T(S)).

We also considered the effects of the exchange interaction:

$H_J=J{\widehat{\mathbf{S}}}_A\cdot {\mathbf{S}}_B(16)$

where J is the exchange coupling. Figure 7 shows that coupling of −50 μT can significantly attenuate the hypomagnetic field effects. A priori for low field effects inter-radical spin-spin interactions would need to be ≤ 50 μT, which requires ≥3.5 nm distance between the radicals. This challenges the radical pair mechanism because electron transfer may be slower than spin relaxation for relatively large distances. However, Ref. [47] showed that LFEs can be significant for much smaller separation of order 2 nm where the effects of exchange and dipolar interactions partially cancel.

FIGURE 7

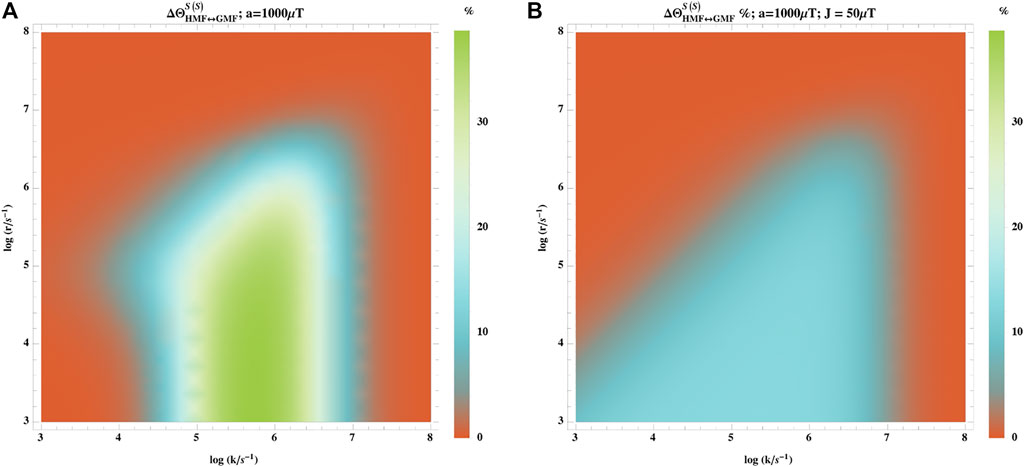
FIGURE 7. Effect of exchange interaction on the hypomagnetic field effects. The hypomagnetic field effect is based on the singlet yield ratio with initial singlet states without (A) and with (B) the exchange interaction. The exchange interaction coupling is −50 μT. In this model, one of the radicals has no hyperfine interaction, and the other is coupled to an isotropic hyperfine coupling constant of a_eiso = 1,000 μT. The exchange interaction significantly attenuates the hypomagnetic field effects.

We also explored the effects of small fluctuations on the hypomagnetic field. We considered an oscillating magnetic field with field with a low frequency and intensity:

$B=B_0+B_1\cos \alpha ,(17)$

where B₁ is the small fluctuating field. As the lifetime of radical pairs is much shorter than the frequency of the applied magnetic field, the effect of the fluctuation can be treated as static during the lifetime of a radical pair [43, 48].

$\overline{{\mathrm{\Phi }}_S\left(B_0,B_1\right)}=\frac{1}{\pi }{\int }_0^{\pi }{\mathrm{\Phi }}_S\left(B\right)d\alpha .(18)$

Figure 8 shows the effect of 5 μT fluctuating magnetic field with low frequency on the hypomagnetic field effect, where including this does not change the results significantly.

FIGURE 8

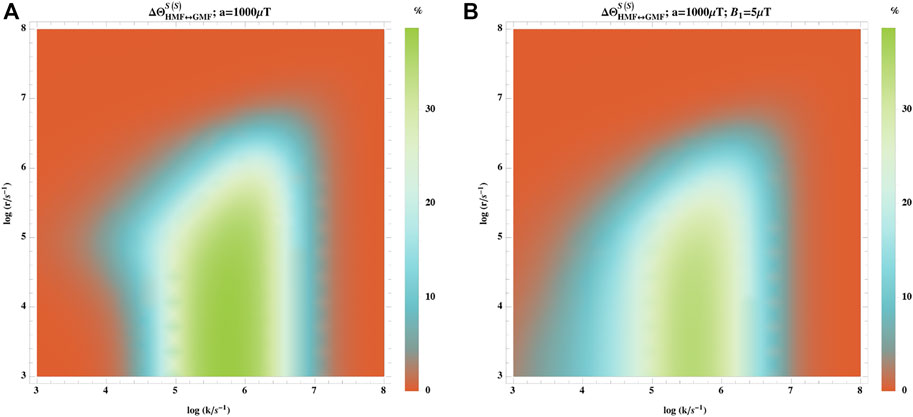
FIGURE 8. Effect of small fluctuation on the hypomagnetic field effects. The hypomagnetic field effect is based on the singlet yield ratio with initial singlet states without (A) and with (B) fluctuating magnetic field of 5 μT with low frequency. In this model, one of the radicals has no hyperfine interaction, and the other one is coupled to an isotropic hyperfine coupling constant of a_eiso = 1,000 μT. The fluctuating field does not change the hypomagnetic field effects significantly.

3 Discussion

In the present work, we aimed to show the hypomagnetic field effects may be an interesting platform for testing the radical pairs models as the underlying mechanism behind the weak magnetic fields in biology. The results indicate that the response of biological systems going from the geomagnetic field strength to the hypomagnetic field regime may be more pronounced than going from the geomagnetic field to higher fields, as shown in Figure 2, which shows clearly that the peak at the low field can be higher than the effect of strong fields. The peak diminishes when the reaction rate is slower than the spin relaxation rate. The hypomagnetic field effects are also more evident when the hyperfine coupling is larger than the spin relaxation and reaction rates. The effects exhibit negligible dependence on the signs of the hyperfine coupling constants, where the effective coupling constant has a larger effective size relative to the individual hyperfine interactions for multi-nuclei interaction. We also explored the impact of the initial state of the radical pairs (singlet or triplet) on the hypomagnetic field effects. We concluded that the effect is more pronounced when it is based on singlet (triplet) yield with triplet (singlet) initial states. We also showed that the exchange interaction can significantly attenuate the hypomagnetic field effects. The effect of small fluctuating magnetic fields on the hypomagnetic field effect was insignificant.

It should be noted that the radical pair model considered in the present work is simplified, where the reaction rates for singlet and triplet yields and the spin relaxation for both radicals are assumed equal. More realistic models of the radical pairs may provide further insight into the underlying mechanism behind these phenomena, e.g., solving the master equation and considering the role of entanglement, dipolar, and exchange interactions in the models.

It should also be noted that an extended version of the radical pair mechanism, the radical triad mechanism [49–51], has been proposed as an explanation for weak magnetic field effects. Radical triads may provide more sensitivity and circumvent issues such as weakening effects from dipolar interactions and fast spin relaxation of superoxide. There are several pieces of evidence that radical pairs or triads may be involved in the response of biological systems to weak magnetic fields [32, 52]. However, both approaches demand more supporting evidence, and this question is under active investigation.

A considerable amount of evidence shows that shielding the geomagnetic field has direct biological consequences, which in some cases could be detrimental. This could also be pertinent for the quest for life on other planets with different magnetic fields, including Mars, which has zero magnetic fields [53, 54].

Studies suggest the Laschamp excursion–the most intense geomagnetic event occurring over the last 50 kyr, with a quasi-reversed polarity of the geomagnetic field–in combination with the Grand Solar Minima, initiated substantial changes in the concentration and circulation of the atmospheric ozone, increased atmospheric ionisation and ultraviolet radiation levels, leading to global climate shifts that caused major environmental changes [55]. They concluded the excursions of the geomagnetic field could be potentially harmful to life. In other words, they proposed an indirect impact of the geomagnetic field deprivation on the mass extinction indirectly via the atmosphere.

In the current work, we reviewed the radical pair mechanism as an arguably plausible explanation for hypomagnetic field effects in biology. We hope this work will inspire our experimental colleagues to test the credibility of this explanation.

Data availability statement

The generated datasets and computational analysis are available from the corresponding author upon reasonable request.

Author contributions

HZ-H and CS conceived the project. HZ-H performed formal analysis, investigation, methodology, software, and visualization with feedback from CS. HZ-H wrote the original draft with help from CS and RR. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Natural Sciences and Engineering Research Council of Canada. National Research Council CSTIP Grant QSP 022 NSERC Discovery Grant RGPIN-2020-03945.

Acknowledgments

The authors would like to thank Aurélien de la Lande, Jean Deviers, and Dennis Salahub for their valuable input.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zadeh-Haghighi H, Simon C. Magnetic field effects in biology from the perspective of the radical pair mechanism. J R Soc. Interf (2022) 19:20220325. doi:10.1098/rsif.2022.0325

CrossRef Full Text | Google Scholar

2. Belyavskaya N. Biological effects due to weak magnetic field on plants. Adv Space Res (2004) 34:1566–74. doi:10.1016/j.asr.2004.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Maffei ME. Magnetic field effects on plant growth, development, and evolution. Front Plant Sci (2014) 5:445. doi:10.3389/fpls.2014.00445

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Binhi VN, Prato FS. Biological effects of the hypomagnetic field: An analytical review of experiments and theories. PLOS ONE (2017) 12:e0179340. doi:10.1371/journal.pone.0179340

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang B, Tian L. Reactive oxygen species: Potential regulatory molecules in response to hypomagnetic field exposure. Bioelectromagnetics (2020) 41:573–80. doi:10.1002/bem.22299

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhang Z, Xue Y, Yang J, Shang P, Yuan X. Biological effects of hypomagnetic field: Ground-based data for space exploration. Bioelectromagnetics (2021) 42:516–31. doi:10.1002/bem.22360

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Xue X, Ali YF, Luo W, Liu C, Zhou G, Liu NA. Biological effects of space hypomagnetic environment on circadian rhythm. Front Physiol (2021) 12:643943. doi:10.3389/fphys.2021.643943

PubMed Abstract | CrossRef Full Text | Google Scholar

8. da Silva JAT, Dobránszki J. Magnetic fields: how is plant growth and development impacted? Protoplasma (2015) 253:231–48. doi:10.1007/s00709-015-0820-7

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tsetlin V, Moisa S, Levinskikh M, Nefedova E. Effect of very small doses of ionizing radiation and hypomagnetic field change physiological characteristics of higher plant seeds. Aerosp Environ Med (2016) 50:51–8. doi:10.21687/0233-528x-2016-50-6-51-58

CrossRef Full Text | Google Scholar

10. Parmagnani AS, Mannino G, Maffei ME. Transcriptomics and metabolomics of reactive oxygen species modulation in near-null magnetic field-induced arabidopsis thaliana. Biomol (2022) 12:1824. doi:10.3390/biom12121824

CrossRef Full Text | Google Scholar

11. Zhang B, Wang L, Zhan A, Wang M, Tian L, Guo W, et al. Long-term exposure to a hypomagnetic field attenuates adult hippocampal neurogenesis and cognition. Nat Commun (2021) 12:1174. doi:10.1038/s41467-021-21468-x

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Raup DM, Sepkoski JJ. Periodicity of extinctions in the geologic past. Proc Natl Acad Sci (1984) 81:801–5. doi:10.1073/pnas.81.3.801

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lipowski A, Lipowska D. Long-term evolution of an ecosystem with spontaneous periodicity of mass extinctions. Theor Biosci (2006) 125:67–77. doi:10.1016/j.thbio.2006.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Becker RO. Relationship of geomagnetic environment to human biology. N.Y State J Med (1963) 63:2215–9.

PubMed Abstract | Google Scholar

15. Beischer DE. The null magnetic field as reference for the study of geomagnetic directional effects in animals and man. Ann N.Y Acad. Sci. (1971) 188:324–30. doi:10.1111/j.1749-6632.1971.tb13107.x

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Beischer DE, Miller EF, Knepton JC. Exposure of man to low intensity magnetic fields in a coil system, 1018. Pensacola, Florida: Naval Aerospace Medical Institute, Naval Aviation Medical Center (1967).

Google Scholar

17. Dubrov AP. The geomagnetic field and life. New York: Springer US (1978).

Google Scholar

18. Alken P, Thebault E, Beggan CD, Amit H, Aubert J, Baerenzung J, et al. International geomagnetic reference field: the thirteenth generation. Earth, Planets Space (2021) 73:49. doi:10.1186/s40623-020-01288-x

CrossRef Full Text | Google Scholar

19. Nordmann GC, Hochstoeger T, Keays DA. Magnetoreception—a sense without a receptor. PLOS Biol (2017) 15:e2003234. doi:10.1371/journal.pbio.2003234

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kirschvink JL, Winklhofer M, Walker MM. Biophysics of magnetic orientation: strengthening the interface between theory and experimental design. J R Soc. Interf (2010) 7:S179–91. doi:10.1098/rsif.2009.0491.focus

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Galvanovskis J, Sandblom J. Amplification of electromagnetic signals by ion channels. Biophys J (1997) 73:3056–65. doi:10.1016/s0006-3495(97)78333-4

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Rosenspire AJ, Kindzelskii AL, Simon BJ, Petty HR. Real-time control of neutrophil metabolism by very weak ultra-low frequency pulsed magnetic fields. Biophys J (2005) 88:3334–47. doi:10.1529/biophysj.104.056663

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Nimpf S, Nordmann GC, Kagerbauer D, Malkemper EP, Landler L, Papadaki-Anastasopoulou A, et al. A putative mechanism for magnetoreception by electromagnetic induction in the pigeon inner ear. Curr Biol (2019) 29:4052–9.e4. doi:10.1016/j.cub.2019.09.048

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Hochstoeger T, Al Said T, Maestre D, Walter F, Vilceanu A, Pedron M, et al. The biophysical, molecular, and anatomical landscape of pigeon CRY4: A candidate light-based quantal magnetosensor. Sci Adv (2020) 6:eabb9110. doi:10.1126/sciadv.abb9110

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Fessenden RW, Schuler RH. Electron spin resonance studies of transient alkyl radicals. J Chem Phys (1963) 39:2147–95. doi:10.1063/1.1701415

CrossRef Full Text | Google Scholar

26. Sagdeev RZ, Molin YN, Salikhov KM, Leshina TV, Kamha MA, Shein SM. Effects of magnetic field on chemical reactions. Org Magn Reson (1973) 5:603–5. doi:10.1002/mrc.1270051212

CrossRef Full Text | Google Scholar

27. Brocklehurst B, Dixon R, Gardy E, Lopata V, Quinn M, Singh A, et al. The effect of a magnetic field on the singlet/triplet ratio in geminate ion recombination. Chem Phys Lett (1974) 28:361–3. doi:10.1016/0009-2614(74)80366-0

CrossRef Full Text | Google Scholar

28. Timmel C, Till U, Brocklehurst B, Mclauchlan K, Hore P. Effects of weak magnetic fields on free radical recombination reactions. Mol Phys (1998) 95:71–89. doi:10.1080/00268979809483134

CrossRef Full Text | Google Scholar

29. Hayashi H. Introduction to dynamic spin chemistry. Singapore: World Scientific (2004).

Google Scholar

30. Steiner UE, Ulrich T. Magnetic field effects in chemical kinetics and related phenomena. Chem Rev (1989) 89:51–147. doi:10.1021/cr00091a003

CrossRef Full Text | Google Scholar

31. Ritz T, Adem S, Schulten K. A model for photoreceptor-based magnetoreception in birds. Biophys J (2000) 78:707–18. doi:10.1016/s0006-3495(00)76629-x

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Xu J, Jarocha LE, Zollitsch T, Konowalczyk M, Henbest KB, Richert S, et al. Magnetic sensitivity of cryptochrome 4 from a migratory songbird. Nature (2021) 594:535–40. doi:10.1038/s41586-021-03618-9

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Smith J, Zadeh-Haghighi H, Salahub D, Simon C. Radical pairs may play a role in xenon-induced general anesthesia. Sci Rep (2021) 11:6287. doi:10.1038/s41598-021-85673-w

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zadeh-Haghighi H, Simon C. Entangled radicals may explain lithium effects on hyperactivity. Sci Rep (2021) 11:12121. doi:10.1038/s41598-021-91388-9

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zadeh-Haghighi H, Simon C. Radical pairs can explain magnetic field and lithium effects on the circadian clock. Sci Rep (2022) 12:269. doi:10.1038/s41598-021-04334-0

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rishabh R, Zadeh-Haghighi H, Salahub D, Simon C. Radical pairs may explain reactive oxygen species-mediated effects of hypomagnetic field on neurogenesis. PLOS Comput Biol (2022) 18:e1010198. doi:10.1371/journal.pcbi.1010198

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zadeh-Haghighi H, Simon C. Radical pairs may play a role in microtubule reorganization. Sci Rep (2022) 12:6109. doi:10.1038/s41598-022-10068-4

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lewis AM, Fay TP, Manolopoulos DE, Kerpal C, Richert S, Timmel CR. On the low magnetic field effect in radical pair reactions. J Chem Phys (2018) 149:034103. doi:10.1063/1.5038558

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Barnes FS, Greenebaum B. The effects of weak magnetic fields on radical pairs. Bioelectromagnetics (2014) 36:45–54. doi:10.1002/bem.21883

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Eveson RW, Brockle B, Timmel CR. The effects of weak magnetic fields on radical recombination reactions in micelles. Int J Radiat Biol (2000) 76:1509–22. doi:10.1080/09553000050176270

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Timmel CR, Henbest KB. A study of spin chemistry in weak magnetic fields. Philos Trans R Soc. Lond. Ser. A: Math. Phys. Eng. Sci. (2004) 362:2573–89. doi:10.1098/rsta.2004.1459

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Maeda K, Henbest KB, Cintolesi F, Kuprov I, Rodgers CT, Liddell PA, et al. Chemical compass model of avian magnetoreception. Nature (2008) 453:387–90. doi:10.1038/nature06834

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Hore P. Upper bound on the biological effects of 50/60 hz magnetic fields mediated by radical pairs. eLife (2019) 8:e44179. doi:10.7554/elife.44179

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Hogben HJ, Efimova O, Wagner-Rundell N, Timmel CR, Hore P. Possible involvement of superoxide and dioxygen with cryptochrome in avian magnetoreception: Origin of zeeman resonances observed by in vivo EPR spectroscopy. Chem Phys Lett (2009) 480:118–22. doi:10.1016/j.cplett.2009.08.051

CrossRef Full Text | Google Scholar

45. Player TC, Baxter EDA, Allatt S, Hore PJ. Amplification of weak magnetic field effects on oscillating reactions. Sci Rep (2021) 11:9615. doi:10.1038/s41598-021-88871-8

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Schulten K, Swenberg CE, Weller A. A biomagnetic sensory mechanism based on magnetic field modulated coherent electron spin motion. Z für Physikalische Chem (1978) 111:1–5. doi:10.1524/zpch.1978.111.1.001

CrossRef Full Text | Google Scholar

47. Efimova O, Hore P. Role of exchange and dipolar interactions in the radical pair model of the avian magnetic compass. Biophys J (2008) 94:1565–74. doi:10.1529/biophysj.107.119362

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Scaiano JC, Mohtat N, Cozens FL, McLean J, Thansandote A. Application of the radical pair mechanism to free radicals in organized systems: Can the effects of 60 hz be predicted from studies under static fields? Bioelectromagnetics (1994) 15:549–54. doi:10.1002/bem.2250150608

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Kattnig DR, Hore PJ. The sensitivity of a radical pair compass magnetoreceptor can be significantly amplified by radical scavengers. Sci Rep (2017) 7:11640. doi:10.1038/s41598-017-09914-7

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kattnig DR. Radical-pair-based magnetoreception amplified by radical scavenging: Resilience to spin relaxation. J Phys Chem B (2017) 121:10215–27. doi:10.1021/acs.jpcb.7b07672

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Ramsay J, Kattnig DR. Radical triads, not pairs, may explain effects of hypomagnetic fields on neurogenesis. PLOS Comput Biol (2022) 18:e1010519. doi:10.1371/journal.pcbi.1010519

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Hiscock HG, Worster S, Kattnig DR, Steers C, Jin Y, Manolopoulos DE, et al. The quantum needle of the avian magnetic compass. Proc Natl Acad Sci (2016) 113:4634–9. doi:10.1073/pnas.1600341113

PubMed Abstract | CrossRef Full Text | Google Scholar

53. McKay DS, Gibson EK, Thomas-Keprta KL, Vali H, Romanek CS, Clemett SJ, et al. Search for past life on mars: Possible relic biogenic activity in martian meteorite ALH84001. Science (1996) 273:924–30. doi:10.1126/science.273.5277.924

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Hyodo R, Usui T. Searching for life on mars and its moons. Science (2021) 373:742. doi:10.1126/science.abj1512

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Cooper A, Turney CSM, Palmer J, Hogg A, McGlone M, Wilmshurst J, et al. A global environmental crisis 42, 000 years ago. Science (2021) 371:811–8. doi:10.1126/science.abb8677

PubMed Abstract | CrossRef Full Text | Google Scholar