Mechanism of supply chain coordination based on price discount with privacy protection in one-supplier-one-buyer system

It is of great economic significance to optimize the total cost and improve the performance of the supply chain. In this paper, we assume that the market demand is random, and the seller and the buyer share information and make decisions together. We analyze the optimal joint order quantity under probabilistic demand and design the quantity discount model and profit distribution mechanism. Under a certain quantity discount mechanism and profit distribution strategy, both the seller and the buyer can reduce costs. The quantity discount model and profit distribution mechanism designed require supply chain members to share information. In order to protect the privacy of members and improve the willingness of supply chain members to share information, we designed a privacy protection joint ordering policy protocol and privacy protection quantity discount policy based on Secure multiparty computation technology. Then, the joint ordering strategy, the privacy-preserving joint ordering strategy, and quantity discount protocol are numerically simulated. The numerical simulation results show that the privacy-preserving quantity discount coordination mechanism designed by us can reduce the cost of supply chain members to varying degrees and effectively protect the shared information of supply chain members. This work is helpful to the research of cost optimization of the system in complex supply chain systems.

1 Introduction

In the social economic network, it is of great economic significance to optimize the total cost and improve the performance of the supply chain. Supply chain literature considers the one-supplier, one-buyer system as the basic building block [1], and in the socio-economic system, the seller can be a manufacturer or wholesaler, and the buyer can be a distributor who faces random market demands. In the traditional mode, the buyer and the seller make decentralized decisions, both based on maximizing their own interests. The buyer usually chooses economic order quantity (EOQ) as his optimal order quantity, however, for the seller, the buyer’s order quantity is different each time, and the buyer’s order time is also uncertain. In order to cope with the uncertainty of order demand, the seller needs to maintain a high inventory, therefore, will inevitably sell to the buyer at a higher price. This leads to the overall high cost and low efficiency of the supply chain system. The efficiency improvement of supply chain systems has become a hot research topic.

The price discount strategy originated from Monahan’s research in 1984 [2]. He assumed that the market demand was constant and had nothing to do with the product price, and the buyer’s order uses a lot-for-lot model, finding that the seller can change the buyer’s order quantity through price discounting strategies to increase profits. Later, many scholars began to apply the price discount strategy in the performance optimization of the supply chain system. At first, scholars assumed that the market demand was constant, and then progressed to the situation that the market demand was random.

Many supply chain cost optimization strategies require supply chain members to share information [3–7]. However, supply chain members may use the shared private cost information [8]. This may cause the supply chain members to lose their competitive advantages and cause them many hidden dangers. For example, in a supply chain cooperation system, the downstream enterprises providing their own private information to the upper will enhance the authority of the upper in the supply chain, making the downstream enterprises at a disadvantage in the negotiations and losing the profit advantage. Although information sharing is the key to achieving enterprise cooperation, driven by the pursuit of individual interests, enterprises may make individual optimal choices that are contrary to the overall optimal. Even, information leakage exists in the supply chain system [9], which will lead to various fraud events, resulting in the loss of enterprise funds.

Privacy information protection [10] and information security [11] have been paid more and more attention, and its related technologies have also been greatly developed, such as blockchain technology [12, 13], secure multi-party computing, and so on. Secure multiparty computation (SMC) originated from Yao Qizhi’s millionaire problem in 1982 [14], and was discussed in detail and systematically by Micali et al. [15]. SMC provides a framework for computing partners, mainly studying how to design secure computing contract functions without a trusted third party. SMC has attracted researchers’ attention. Scholars began to study the application of secure multi-party computing to privacy protection in information-sharing scenarios.

In this paper, we are interested in the mechanism of supply chain coordination based on price discount and privacy protection in a one-supplier-one-buyer system, and the reasons are, on one hand, quantity discount mechanism for joint-ordering in a one-supplier-one-buyer system has yet not been reported, on the other hand, the privacy protection of information sharing in price discount mechanism using SMC technology has not been studied. The main contributions and significance of this paper are summarized as follows:

1) In the classic one-supplier-one-buyer supply chain system, the buyer’s order adopts the economic order quantity mode; the buyer and seller make independent decisions, and the cost of the overall supply chain system is high. We assume that the market demand is random, and the seller and the buyer share information and make decisions together like two departments of the same company. We analyze the optimal joint order quantity under probabilistic demand and design the quantity discount model and profit distribution mechanism. Under a certain quantity discount mechanism and profit distribution strategy, both the seller and the buyer can reduce costs.

2) The quantity discount model and profit distribution mechanism designed require supply chain members to share information. However, after all, the seller and the buyer are independent companies. On one hand, they may not want the other party to know their private information; On the other hand, even though both parties are willing to share information, they are afraid to share information because they are worried about the harm caused by information leakage. In order to protect the privacy of members and improve the willingness of supply chain members to share information, we designed a privacy protection joint ordering policy protocol and privacy protection quantity discount policy based on SMC technology. It is implemented without using intermediaries and does not disclose the private information of members. Then, the joint ordering strategy, the privacy-preserving joint ordering strategy and the quantity discount protocol are numerically simulated. The numerical simulation results show that the privacy-preserving quantity discount coordination mechanism designed by us can reduce the cost of supply chain members to varying degrees and effectively protect the shared information of supply chain members.

The rest of the paper is organized as follows. Section 2 introduces the work of other researchers related to this paper; Section 3 describes the basic model based on EOQ; In section 4, We designed the improved model based on price discount and quantity coordination; We designed a privacy protection joint ordering policy protocol and privacy protection quantity discount policy based on SMC technology in Section 5; some simulations are performed to validate the effectiveness and feasibility of the proposed mechanism of supply chain coordination based on price discount and privacy protection in Sections 6, 7 is conclusion and discussion. The construction of the basic sub-protocol oblivious transfer (OT) and the content of the privacy protocol are introduced in Supplementary Appendix S1–S4, where Supplementary Appendix S1 (protocol 1: an oblivious transfer protocol) and Supplementary Appendix S2 (protocol 2: a secure two-party real product protocol) are the basic protocols of cryptography and are the basis for constructing Supplementary Appendix S3, S4.

2 Related work

2.1 Economic order quantity

In a supply chain system, in the order decision of the seller, how to determine the quantity of raw materials ordered for the production of certain products is a difficult problem; which batch can obtain the best investment benefit is an important issue. Economic order quantity (EOQ) balances the purchase cost and storage cost accounting, which achieves the best order quantity with the lowest total inventory cost. Mokhtari [16] presented an EOQ model to optimize the total system cost. In the context of uncertain demands, Braglia et al. [17] studied the stochastic periodic-review joint replenishment problem (JRP). Tayebi et al. [18] formulated the joint order (1, T) policy with Poisson demands while ensuring reduced supply chain costs. Güler et al. [19] considered the JRP when the holding cost rate and demand rate are private information and presented a mechanism to allocate costs in the JRP. That quantity coordination strategy can improve the supply chain performance of traditional decentralized system.

2.2 Price discount policy

In the 1990s, scholars began to use quantity-based price discount strategy to achieve supply chain coordination [20–22]. Weng [20] assumed that demand is elastic and affected by price, and found that quantity discount can effectively stimulate the increase of market demand and ensure Pareto Optimality. Under the condition of price elasticity of demand, Gao et al. [21] studied the problem of determining price discount in a supply chain contract composed of one buyer and one seller. Munson et al. [22] studied the overall profit maximization problem of the three-level chain (supplier-manufacturer-retailer) supply chain system. These studies assume that market demand is a constant or a decreasing function of product price. Some scholars further assume that market demand is a random variable, and study the cost optimization problem of supply chain system [23].

2.3 Secure multiparty computing

The research of SMC is mainly aimed at how to calculate a contract function safely without a trusted third party, which is the password basis for many applications [15] such as electronic voting, threshold signatures, and electronic auctions. The application of SMC is a possible mean to solve private information preserving problems [24], which has now become a subfield of cryptography [25].

Scholars began to study the application of SMC in the supply chain system. Atallah et al. [26] proposed the secure supply chain collaboration (SSCC) protocol for capacity allocation while preserving parties’ private information. Clifton et al. [27] proposed a secure protocol for swapping loads while preserving trucking companies’ private information, but they did not explicitly consider benefit sharing. Xie et al. [28] addressed SMC in the context of joint ordering under deterministic demand to minimize total supply chain expected costs. Pibernik et al. [29] described a privacy-preserving protocol for determining the EOQ with stochastic benefit sharing under deterministic demand with any private (cost and capacity) information preservation. Yang et al. [30] proposed a blockchain-based secure multi-party computation architecture for data sharing. Wang et al. [31] explored a novel approach to support energy storage sharing with privacy protection, based on privacy-preserving blockchain and secure multi-party computation.

2.4 Oblivious transfer protocol

The oblivious transfer (OT) protocol is a basic protocol in cryptography that enables the receiver of a service to obtain messages input by the sender of the service inadvertently, thus protecting the privacy of the receiver from the sender. Long et al. [32] proposed a privacy protection method based on server-assisted reverse oblivious transfer, which includes the protocol of a cloud server and can calculate the result of encrypting the sensing data to avoid fully trusting the sensing platform. Wang et al. [33] proposed a casual transmission protocol and a private set intersection protocol to protect the privacy of users. Based on smart contracts and OT, Li et al. [34] proposed a privacy-preserving big data exchange scheme that allows buyers and sellers to complete transactions independently and fairly without involving any third-party middleman.

3 Basic model based on EOQ

The classical EOQ model was created by Harris [35]. Based on the assumptions of the classical model, the basic model assumptions in this study are as follows:

a. The research object of this study is a two-level supply chain, and the current status of the supply chain is assumed to be balanced [36].

b. The seller makes the product, and the unit production cost is constant.

c. The supply capacity of the seller is much greater than the demand of the buyer, so the out-of-stock cost can be ignored.

d. When the market demand tends to be stable, the demand follows the normal distribution, and the buyer’s demand expectation is $D$.

e. The buyer is a price taker in a free competitive market, and he can accept the shortage in the market. The buyer uses EOQ to determine the quantity of each purchase, and its ordering strategy uses $\left(s,Q\right)$ strategy.

f. The seller’s unit order preparation cost consists of two parts: the order processing cost and the production preparation cost.

g. The lead time of the buyer’s order is constant.

The notations adopted in this paper are presented in Table 1.

TABLE 1

TABLE 1. Parameter definitions.

According to the previous assumption, the buyer’s order lead time is constant, so the demand in the lead time is only related to the demand quantity. Assuming that the buyer’s order amount is $Q$ each time and the product price given by the seller is $w$, the buyer’s total annual cost is:

${TC}_b\left(Q,w\right)=wD+\frac{S_{b}D}{Q}+\left(\frac{Q}{2}+k\delta \right)h_b+B_b\delta G\left(k\right)D/Q(1)$

where $wD$ is the acquisition cost, $\frac{S_{b}D}{Q}$ is the ordering cost, $\left(\frac{Q}{2}+k\delta \right)h_b$ is the inventory holding cost, and $B_b\delta G\left(k\right)D/Q$ is the expected penalty and opportunity cost.

In Formula 1, $\delta G\left(k\right)$ represents the expected shortages [37]:

$G\left(k\right)={\int }_k^{\infty }\left(u-k\right)\frac{1}{\sqrt{2\pi }}\mathit{exp}\left(-\frac{u^2}{2}\right)du(2)$

In Formula 2, $G\left(k\right)$ represents the distribution function of standard normal variables.

According to Formula 1, the optimal order quantity of the buyer can be obtained:

$Q^{*}=\sqrt{2D\left[S_b+B_b\delta G\left(k\right)\right]/h_b}(3)$

So, the buyer’s total annual cost is:

${TC}_b\left(Q^{*},w\right)=wD+k\delta h_b+\sqrt{2D\left[S_b+B_b\delta G\left(k\right)\right]/h_b}(4)$

Then, the cost of the seller needed to be studied. We have assumed that the buyer’s order amount is $Q$ each time. When the buyer’s annual demand is $D$, the buyer needs to order $D/Q$ times in a year. So the buyer needs to place an order with the seller every $Q*365/D$ days. For such order flow, the seller’s production quantity should be a multiple of the buyer’s order quantity within 1 year. In order to facilitate the account, we define the total cost of the seller as the sum of the cost of production, the fixed cost, and the inventory holding cost minus the sales return. Therefore, the total annual cost of the seller is expressed as:

${TC}_s\left(Q,w\right)=CD+\frac{h_{s}Q}{2}+\frac{S_{s}D}{Q}-wD(5)$

Let $Q_s^{*}$ be the order quantity that the seller expects from the buyer to minimize the seller’s cost. We can get $Q_s^{*}=\sqrt{2S_{s}D/h_s}$. By substituting $Q_s^{*}$ into (5), we can infer the annual total cost of the seller.

${TC}_s\left(Q_s^{*},w\right)=\left(C-w\right)D+\sqrt{2h_s{S}_{s}D}(6)$

When the buyer adopts EOQ ordering mode, the Seller’s cost is as follows: [by substituting $Q^{*}$ into (5)]

${TC}_s\left(Q^{*},w\right)=\left(C-w\right)D+\left(\frac{S_s}{\left[S_b+B_b\delta G\left(k\right)\right]}+h_s/h_b\right)\sqrt{D\left[S_b+B_b\delta G\left(k\right)\right]h_b/2}(7)$

Comparing Formulas 6, 7, we can find that ${TC}_s\left(Q^{*},w\right)\ge {TC}_s\left(Q_s^{*},w\right)$, and the equation is established when $\frac{S_s}{\left[S_b+B_b\delta G\left(k\right)\right]}=h_s/h_b$.

4 The improved model based on price discount and quantity coordination

According to the basic model, in the case of decentralized decision-making, each member of the supply chain system makes decisions from the perspective of maximizing their own interests, and the strategies of the buyer and the seller are prone to conflict, resulting in high transaction costs for each member.

If the seller and buyer in the system can cooperate, share information with each other, and make joint decisions together, just like two departments in the same large company, their respective costs may be reduced in this case. Based on this idea, we first study the optimal joint order quantity of seller and buyer under probabilistic demand, and then design the quantity discount and profit distribution mechanism.

4.1 Optimal joint-ordering quantity under probabilistic demand

When the seller and the buyer share information and make joint decisions, the overall cost of the system should be the sum of the costs of the seller and the buyer. We use $TC$ to express the joint cost.

The buyer’s cost is shown in Formula 1, and the seller’s cost is shown in Formula 5, $TC={TC}_b\left(Q,w\right)+{TC}_s\left(Q,w\right)$, so we can obtain:

$TC=\frac{\left[S_b+S_s+B_b{\delta }_{L}G\left(k\right)\right]D}{Q}+\frac{\left(h_b+h_s\right)Q}{2}+h_{b}k\delta +CD(8)$

When the joint cost $TC$ takes the minimum value, that is, calculate the first derivative of $TC$, the order quantity $Q^j$ of the buyer can be calculated:

$Q^j=\sqrt{2D\left[S_b+S_s+B_b\delta G\left(k\right)\right]/\left(h_b+h_s\right)}(9)$

Now, the minimum annul joint cost $TC\left(Q^j\right)$ of the system is as follows:

$TC\left(Q^j\right)=\sqrt{2D\left(h_b+h_s\right)\left[S_b+S_s+B_b\delta G\left(k\right)\right]}+h_{b}k\delta +CD(10)$

When the seller and the buyer make decentralized decision, the buyer’s total annual cost is ${TC}_b\left(Q^{*},w\right)$ (Formula 4), and the seller’s total annual cost is ${TC}_s\left(Q^{*},w\right)$ (Formula 7), then, the sum of the total annual costs of the seller and the buyer is $TC\left(Q^{*}\right)=T{C}_b\left(Q^{*},w\right)+T{C}_s\left(Q^{*},w\right)$.

Comparing the expressions $TC\left(Q^{*}\right)$ and $TC\left(Q^j\right)$, it is easy to get

$TC\left(Q^{*}\right)\ge TC\left(Q^j\right)(11)$

That is to say, when the buyer orders with the order quantity T under the joint decision, the overall cost of the supply chain system is less than the sum of the respective costs under the decentralized decision of the buyer and the seller. However, for the buyer, when he chooses the order quantity $Q^j$ of joint decision rather than the optimal order quantity $Q^{*}$ of decentralized decision, his cost will increase, as $T{C}_b\left(Q^{*},w\right)\le T{C}_b\left(Q^j,w\right)$. Therefore, the buyer is unwilling to use the order quantity of joint strategy.

The reason for this situation is that under the joint strategy, the cost reduced by the seller is greater than the cost increased by the buyer, that is $T{C}_s\left(Q^j,w\right)-T{C}_s\left(Q^{*},w\right)<T{C}_b\left(Q^{*},w\right)-T{C}_b\left(Q^j,w\right)$.

In order to encourage the buyer to increase the order quantity of independent decision to the order quantity of joint decision, the seller needs to provide price discount to compensate the buyer for the increased cost. Suppose that the price provided by the seller to the buyer decreases from $w$ to $w_1$, and at the same time he requires the buyer to increase the order quantity from $Q^{*}$ to $Q^{\prime }$. Then, only when the cost of the buyer is lower than the cost without price discount will he accept the price discount strategy. Therefore, there is the following constraint:

$T{C}_b\left(Q^{\prime },w_1\right)\le T{C}_b\left(Q^{*},w\right)(12)$

Formula 12 can be converted to:

$wD-S_b\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)-\left(\frac{Q^{\prime }}{2}-\frac{Q^{*}}{2}\right)h_b-B_b\delta G\left(k\right)\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)\ge w_{1}D(13)$

Then, we can infer that under the price discount strategy, the seller’s wholesale price $w_1$ has a maximum value.

$w_1^{\mathit{max}}=w-\left\{\frac{h_b\left(Q^{\prime }-Q^{*}\right)}{2}+\left[S_b+B_b\delta G\left(k\right)\right]\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)\right\}/D(14)$

Similarly, for the seller, he hopes that after implementing the price discount strategy, his cost cannot increase, that is, the following condition should be met:

$T{C}_s\left(Q^{\prime },w_1\right)\le T{C}_s\left(Q^{*},w\right)(15)$

Formula 15 can be rewritten as

$\frac{h_s\left(Q^{\prime }-Q^{*}\right)}{2}+S_s\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)+wD\le w_{1}D(16)$

Then, we can infer that under the price discount strategy, the seller’s wholesale price $w_1$ has a minimum value.

$w_1^{\mathit{min}}=w-\left[S_s\left(\frac{D}{Q^{*}}-\frac{D}{Q^{\prime }}\right)-\frac{h_s\left(Q^{\prime }-Q^{*}\right)}{2}\right]/D(17)$

Now, the optimal joint order quantity can benefit both the buyer and the seller without increasing the cost of either party.

We have the following proposition that describes the amount of cost saved:

Proposition 1. Under the joint strategy, the supply chain cost is $TC\left(Q^j\right)$, and under the decentralized decision, the supply chain cost is $TC\left(Q^{*}\right)$, which satisfies:

$TC\left(Q^{*}\right)-TC\left(Q^j\right)=D\times \left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)(18)$

4.2 Profit distribution and quantity discounts design

According to the previous proposition, when the seller and the buyer adopt a joint strategy, the overall cost saved by the supply chain system is $D\left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)$. In order to promote cooperation between the seller and the buyer, it is necessary to ensure that their respective costs under the joint strategy are lower than those of the previous independent decisions. Therefore, after the cooperation between the seller and the buyer, it is necessary to reasonably allocate the overall saved cost of the supply chain system to the seller and the buyer.

So we design such an implementation strategy, allocate the cost saved by the whole supply chain system, the proportion obtained by the buyer is $\alpha$, and the proportion obtained by the seller is $1-\alpha$. Here, $\alpha \in \left(\mathrm{0,1}\right)$ is a random number, named coordination factor. In fact, $\alpha$ means the allocation of the saved costs. If the buyer in the supply chain is stronger than the seller, for example, the buyer has the right to speak and decide, the buyer will save more costs, $\alpha$ will increase and be close to 1.

The cost savings allocated to the buyer is $\alpha D\left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)$, and the cost savings allocated to the seller is $\left(1-\alpha \right)D\left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)$. The implementation strategy can be expressed by the following proposition:

Proposition 2. To encourage the buyer to increase the independent decision-making order quantity to equal the joint order quantity $Q^j$, the seller changes the sales price from $w$ to $w_1$, and the quantity discount provided by the seller can be expressed as

$w_1=w_1^{\mathit{max}}-\alpha \left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)(19)$

Where $w_1^{\mathit{max}}$ and $w_1^{\mathit{min}}$ are given in Eqs 14, 17.

5 Joint ordering strategy and quantity discount design with privacy protection

We assume that the seller and the buyer share information and make decisions together like two departments of the same company. Under a certain quantity discount mechanism and profit distribution strategy, both the seller and the buyer can reduce costs. However, after all, the seller and the buyer are independent companies. On one hand, they may not want the other party to know their private information; On the other hand, even though both parties are willing to share information, they are afraid to share information because they are worried about the harm caused by information leakage. Therefore, a mechanism is needed to realize secure information sharing. In this section, we apply SMC protocols to joint ordering policy and quantity discount design with privacy protection under probabilistic demand.

5.1 Privacy preserving joint-ordering policy protocols

To calculate the minimum joint cost under the joint ordering strategy, the buyer and the seller need to provide the total annual cost when making independent decisions. Therefore, the information that both parties need to provide and obtain is as follows:

5.1.1 Inputs

The buyer supplies $T{C}_b\left(Q,w\right)=wD+\frac{S_{b}D}{Q}+\left(\frac{Q}{2}+k\delta \right)h_b+B_b\delta G\left(k\right)D/Q$, where $S_b$, $h_b$, $k$, $B_b$, $\delta$, and $G\left(k\right)$ are the buyer’s private (cost and capacity) information.

The seller supplies $T{C}_s\left(Q,w\right)=CD+\frac{h_{s}Q}{2}+\frac{S_{s}D}{Q}-wD$,where $h_s$, $S_s$, and $C$ are the seller’s private (cost and capacity) information.

5.1.2 Outputs

The partners learn $Q^j=\sqrt{2D\left[S_b+S_s+B_b\delta G\left(k\right)\right]/\left(h_b+h_s\right)}$ with any private (cost and capacity) information preservation.

5.1.3 Assumptions

The formula $Q^j=\sqrt{2D\left[S_b+S_s+B_b\delta G\left(k\right)\right]/\left(h_b+h_s\right)}$ is public information.

Therefore, the buyer and seller’s goals are to compute the formula for $Q^j$ while preserving their private information.

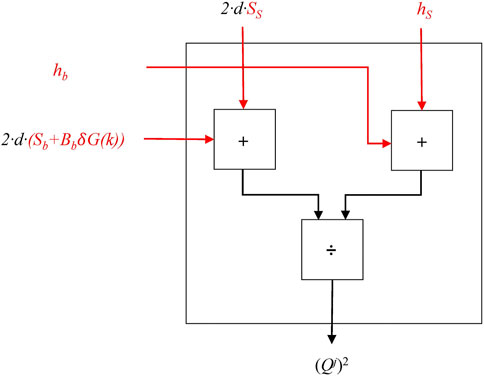
In computer science, formulas are often represented by circuits. So, we construct a circuit for the computation of $Q^j$, which is displayed in Figure 1.

FIGURE 1

FIGURE 1. Circuit for computation of privacy preserving joint-ordering.

In Figure 1, in the circuit, on the top, the red values denote the private part of the seller’s input, and on the left, the red values denote those of the buyer.

5.1.4 Protocol steps

The buyer holds two values $\left(h_b,S_b+B_b\delta G\left(k\right)\right)$, and the seller holds two values $\left(h_s\right.$, $S_s)$.

The common goal is to compute $\left[S_b+S_s+B_b\delta G\left(k\right)\right]/\left(h_b+h_s\right)$ because $2D$ is public information.

Step 1 The buyer generates $U_1$ (random number), and the seller generates $U_2$ (random number).

Step 2 The buyer and the seller use Secure two-party add-product protocol (Supplementary Appendix S3), the buyer obtains $d_1$, and the seller obtains $d_2$, where $d_1+d_2=\left(U_1+U_2\right)\left(S_b+B_b\delta G\left(k\right)+S_s\right)\times 2D$.

Step 3 The buyer and the seller use secure two-party add-product protocol, which are as follows:Inputs: the buyer has two reals $\left(x_1,y_1\right)$, and the seller has two reals $\left(x_2,y_2\right)$.Outputs: the buyer obtains $r_1$, and the seller obtains $r_2$, where $r_1+r_2=\left(x_1+x_2\right)\left(y_1+y_2\right)$.The detailed demonstration process is in Supplementary Appendix S3.The buyer receives $n_1$, and the seller receives $n_2$, where $n_1+n_2=\left(U_1+U_2\right)\left(h_b+h_s\right)$.

Step 4 The buyer sends $n_1$ to the seller, the seller computes ${n=n}_1+n_2$, and the seller sends $n$ to the buyer.

Step 5 The buyer and the seller independently compute $s_1=\frac{d_1}{n},s_2=\frac{d_2}{n}$, and $s_1$, $s_2$ obey the equation:

$s_1+s_2=\frac{d_1+d_2}{n_1+n_2}=\left(S_b+B_b\delta G\left(k\right)+S_s\right)\times 2D/\left(h_b+h_s\right)={\left(Q^j\right)}^2$

5.1.5 Analysis of the protocol

• Information disclosure:

The security in the second (third) step is guaranteed by secure two-party add-product protocol (Supplementary Appendix S3). The independent computation in the 5th step is private. Next, the security of computation in the 4th step is discussed.

The buyer and the seller know the following equation:

$d_1+d_2=\left(U_1+U_2\right)\left(S_b+B_b\delta G\left(k\right)+S_s\right)\times 2D(20)$

${n=n}_1+n_2=\left(U_1+U_2\right)\left(h_b+h_s\right)(21)$

For the buyer (the seller), there are 5 unknown reals: $d_2$, $U_2$, $n_2$, $h_s$, $S_s$$\left(d_1,U_1,n_1,h_b,S_b+B_b\delta G\left(k\right)\right)$. Neither party can know the secret input of another participant.

• Computational complexity:

The protocol used two times Secure two-party add-product protocol (Supplementary Appendix S3).

• Communication complexity:

The protocol only requires communication between the buyer and the seller; both sides know the value of $Q^j$.

5.2 Privacy preserving quantity discounts design

To implement the quantity discount, that is, to let the seller adjust the sales price from $w$ to $w_1$, the buyer and the seller need to provide the total annual cost when making their own decisions, and then inform both parties of the quantity discount information $w_1$, which are as follows:

5.2.1 Inputs

The buyer supplies $T{C}_b\left(Q,w\right)=wD+\frac{S_{b}D}{Q}+\left(\frac{Q}{2}+k\delta \right)h_b+B_b\delta G\left(k\right)D/Q$,where $S_b$, $h_b$, $k$, $B_b$, $\delta$, and $G\left(k\right)$ are the buyer’s private information.

The seller supplies $T{C}_s\left(Q,w\right)=CD+\frac{h_{s}Q}{2}+\frac{S_{s}D}{Q}-wD$,where $h_s$, $S_s$, and $C$ are the private information of the seller.

Coordination factor $\alpha$, where $\alpha \in \left(\mathrm{0,1}\right)$ is a random number, which is determined by the bargaining power of both sides, the seller generates a random number $\alpha$.

5.2.2 Outputs

The seller and buyer learn the quantity discount $w_1$ while preserving their private information.

5.2.3 Assumptions

The seller and the buyer’s goal is to compute $w_1$ with stochastic quantity discounts because $Q^j$ is public information.

We reformulate the stochastic quantity discounts to $w_1=w_1^{\mathit{max}}-\alpha \left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)$,where $\alpha \in \left(\mathrm{0,1}\right)$ is a random number.

${\because w}_1^{\mathit{max}}=w-\left\{\frac{h_b\left(Q^{\prime }-Q^{*}\right)}{2}+\left[S_b+B_b\delta G\left(k\right)\right]\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)\right\}÷D$

$w_1^{\mathit{min}}=w-\left[S_s\left(\frac{D}{Q^{*}}-\frac{D}{Q^{\prime }}\right)-\frac{h_s\left(Q^{\prime }-Q^{*}\right)}{2}\right]÷D$

$\therefore w_1=w_1^{\mathit{max}}-\alpha \left(w_1^{\mathit{max}}-w_1^{\mathit{min}}\right)$

$=w_1^{\mathit{max}}-\alpha \left(w_1^{\mathit{max}}-w\right)-\alpha \times \frac{S_s}{Q^{*}}-\alpha \times \frac{h_s{Q}^{*}}{2D}+\alpha \times \left(\frac{S_s}{Q^{\prime }}+h_s{Q}^{\prime }/2D\right)$

Therefore, $w_1$ is only a function that requires inputs $\left(w_1^{\mathit{max}},w_1^{\mathit{max}}-w,\frac{1}{Q^{*}},Q^{*}\right)$ from the buyer and $\left(-\alpha ,-\alpha \times S_s,-\alpha \times \frac{h_s}{2D},\alpha \times \left(\frac{S_s}{Q^{\prime }}+h_s{Q}^{\prime }/2D\right)\right)$ from the seller.

Because $w$ and $Q^j$ (public information) are known to the buyer, then the buyer can dependably compute $\left(w_1^{\mathit{max}},w_1^{\mathit{max}}-w,\frac{1}{Q^{*}},Q^{*}\right)$.

Because $\alpha$ is a random number, that is, in contrast, determined by the bargaining power of both sides, the seller generates a random number $\alpha$.

The seller can compute $\left(-\alpha ,-\alpha \times S_s,-\alpha \times \frac{h_s}{2D},\alpha \times \left(\frac{S_s}{Q^{\prime }}+\frac{h_s{Q}^{\prime }}{2D}\right)\right)$.

Where, $w_1^{\mathit{max}}-\alpha \left(w_1^{\mathit{max}}-w\right)-\alpha \times \frac{S_s}{Q^{*}}-\alpha \times \frac{h_s{Q}^{*}}{2D}+\alpha \times \left(\frac{S_s}{Q^{\prime }}+\frac{h_s{Q}^{\prime }}{2D}\right)$

$=\left(w_1^{\mathit{max}},w_1^{\mathit{max}}-w,\frac{1}{Q^{*}},Q^{*},1\right)\times (1,-\alpha ,-\alpha \times S_s,-\alpha \times \frac{h_s}{2D},\alpha \times \left(\frac{S_s}{Q^{\prime }}+h_s{Q}^{\prime }/2D\right))$

The flowchart of privacy preserving quantity discounts design is shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of privacy preserving quantity discounts design.

In Figure 2, the buyer independently computes vector $\mathit{X}$, and the seller independently computes vector $\mathit{Y}$ based on $Q^j$ and $\alpha$. The red values denote the private information of the buyer and the seller. The buyer and the seller determine the allocation of overall reduced costs, which is determined by the bargaining power of both parties to the contract, and the seller generates a random number $\alpha$. Based on the foundation of OT, the calculation framework of privacy preserving quantity discounts design is given in Figure 2.

5.2.4 Protocol steps

Step 1 The buyer and the seller use privacy-preserving optimal joint-ordering quantity protocols, and the seller obtain $Q^j$.

Step 2 The buyer and the seller determine the allocation of overall reduced costs, which is determined by the bargaining power of both parties to the contract, and the seller generates a random number $\alpha$.

Step 3 The buyer independently computes vector $\mathit{X}=\left(w_1^{\mathit{max}},w_1^{\mathit{max}}-w,\frac{1}{Q^{*}},Q^{*},1\right)$, and the seller independently computes vector $\mathit{Y}=\left(1,-\alpha ,-\alpha \times S_s,-\alpha \times \frac{h_s}{2D},\alpha \times \left(\frac{S_s}{Q^{\prime }}+\frac{h_s{Q}^{\prime }}{2D}\right)\right)$.

Step 4 The buyer and the seller using secure two-party real product protocol (Supplementary Appendix S2), the buyer obtains $u=\mathit{X}\times {\mathit{Y}}^T+v$, and the seller obtains $v$, where the letter T stands for ‘transpose’.

5.2.5 Analysis of protocol

• Information disclosure:

Protocol 5.1 guarantees security in the first step. The independent computation in the 2nd and 3rd steps is secure. Secure two-party real product protocol (Supplementary Appendix S2) guarantees security in the fourth step.

• Computational complexity:

The protocol uses secure two-party add-product protocol (Supplementary Appendix S3) twice and Secure two-party real product protocol (Supplementary Appendix S2) once.

• Communication complexity:

The protocol requires communication between the buyer and the seller only; both sides of the calculation know the value of $w_1$.

6 Numerical simulation

In this section, we carry out a numerical simulation on joint ordering, joint ordering for privacy protection, and quantity discount for privacy protection.

6.1 Numerical simulation of joint ordering strategy

According to the previous conclusions, the annual costs of the buyer and the seller under independent decision-making and joint decision-making should be numerically simulated and then compared. The details are as follows.

6.1.1 Steps

First, assume the target stock-out probability $p\left(k\right)$ determined by the buyer is 0.1 (0.1 is randomly selected, and other values are also acceptable).

Second, as $G\left(k\right)$ represents the distribution function of standard normal variables, query standard normal distribution function table, and $k=1.28$, and $G\left(k\right)=0.048$ can be obtained. Other parameters of the buyer and the seller, such as $D$, $S_b$, $h_b$, $B_b$, etc., are listed in Table 2. Assume that the cost allocation mechanism negotiated by the buyer and the seller is $\alpha =0.4$.

TABLE 2

TABLE 2. Numerical value of simulation parameters.

Third, no price discount is considered in Table 3. The results from the model based on quantity coordination are shown in Table 4. A negative cost for the seller means that it is his profit.

TABLE 3

TABLE 3. Basic model without price discount.

TABLE 4

TABLE 4. The improved model of quantity coordination.

6.1.2 Results

Comparing the seller’s pricing and the buyer’s order under the above two conditions reveals that when adopting the quantity coordination strategy, the buyer’s order quantity increases significantly, and the costs of both parties are reduced. These two benefits greatly reduce the costs of both buyers and sellers, and the supply chain achieves efficient operations and a win-win outcome.

Then, adjust the value of $\alpha$ to observe the cost change of the supply chain system, and the results are listed in Table 5. From Table 5, it can be inferred that the strength of negotiation between buyers and sellers determines the flow of overall profit savings in the supply chain, but the total cost savings are fixed.

TABLE 5

TABLE 5. Cost change under different $\alpha$ ($w^{\mathit{min}}=48.72$, $w^{\mathit{max}}=49.62$).

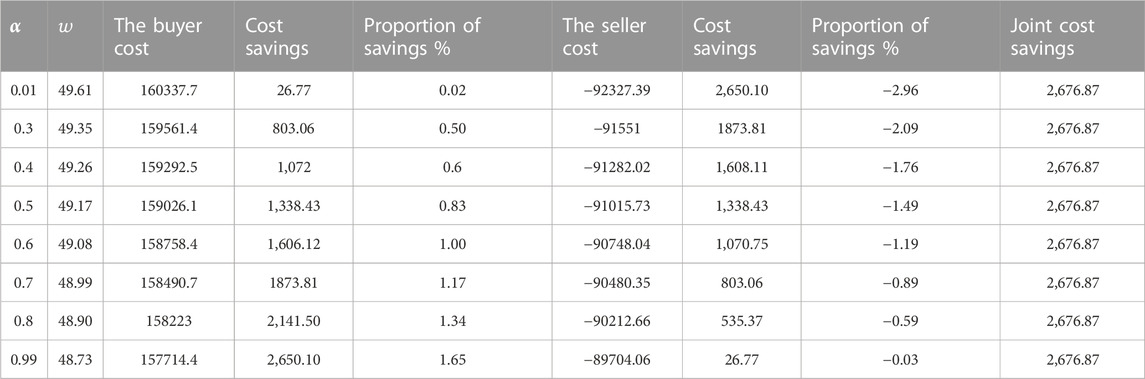
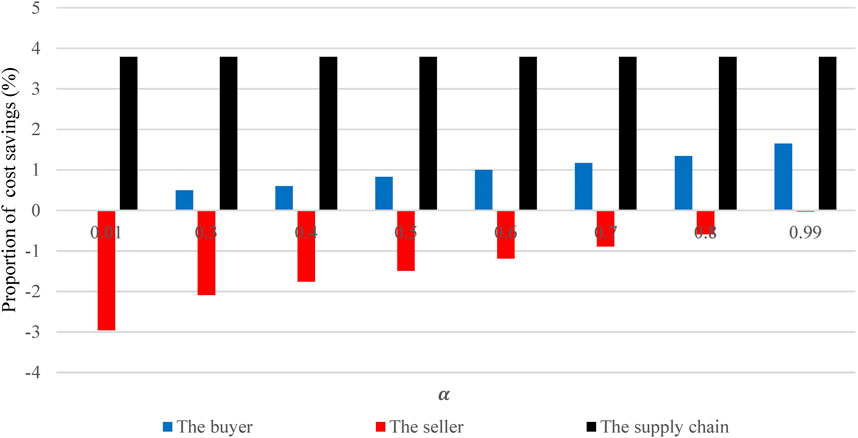
Furthermore, from Table 5, we extract the cost saving ratio of all parties in the supply chain system and plot it in the coordinate system, as shown in Figure 3.

FIGURE 3

FIGURE 3. Cost saving ratio of all parties in the supply chain system.

In Figure 3, the abscissa $\alpha$ represents the proportion obtained by the buyer when allocate the cost saved through coordination between the buyer and the seller; and the vertical coordinate represents the proportion of cost savings (%). The blue bar chart represents the buyer, the red bar chart represents the seller, and the black bar chart represents the overall supply chain. For the seller, a negative cost means that it is his profit.

When the buyer makes an independent decision, the optimal ordering strategy of individual cost is adopted. The ordering quantity is 243, the purchase price is 50, the cost is 160,364, the ordering cost of the seller is −89,673, and the total supply chain cost is 70,690. When the buyer and the seller use privacy-preserving joint-ordering policy protocols, the order quantity is 423, and the buyer gets 40% of the cost saved by the supply chain. The order price is 49.26, the buyer’s cost is 159,292.5, the seller’s cost is −91,282.02, and the total supply chain cost is 68,010.48. Through collaborative ordering, the buyer’s cost, the seller’s cost, and the total supply chain’s cost all decrease.

Figure 3 shows the comparative analysis of the cost savings ratio between buyers and sellers under different profit distribution ratios. As can be seen from Figure 3, the total cost savings are fixed; the larger the $\alpha$ is, the more cost savings in the supply chain will flow to buyers; the smaller the $\alpha$ is, the more the cost savings in the supply chain flow to selling.

6.2 Numerical simulation of joint ordering for privacy protection

Taking the data in Table 2 as an example, the following calculates the privacy-preserving joint-ordering policy protocols.

6.2.1 Steps

Step 1 The buyer uses $B_b,\delta ,G\left(k\right)$ and private information $S_b$ to independently compute private information $S_b^{*}=2D\times \left(S_b+B_b\delta G\left(k\right)\right)$, and $H_b^{*}=h_b$. The seller uses $D$ and private information $S_s$, $h_s$ to independently compute private information $S_s^{*}=2D\times S_s$, $H_s^{*}=h_s$. The buyer holds two values (1772832, 30), and the seller holds two values (5400000, 10).

Step 2 The buyer generates $U_1$ (random number 1024), and the seller generates $U_2$ (random number 2560). The buyer holds two values $\left(S_b^{*}=2D\times \left(S_b+B_b\delta G\left(k\right)\right),H_b^{*}=h_b\right)$, and the seller holds two values $\left(S_s^{*}=2D\times S_s,H_s^{*}=h_s\right)$. The seller uses Secure two-party add-product protocol (Supplementary Appendix S3), and the calculation steps and principles are reported in Supplementary Appendix S3. The buyer obtains $d_1$ (10675782451.2), and the seller obtains $d_2$ (15031647436.8), where

$d_1+d_2=\left(U_1+U_2\right)\left(S_b+B_b\delta G\left(k\right)+S_s\right)\times 2D=2507429888.$

Step 3 The buyer and the seller use secure two-party add-product protocol (Supplementary Appendix S3), and the calculation steps and principles and principles are reported in Supplementary Appendix S3. The buyer obtains $n_1$ (86016), and the seller obtains $n_2$ (57344), where

$n_1+n_2=86016+57344=\left(U_1+U_2\right)\left(h_b+h_s\right)=143360.$

Step 4 The buyer sends $n_1$ to the seller, the seller computes $n=n_1+n_2=143360$, and the seller sends $n$ to the buyer.

Step 5 The buyer and the seller independently compute $s_1=\frac{d_1}{n}=74468.35$, and $s_2=\frac{d_2}{n}=104852.5$, and $s_1$, $s_2$ obey the equation:

$s_1+s_2=\frac{d_1+d_2}{n_1+n_2}=179320.9=\frac{\left(U_1+U_2\right)\left(S_b+B_b\delta G\left(k\right)+S_s\right)\times 2D}{\left(U_1+U_2\right)\left(h_b+h_s\right)}=179320.9$

so, we can obtain $Q^j=\sqrt{179320.9}$.

6.2.2 Analysis

• Information disclosure:

The security in the second and third step is guaranteed by secure two-party add-product protocol (Supplementary Appendix S3). The independent computation in the 5th step is private. Then, the security of computation in the 4th step is discussed.

The buyer and the seller know the Equations 20, 21, for the buyer (the seller), there are 5 unknown reals:$d_2$, $U_2$, $n_2$, $h_s$, $S_s$ ($d_1$, $U_1$, $n_1$, $h_b$, $S_b+B_b\delta G\left(k\right)$. Neither party can know the secret input of another participant.

• Computational complexity:

The protocol used two times secure two-party add-product protocol (Supplementary Appendix S3).

• Communication complexity:

The protocol only requires communication between the buyer and the seller; both sides know the value of $Q^j$.

6.3 Numerical simulation of quantity discount for privacy protection

The following calculates the privacy-preserving quantity discount.

6.3.1 Steps

Step 1 The buyer and the seller use privacy-preserving joint-ordering policy protocols, and the buyer and the seller obtain $Q^j=\sqrt{179320.9}=423$.

Step 2 The buyer and the seller determine the allocation of overall reduced costs, and the seller generates a random number $\alpha =0.4$.

Step 3 The buyer independently computes vector:

$\mathit{X}=\left(w_1^{\mathit{max}},w_1^{\mathit{max}}-w,\frac{1}{Q^{*}},Q^{*},1\right)=\left(49.62,-\mathrm{0.38,0.0041,243,1}\right)$

where $w_1^{\mathit{max}}=w-\left\{\frac{h_b\left(Q^{\prime }-Q^{*}\right)}{2}+\left[S_b+B_b\delta G\left(k\right)\right]\left(\frac{D}{Q^{\prime }}-\frac{D}{Q^{*}}\right)\right\}÷D=49.62$The seller independently computes vector:

$\mathit{Y}=\left(1|,|-|\alpha |,|-|\alpha |\times |S_s|,|-|\alpha |\times |\frac{h_s}{2D}|,|\alpha |\times |\left(\frac{S_s}{Q^{\prime }}+\frac{h_s{Q}^{\prime }}{2D}\right)|=|\left(1,-0.4,-360,-\mathrm{0.00067,1.333}\right)\right)$

where $w_1^{\mathit{min}}=w-\left[S_s\left(\frac{D}{Q^{*}}-\frac{D}{Q^{\prime }}\right)-\frac{h_s\left(Q^{\prime }-Q^{*}\right)}{2}\right]÷D=48.72$

Step 4 The buyer and the seller use secure two-party real product protocol (Supplementary Appendix 2), and the calculation steps and principles are presented in Supplementary Appendix S4, The buyer obtains $u=\mathit{X}\times {\mathit{Y}}^T+v=49.26+10.34=59.60$, and the seller obtains $v\left(10.34\right)$, where the letter T stands for ‘transpose’.

6.3.2 Analysis

• Information disclosure:

Secure two-party real product protocol guarantees security in the first step. The independent computation in the 2nd and 3rd steps is secure. Secure two-party real product protocol (Supplementary Appendix S2) guarantees security in the fourth step.

• Computational complexity:

The protocol uses secure two-party add-product protocol (Supplementary Appendix S3) twice and Secure two-party real product protocol (Supplementary Appendix S2) once.

• Communication complexity:

The protocol requires communication between the retailer and the seller only; both sides of the calculation know the value of $w_1$.

6.4 Global analysis

In brief, there is no information sharing, that is, when the buyer makes independent decisions, he can not get a discount subsidy, and the order cost is very high at this time; under the perfect information sharing, the use of collaborative ordering can reduce various costs; however, due to fear of private information leakage, perfect information sharing cannot be carried out in reality. Collaborative ordering under perfect information sharing through SMC was realized, and all costs of the supply chain system were reduced, which was further verified by the numerical simulation.

7 Conclusion and discussion

In this paper, we assume that the market demand is random, and the seller and the buyer share information and make decisions together like two departments of the same company. We analyze the optimal joint order quantity under probabilistic demand, and design the quantity discount model and profit distribution mechanism. Under a certain quantity discount mechanism and profit distribution strategy, both the seller and the buyer can reduce costs. The quantity discount model and profit distribution mechanism designed require supply chain members to share information. In order to protect the privacy of members and improve the willingness of supply chain members to share information, we designed a privacy protection joint ordering policy protocol and privacy protection quantity discount policy based on SMC technology. Then, the joint ordering strategy, the privacy-preserving joint ordering strategy and the quantity discount protocol are numerically simulated. The numerical simulation results show that the privacy-preserving quantity discount coordination mechanism designed by us can reduce the cost of supply chain members to varying degrees and effectively protect the shared information of supply chain members.

Our research is based on the classic one buyer and one seller supply chain system, and the proposed joint ordering strategy and quantity discount design with privacy protection have a certain practical significance, which is helpful to the research of cost optimization of the system in complex supply chain systems. But there are several limitations. First, the shared information discussed in this paper is all quantitative information. There are still a lot of qualitative information to be shared in supply chain collaborative optimization. Whether supply chain collaborative optimization can make cooperative decisions under the protection of qualitative information deserves further study. Second, enterprises participating in collaborative optimization of supply chain under the protection of private information share their own information, but different private information shared by enterprises will bring different benefits to collaborative optimization. The rational distribution mechanism should be to distribute the value of collaborative optimization reasonably according to private information. Therefore, how to distribute the additional benefits of collaborative optimization reasonably according to the utility of information is the direction that needs further research. Third, there are more buyers or multitier supply chain structures in reality, under these complex circumstances, the joint ordering strategy with privacy protection and quantity discount scheme need to be designed and solved urgently.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

C-HX provided this topic; S-YH wrote and guided the manuscript. S-YH, J-CZ, C-HX, and L-TZ discussed and modified the manuscript. All authors contributed to the manuscript and approved the submitted version.

Funding

This research is supported by the following projects: The Zhejiang Philosophy and Social Sciences Foundation (Grand No. 19NDJC145YB); The Zhejiang Province Soft Science Research Program in China under Grant 2022C25034; The Wenzhou Social Science Association Project (key project): 22WZX01; The Zhejiang First-class Undergraduate Curriculum Project in 2022 (970); The Zhejiang Curriculum Ideological and Political Demonstration Grass-roots Teaching Organization Project in 2022(55); The Doctoral fund project of Changzhou Vocational Institute of Technology under Grant BS202213101007.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1017251/full#supplementary-material

References

1. Jin MZ. Game theoretic analysis for supply chain coordination: Modeling electronic intermediation, coalition formation, and capacity reservation. [dissertation]. Bethlehem: Lehigh University (2001).

Google Scholar

2. Monahan JP. A quantity discount pricing model to increase vendor profits. Manag Sci (1984) 30(6):720–6. doi:10.1287/mnsc.30.6.720

CrossRef Full Text | Google Scholar

3. Li JL, Liu LW. Supply chain coordination with quantity discount policy. Int J Prod Econ (2006) 101(1):89–98. doi:10.1016/j.ijpe.2005.05.008

CrossRef Full Text | Google Scholar

4. Mesmer-Magnus JR, DeChurch LA. Information sharing and team performance: A meta-analysis. J Appl Psychol (2009) 94(2):535–46. doi:10.1037/a0013773

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang LQ, Liu HF, Cai Z. Addressing the consensus on information sharing in CPFR information systems: Insights from manufacturer–retailer dyads. Int J Prod Res (2022) 60(11):3569–88. doi:10.1080/00207543.2021.1926569

CrossRef Full Text | Google Scholar

6. Fu K, Wang C, Xu JY. The impact of trade credit on information sharing in a supply chain. Omega:. Int J Manag Sci (2022) 110:102633. doi:10.1016/j.omega.2022.102633

CrossRef Full Text | Google Scholar

7. Wijewickrama MKCS, Chileshe N, Rameezdeen R, Ochoa JJ. Information sharing in reverse logistics supply chain of demolition waste: A systematic literature review. J Clean Prod (2021) 280:124359. doi:10.1016/j.jclepro.2020.124359

CrossRef Full Text | Google Scholar

8. Lee HL, Whang S. Information sharing in a supply chain. Int J Tech Manag (2000) 1:79–93. doi:10.1504/ijmtm.2000.001329

CrossRef Full Text | Google Scholar

9. Wu JJ, Xu H. Information leakage and financing decisions in a supply chain with corporate social responsibility and supply uncertainty. Sustainability (2021) 13(21):11917. doi:10.3390/su132111917

CrossRef Full Text | Google Scholar

10. Rockwern B, Johnson D, Sulmasy LS. Health information privacy, protection, and use in the expanding digital health ecosystem: A position paper of the American college of physicians. Ann Intern Med (2021) 174(7):994–8. doi:10.7326/m20-7639

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Deb R, Roy S. A software defined network information security risk assessment based on pythagorean fuzzy sets. Expert Syst Appl (2021) 183:115383. doi:10.1016/j.eswa.2021.115383

CrossRef Full Text | Google Scholar

12. He B, Li RD, Wang SS, Liu JG. A social mobilized inspection system against external damage of power grid based on block chain technology. J Phys Conf Ser (2020) 1453:012104. doi:10.1088/1742-6596/1453/1/012104

CrossRef Full Text | Google Scholar

13. Ugochukwu NA, Goyal SB, Arumugam S. Blockchain-based IoT-enabled system for secure and efficient logistics management in the era of IR 4.0. J Nanomater (2022) 2022:1–10. doi:10.1155/2022/7295395

CrossRef Full Text | Google Scholar

14. Yao AC. Protocols for secure computations. In: Proceeding of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982); 1982 November 3-5; Chicago, IL, USA. IEEE (1982). p. 160–4.

CrossRef Full Text | Google Scholar

15. Micali S, Goldreich O, Wigderson A. How to play any mental game. In: Proceedings of the Nineteenth ACM Symp. on Theory of Computing, STOC; May 1987; New York, NY, USA. New York: ACM (1987). p. 218–29.

CrossRef Full Text | Google Scholar

16. Mokhtari H. Economic order quantity for joint complementary and substitutable items. Mathematics Comput Simulation (2018) 154:34–47. doi:10.1016/j.matcom.2018.06.004

CrossRef Full Text | Google Scholar

17. Braglia M, Castellano D, Song D. Distribution-free approach for stochastic Joint-Replenishment Problem with backorders-lost sales mixtures, and controllable major ordering cost and lead times. Comput Operations Res (2017) 79:161–73. doi:10.1016/j.cor.2016.11.002

CrossRef Full Text | Google Scholar

18. Tayebi H, Haji R, Jeddi BG. Joint order (1, T) policy for a two-echelon, single-item, multi-retailer inventory system with Poisson demand. Comput Ind Eng (2018) 119:353–9. doi:10.1016/j.cie.2018.04.009

CrossRef Full Text | Google Scholar

19. Güler K, Körpeoğlu E, Şen A. Design and analysis of mechanisms for decentralized joint replenishment. Eur J Oper Res (2017) 3:992–1002. doi:10.1016/j.ejor.2016.11.029

CrossRef Full Text | Google Scholar

20. Weng ZK. Modeling quantity discounts under general price-sensitive demand functions: Optimal policies and relationships. Eur J Oper Res (1995) 86(2):300–14. doi:10.1016/0377-2217(94)00104-k

CrossRef Full Text | Google Scholar

21. Gao JJ, Wang YJ, Guo YJ, Zhao XD. Pareto optimization problems in supply chain contract under elastic demand. J Syst Manag (2002) 11(1):36–40. doi:10.3969/j.issn.1005-2542.2002.01.008

CrossRef Full Text | Google Scholar

22. Munson CL, Rosenblatt MJ. Coordinating a three-level supply chain with quantity discounts. IIE Trans (2001) 33:371–84. doi:10.1080/07408170108936836

CrossRef Full Text | Google Scholar

23. Li JL, Liu LW. Two mechanisms of supply chain coordination based on price discount under probabilistic demand. Chin J Manag Sci (2005) 13(3):37–43. doi:10.1007/s11769-005-0030-x

CrossRef Full Text | Google Scholar

24. Bayatbabolghani F, Blanton M. Secure multi-party computation. In: Proceedings of the CCS '18: 2018 ACM SIGSAC Conference on Computer and Communications Security; 2018 October 15–19; Toronto, Canada. New York: Association for Computing Machinery (2018). p. 2157–9.

CrossRef Full Text | Google Scholar

25. Balasubramanian K, Rajakani M. Secure multiparty computation. In: Algorithmic strategies for solving complex problems in cryptography. Hershey, Pennsylvania: IGI global (2017). p. 154–66.

Google Scholar

26. Atallah MJ, Elmongui HG, Deshpande V, Schwarz LB. Secure supply-chain protocols. In: Proceedings of the IEEE International Conference on E-Commerce, 2003; 2003 Jun 24-27; Newport Beach, CA, USA. IEEE (2003). p. 293–302.

Google Scholar

27. Clifton C, Iyer A, Cho R, Jiang W, Kantarc LM, Vaidya J. An approach to securely identifying beneficial collaboration in decentralized logistics systems. Manufacturing Serv Operations Manag (2008) 10:108–25. doi:10.1287/msom.1070.0167

CrossRef Full Text | Google Scholar

28. Xie CH, Zhong WJ, Zhang YL. A study of privacy preserving joint-ordering policy. In: Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing; 2008 Oct 12-14; Dalian, China. IEEE (2008). p. 1–4.

CrossRef Full Text | Google Scholar

29. Pibernik R, Zhang Y, Kerschbaum F, Schröpfer A. Secure collaborative supply chain planning and inverse optimization–The JELS model. Eur J Oper Res (2011) 208:75–85. doi:10.1016/j.ejor.2010.08.018

CrossRef Full Text | Google Scholar

30. Yang YH, Wei LJ, Wu J, Long CN. Block-smpc: A blockchain-based secure multi-party computation for privacy-protected data sharing. In: Proceedings of the 2020 The 2nd International Conference on Blockchain Technology; March 12–14, 2020; Shanghai Jiao Tong University, Huazhong University of Science and Technology, China. New York. New York: Association for Computing Machinery (2020). p. 46–51.

Google Scholar

31. Wang N, Chau SC, Zhou Y. Privacy-preserving energy storage sharing with blockchain and secure multi-party computation. ACM SIGENERGY Energ Inform Rev (2021) 1:32–50. doi:10.1145/3508467.3508471

CrossRef Full Text | Google Scholar

32. Long H, Zhang S, Zhang Y, Zhang L, Wang L. A privacy-preserving method based on server-aided reverse oblivious transfer protocol in MCS. IEEE Access (2019) 7:164667–81. doi:10.1109/access.2019.2953221

CrossRef Full Text | Google Scholar

33. Wang X, Kuang X, Li J, Li J, Chen X, Liu Z. Oblivious transfer for privacy-preserving in VANET's feature matching. IEEE Trans Intell transportation Syst (2020) 22(7):4359–66. doi:10.1109/tits.2020.2973738

CrossRef Full Text | Google Scholar

34. Li T, Ren W, Xiang Y, Zheng X, Zhu T, Choo KR, et al. Faps: A fair, autonomous and privacy-preserving scheme for big data exchange based on oblivious transfer, ether cheque and smart contracts. Inf Sci (2021) 544:469–84. doi:10.1016/j.ins.2020.08.116

CrossRef Full Text | Google Scholar

35. Harris FW. How many parts to make at once. Operations Res (1990) 38:947–50. doi:10.1287/opre.38.6.947

CrossRef Full Text | Google Scholar

36. Venegas BB, Ventura JA. A two-stage supply chain coordination mechanism considering price sensitive demand and quantity discounts. Eur J Oper Res (2018) 2:524–33. doi:10.1016/j.ejor.2017.06.030

CrossRef Full Text | Google Scholar

37. Silver EA, Pyke DF, Peterson R. Inventory management and production planning and scheduling. Wiley New York (1998) 3:722–3. doi:10.1016/S0278-6125(99)90116-4

CrossRef Full Text | Google Scholar