Formalism of the NanOx biophysical model for radiotherapy applications

Introduction: NanOx is a theoretical framework developed to predict cell survival to ionizing radiation in the context of radiotherapy. Based on statistical physics, NanOx takes the stochastic nature of radiation at different spatial scales fully into account. It extends concepts from microdosimetry to nanodosimetry, and considers as well the primary oxidative stress. This article presents in detail the general formalism behind NanOx.

Methods: Cell death induction in NanOx is modeled through two types of biological events: the local lethal events, modeled by the inactivation of nanometric sensitive targets, and the global events, represented by the toxic accumulation of oxidative stress and sublethal lesions. The model is structured into general premises and postulates, the theoretical bases compliant with radiation physics and chemistry, and into simplifications and approximations, which are required for its practical implementation.

Results: Calculations performed with NanOx showed that the energy deposited in the penumbra of ion tracks may be neglected for the low-energy ions encountered in some radiotherapy techniques, such as targeted radionuclide therapy. On the other hand, the hydroxyl radical concentration induced by ions was shown to be larger for low-LET ions and to decrease faster with time compared to photons. Starting from the general formalism of the NanOx model, an expression was derived for the cell survival to local lethal events in the track-segment approximation.

Discussion: The NanOx model combines premises of existing biophysical models with fully innovative features to consider the stochastic effects of radiation at all levels in order to estimate cell survival and the relative biological effectiveness of ions. The details about the NanOx model formalism given in this paper allow anyone to implement the model and modify it by introducing different approximations and simplifications to improve it, or even adapt it to other medical applications.

1 Introduction

Innovative radiotherapy techniques such as hadrontherapy, boron neutron capture therapy (BNCT) and targeted radionuclide therapy (TRT) exploit the advantages of ions for an improved irradiation of tumors.

From the radiobiological point of view ions have, due to their track structure, an enhanced efficacy in killing tumor cells, quantified through the relative biological effectiveness (RBE). The RBE associated with a radiation quality is defined as the ratio of the absorbed dose delivered by a reference radiation to the one delivered by a particle or by a given mixed field of different particles resulting in the same biological effect [1,2]. The RBE is a complex function which depends on physical parameters like the dose, the radiation type and energy, and on biological parameters such as the cell line, the cell cycle phase and the cell environment. It is normally assumed to be 1.1 along the whole path for protons [3], while for heavier ions it may be predicted with a biophysical model or via an empirical approach, e.g., from irradiation experiments with different cell lines [4,5].

Biophysical models are important tools often used to evaluate the biological effects of ionizing radiation in radiotherapy. In particular, two different biophysical models are currently implemented in the treatment planning systems (TPS) of hadrontherapy facilities all over the world: the first version of the local effect model (LEM) [6] and the modified microdosimetric kinetic model (mMKM) [7,8].

Improved versions of those models have been developed to solve some of their shortcomings [9–12]. Furthermore, other biophysical models have emerged as well in recent years proposing alternative frameworks to describe the radio-induced biological effects at different scales and using a variable number of free parameters [13–17].

In this context, we developed and published in 2017 [13] the NanOx biophysical model, a theoretical framework which gathered and combined the premises of some of the models proposed in the literature, while considering the stochastic nature of energy deposition down to the nanometric scale. The latter leads to a rigorous framework to describe radiation effects without, for instance, the need of non-Poissonian corrections.

Among the ideas that inspired us from the literature we can mention for instance the concept of local events defined in the three first versions of the LEM [6,9,10]. This notion was reused to describe processes leading to cell death due to energy deposition at the nanometric scale. However, as it was shown that the magnitude of fluctuations of such energy deposition cannot be disregarded [18], the local dose was replaced in NanOx by a stochastic quantity representing the physico-chemical mechanisms. This is in contrast to the latest version of the LEM [11,19], where the biological effect of ions is primarily linked to the initial distribution of DNA double-strand breaks (DSB) induced by radiation rather than the local dose itself. In addition, the LEM IV still applies the radial dose with an amorphous track model to describe the energy depositions by ions, without taking into account the significant stochastic effects in ion tracks. The LEM IV also introduces a second-order of spatiality (micrometer scale) beyond the nanometric scale, showing the relevance of accounting for both in comparison to experiments [20].

Moreover, as explained in [21,22], local lethal events alone do not allow to reproduce the shoulders in cell survival curves. For this reason, we introduced non-local lethal events in the NanOx model. The combination of “local” and “non-local” lethal events was inspired by the incorporation of the “ion-kill” and “γ-kill” components in the model developed by Katz et al. [23,24]. On the whole, NanOx is a framework that allows to predict cell survival to ionizing radiation consistently with the stochastic nature of the latter down to a nanometric scale. Since it takes into account not only the physical processes, but also the chemical ones, its name refers to the concepts of NANodosimetry and OXidative stress. Some predictions of this model for monoenergetic irradiations have already been published [13,25–28] and showed good agreement with experimental data.

While a short description of the NanOx main principles and postulates was given in [13], no exhaustive and complete presentation of the model had been published until now. Moreover, this model was initially developed for hadrontherapy [13,28]. The present paper provides the general theoretical framework so it can be applied to any radiotherapy technique, including BNCT and TRT. It is structured as follows. Section 2 presents the basic concepts and the detailed mathematical formalism behind the NanOx model. In Section 3, we report some relevant results derived from the NanOx model formalism, as well as an example of application for computing the cell survival probability to local lethal events within the range of validity of the track-segment approximation. Section 4 discusses the positioning of NanOx in respect to other biophysical models proposed in the literature. Finally, conclusions are drawn in Section 5.

2 Materials and methods

The formalism behind the NanOx model is detailed in this section. Our discussion follows a top-down approach, i.e., the general premises and main postulates of the model are presented first (Sections 2.1 and Section 2.2); then, the simplifications and approximations necessary for the practical implementation of the model are introduced (Section 2.3). Lastly, a summary of the parameters required for NanOx calculations is provided in Section 2.4.

2.1 General premises of the NanOx model

The main premise of the NanOx model is that cell survival is the result of cell response to two types of biological events that take place in the sequence of an irradiation and occur at different spatial scales: the “local” and “non-local” lethal events.

The NanOx model relies on a completely stochastic theory, according to which cell survival is averaged over all irradiation configurations c_K. Depending on the application field, c_K may account for the set of parameters characterizing the nature of irradiation, such as the type of particles, their initial position, direction and energy. Each configuration consists of a stochastic number K of radiation tracks with a stochastic distribution of energy transfer points and radical species. A radiation track may correspond, for instance, to a track generated by an ion or an electron; to the interactions of photons or neutrons that lead to the ejection of secondary particles (electrons or ions); or to the different particles emitted in a radioactive decay. Radiation tracks are produced by means of Monte Carlo (MC) simulations of particle transport in matter (with a nanometric resolution), including physico-chemical and chemical processes [29].

As Figure 1 shows, the spatial distributions of energy transfer points and of primary radical species constitute the main input for the NanOx model. The spatial distribution of energy transfer points is used to compute the restricted specific energy (see Definition 2, Section 2.2.2) in nanometric targets associated with local lethal events. On the other hand, the distribution of primary radicals is used to model the effects induced by global events (a particular case of non-local lethal events) via the chemical specific energy (see Definition 5, Section 2.3.3.3).

FIGURE 1

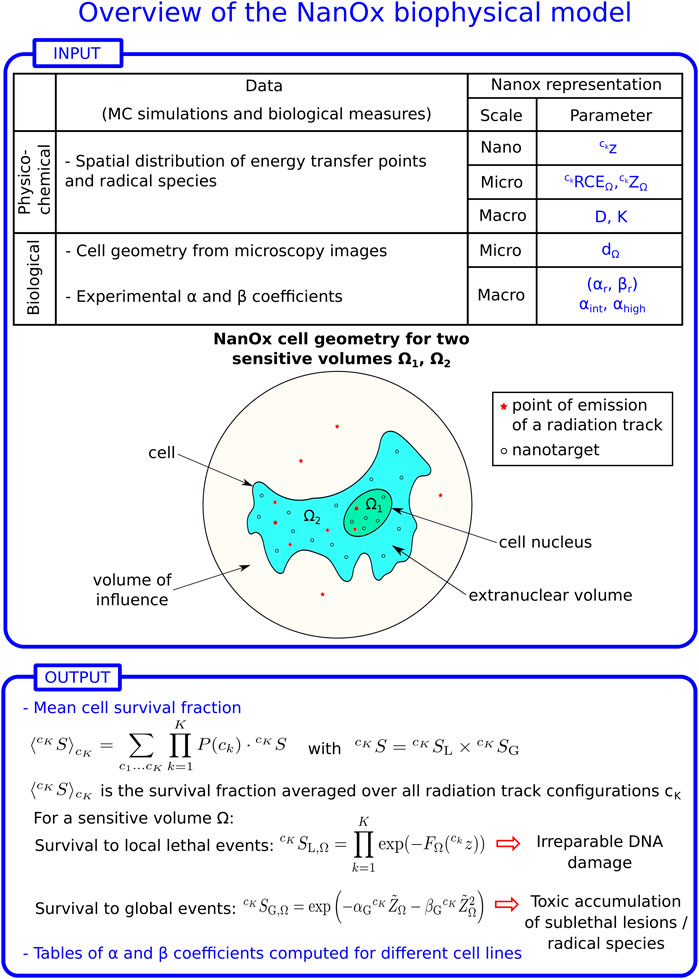
FIGURE 1. Overview of the NanOx biophysical model. z: restricted specific energy distribution in local targets; Z_Ω: restricted specific energy distribution in the sensitive volume Ω; RCE_Ω: relative chemical effectiveness; D: macroscopic dose; K: number of radiation tracks in the volume of influence (see Definition 1). Each radiation track k may correspond to a track generated by an ion or an electron, to the interactions of photons or neutrons that lead to the ejection of secondary particles, or to the particles emitted in a radioactive decay; P (c_k): probability of a radiation configuration c_k; d_Ω: diameter of the sensitive volume Ω; α_r, β_r: linear-quadratic (LQ) coefficients for reference radiation; α_int, α_high: linear coefficient for intermediate- and high-LET radiation, respectively; F_Ω: effective local lethal function for a sensitive volume Ω; ${}^{}\tilde{Z}_{\mathrm{\Omega }}$: chemical specific energy distribution in the sensitive volume Ω; α_G, β_G: LQ coefficients for global events. The illustrative geometry is not to scale.

The procedure required for the calculation of the cell survival fraction, illustrated schematically in Figure 1, may be easily generalized to any mixed field.

2.1.1 Locality and local lethal events

The notion of locality means that we can consider a volume small enough such that the probability that two or more particle tracks deposit a significant specific energy inside that volume is negligible at clinical doses. This is the case of biological targets of the order of tens of nanometers ($<$ 100 nm) [21]. By definition, a local lethal event is able to induce cell death on its own; it is triggered by physical and chemical processes induced at local scale by an irradiation. As an example, a local lethal event may correspond to severe clustered DNA damage which is not managed by the cell, and thus leads to its death. Local lethal events are biologically independent, in other words the probability that a local energy deposition induces cell death is independent of any other energy deposition and biological event. Moreover, it has been demonstrated that these events yield cell survival curves that do not show any shoulder [21]. The local action of radiation is represented in NanOx by the quantity x, determined according to the physical or chemical phenomenon considered for representing an irradiation. For example, it may range from the distributions of ionization cluster size [30] and the descriptors of DNA damage [31], to the thermal spikes generated by high linear energy transfer (LET) ions [32] and the consequent shock waves [33]. While the aforementioned processes may be investigated in the future, in the current version of NanOx x = z, i.e., the restricted specific energy (see Section 2.2.2).

2.1.2 Non-local lethal events

Non-local lethal events constitute, by definition, the complementary class to that of local lethal events. They may be associated with physico-chemical mechanisms occurring at a larger scale than the local ones, but they may also correspond to a distribution of several local events, the single action of which being non-lethal. A common example of non-local lethal events used in microdosimetric models is the interaction between two sublethal cellular lesions separated by distances of the order of the micrometer. The combination of these events, by an effect of accumulation and/or interaction, may result in cell death by triggering apoptosis or via any other cell death pathway. In the current version of NanOx, we introduce “global” events to describe a phenomenon of toxic accumulation. This accumulation may refer to the generation of numerous sublethal lesions which become complex to manage for the cell, or refer to an imbalance between the amount of antioxidant defenses and reactive chemical species. This choice allows us to explore a mechanism that is usually not considered in other biophysical models reported in the literature. Moreover, this choice does not exclude the possibility of exploring other processes in the future, such as the radio-induced damage on cellular targets other than the nucleus (e.g., in the cell membrane or the mitochondria), the communications of type bystander, and the mechanisms underpinning the oxygen effect on tumor resistance to radiotherapy [34].

In a general way, we set X the quantity that represents the action that triggers global events. In this context, the production of primary reactive chemical species seemed to us of particular interest and we decided to take it as a parameter to account for all global events in the current version of NanOx. Indeed, radical species are responsible for causing oxidative stress and inducing a significant part of sublethal damage [35,36].

It should be noted that there is no straightforward correspondence between the direct effects of ionizing radiation and the local lethal events in the NanOx model; similarly, no one-to-one correspondence can be established between the indirect effects of ionizing radiation and the global events as defined in NanOx. As a matter of fact, both local and global events might have contributions of both direct and indirect effects.

2.2 Postulates of the NanOx model

This section requires the introduction of some definitions and notations, which are summarized in Table 1. The NanOx postulates, previously presented in [13], are listed; the equations derived from Postulate 3 are, however, more general here.

TABLE 1

TABLE 1. List of the main notations used in the NanOx model, their name and definition.

With NanOx, we look to perform a simulation close to reality. In that sense, to each cell in a population corresponds a unique radiation track configuration that represents the radiation impacts inside that cell, as well as the impacts taking place outside of it but which are able to induce energy deposition or ionizations in the cell.

Let us consider a large number N of cells irradiated with an absorbed dose D. Experimentally, the average cell survival for a cell population, ⟨S_pop⟩, can be computed as:

$⟨S_{\text{pop}}⟩=\frac{1}{N}\sum _{i=1}^N{S}_i.(1)$

Alternatively, we could consider a representative cell such that:

$\langle S_{\text{pop}}\rangle \approx \langle S_{\text{cell}}{\rangle }_{\text{IR}},(2)$

where the subscript IR denotes the set of N irradiation configurations impacting the N cells in the previous approach (Eq. 1). Ideally, N would be infinite to minimize statistical fluctuations.

The previous considerations lead us to the following simplification.

Simplification 1 (Representative cell associated with a cell population)We consider that the cell survival probability can be computed starting from a representative cell. The latter means that we calculate the average survival of the representative cell over many configurations of radiation tracks.he latter simplification implies that in NanOx we do not consider explicitly the effect of communications between cells. However, such processes are implicitly included in NanOx’s predictions because the model’s parameters are adjusted with experimental data, which clearly include all types of cell communications.

2.2.1 Sensitive volumes and volume of influence

Postulate 1 (Sensitive volumes associated with local and non-local lethal events)The cell survival fraction after an irradiation is characterized by the effect of such an irradiation on several sensitive volumes, some associated with local lethal events and some associated with non-local lethal events.

Definition 1. (Volume of influence)The volume of influence is a volume large enough that the track of a particle outside this volume leads to a negligible transfer of energy into the sensitive volumes associated with local and non-local lethal events.

2.2.2 Restricted specific energy

Microdosimetry introduced the specific energy as the stochastic analogue of the dose; this quantity is in fact defined as the ratio of the energy imparted by one or more events in a site, to the mass of the site. We propose an alternative computation, disregarding the energy that simply causes the heating of the medium (e.g., molecular vibrations, interactions between electrons and water phonons, geminate recombinations).

Definition 2. (Restricted specific energy)The restricted specific energy z defined for a given target corresponds to the specific energy in that target obtained by considering only the energy transfers that may lead to events which are relevant for the biological effects of radiation (e.g., ionizations, excitations and attachments of electrons). For a sufficiently large target:

$⟨z⟩=\eta \cdot D,(3)$

Where η ∼ 80% according to calculations with LQD [29] (see Section 3.1). The considered processes and their energies are listed in Table 2. Let us note that the value of η might depend on the set of interaction cross sections used in the simulations [37] and it is not measurable. On the other hand, the good agreement obtained for radical yields [38–40] and in the prediction of the mean ionization energy (or W-value, an indication of the fraction of energy related to ionization) [41,42] give confidence about the value of η reported here.

TABLE 2

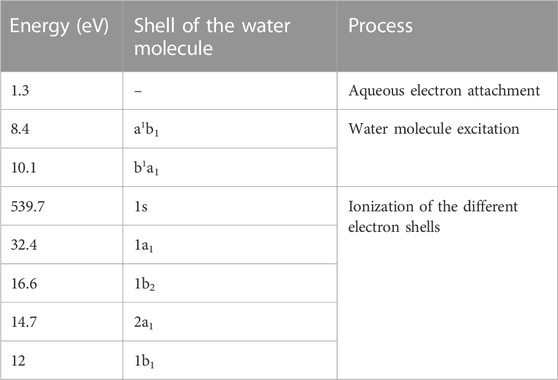
TABLE 2. Energy of the processes considered in the Monte Carlo simulations for NanOx [59].

2.2.3 Cell survival to local and non-local lethal events

Postulate 2 (Independence of local and non-local lethal events)Local and non-local lethal events are independent. Thus, the probability of cell survival to a configuration of radiation tracks c_K (${}^{{\mathrm{c}}_K}S$) is given by the following expression:

${}^{{\mathrm{c}}_K}S_{}={}^{{\mathrm{c}}_K}S_{\mathrm{L}}\times {}^{{\mathrm{c}}_K}S_{\mathrm{N}\mathrm{L}}(4)$

Where ${}^{{\mathrm{c}}_K}S_{\mathrm{L}}$ (resp. ${}^{{\mathrm{c}}_K}S_{\mathrm{N}\mathrm{L}}$) represents the probability of cell survival to local lethal events (non-local lethal events). In Equation 4, K is the number of particle tracks in the volume of influence and c_K denotes their configuration, i.e., their spatial distribution and track description.In order to compare predictions and experimental data often measured after a macroscopic dose D of irradiation, ${}^{{\mathrm{c}}_K}S$ has to be averaged over the whole set of different radiation track configurations that deposit a macroscopic dose D in the volume of influence.

2.2.3.1 Cell survival to local lethal events

The modeling of cell survival probability to local lethal events is based on the single-hit, single-target theory [43]. Therefore cell killing is induced by the inactivation of one single target among N. The size of the latter is small enough (nanometric) to allow classifying this inactivation mechanism as a local lethal event.

Postulate 3 (Definition of the probability of cell survival to local lethal events)The probability of cell survival to local lethal events (${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}$) for a given configuration of N targets (c_N) and K particle tracks (c_K) is equal to the probability that no target is inactivated. The biological response of a target i depends only on the quantity ${}^{{\mathrm{c}}_i,{\mathrm{c}}_K}x_{}$ in that same target i.Since Postulate 3 entails that target responses are independent, ${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}$ is expressed as:

${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}=\prod _{\mathrm{\Omega }}\prod _{{\mathrm{c}}_i\in \mathrm{\Omega }}\left(1-{}^{{\mathrm{c}}_i}f_{}({}^{{\mathrm{c}}_i,{\mathrm{c}}_K}x_{})\right),(5)$

where ${}^{{\mathrm{c}}_i}f_{}({}^{{\mathrm{c}}_i,{\mathrm{c}}_K}x_{})$ is the probability that the target i belonging to the sensitive volume Ω is inactivated following an irradiation by a configuration c_K of tracks that induced the quantity ${}^{{\mathrm{c}}_i,{\mathrm{c}}_K}x_{}$ in the target i. Since c_i ∈ Ω, the response function ${}^{{\mathrm{c}}_i}f_{}$ may be classified by the category Ω, such that ${}^{{\mathrm{c}}_i}f_{}=f_{\mathrm{\Omega }}$. Ω may correspond to the nucleus, the cytoplasm, a lysosome and, in general, any organelle or cell structure of interest. Moreover, the positions of the targets define the sensitive volume Ω, where the total number of targets N is given by:

$N=\sum _{\mathrm{\Omega }}{N}_{\mathrm{\Omega }},(6)$

with N_Ω the number of targets inside the sensitive volume Ω. For example, if the mitochondrion unit was considered as target, then the domain would correspond to the mitochondrial network. Considering that the size of the targets associated with local lethal events is defined so that the probability that two particle tracks deposit energy into the same target is negligible, the following approximation holds:

${}^{{\mathrm{c}}_i,{\mathrm{c}}_K}x_{}\sim {}^{{\mathrm{c}}_i,{\mathrm{c}}_{k_i}}x_{}(7)$

where k_i is the index of the particle track responsible for the physical or chemical quantity associated with the target i. Obviously, if the target i does not suffer any physico-chemical process, ${}^{{\mathrm{c}}_i,{\mathrm{c}}_{k_i}}x_{}=0$. Regrouping the factors by track index in Eq. 5 we obtain:

$\begin{array}{cc}\hfill {}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}& =\prod _{\mathrm{\Omega }}\prod _{{\mathrm{c}}_i\in \mathrm{\Omega }}\left(1-f_{\mathrm{\Omega }}({}^{{\mathrm{c}}_i,{\mathrm{c}}_{k_i}}x_{})\right)\hfill \\ =\prod _{\mathrm{\Omega }}\prod _{k=1}^K\prod _{{\mathrm{c}}_i\in \mathrm{\Omega }}\left(1-f_{\mathrm{\Omega }}({}^{{\mathrm{c}}_i,{\mathrm{c}}_k}x_{})\right);\hfill \end{array}(8)$

As it will be shown in Section 3.2, it is possible to write ${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}$ in terms of the average effective number of local lethal events (ENLLE).

2.2.3.2 Cell survival to non-local lethal events

In the present version of NanOx, we use the class of global events to describe a phenomenon of toxic accumulation, which may encompass the production of sublethal lesions that would saturate at a certain point the repair capacities of the cell, or the oxidative stress induced by reactive chemical species.

Postulate 4 (Non-local lethal events limited to global events)In this version of the NanOx model non-local lethal events are limited to the class of global events, for which a function representing the toxic accumulation of sublethal lesions or oxidative stress induced by reactive chemical species is introduced.

Postulate 5 (Probability of cell survival to global events)The probability of cell survival to global events ${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{G}}$ is a function of the quantity X generated by the configuration of radiation tracks c_K in the sensitive volumes. X may be a matrix of quantities defined at non-local scale, or defined at local scale provided that the function ${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{G}}$ integrates some biological correlations between such local quantities.For example, X may represent a vector describing the formation of local sublethal lesions and ${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{G}}$ could translate the interaction between them. X may also be a matrix describing an oxidative stress in terms of the production of various chemical species in several cellular substructures. Currently, X is the chemical specific energy (see Section 2.3.3.3) associated with OH^•, but ${{\text{O}}_2}^{-•}$ and ${{\text{HO}}_2}^{•}$ could be included as well to take into account the oxygen effect [44].

2.3 Implementation of NanOx

NanOx was defined in the previous sections, however its implementation requires some approximations and simplifications to drastically reduce the amount of computing resources required.

2.3.1 Core and penumbra for ion tracks

For ions we can consider a track segment of length L small enough to consider a straight trajectory over which the energy remains constant. For sufficiently high-energy ions, L may be equal or even larger than the size of the cell. The previous assumption is made basically to exploit the track-segment approximation in hadrontherapy applications. Let us note, however, that this approximation is not always verified, particularly when projectile or target fragmentation occurs. Indeed, it has been shown in the literature that even for proton beams target fragmentation modifies the biological dose calculation, especially in the entrance channel, while minor effects are expected in the Bragg peak region [45]. The impact of fragment species is currently not included in NanOx, but it may be investigated in future versions of the model along with low-energy ion irradiations.

To simplify the implementation of the model and the calculations, we exploited a feature that characterizes ion tracks: the presence of two regions in which the energy deposition patterns are totally distinct. The inner core may be distinguished by a high concentration of energy transfer points around the ion’s path, while the remainder of the track, designated as penumbra, consists of sparser energy depositions issued from fast δ electrons; its extension is delimited by the farthest energy transfer points from the ion trajectory. The two regions may be easily identified in Figure 2, where the spatial pattern of energy depositions in water by a 2.6 MeV proton and a 12 MeV/u carbon ion is depicted.The delimitation of the two track components is not straightforward, since the typical extension of the inner region may vary according to the radiation quality. The interest in treating the track core and penumbra differently is to describe the physical and chemical events that compose the latter region in the same way as those induced by the reference radiation, i.e., photons (corresponding to LET values $<$ 1 keV/μm). In other words, the extension of the track core has to be sufficiently large so that the density of physical and chemical events in the track penumbra is comparable to that of the reference radiation. At the same time, such a discretization should be fine enough in order to minimize any edge effects (as in the case where the track core intercepts the border of the sensitive volumes).Let us consider the path of an ion traversing the volume of influence of a sensitive volume Ω. The energy ${}^{{\mathrm{c}}_k}E_{\mathrm{\Omega }}$ deposited in the sensitive volume is equal to the sum of the contributions from the track core ${}^{{\mathrm{c}}_k}E_{\mathrm{\Omega },\mathrm{c}}$ and the track penumbra ${}^{{\mathrm{c}}_k}E_{\mathrm{\Omega },\mathrm{p}}$:

${}^{{\mathrm{c}}_k}E_{\mathrm{\Omega }}={}^{{\mathrm{c}}_k}E_{\mathrm{\Omega },\mathrm{c}}+{}^{{\mathrm{c}}_k}E_{\mathrm{\Omega },\mathrm{p}},(9)$

Where ${}^{{\mathrm{c}}_k}E_{\mathrm{\Omega },\mathrm{c}}=0$ when the path of the ion is outside the sensitive volume Ω.

FIGURE 2

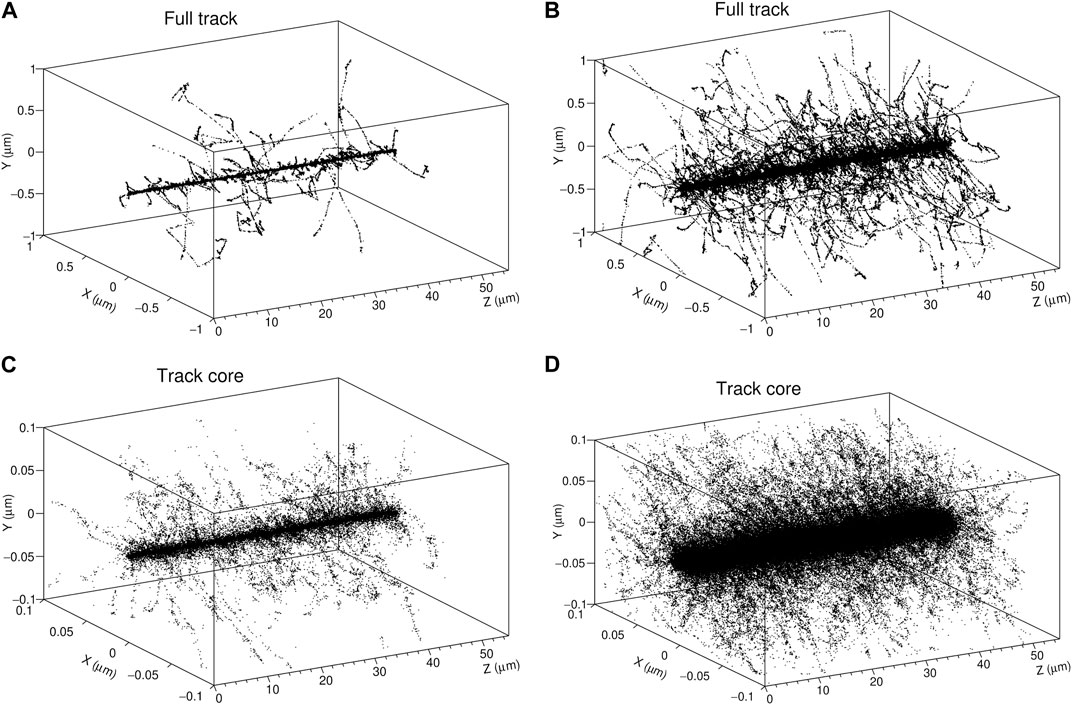
FIGURE 2. 3D plots of the tracks of a 2.6 MeV proton (A) and a 12 MeV/u carbon ion (B) with a LET in water of 13.5 and 151 keV/μm, respectively. Each point corresponds to an energy transfer point simulated with LQD (C, D) correspond to a zoom over the inner region of the tracks (core volume).

It is worth mentioning that for low-energy ions the track-segment approximation becomes more questionable than in hadrontherapy and therefore another strategy has to be developed. For instance, for sufficiently low energies, the penumbra may be neglected (see Section 3.3). This could be applied for instance to TRT with α-particle emitters, BNCT, or neutron irradiations in general. Ongoing work is devoted to extend the model to low-energy ion irradiations, which will allow to take into account as well the impact of fragmentation on NanOx predictions.

2.3.2 Local lethal events

2.3.2.1 Strategy: From nanoscale to microscale

In order to implement the modeling of cell survival to local lethal events, we present several approximations; the purpose is to disregard, when possible, the details at nanoscale in favor of some generalizations and to replace, when justified, some quantities with their mean values.

First, we provide a generic representation of local targets to treat them as N undifferentiated entities and neglect the specific features that each one may present. This will allow to introduce in Section 3.2 an “effective local lethal function” (ELLF), which characterizes the response of each cell line instead of the one of each target [46].

Second, for each radiation quality we establish a link between the effective number of local lethal events (ENLLE, written as n^∗, see Section 3.2) and the restricted specific energy deposited in each sensitive volume Ω by K tracks (Z_Ω). Indeed calculating the number of effective local lethal events for each configuration of targets and radiation tracks would be cumbersome, thus some simplifications are strongly recommended. For this reason, we introduce coefficient α defined generically as follows:

$n^{\ast }=\alpha Z.(10)$

2.3.2.2 Characterization of the local targets

Approximation 1 (Definition of the number N_Ω of local targets in the sensitive volume Ω)The number N_Ω of local targets in the sensitive volume Ω is large enough so that the fluctuations in the ENLLE (Section 3.2) become negligible.

Simplification 2 (Identical local targets in the sensitive volume Ω)All local targets in a sensitive volume Ω have the same geometry and their response is characterized by the same law. We will use in the following the index ${\mathrm{t}}_{N_{\mathrm{\Omega }}}$ to represent the average response of N_Ω targets.

Simplification 3 (Homogeneous distribution of the targets associated with local lethal events)The targets associated with local lethal events are homogeneously distributed inside the sensitives volumes of the cell.

Simplification 4 (Characterization of the targets associated with local lethal events)The local targets are modeled as cylinders with length L_t = 10 nm and diameter d_t = 20 nm, oriented along a single direction. For instance, the direction of an incident photon beam or the ion’s trajectory for track-segment conditions.The size of the local targets is independent of radiation quality and cell line. The chosen dimensions correspond roughly to the extension of a DSB, taking the diffusion of reactive chemical species into account. Indeed, a DSB may extend up to over 20 base pairs or 6 nm [9,21,47], while the reactive species can cause damage up to 4 nm away from the hit site [9,48].

2.3.2.3 Alpha coefficient for reference radiation

Definition 3. (Low-LET as reference radiation)The reference radiation corresponds to low-LET radiation (LET $<$ 1 keV/μm). Since in the case of low-LET radiation the number of tracks K is very high at clinical doses, the ENLLE exhibits only a slight dependency on the configurations c_K, leading to the following approximation.

Approximation 2 (α coefficient for reference radiation)The average ENLLE (see Section 3.2) induced in the sensitive volume Ω by reference radiation at clinical doses is proportional to the restricted specific energy deposited in the sensitive volume Ω:

${}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_K}{n}^{\ast }_{\mathrm{r}}={}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}}}\alpha _{\mathrm{r},\mathrm{L},\mathrm{\Omega }}{}^{{\mathrm{c}}_K}{Z}_{\mathrm{\Omega }}_{}(11)$

where ${}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}}}\alpha _{\mathrm{r},\mathrm{L},\mathrm{\Omega }}$ is the proportionality coefficient for the reference radiation relative to local lethal events, independent of the irradiation configurations. We would like to stress that ${}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}}}\alpha _{\mathrm{r},\mathrm{L},\mathrm{\Omega }}$ is not deduced from the experimental value for photons, but calculated in the same way as for any ionizing radiation.In the case of ions, in turn, the number of local lethal events depends on the track configuration because the interaction with matter is characterized by a high density of ionizations in the region closest to the ion path (core) as opposed to the complementary outer region (penumbra). Such a structure of the ion track implies that the number of local lethal events in a sensitive volume may be substantially different according to whether the core volume is located inside or outside. Moreover one expects ${}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_k}\alpha _{}$ to strongly vary from track to track due to the contribution to ${}^{{\mathrm{t}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_k}{n}^{\ast }_{}$ from the penumbra, since the generation of δ electrons may be a rare event. These issues must be addressed according to the specific domain of application (see [28] explaining the methodology applied for hadrontherapy).

2.3.3 Non-local lethal events

2.3.3.1 Cell survival probability to global events

Simplification 5 (The cell survival to global events has a linear-quadratic (LQ) shape)The probability of cell survival to global events computed over all sensitive volumes is written as:

${}^{{\mathrm{c}}_K}S_{\mathrm{G}}\left({}^{{\mathrm{c}}_K}Y_{}\right)=\prod _{\mathrm{\Omega }}{}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}\left({}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}\right)(12)$

where ${}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}$ and ${}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}$ are the probability of cell survival and the concentration of radical species in the sensitive volume Ω associated with global events, respectively. ${}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}$ is a linear-quadratic function of ${}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}$:

${}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}\left({}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}\right)=\exp \left(-a{}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}-b{{}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}}^2\right),(13)$

with a and b representing cell line-dependent parameters. Indeed, to predict the shoulder seen in cell suvival curves it is necessary to have a quadratic term in the cell survival to global events.

Simplification 6 (Representative chemical species)Primary hydroxyl radicals (OH^•) produced by water radiolysis at a time T_RCE (where the subscript RCE refers to the relative chemical effectiveness defined in Section 2.3.3.3), elapsed after each radiation track, are chosen to represent the reactive chemical species. OH^• radicals are indeed among the most effective reactive chemical species in causing cell damage [49].

2.3.3.2 Strategy: From nanoscale to microscale

${}^{{\mathrm{c}}_K}{Y}_{\mathrm{\Omega }}_{}$ is a microscopic quantity since it corresponds to a concentration inside the sensitive volume Ω, but relies on calculations that have to be performed at nanometric scale to take into account the OH^• radicals production and diffusion along the ion tracks (heterogeneous chemistry). In order to deal with this laborious work, we propose a series of approximations that lead to the introduction of the chemical specific energy ($\tilde{Z}$). In this way, Eq. 13 may be reformulated as:

${}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}\left({}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_{\mathrm{G}}{}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}-{\beta }_{\mathrm{G}}{{}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}}^2\right).(14)$

${\tilde{Z}}_{\mathrm{\Omega }}$ and the LQ coefficients α_G and β_G will be introduced in the next section; as it will be pointed out, the latter are of particular interest since they allow to draw a simple relation with the β coefficient characterizing the survival curves for low-LET radiation types. Further simplifications are required for this development; first, by dealing only with primary radicals and moderate clinical doses, tracks may be considered as independent; second, the separation between core and penumbra and the micrometric size of the sensitive volumes allow to approximate certain quantities by their mean values.

2.3.3.3 Chemical specific energy

Definition 4. (Chemical yield)The chemical yield G is defined as the ratio between the concentration of a given reactive chemical species and the irradiation dose that induces such a concentration. More precisely, G represents the number of reactive chemical species generated per 100 eV.

Definition 5. (Chemical specific energy)The chemical specific energy ${}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}$ in the sensitive volume Ω resulting from an irradiation with a configuration of radiation tracks c_K may be determined as follows:

${}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}={}^{{\mathrm{c}}_K}\mathrm{R}\mathrm{C}\mathrm{E}_{\mathrm{\Omega }}\cdot {}^{{\mathrm{c}}_K}Z_{\mathrm{\Omega }}(15)$

In Eq. 15, ${}^{{\mathrm{c}}_K}Z_{\mathrm{\Omega }}$ is the specific energy deposited in the sensitive volume Ω by K radiation tracks, computed with the LQD MC code; ${}^{{\mathrm{c}}_K}\mathrm{R}\mathrm{C}\mathrm{E}_{\mathrm{\Omega }}$ is the relative chemical effectiveness in the sensitive volume Ω, defined from the chemical yields of the reference radiation, G_r, and that of the considered particle, ${}^{{\mathrm{c}}_K}G_{\mathrm{\Omega }}$:

${}^{{\mathrm{c}}_K}\mathrm{R}\mathrm{C}\mathrm{E}_{\mathrm{\Omega }}=\frac{{}^{{\mathrm{c}}_K}G_{\mathrm{\Omega }}}{G_{\mathrm{r}}}(16)$

and computed with the LQD/PHYCHEML/CHEM MC codes [29].

Property 1. (Tracks of primary reactive chemical species)As the chemical yields are computed for primary reactive chemical species, the tracks may be considered as independent:

${}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}=\sum _{k=1}^K{}^{{\mathrm{c}}_k}\mathrm{R}\mathrm{C}\mathrm{E}_{\mathrm{\Omega }}\cdot {}^{{\mathrm{c}}_k}Z_{\mathrm{\Omega }}(17)$

At this stage, it is possible to express the probability of cell survival to global events (Eq. 13) as a function of the chemical specific energy. The concentration of primary reactive chemical species after a configuration of K radiation tracks may be expressed as:

${}^{{\mathrm{c}}_K}Y_{\mathrm{\Omega }}=\frac{{}^{{\mathrm{c}}_K}G_{\mathrm{\Omega }}}{\eta }\cdot {}^{{\mathrm{c}}_K}Z_{\mathrm{\Omega }}=\frac{G_{\mathrm{r}}}{\eta }\cdot {}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}.(18)$

The factor η, previously presented in Eq. 3, is due to the fact that we chose to discard the fraction of deposited energy leading exclusively to the heating of the medium in our calculations, while the definition of the yield relies on the standard notion of specific energy. By replacing the second term of Eq. 18 in Eq. 13, one obtains:

$\begin{array}{cc}\hfill {}^{{\mathrm{c}}_K}S_{\mathrm{G},\mathrm{\Omega }}\left({}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}\right)& =\exp \left[-a\frac{G_{\mathrm{r}}}{\eta }\cdot {}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}-b{\left(\frac{G_{\mathrm{r}}}{\eta }\cdot {}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}\right)}^2\right]\hfill \\ \hfill & =\exp \left(-{\alpha }_{\mathrm{G}}{}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}-{\beta }_{\mathrm{G}}{{}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}}^2\right),\hfill \end{array}(19)$

where the new coefficients read α_G = a ⋅ G_r/η and ${\beta }_{\mathrm{G}}=b\cdot {(G_{\mathrm{r}}/\eta )}^2$.

2.3.4 Calculation of cell survival for reference radiation

The α_G and β_G coefficients introduced in the previous section are determined by imposing that NanOx predictions reproduce a LQ expression for the survival of reference radiation. The calculation is detailed below. For the sake of simplicity we restrict the following discussion to the case of one sensitive volume, thus the index Ω will be omitted. For an irradiation with dose D, the average probability of cell survival corresponds to:

$S_{\mathrm{r}}(D)=\sum _{K=0}^{\infty }{P}_{\mathrm{r}}(K,D)\cdot S_{\mathrm{r}}(K)(20)$

where P_r(K, D) is the probability that K radiation tracks are located inside the chosen volume of influence for a dose D delivered by the reference radiation and

$S_{\mathrm{r}}(K)=\sum _{{\mathrm{c}}_K}{P}_{\mathrm{r}}({\mathrm{c}}_K)\cdot {}^{{\mathrm{c}}_K}S_{\mathrm{r}}.(21)$

Due to Approximation 2 and to the fact that for reference radiation RCE_r = 1 and thus ${}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{r}}={}^{{\mathrm{c}}_K}Z_{\mathrm{r}}$, the probability of cell survival depends on the configuration of radiation tracks c_K only via ${}^{{\mathrm{c}}_K}Z_{\mathrm{r}}$:

$\begin{array}{cc}\hfill S_{\mathrm{r}}(K)& =\sum _{{\mathrm{c}}_K}{P}_{\mathrm{r}}({\mathrm{c}}_K)\cdot S_{\mathrm{r}}({}^{{\mathrm{c}}_K}Z_{\mathrm{r}})\hfill \\ \hfill & =\sum _{{\mathrm{c}}_K}{\int }_0^{\infty }dZ\left[P_{\mathrm{r}}({\mathrm{c}}_K)\cdot S_{\mathrm{r}}(Z)\cdot \delta (Z-{}^{{\mathrm{c}}_K}Z_{\mathrm{r}})\right],\hfill \end{array}(22)$

where the Dirac delta function allowed for a reformulation of the same mathematical entity. Eq. 20 may, thus, be expressed as follows:

$S_{\mathrm{r}}(D)={\int }_0^{\infty }dZ\left[S_{\mathrm{r}}(Z)\left(\sum _{K=0}^{\infty }{P}_{\mathrm{r}}(K,D)\sum _{{\mathrm{c}}_K}{P}_{\mathrm{r}}({\mathrm{c}}_K)\cdot \delta (Z-{}^{{\mathrm{c}}_K}Z_{\mathrm{r}})\right)\right].(23)$

Finally, by renaming ∂P_D/∂Z the weighting factor which represents the distribution of specific energy in the sensitive volume corresponding to a macroscopic dose D, one obtains:

$S_{\mathrm{r}}(D)={\int }_0^{\infty }dZ\left[S_{\mathrm{r}}(Z)\cdot \frac{\partial P_D}{\partial Z}\right].(24)$

Approximation 3 (The distribution of energy depositions of reference radiation at a microscopic scale is modeled with a Gaussian law)If the dose deposited by reference radiation in the sensitive volume is higher than a few cGy and lower than a few tens of Gy, i.e., belongs to a range in which the linear-quadratic approximation for cell survival is appropriate, ∂P_D/∂Z corresponds to a Gaussian law:

${\left(\frac{\partial P_D}{\partial Z}\right)}_{\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}}=\frac{1}{{\sigma }_Z\sqrt{2\pi }}\exp \left[\frac{-{(Z-⟨Z⟩)}^2}{2{\sigma }_Z^2}\right](25)$

with:

$⟨Z⟩=\eta D.(26)$

We remind that the factor η was mentioned in the description of the restricted specific energy (Definition 2), and its value corresponds almost to 80% (see also Section 3.1).Figure 3 reports, as an example, the specific energy distribution obtained after an irradiation with photons from a ⁶⁰Co source depositing 0.1 Gy in cylinders of 4.89 µm radius and 1 µm thickness. The curve is a Gaussian peaked around 0.08 Gy, corresponding to the irradiation dose rescaled by the factor η.Once analyzed the factor ∂P_D/∂Z, Eq. 24 may be used to derive the coefficients α_G and β_G, which have been introduced for the modeling of global events, and α_rL for the description of local events. The term on the left represents the LQ description of cell survival probability to reference radiation in terms of the macroscopic dose D, by definition:

$S_{\mathrm{r}}(D)=\exp \left(-{\alpha }_{\mathrm{r}}D-{\beta }_{\mathrm{r}}{D}^2\right).(27)$

The term on the right of Eq. 24, on the other hand, corresponds to a convolution between a Gaussian and the NanOx representation of the cell survival probability to reference radiation as a function of the microscopic restricted specific energy. The latter equals:

$S_{\mathrm{r}}(Z)=\exp \left(-{\alpha }_{\mathrm{r}}^{\prime }Z-{\beta }_{\mathrm{r}}^{\prime }{Z}^2\right),(28)$

where ${\alpha }_{\mathrm{r}}^{\prime }$ and ${\beta }_{\mathrm{r}}^{\prime }$ are given by:

$\begin{array}{cc}\hfill {\alpha }_{\mathrm{r}}^{\prime }& ={\alpha }_{\mathrm{r},\mathrm{L}}+{\alpha }_{\mathrm{G}}\hfill \\ \hfill {\beta }_{\mathrm{r}}^{\prime }& ={\beta }_{\mathrm{G}}.\hfill \end{array}(29)$

The integral from 0 to infinity in Eq. 24 may be approximated to the one from −∞ to ∞ provided that D is sufficiently larger than 0 Gy. In this way, knowing the result of the Euler-Poisson integral, the convolution becomes:

$\begin{array}{l}\hfill S_{\mathrm{r}}(D)=\frac{\exp \left(\frac{{\sigma }_Z^2{\alpha }_{\mathrm{r}}^{2\prime }}{2\cdot (1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2)}\right)}{\sqrt{1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2}}\\ \hfill \cdot \exp \left(-\frac{1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2}{\eta }{\alpha }_{\mathrm{r}}⟨Z⟩-\frac{{\beta }_{\mathrm{r}}}{{\eta }^2-2{\beta }_{\mathrm{r}}{\sigma }_Z^2}⟨Z^2⟩\right)\end{array}(30)$

Given that $\frac{\exp \left(\frac{{\sigma }_Z^2{\alpha }_{\mathrm{r}}^{2\prime }}{2\cdot (1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2)}\right)}{\sqrt{1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2}}\sim 1$, Eq. 30 reads:

$S_{\mathrm{r}}(D)\sim \exp \left(-\frac{1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2}{\eta }{\alpha }_{\mathrm{r}}⟨Z⟩-\frac{{\beta }_{\mathrm{r}}}{{\eta }^2-2{\beta }_{\mathrm{r}}{\sigma }_Z^2}⟨Z^2⟩\right).(31)$

In the framework of this approximation, the coefficients of cell survival at a microscopic scale for a low-LET irradiation are finally determined:

$\begin{array}{cc}\hfill {\beta }_{\mathrm{r}}^{\prime }& =\frac{{\beta }_{\mathrm{r}}}{{\eta }^2-2{\beta }_{\mathrm{r}}{\sigma }_Z^2}\hfill \\ \hfill {\alpha }_{\mathrm{r}}^{\prime }& =\frac{1+2{\beta }_{\mathrm{r}}^{\prime }{\sigma }_Z^2}{\eta }{\alpha }_{\mathrm{r}},\hfill \end{array}(32)$

with the previous expressions simplifying to:

$\begin{array}{cc}\hfill {\beta }_{\mathrm{r}}^{\prime }& =\frac{{\beta }_{\mathrm{r}}}{{\eta }^2}\hfill \\ \hfill {\alpha }_{\mathrm{r}}^{\prime }& =\frac{{\alpha }_{\mathrm{r}}}{\eta }\hfill \end{array}(33)$

When σ_Z ≪⟨Z⟩ = ηD.Let’s recall that for our calculations we did not applied such approximations, and we defined the coefficient C_L as:

$C_{\mathrm{L}}=\frac{{\alpha }_{\mathrm{r},\mathrm{L}}}{{\alpha }_{\mathrm{r},\mathrm{L}}+{\alpha }_{\mathrm{G}}}(34)$

to represent the fraction of the linear component of the cell survival probability at a microscopic scale due to local lethal events after reference radiation. C_L is set to 1 in this version of the model, resulting in α_G = 0 Gy⁻¹, which allows for an independent adjustment of the local and the global events. We obtain then:

$\begin{array}{cc}\hfill {\alpha }_{\mathrm{r},\mathrm{L}}& ={\alpha }_{\mathrm{r}}^{\prime }\hfill \\ \hfill {\beta }_{\mathrm{G}}& ={\beta }_{\mathrm{r}}^{\prime }.\hfill \end{array}(35)$

FIGURE 3

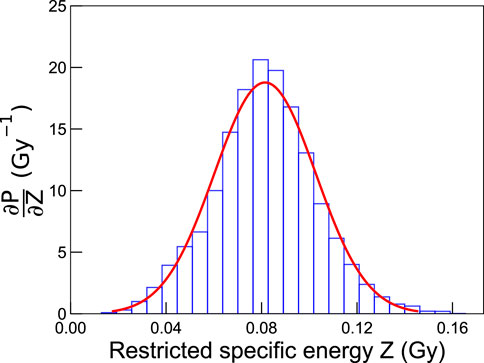
FIGURE 3. Probability distribution of specific energies in cylinders of 4.89 µm radius and 1 µm thickness for an irradiation of 0.1 Gy with photons from a ⁶⁰Co source. The simulations were carried out with LQD, and the bin width was defined as 6 × 10⁻³ Gy.

2.4 Summary of the NanOx model parameters

To conclude the characterization of the model, which proceeded first via the presentation of the main postulates and then with the list of approximations and simplifications currently implemented, it is interesting to consider the parameters required for NanOx calculations. The main input parameters required for NanOx predictions are summarized in Table 3.

TABLE 3

TABLE 3. NanOx model parameters and classes of events with which they are associated.

The modeling of local and non-local lethal events is based on the definition of critical cellular regions called “sensitive volumes”. The latter may correspond for instance to the cell nucleus and to the cytoplasm, if the modeling considers two sensitive volumes. For the sake of simplicity, and to reduce computing time, the sensitive volumes are modeled by default in NanOx simulations as cylinders. However, calculations may be extended to complex and more realistic cell geometries (e.g., obtained from microscopy images, see Figure 1).

The modeling of local lethal events relies on the inactivation of nanometric biological targets designated via their diameter d_t and thickness L_t. A convenient representation of this process is given in terms of an “effective local lethal function” (ELLF), F_Ω, expressing the response of the specific cell line instead of the one of each single local target (see Section 3.2). By initially defining F_Ω as a linear combination of basis functions, it has been shown in [46] that this function presents a threshold and a saturation for the 3 cell lines (V79, CHO-K1 and HSG) considered in that study. In order to reproduce the function’s main features while reducing the number of parameters, an error-like function was then used with the three following parameters: h, the height of the response, z₀, the restricted specific energy threshold and σ, the extent of the increase.

On the other hand, the modeling of global events, a particular case of non-local lethal events, requires the parameters α_G, β_G and T_RCE. Nevertheless, an extensive study of the influence of NanOx parameters [26] demonstrated that the prediction of the biological effect of ions for a wide LET range may be based, when considering a single sensitive volume, on only five parameters characterizing a given cell line (d_Ω, h, z₀, σ, β_G), while the other parameters can be fixed according to specific considerations.

3 Results

3.1 Computation of η

As mentioned in Section 2.2.2, the restricted specific energy z takes into account only the fraction of energy deposits that may contribute to biological damage. Such fraction, denoted as η in our model, is the ratio of the energy deposited in the medium to the total energy lost by radiation. We computed by means of the LQD MC code [29] the value of η for different radiation types and incident energies. The results are presented in Table 4. It can be seen that regardless of the radiation quality, η is approximately equal to 0.8 for all practical purposes.

TABLE 4

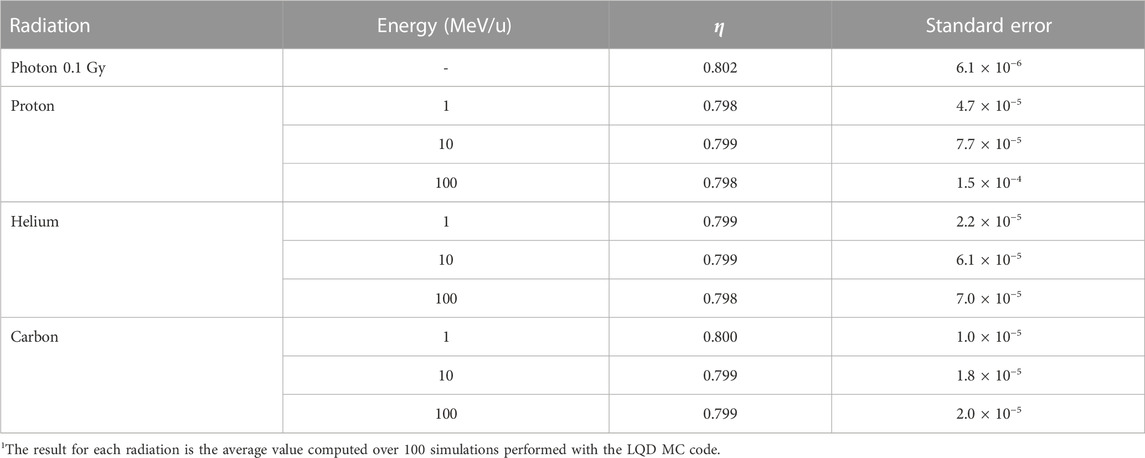
TABLE 4. Values for the factor η, i.e., the ratio of the energy deposited in the medium to the total energy lost by radiation¹.

3.2 Effective number of local lethal events and effective local lethal function

The average number of local lethal events in a local target i belonging to the sensitive volume Ω, determined over the whole set of possible biological responses in the sequence of an irradiation leading to a quantity x_i in the target i, is:

${}^{{\mathrm{c}}_i,{\mathrm{c}}_k}n_{}={}^{{\mathrm{c}}_i}f_{}\left({}^{{\mathrm{c}}_i,{\mathrm{c}}_k}x_{}\right)=f_{\mathrm{\Omega }}\left({}^{{\mathrm{c}}_i,{\mathrm{c}}_k}x_{}\right),(36)$

since c_i ∈ Ω. We introduce here a quantity more convenient for the practical implementation of the model, which we designate as the average (over the whole set of possible biological responses) effective number of local lethal events (ENLLE) in the target i:

${}^{{\mathrm{c}}_i,{\mathrm{c}}_k}{n}^{\ast }_{}=-\ln \left(1-f_{\mathrm{\Omega }}({}^{{\mathrm{c}}_i,{\mathrm{c}}_k}x_{})\right).(37)$

Given that, by definition, local lethal events are mutually independent, the average ENLLE induced by the track k in the sensitive volume Ω with N_Ω targets is:

${}^{{\mathrm{c}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_k}{n}^{\ast }_{}=\sum _{{\mathrm{c}}_i\in \mathrm{\Omega }}{}^{{\mathrm{c}}_i,{\mathrm{c}}_k}{n}^{\ast }_{}.(38)$

Or taking into account the total number of targets N in the sensitive volumes:

${}^{{\mathrm{c}}_N,{\mathrm{c}}_k}{n}^{\ast }_{}=\sum _{\mathrm{\Omega }}{}^{{\mathrm{c}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_k}{n}^{\ast }_{}.(39)$

The cell survival fraction to local lethal events for a configuration of N targets and K particle tracks (Eq. 8) can then be written as:

${}^{{\mathrm{c}}_N,{\mathrm{c}}_K}S_{\mathrm{L}}=\prod _{k=1}^K\exp (-{}^{{\mathrm{c}}_N,{\mathrm{c}}_k}{n}^{\ast }_{})=\exp (-{}^{{\mathrm{c}}_N,{\mathrm{c}}_K}{n}^{\ast }_{}),(40)$

$\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{}^{{\mathrm{c}}_N,{\mathrm{c}}_K}{n}^{\ast }_{}=\sum _{k=1}^K{}^{{\mathrm{c}}_N,{\mathrm{c}}_k}{n}^{\ast }_{.}(41)$

At this stage it is possible to define the effective local lethal function F_Ω(z) (ELLF) for a sensitive volume Ω:

${}^{{\mathrm{c}}_{N_{\mathrm{\Omega }}},{\mathrm{c}}_K}{n}^{\ast }_{}={\int }_0^{+\infty }{\left[\frac{\mathrm{d}P}{\mathrm{d}z}\right]}_{\mathrm{\Omega },{\mathrm{c}}_K}{F}_{\mathrm{\Omega }}(z)\mathrm{d}z,(42)$

with

$F_{\mathrm{\Omega }}(z)=-N_{\mathrm{\Omega }}\ln (1-f_{\mathrm{\Omega }}(z)),(43)$

and

${\left[\frac{\mathrm{d}P}{\mathrm{d}z}\right]}_{\mathrm{\Omega },{\mathrm{c}}_K}=\sum _{{\mathrm{c}}_i\in \mathrm{\Omega }}\delta (z-{}^{{\mathrm{c}}_i,{\mathrm{c}}_K}z_{}).(44)$

${\left[\frac{\mathrm{d}P}{\mathrm{d}z}\right]}_{\mathrm{\Omega },{\mathrm{c}}_K}$ represents the density of probability, for the configuration of radiation tracks c_K, to deposit the restricted specific energy z in a local target i in the sensitive volume Ω.

3.3 Energy deposited in the core and penumbra of ion tracks

Table 5 shows the average ratio of the energy deposited in the penumbra (E_p) to the energy deposited in the core (E_c) of ion tracks for protons, helium and carbon ions with energies in the range from 1 MeV/u to 150 MeV/u. The values were computed with the LQD MC code considering a core volume defined as a parallelepiped with a square cross section of 200 nm edge. It can be seen that the ratio depends essentially on the ion’s energy, but not its type, and that a maximum value is reached for energies between 50 MeV/u and 100 MeV/u. The fact that the maximum value of the ratio does not correspond to the highest ion energy might be due to the enhanced forward emission (i.e., in the direction of the ion’s trajectory) of secondary electrons. The latter would increase the energy deposited in the core, thus explaining the overall decrease in the ratio. Furthermore, the results indicate that the energy deposited in the penumbra represents about 12% of the energy deposited in the core at 3 MeV/u, and only about 6% at 2 MeV/u. Thus, the contribution of the penumbra may be neglected for low-energy ions such as the ones used in BNCT and TRT with α-particle emitters.

TABLE 5

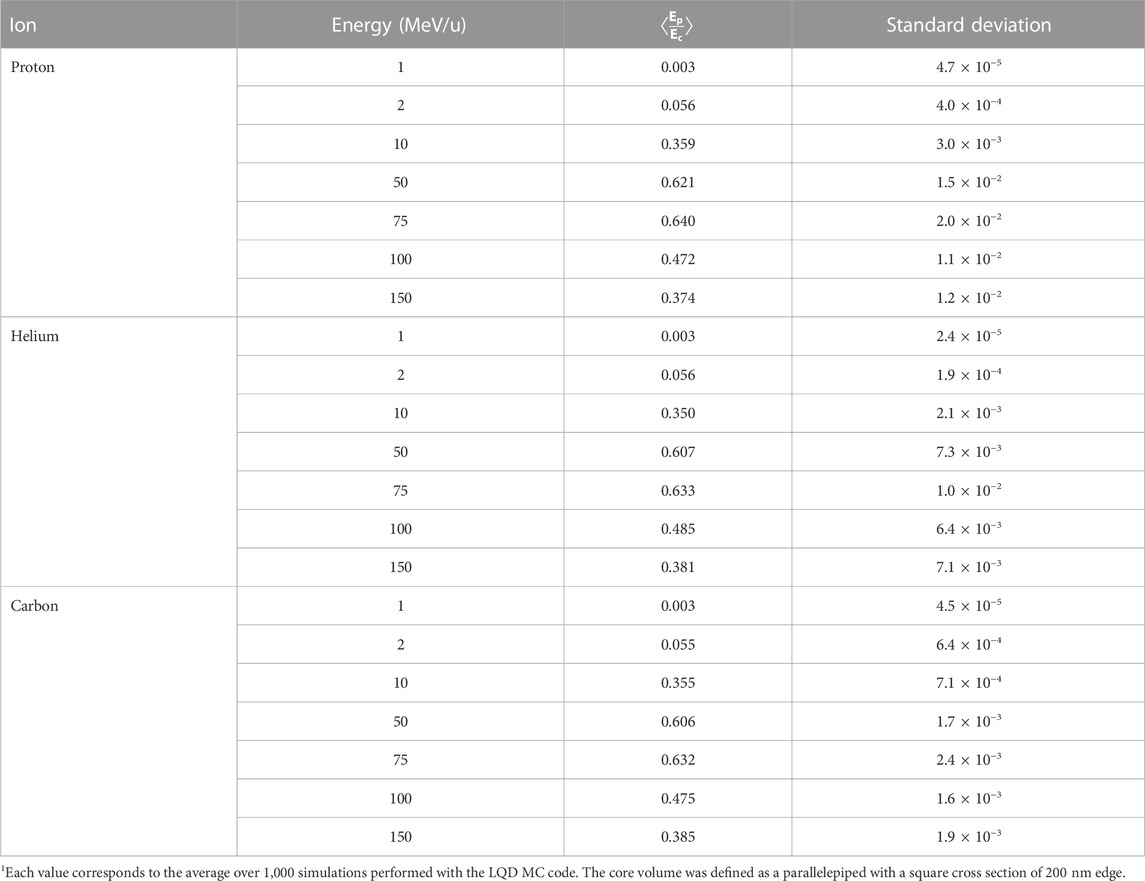
TABLE 5. Average ratio of the energies in the penumbra (E_p) and the core (E_c) for different ions and incident energies¹.

3.4 Relative chemical effectiveness and β coefficient

The production and diffusion of OH^• radicals has been simulated for different radiation types and energy values. The obtained evolution with time of RCE² (since this quantity appears squared in the expression of cell survival to global events, Eq. 19) is plotted in Figure 4. The plots show that the hydroxyl radical concentration induced by ions as a function of time decreases faster than the one obtained in response to photons, an effect due to the different spatial distribution of the reactive chemical species produced in the two cases. When they are located along the ion tracks, indeed, they may easily recombine to give water or other (non-radical) molecules, while when they are sparsely distributed the interactions between them are strongly reduced. Even if the OH^• recombination is a complex phenomenon, the simulations suggest that the value of RCE increases with decreasing LET, as a general trend. Only one exception is noticed in Figure 4 for 70 MeV protons. The general behavior is illustrated as well in Figure 5, where we have plotted the RCE as a function of LET for protons, helium and carbon ions at a time T_RCE = 10^–11 s. Let us remind that T_RCE is the time interval separating the impact of the incident particles and the moment at which the concentration of OH^• radicals is considered. It was shown in a previous work [26] that the influence of T_RCE on NanOx predictions is limited and almost independent of the cell line. In particular, it was observed that changing T_RCE from 10^–11 s to 10^–8 s did not affect the linear coefficient α. This is not surprising, as the term ${\beta }_{\mathrm{G}}{{}^{{\mathrm{c}}_K}\tilde{Z}_{\mathrm{\Omega }}}^2$ has a low impact on α. On the other hand, the dose deposited to achieve 1% of cell survival (D_1%) slightly increased with T_RCE for low-LET ions, while no effect was seen for high-LET ions. Overall, the maximum relative difference in D_1% was ≲ 15%. Therefore, and for practical reasons, T_RCE is fixed to 10^–11 s in all our simulations. The value of 10^–11 s was chosen because it slightly improves the results when we compare the cell survival curves predicted by NanOx with experimental ones. This time corresponds to the primary production of radicals just after the very fast reactions involving the chemical species that are almost in contact [26].

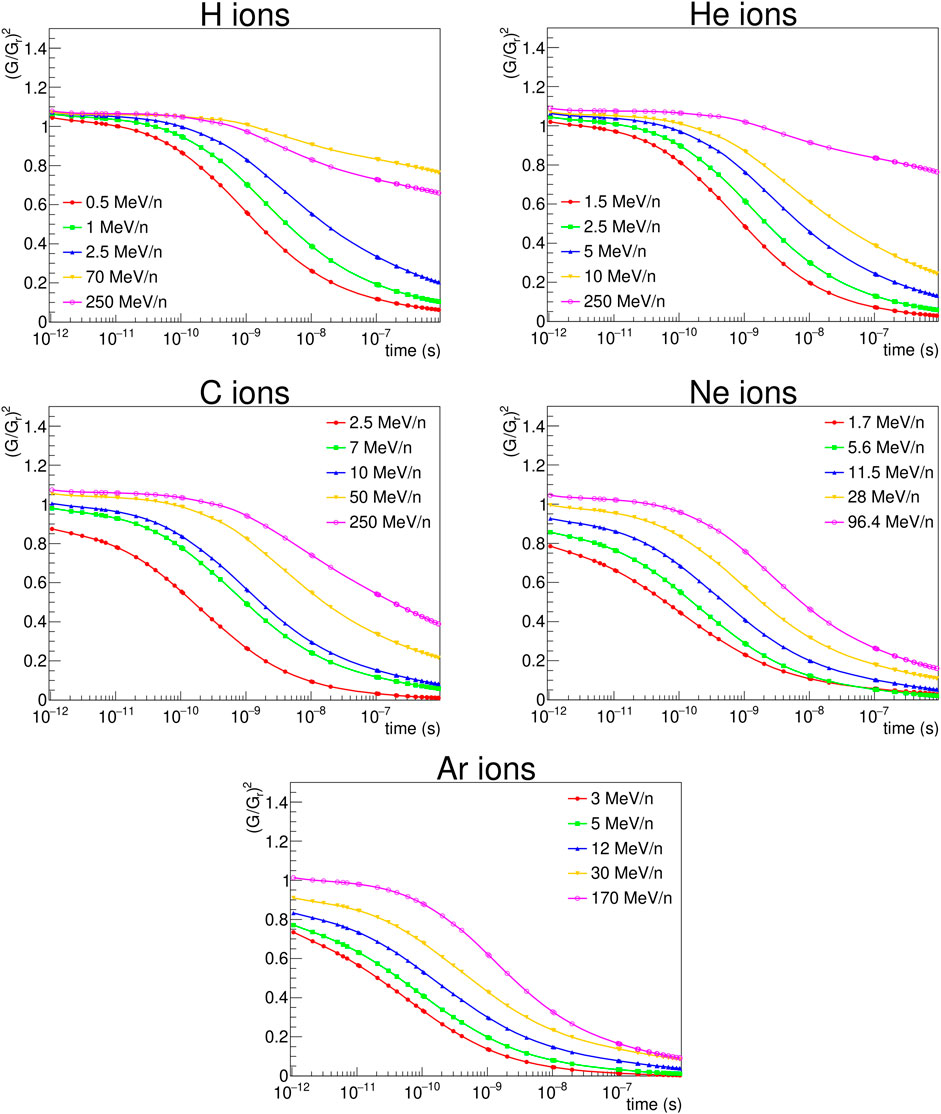
FIGURE 4

FIGURE 4. ${\mathrm{R}\mathrm{C}\mathrm{E}}^2={\left(\frac{G}{G_{\mathrm{r}}}\right)}^2$ as a function of time for hydrogen, helium, carbon, neon and argon ions. G and G_r are, respectively, the chemical yield of the OH^• radical produced by a given radiation and by the reference radiation (here ⁶⁰Co photons). The solid curves that connect the calculated values are for visualization purposes only.

FIGURE 5

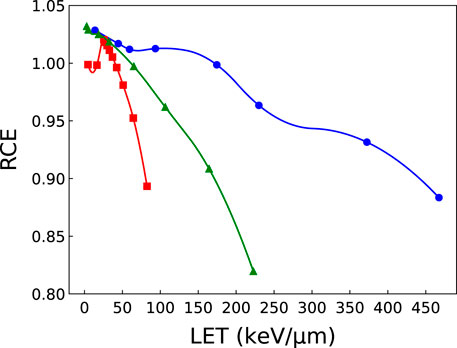
FIGURE 5. RCE as a function of LET for protons (squares), helium (triangles) and carbon (circles) ions computed at a time of 10^–11 s. The solid curves connecting the calculated points are for visualization purposes only. Error bars are not shown given the small value of the standard deviation: σ ≤2×10⁻⁴ for protons and helium ions; σ ≤3×10⁻³ for carbon ions.

It is clear from Figure 5 that while the RCE increases with decreasing LET for all ions, the curves do not exhibit a linear trend. Moreover, the variations in the RCE become more important for low-LET ions.

We have plotted in Figure 6 the ratio β/β_r as a function of RCE² for protons, helium and carbon ions. We remind the reader that β is the macroscopic coefficient of the quadratic term in the LQ model corresponding to ion irradiation, and that β_r is the value for reference photon radiation. The coefficient β was obtained by performing a LQ fit on the cell survival fractions computed with NanOx for the human salivary gland (HSG) cell line (β_r = 0.0615 Gy⁻²), taking the cell nucleus as the sole sensitive volume (cylindrical volume with a radius of 7 µm and thickness of 1 µm). As usual, the RCE was computed considering the chemical yields of OH^• radicals at a time of 10^–11 s for all ions. It can be seen that the ratio β/β_r varies with RCE². Moreover, in the region in which RCE = 1, there is an important variation in β, which indicates that β does not correspond directly to β_G⋅RCE² and that the averaging process over all irradiation configurations plays an important role on the value of β. We obtain different results when we fix RCE = 1 and when we consider the RCE at a time of 10^–11 s. Since the latter condition leads to a better agreement with experimental data when comparing cell survival fractions [28], it seems that taking into account the chemical specific energy improves the modeling of biological effects.

FIGURE 6

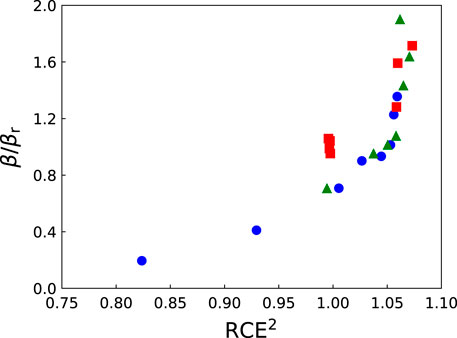
FIGURE 6. The ratio β/β_r as a function of RCE² for protons (squares), helium (triangles) and carbon (circles) ions. The RCE was computed at a time of 10^–11 s for all ions. The coefficient β was obtained by performing a linear-quadratic fit on the cell survival fractions computed with NanOx for the HSG cell line (β_r =0.0615 Gy⁻², cylindrical nucleus with radius of 7 µm and thickness of 1 µm).

3.5 An example of application: Cell survival to local lethal events in the track-segment approximation

In this section we illustrate a simple application example of the NanOx model. Let us consider the irradiation of a single sensitive volume by a monoenergetic, monotype, parallel ion beam. In addition, we will assume that track-segment conditions are fulfilled, that the beam delivers a uniform radiation dose in the surface of influence, and that the particles in the beam are independent. Finally, we will consider that the effect on cell survival of non-local lethal events can be neglected in order to keep only the term ${}^{{\mathrm{c}}_K}S_{\mathrm{L}}$ in Eq. 4. Under these conditions, the cell survival probability as a function of the macroscopic dose D is given by:

$S(D)=\sum _{K=0}^{\infty }P(K,D)\cdot {\langle }^{{\mathrm{c}}_K}{S}_{\mathrm{L}}{\rangle }_{{\mathrm{c}}_K},(45)$

with P(K, D) the probability, modeled with a Poisson distribution, to achieve K impacts in the volume of influence with the dose D; ${⟨{}^{{\mathrm{c}}_K}S_{\mathrm{L}}⟩}_{{\mathrm{c}}_K}$ is the cell survival probability to local lethal events averaged over c_K irradiation configurations. Since the particles are considered as independent, we have from Eq. 40:

$\begin{array}{lll}\hfill {⟨{}^{{\mathrm{c}}_K}S_{\mathrm{L}}⟩}_{{\mathrm{c}}_K}& =\sum _{c_1\dots {\mathrm{c}}_K}\prod _{k=1}^{K}P\left({\mathrm{c}}_k\right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(-\sum _{k=1}^K{}^{{\mathrm{c}}_k}{n}^{\ast }_{}\right)\hfill & \hfill =\prod _{k=1}^K\left[\sum _{{\mathrm{c}}_k}P\left({\mathrm{c}}_k\right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(-{}^{{\mathrm{c}}_K}{n}^{\ast }_{}\right)\right]\end{array}(46)$

By defining the mean cell survival to one impact as:

$S_{1,\mathrm{L}}={\langle }^{{\mathrm{c}}_k}{S}_{\mathrm{L}}{\rangle }_{{\mathrm{c}}_k},(47)$

it follows from Eq. 46 that:

${\langle }^{{\mathrm{c}}_K}{S}_{\mathrm{L}}{\rangle }_{{\mathrm{c}}_K}={\left(S_{1,\mathrm{L}}\right)}^K.(48)$

By substituting the right side of Eq. 48 into Eq. 45 and writing P(K, D) as a Poisson distribution:

$S(D)=\sum _{K=0}^{\infty }\mathrm{e}\mathrm{x}\mathrm{p}(-\lambda )\cdot \frac{{\lambda }^K}{K!}\cdot {\left(S_{1,\mathrm{L}}\right)}^K=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\lambda \left(1-S_{1,\mathrm{L}}\right)\right].(49)$

On the other hand:

$\lambda =\mathcal{F}\cdot \mathrm{\Sigma }=\frac{D\cdot \mathrm{\Sigma }}{a\cdot \mathrm{L}\mathrm{E}\mathrm{T}},(50)$

where $\mathcal{F}$ is the beam fluence in μm⁻², Σ is the surface of influence in μm², D is the dose in Gy, a is a unit conversion factor equal to 0.1602 Gy ⋅keV⁻¹ ⋅μm³, while the LET is in keV/μm. Substituting the right side of Eq. 50 into the one of Eq. 49:

$S(D)=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{\mathrm{\Sigma }}{a\cdot \mathrm{L}\mathrm{E}\mathrm{T}}\left(1-S_{1,\mathrm{L}}\right)\cdot D\right].(51)$

We can observe from Eq. 51 that when only the local lethal events are taken into account, the cell survival probability is given by a pure decreasing exponential, i.e.,:

$S(D)=\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha \cdot D),(52)$

with:

$\alpha =\frac{\mathrm{\Sigma }\left(1-S_{1,\mathrm{L}}\right)}{a\cdot \mathrm{L}\mathrm{E}\mathrm{T}}=\frac{\varsigma }{a\cdot \mathrm{L}\mathrm{E}\mathrm{T}},(53)$

where $\varsigma =\mathrm{\Sigma }\left(1-S_{1,\mathrm{L}}\right)$ is the inactivation cross section. This result can be readily extended to mixed radiation fields, in which case we obtain the equation of Kanai et al. [4].Finally, it is worth showing that the size of the surface of influence has no impact whatsoever on ς or α. To understand this fact, let us consider two surfaces of influence Σ₁ and Σ₂, the latter encompassing the former. The inactivation cross section for Σ₁ is:

${\varsigma }_1={\mathrm{\Sigma }}_1\left(1-S_{1,{\mathrm{\Sigma }}_1}\right).(54)$

Similarly, for Σ₂:

${\varsigma }_2={\mathrm{\Sigma }}_2\left(1-S_{1,{\mathrm{\Sigma }}_2}\right),(55)$

which can be written as well as:

${\varsigma }_2={\mathrm{\Sigma }}_1\left(1-S_{1,{\mathrm{\Sigma }}_1}\right)+\left({\mathrm{\Sigma }}_2-{\mathrm{\Sigma }}_1\right)\left(1-S_{1,{\mathrm{\Sigma }}_2-{\mathrm{\Sigma }}_1}\right).(56)$

However, by Definition 1, the ions cannot deposit energy outside the surface of influence Σ₁, so $S_{1,{\mathrm{\Sigma }}_2-{\mathrm{\Sigma }}_1}=1$ and the second term on the right of Eq. 56 vanishes. Thus:

${\varsigma }_2={\varsigma }_1.(57)$

4 Discussion

The NanOx model was firstly developed for applications in hadrontherapy [13,50,51]. Its development followed a theoretical study which showed that the local effects (at the nanometric scale) were not enough for describing cell survival, and that it was necessary to include non-local effects [21,22].

NanOx combines some premises from other biophysical models proposed in the literature with some fully innovative aspects. The present section details further the positioning of the NanOx model in the context of the state of the art in particle beam radiation biophysical models.

The extension or adaptation of the existing premises is seen in the following features of the model:

• Usage of the concept of specific energy introduced in microdosimetry; however, the use of this specific energy was extended in NanOx to the nanoscale.

• Introduction of the postulate that the cell survival can be modeled with the product of two components, similar to what was done in the model by Katz et al. [23,24]. However, in the latter model the two components refer to the same mechanism (activation of N targets), while in the NanOx model they are related to two different lethal mechanisms.

• NanOx took the notion of local lethal event introduced in the first version of the LEM [6], but without the assumption that the expression relating the cell survival to the number of local lethal events is a Poisson law.

The fully innovative aspects introduced in the NanOx model were:

• The notion of global events that intends to model the lethal effects of the oxidative stress and of the accumulation of sublethal lesions, induced at the scale of the cell sensitive volumes (the NanOx model in the present version does not consider the interaction by pair of sublethal lesions).

• The notion of chemical specific energy, representing the toxic accumulation of oxidative stress, i.e., the imbalance between the production of reactive oxygen species and antioxidant defenses, or sublethal damage at a cellular level. To the best of our knowledge, for the first time chemical yields were used as an input for a RBE model of cell survival.

• The construction of the ELLF related to the inactivation of nanotargets. With no a priori assumptions on this function except for the monotonic increase, its shape was resolved by means of a linear combination of basis functions and a fit of the weight values of this linear combination to get a good agreement with experimental data. The resulting ELLF presented a threshold and a saturation that were discussed in respect to features of other models [46].

Moreover, two important aspects that deserve further discussion are the scales and the level of detail at which biophysical models describe the radiation effects and the way they integrate (or not) non-Poissonian effects. As already mentioned, in the current version of NanOx, the nanometric scale is integrated via the restricted specific energy distributions in 10 nm targets, a size that covers the extension of a DSB, including the diffusion of reactive chemical species. These nanotargets are distributed uniformly in micrometric sensitive volumes (e.g., the cell nucleus or, more generally, any other cell organelle). Moreover, the chemical specific energy is calculated also at the micrometric scale. Therefore, the target geometry covers the microscale and the nanoscale. Besides, stochastic effects inherent to ionizing radiations are fully taken into account. Indeed, each configuration of irradiation is characterized by 1) the distribution of radiation tracks and 2) for each track, by the distribution of energy depositions and radicals with nanoscale resolution.

It is important to point out that the concepts of local lethal and global events in NanOx are intentionally formulated in a sufficiently general way to allow testing distinct mechanisms in the future as the model evolves. For this reason, we do not explicitly deal in NanOx with the different types of DNA damages or their yield.

The question related to using a Poisson or non-Poisson law appears at two levels. At the level of the local events, contrary to the LEM, the NanOx model does not assume a Poisson law. At the level of the radiation track configurations, in the same way as the LEM, the cell survivals are averaged over all the possible values of the number of tracks and their positions. In contrast, the MKM calculates a mean number of lethal events over these irradiation configurations and assumes a Poisson law for calculating the mean cell survival. As this assumption is not valid for high-LET, “non-Poissonian” corrections have been introduced in the extended and derived versions of the model.

It should be noted that the LEM IV [11,19] is very different from the previous versions of the model. The locality is no longer associated to point-like events. The biological effect is determined from the initial spatial distribution of DSB induced by radiation. The calculation of the DSB distribution is based on the local dose (derived from radial dose profiles) deposited in subvolumes of the cell nucleus. MC methods are applied for sampling the DSB location. The LEM IV considers three spatial scales of DNA damage formation assumed to be relevant for cell survival, extending from the nm level to about 10 µm. It does not take into account, however, the degree of complexity of DSB at the nm scale or the formation of chromosome aberrations [20]. The LEM IV assumes a linear-quadratic-linear (LQL) behavior of cell survival, with a threshold dose marking the transition from a LQ to a purely linear behavior.

Similarly to the LEM IV, the MKM [52] divides the sensitive target (cell nucleus) into subunits called domains, having a variety of shapes. Radiation is assumed to create two types of DNA damages: type I lesions are lethal; type II lesions are sublethal, i.e., they can be repaired or converted into lethal lesions (either by spontaneous conversion or binary combination with another sublethal lesion). Cell death occurs if at least one domain contains a lethal lesion. The initial number of lesions in a domain is considered proportional to the specific energy in the domain. Then the evolution of the average number of lesions per domain is computed by solving a set of coupled ordinary differential equations. To connect the number of lesions to the cell survival probability, the original MKM assumed a Poisson distribution of the lethal lesions and a linear-quadratic behavior of cell survival. Later improvements and extensions were made to the MKM, which essentially added ad hoc corrections to account for non-Poissonian effects [7,8,53]. Moreover, other developments have been required to compensate the partial accounting of the stochastic nature of energy deposition in the MKM, which leads to disagreements for high-dose and high-LET irradiations, notably in the prediction of the behavior of the β coefficient [12]. For more details, we refer the reader to the excellent review on the MKM and derived models recently carried out by Bellinzona et al. [54].

The local and global events defined in NanOx are somewhat analogous to the type I and II lesions of the MKM, respectively. However, the notion of global event in NanOx is different at least in two points: 1) it currently does not consider the binary interaction of sublethal lesions, only represents the deleterious effect of their accumulation; 2) NanOx stresses the role of reactive chemical species in radiation damage induction. On the other hand, an interesting aspect of the MKM is the possibility to account for arbitrary dose-rates, something that is currently not considered in the LEM and NanOx.

BIANCA (BIophysical ANalysis of Cell death and chromosome Aberrations) [16,55,56] is a biophysical model allowing to compute cell survival probabilities as well as chromosome aberration dose-response curves for different types of irradiation. The basic idea behind BIANCA is that some radio-induced DNA damages (called cluster lesions) produce two independent chromosome fragments, after which distance-dependent fragment mis-rejoining or un-rejoining give rise to chromosome aberrations. Some of these aberrations (dicentrics, rings and large deletions) lead to cell death. While in the first version of BIANCA the cell survival was computed considering a Poisson distribution of the number of lethal aberrations, the calculation is now performed on a cell-by-cell basis. A cell with at least one lethal aberration is counted as a dead cell, whereas a cell with zero lethal aberrations is counted as a surviving cell. The treatment of lethal aberrations in BIANCA is thus similar to the one of local lethal events in NanOx. Since BIANCA assumes that cell death is only due to chromosome aberrations, it does not consider other origins of cell death. As in NanOx, dose-rate is currently not taken into account in BIANCA.

Finally let us note that similarly to NanOx, other models have been recently proposed to overcome the need of ad hoc non-Poissonian corrections in the MKM and related models. One of them is the generalized stochastic microdosimetric model (GSM2) [14,57], which picks up some of the main assumptions of the MKM to derive a more general and rigorous mathematical formalism. The GSM2 considers both DNA lesion formation and time evolution via a microdosimetric master equation. As other models, it uses microdosimetry spectra (obtained from radiation transport simulations with MC codes such as TOPAS [58]) to include the stochastic nature of energy deposition. Some processes that GSM2 currently does not include are time-delayed repair of DSB and cell apoptosis.

In summary, it is clear that much progress has been achieved in recent years regarding the development of biophysical models able to manage multi-scale approaches and non-Poissonian effects in the description of ionizing radiation effects. We have mentioned here the principles and assumptions on which some of those models are based in order to highlight some similarities and differences with respect to the NanOx model. However, it is out of the scope of this paper to perform a in-depth comparison of NanOx with other models either in terms of predictions or underlying concepts.

Furthermore, it should be mentioned that the implementation in NanOx of radiation stochastic effects at all levels represents a major challenge in terms of computing resources. Relevant approximations were therefore introduced according to the domain of application of the NanOx model. An example of these approximations, quite innovative in RBE modeling, is the separation of the track in core and penumbra, taking advantage of an ion’s track properties for hadrontherapy applications [28]. Finally, very optimized algorithms have been developed in order to make the implementation of the model tractable. They were not mentioned in the paper for the sake of simplicity.

Two aspects that are currently not considered in NanOx are the explicit modeling of radio-induced bystander effects, which are related to the communication between adjacent or nearby cells, and the influence of radiation dose-rate. However, since NanOx predictions are tuned based on experimental data, bystander effects are somehow implicitly included. On the other hand, dose-rate effects may be taken into account in future developments of the model.

5 Conclusion

This work presents a complete description of the formalism of the NanOx model through an exhaustive listing of its main postulates.

The model allows to predict cell survival fractions following irradiations with ions or photons, and consequently to estimate the relative biological effectiveness. NanOx is based on a multiscale description of the interactions between radiation and biological tissues, and accounts for the fluctuations in the energy deposition at several levels: the fluctuations in the number of radiation tracks (or the number of impacts produced by a given macroscopic dose), the stochasticity of the energy pattern along each track, and of the inter-track processes.

The intent of the paper is to stress the fact that the NanOx model offers perspectives of evolution and improvement that are intrinsically related to its formalism. Indeed, by working on NanOx postulates and simplifications, one may explore different scenarios to explain the enhanced radiobiological efficacy of the ions used in innovative radiotherapy techniques such as hadrontherapy, BNCT and TRT with α-particle emitters.

On the other hand, some of the approximations made in the model may be relaxed, and the impact of each one quantitatively evaluated.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MA-A, CM, and MC performed the simulations and wrote the first draft of the paper. MC, ÉT, and MB conceived and developed the NanOx model. ÉT and MB designed and supervised the work and revised the final manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was performed in the framework of the LabEx PRIMES (ANR-11-LABX-0063) of the Université de Lyon, within the program “Investissements d’ Avenir” (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). We acknowledge the financial support of the French National Institute of Health and Medical Research (Inserm), through the grant “Apports à l’oncologie de la physique, de la chimie et des sciences de l’ingénieur,” no. 20CP176-00.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Schardt D, Elsässer T, Schulz-Ertner D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev Mod Phys (2010) 82:383–425. doi:10.1103/RevModPhys.82.383

CrossRef Full Text | Google Scholar

2. Karger CP, Peschke P. RBE and related modeling in carbon-ion therapy. Phys Med Biol (2018) 63:01TR02. doi:10.1088/1361-6560/aa9102

CrossRef Full Text | Google Scholar

3. Paganetti H, Niemierko A, Ancukiewicz M, Gerweck LE, Goitein M, Loeffler JS, et al. Relative biological effectiveness (RBE) values for proton beam therapy. Int J Radiat Oncol Biol Phys (2002) 53:407–21. doi:10.1016/S0360-3016(02)02754-2

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kanai T, Furusawa Y, Fukutsu K, Itsukaichi H, Eguchi-Kasai K, Ohara H. Irradiation of mixed beam and design of spread-out Bragg peak for heavy-ion radiotherapy. Radiat Res (1997) 147:78–85. doi:10.2307/3579446

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Furusawa Y, Fukutsu K, Aoki M, Itsukaichi H, Eguchi-Kasai K, Ohara H, et al. Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated ³He-, ¹²C- and ²⁰Ne-ion beams. Radiat Res (2000) 154:485–96. doi:10.1667/0033-7587(2000)154[0485:IOAAHC]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy. Radiat Environ Biophys (1997) 36:59–66. doi:10.1007/s004110050055

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kase Y, Kanai T, Matsumoto Y, Furusawa Y, Okamoto H, Asaba T, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat Res (2006) 166:629–38. doi:10.1667/RR0536.1

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Inaniwa T, Furukawa T, Kase Y, Matsufuji N, Toshito T, Matsumoto Y, et al. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys Med Biol (2010) 55:6721–37. doi:10.1088/0031-9155/55/22/008

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Elsässer T, Scholz M. Cluster effects within the local effect model. Radiat Res (2007) 167:319–29. doi:10.1667/RR0467.1

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Elsässer T, Krämer M, Scholz M. Accuracy of the Local Effect Model for the prediction of biologic effects of carbon ion beams in vitro and in vivo. Int J Radiat Oncol Biol Phys (2008) 71:866–72. doi:10.1016/j.ijrobp.2008.02.037

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Elsässer T, Weyrather WK, Friedrich T, Durante M, Iancu G, Krämer M, et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: Direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int J Radiat Oncol Biol Phys (2010) 78:1177–83. doi:10.1016/j.ijrobp.2010.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Sato T, Furusawa Y. Cell survival fraction estimation based on the probability densities of domain and cell nucleus specific energies using improved microdosimetric kinetic models. Radiat Res (2012) 178:341–56. doi:10.1667/rr2842.1

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Cunha M, Monini C, Testa E, Beuve M. NanOx: A new model to predict cell survival in the context of particle therapy. Phys Med Biol (2017) 62:1248–68. doi:10.1088/1361-6560/aa54c9

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Cordoni F, Missiaggia M, Attili A, Welford SM, Scifoni E, La Tessa C. Generalized stochastic microdosimetric model: The main formulation. Phys Rev E (2021) 103:012412. doi:10.1103/PhysRevE.103.012412

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kamp F, Carlson D, Wilkens J. Rapid implementation of the repair-misrepair-fixation (RMF) model facilitating online adaption of radiosensitivity parameters in ion therapy. Phys Med Biol (2017) 62:N285–96. doi:10.1088/1361-6560/aa716b

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ballarini F, Carante MP. Chromosome aberrations and cell death by ionizing radiation: Evolution of a biophysical model. Radiat Phys Chem (2016) 128:18–25. doi:10.1016/j.radphyschem.2016.06.009

CrossRef Full Text | Google Scholar

17. Conte V, Selva A, Colautti G, Hilgers G, Rabus H, Bantsar A, et al. Nanodosimetry: Towards a new concept of radiation quality. Radiat Prot Dosim (2018) 180:150–6. doi:10.1093/rpd/ncx175

CrossRef Full Text | Google Scholar

18. Cunha M, Testa E, Komova OV, Nasonova EA, Mel’nikova LA, Shmakova NL, et al. Modeling cell response to low doses of photon irradiation—Part 1: On the origin of fluctuations. Radiat Environ Biophys (2016) 55:19–30. doi:10.1007/s00411-015-0621-6

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Friedrich T, Scholz U, Elsässer T, Durante M, Scholz M. Calculation of the biological effects of ion beams based on the microscopic spatial damage distribution pattern. Int J Radiat Biol (2012) 88:103–7. doi:10.3109/09553002.2011.611213

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Friedrich T, Ilicic K, Greubel C, Girst S, Reindl J, Sammer M, et al. DNA damage interactions on both nanometer and micrometer scale determine overall cellular damage. Sci Rep (2018) 8:16063. doi:10.1038/s41598-018-34323-9

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Beuve M, Colliaux A, Dabli D, Dauvergne D, Gervais B, Montarou G, et al. Statistical effects of dose deposition in track-structure modelling of radiobiology efficiency. Nucl Instrum Methods Phys Res B (2009) 267:983–8. doi:10.1016/j.nimb.2009.02.016

CrossRef Full Text | Google Scholar

22. Beuve M. Formalization and theoretical analysis of the local effect model. Radiat Res (2009) 172:394–402. doi:10.1667/RR1544.1

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Katz R, Sharma SC. Response of cells to fast neutrons, stopped pions, and heavy ion beams. Nucl Instrum Meth (1973) 111:93–116. doi:10.1016/0029-554X(73)90101-8

CrossRef Full Text | Google Scholar

24. Katz R, Zachariah R, Cucinotta FA, Zhang C. Survey of cellular radiosensitivity parameters. Radiat Res (1994) 140:356–65. doi:10.2307/3579113

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Monini C, Testa E, Beuve M. NanOx predictions of cell survival probabilities for three cell lines. Acta Phys Pol B (2017) 48:1653. doi:10.5506/APhysPolB.48.1653

CrossRef Full Text | Google Scholar

26. Monini C, Cunha M, Testa E, Beuve M. Study of the influence of NanOx parameters. Cancers (2018) 10:87. doi:10.3390/cancers10040087

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Monini C, Alphonse G, Rodriguez-Lafrasse C, Testa E, Beuve M. Comparison of biophysical models with experimental data for three cell lines in response to irradiation with monoenergetic ions. Phys Imaging Radiat Oncol (2019) 12:17–21. doi:10.1016/j.phro.2019.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Alcocer-Ávila M, Monini C, Cunha M, Testa E, Beuve M. Cell survival prediction in hadrontherapy with the NanOx biophysical model. Front Phys (2022) 10. doi:10.3389/fphy.2022.1011063

CrossRef Full Text | Google Scholar

29. Gervais B, Beuve M, Olivera G, Galassi M. Numerical simulation of multiple ionization and high LET effects in liquid water radiolysis. Radiat Phys Chem (2006) 75:493–513. doi:10.1016/j.radphyschem.2005.09.015

CrossRef Full Text | Google Scholar

30. Grosswendt B. Recent advances of nanodosimetry. Radiat Prot Dosim (2004) 110:789–99. doi:10.1093/rpd/nch171

CrossRef Full Text | Google Scholar

31. Garty G, Schulte R, Shchemelinin S, Leloup C, Assaf G, Breskin A, et al. A nanodosimetric model of radiation-induced clustered DNA damage yields. Phys Med Biol (2010) 55:761–81. doi:10.1088/0031-9155/55/3/015

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Toulemonde M, Surdutovich E, Solov’yov AV. Temperature and pressure spikes in ion-beam cancer therapy. Phys Rev E (2009) 80:031913. doi:10.1103/PhysRevE.80.031913

CrossRef Full Text | Google Scholar

33. Surdutovich E, Yakubovich AV, Solov’yov AV. Biodamage via shock waves initiated by irradiation with ions. Sci Rep (2013) 3:1289. doi:10.1038/srep01289

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Wozny AS, Gauthier A, Alphonse G, Malésys C, Varoclier V, Beuve M, et al. Involvement of HIF-1α in the detection, signaling, and repair of DNA double-strand breaks after photon and carbon-ion irradiation. Cancers (2021) 13:3833. doi:10.3390/cancers13153833

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ravanat JL, Douki T, Cadet J. Direct and indirect effects of UV radiation on DNA and its components. J Photoch Photobio B (2001) 63:88–102. doi:10.1016/s1011-1344(01)00206-8

CrossRef Full Text | Google Scholar

36. Douki T, Ravanat JL, Pouget JP, Testard I, Cadet J. Minor contribution of direct ionization to DNA base damage induced by heavy ions. Int J Radiat Biol (2006) 82:119–27. doi:10.1080/09553000600573788

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Villagrasa C, Rabus H, Baiocco G, Perrot Y, Parisi A, Struelens L, et al. Intercomparison of micro- and nanodosimetry Monte Carlo simulations: An approach to assess the influence of different cross-sections for low-energy electrons on the dispersion of results. Radiat Meas (2022) 150:106675. doi:10.1016/j.radmeas.2021.106675

CrossRef Full Text | Google Scholar

38. Gervais B, Beuve M, Olivera G, Galassi M, Rivarola R. Production of HO₂ and O₂ by multiple ionization in water radiolysis by swift carbon ions. Chem Phys Lett (2005) 410:330–4. doi:10.1016/j.cplett.2005.05.057

CrossRef Full Text | Google Scholar

39. Colliaux A, Gervais B, Rodriguez-Lafrasse C, Beuve M. Simulation of ion-induced water radiolysis in different conditions of oxygenation. Nucl Instrum Methods Phys Res B (2015) 365:596–605. doi:10.1016/j.nimb.2015.08.057

CrossRef Full Text | Google Scholar

40. Ali Y, Auzel L, Monini C, Kriachok K, Létang JM, Testa E, et al. Monte Carlo simulations of nanodosimetry and radiolytic species production for monoenergetic proton and electron beams: Benchmarking of GEANT4-DNA and LPCHEM codes. Med Phys (2022) 49:3457–69. doi:10.1002/mp.15609

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Tessaro V, Poignant F, Gervais B, Beuve M, Galassi M. Theoretical study of W-values for particle impact on water. Nucl Instrum Methods Phys Res B (2019) 460:259–65. doi:10.1016/j.nimb.2018.11.031

CrossRef Full Text | Google Scholar

42. Tessaro VB, Gervais B, Poignant F, Beuve M, Galassi ME. Monte Carlo transport of swift protons and light ions in water: The influence of excitation cross sections, relativistic effects, and Auger electron emission in w-values. Phys Med (2021) 88:71–85. doi:10.1016/j.ejmp.2021.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Lea DE. Action of radiation on living cells. Cambridge: Cambridge University Press (1946).

Google Scholar

44. Colliaux A, Gervais B, Rodriguez-Lafrasse C, Beuve M. O₂ and glutathione effects on water radiolysis: A simulation study. J Phys Conf Ser (2011) 261:012007. doi:10.1088/1742-6596/261/1/012007

CrossRef Full Text | Google Scholar

45. Bellinzona EV, Grzanka L, Attili A, Tommasino F, Friedrich T, Krämer M, et al. Biological impact of target fragments on proton treatment plans: An analysis based on the current cross-section data and a full mixed field approach. Cancers (2021) 13:4768. doi:10.3390/cancers13194768

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Monini C, Cunha M, Chollier L, Testa E, Beuve M. Determination of the effective local lethal function for the NanOx model. Radiat Res (2020) 193:331. doi:10.1667/RR15463.1

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Schipler A, Iliakis G. DNA double-strand-break complexity levels and their possible contributions to the probability for error-prone processing and repair pathway choice. Nucleic Acids Res (2013) 41:7589–605. doi:10.1093/nar/gkt556

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Nikjoo H, O’Neill P, Goodhead DT, Terrissol M. Computational modelling of low-energy electron-induced DNA damage by early physical and chemical events. Int J Radiat Biol (1997) 71:467–83. doi:10.1080/095530097143798

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Pouget JP, Mather SJ. General aspects of the cellular response to low- and high-LET radiation. Eur J Nucl Med (2001) 28:541–61. doi:10.1007/s002590100484

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Chollier L. Modélisation biophysique de l’interaction des ions à hautes énergies avec de la matière vivante: Application aux traitements de tumeurs par hadronthérapie. Ph.D Thesis. Université Claude Bernard Lyon 1 (2012).

Google Scholar

51. Beuve M, Testa E, Dos Santos Cunha M. Procédé d’estimation automatique d’un taux de survie d’une lignée cellulaire irradiée par une dose d d’un rayonnement ionisant (2015). p. FR1554411.

Google Scholar

52. Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res (1994) 140:366–74. doi:10.2307/3579114

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET. Radiat Res (2003) 160:61–9. doi:10.1667/RR3010

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Bellinzona VE, Cordoni F, Missiaggia M, Tommasino F, Scifoni E, La Tessa C, et al. Linking microdosimetric measurements to biological effectiveness in ion beam therapy: A review of theoretical aspects of MKM and other models. Front Phys (2021) 8:578492. doi:10.3389/fphy.2020.578492

CrossRef Full Text | Google Scholar

55. Carante MP, Aimè C, Cajiao JJT, Ballarini F. BIANCA, a biophysical model of cell survival and chromosome damage by protons, C-ions and He-ions at energies and doses used in hadrontherapy. Phys Med Biol (2018) 63:075007. doi:10.1088/1361-6560/aab45f

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Carante MP, Embriaco A, Aricò G, Ferrari A, Mairani A, Mein S, et al. Biological effectiveness of He-3 and He-4 ion beams for cancer hadrontherapy: A study based on the BIANCA biophysical model. Phys Med Biol (2021) 66:195009. doi:10.1088/1361-6560/ac25d4

CrossRef Full Text | Google Scholar

57. Cordoni FG, Missiaggia M, Scifoni E, Tessa CL. Cell survival computation via the generalized stochastic microdosimetric model (GSM2); Part I: The theoretical framework. Radiat Res (2022) 197:218–32. doi:10.1667/RADE-21-00098.1

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Zhu H, Chen Y, Sung W, McNamara AL, Tran LT, Burigo LN, et al. The microdosimetric extension in TOPAS: Development and comparison with published data. Phys Med Biol (2019) 64:145004. doi:10.1088/1361-6560/ab23a3

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Cunha M, Testa E, Beuve M, Balosso J, Chaikh A. Considerations on the miniaturization of detectors for in vivo dosimetry in radiotherapy: A Monte Carlo study. Nucl Instrum Methods Phys Res B (2017) 399:20–7. doi:10.1016/j.nimb.2017.03.078

CrossRef Full Text | Google Scholar