ResAttn-recon: Residual self-attention based cortical surface reconstruction

Introduction: The accurate cerebral cortex surface reconstruction is crucial for the study of neurodegenerative diseases. Existing voxelwise segmentation-based approaches like FreeSurfer and FastSurfer are limited by the partial volume effect, meaning that reconstruction details highly rely on the resolution of the input volume. In the computer version area, the signed distance function has become an efficient method for 3D shape representation, the inherent continuous nature makes it easy to capture the fine details of the target object at an arbitrary resolution. Additionally, as one of the most valuable breakthroughs in deep learning research, attention is a powerful mechanism developed to enhance the performance of the encoder-decoder architecture.

Methods: To further improve the reconstruction accuracy of the cortical surface, we proposed ResAttn-Recon, a residual self-attention based encoder-decoder framework. In this framework, we also developed a lightweight decoder network with skip connections. Furthermore, a truncated and weighted L1 loss function are proposed to accelerate network convergence, compared to simply applying the L1 loss function.

Results: The intersection over union curve in the training process achieved a steeper slope and a higher peak (0.948 vs. 0.920) with a truncated L1 loss. Thus, the average symmetric surface distance (AD) for the inner and outer surfaces is 0.253 ± 0.051 and the average Hausdorff distance (HD) is 0.629 ± 0.186, which is lower than that of DeepCSR, whose absolute distance equals 0.283 ± 0.059 and Hausdorff distance equals 0.746 ± 0.245.

Discussion: In conclusion, the proposed residual self-attention-based framework can be a promising approach for improving the cortical surface reconstruction performance.

1 Introduction

In neural image processing, the brain cortical surface reconstruction plays an essential role in the study of neurodegenerative diseases [1] and psychological disorders [2]. Specifically, the cortical surface reconstruction aims to extract two surface meshes from brain magnetic resonance imaging (MRI). The inner white matter surface separates the white matter and the gray matter tissues, and the outer pial surface separates the gray matter tissue and the cerebrospinal fluid [3]. Considering the highly curved and folded intrinsic folding pattern of the cortical surface [4], it is challenging to extract anatomically plausible and topologically correct cortical surfaces in practice.

To address this, traditional approaches use a series of lengthy and computationally intensive processing algorithms, with manual intervention for hyperparameter fine-turning [5–11]. For instance, the widely used and reliable [9] toolkit usually takes hours to process a MRI volume data. In recent years, several deep learning approaches have emerged to overcome this shortage, and according to the data format being processed, these approaches can be categorized as voxel-based, mesh-based, and implicit surface representation-based. Voxel-based approaches first obtain the brain white matter tissue segmentation based on 3D-CNN [12] or 3D-Unet-like [13] architecture. Then the triangular mesh of the inner surface is extracted by applying mesh tessellation to the segmentation masks, with surface mesh smoothing and topology correction [14]. The outer pial surface mesh can then be derived from inflating the white matter surface mesh [15]. Leonie et al. [15] proposed FastSurfer to accelerate the FreeSurfer pipeline by replacing the traditional white matter segmentation algorithm with a 3D-CNN network. [16] proposed the SegRecon framework for cortical surface reconstruction and segmentation. Due to the partial volume effect (PVE) [17], voxel-based approaches have inherent limitations in capturing fine details at high resolution. Mesh-based approaches are mainly implemented by deforming the initial surface mesh to the target surface mesh, with a geometric deep-learning model. For instance, [18] proposed PialNN to reconstruct the pial surface from the white matter surface handled by the FreeSurfer pipeline. [19] proposed Voxel2Mesh to deform predefined sphere template meshes to cortical surfaces. [20] Proposed Vox2Cortex that leverages convolutional and graph convolutional neural networks to deform the template mesh to densely folded target cortical surface. Despite fast processing, theoretical guarantees are to be further developed to prevent self-intersections of the surface mesh. Implicit surface representation-based methods reformulate cortical surface reconstruction as the prediction of the implicit surface representation [21]. Typically, [3] proposed the DeepCSR network to learn an implicit surface function in a continuous coordinate system, with topology correction algorithm to ensure the geometric accuracy of the target surface.

Given brain MRI volume, existing deep learning approaches spend less time reconstructing cortical surface compared to traditional pipeline, with high reliability. Most of these approaches require voxelwise or vertexwise features extracted from the input MRI volume, however, none of them considered the long range feature dependencies, which plays an important role in model performance improvement. For instance, DeepCSR [3] directly concatenates the local and global features from the encoder feature maps, combined with the location coordinates of the query point as the input of the decoder network, PialNN [18] combined the norm and the location coordinate of the initial mesh vertex with the volumetric features extracted from local convolution, to predict the deformation displacement in the inflating process. Both approaches ignored the relationship between query points or mesh vertices. In this work, to efficiently model the long range feature dependencies in cortical surface reconstruction, the concept of the self-attention mechanism is introduced from neural language processing [22–24] and computer version [25–27] area. For pioneer works that apply self-attention to vision tasks [28], proposed Vision Transformer (ViT) for image recognition [29], proposed Tokens-To-Token Vision Transformer (T2T-ViT) to improve classification accuracy [30], proposed Swin Transformer, a general framework for image classification and segmentation, all the above works are discussed around 2D images. In this work, firstly, the input MRI volume is registered to a standard brain space, such as MNI105. Secondly, after the 3D Convolution block, the residual connected multi-head self-attention block and global flatten block, multi-scale feature maps and global feature vector are prepared to obtain volumetric features of sampling points at any given resolution. Then combined with location coordinates in standard space, the signed distance values of sampling points toward four cortical surfaces are predicted, Thirdly, after topology correction and iso-surface extraction operation, the inner and outer surface of the left and right hemispheres are reconstructed in parallel.

In this paper, we proposed ResAttn-Recon, a novel implicit surface representation approach based framework for inner and outer cortical surface reconstruction. In this work, we propose employing the concept of the self-attention mechanism and residual connection trick to the 3D convolutional neural network (3D CNN) encoder, 1 × 1 convolution is embedded into a multi-head self-attention block to fit the 3D feature map input. The proposed framework is able to reconstruct the cortical surface at an arbitrary resolution and benefit from the theoretical support of the implicit surface representation approach. The experimental performance has been substantially improved compared to the DeepCSR and the simple encoder-decoder framework without the attention block. The main contributions of this paper are as follows.

1) To the best of our knowledge, this is the first exploration in employing the residual self-attention mechanism in 3D cortical surface reconstruction.

2) A Commit2 from Review4 with skip connections is developed as an improvement over the DeepCSR decoder network, to simplify the network structure without losing performance.

3) The prior constraints are imposed on the network training with the proposed truncated L1 loss and Gaussian decay weighted L1 loss, as a new strategy for model performance improvement.

The rest of this paper is organized as follows. Section 2 introduces the basic theories and the proposed framework, as well as the dataset enrolled in this work, In Section 3, the details of the experimental evaluation and analysis are given. Section 4 and Section 5 provide a discussion and conclude this paper.

2 Materials and methods

In this section, we introduced ResAttn-Recon, a residual self-attention-based cortical surface reconstruction network. Simultaneously, the lightweight decoder networks and the loss function with prior constrains are also explored to improve the reconstruction performance. As shown in Figure 1, the proposed framework consists of four main parts: 1) data preprocessing, including data acquisition from FreeSurfer toolkit and MRI volume registration; 2) feature extraction; 3) implicit surface representation performed with the proposed ResAttn-Recon network; and 4) post-processing to extract the target inner and outer cortical surfaces from the predicted signed distance function representation. The residual self-attention block is embedded in the encoder network following the intermediate feature map.

FIGURE 1

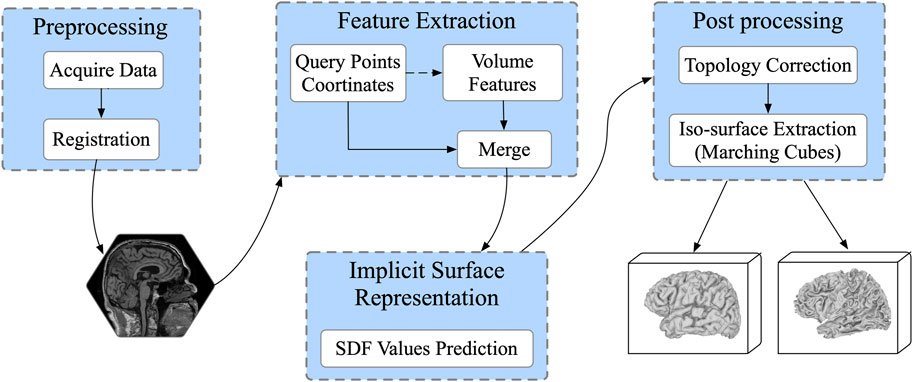
FIGURE 1. The workflow for cortical surface reconstruction. Input the 3D MRI volume, given enough sampling points, it predicts 4 mesh surfaces of arbitrary resolution in parallel.

2.1 Data acquisition

In this paper, we used the publicly available dataset from Alzheimer’s Disease Neuroimaging Initiative (ADNI) [31], MRI scans of 560 T1 original images are enrolled in this work, 470 images for training, 30 images for validation and the remaining 60 images for testing. Ground-truth of inner and outer surfaces from the left and right hemispheres are extracted by the FreeSurfer pipeline. Images are normalized to the size of 182 × 218 × 182, with voxel spacing to [1, 1, 1]. To unify the coordinate systems of the input MRI scans, affine registration is first performed to the MNI105 brain template [32].

2.2 Surface representation

The signed distance function (SDF) is a continuous function to represent the surface distribution, and has been widely employed in 3D shape representation.

The SDF function can be defined as follows:

$\begin{array}{c}SD{F}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}\left({\mathit{x}}_{\mathit{i}}\right)=s_i,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\mathit{x}}_{\mathit{i}}\in {\mathcal{R}}^3,s_i\in \mathcal{R}\end{array}(1)$

Here, $x_i$ stands for any point in Euclidean space represented by its 3D location coordinate, and $s_i$ is the shortest Euclidean distance from the point $x_i$ to the surface, with a positive sign if the point is inside the watertight surface or negative sign if the point is outside the surface.

With the SDF values of given spatial points, the target surface can be expressed as a set consisting of all points satisfying the following:

$\begin{array}{c}SD{F}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}\left(\cdot \right)=0\end{array}(2)$

Then, after Gaussian smoothing and topology correction processing, the target surface is extracted with a zero iso-surface extraction algorithm, such as marching cubes [33].

In this work, the continuous SDF in Ω space is approximated by the deep learning model. Given query point, the well-trained network predicts its SDF value to the target surface directly. This provides theoretical support for reconstructing surfaces of arbitrary resolutions. In detail, the approximator is implemented by a decoder network parameterized by θ, which is further described below.

2.3 ResAttn-recon framework

2.3.1 Feature extraction encoder module

The network architecture is illustrated in Figure 2, and the raw brain MRI need to be firstly registered to MNI105 space before being sent to the network. The feature extraction encoder module consists of three subblocks, the 3D Convolution (Conv3D) block, the Residual Self-Attention block, and the Global Flatten block. The Conv3D block consists of five Conv3D layers, each of which is followed by a Rectified Linear Units (ReLU) activation, with the 3D max pooling operation before the fourth convolution. The number of convolution output channels is sequentially increased to $2^3$; $2^4$; $2^5$; $2^6$; $2^7$ after each convolution. The convolutional kernel is set to $3\times 3\times 3$, with the stride equal to two and padding equal to one. The fourth output feature map is then input into the residual self-attention block, followed by the global flatten block to generate the global feature map. The image features represented by the encoder intermediate feature maps and outputs are firstly extracted by the proposed feature extraction encoder module from the registered MRI, then we construct a bounding box grid with evenly spaced points at a predefined desired resolution (e.g;, $512\times 512\times 512$), which is capable of covering the registered brain MRI in MNI105 standard registration space. After that, the relative position coordinates of the predefined sampling points in MNI105 space as mentioned above are projected to the multiscale feature maps generated by the Conv3D block and the residual self-attention block. The interpolated values obtained from the projected locations and the global feature vector after the Global Flatten block are concatenated as the feature vector of the sampling point.

FIGURE 2

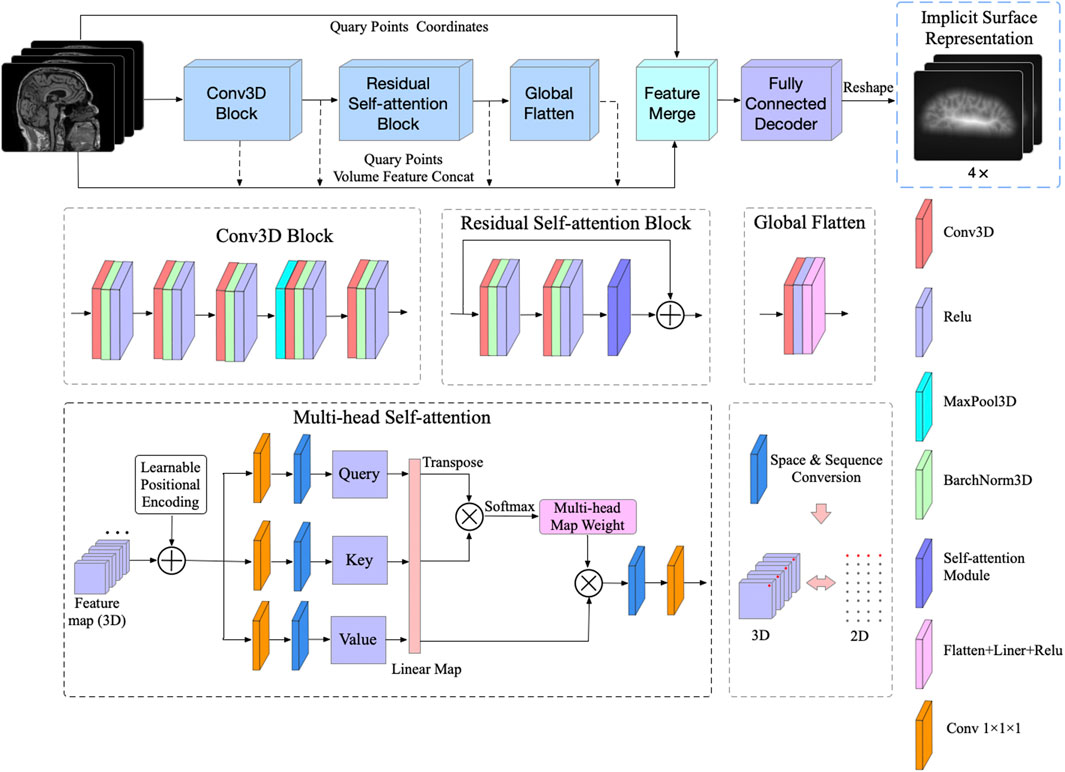
FIGURE 2. The proposed ResAttn-recon architecture for cortical surface reconstruction. The concept of the multi-head self-attention mechanism was introduced to our residual self-attention block.

2.3.2 Residual self-attention mechanism

To better aggregate the feature representation of the sampled points, the widely used self attention mechanism is introduced to our proposed encoder-decoder network architecture, where the detail operation can be described as follows:

$\begin{array}{c}\widehat{X}=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{\theta \left(X\right)\varphi \left(X\right)}{\sqrt{d_{feat}}}\right)\phi \left(X\right)\end{array}(3)$

Where $X\in N\times L$ stands for the local and global feature representation extracted from encoder feature maps, $N$ is the number of sampled points, and $L$ is the dimension of the corresponding feature vector. After the $1\times 1$ convolution and reshape operation, linear transformation of $\theta \left(\cdot \right)$, $\varphi \left(\cdot \right)$ and $\phi \left(\cdot \right)$ are implemented by three single-layer perceptrons (Linear map) in this work. The point-to-point affinity is calculated by the inner product of $\theta \left(X\right)$ and $\phi \left(X\right)$.

In this work, the multi-head self-attention mechanism [22] is applied to improve the expression ability of the attention module. For this 3D reconstruction work, as illustrated in Figure 2, the residual connection in the Residual Self-attention Block indicates that this block does not change the dimension of the input feature map, which equals $\left(batch\_size\times num\_channels\times d\times w\times h\right)$ for single image. From another point of view, the input feature map can be considered as a token array (with the shape of $\left(d\times w\times h\right)$), each token corresponds to a 128-dimensional feature embedding vector alone the channel direction (number of channels equals 128 in this case). Therefore, the input feature map of the Residual Self-attention Block is converted to a 2 days array squence input $X$ with the shape of $\left(\left(d\times w\times h\right),128\right)$, by reshape and transpose operations. After that, mulit-head self-attention operation can be easily applied to $X$. In this case, the number of heads equals 4, therefore $X$ is projected to subdimension space 4 times in parallel; after four self-attention operations, the outputs are concatenated and further projected. The sequence output is reshaped again by the reverse operation of “space and sequence conversion” as shown in Figure 2, and output the attentioned 3D feature map, followed by a $1\times 1\times 1$ convolution. The “space and sequence conversion” operation means taking feature in the same spatial location across all channels.

$\begin{array}{c}\begin{array}{c}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}\left(Q,K,V\right)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,\dots ,{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_n\right)W^O\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}hea{d}_i=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)\end{array}\end{array}(4)$

Here, $Q$, $K$ and $V$ represent the Query, Key and Value matrix as shown in Figure 2, and $n=4$, $W_i^Q=W_i^K=W_i^V\in {\mathcal{R}}^{128\times 32}$, $W^O\in {\mathcal{R}}^{128\times 128}$ in this work.

It is worth noting that to fully take advantage of the spatial sequence information extracted by sampling, the absolute positional coding strategy is applied in this work, where the positional coding is directly added to the input of the self attention module. Specifically, one raw MRI input is firstly normalized and reshaped to $1\times 182\times 218\times 182$, and the size of feature representation $X$ becomes $128\times 12\times 14\times 12$ after the Conv3D block, where the first dimension represents the number of channels. The shape of positional coding $P$ can be expressed as: $\left(batch\_size\times embedded\_dim\times width\times height\times depth\right.$), where embedded_dim is the dimension of positional vector and equals 128 in this case. In this work, during network training, we initialized the positional coding $P$ with standard normal distribution where $P\sim N\left(0,1\right)$, and then taking $P$ as trainable parameters to update with backpropagation. As seen in Figure 2, the learnable positional encoding matrix $P$ was simply added to the input feature map, inspired by Sequence to Sequence Learning [34].

For the residual self-attention block, before the self-attention module, two 3D convolution operations are performed, each followed by 3D batch normalization and ReLU activation. Notably, we added the residual connection between the Conv3D block output and the self-attention module output to help improve the learning.

2.3.3 Decoder with skip connections

To further simplify the decoder network without losing performance, the feed-forward network is composed of six fully connected layers, and feature vectors extracted from feature maps and corresponding coordinates of sampling points are concatenated as the input of the decoder network. Since position coordinates are critical for 3D shape representation [21], we introduced skip-connection to maintain the proportion of location information. As shown in Figure 3, the input feature vector is concatenated with the intermediate output of the following four fully connected layers. The output vector of the decoder network representing the SDF values of four corresponding cortical surfaces for each voxel is a vector with length 4.

FIGURE 3

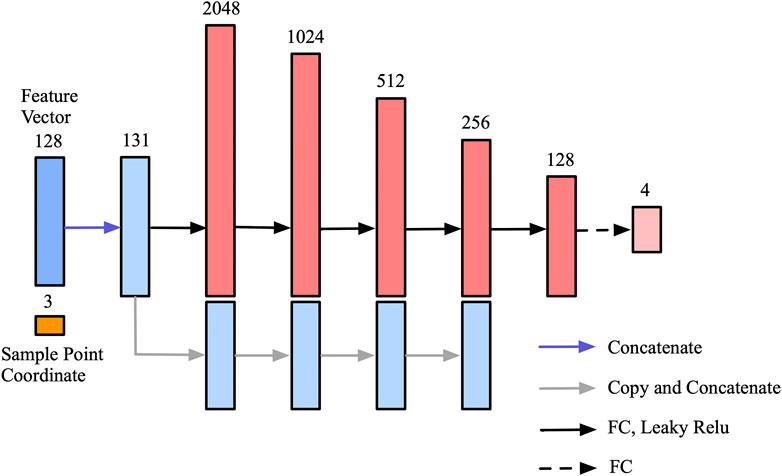
FIGURE 3. Decoder network for SDF values prediction. The skip-connection mechanism is introduced to make full use of the location information of the sampling points.

2.3.4 Loss function

In 3D object reconstruction, L1 loss is the most frequently used loss function, and the basic form of L1 loss for one cortical surface can be written as follows, where $N$ represents the number of sampling points and $B$ represents batch size during training:

$\begin{array}{c}\mathcal{L}\left(f_{\theta }\left(X\right),S\right)=\frac{1}{B}{\displaystyle \sum }_b^B{\displaystyle \sum }_{i=1}^N\left|f_{\theta }\left({\mathit{x}}_i\right)-s_i\right|\end{array}(5)$

And for parallel training with four cortical surfaces, the formula becomes:

$\begin{array}{c}\mathcal{L}\left(f_{\theta }\left(X\right),S\right)=\frac{1}{B}{\displaystyle \sum }_b^B{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^4\left|f_{\theta }\left({\mathit{x}}_i^j\right)-s_i^j\right|\end{array}(6)$

For cortical surface representation with signed distance function values, sampling points close to the cortical surface are critical for reconstruction details, while sampling points away from the cortical surface contribute less to the reconstruction process. To help the training network capture more detailed information around the surface, the truncate interval $\left[-\delta ,\delta \right]$ is applied to the ground-truth and the predicted signed distance values, where the truncated L1 loss can be expressed as follows:

$\begin{array}{c}T\left(\lambda ,\delta \right)≔\mathit{min}\left(\mathit{max}\left(\lambda ,-\delta \right),\delta \right)\end{array}(7)$

$\begin{array}{c}{\mathcal{L}}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{e}}\left(f_{\theta }\left(X\right),S\right)=\frac{1}{B}{\displaystyle \sum }_b^B{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^4\left|T\left(f_{\theta }\left({\mathit{x}}_i^j\right),\delta \right)-T\left(s_i^j,\delta \right)\right|\end{array}(8)$

$T\left(\cdot \right)$ is defined as the truncated function with parameter $\delta$. Given proper small hyperparameter values of $\delta$, the network can focus more on surface details, while for larger value of $\delta$, more samples are used for model weight updates. In general, the basic form of L1 loss is the special case of its truncated form.

Furthermore, we also propose exploring the potential of the L1 loss function with a Gaussian decay coefficient. The Gaussian function in this case is of the following form:

$\begin{array}{c}G\left(s_i\right)=\frac{A}{\sigma \sqrt{2\pi }}\exp \left(-\frac{1}{2}\frac{{\left(s_i-\mu \right)}^2}{{\sigma }^2}\right)\end{array}(9)$

where A is the amplitude coefficient. Due to the smooth decay characteristic of the Gaussian function, as the distance between the sampling point and the ground-truth surface increases, the loss weight of the corresponding sampling point decreases. We hope this design can perform dynamic loss constraint during network training, and help the network to better converge to the optimal solution. The Gaussian decay L1 loss can be described as follows:

$\begin{array}{c}{\mathcal{L}}_{gaussian}\left(f_{\theta }\left(X\right),S\right)=\frac{1}{B}{\displaystyle \sum }_b^B{\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^{4}G\left(s_i^j\right)\cdot \left|f_{\theta }\left({\mathit{x}}_i^j\right)-s_i^j\right|\end{array}(10)$

The amplitude coefficient A, $\mu$ and $\theta$ are hyperparameters based on experience. In this work, A equals 20, $\mu$ equals 0, and $\theta$ equals 1.5. For the netwok training, the Adam optimizer was employed with a fixed learning rate equals 0.0001.

2.4 Cortical surface extraction

For the cortical surface extraction pipeline, firstly, the input MRI volume is registered into the MNI105 space; secondly, given arbitrary reconstruction resolution, i.e., $512\times 512\times 512$ by uniform sampling from MNI105 space, the attention-based encoder-decoder network outputs the SDF representation with the shape of $512\times 512\times 512$, followed by a Gaussian filter smoothing with a standard deviation of 0.5.

To prevent grid self-intersection, and to ensure that the predicted signed distance function values is homeomorphic to a sphere, in this work, we apply a topology propagation algorithm using a fast marching technique proposed by bazin. et.al [35], that enforces the network prediction result to a desired topology.

Algorithm 1:. Marching cubes pseudocode

Data: the SDF value of the $i$-th vertex of the $n$-th cube $V_n^i$, the 3D coordinate of the $i$-th vertex of the $n$-th cube $P_n^i$, $N$ cubes to iterate, the scale surface level set $l$, the adjacency vertex index $\mathcal{N}\left(i\right)$ of the index $i$ in the query cube

Result: Extracted surface mesh vertices coordinates $M_{vertices}$

1 M_vertices←[];

2 $M_v\leftarrow 0;$

3 While $n\le$ N do

4 if $l\ge V_n^i\mathrm{a}\mathrm{n}\mathrm{d}l\le V_n^{\mathcal{N}\left(i\right)}\left(i=1..8\right)$ then

5 $\Delta P\leftarrow \frac{\left(l-V_n^i\right)\left(\left|{\mathit{P}}_n^{\mathcal{N}\left(i\right)}-{\mathit{P}}_n^i\right|\right)}{V_n^{\mathcal{N}\left(i\right)}-V_n^i}$

6 ${\mathit{M}}_{\mathit{v}}\leftarrow {\mathit{P}}_n^i+\Delta P;$/* Coordinate interpolation */

7 $M_{vertices}.append\left(M_v\right);$/* Accumulate mesh vertex coordinates */

8 else

9 continue

10 end

11 end

Then, the marching cubes algorithm proposed by [33] is further employed to cortical surface extraction, followed by Laplacian smoothing. The core idea of the marching cubes algorithm can be summarized as Algorithm 1 For vertices $v_i\in M$, where M represents the extracted surface mesh, the Laplacian smoothing operation can be described as follows:

$\begin{array}{c}\mathrm{S}\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{h}\left({\mathit{v}}_i\right)={\displaystyle \sum }_{k\in \mathcal{N}\left(i\right)}\frac{{\mathit{v}}_k}{\left|\mathcal{N}\left(i\right)\right|}\end{array}(10)$

where $N\left(i\right)$ is the adjacency vertices of the $i$-th vertex. Note that the post-processing operation of the four surfaces is performed in parallel, for efficiency.

4 Results

To verify the effectiveness of our method, we first designed a series of ablation studies to explore the importance of prior constraints and the skip connections mechanism, after which we evaluated the performance of three loss function. Finally, the precision analysis is performed compared with DeepCSR for challenging pial surface reconstruction.

4.1 Ablation experiment

As shown in Table 1, the ablation experiment is conducted to measure the importance of the proposed components.

TABLE 1

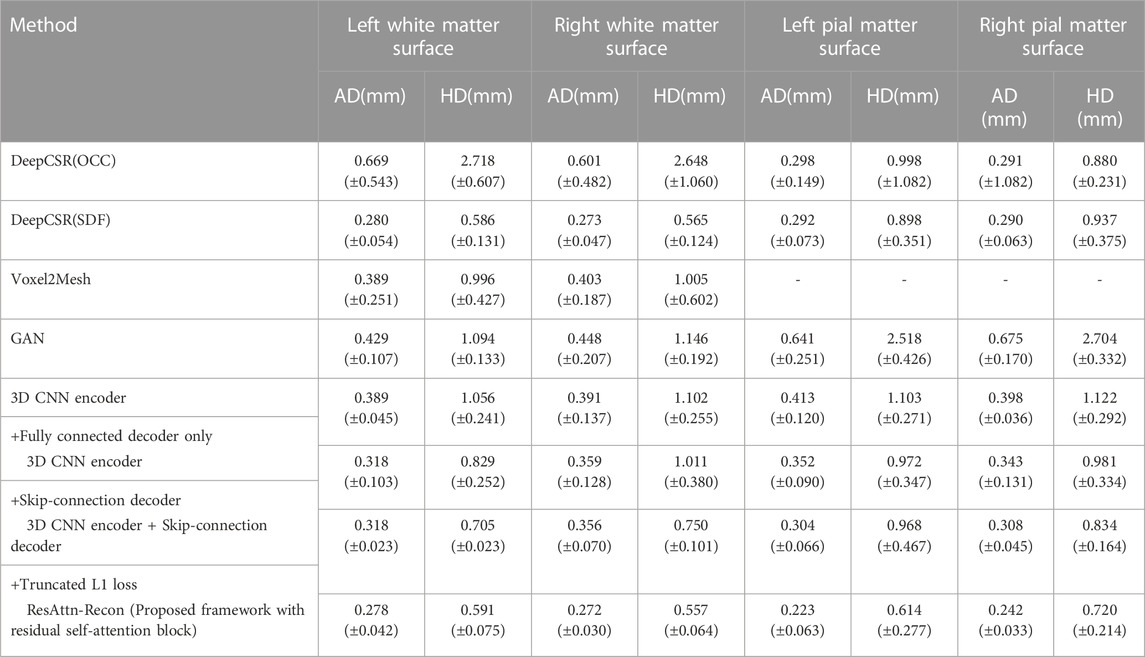
TABLE 1. Results of comparison analysis with DeepCSR and the ablation study on the proposed ResAttn-Recon framework for cortical surface reconstruction. Including the white matter surface and the pial matter surface, where AD = Average symmetric surface distance, HD = Hausdorff distance.

The average absolute distance (AD) and the Hausdorff distance (HD) [36,37] are employed as the surface evaluation metrics, and the lower the values, the better the reconstruction results.

4.1.1 Decoder network with skip connections

In this experiment we explored the expressive capability of fully connected layers in the decoder network architecture with the skip connections mechanism. As shown in Table 1, row 4 records the baseline encoder-decoder network where the decoder network is the fully connected layers without skip connections mechanism, and the feature vectors and location coordinates are simply concatenated from the decoder input. It was found that the decoder with skip-connection (row 4) shows lower AD and HD indicators than that without skip connections (row 5). The results indicate that the location information of the sampling points make a considerable contribution to reconstruction work. Nevertheless, there is still much room for improvement in the reconstruction indicators, compared with the DeepCSR framework (row 3).

In order to further validate the performance of the proposed lightweight decoder network, different indicators are used to compare with the decoder network in DeepCSR framework. As shown in Table 2, the proposed decoder network outperforms DeepCSR’s decoder network in the number of parameters (2636527 vs. 3549188), parameters size (10.05 MB vs. 13.53 MB), and the average inference speed (0.47 ± 0.02 vs. 6.34 ± 0.02) for testing dataset. The average L1 Loss (computational cost shown in formula 5) of the proposed framework is 1,291.89 ± 10.50, lower than that of the DeepCSR framework (1,452.85 ± 28.98). By the way, the computational cost looks larger, because the distance space is not normalized to the [-0.5,0.5] interval.

TABLE 2

TABLE 2. Lightweight decoder analysis.

4.1.2 Loss function with prior constraints

The performance of the proposed framework between employing prior constraints (trained with a truncated L1 loss or Gaussian decay L1 loss) and without prior constraints (trained with a basic L1 loss) are compared, as shown in row five and row six of Table 1, Additionally, the reconstruction results improved with the help of prior constraints imposed on the loss function from the perspective of AD and HD indicators. For fairness, the training process of the DeepCSR-SDF network also employs the L1 loss and its variants, and take the optimal result for performance comparison and analysis.

4.2 Methods comparision

For further comparison and analysis, besides the DeepCSR framework, Voxel2Mesh and GAN [38] were added to the experiments. Since the Voxel2Mesh framework cannot reconstruct the inner and outer surfaces in parallel, analysis of white matter surface reconstruction performance is considered for convenience.

For GAN model, the 3D-UNet is employed as the backbone of the generator network. The generator predicts the SDF representation (output channel equals 4) relevant to four cortical surfaces. The discriminator takes the MRI volume and the ground truth/predicted SDF representation as input, and discriminate true or false label, where cross entropy loss is used as the discriminator loss function. As shown in Table 3, the AD and HD values derived from Voxel2Mesh and GAN model are significantly higher than that from the proposed framework. The GAN model shows the worst performance for AD and HD indicators.

TABLE 3

TABLE 3. The maximum IOU values with different loss functions: the L1 loss, Gaussian decay L1 loss and Truncate L1 loss functions.

From another persperctive, according to the data format being processed, the GAN model reconstruct the cortical surface based on MRI voxels, 1) Due to the partial volume effect, the reconstruction accuracy is limited by the resolution of MRI volume, 2) The idea of generative adversarial network is to infer whether each voxel is inside or outside the surface of the cerebral cortex by training the generator, and then give a true or false judgment through the decision network. Each voxel has only binary information (inside or outside), while ignoring the distance information to the surface. Mesh based Voxel2Mesh model deform predefined sphere template meshes to cortical surfaces. 1) Despite fast processing, theoretical guarantees are lack to prevent self-intersections of the surface mesh. 2) Besides, a Voxel2Mesh model only able to reconstruct a single surface once (outer or inner surface). The proposed framework reconstruct the surface based on sampling points, and therefore has the theoretical support to reconstruct cortical surfaces of arbitrary resolution.

4.3 Visualization analysis

As illustrated in Figure 4, the reconstruction of the pial surface is more challenging than that of the white matter surface. The reconstructed pial surface of the left hemisphere is shown in the first row. The proposed ResAttn-Recon framework achieves the best reconstruction result, and the reconstruction result with DeepCSR has obvious surface bumps in the red rectangle area. The encoder-decoder architecture without the attention module (no attention version) has several reconstruction defects. The upper rectangular frame area shows severe reconstruction noise near the surface, and the lower rectangular frame area has multiple grid self-intersections. For the white matter reconstruction surface of the left hemisphere shown in the second row, there is no major visual difference between the three network structures in this case.

FIGURE 4

FIGURE 4. Visual assessment of cerebral cortical reconstruction results. The first row corresponds to the pial matter surface of the left hemisphere, and the second row corresponds to the white surface of the left hemisphere.

It is also worth noting that the ground-truth surfaces handled by FreeSurfer look rougher than the actual physiological surface. To address this, both the proposed framework and the DeepCSR framework have moderately smoothed the predicted surface through a post-processing algorithm. To further visualize the robustness of the proposed model, another eight examples of cortical surfaces (prediction and corresponding ground-truth) were illustrated in Figure 5.

FIGURE 5

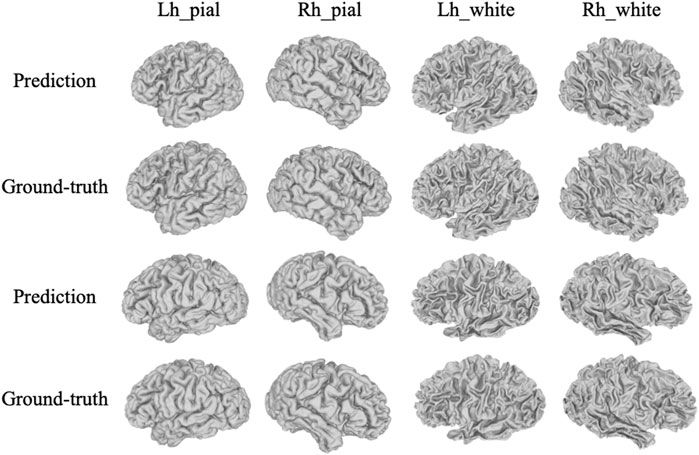
FIGURE 5. More visualization examples of the prediction results by the proposed method with corresponding ground-truth, including pial and white matter surfaces of left and right hemispheres.

4.4 Loss function evaluation

As seen in Figure 6, we compared the convergence curve of the intersection over union (IOU) based on the three loss functions mentioned above. By the way, for IOU, the SDF representation of the cortical surface could be further converted to the binarized SDF mask, 0 for inner surface points and one for outer surface points, then the binarized SDF mask based IOU could be further calculated between the ground-truth SDF and the predicted SDF. It is clear that the IOU curve based on the truncated L1 loss is distributed over the other two curves throughout the training process. For the other two curves, before 10 k training steps, the slope of the IOU curve based on the basic L1 loss is larger than that based on the Gaussian decay L1 loss, after which the IOU curve of the latter surpassed that of the former.

FIGURE 6

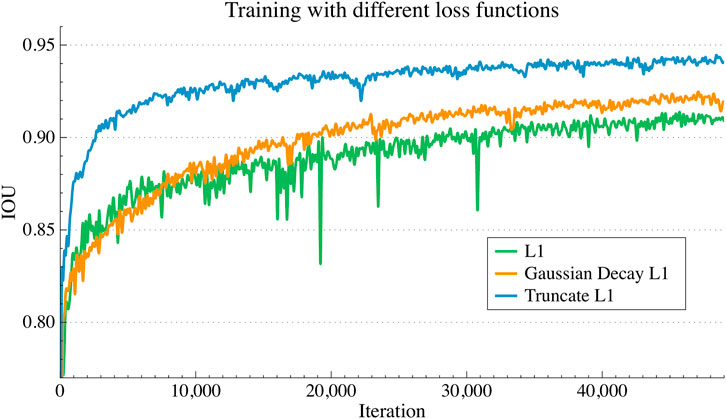
FIGURE 6. IOU convergence curves during training process with different loss functions. L1 loss, the truncated L1 loss and the Gaussian decay L1 loss were compared for analysis.

As shown in Table 3, the maximum IOU value of the trained with truncated L1 loss is 0.948 after convergence, followed by the loss function based on the Gaussian decay coefficient with a maximum IOU equals 0.935. The maximum IOU value based on the basic L1 loss is 0.92, which is considerably lower than the former. Also, thecorresponding convergence trend of the training curve can be confirmedfrom Figure 6.

The experimental results show that training with the truncated L1 loss and Gaussian decay L1 loss outperform the basic L1 loss, and among them, the truncated L1 is more effective. For the Gaussian decay L1 loss, the loss weighting coefficients tend to zero for sampling points away from the ground-truth surface, which leads to these points making less of a contribution for network training.

4.5 Precision analysis

To measure the precision of the reconstructed cortical surface, the average absolute distance (AD) is employed in millimeters (mm). Mesh vertices with an AD greater than 1 mm, 2mm and 5 mm as a percentage of the total number of mesh vertices are calculated.

Due to the highly folded and curved geometry, pial surface reconstruction is much more challenging than white surface reconstruction. Moreover, 60 ADNI test datasets with pial surface ground-truth are enrolled for precision analysis. As shown in Table 4, compared with DeepCSR, the AD percentage greater than 1 mm (3.616 vs 5.582 for left pial), 2 mm (1.467 vs 2.432 for left pial) and 5 mm (0.131 vs 0.249 for the left pial) are lower than those of the DeepCSR framework, indicating that the proposed method has a good robustness of the overall reconstruction.

TABLE 4

TABLE 4. Precision analysis for left pial matter surface and right pial matter surface: with range greater than 1mm, 2mm and 5 mm.

5 Discussion

We successfully developed a residual self-attention-based architecture to reconstruct the inner and outer surface of the left and right hemispheres in parallel. In the current work of cortical surface reconstruction, including the voxel-based, mesh-based, and the implicit surfaces representation-based approaches, none of them considered the importance of capturing long range feature dependencies, during voxelwise or mesh vertex wise or sampling pointwise feature extraction, which is essential for 3D geometric surfaces representation is not considered. Given enough sampling points, the implicit surface representation-based approach has the theoretical support to reconstruct cortical surfaces of arbitrary resolution, our study is developed based on this direction and compared with the typical DeepCSR architecture. To adapt the residual connected multi-head self-attention to the 3D shape representation task, the $1\times 1$ convolution is embedded in this module, with a learnable positional encoding matrix.

Ablation studies are undertaken to evaluate the impact of the residual self-attention module, the skip connections trick in decoder network, and the loss function with prior constraints. Experiments show that these components are effective in improving the reconstruction performance. We proposed the truncated L1 loss and the Gaussian decay weighted L1 loss to explore the effect of loss function on model expression potential. The truncated L1 loss achieves optimal results compared to simply applying the basic L1 loss function, and the training process achieved a higher IOU value (0.948 vs. 0.920) with the proposed truncated L1 loss. The average symmetric surface distance (AD) for the inner and outer surfaces is 0.253 ± 0.051, the average Hausdorff distance (HD) is 0.629 ± 0.186, which is lower than that of DeepCSR, whose AD equals 0.283 ± 0.059, and HD equals 0.746 ± 0.245. In addition, to measure the robustness of the overall reconstruction process, the AD greater than 1 mm, 2 mm and 5 mm as a percentage of the total number of mesh vertices are calculated, and we evaluated the challenging pial cortical surface result compared with DeepCSR, in 1 mm (3.616 vs. 5.582) and 2 mm (1.467 vs. 2.432) and 5 mm (0.131 vs. 0.249). From the perspective of visual analysis, the proposed ResAttn-Recon outperforms DeepCSR and the simple encoder-decoder architecture without the attention module. From Figure 5, it was found that the SDFs of pial matter surfaces are harder to approximate than the white matter surfaces during network training in parallel. Our proposed framework can better capture the surface details in a limited data size. Thus, the proposed residual self-attention-based framework can be a promising approach for improving the cortical surface reconstruction performance.

Our study has one main limitation: due to the lengthy processing time by the FreeSurfer pipeline, only a total of 560 T1 weighted images are enrolled in our dataset. In the future, more MRI volumes will be retrieved to expand the training dataset. Furthermore, it is desirable to enroll a larger pool of multicenter data to demonstrate the clinical value of this framework. Since topology correction algorithm during post processing usually takes a few minutes to enforce the prediction result to a desired topology, we will also pay more attention to the optimization of the post processing algorithm to further shorten the time of cortical surface reconstruction pipeline.

6 Conclusion

In this paper, we proposed ResAttn-Recon for challenging cerebral cortical surface reconstruction tasks. Firstly, we explored the concept of residual self-attention to the encoder-decoder architecture. Secondly, a lightweight decoder network with skip connection is developed to simplify the network without losing performance. In addition, experiments show that the proposed truncated L1 loss and Gaussian decay weighted L1 loss function contribute to the network training and performance improvement. The superior performance is achieved by the proposed framework compared with DeepCSR and a simple encoder-decoder framework without an attention block. The proposed framework can be a promising approach for improving the cortical surface reconstruction performance. We hope our work can inspire insights and show new directions toward cortical surface reconstruction study.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Ethics statement

The studies involving human participants were reviewed and approved by the Institutional Review Boards of all of the participating institutions. Informed written consent was obtained from all participants at each site. The patients/participants provided their written informed consent to participate in this study.

Author contributions

MA performed all the experiments and wrote the manuscript, ZL analyzed and optimized the proposed algorithm. JC collected and cleaned the raw data. YC and KT conceived and supervised the project. JW, CW, and KZ reviewed the content of the manuscript and revised the grammar, they also provided valuable suggestions for modification of figures and tables. All authors contributed to the critical reading and writing of the manuscript.

Acknowledgments

The authors express special thanks to the Alzheimer’s Disease Neuroimaging Initiative for available data providing, and all the medical students for assisting with the collection of the data.

Conflict of interest

Author KZ was employed by the company Inspur Electronic Information Industry Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1003874/full#supplementary-material

References

1. Du A-T, Schuff N, Kramer JH, Rosen HJ, Gorno-Tempini ML, Rankin K, et al. ‘Different regional patterns of cortical thinning in Alzheimer’s disease and frontotemporal dementia’. Brain (2006) 130(4):1159–66. doi:10.1093/brain/awm016

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rimol LM, Nesvag R, Hagler DJ, Bergmann O, Fennema-Notestine C, Hartberg CB, et al. ‘Cortical volume, surface area, and thickness in schizophrenia and bipolar disorder’. Biol Psychiatry (2012) 71(6):552–60. doi:10.1016/j.biopsych.2011.11.026

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Cruz RS, Lebrat L, Bourgeat P, Fookes C, Fripp J, Salvado O. DeepCSR: A 3D deep learning approach for cortical surface reconstruction, In: 2021 IEEE Winter Conference on Applications of Computer Vision (WACV); January 5-9, 2021; Waikoloa, HI, USA (2021). 806–15. doi:10.1109/WACV48630.2021.00085

CrossRef Full Text | Google Scholar

4. Duan D, Xia S, Rekik I, Meng Y, Wu Z, Wang L, et al. ‘Exploring folding patterns of infant cerebral cortex based on multi-view curvature features: Methods and applications’. NeuroImage (2019) 185:575–92. doi:10.1016/j.neuroimage.2018.08.041

PubMed Abstract | CrossRef Full Text | Google Scholar

5. MacDonald D, Kabani N, Avis D, Evans AC. ‘Automated 3-D extraction of inner and outer surfaces of cerebral cortex from MRI’. NeuroImage (2000) 12(3):340–56. doi:10.1006/nimg.1999.0534

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kriegeskorte N, Goebel R. ‘An efficient algorithm for topologically correct segmentation of the cortical sheet in anatomical MR volumes’. NeuroImage (2001) 14(2):329–46. doi:10.1006/nimg.2001.0831

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Shattuck DW, Leahy RM. ‘BrainSuite: An automated cortical surface identification tool’. Med Image Anal (2002) 6:129. doi:10.1016/s1361-8415(02)00054-3

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kim JS, Singh V, Lee JK, Lerch J, Ad-Dab'bagh Y, MacDonald D, et al. ‘Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification’. NeuroImage (2005) 27(1):210–21. doi:10.1016/j.neuroimage.2005.03.036

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fischl B. ‘FreeSurfer’. NeuroImage (2012) 62(2):774–81. doi:10.1016/j.neuroimage.2012.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dahnke R, Yotter RA, Gaser C. ‘Cortical thickness and central surface estimation’. NeuroImage (2013) 65:336–48. doi:10.1016/j.neuroimage.2012.09.050

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. Neuroimage (2012) 9:197. doi:10.1006/nimg.1998.0395

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Rao C, Liu Y. ‘Three-dimensional convolutional neural network (3D-CNN) for heterogeneous material homogenization’. Comput Mater Sci (2020) 184:109850. doi:10.1016/j.commatsci.2020.109850

CrossRef Full Text | Google Scholar

13. Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. (2016). 3d u-net: learning dense volumetric segmentation from sparse annotation. In International conference on medical image computing and computer-assisted intervention (Springer), 424–432.

14. Segonne F, Pacheco J, Fischl B. ‘Geometrically accurate topology-correction of cortical surfaces using nonseparating loops’. IEEE Trans Med Imaging (2007) 26(4):518–29. doi:10.1109/tmi.2006.887364

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Henschel L, Conjeti S, Estrada S, Diers K, Fischl B, Reuter M. ‘FastSurfer - a fast and accurate deep learning based neuroimaging pipeline’. NeuroImage (2020) 219:117012. doi:10.1016/j.neuroimage.2020.117012

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Gopinath K, Desrosiers C, Lombaert H. ‘SegRecon: Learning joint brain surface reconstruction and segmentation from images’. In: Medical image computing and computer assisted intervention – miccai 2021. Cham: Springer International Publishing (2021). p. 650–9.

CrossRef Full Text | Google Scholar

17. Gonzalezballester M. ‘Estimation of the partial volume effect in MRI’. Med Image Anal (2002) 6(4):389–405. doi:10.1016/s1361-8415(02)00061-0

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ma Q, Robison EC, Kainz B, Rueckert D, Alansary A. (2021). Pialnn: A fast deep learning framework for cortical pial surfacereconstruction. In International Workshop on Machine Learning in ClinicalNeuroimaging (Springer), 73–81.

19. Wickramasinghe U, Remmelli E, Knott G, Fua P. (2020). Voxel2mesh: 3d mesh model generation from volumetric data. InInternational Conference on Medical Image Computing and Computer-Assisted Intervention (Springer), 299–308.

Google Scholar

20. Bongratz F, Rickman AM, Polserl S, Wachinger C. Vox2Cortex: Fast explicit reconstruction of cortical surfaces from 3D MRI scans with geometric deep neural networks. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); June 18 2022 to June 24 2022; New Orleans, LA, USA (2022). 20741–51. doi:10.1109/CVPR52688.2022.02011

CrossRef Full Text | Google Scholar

21. Park JJ, Florence P, Straub J, Newcombe R, Lovergrove S. (2019). Deepsdf: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 165–174.

Google Scholar

22. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. (2017) Attention is all you need. Advances in neural information processing systems, 30.

23. Shi H, Gao J, Ren X, Xu H, Liang X, Li Z, et al. (2021) Sparsebert: Rethinking the importance analysis in self-attention. In International Conference on Machine Learning (PMLR), 9547–9557.

24. Shen T, Zhou T, Long G, Jiang J, Pan S, Zhang C. (2018) DiSAN: Directional self-attention network for RNN/CNN-free language understanding, arXiv.

CrossRef Full Text | Google Scholar

25. Ramachandran P, Parmar N, Vaswani A, Bello I, Levskaya A, Shlens J, et al. (2019) Stand-alone self-attention in vision models. Advances in Neural Information Processing Systems, 32.

26. Zhao H, Jia J, Koltun V. Exploring self-attention for image recognition. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); June 13 2020 to June 19 2020; Seattle, WA, USA (2020). 10073–82. doi:10.1109/CVPR42600.2020.01009

CrossRef Full Text | Google Scholar

27. Vaswani A, Ramachandran P, Srinivas A, Parmar N, Hetchman B, Shlens J. Scaling local self-attention for parameter efficient visual backbones. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); June 20 2021 to June 25 2021; Nashville, TN, USA (2021). p. 12889–99. doi:10.1109/CVPR46437.2021.01270

CrossRef Full Text | Google Scholar

28. Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, et al. (2020) An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929.

29. Yuan L, Chen Y, Wang Y, Yu W, Shi Y, Jiang Z, et al. Tokens-to-Token ViT: Training vision transformers from scratch on ImageNet. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV); Oct. 11 2021 to Oct. 17 2021; Montreal, QC, Canada (2021). p. 538–47. doi:10.1109/ICCV48922.2021.00060

CrossRef Full Text | Google Scholar

30. Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, et al. (2021) Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF international conference on computer vision, 10012–10022.

31. Petersen RC, Aisen PS, Beckett LA, Donohue MC, Gamst AC, Harvey DJ, et al. ‘Alzheimer’s disease neuroimaging initiative (ADNI): Clinical characterization’. Neurology (2010) 74(3):201–9. doi:10.1212/wnl.0b013e3181cb3e25

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. ‘A probabilistic atlas of the human brain: Theory and rationale for its development’. Neuroimage (1995) 2(2):89–101. doi:10.1006/nimg.1995.1012

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lorensen WE, Cline HE. Computer graphics. J Comp (1987) 21, 7.

Google Scholar

34. Gehring J, Auli M, Grangier D, Yarats D, Dauphin YN. (2017) ‘Convolutional sequence to sequence learning’. arXiv. doi:10.48550/arXiv.1705.03122

CrossRef Full Text | Google Scholar

35. Bazin P-L, Pham DL. ‘Topology correction of segmented medical images using a fast marching algorithm’. Comp Methods Programs Biomed (2007) 88(2):182–90. doi:10.1016/j.cmpb.2007.08.006

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tosun D, Rettmann ME, Naiman DQ, Resnick SM, Kraut MA, Prince JL. ‘Cortical reconstruction using implicit surface evolution: Accuracy and precision analysis’. NeuroImage (2006) 29(3):838–52. doi:10.1016/j.neuroimage.2005.08.061

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Taha AA, Hanbury A. ‘Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool’. BMC Med Imaging (2015) 15(1):29. doi:10.1186/s12880-015-0068-x

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Ning Z, Zhang Y, Pan Y, Zhong T, Liu M, Shen D. (2020). “Ldgan: Longitudinal-diagnostic generative adversarial network for disease progression prediction with missing structural MRI,” in M Liu. (eds) Machine learning in medical imaging. Cham: Springer International Publishing(Lecture Notes in Computer Science), 170–9. doi:10.1007/978-3-030-59861-7_18

CrossRef Full Text | Google Scholar