Stabilization of skyrmions in two-dimensional systems with next-nearest-neighbor exchange interactions

We study, in the absence of a magnetic field, the stabilization of skyrmions in a single-layered ferromagnet in the presence of next-nearest-neighbor exchange interactions including both the ferromagnetic exchange interaction and Dzyaloshinskii–Moriya exchange interaction. The stabilization of skyrmion depends on not only magnetic anisotropy but also the next-nearest-neighbor ferromagnetic exchange interaction. The latter stabilizes bimeron in the presence of in-plane magnetic anisotropy, while it enhances the stabilization of the ferromagnetic background in the presence of perpendicular magnetic anisotropy. Numerical simulations show that the next-nearest-neighbor ferromagnetic exchange interaction is a viable tool to control the creation and annihilation of skyrmionic states with a small size. This study may open an alternative avenue to the generation, stabilization, and control of magnetic skyrmions in the two-dimensional thin films.

1 Introduction

Since the discovery of graphene by Novoselov et al., two-dimensional materials have attracted considerable attention [1]. Graphene has a conical band structure with a pair of degenerate valleys, a high carrier mobility, and a long spin coherent length, regarded as a promising candidate for spintronic devices [2]. Nevertheless, graphene has absence of ferromagnetism. Hence, the spin manipulations in graphene are proposed to dope with magnetic impurities [3], exchange with an adjacent magnetic substrate [4], or utilize an external magnetic field. Recently, ferromagnetic CrI₃ has been first reported [5]. Later, Fe₃GeTe₂ [6], even for room-temperature ferromagnets such as VSe₂ [7] and Fe₅GeTe₂ [8], has also been reported. The layered ferromagnetic materials such as Fe₃GeTe₂ integrate the conducting and ferromagnetism into the same materials, leading to the potential applications in ultra-thin spintronic devices. Furthermore, unlike the ferromagnetic metal, the saturation of magnetization is lowered, and magnetization is much easier to tilt or flip due to the suppression of exchange correlation in the presence of Ge and Te elements. In addition, the elements of Ge and Te also cause the broken inversion symmetry of the film and induce the (Dzyaloshinskii–Moriya) DM interaction. The competitions among the DM interaction, exchange interaction, and magnetic field could give rise to an isolated skyrmion or skyrmion lattices [9–12]. For bulk Fe₃GeTe₂, the diameter of skyrmion is relatively large due to the weak spin–orbit coupling. The diameter of skyrmion can be further decreased by interacting with a substrate such as ferromagnet or WTe₂ [13]. For a system with skyrmions around 100 nm, the long-range first-nearest-neighbor ferromagnetic exchange interactions dominate the system. However, when the size of skyrmion decreases to 10 nm or even smaller, the high-order exchange such as the next-nearest-neighbor exchange interactions should be considered in a thin film and may hold a strong coupling with the substrate. For example, Lohani et al. showed the influence of next-nearest-neighbor exchange interactions on the magnetic correlations and ground states in frustrated magnets [14]. The next-nearest-neighbor exchange interactions compete with the other exchange interactions and stabilize the small-size skyrmion [15]. The skyrmion has not only a spin configuration of skyrmion–antiskyrmion pairs but also a tunneling effect behavior as a quasi-particle. Zhang et al. studied the stabilization and motion of skyrmions driven by spin–orbit torques in frustrated ferromagnets in the presence of next-nearest-neighbor exchange interactions [16]. The next-nearest-neighbor exchange interactions lower the total energy of systems and stabilize the spin configurations of skyrmion with high topological numbers.

In this study, we explore the viability of stabilizing skyrmionic states in the presence of next-nearest-neighbor exchange interactions in chiral magnets. Unlike the previous results [15, 17], we find that the role of next-nearest-neighbor exchange interactions depends on the type of magnetic anisotropy. We show that in the presence of perpendicular magnetic anisotropy, the stabilization of Néel skyrmionic states could be shortened in a parametric range. By contrast, in the presence of in-plane magnetic anisotropy, the bimeron is stabilized by the next-nearest-neighbor exchange interactions in a broad parametric range.

2 Theoretical model

We consider a single-layered ferromagnet with a hexagonal lattice as shown in Figure 1A. r₁, r₂, and r₃ denote the original point, the first nearest-neighbor site, and the next nearest-neighbor site, respectively. d₁ and d₂ denote the exchange length of the first nearest-neighbor and the next nearest-neighbor, respectively. When a system or a local region is dominated by the ferromagnetic exchange interaction, both the first-nearest-neighbor exchange and the next-nearest-neighbor exchange prefer the parallel spins and retain the system to be ferromagnetic. However, when the DM interaction is strong and the system stabilizes to a helical state or a skyrmion, the next-nearest-neighbor ferromagnetic exchange prefers a canted spin configuration as shown in Figure 1B. Furthermore, the trend is more evident when the diameter of skyrmion is relatively small such as a bimeron. In the opposite limit, the DM interaction is weak and the helical period is very long, the diameter of skyrmion goes to the infinite range, and the next-nearest-neighbor exchange recovers to stabilize the ferromagnetic exchange.

FIGURE 1

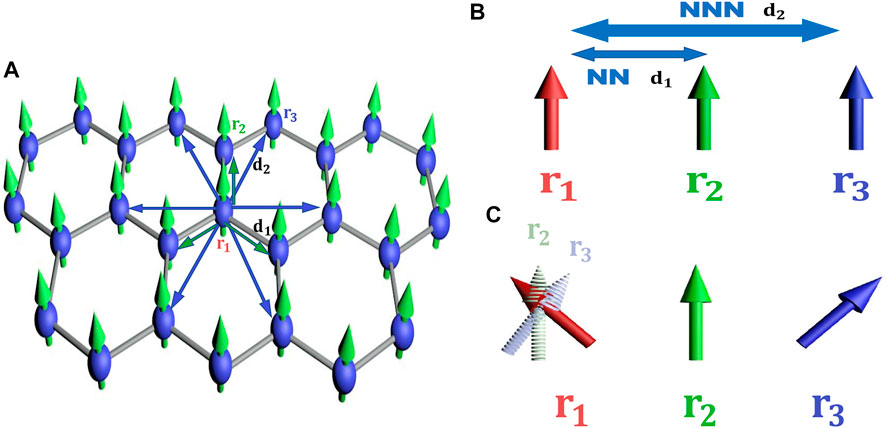
FIGURE 1. Schematic view of the role of next-nearest-neighbor exchange interactions on the spin textures. (A) Single-layered ferromagnetic material with a hexagonal lattice, where r₁, r₂, and r₃ denote the original point, the first nearest-neighbor position, and the next nearest-neighbor position, respectively. (B) Both the first-nearest-neighbor and next-nearest-neighbor exchange interactions prefer the parallel spins in a ferromagnetic state. (C) First-nearest-neighbor and next-nearest-neighbor exchange interactions prefer the tilted spins for different directions in a nonferromagnetic state.

3 Atomistic spin simulations

In order to ascertain the role of the next-nearest-neighbor ferromagnetic exchange interactions J₂ in the stabilization of magnetic skyrmions in our proposed model, we conduct comparative spin dynamics simulations on two setups, namely, the system with and without the next-nearest-neighbor exchange interactions J₂. Within the micro-magnetism framework, the dynamics of the magnetization of the ith magnetic atom M_i is governed by the Landau–Lifshitz–Gilbert (LLG) equation given as follows:

$\frac{\partial {\mathbf{M}}_i}{\partial t}=-\frac{\gamma }{\left(1+{\alpha }^2\right){\mu }_i}{\mathbf{M}}_i\times {\mathbf{B}}_i^{\text{eff}}-\frac{\gamma \alpha }{\left(1+{\alpha }^2\right){\mu }_i}{\mathbf{M}}_i\times \frac{\partial {\mathbf{M}}_i}{\partial t},(1)$

where γ is the gyromagnetic ratio and α is the Gilbert damping constant. In Eq. 1, ${\mathbf{B}}_i^{\text{eff}}=-\partial \mathbf{H}/({\mu }_0\partial {\mathbf{M}}_i)$ is the effective field of the ith magnetic atom, μ_i is the permeability of magnetic material with μ_i = 1 [18], and H is the Hamiltonian of the system that incorporates magnetic interactions such as exchange, anisotropy, DM, and magneto-static interactions in the system. The Hamiltonian reads:

$\begin{array}{ccc}\hfill \mathbf{H}& =\hfill & -\sum _{i,j}{\mathcal{J}}_{ij}{\mathbf{S}}_i\cdot {\mathbf{S}}_j-\sum _{i,j}{\mathcal{D}}_{ij}\left({\mathbf{S}}_i\times {\mathbf{S}}_j\right)+\sum _j\mathcal{K}{\left(S_i^z\right)}^2\hfill \\ \hfill & +\hfill & \frac{1}{2}\frac{{\mu }_0}{4\pi }\sum _{i,j}{\mu }_i{\mu }_j\frac{\left({\mathbf{n}}_i\cdot {\widehat{\mathbf{r}}}_{ij}\right)\left({\mathbf{n}}_j\cdot {\widehat{\mathbf{r}}}_{ij}\right)-{\mathbf{n}}_{\mathrm{i}}{\mathbf{n}}_{\mathrm{j}}}{{{\widehat{r}}_{ij}}^3},\hfill \end{array}(2)$

where J_ij is the ferromagnetic exchange constant, K is the magnetic anisotropy constant, and D_ij quantifies the strength of the DM interaction [19]. i and j denote the summation over the interaction pairs for the first and next nearest-neighbor, respectively. Atomistic spin simulations are performed using the Spirit package [20]. In all our simulations, unless otherwise specified, we used the parameters: K_u = 0.55 meV, J_ij = 0.4, or 0.5 meV for the next-nearest-neighbor ferromagnetic exchange interaction and D_ij = 2 meV for the first-nearest-neighbor DM exchange interaction [21], while the size of the system was set to 58 × 58 × 1, and the lattice constant a is set to 0.693 nm.

The DM interaction in our system arises from a spin–orbit coupling at the interface between a thin magnetic film and substrate such as Fe₃GeTe₂/Wse₂ and Fe₃GeTe₂ itself. For an individual skyrmion in an ultra-thin film of thickness d and radius R, the contribution to the magnetic energy from the DM interaction and demagnetization can be estimated as 2π²DRd and $-2\pi {\mu }_0{M}_s^{2}WRd$, respectively, for a given skyrmion wall width W = πd/4K_u [22]. To obtain the final spin state, we consider initial state for the magnetization configuration, namely, random skyrmion and Néel skyrmion. At zero temperature, the initial state evolves according to the LLG equation.

4 Numerical results

We first show, in the presence of perpendicular magnetic anisotropy, phase diagrams of final spin states as a function of the strength of ferromagnetic exchange interactions J₁ and J₂ in Figure 2A. When J₁ is weak (J₁ < 6 meV) and J₂ is absent, there are skyrmionic states and labyrinth-like domain walls, in agreement with the previous results [23]. With the increasing of J₁, the diameter of skyrmion increases and the number of skyrmion decreases. This is because the diameter of skyrmion is proportional to A_ex/D in a two-dimensional system with dense skyrmions or a skyrmion lattice. However, when the distance between skyrmions is larger than the period of the helical state, the interaction between the skyrmions is weakened. The spin configuration of a skyrmion lattice degenerates to an isolated skyrmion. The skyrmion diameter is decreased with the further increasing of the ferromagnetic exchange interaction J₁. This is similar to the skyrmion in a confined nanodisk [24]. When the exchange interaction is sufficiently strong (J₁ = 14 meV), the role of DM interaction is totally suppressed and the system is dominated by the ferromagnetic state.

FIGURE 2

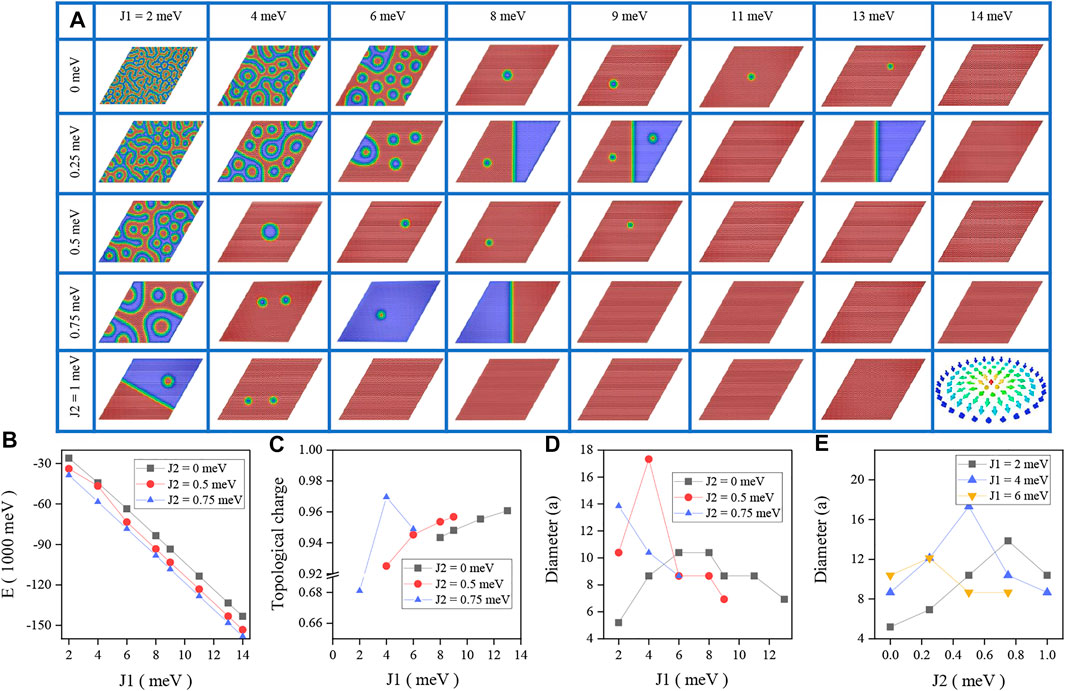
FIGURE 2. (A) Profile of the magnetization of the final state for different J₁ and J₂ in the presence of perpendicular magnetic anisotropy. (B) Total energy, (C) topological charge, and the skyrmion size (in unit of lattice constant a) as a function of (D) the first-nearest-neighbor ferromagnetic exchange interaction J₁ and (E) the next-nearest-neighbor ferromagnetic exchange interaction J₂. A skyrmion sketched by arrows denotes the magnetization direction.

When the ferromagnetic exchange interaction J₂ is turned on and increased, the skyrmion density decreases with increasing J₂. At weak J₂ (J₂ < 0.25 meV), the diameter of skyrmion increases with J₂ when J₁ < 8 meV, in agreement with the analytical expression [25]. With further increasing of J₂, the skyrmion size decreases as shown in Figures 2A,D. This is similar to the case without the exchange interaction J₂. We further plot the total energy of the system as a function of exchange interaction J₁ in Figure 2B. The total energy is decreased when J₁ is increased. This indicates that the skyrmion is in a metastable state. The presence of J₂ leads to the further decreasing of total energy, that is, the role of J₂ in the ferromagnetic region prefers the stabilization of the ferromagnetic state as sketched in Figure 1A and thus leads to the decrease of total energy and the parametric range of skyrmion stabilization. Moreover, we also find that the topological number increases, as shown in Figure 2C, when J₁ increases. This is related to the decreasing of the quasi-uniform ferromagnetic region around the skyrmion core. For a ferromagnetic exchange coupling J₂, it further enhances the ferromagnetic exchange interaction, and ferromagnetic domain increases with J₁ as shown in Figure 2A. In contrast, for an antiferromagnetic exchange coupling J₂, it behaves as a DM coupling. It could shorten the period of helical states and increase the density of skyrmion [17].

In order to further understand the influence of exchange interaction J₂ on the stabilization of skyrmion, we plot, in the presence of in-plane magnetic anisotropy, the magnetization of the final states as a function of exchange interactions J₁ and J₂ in Figure 3A. For a weak exchange interaction J₁, the skyrmions and labyrinth-like domain walls are randomly distributed. With the exchange interaction J₁ increasing, the skyrmion evolves to a meron due to the presence of in-plane magnetic anisotropy, and the width of labyrinth-like domain walls becomes inhomogeneous. When the exchange interaction J₁ further increases, the skyrmion and domain wall totally disappears and are replaced by meron chains. When the exchange interaction J₁ exceeds a certain threshold value, the meron chains become independent merons due to the suppression of the period of the helical state. However, when J₂ is present, the spin configurations of skyrmion are not switched to a meron. Interestingly, the parametric range J₁ of skyrmion stabilization is not narrowed. The spin configuration of skyrmion is just changed from a Néel type to a bimeron type, and the bimeron retains for a wide range of J₁. In comparison to the magnetization of skyrmion, only the mirror symmetry of the z-component of magnetization of bimeron is broken by in-plane magnetic anisotropy. That is, the period of spin spiral of bimeron is retained. Hence, in this case, the exchange interaction J₂ plays the role to stabilize the spin spiral configuration as sketched in Figure 1B. The total energy as a function of exchange interaction J₁ is plotted in Figure 3B in the presence of an isolated meron (black line) and bimerons (red line). The total energy is dominated by the ferromagnetic region and thus decreased when J₁ is increased [26]. The topological number of merons almost remains the same as shown in Figure 3C, while the diameter of merons decreases with the increasing J₁ as shown in Figure 3D. For bimerons, the topological number is robust to J₁, while the diameter of bimerons increases with J₁. For a meron, it is a totally suppressed skyrmion, and its diameter is robust to the variation of exchange interaction J₁. For a bimeron, it is a partly suppressed skyrmion, and its stabilization depends on the physical boundary or merons. Hence, the size of a bimeron is still sensitive to the exchange interaction J₁. The diameter of meron and bimeron as a function of J₂ is plotted in Figure 3E. Unlike the variations of skyrmion diameter in 3D, the diameter of bimeron oscillates with increasing J₂, indicating that the role of J₂ is indeed different from J₁. In comparison to increasing J₂ in the presence of the perpendicular magnetic anisotropy, bimerons exist in a more broad parametric range with the increasing J₂ in the presence of in-plane magnetic anisotropy.

FIGURE 3

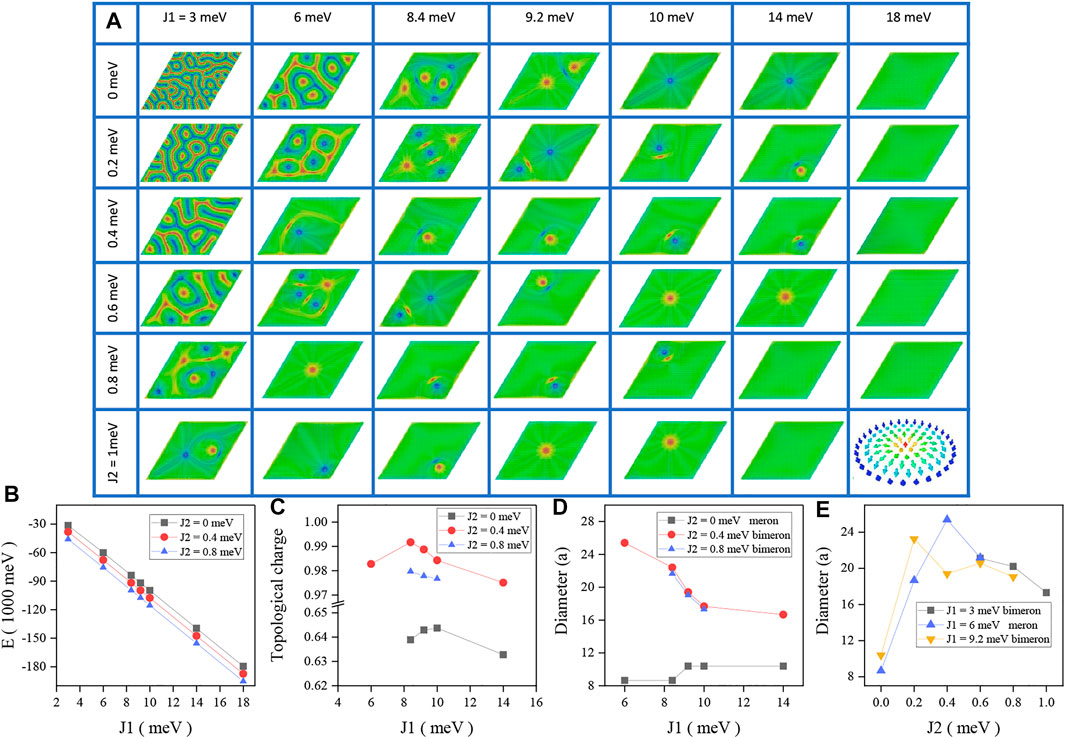
FIGURE 3. (A) Profile of the magnetization of the final state for different J₁ and J₂ in the presence of in-plane magnetic anisotropy. (B) Total energy, (C) topological charge, and diameter of skyrmion (in unit of lattice constant a) as a function of (D) the first-nearest-neighbor exchange interaction J₁ and (E) the next-nearest-neighbor exchange interaction J₂.

Finally, we plot the phase diagram of magnetization of the final states as a function of J₁ and D₂ in Figure 4A. When J₁ is weak, a meron lattice can be found. When J₁ is ranged from 9.2 to 14 meV, the meron lattice evolves into meron chains. With J₁ further increases, the meron chains further evolve to a trimeron. This indicates that the role of J₂ is similar to the role of D₂ and leads to meron-like spin textures. Nevertheless, it is a short-ranged exchange interaction, only resulting in bimerons instead of meron chains or trimerons [27]. In this case, the total energy shown in Figure 4B is similar to the tendency in the presence of exchange interaction in Figure 3B not sensitive to the strength of DM coupling and the difference of spin configurations. The topological number almost remains the same as shown in Figure 4C, while the diameter of bimerons decreases and that of merons almost remains the same with the increasing J₁ in Figure 4D. As mentioned previously, the meron is totally suppressed, while bimeron is stabilized by the meron or physical boundary.

FIGURE 4

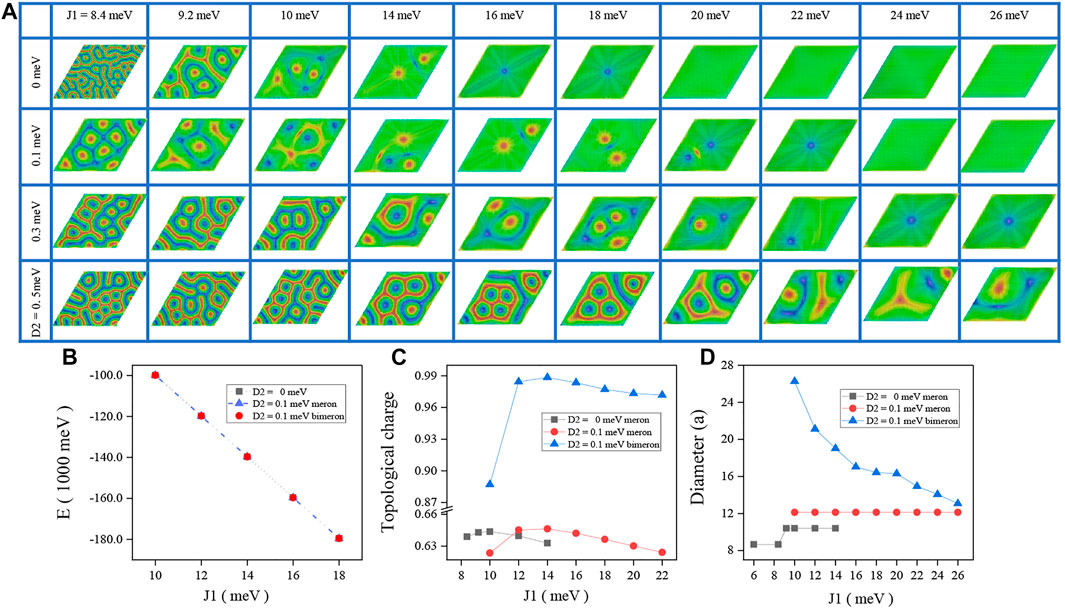
FIGURE 4. Panel (A) Spatial profile of the magnetization of the final state for different J₁ and D₂ with in-plane magnetic anisotropy. (B) Total energy, (C) topological charge, and (D) diameter of skyrmion as a function of the first-nearest-neighbor exchange interactions J₁.

5 Conclusion

We study the stabilization of spin textures in a single-layered ferromagnet with next-nearest-neighbor exchange interactions. It stabilizes the ferromagnetic state and shortens the parametric range of stabilization of Néel skyrmion in the presence of perpendicular magnetic anisotropy and stabilizes bimerons in a wide range of exchange interactions in the presence of in-plane magnetic anisotropy. Numerical simulation shows that creation and annihilation of skyrmionic states with a small size could be tuned by next-nearest-neighbor exchange interactions. This study may open an alternative avenue to the generation, stabilization, and control of magnetic skyrmions in two-dimensional materials.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

HL conceived the idea of the research, WW performed the numerical calculations, and HL and JS wrote the manuscript.

Funding

WW and HL acknowledges the support from the National Natural Science Foundation of China (Grant No. 11804078) and Henan University (Grant No. CJ3050A0240050).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, et al. Electric field effect in atomically thin carbon films. Science (2004) 306:666–9. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Neto AC, Guinea F, Peres NM, Novoselov KS, Geim AK. The electronic properties of graphene. Rev Mod Phys (2009) 81:109–62. doi:10.1103/RevModPhys.81.109

CrossRef Full Text | Google Scholar

3. Santos EJ, Sánchez-Portal D, Ayuela A. Magnetism of substitutional Co impurities in graphene:Realization of single π vacancies. Phys Rev B (2010) 81:125433. doi:10.1103/PhysRevB.81.125433

CrossRef Full Text | Google Scholar

4. Swartz AG, Odenthal PM, Hao Y, Ruoff RS, Kawakami RK. Integration of the ferromagnetic insulator EuO onto graphene. ACS Nano (2012) 6:10063–9. doi:10.1021/nn303771f

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Goerbig MO, Moessner R, Douçot B. Electron interactions in graphene in a strong magnetic field. Phys Rev B (2006) 74:161407. doi:10.1103/PhysRevB.74.161407

CrossRef Full Text | Google Scholar

6. Huang B, Clark G, Klein DR, MacNeill D, Navarro-Moratalla E, Seyler KL, et al. Electrical control of 2D magnetism in bilayer CrI₃. Nat Nanotechnol (2018) 13:544–8. doi:10.1038/s41565-018-0121-3

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bonilla M, Kolekar S, Ma Y, Diaz HC, Kalappattil V, Das R, et al. Strong room-temperature ferromagnetism in VSe₂ monolayers on van der Waals substrates. Nat Nanotechnol (2018) 13:289–93. doi:10.1038/s41565-018-0063-9

PubMed Abstract | CrossRef Full Text | Google Scholar

8. May AF, Ovchinnikov D, Zheng Q, Hermann R, Calder S, Huang B, et al. Ferromagnetism near room temperature in the cleavable van der Waals crystal Fe₅GeTe₂. ACS Nano (2019) 13:4436–42. doi:10.1021/acsnano.8b09660

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ding B, Li Z, Xu G, Li H, Hou Z, Liu E, et al. Observation of magnetic skyrmion bubbles in a van der Waals ferromagnet Fe₃GeTe₂. Nano Lett (2019) 20:868–73. doi:10.1021/acs.nanolett.9b03453

CrossRef Full Text | Google Scholar

10. Wang Y, Wang L, Xia J, Lai Z, Tian G, Zhang X, et al. Electric-field-driven non-volatile multi-state switching of individual skyrmions in a multiferroic heterostructure. Nat Commun (2020) 11:3577. doi:10.1038/s41467-020-17354-7

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hou Z, Wang Y, Lan X, Li S, Wan X, Meng F, et al. Controlled switching of the number of skyrmions in a magnetic nanodot by electric fields. Adv Mater (2022) 34:e2107908. doi:10.1002/adma.202107908

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li S, Du A, Wang Y, Wang X, Zhang X, Cheng H, et al. Experimental demonstration of skyrmionic magnetic tunnel junction at room temperature. Sci Bull (Beijing) (2022) 67:691–9. doi:10.1016/j.scib.2022.01.016

CrossRef Full Text | Google Scholar

13. Yang M, Li Q, Chopdekar R, Dhall R, Turner J, Carlstrom J, et al. Creation of skyrmions in van der Waals ferromagnet Fe₃GeTe₂ on (Co/Pd)_n superlattice. Sci Adv (2020) 6:eabb5157. eabb5157. doi:10.1126/sciadv.abb5157

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lohani V, Hickey C, Masell J, Rosch A. Quantum skyrmions in frustrated ferromagnets. Phys Rev X (2019) 9:041063. doi:10.1103/PhysRevX.9.041063

CrossRef Full Text | Google Scholar

15. Paul S, Haldar S, von Malottki S, Heinze S. Role of higher-order exchange interactions for skyrmion stability. Nat Commun (2020) 11:4756. doi:10.1038/s41467-020-18473-x

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhang X, Xia J, Shen L, Ezawa M, Tretiakov OA, Zhao G, et al. Static and dynamic properties of bimerons in a frustrated ferromagnetic monolayer. Phys Rev B (2020) 101:144435. doi:10.1103/PhysRevB.101.144435

CrossRef Full Text | Google Scholar

17. Oliveira S, Silva R, Silva R, Pereira R. Effects of second neighbor interactions on skyrmion lattices in chiral magnets. J Phys : Condens Matter (2017) 29:205801. doi:10.1088/1361-648X/aa63dd

PubMed Abstract | CrossRef Full Text | Google Scholar

18. May AF, Calder S, Cantoni C, Cao H, McGuire MA. Magnetic structure and phase stability of the van der Waals bonded ferromagnet Fe_3−xGeTe₂. Phys Rev B (2016) 93:93014411. doi:10.1103/PhysRevB.93.014411

CrossRef Full Text | Google Scholar

19. Bogdanov A, Hubert A. Thermodynamically stable magnetic vortex states in magnetic crystals. J Magn Magn Mater (1994) 138:255–69. doi:10.1016/0304-8853(94)90046-9

CrossRef Full Text | Google Scholar

20. Muller GP, Hoffmann M, Dibelkamp C, Schurhoff D, Mavros S, Sallermann M, et al. Spirit: Multifunctional framework for atomistic spin simulations. Phys Rev B (2019) 99:224414. doi:10.1103/PhysRevB.99.224414

CrossRef Full Text | Google Scholar

21. Yang HH, Bansal N, RuBmann P, Hoffmann M, Zhang L, Go D, et al. Magnetic domain walls of the van der Waals material Fe₃GeTe₂. 2d Mater (2022) 9:025022. doi:10.1088/2053-1583/ac5d0e

CrossRef Full Text | Google Scholar

22. Li H, Akosa CA, Yan P, Wang Y, Cheng Z. Stabilization of skyrmions in a nanodisk without an external magnetic field. Phys Rev Appl (2020) 13:034046. doi:10.1103/PhysRevApplied.13.034046

CrossRef Full Text | Google Scholar

23. Woo S, Litzius K, Krüger B, Im MY, Caretta L, Richter K, et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat Mater (2016) 15:501–6. doi:10.1038/nmat4593

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Sun W, Wang W, Li H, Zhang G, Chen D, Wang J, et al. Controlling bimerons as skyrmion analogues by ferroelectric polarization in 2D van der Waals multiferroic heterostructures. Nat Commun (2020) 11:5930. doi:10.1038/s41467-020-19779-6

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhu Y, Fan JY, Wu R. Extend NdJ relationship with the size, multiple exchanges and Dzyaloshinskii-Moriya interaction for Néel skyrmions in hexagonal magnetic interfaces. J Magn Magn Mater (2020) 507:166805. doi:10.1016/j.jmmm.2020.166805

CrossRef Full Text | Google Scholar

26. Hao X, Zhuo F, Manchon A, Wang X, Li H, Cheng Z. Skyrmion battery effect via inhomogeneous magnetic anisotropy. Appl Phys Rev (2021) 8:021402. doi:10.1063/5.0035622

CrossRef Full Text | Google Scholar

27. Sun W, Wang W, Zang J, Li H, Zhang G, Wang J, et al. Manipulation of magnetic skyrmion in a 2D van der Waals heterostructure via both electric and magnetic fields. Adv Funct Mater (2021) 31:2104452. doi:10.1002/adfm.202104452

CrossRef Full Text | Google Scholar