Study on the stability of particle packing structure based on cells

The macroscopic mechanical property and the stability of granular mechanics system are determined by packing structure. Cells play a fundamental role in granular statistical mechanics and thus cells were utilized in this paper to research the packing structure of disk particles and gear particles in a two-dimensional cubic container. The probability distribution of cell order satisfies the exponential function distribution and is independent of intergranular friction, the size of system and vibration. Furthermore, it is observed that friction and system size are the key factors affecting the stability of particle packing structure. Significantly, the relationship between volume fraction and packing structure of disk particles is established under vibration. The experimental results reveal the characteristics of ordered packing structure of disordered particle system in mesoscale and provide data reference for perfecting the theory of particle mechanics.

Introduction

Granular materials constitute a unique and complex class of matter [1–3]. When driven by external forces, granular materials show a highly complex response, mainly due to the strongly dissipative, hysteretic, and nonlinear interactions. The structures of such systems is self-organized dynamically, which is of great significance in science and engineering [4–9]. A central task in this field is to study the change law of particle packing structure in self-organized systems [10].

In the past few decades, different methods have been used to quantify the packing structure of particles. Packing density, coordination number (CN), radial distribution function (RDF) and angular distribution function (ADF) are important parameters to describe structural characteristics [11]. Jalali et al. [12] used a hard sphere model combined with a newly developed densification algorithm to study how a hard sphere system eventually form amorphous or glassy states. The result showed that glass formability is an intrinsic material property necessarily connected to crystal formability. At present, researchers usually use cyclic shear and vibration to achieve densification of particle packing structure [13, 14]. Nicolas et al. [13] studied the densification process of granular materials driven by cyclic shear in experiments. They showed that the dynamics of the system is slow and continuous when the amplitude of the shear is constant, while the volume fraction of the system shows a rapid evolution when the shear amplitude changes suddenly. An [14] used DEM to simulate the packing densification of equal spheres subjected to one-dimensional and three-dimensional vibrations, and obtained the amorphous state and crystalline state with the maximum packing densities of 0.64 and 0.74, respectively. He analyzed in terms of CN, RDF and ADF. It was shown that the distributions of CN have the peak values of 7 and 12 for the amorphous state and crystalline state, respectively. The distributions of RDF and ADF showed isolated peaks and orientation preferences for the crystalline state, indicating the long range and angle correlation among particles commonly observed in the crystalline state. Voronoi tessellation, as a straightforward way to tessellate packing volume, is widely used in particle flow fields [15, 16]. Meyer et al. [4] used the Voronoi diagram to partition the volume. They investigated the existence of random close and random loose packing limits of monodisperse hard disks in a two-dimensional particle system. They used a statistical mechanics approach based on several approximations to predict the probability distribution of volumes, indicating that the limiting densities of the jammed packings exist according to their coordination number and compactivity. This result has implications for the understanding of disordered states in the disk packing problem and the existence of a putative glass transition in two-dimensional systems. In recent years, a new method to describe local random structures has emerged, which consists of constructing space-tessellating volume elements, called quadrons [17, 18]. Matsushima et al. [18] have studied in detail the effects of intergranular friction and initial conditions on the structural characteristics of two-dimensional granular assemblies. They have shown that structure can be analyzed quantitatively by using the quadron description. In particular, they have established that a number of distributions collapse onto single curves, pointing out that structural characteristics are independent of initial states and friction coefficients.

Cells which defined as the smallest closed loops of contacts between particles that touch at least two neighbors are closely related to quadrons [19]. Cells can accurately describe the local structural features and characterize the mechanical stability of the particle system. Establishing the relationship between structural features and mechanical stability of particle systems plays an important role in understanding the properties of the system [6, 19, 20]. Sun et al. [19] used cells to determine the structure characteristics of the particle system under different particle friction coefficients. They found that the probability distribution of cell order satisfies the exponential function distribution, which indicates that the structure of the particle system is self-organized and the distribution characteristics are independent of the friction coefficients. Furthermore, they showed that very high-order cells are short-lived in such systems, implying that the system is liquid-like rather than glassy.

In this paper, cells are used to study the characteristics of packing structure in two-dimensional cubic container under different external forces driving. By comparing the cells differences of disk particles and gear particles in the cubic container under different external forces driving, the rules of the structural characteristics were studied. The paper is organized as follows. In Section 2, we introduce the experimental setup system and cell construction method. In Section 3, we analyze the effects of intergranular friction, the size of system, and vibration on the packing structure characteristics of the disordered two-dimensional particle systems. Finally, the main conclusions of the study are presented in Section 4.

Experiment setup

Experiment parameters

As shown in Figure 1, the whole system consists of a two-dimensional cubic container, a vibrator, a camera and a light source. The two-dimensional cubic container is made of 5 mm toughened glass, with a height of 50 cm, a thickness of 5cm, and a width adjustable within the range of 20–35 cm. The height of camera (3F04M, Revealer, China) can be adjusted to exactly capture the center of the cubic container. The resolution of camera is 1,691 × 1,489 pixels, and the spatial resolution of the image captured by the camera is calculated to be 0.042 mm/px by proportional approximation. The LED (SL-200W, Godox, China) light source has output power of 200 W and beam diameter of 400 mm. The particles we used were made of plexiglass, including gear particles with a diameter of 9.8 mm and a thickness of 4.7 mm, and disk particles with a diameter of 10 mm and a thickness of 4.4 mm.

FIGURE 1

FIGURE 1. Figure of the experimental setup.

First, the experiment should determine the width of the container. Then, the cubic container was placed on the workbench and the particles ware loaded into the container by distributed filling [21]. The light is evenly irradiated on the particles by adjusting the position of the light source. Finally, the aperture and focal length of the camera should be adjusted so that the central point of each particle can be clearly captured.

Similarly, to ensure that uniform force is obtained, the cubic container was placed in the center of the vibrator after the disk particles are loaded by distributed filling in the experiment. The exposure time for the camera is set to 1,000 μs and the sampling rate is 100 fps.

Cells

Figures 2A,B show the images of a certain region of the gear particles and disk particles collected in an experiment, respectively. In order to accurately draw the cell distribution map of particles, a series of processes are performed on the collected images. Firstly, the global threshold segmentation method [22] is used to segment the initial image, and the particles are separated from the image background to obtain a binary image. The global threshold segmentation method is shown in Eq. 1:

$B\left(x,y\right)=\{\begin{array}{c}0,F\left(x,y\right)<\mathrm{T}\\ 1,F\left(x,y\right)\ge \mathrm{T}\end{array}(1)$

where, B(x, y) is the pixel value of the point (x, y) of the binary image after threshold segmentation, 0 represents black, 1 represents white, F(x, y) is the pixel gray value of the point (x, y) in the initial image and T is the best gray threshold. The best gray threshold is selected by the bimodal method. The principle of the bimodal method is that the distribution of the one-dimensional gray histogram of the initial image is bimodal and the two peaks represent the target and the background in the initial image respectively. While the trough represents the edge between the target and the background, which is the best threshold value selected.

FIGURE 2

FIGURE 2. Particle characterization diagram; (A) Initial image of gear particles; (B) Characterization result of gear particles; (C) Initial image of disk particles; (D) Characterization result of disk particles.

Then, the center point of the particle is positioned and the particle is replaced by the center coordinate point. The center point coordinates ($\overline{X}$, $\overline{Y}$) of the particles can be expressed as Eq. 2:

$\{\begin{array}{c}\overline{X}=\frac{\mathit{1}}{S}{\displaystyle \sum }_{x=\mathit{0}}^{M-\mathit{1}}{\displaystyle \sum }_{y=\mathit{0}}^{N-\mathit{1}}yB\left(x,y\right)\\ \overline{Y}=-\frac{\mathit{1}}{S}{\displaystyle \sum }_{x=\mathit{0}}^{M-\mathit{1}}{\displaystyle \sum }_{y=\mathit{0}}^{N-\mathit{1}}xB\left(x,y\right)\\ S={\displaystyle \sum }_{x=\mathit{0}}^{M-\mathit{1}}{\displaystyle \sum }_{y=\mathit{0}}^{N-\mathit{1}}B\left(x,y\right)\end{array}(2)$

where, S represents the area of the connected domain in the binary image, (x, y) represents the coordinates of the pixels in the binary image, (M, N) is the maximum value of pixel coordinates (x, y) in connected domain and B(x, y) is the pixel value corresponding to (x, y) in the binary image.

Finally, determine whether the two particles are in contact with each other. The Euclidean distance method is used to calculate the distance between the center points of two particles, as shown in Eq. 3:

$d\left(\left[{\overline{X}}_{\mathit{1}},{\overline{Y}}_{\mathit{1}}\right],\left[{\overline{X}}_{\mathit{2}},{\overline{Y}}_{\mathit{2}}\right]\right)=\sqrt{{\left({\overline{X}}_{\mathit{1}}-{\overline{X}}_{\mathit{2}}\right)}^{\mathit{2}}+{\left({\overline{Y}}_{\mathit{1}}-{\overline{Y}}_{\mathit{2}}\right)}^{\mathit{2}}}(3)$

For gear particles, set the distance between the center points of adjacent particles as d_g ϵ [d₁, d₂], where d₁ is the inner diameter and d₂ is the outer diameter of the gear particles. When d₁ ≤ d ≤ d₂, the two gear particles are judged to be in contact with each other and the center point coordinates of the two particles are connected. The above calculation process is repeated and the coordinates of the center points of all gear particles that meet the threshold conditions are connected to complete the cell construction. In this way, we can accurately characterize the cell of gear particles as shown in Figure 2B. For disk particles, the diameter d_d = 10 mm of the disk particles is set as the threshold condition to judge whether the two particles are in contact. When d ≤ d_d, the two disk particles are judged to be in contact with each other and the disk particles are operated like the above gear particles to complete the cell construction, as shown in Figure 2D.

The cell order n is equal to the contacts contained in the cell. The blue shadow in Figure 2B indicates the schematic diagram of cell order n = 11 (11-Cell). The blue shadow in Figure 2D indicates the schematic diagram of cell order n = 3 (3-Cell), which is the smallest cell. P(n) is the occurrence probability of cell order n. In the experiment, P(n) can be obtained by counting cell order n in all collected images. Compared with the initial image, we find that there are still errors in judging whether the particles are in contact. The errors are mainly caused by the inevitable distortion at the edges of the initial image. Hence, there is a slight error in the characterization of the particles at the edges of the image. In this regard, we placed the camera as far away from the cubic container as possible to effectively reduce the error.

Results and discussion

Probability distribution of cell order

Figures 3A,B indicate the distribution of gear particles and disk particles in the 35*30 cm container respectively. We can see that the cell distribution of gear particles is relatively loose under gravity, while the cell distribution of disk particles of the same size is relatively concentrated. These results above suggest that the system of disk particles with less friction is more likely to form crystals, while the gear particle system with the friction close to infinity is more likely to form high-order cells [23].

FIGURE 3

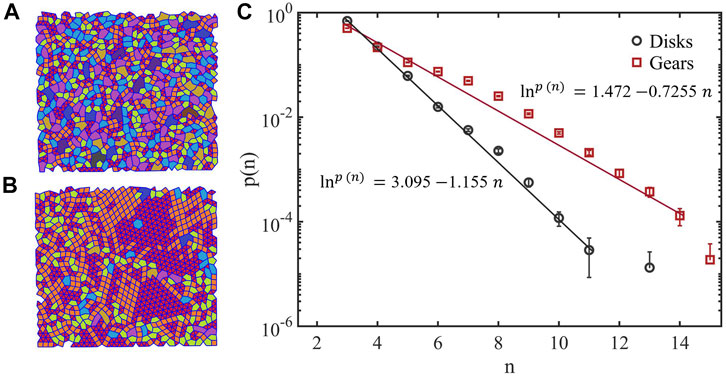
FIGURE 3. The structure characteristics of gear particles and disk particles; (A) Cell distribution of gear particles; (B) Cell distribution of disk particles, different colors are used in the figure to distinguish cells with different orders; (C) Cell order probability of gear particles and disk particles. The abscissa n represents cell order, and the ordinate P(n) represents the occurrence probability of cell order n. The least-square method is used to fit the raw data, and the fitting error is less than 5%.

By counting the cells of each order in 50 experiments, the probability distribution of cell order was obtained, and the result is shown in Figure 3C. It can be seen that the probability distribution of cell order of gear particles and disk particles both obey the exponential function distribution. The cell order probability distribution curve of particle packing satisfies Eq. 4:

$\mathrm{l}{\mathrm{n}}^{p\left(n\right)}=\mathrm{a}+\mathrm{b}n(4)$

where a and b are fitting parameters. The fitting parameter b can characterize the loose degree of the packing structure. The fitting parameter b of gear particles is bigger than that of disk particles, which indicates that the cell distribution of gear particles packing is more loosely. Furthermore, the occurrence probability of cell order n = 3 of disk particles is greater than that of gear particles, the occurrence probability of cell order n = 4 of gear particles and disk particles is about equal. When order n ≥ 5, the occurrence probability of cells order n of gear particles is greater than that of disk particles. Note that the occurrence probability of cell order n = 13 of disk particles and occurrence probability of the cell order n = 15 of gear particles both deviate from the exponential function curve, because the probability of high-order cells appearing is random, which is consistent with the results of self-organized criticality model [24].

Size effect

Figure 4A illustrates the cell order probability distribution of gear particles under different size of system. It can be found that, the cell order probability distribution still satisfies the exponential function distribution after changing the size of system. However, the fitting parameter b of the curve shows an upward trend with the increase of the container width as shown in Figure 4B. This reveals that the increase of the width would lead to the loose packing structure of cells within a certain range of container width, thus reducing the mechanical stability of the particle system. Although the friction of disk particles is different from that of gear particles, the similar phenomenon can also be observed in the disk particles system after changing the size of system, as shown in Figures 4C,D. This shows that the increase of the size of system will reduce the mechanical stability of packing particles [25], which has nothing to do with intergranular friction. However, we need to emphasize that this behavior will likely not continue in the large system limit. On the other hand, we find that the fitting parameter b1 ϵ [-0.742, -0.734] of gear particles is larger than that b2 ϵ [-1.43, -1.38] of disk particles. The slope of b2 with the change of container width is significantly greater than that of b1, which indicates that the smaller the friction between particles, the greater the effect of the size of system on the mechanical stability of particle packing.

FIGURE 4

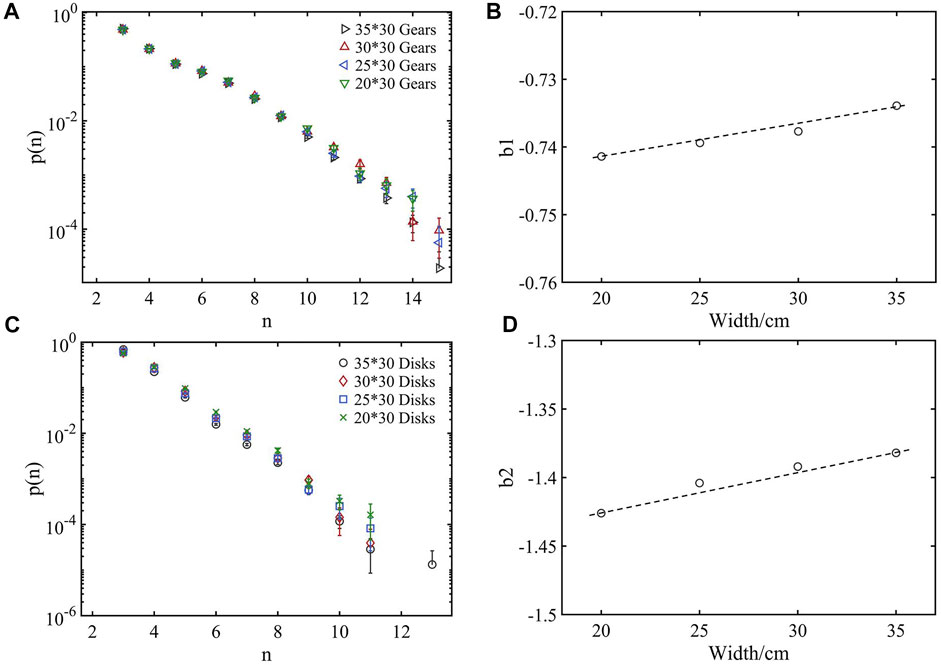
FIGURE 4. The cell order probability distribution of gear particles and disk particles with different container width; (A) Cell order distribution of gear particles; (B) Changes of the fitting parameter b1 for gear particles; (C) Cell order distribution of disk particles; (D) Changes of the fitting parameter b2 for disk particles.

Influence of vibration on structural characteristics of disk particles

Figure 5A shows the probability distribution of cell order of disk particles in the 35*30 cm container under vibration. The vertical frequency is 10 Hz and the amplitude is 0.4 mm. It is observed that the cell order probability distribution always meets the exponential distribution under vibration. It reveals the ordered structure characteristics of particle packing system under external force driving. Moreover, the occurrence probability of cell order n = 3 significantly increases about 22%, while the occurrence probability of cells of other order decreases. This indicates that under the condition of external force driving, the structure of high-order cell is more likely to be destroyed to form 3-Cell, which is the smallest cell.

FIGURE 5

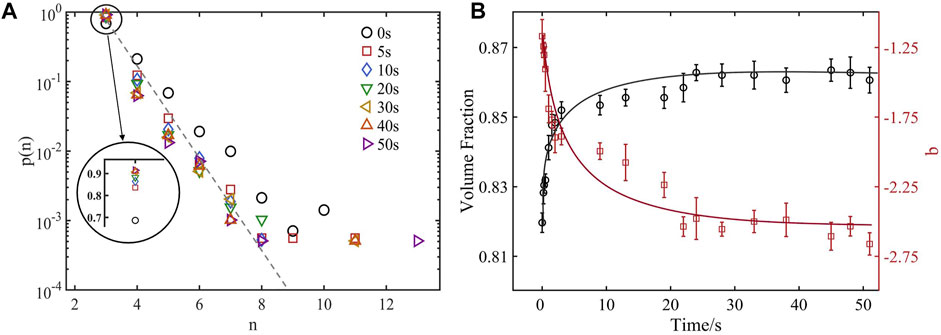
FIGURE 5. Influence of vibration on structural characteristics of disk particles; (A) Cell order distribution of disk particles under vibration; (B) The change of the volume fraction and the fitting parameter b of the disk particles system under vibration.

Figure 5B shows the variation curves of volume fraction and fitting parameter b of disk particles under vibration. Obviously, in the process of vibration, the volume fraction of disk particles is inversely proportional to the fitting parameter b which can describe the loose degree of the packing structure. When t = 0s, the volume fraction of disk particles is the smallest, φ = 0.82, and the value of the fitting parameter b is the largest, b = -1.22. At this moment, the packing structure of disk particles in the cubic container is at its loosest. In the range of t ϵ [0s, 25s], the volume fraction of disk particles increases with the increase of vibration time, while the value of the fitting parameter b decreases. When t > 25 s, the disk particles in the cubic container are in steady state, and the volume fraction of the particle system and the fitting parameter b are basically unchanged.

Conclusion

To conclude, we have studied the effects of intergranular friction, the size of system, and vibration on the packing structure characteristics in disordered 2D granular systems. By measuring the cells of gear particles and disk particles in the 2D cubic container, we found that the cell order probability distribution of particle packing meets exponential function distribution, which is independent of intergranular friction, the size of system and vibration. Furthermore, cell order probability distribution always meets exponential function distribution under different size of system. Within a certain width range, the fitting parameter b shows an upward trend with the increase of the container width, which indicates that the larger the particle system, the worse the stability of the particle packing structure. It is worth noting that the volume fraction of disk particles is inversely proportional to the fitting parameter b under vibration. The experimental results reveal the ordered packing structure characteristics of disordered particle system in mesoscale and provide reference data for improving the transportation and processing technology of granular materials in industrial production.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HY:Writing—original draft, Investigation. XY:Writing—original draft. DH:Writing—original draft. YH:Writing—review and editing. CZ:data curation. LR:Validation, Funding acquisition.

Funding

This work has been supported by the National Natural Science Foundation of China (11972212, 11902190, 12072200, 12002213). I would like to express my gratitude to Jie Zhang of Shanghai Jiao Tong University and other relevant teachers and students for their help and support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jaeger HM, Nagel SR, Behringer RP. Granular solids, liquids, and gases. Rev Mod Phys (1996) 68(4):1259–73. doi:10.1103/RevModPhys.68.1259

CrossRef Full Text | Google Scholar

2. Yang H, Zhang BF, Li R, Zheng G, Zivkovic V. Particle dynamics in avalanche flow of irregular sand particles in the slumping regime of a rotating drum. Powder Technol (2017) 311:439–48. doi:10.1016/j.powtec.2017.01.064

CrossRef Full Text | Google Scholar

3. Papadopoulos L, Porter MA, Daniels KE, Bassett DS. Network analysis of particles and grains. J Complex Netw (2018) 6(4):485–565. doi:10.1093/comnet/cny005

CrossRef Full Text | Google Scholar

4. Meyer S, Song C, Jin Y, Wang K, Makse HA. Jamming in two-dimensional packings. Physica A: Stat Mech its Appl (2010) 389(22):5137–44. doi:10.1016/j.physa.2010.07.030

CrossRef Full Text | Google Scholar

5. Wang P, Song C, Jin Y, Makse HA. Jamming II: Edwards’ statistical mechanics of random packings of hard spheres. Physica A: Stat Mech its Appl (2011) 390(3):427–55. doi:10.1016/j.physa.2010.10.017

CrossRef Full Text | Google Scholar

6. Baule A, Morone F, Herrmann HJ, Makse HA. Edwards statistical mechanics for jammed granular matter. Rev Mod Phys (2018) 90(01):015006. doi:10.1103/RevModPhys.90.015006

CrossRef Full Text | Google Scholar

7. Kato A, Thau D, Hudak AT, Meigs GW, Moskal LM. Quantifying fire trends in boreal forests with Landsat time series and self-organized criticality. Remote Sensing Environ (2020) 237:111525. doi:10.1016/j.rse.2019.111525

CrossRef Full Text | Google Scholar

8. Filho ASN, Araújo MLV, Miranda JGV, Murari TB, Saba H, Moret MA. Self-affinity and self-organized criticality applied to the relationship between the economic arrangements and the dengue fever spread in Bahia. Physica A: Stat Mech its Appl (2018) 502:619–28. doi:10.1016/j.physa.2018.03.024

CrossRef Full Text | Google Scholar

9. Mauro JC, Diehl B, Marcellin RF, Vaughn DJ. Workplace accidents and self-organized criticality. Physica A: Stat Mech its Appl (2018) 506:284–9. doi:10.1016/j.physa.2018.04.064

CrossRef Full Text | Google Scholar

10. Matsushima T, Blumenfeld R. Universal structural characteristics of planar granular packs. Phys Rev Lett (2014) 112(9):098003. doi:10.1103/PhysRevLett.112.098003

PubMed Abstract | CrossRef Full Text | Google Scholar

11. An XZ, Yang RY, Zou RP, Yu AB. Effect of vibration condition and inter-particle frictions on the packing of uniform spheres. Powder Technol (2008) 188(2):102–9. doi:10.1016/j.powtec.2008.04.001

CrossRef Full Text | Google Scholar

12. Jalali P, Li M. Atomic size effect on critical cooling rate and glass formation. Phys Rev B (2005) 71(1):014206. doi:10.1103/PhysRevB.71.014206

CrossRef Full Text | Google Scholar

13. Nicolas M, Duru P, Pouliquen O. Compaction of a granular material under cyclic shear. The Eur Phys J E (2000) 3:309–14. doi:10.1007/s101890070001

CrossRef Full Text | Google Scholar

14. An XZ. Densification of the packing structure under vibrations. Int J Miner Metall Mater (2013) 20(5):499–503. doi:10.1007/s12613-013-0757-9

CrossRef Full Text | Google Scholar

15. Song J, Yang H, Li R, Chen Q, Zhang YJ, Wang YJ, et al. Improved PTV measurement based on Voronoi matching used in hopper flow. Powder Technol (2019) 355:172–82. doi:10.1016/j.powtec.2019.07.003

CrossRef Full Text | Google Scholar

16. Asahina D, Bolander JE. Voronoi-based discretizations for fracture analysis of particulate materials. Powder Technol (2011) 213(1):92–9. doi:10.1016/j.powtec.2011.07.010

CrossRef Full Text | Google Scholar

17. Blumenfeld R, Edwards SF. Geometric partition functions of cellular systems: Explicit calculation of the entropy in two and three dimensions. Eur Phys J E (2006) 19:23–30. doi:10.1140/epje/e2006-00014-7

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Matsushima T, Blumenfeld R. Fundamental structural characteristics of planar granular assemblies: Self-organization and scaling away friction and initial state. Phys Rev E (2017) 95(3):032905. doi:10.1103/PhysRevE.95.032905

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sun X, Kob W, Blumenfeld R, Tong H, Wang Y, Zhang J. Friction-controlled entropy-stability competition in granular systems. Phys Rev Lett (2020) 125(26):268005. doi:10.1103/PhysRevLett.125.268005

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Blumenfeld R, Edwards SF. Granular entropy: Explicit calculations for planar assemblies. Phys Rev Lett (2003) 90(11):114303. doi:10.1103/PhysRevLett.90.114303

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Nielsen J. Pressures from flowing granular solids in silos. Philos Trans R Soc Lond Ser A: Math Phys Eng Sci (1998) 356(1747):2667–84. doi:10.1098/rsta.1998.0292

CrossRef Full Text | Google Scholar

22. Yu BW, Liu YF, Zhao T. Counting of pine wood nematode disease trees based on threshold segmentation. J Phys : Conf Ser (2021) 1961(1):012033. doi:10.1088/1742-6596/1961/1/012033

CrossRef Full Text | Google Scholar

23. Papanikolaou S, O’Hern CS, Shattuck MD. Isostaticity at frictional jamming. Phys Rev Lett (2013) 110(19):198002. doi:10.1103/PhysRevLett.110.198002

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Marković D, Gros C. Power laws and self-organized criticality in theory and nature. Phys Rep (2014) 536(2):41–74. doi:10.1016/j.physrep.2013.11.002

CrossRef Full Text | Google Scholar

25. Hummel M, Böhm C, Verestek W, Schmauder S. Introducing a method of constructing realistic closed cell nano-porous iron crystals and MD simulations to investigate the influence of the system size on the stability and the mechanical properties. Comput Mater Sci (2019) 166:150–4. doi:10.1016/j.commatsci.2019.04.035

CrossRef Full Text | Google Scholar