- 1Center for Cognition and Neuroergonomics, State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Zhuhai, China
- 2Faculty of Science, University of Kragujevac, Kragujevac, Serbia
- 3Department of Mechanical Engineering, City University of Hong Kong, Hong Kong, China
- 4Department of Electrical Engineering, Ajman University, Ajman, United Arab Emirates
We analyze the effect of launch beam distribution on space-division multiplexing (SDM) performance in multimode multicore silica optical fibers (MM MC SOF) with seven cores. The time-independent power flow equation (TI PFE) is used to explore the effect of the width of the distribution of the Gaussian launch beam on power flow in each of the seven cores. We show that the optical fiber length at which the equilibrium mode distribution (EMD) and steady-state distribution (SSD) are obtained is greatly influenced by the width of the Gaussian launch beam distribution. We further show that when the width of the Gaussian launch beam distribution widens, the optical fiber length at which angular division multiplexing (ADM) in each of the seven cores can be realized with minimal crosstalk between neighboring angular optical channels decreases. We demonstrate that, for increasing the capacity of an optical fiber transmission system, an SDM system with two- and three-channel ADM and multicore optical fiber multiplexing can be implemented with the proposed seven-core MM MC SOF at optical fiber lengths up to ≈1 km (2 ADM channels × 7 cores) and ≈200 m (3 ADM channels × 7 cores), respectively. Such characterization of MM MC SOFs under various launch conditions is important for building a multicore optical fiber SDM transmission system.
Introduction
Optical fiber communication is the backbone of worldwide telecommunications infrastructure. In the last two decades, the capacity of optical fiber transmission systems has increased as a result of technological advancements such as low-loss single-mode and multimode fibers, spectral coding, fiber amplifiers, and multiplexing [1]. Optical signal multiplexing is usually realized in wavelength, polarization, time, phase, and space [1, 2]. Although wavelength-division multiplexed (WDM) systems using typical commercial single-mode single-core fibers (SM SCFs) can enhance the transmission capacity by two orders of magnitude, current studies suggest that WDM systems are rapidly nearing their Shannon capacity limit [3]. SDM, including mode division multiplexing via MM or few-mode fibers and/or core multiplexing using multicore fibers (MCFs) [4], has gotten much attention in the last decade as the next step in multiplicative capacity growth in optical fiber transmission systems [5–9].
Research on SDM transmission in MM SCFs has recently seen tremendous progress, with efficient solutions for signal multiplexing/de-multiplexing in MM fibers and integrated MM amplification. For example, every ADM channel inside the carrier MM SCF is assigned radially distributed, dedicated spatial positions in the case of SDM when using the same wavelength [10]. The launch angle and mode coupling strength determine where each channel is located inside the MM SCF. To further increase the capacity of SDM in MM fibers, MM MCF has been proposed as a promising spatial avenue.
SM SOFs have been the chosen solution for long-distance and high-capacity communications networks, laser beam delivery, sensing systems, lane control signaling devices, and other applications for decades. To increase the capacity of SOF systems, we here present an SDM scheme in a custom-designed MM MC SOFs which have seven cores arrayed in a hexagonal arrangement. The differential mode attenuation and the rate of mode coupling both influence the optical signal transmission characteristics of MM optical fibers [11–17]. By solving the TI PFE, we explore the effect of the width of the Gaussian launch beam distribution on the state of mode coupling, EMD and SSD in MM MC SOFs with seven cores. In the core-cladding interface, the refractive index (RI) profile of homogenous cores shows a gap between two constant values. The effect of mode coupling changes the input angular power distribution that comes from a particular launch as the distance from the input end of the optical fiber increases. As a result, the far-field radiation patterns are changed [18]. For example, a ring pattern can be obtained at the output optical fiber end in the case of a short optical fiber, for a centrally symmetric launch (along a cone) at an angle θ0 from the fiber axis. With increasing optical fiber length, the boundaries of the ring will blur, and the ring progressively morphs into a disk, which is a consequence of the mode coupling that occurs in optical fiber. At coupling length Lc, the distribution of the highest order guiding modes shifts the mid-point to θ = 0o, when an EMD is attained. The unique angular power distribution will become fixed and centered (independently on the launch beam angle θ0 and the width of the launch beam distribution) when the optical fiber is lengthened beyond the value known as zs, denoting that an SSD is established.
The modelling of propagation and SDM in MM optical fibers is still a challenging task since until recently, commercial simulation software packages were not designed neither for MM SCFs nor MM MCFs. This deficiency has been addressed in our previous works for modeling a different types of conventional MM SCFs [10, 13, 15, 17, 18]. In this work, by numerically solving the TI PFE for varying widths of the launch beam distribution, we calculate the length at which the EMD and an SSD is attained in each of the seven cores of the MM MC SOF. Also, an analysis is conducted on how the width of the Gaussian launch beam distribution affects the optical fiber length at which ADM in each of the seven cores may be achieved with minimum crosstalk among neighboring angular optical channels.
Time-independent power-flow equation
Gloge’s TI PFE for simulation of the power distribution within a multimode SI optical fiber is [11]:
where P(θ,z) denotes the angular power distribution, θ is the propagation angle to the core axis, z is the distance from the input end of the optical fiber, D is the coupling coefficient (which is assumed constant [11, 14, 17, 18]), and α(θ) is the modal attenuation. Since α(θ) need not be considered when accounting for mode coupling in Eq. 1 and Eq. 1 becomes [15]:
The boundary conditions are P(θc,z) = 0, where θc is the critical angle of the fiber, and D(∂P/∂θ) = 0 at θ = 0. Condition P(θc,z) = 0 implies that modes with infinitely high loss do not carry power. Condition D(∂P/∂θ) = 0 at θ = 0 indicates that the coupling is limited to the modes propagating with θ > 0. We used the explicit finite-difference method [15] to obtain a numerical solution for the TI PFE (2) for Gaussian launch-beam distribution:
Here, 0≤θ≤θc, θ0 is the incidence angle distribution’s mean value, θc denotes the critical angle, and σ specifies the standard deviation (FWHM =
Numerical results and discussion
The SDM capability of MM MC SOFs with seven cores, which is designed based on the SC SOF experimentally examined by [19], is investigated in this article. Figure 1A shows the cross-section of the MM MC SOF with seven cores placed in a hexagonal arrangement. Individual cores and cladding for the MM MC SOF are presumed to be composed of the same material as the core and cladding of SC SOF. The MM SC SOF has a diameter of 600 μm, NA = 0.22, core RI n1 = 1.4570 at λ = 633 nm, and a critical angle of θc = 8.8. To avoid core-to-core mode coupling, the MM MC SOF with a diameter d = 600 μm has seven cores with a radius a = 25 μm, with inter-core distance Λ = 250 µm (the cores are uncoupled for Λ ≥ 7a) [3] (see Figure 1). The coupling coefficient for the MM SC SOF investigated by [19] was D = 4.9 × 10–7 rad2/m, which is used in this work in modeling mode coupling in MM MC SOF.
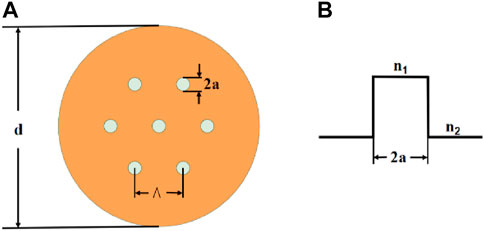
FIGURE 1. Schematic of (A) the cross-section of MM MC SOF, and (B) the index profile of the core structure.
Using the following equation
we obtain a number of modes N = 1,490 in each of the seven cores of the proposed MM MC SOF. A large number of modes can be seen as a modal continuum, which is necessary for the employment of Eq. 2.
To make comparisons easier, we solved the TI PFE (2) and calculated the lengths at which the EMD and SSD are attained in each of the seven cores of the MM MC SOF for various widths of the Gaussian distribution of the launch beam. Figure 2 shows the normalized output angular power distribution for different optical fiber lengths, when a Gaussian beam with (FWHM)z=0 = 1 was launched at different input angles θ0 = 0, 4, and 8 (three different angular optical channels).
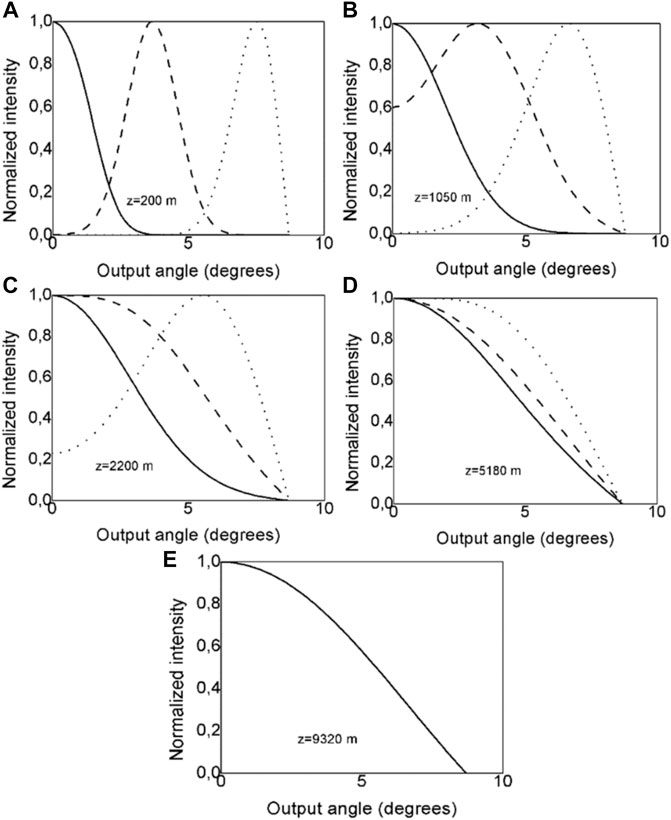
FIGURE 2. Normalized output angular power distributions of different locations along each carrier seven cores of the MM MC SOF, for different Gaussian input angles θ0 = 0 (solid line), 4 (dashed line) and 8o (dotted line), with (FWHM)z=0 = 1 for: (A) z = 200 m; (B) z = 1,050 m; (C) z = 2,200 m; (D) z = Lc = 5,180 m and (E) z = zs = 9,320 m (The solid line, dashed line and dotted line are overlapped at fiber length zs at which SSD is established).
If the launch beam distribution at the input of the optical fiber is centered at θ0 = 0, by increasing the optical fiber length, the width of the angular power distribution grows, owing to mode coupling, as shown in Figure 2. The radiation patterns of non-centrally launched Gaussian beams, as Figure 2A shows, are centered near their initial values, which leads to minimization of crosstalk between the neighboring co-propagating optical channels. With increasing optical fiber length, all radiation patterns become broader, thus increasing crosstalk among the three co-propagating channels. At coupling length Lc = 5,180 m (Figure 2D), where the highest order guiding modes centered their mode-distribution at θ = 0, the EMD is achieved. At zs = 9,320 m, an SSD is established (Figure 2E). One should see from Figure 2E that the solid line, dashed line and dotted line, which represent angular power distributions for different launch angles, are overlapped at fiber length zs at which SSD is established. This unique angular power distribution, shown as a solid line, became fixed and centered, denoting that an SSD is established. Mode coupling restricts the length of the proposed MM MC SOF at which an ADM may be implemented, as can be seen. In each carrier seven cores of the investigated MM MC SOF, a three-channel ADM (with launch angles θ0 = 0, 4, and 8) and two-channel (with launch angles θ0 = 0 and 8°) can be realized at a maximum length of 200 m (Figure 2A) and 1,050 m (Figure 2B), respectively.
Table 1 shows that as the width of the distribution of the Gaussian launch beam increases, the length Lc required for obtaining the EMD, and the length zs required for establishing the SSD, decreases. Due to the energy of a wide Gaussian launch beam being divided more evenly between guided modes in the optical fiber, wide beams realizing EMD and SSD are forced to travel shorter distances than narrow Gaussian launch beams (Figure 3). As a result, the three-channel and two-channel ADM in each carrier seven cores of the MM MC SOF can be realized at longer fiber lengths for narrower Gaussian launch beam distributions.

TABLE 1. The calculated length Lc for obtaining the EMD, length

FIGURE 3. Length Lc for obtaining the EMD and length.
For increasing the capacity of an optical fiber transmission system, an SDM with two- and three-channel ADM and multicore multiplexing is feasible with a seven-core MM MC SOF at fiber lengths up to ≈1 km (2 ADM channels × 7 cores) and ≈200 m (3 ADM channels × 7 cores), respectively. In general, an MM optical fiber that has weaker mode coupling is a good potential candidate for SDM. These MM MC SOF’s characteristics could be useful in their potential applications as a part of a telecommunication and sensory systems [20–22]. As a comparison, due to much stronger mode coupling in multimode seven-core plastic optical fibers (D≃10−4 rad2/m), SDM with two-channel ADM and multicore multiplexing can be realized at fiber length of ≈7 m [23].
Finally, it is interesting to note that the theoretical approach of modal diffusion in MM MC SOF employed in this work can be used for calculation of fiber’s bandwidth, but instead of time-independent power flow Eq. 2 which is solved in this work, one has to solve the time-dependent power flow equation.
Conclusion
To further enhance the SDM capability of MM SOFs, we designed a MM MC SOF with seven cores. By employing the TI PFE, the effect of the width of the Gaussian launch beam distribution on EMD and SSD in each carrier seven cores of the MM MC SOF is examined. The numerical solutions of the TI PFE demonstrate that with increasing width of the Gaussian launch beam distribution, the length Lc required to obtain EMD and the length zs required to establish SSD decreases. We showed that mode coupling is a mechanism that limits the length for practical realizations of three-channel and two-channel ADM in the MM MC SOF. We found that an SDM with two- and three-channel ADM and multicore multiplexing in the MM MC SOF investigated in this work can be realized at optical fiber lengths up to ≈1 km (2 ADM channels × 7 cores) and ≈200 m (3 ADM channels × 7 cores), respectively. The findings of this study should be taken into account when constructing MM MC SOF transmission systems for SDM with various launch beam characteristics.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SS: Methodology, Conceptualization, Formal analysis, Validation, Writing—original draft. WD: Formal analysis, Validation. AD: Formal analysis, Validation, Writing—review and editing. KA: Validation, Writing—review and editing. ZL: Validation, Writing—review and editing. RM: Conceptualization, Formal analysis, Funding acquisition, Writing—review and editing.
Funding
National Natural Science Foundation of China (62003046, 6211101138); Strategic Research Grant of City University of Hong Kong (CityU 7004600); Serbian Ministry of Education, Science and Technological Development grant (451-03-68/2022-14/200122); Science Fund of the Republic Serbia (CTPCF-6379382); Guangdong Basic and Applied Basic Research Foundation (2021A1515011997); Special project in key field of Guangdong Provincial Department of Education (2021ZDZX1050); The Innovation Team Project of Guangdong Provincial Department of Education (2021KCXTD014).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Richardson DJ, Fini JM, Nelson LE. Space-division multiplexing in optical fibres. Nat Photon (2013) 7(5):354–62. doi:10.1038/nphoton.2013.94
2. Montero DS, Garcilópez IP, García CV, Lallana PC, Moraleda AT, Castillo PJP. Recent advances in wavelength-division-multiplexing plastic optical fiber technologies. Rijeka: InTech (2015).
3. Ortiz AM, Sáez RL. Multi-core optical fibers: Theory, applications and opportunities. In: Selected topics on optical fiber technologies and applications. London, UK: IntechOpen (2017). p. 63–102.
4. Saitoh K, Matsuo S. Multicore fibers for large capacity transmission. Nanophotonics (2013) 2(5-6):441–54. doi:10.1515/nanoph-2013-0037
5. Kokubun Y, Koshiba M. Predictable and unpredictable phenomena in optical fibers for space-division/mode-division multiplexing transmission: Statistical analysis of coupling and mysterious behavior of modes. IEICE Electron Express (2020) 17(15):20202001. doi:10.1587/elex.17.20202001
6. Malhotra A, Kaur G, Goyal R, Rani M. Design and investigation of high-capacity spatial-division multiplexing network employing a multimode fiber. J Russ Laser Res (2020) 41:544–51. doi:10.1007/s10946-020-09909-2
7. Brunet C, Ung B, Bélanger PA, Messaddeq Y, LaRochelle S, Rusch LA. Vector mode analysis of ring-core fibers: Design tools for spatial division multiplexing. J Lightwave Technol (2014) 32(23):4648–59. doi:10.1109/jlt.2014.2361432
8. Zhou Y, Su H. Research on mode-coupled multi-mode fiber mode-division in multiplexing transmission system, Journal of Physics: Conference Series, Vol. 2246. In: 8th International Symposium on Sensors, Mechatronics and Automation System (2022).
9. Murshid SH, Chakravarty A, Biswas R. Attenuation and modal dispersion models for spatially multiplexed co-propagating helical optical channels in step index fibers. Opt Laser Technology (2011) 43(3):430–6. doi:10.1016/j.optlastec.2010.06.004
10. Savović S, Djordjevich A, Simović A, Drljača B. Influence of mode coupling on three, four and five spatially multiplexed channels in multimode step-index plastic optical fibers. Opt Laser Technology (2018) 106:18–21. doi:10.1016/j.optlastec.2018.03.015
11. Gloge D. Optical power flow in multimode fibers. Bell Syst Tech J (1972) 51(8):1767–83. doi:10.1002/j.1538-7305.1972.tb02682.x
12. Gambling WA, Payne DN, Matsumura H. Mode conversion coefficients in optical fibers. Appl Opt (1975) 14(7):1538–42. doi:10.1364/ao.14.001538
13. Savović S, Djordjevich A. Influence of the angle-dependence of mode coupling on optical power distribution in step-index plastic optical fibers. Opt Laser Technology (2012) 44(1):180–4. doi:10.1016/j.optlastec.2011.06.015
14. Rousseau M, Jeunhomme L. Numerical solution of the coupled-power equation in step-index optical fibers. IEEE Trans Microw Theor Tech (1977) 25(7):577–85. doi:10.1109/tmtt.1977.1129162
15. Djordjevich A, Savović S. Investigation of mode coupling in step index plastic optical fibers using the power flow equation. IEEE Photon Technol Lett (2000) 12(11):1489–91. doi:10.1109/68.887704
16. Garcés I, Mateo J, Salinas I, Lou J, Zubía J, Zubia J. Mode coupling contribution to radiation lossesin curvatures for high and low numerical aperture plastic optical fibers. J Lightwave Technol (2002) 20(7):1160–4. doi:10.1109/jlt.2002.800377
17. Savović S, Djordjevich A. Mode coupling and its influence on space division multiplexing in step-index plastic-clad silica fibers. Opt Fiber Technology (2018) 46:192–7. doi:10.1016/j.yofte.2018.10.005
18. Savović S, Djordjevich A. Calculation of the coupling coefficient in strained step index plastic optical fibers. Appl Opt (2008) 47(27):4935–9. doi:10.1364/ao.47.004935
19. Hurand S, Chauny LA, El-Rabii H, Joshi S, Yalin AP. Mode coupling and output beam quality of 100–400 μm core silica fibers. Appl Opt (2011) 50(4):492–9. doi:10.1364/ao.50.000492
20. Mishra GP, Kumar D, Chaudhary VS, Murmu G. Cancer cell detection by a heart-shaped dual-core photonic crystal fiber sensor. Appl Opt (2020) 59(33):10321–9. doi:10.1364/ao.409221
21. Mishra GP, Kumar D, Chaudhary VS, Sharma S. Terahertz refractive index sensor with high sensitivity based on two-core photonic crystal fiber. Microw Opt Technol Lett (2021) 63(1):24–31. doi:10.1002/mop.32573
22. Chaudhary VS, Kumar D, Mishra R, Sharma S. Twin core photonic crystal fiber for temperature sensing. Mater Today Proc (2020) 33(5):2289–92. doi:10.1016/j.matpr.2020.04.197
Keywords: launch beam distribution, power flow, coupling length, angular division multiplexing, multicore optical fiber
Citation: Savović S, Dai W, Djordjevich A, Aidinis K, Li Z and Min R (2022) Influence of launch beam distribution on power flow and angular division multiplexing in seven-core silica optical fibers. Front. Phys. 10:993738. doi: 10.3389/fphy.2022.993738
Received: 14 July 2022; Accepted: 25 July 2022;
Published: 01 September 2022.
Edited by:
Sushank Chaudhary, Quanzhou Institute of Equipment manufacturing, Chinese academy of Sciences, China, ChinaReviewed by:
Dharmendra Kumar, Madan Mohan Malaviya University of Technology, IndiaYongxing Guo, Wuhan University of Science and Technology, China
Copyright © 2022 Savović, Dai, Djordjevich, Aidinis, Li and Min. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zheng Li, bHpAYm51LmVkdS5jbg==; Rui Min, cnVtaUBkb2N0b3IudXB2LmVz
 Svetislav Savović
Svetislav Savović Wenjing Dai1
Wenjing Dai1 Zheng Li
Zheng Li Rui Min
Rui Min