Shear-induced diffusion and dynamic heterogeneities in dense granular flows

We study two-dimensional dense granular flows by molecular dynamics simulations. We quantify shear-induced diffusion of granular particles by the transverse component of particle displacements. In long time scales, the transverse displacements are described as normal diffusion and obey Gaussian distributions, where time correlations of particle velocities entirely vanish. In short time scales, the transverse displacements are strongly non-Gaussian if the system is dense and sheared quasistatically though memory effects on the particle velocities are further suppressed. We also analyze spatio-temporal structures of the transverse displacements by self-intermediate scattering functions and dynamic susceptibilities. We find that the relation between the maximum intensity and characteristic time scale for dynamic heterogeneities is dependent on the models of contact damping (which exhibit different rheological properties such as the Newtonian fluids’ behavior and shear thickening). In addition, the diffusion coefficient over the shear rate is linear (sub-linear) in the maximum of dynamic susceptibility if the damping force is not restricted (restricted) to the normal direction between the particles in contact.

1 Introduction

Flows of granular materials are of great importance to engineering technology [1, 2] and a better understanding of their transport phenomena is crucial to many industrial processes such as mixing and segregation [3]. Because constituent grains are macroscopic in size, e.g., are typically from few μm to mm in diameter [4], thermal fluctuations do not play a role in flows and transport phenomena of granular materials. This means that granular flows are induced only by external forces and “mechanically driven” particle motions have extensively been studied by experiments [5–12] and numerical simulations [13–19]. It now seems to be a common consensus that collective motions of granular particles are more pronounced as the system approaches the jamming transition [20].

In recent years, diffusion of the particles under shear, i.e. shear-induced diffusion, has widely been investigated by experiments [21–25] and molecular dynamics (MD) simulations [26–31]. From a scaling argument, the shear-induced diffusion coefficient scales as $D\sim d_0^2\dot{\gamma }$ with the particle diameter d₀ and externally imposed shear rate $\dot{\gamma }$ [21–23]. The scaling argument implies that the diffusion coefficient is proportional to the shear rate. However, a crossover from $D\propto \dot{\gamma }$ to ${\dot{\gamma }}^{0.8}$ (with increasing $\dot{\gamma }$) was observed in MD simulations of two- and three-dimensional particles [16, 26]. These results agree with laboratory experiments of colloidal glasses under shear [24] and suggest that the shear-induced diffusion does not depend on spatial dimensions. Another crossover from $D\propto \dot{\gamma }$ to ${\dot{\gamma }}^{1/2}$ was also found in a model of amorphous solids [29]. In addition, sub-linear scaling, $D\propto {\dot{\gamma }}^{q_D}$, was examined near the jamming transition density ϕ_J, where the exponent varies as q_D = 1 (ϕ < ϕ_J), 0.78 (ϕ ≃ ϕ_J), and 0.68 (ϕ > ϕ_J) with the increase of particle packing fraction ϕ [27].

The collective motions of the particles enhance self-diffusion and thus the scaling argument was revised as $D\sim d_0\xi \dot{\gamma }$ with a typical size of collective motions, ξ [28]. The typical size can be extracted, e.g. from a spatial correlation function of particle velocities, and it has been suggested that $\xi \sim {\dot{\gamma }}^{-0.23}$ near jamming (ϕ ≃ ϕ_J) [16] and $\xi \sim {\dot{\gamma }}^{-1/2}$ above jamming (ϕ > ϕ_J) [28, 29]. If the system is below jamming (ϕ < ϕ_J), critical divergence of the size was found as ξ ∼|Δϕ|^−0.6 in overdamped MD simulations [20], where Δϕ ≡ ϕ − ϕ_J is the proximity to jamming. However, ξ ∼|Δϕ|⁻¹ was reported in quasi-static simulations [32].

In addition to the shear-induced diffusion, analogies with dynamic heterogeneities [33, 34] have also been made by experiments [9, 10] and numerical simulations [15–17]. Associating the mechanical driving with thermal fluctuations, the physicists have analyzed heterogeneous nature of particle motions both in space and time. Then, a link between the shear-induced diffusion and dynamic heterogeneities was suggested as $D\sim {\chi }_s^{\ast }\dot{\gamma }$ by the elastoplastic model in two-dimension (not in three-dimension) [35], where ${\chi }_s^{\ast }$ represents the maximum intensity of dynamic heterogeneities. Results in prior works, however, are controversial, e.g. the maximum intensity scales as ${\chi }_s^{\ast }\sim |\mathrm{\Delta }\varphi {|}^{-1.8}$ for ϕ < ϕ_J and ${\chi }_s^{\ast }\sim \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.$ for ϕ > ϕ_J in quasi-static simulations [17], while ${\chi }_s^{\ast }\sim |\mathrm{\Delta }\varphi {|}^{-1.2}{\dot{\gamma }}^{-0.3}$ was suggested for both below and above jamming by experiments [10]. Moreover, the scaling, $D\sim {\chi }_s^{\ast }\dot{\gamma }$, has not yet been tested by MD simulations of sheared granular materials. Interestingly, particle motions in oscillatory sheared granular materials [6], air-fluidized bed [7], and horizontally vibrated granular media [36] have similarities to glass forming liquids [33, 34], where both length and time scales for dynamic heterogeneities diverge at the jamming transition density.

In this paper, we study the shear-induced diffusion and dynamic heterogeneities in dense granular flows by MD simulations. We investigate wide ranges of control parameters, i.e. the packing fraction of the particles ϕ and shear rate $\dot{\gamma }$, to examine the scaling relation, $D\sim {\chi }_s^{\ast }\dot{\gamma }$, both below and above jamming, and in both quasi-static and fast flow regimes. In the following sections, we introduce our numerical method in Section 2 and show our results in Section 3. Then, we discuss our results in Section 4 and conclude our findings in Section 5.

2 Method

We study dense granular flows in two dimensions by MD simulations. To avoid crystallization of the system, we randomly distribute a 50 : 50 binary mixture of N = 2048 particles in a L × L square periodic box. Different kinds of particles have the same mass m and different diameters, d_S and d_L = 1.4d_S [20, 37]. Repulsive force between the particles, i and j, in contact is modeled as elastic force, ${\mathit{f}}_{ij}^{\text{e}}=k_{\text{e}}{l}_{ij}{\mathit{n}}_{ij}$, where k_e is a spring constant and n_ij ≡r_ij/|r_ij| with the relative position between the particles, r_ij, is the normal unit vector. Here, l_ij ≡ R_i + R_j − |r_ij| > 0 represents an overlap between the particles, where R_i (R_j) is the radius of i(j)-th particle. Damping force is also introduced between the particles in contact as ${\mathit{f}}_{ij}^{\text{d}}$, where we examine two different force laws according to Ref. [38]: (i) The damping force is given by ${\mathit{f}}_{ij}^{\text{d}}=-{\eta }_{\text{d}}{\mathit{v}}_{ij}$, where η_d is a damping constant and v_ij is the relative velocity between the particles. We refer to this model as model A. (ii) The damping force is restricted to the normal direction as ${\mathit{f}}_{ij}^{\text{d}}=-{\eta }_{\text{d}}\left({\mathit{v}}_{ij}\cdot {\mathit{n}}_{ij}\right){\mathit{n}}_{ij}$, which is often used for a model of “frictionless granular particles” [39]. We refer to this model as model B. In both the models A and B, we choose the spring and damping constants as the normal restitution coefficient is given by $e=\exp (-\pi /\sqrt{2m{k}_{\text{e}}/{\eta }_{\text{d}}^2-1})\simeq 0.8$ [40].

We simulate simple shear flows of the system under the Lees-Edwards boundary condition. In each time step, every particle position r_i = (x_i, y_i) is replaced with (x_i + Δγy_i, y_i) (i = 1, …, N) and then equations of motion, $m{\ddot{\mathit{r}}}_i={\sum }_j({\mathit{f}}_{ij}^{\text{e}}+{\mathit{f}}_{ij}^{\text{d}})$, are numerically integrated with a small time increment, Δt = 0.1t₀. Here, t₀ ≡ η_d/k_e is a time unit and Δγ is a strain increment such that the shear rate is defined as $\dot{\gamma }=\mathrm{\Delta }\gamma /\mathrm{\Delta }t$. In the following, we analyze the data in a steady state (where the amount of shear strain exceeds unity) and scale every mass, time, and length by m, t₀, and the mean particle diameter, d₀ ≡ (d_S + d_L)/2, respectively.

3 Results

In this section, we show our numerical results of shear-induced diffusion and dynamic heterogeneities in dense granular flows. We clarify the role of packing fraction of the particles ϕ and shear rate $\dot{\gamma }$. In addition, we examine how rheological properties of the particles affect our results. Figure 1 displays our numerical results of shear viscosity $\eta =\sigma /\dot{\gamma }$, where σ is shear stress. The shear stress is calculated as $\sigma =-L^{-2}{\sum }_{i<j}{f}_{\mathit{ijx}}^{\text{e}}{r}_{\mathit{ijy}}$ with the x- and y-components of the elastic force and relative position, $f_{\mathit{ijx}}^{\text{e}}$ and r_ijy, respectively, and is averaged over 10³ different configurations of the particles in a steady state. In this figure, we used the models (A) A and (B) B for the contact damping, ${\mathit{f}}_{ij}^{\text{d}}$, and changed the packing fraction from ϕ = 0.80 to 0.90 (symbols). If the packing fraction is much smaller than the jamming transition density, ϕ_J ≃ 0.8433 [20], the model A exhibits the Newtonian fluids’ behavior, i.e. η ∼const., for sufficiently small shear rates. In contrast, the model B shows the Bagnold scaling, $\sigma \sim {\dot{\gamma }}^2$, i.e. $\eta \sim \dot{\gamma }$ (dashed line). If the packing fraction is larger than ϕ_J, both the models exhibit the rate-independent yield stress, σ = σ_Y, so that one observes shear thinning as $\eta \sim {\dot{\gamma }}^{-1}$ (solid lines). See also the Supplementary Material (SM) [41] for our numerical results of flow curves, i.e., σ vs. $\dot{\gamma }$. In the following analyses, we explain how the difference between the models A and B influences the shear-induced diffusion and dynamic heterogeneities.

FIGURE 1

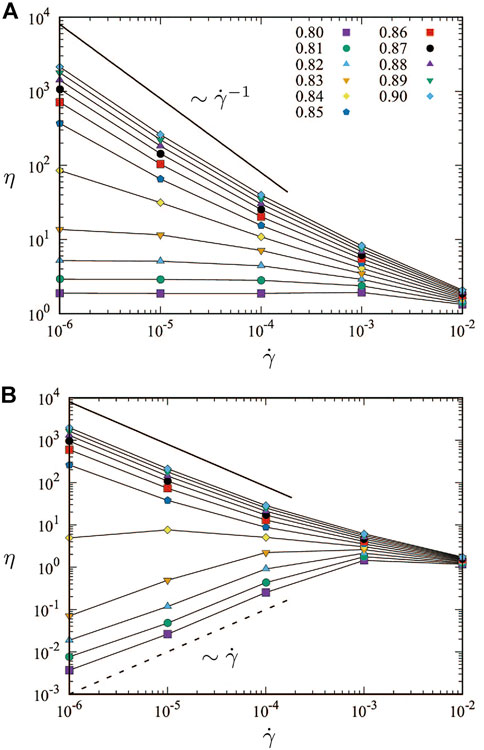
FIGURE 1. Double logarithmic plots of the shear viscosity η and shear rate $\dot{\gamma }$, where the models (A) A and (B) B are used for the damping force, ${\mathit{f}}_{ij}^{\text{d}}$. The packing fraction of the particles ϕ increases as listed in the legend of (A). The solid lines indicate shear thinning, $\eta \sim {\dot{\gamma }}^{-1}$, whereas the dashed line in (B) represents the Bagnold scaling (shear thickening), $\eta \sim \dot{\gamma }$.

Since our system is homogeneously sheared along the x-direction, we analyze fluctuating transverse motions of the particles along the y-direction. We introduce a transverse displacement of the particle i (= 1, …, N) as the time integral,

$\delta y_i\left(\tau \right)={\int }_{t_a}^{t_a+\tau }{v}_{iy}\left(t\right)dt,(1)$

where τ is a time interval and v_iy(t) is the y-component of particle velocity [42]. Note that the initial time t_a can arbitrary be chosen during a steady state.

In the following, we associate the fluctuating transverse motions of the particles (Eq. 1) with thermally activated molecular motions in glasses [33]. We show how the shear-induced diffusion is controlled by the parameters, ϕ and $\dot{\gamma }$ (Section 3.1), and analyze dynamic heterogeneities (Section 3.2). Then, we examine the relation between the maximum intensity and characteristic time scale for dynamic heterogeneities (Section 3.3) and discuss the link between the shear-induced diffusion and dynamic heterogeneities (Section 3.4).

3.1 Shear-induced diffusion

We quantify shear-induced diffusion of the particles by the transverse component of mean squared displacement (MSD) [42],

${\mathrm{\Delta }}^2\left(\tau \right)={⟨\frac{1}{N}\sum _{i=1}^N\delta y_i{\left(\tau \right)}^2⟩}_{t_a},(2)$

where the ensemble average ${⟨\dots ⟩}_{t_a}$ is taken over different choices of the initial time t_a (see Eq. 1). Figures 2A,B display the MSDs with different values of the control parameters, (A) ϕ and (B) $\dot{\gamma }$, where the scaled shear rate and packing fraction are fixed to (A) $\dot{\gamma }{t}_0=10^{-4}$ and (B) ϕ = 0.84, respectively. The horizontal axes are the time interval τ scaled by the shear rate $\dot{\gamma }$, i.e. the shear strain applied to the system for the duration, $\gamma \equiv \dot{\gamma }\tau$. In this figure, we used the model A for the damping force (see SM [41] for the results of model B, where we confirm that the results are qualitatively the same). As can be seen, every MSD exhibits a cross-over from super-diffusion to normal diffusion, ${\mathrm{\Delta }}^2(\tau )\sim \dot{\gamma }\tau$ (dashed lines), around a cross-over strain, γ = γ_c < 1 [17]. The MSDs monotonously increase with the increase of packing fraction ϕ (Figure 2A), whereas they decrease with the increase of shear rate $\dot{\gamma }$ (Figure 2B). In simple shear flows, transverse motions of the particles are induced by contacts. The denser the system is, the more likely the particles make contacts. In addition, the particles can travel long distance during a certain strain interval if the shear rate is small. Therefore, transverse motions of the particles are most enhanced in quasi-static flows of dense systems [19]. Different from glass forming liquids [33], any plateaus are not observed in the MSDs. This means that neither caging nor sub-diffusion of the particles exists in our system [15–17]. Note that the MSDs defined by non-affine displacements show qualitatively the same results (data are not shown).

FIGURE 2

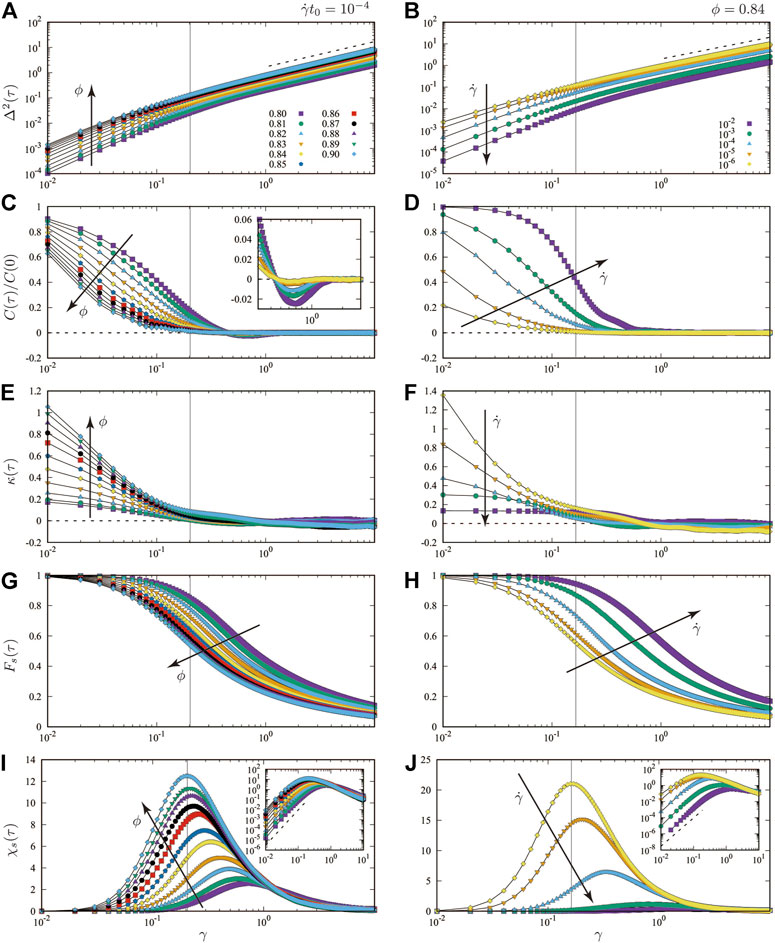
FIGURE 2. The MSD Δ²(τ) ((A) and (B)), normalized VACF C(τ)/C(0) ((C) and (D)), non-Gaussian parameter κ(τ) ((E) and (F)), self-intermediate scattering function F_s(τ) ((G) and (H)), and dynamic susceptibility χ_s(τ) ((I) and (J)) as functions of the shear strain $\gamma =\dot{\gamma }\tau$, where we used the model A for the damping force (see the SM [41] for the results of model B). In (A), (C), (E), (G), and (I), we increase the packing fraction of the particles ϕ as listed in the legend of (A), where the scaled shear rate is given by $\dot{\gamma }{t}_0=10^{-4}$. In (B), (D), (F), (H), and (J), we decrease the scaled shear rate $\dot{\gamma }{t}_0$ as listed in the legend of (B), where the packing fraction is fixed to ϕ = 0.84. The dashed lines in (A) and (B) indicate the normal diffusion, ${\mathrm{\Delta }}^2\sim \dot{\gamma }\tau$, while those in (C)–(F) represent zero. The inset to (C) is a zoom-in to the data for ϕ < ϕ_J ≃ 0.8433 and $\dot{\gamma }{t}_0=10^{-4}$. The insets to (I) and (J) are double logarithmic plots, where the dashed lines indicate the power-law behavior (with the slope 3.5). The vertical solid lines represent the peak positions of the dynamic susceptibility, i.e. ${\gamma }^{*}=\dot{\gamma }{\tau }^{*}$, for ϕ = 0.90 ((A), (C), (E), (G), and (I)) and $\dot{\gamma }{t}_0=10^{-6}$ ((B), (D), (F), (H), and (J)). Note that all the results have been averaged over 10² samples.

We also analyze time correlations of transverse motions by the velocity auto-correlation function (VACF),

$C\left(\tau \right)={⟨\frac{1}{N}\sum _{i=1}^N{v}_{iy}\left(t_a+\tau \right)v_{iy}\left(t_a\right)⟩}_{t_a}.(3)$

Figures 2C,D show the normalized VACFs, C(τ)/C(0), where ϕ and $\dot{\gamma }$ vary as in Figures 2A,B, respectively. As can be seen, every VACF decays to zero if the shear strain exceeds the cross-over strain, γ > γ_c. Therefore, transverse velocities of the particles completely lose their memory when the system exhibits the normal diffusion (dashed lines in Figures 2A,B). If the packing fraction is small enough, i.e. ϕ < ϕ_J, one observes that the VACFs are lowered to negative values and then converge to zero (see the inset to (C)), indicating backscattering of the particles [43]. Note that the backscattering effects are weakened if we use the model B for the damping force (see SM [41]). In short time scales, γ < γ_c, the VACF decays faster if we increase ϕ (Figure 2C) or decrease $\dot{\gamma }$ (Figure 2D). Thus, the time correlations, as well as memory effects on transverse motions, are strongly suppressed in quasi-static flows of dense systems.

The probability distribution function (PDF) of particle displacements is associated with the self-van Hove function which is another important measure of diffusion [43]. Figure 3 shows our numerical results of the PDFs of transverse displacements, P(δy_i(τ)), where the models (A) A and (B) B are used for the contact damping. In this figure, each PDF has been averaged over 10² samples. As can be seen, the PDFs are quite insensitive to the models and are symmetric around δy_i(τ) = 0, indicating that the anisotropy is negligible in our systems [44].

FIGURE 3

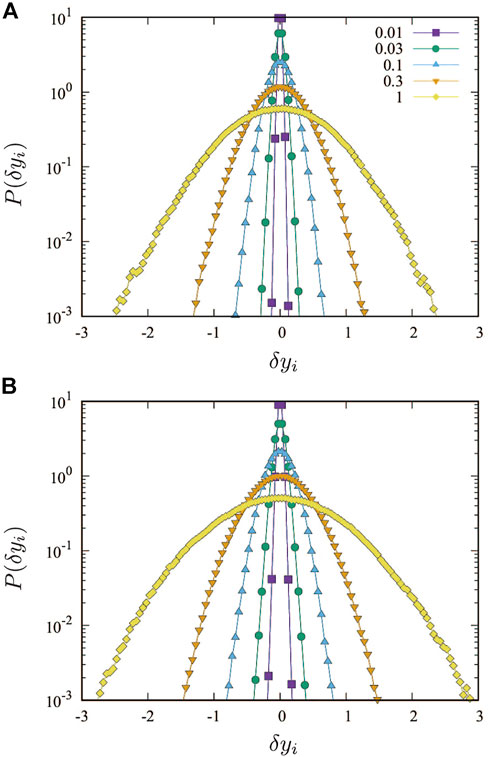
FIGURE 3. Semi-logarithmic plots of the PDFs of transverse displacements δy_i(τ) (i = 1, …, N), where the models (A) A and (B) B are used for the damping force. The shear strain increases from $\gamma =\dot{\gamma }\tau =10^{-2}$ to 1 as listed in the legend of (A), where the control parameters are given by ϕ = 0.84 and $\dot{\gamma }{t}_0=10^{-4}$.

The width (variance) of the PDF is equivalent to the MSD, while the shape of the PDF is characterized by the non-Gaussian parameter,

$\kappa \left(\tau \right)=\frac{\langle N^{-1}{\sum }_{i=1}^N\delta y_i{\left(\tau \right)}^4{\rangle }_{t_a}}{\langle N^{-1}{\sum }_{i=1}^N\delta y_i{\left(\tau \right)}^2{\rangle }_{t_a}^2}-3.(4)$

The non-Gaussian parameter is defined as the kurtosis subtracted by three, which quantifies how the PDF deviates from the normal distribution (where κ(τ) = 0). Figures 2E,F display the time development of non-Gaussian parameters, κ(τ), where the control parameters change as in Figures 2A,B. In this figure, we used the model A for the damping force (see SM [41] for the results of model B). The non-Gaussian parameters converge to zero if the strain exceeds the cross-over strain, γ > γ_c, regardless of ϕ and $\dot{\gamma }$. This means that the transverse displacements obey Gaussian distributions and thus are uncorrelated in space when the shear-induced diffusion is described as the normal diffusion. When molecules in a glass escape from a cage, the self-van Hove function strongly deviates from the normal distribution [45] so that the non-Gaussian parameter exhibits a characteristic peak. In our system, the non-Gaussian parameters do not show peaks because the particles are not trapped by cages and do not undergo sub-diffusion. Nevertheless, in short time scales (γ < γ_c), the non-Gaussian parameter tends to be large for ϕ > ϕ_J (Figure 2E) and $\dot{\gamma }{t}_0\ll 1$ (Figure 2F), implying that “transverse velocities” in quasi-static flows of dense systems are strongly non-Gaussian and may be spatially correlated [19].

3.2 Dynamic heterogeneities

Next, we examine dynamic heterogeneities of transverse motions of the particles. To quantify the dynamics of single particles, we introduce the self-intermediate scattering function as $F_s(\tau )={⟨{\widehat{f}}_s(\tau )⟩}_{t_a}$, where the function is defined as

${\widehat{f}}_s\left(\tau \right)=\frac{1}{N}\sum _i\frac{\sin \left[k\delta y_i\left(\tau \right)\right]}{k\delta y_i\left(\tau \right)}(5)$

with the wave number, k = 2π/d₀. Figures 2G,H show the time development of self-intermediate scattering functions, F_s(τ), where the parameters, ϕ and $\dot{\gamma }$, vary as in Figures 2A,B, respectively (see SM [41] for the results of model B). In these figures, F_s(τ) monotonously decreases from one to zero and does not exhibit a plateau as we do not observe any plateaus in the MSDs. In addition, it becomes sufficiently small, F_s(τ) < 0.5, when the shear-induced diffusion is described as the normal diffusion. This means that most of the transverse displacements are greater than the particle radius if γ > γ_c (as can be seen in the data of MSDs). In short time scales (γ < γ_c), F_s(τ) decays faster if we increase ϕ (Figure 2G) or decrease $\dot{\gamma }$ (Figure 2H). Therefore, the magnitude of transverse displacements is most enhanced in quasi-static flows of dense systems [19].

To further investigate spatio-temporal heterogeneous structures of transverse motions, we calculate the dynamic susceptibility as the variance of the function ${\widehat{f}}_s(\tau )$, i.e.

${\chi }_s\left(\tau \right)=N\left\{\langle {\widehat{f}}_s{\left(\tau \right)}^2\rangle -\langle {\widehat{f}}_s{\left(\tau \right)\rangle }^2\right\}.(6)$

Figures 2I,J display the time development of dynamic susceptibilities, χ_s(τ), where the control parameters change as in Figures 2A,B (see SM [41] for the results of model B). As in the case of glass forming liquids [34], χ_s(τ) has a single peak at a characteristic time scale, τ*. The height of the peak, ${\chi }_s^{\ast }\equiv {\chi }_s({\tau }^{*})$, representing the maximum intensity of the heterogeneities, grows with the increase of ϕ (Figure 2I) [17] and decrease of $\dot{\gamma }$ (Figure 2J). On the other hand, the peak position $\dot{\gamma }{\tau }^{*}$ decreases with increasing ϕ and decreasing $\dot{\gamma }$. This is in sharp contrast to the dynamic heterogeneities in glasses [34] and homogeneously driven granular materials [7], where both the peak height and position, ${\chi }_s^{\ast }$ and τ*, increase when the systems approach the glass and jamming transitions. Note that the peak position $\dot{\gamma }{\tau }^{*}$ (vertical solid lines in Figure 2) is around (or less than) the cross-over strain γ_c. Moreover, we also find the power-law growth of dynamic susceptibility before the peak (dashed lines in the insets to (I) and (J)) as previously reported by experiments of two-dimensional granular materials under shear [6].

3.3 Dynamic criticality

In the case of glass forming liquids and homogeneously driven granular materials, both the peak height ${\chi }_s^{\ast }$ and position τ* of dynamic susceptibility are increased by e.g. the decrease of temperature [33] and the increase of packing fraction [7]. This implies the existence of dynamic criticality in thermally/athermally driven disordered systems, i.e. critical slowing down (the divergence of relaxation time τ*) is accompanied by the divergence of correlation length ξ*, where the correlation length is roughly estimated as ${\xi }^{*}\sim {\chi }_s^{\ast 1/d}$ in d-dimension [34].

In our MD simulations, however, we find that ${\chi }_s^{\ast }$ grows while τ* shifts to short time scales if the system is dense and sheared quasistatically (Figures 2I,J). This means that instantaneous transverse motions, or “transverse velocities”, become more heterogeneous in space than the displacements in long time scales (γ > γ_c). To extract relations between the peak height and position of dynamic susceptibility, we make scatter plots of ${\chi }_s^{\ast }$ and $\dot{\gamma }{\tau }^{*}$ in Figure 4A. Here, the solid (open) symbols are the results of model A (B), where the shear rate is limited to quasi-static values, $\dot{\gamma }{t}_0\le 10^{-5}$ (10^–4). We find that the relations between ${\chi }_s^{\ast }$ and $\dot{\gamma }{\tau }^{*}$ are well described by the power-laws, where the data of models A and B are fitted to $\dot{\gamma }{\tau }^{*}\sim {\chi }_s^{\ast -0.82}$ (solid line) and ${\chi }_s^{\ast -0.51}$ (dashed line), respectively. The data cannot be described by the power-laws if the shear rate is sufficiently large. Furthermore, the difference between the models becomes significant as ${\chi }_s^{\ast }$ decreases and $\dot{\gamma }{\tau }^{*}$ increases (Figure 4A), where the two models exhibit different rheological properties, i.e. the Newtonian fluids’ behavior and shear thickening, for ϕ < ϕ_J and $\dot{\gamma }{t}_0\ll 1$ (Figure 1). On the other hand, the difference between them is less pronounced if ${\chi }_s^{\ast }$ increases and $\dot{\gamma }{\tau }^{*}$ decreases (Figure 4A), where both the models show the same rheological behavior, i.e. shear thinning, for ϕ > ϕ_J and $\dot{\gamma }{t}_0\ll 1$ (Figure 1).

FIGURE 4

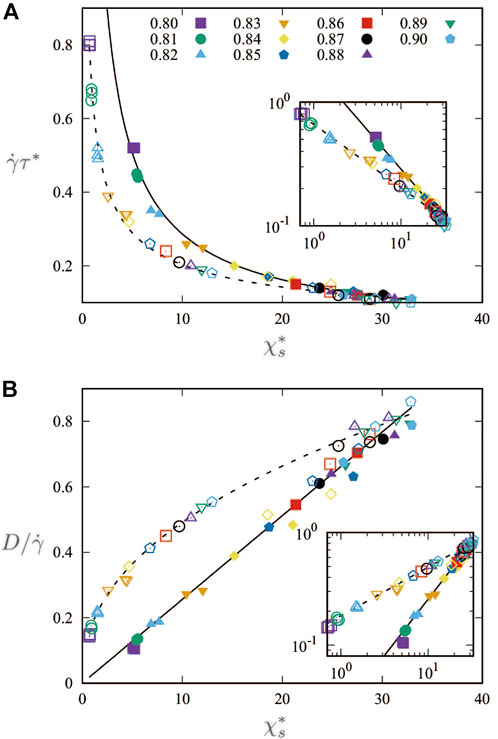
FIGURE 4. (A) The peak position of dynamic susceptibility, $\dot{\gamma }{\tau }^{*}$, and (B) diffusion coefficient over the shear rate, $D/\dot{\gamma }$, as functions of the maximum intensity of dynamic heterogeneities, ${\chi }_s^{\ast }$, where the packing fraction ϕ increases as listed in the legend of (A). The solid (open) symbols are the results of model A (B), where we only show the data in a quasi-static regime, $\dot{\gamma }{t}_0\le 10^{-5}$ (10^–4). In (A), the solid (dashed) line is a power-law fit, $\dot{\gamma }{\tau }^{*}\sim {{\chi }_s^{\ast -0.82}}^{}$ $({{\chi }_s^{\ast -0.51}}^{})$, to the data of model A (B). In (B), the solid line is the linear scaling, $D/\dot{\gamma }\sim {\chi }_s^{\ast }$, for the results of model A, while the dashed line is a power-law fit, $D/\dot{\gamma }\sim {{\chi }_s^{\ast 0.43}}^{}$, to the data of model (B). The insets are double logarithmic plots.

3.4 Shear-induced diffusion coefficient

It had been suggested by the elastoplastic model [35] that the diffusion coefficient of sheared athermal system is linked to the peak height of dynamic susceptibility as

$D\sim {\chi }_s^{\ast }\dot{\gamma }.(7)$

We examine this linear scaling relation between D and ${\chi }_s^{\ast }\dot{\gamma }$ by our numerical data. Extracting the shear-induced diffusion coefficient over the shear rate from the slope of MSD as $D/\dot{\gamma }=\underset{\tau \to \infty }{\lim }{\mathrm{\Delta }}^2(\tau )/2\gamma$ [42], we make scatter plots of $D/\dot{\gamma }$ and ${\chi }_s^{\ast }$ in Figure 4B. We find that the results of model A (solid symbols) obey the linear scaling, Eq. 7 (solid line), regardless of the packing fraction ϕ, where the shear rate is limited to the quasi-static values, $\dot{\gamma }{t}_0\le 10^{-5}$. However, the model B (open symbols) exhibits a different scaling, $D/\dot{\gamma }\sim {\chi }_s^{\ast 0.43}$ (dashed line), for any ϕ and $\dot{\gamma }{t}_0\le 10^{-4}$. Though the scaling for the results of model B is controversial, the difference between the models for small ${\chi }_s^{\ast }$ can be associated with the different rheological properties in ϕ < ϕ_J and $\dot{\gamma }{t}_0\ll 1$ (Figure 1). In contrast, the difference becomes small if ${\chi }_s^{\ast }$ increases, where the same shear thinning, $\eta \sim {\dot{\gamma }}^{-1}$, is observed in both the models (Figure 1). Interestingly, the product of shear-induced diffusion coefficient D and time scale τ* is almost constant, Dτ* ∼const., if the maximum intensity increases to ${\chi }_s^{\ast }>20$ (see SM [41]). This relation, Dτ* ∼const., is insensitive to the models and mimics the Stokes-Einstein relation [46, 47]. However, the dependence of shear viscosity η on either ${\chi }_s^{\ast }$ or τ* is not monotonous (see SM [41]) and we cannot find a clear relationship between the viscosity and diffusion coefficient.

4 Discussion

In this study, we have numerically investigated shear-induced diffusion and dynamic heterogeneities in two-dimensional dense granular flows. Applying simple shear deformations to the system, we analyzed fluctuating transverse motions of the particles, where we focused on the role of packing fraction of the particles ϕ and shear rate $\dot{\gamma }$. To examine the influence of different rheological properties, we introduced two different force laws to the damping force between the particles in contact (as the models A and B). We found that the transverse displacements (Eq. 1) are described as the normal diffusion if the applied strain exceeds the cross-over strain, γ_c < 1. In long time scales, γ > γ_c, the time correlations of transverse velocities vanish and the transverse displacements obey Gaussian distributions, where most of the transverse displacements exceed the particle radius. In short time scales, γ < γ_c, memory effects on the transverse velocities are strongly suppressed and the transverse displacements become highly non-Gaussian if the system is dense (ϕ > ϕ_J) and sheared quasistatically ($\dot{\gamma }$t₀ ≪ 1). We confirmed that the dependence of the MSDs, VACFs, and non-Gaussian parameters on the control parameters, ϕ and $\dot{\gamma }$, is qualitatively the same even if we change the model of contact damping. Different from thermally activated molecular motions in glasses [33], we did not observe any plateaus in the MSDs and self-intermediate scattering functions, and did not find any peaks in the non-Gaussian parameters. Therefore, neither the caging nor sub-diffusion exists in our shear-driven granular systems. In contrast, the dynamic susceptibility exhibits a peak at a characteristic time scale τ*. Increasing ϕ and decreasing $\dot{\gamma }$, we found that the maximum of dynamic susceptibility ${\chi }_s^{\ast }$ increases though the peak position $\dot{\gamma }{\tau }^{*}$ shifts to short time scales. This trend is opposite to the dynamic criticality observed in glasses [48] and homogeneously driven granular materials [7], where we described our numerical results in a quasi-static regime as a power-law, $\dot{\gamma }{\tau }^{*}\sim {\chi }_s^{\ast -\nu }$, with the model-dependent exponent ν. Moreover, the diffusion coefficient over the shear rate, $D/\dot{\gamma }$, is linear in the maximum of dynamic susceptibility ${\chi }_s^{\ast }$ (Eq. 7) if the model A is used for the contact damping. On the other hand, we found a sub-linear scaling between them, which is in conflict to the prediction made by the elastoplastic model [35], if the model B is used in MD simulations.

Though we have examined two different models of contact damping, where they exhibit the Newtonian fluids’ behavior and Bagnold scaling for sufficiently small ϕ and $\dot{\gamma }$ [38], more systematic studies of the damping force are also possible [38, 49]. Furthermore, the effect of particle inertia which we have not studied here is also crucial to the rheology [50]. In general, interactions between the particles in contact drastically change the rheological behavior, e.g. frictional contacts induce discontinuous shear thickening [51, 52], whereas cohesive contacts result in discontinuous shear thinning [53]. Because our results suggest that the relation between the maximum intensity and characteristic time scale for dynamic heterogeneities, as well as the link between the shear-induced diffusion and dynamic heterogeneities, is dependent on rheological properties, further studies of the effect of particle inertia and interaction forces are necessary in future. In addition, different models of elastic forces, e.g. the Hertzian contact which takes account of the particle curvature, should also be examined. Moreover, non-spherical particle shapes [54] and the study in three dimensions [55, 56] are also important for experiments and industrial applications of this study.

5 Conclusion

In conclusion, we found that shear-induced transverse motions of granular particles are totally different from thermally activated molecular motions in glasses. The scaling relations between the maximum intensity of dynamic heterogeneities, characteristic time scale, and diffusion coefficient of the particles were confirmed in quasi-static flows, where the scaling exponents are dependent on the model of contact damping.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KS and TK designed the research and wrote the article. KS performed the research.

Funding

This work was supported by KAKENHI Grant Nos. 20H01868, 21H01006, 22K03459, JPMJFR212T, 20H05157, 20H00128, 19K03767, 18H01188 from JSPS.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.992239/full#supplementary-material

References

1. Jeager H, Nagel S, Behringer R. Granular solids, liquids, and gases. Rev Mod Phys (1996) 68:1259. doi:10.1103/RevModPhys.68.1259

CrossRef Full Text | Google Scholar

2. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield stress materials in soft condensed matter. Rev Mod Phys (2017) 89:035005. doi:10.1103/revmodphys.89.035005

CrossRef Full Text | Google Scholar

3. Aranson IS, Tsimring LS. Patterns and collective behavior in granular media: Theoretical concepts. Rev Mod Phys (2006) 78:641–92. doi:10.1103/revmodphys.78.641

CrossRef Full Text | Google Scholar

4. Castellanos A. The relationship between attractive interparticle forces and bulk behaviour in dry and uncharged fine powders. Adv Phys X (2005) 54:263–376. doi:10.1080/17461390500402657

CrossRef Full Text | Google Scholar

5. Pouliquen O. Velocity correlations in dense granular flows. Phys Rev Lett (2004) 93:248001. doi:10.1103/physrevlett.93.248001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dauchot O, Marty G, Biroli G. Dynamical heterogeneity close to the jamming transition in a sheared granular material. Phys Rev Lett (2005) 95:265701. doi:10.1103/physrevlett.95.265701

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Keys AS, Abate AR, Glotzer SC, Durian DJ. Measurement of growing dynamical length scales and prediction of the jamming transition in a granular material. Nat Phys (2007) 3:260–4. doi:10.1038/nphys572

CrossRef Full Text | Google Scholar

8. Candelier R, Dauchot O, Biroli G. Building blocks of dynamical heterogeneities in dense granular media. Phys Rev Lett (2009) 102:088001. doi:10.1103/physrevlett.102.088001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Katsuragi H, Abate AR, Durian DJ. Jamming and growth of dynamical heterogeneities versus depth for granular heap flow. Soft Matter (2010) 6:3023. doi:10.1039/b918991b

CrossRef Full Text | Google Scholar

10. Nordstrom KN, Gollub JP, Durian DJ. Dynamical heterogeneity in soft-particle suspensions under shear. Phys Rev E (2011) 84:021403. doi:10.1103/physreve.84.021403

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rahmani Y, van der Vaart K, van Dam B, Hu Z, Chikkadi V, Schall P. Dynamic heterogeneity in hard and soft sphere colloidal glasses. Soft Matter (2012) 8:4264. doi:10.1039/c2sm25267h

CrossRef Full Text | Google Scholar

12. Sanlí C, Saitoh K, Luding S, van der Meer D. Collective motion of macroscopic spheres floating on capillary ripples: Dynamic heterogeneity and dynamic criticality. Phys Rev E (2014) 90:033018. doi:10.1103/physreve.90.033018

CrossRef Full Text | Google Scholar

13. Heussinger C, Barrat JL. Jamming transition as probed by quasistatic shear flow. Phys Rev Lett (2009) 102:218303. doi:10.1103/physrevlett.102.218303

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Vågberg D, Olsson P, Teitel S. Universality of jamming criticality in overdamped shear-driven frictionless disks. Phys Rev Lett (2014) 113:148002. doi:10.1103/physrevlett.113.148002

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tsamados M. Plasticity and dynamical heterogeneity in driven glassy materials. Eur Phys J E (2010) 32:165–81. doi:10.1140/epje/i2010-10609-0

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Hatano T. Rheology and dynamical heterogeneity in frictionless beads at jamming density. J Phys : Conf Ser (2011) 319:012011. doi:10.1088/1742-6596/319/1/012011

CrossRef Full Text | Google Scholar

17. Heussinger C, Berthier L, Barrat JL. Superdiffusive, heterogeneous, and collective particle motion near the fluid-solid transition in athermal disordered materials. Eur Phys Lett (2010) 90:20005. doi:10.1209/0295-5075/90/20005

CrossRef Full Text | Google Scholar

18. Goldenberg C, Tanguy A, Barrat JL. Particle displacements in the elastic deformation of amorphous materials: Local fluctuations vs. non-affine field. Europhys Lett (2007) 80:16003. doi:10.1209/0295-5075/80/16003

CrossRef Full Text | Google Scholar

19. Saitoh K, Mizuno H. Anomalous energy cascades in dense granular materials yielding under simple shear deformations. Soft Matter (2016) 12:1360–7. doi:10.1039/c5sm02760h

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Olsson P, Teitel S. Critical scaling of shear viscosity at the jamming transition. Phys Rev Lett (2007) 99:178001. doi:10.1103/physrevlett.99.178001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Geng J, Behringer RP. Diffusion and mobility in a stirred dense granular material. Phys Rev Lett (2004) 93:238002. doi:10.1103/physrevlett.93.238002

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Eisenmann C, Kim C, Mattsson J, Weitz DA. Shear melting of a colloidal glass. Phys Rev Lett (2010) 104:035502. doi:10.1103/physrevlett.104.035502

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wandersman E, Dijksman JA, van Hecke M. Particle diffusion in slow granular bulk flows. Eur Phys Lett (2012) 100:38006. doi:10.1209/0295-5075/100/38006

CrossRef Full Text | Google Scholar

24. Besseling R, Weeks ER, Schofield AB, Poon WCK. Three-dimensional imaging of colloidal glasses under steady shear. Phys Rev Lett (2007) 99:028301. doi:10.1103/physrevlett.99.028301

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Möbius ME, Katgert G, van Hecke M. Relaxation and flow in linearly sheared two-dimensional foams. Eur Phys Lett (2010) 90:44003. doi:10.1209/0295-5075/90/44003

CrossRef Full Text | Google Scholar

26. Ono IK, Tewari S, Langer SA, Liu AJ. Velocity fluctuations in a steadily sheared model foam. Phys Rev E (2003) 67:061503. doi:10.1103/physreve.67.061503

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Olsson P. Diffusion and velocity autocorrelation at the jamming transition. Phys Rev E (2010) 81:040301(R). doi:10.1103/physreve.81.040301

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kharel P, Rognon P. Vortices enhance diffusion in dense granular flows. Phys Rev Lett (2017) 119:178001. doi:10.1103/physrevlett.119.178001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lemaitre A, Caroli C. Rate-dependent avalanche size in athermally sheared amorphous solids. Phys Rev Lett (2009) 103:065501. doi:10.1103/physrevlett.103.065501

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Clemmer JT, Salerno KM, Robbins MO. Criticality in sheared, disordered solids. II. Correlations in avalanche dynamics. Phys Rev E (2021) 103:042606. doi:10.1103/physreve.103.042606

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Cai R, Xiao H, Zheng J, Zhao Y. Diffusion of size bidisperse spheres in dense granular shear flow. Phys Rev E (2019) 99:032902. doi:10.1103/physreve.99.032902

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Heussinger C, Barrat JL. Jamming transition as probed by quasistatic shear flow. Phys Rev Lett (2009) 102:218303. doi:10.1103/physrevlett.102.218303

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials. Rev Mod Phys (2011) 83:587–645. doi:10.1103/revmodphys.83.587

CrossRef Full Text | Google Scholar

34. Berthier L. Dynamic heterogeneity in amorphous materials. Physics (2011) 4:42. doi:10.1103/physics.4.42

CrossRef Full Text | Google Scholar

35. Martens K, Bocquet L, Barrat JL. Connecting diffusion and dynamical heterogeneities in actively deformed amorphous systems. Phys Rev Lett (2011) 106:156001. doi:10.1103/physrevlett.106.156001

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lechenault F, Dauchot O, Biroli G, Bouchaud JP. Lower bound on the four-point dynamical susceptibility: Direct experimental test on a granular packing. Europhys Lett (2008) 83:46002. doi:10.1209/0295-5075/83/46002

CrossRef Full Text | Google Scholar

37. Saitoh K, Hatano T, Ikeda A, Tighe BP. Stress relaxation above and below the jamming transition. Phys Rev Lett (2020) 124:118001. doi:10.1103/physrevlett.124.118001

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Vågberg D, Olsson P, Teitel S. Dissipation and rheology of sheared soft-core frictionless disks below jamming. Phys Rev Lett (2014) 112:208303. doi:10.1103/physrevlett.112.208303

CrossRef Full Text | Google Scholar

39. Luding S. Anisotropy in cohesive, frictional granular media. J Phys : Condens Matter (2005) 17:S2623–40. doi:10.1088/0953-8984/17/24/017

CrossRef Full Text | Google Scholar

40.In our MD simulations, numerical values of k_e and η_d are given by 1.0 and 0.1, respectively.

41.See Supplemental Material at [URL will be inserted by publisher] for full details.

42. Saitoh K, Kawasaki T. Critical scaling of diffusion coefficients and size of rigid clusters of soft athermal particles under shear. Front Phys (2020) 8:99. doi:10.3389/fphy.2020.00099

CrossRef Full Text | Google Scholar

43. Boon JP, Yip S. Molecular hydrodynamics. New York: Dover (1991).

Google Scholar

44. Saitoh K, Mizuno H. Anisotropic decay of the energy spectrum in two-dimensional dense granular flows. Phys Rev E (2017) 96:012903. doi:10.1103/physreve.96.012903

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Chaudhuri P, Berthier L, Kob W. Universal nature of particle displacements close to glass and jamming transitions. Phys Rev Lett (2007) 99:060604. doi:10.1103/physrevlett.99.060604

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Kawasaki T, Onuki A. Slow relaxations and stringlike jump motions in fragile glass-forming liquids: Breakdown of the Stokes-Einstein relation. Phys Rev E (2013) 87:012312. doi:10.1103/physreve.87.012312

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Kawasaki T, Kim K. Identifying time scales for violation/preservation of Stokes-Einstein relation in supercooled water. Sci Adv (2017) 3:e1700399. doi:10.1126/sciadv.1700399

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Lačević N, Starr FW, Schrøder TB, Glotzer SC. Spatially heterogeneous dynamics investigated via a time-dependent four-point density correlation function. J Chem Phys (2003) 119:7372–87. doi:10.1063/1.1605094

CrossRef Full Text | Google Scholar

49. Andreotti B, Barrat JL, Heussinger C. Shear flow of non-brownian suspensions close to jamming. Phys Rev Lett (2012) 109:105901. doi:10.1103/physrevlett.109.105901

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Kawasaki T, Ikeda A, Berthier L. Thinning or thickening? Multiple rheological regimes in dense suspensions of soft particles. Eur Phys Lett (2014) 107:28009. doi:10.1209/0295-5075/107/28009

CrossRef Full Text | Google Scholar

51. Otsuki M, Hayakawa H. Critical scaling near jamming transition for frictional granular particles. Phys Rev E (2011) 83:051301. doi:10.1103/physreve.83.051301

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Seto R, Mari R, Morris JF, Denn MM. Discontinuous shear thickening of frictional hard-sphere suspensions. Phys Rev Lett (2013) 111:218301. doi:10.1103/physrevlett.111.218301

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Irani E, Chaudhuri P, Heussinger C. Impact of attractive interactions on the rheology of dense athermal particles. Phys Rev Lett (2014) 112:188303. doi:10.1103/physrevlett.112.188303

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Marschall T, Keta YE, Olsson P, Teitel S. Orientational ordering in athermally sheared, aspherical, frictionless particles. Phys Rev Lett (2019) 122:188002. doi:10.1103/physrevlett.122.188002

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Oyama N, Mizuno H, Saitoh K. Avalanche interpretation of the power-law energy spectrum in three-dimensional dense granular flow. Phys Rev Lett (2019) 122:188004. doi:10.1103/physrevlett.122.188004

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Olsson P. Dimensionality and viscosity exponent in shear-driven jamming. Phys Rev Lett (2019) 122:108003. doi:10.1103/physrevlett.122.108003

PubMed Abstract | CrossRef Full Text | Google Scholar