A graphene-based THz metasurface sensor with air-spaced structure

Owing to the unique electromagnetic response ability, electromagnetic metasurface have potential applications in medical, imaging, sensing, and other fields. In this paper, a graphene-based THz metasurface sensor with an air spacer layer is designed by combining the advantages of the air spacer structure and the dynamic tunability of graphene materials. The proposed metasurface sensor consists of six layers, which are silicon dioxide (SiO₂) substrate, metal reflector, air layer, graphene metasurface etched with microstructure, ion-gel layer and silicon dioxide dielectric layer from bottom to top. A comprehensive study of the absorption properties and sensing performance are carried out which is simulated and analyzed with the help of CST Microwave Studio software. The calculation results show that the two obvious resonance absorption peaks located at 0.95 THz and 1.53 THz with absorption of 94.9% and 79%, respectively, and there is a good linear relationship between the absorption peak and dielectric parameters of analyte. The frequency shift sensitivity of the two resonance peaks M1 and M2 can reach 450 GHz/RIU and 717 GHz/RIU, respectively. By changing the thickness of the air layer, when the two resonance peaks M1 and M2 reach the maximum absorption at $h_{\mathit{2}}=\mathit{140}\mu \mathrm{m}$ and $h_{\mathit{2}}=\mathit{280}\mu \mathrm{m}$, respectively, the frequency shift sensitivity is still as high as close to 450 GHz/RIU. The influence of structure parameters and incident angle on the absorption spectrum shows that the proposed structure has good stability and reliability. The proposed graphene-based absorption sensor has good biocompatibility, broadening the application range of terahertz functional devices.

Introduction

Terahertz (THz) wave, generally defined in the frequency range of 0.1–10 THz, lie between the microwave and infrared frequencies in the electromagnetic spectrum. THz waves have both analyte penetration and analyte fingerprint recognition characteristics, making it widely used for analyte detection. Moreover, THz waves are non ionizing. So, when THz waves are used to detect analyte, they will not cause changes in material properties and structural damage due to ionization and high-intensity radiation, and can achieve non-destructive testing of analyte [1]. Metamaterials are composite materials made by artificial design. The properties are not only related to the physical properties of the constituent materials, but also related to the effect of the unit structure on waves, and have a single electromagnetic response characteristic that is not found in nature. This material consists of periodically arranged subwavelength units [2, 3], which can realize the local enhancement of electromagnetic fields [4–7]. It is also quite sensitive to the change of the dielectric environment around the structure [8, 9]. THz metamaterial sensor is an important functional device in the THz frequency band [10–13]. It realizes the detection of analyte by changing the resonance characteristics of the sensor due to the difference of the electromagnetic parameters of the measured analyte in the THz frequency band [14–17]. In 2017, Geng et al. reported A microfluidic-integrated terahertz metamaterial biosensor produces 19 GHz resonance shift (5 mu/ml) and 14.2 GHz resonance shift (0.02524 μg/ml) when detecting Alpha fetoprotein (AFP) and Glutamine transferase isozymes II (GGT-II), which can be used for the detection of early-stage liver cancer biomarkers [18]. At present, THz metamaterial sensors are mainly divided into transmissive metamaterial sensors and reflective metamaterial sensors [19], the designed and processed metamaterial sensor have a wide applicable occasion in biomolecule recognition, food quality control, environmental detection, and many other fields [20–22].

During the process of designing metamaterial absorbers, spacers can be incorporated in such a design (in terms of thickness and dielectric function) that it is critical to realize various applications [23, 24]. For example, partially etched partitions can be replaced with liquid crystals to achieve electrically tunable metamaterial absorbers [25–28]. Alternatively, VO₂ can be used as the material of the air spacer. Can control the change of the material from the insulating layer to the air layer by changing the temperature. Meanwhile, the absorption resonance will be turned on and off due to the change of the material [29–32]. In addition, nonlinear characteristics can be introduced by integrating semiconductor materials in spacers [33–36]. Importantly, metamaterial absorbers typically have a higher quality factor than single-layer metamaterial, making them more suitable for sensing applications. However, the physical presence of dielectric spacers impedes access to volumes between the metamaterial layer and the ground plane, where the electric field is highly concentrated. In addition, dielectric loss of spacer materials will reduce the quality factor [37].

Graphene is a two-dimensional material made of carbon atoms arranged in a regular hexagonal shape similar to benzene rings. The surface conductivity of graphene can be artificially modulated by applying bias voltage or chemical doping to change the carrier concentration of graphene. Therefore, graphene can be dynamically modulated. Therefore, graphene may be a good candidate for the design and engineering of some tunable devices to the above modulation properties. It has been widely used in sensors, and the position of the resonance wavelength on the spectrum can be affected by the Fermi level, which can easily realize a wide range of graphene sensing [38–40].

In this paper, we combine an air-spaced structure with a highly concentrated electric field and a tunable graphene material to propose a graphene-based THz metasurface sensor with air-spaced structure which is simulated and analyzed with the help of CST Microwave Studio software, two resonance peaks located at 0.95 THz and 1.53 THz are observed. At the same time, the resonance mechanism is analyzed from impedance matching and electric field mode. In addition, the sensing characteristics of the sensor were also studied, and the sensitivity of the two resonance peaks M1 and M2 of the graphene absorption sensor can reach 450 GHz/RIU and 717 GHz/RIU, respectively. Furthermore, when the two peaks reach the maximum absorption, the sensitivity is still as high as close to 450 GHz/RIU.

Structure and design

The proposed graphene-based THz metasurface sensor consists of six layers, which are silicon dioxide (SiO₂) substrate, metal reflector, air layer, graphene metasurface etched with the microstructure, ion-gel layer and silicon dioxide dielectric layer from bottom to top. The side view of the unit cell is shown in Figure 1A. The repeat period is $P_x=P_y=\mathit{50}\mu \mathrm{m}$. The SiO₂ whose relative dielectric constant is 3.9, are used as substrate and the dielectric layer, and the thicknesses of the dielectric layer and the substrate layer are $h_{\mathit{4}}=\mathit{10}\mu \mathrm{m}$ and $h=\mathit{5}\mu \mathrm{m}$ , respectively. The metal reflection layer is made of gold (Au), the conductivity is $\mathit{4.56}\times {\mathit{10}}^{\mathit{7}}\mathrm{S}/\mathrm{m}$, and the thickness is $h_{\mathit{3}}=\mathit{0.2}\mu \mathrm{m}$. The air layer is located between the graphene microstructure layer and the metal reflective layer, with a thickness of $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$. The E_f and conductivity of graphene can be changed by applying static bias, so as to realize the tunable function of graphene sensor. In order to easily adjust the electrical conductivity of graphene in the graphene microstructure layer, an Ion-gel thin film layer is added on the top of the graphene microstructure layer as a conductive layer, the thickness of which is $h_{\mathit{1}}=\mathit{2}\mu \mathrm{m}$. The ion-gel is a solid-state mixture composed of polymer materials and electrolyte materials with good electrical conductivity, and the relative permittivity is ${\epsilon }_{Ion-gel}=\mathit{1.82}$. The top view of the graphene microstructure is shown in Figure 1B, the dotted line is the auxiliary line. Two identical rings placed vertically are etched away from the graphene layer. The long radius of the outer ring is $R_{out}=\mathit{25}\mu \mathrm{m}$, and the short radius is $r_{out}=\mathit{16.5}\mu \mathrm{m}$, the long radius of the inner ring is $R_{in}$, and the short radius is $r_{in}=\mathit{0.65}{R}_{in}\mu \mathrm{m}$. The entire structure is illuminated by planar light propagating along the negative Z axis, and the position of the electric field monitor is the same as that of the graphene layer and larger than the graphene layer boundary.

FIGURE 1

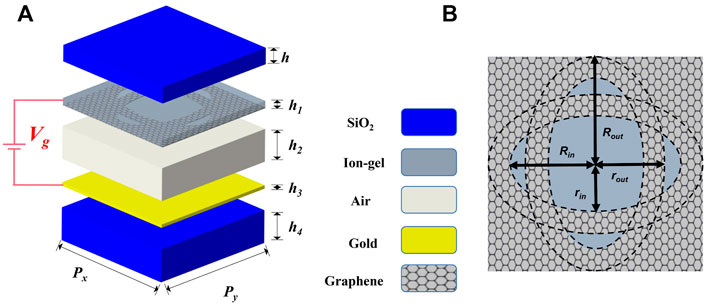
FIGURE 1. (A) Layered structure diagram of the graphene-based THz metasurface sensor. (B) Schematic diagram of the graphene microstructure, respectively.

In this paper, the conductivity model of graphene is mainly explained by the Kubo formula. Eqs 2, 3 represent the intraband conductivity and interband conductivity of graphene, respectively, where e is the electron charge, T is the temperature of the environment, $\omega$ is the circular frequency of the incidence wave, $k_B$ is Boltzmann’s constant, $\hslash$ is the reduced Planck’s constant, $E_f$ is the Fermi energy of graphene, and $\tau =\left({\mu }_v{E}_f\right)/\left(e{V}_f^{\mathit{2}}\right)$ is the relaxation time. The Fermi velocity $V_f={\mathit{10}}^{\mathit{6}}\mathrm{m}/\mathrm{s}$ in graphene, and ${\mu }_v$ is the carrier mobility, which decreases with the carrier density increasing (high Fermi energy). The experimental results show that the mobility range is 2000–40,000 cm² V⁻¹• s⁻¹, in this paper, a compromise value of 10,000 is taken for the convenience of calculation [41–43],

${\sigma }_g={\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}ra}+{\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}er}(1)$

${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}ra}\left(\omega ,T,\tau ,E_f\right)=j\frac{e^2{k}_{B}T}{\pi {\mathrm{\hslash }}^2\left(\omega -j{\tau }^{-1}\right)}\left[\frac{E_f}{k_{B}T}+2\ln \left(e^{-E_f/k_{B}T}+1\right)\right](2)$

${\sigma }_{\mathrm{i}\mathrm{n}\mathrm{t}er}\left(\omega ,T,\tau ,E_f\right)=j\frac{e^2}{4\pi \mathrm{\hslash }}\ln \left(\frac{2\left|E_f\right|-\left(\omega +j{\tau }^{-1}\right)\mathrm{\hslash }}{2\left|E_f\right|+\left(\omega +j{\tau }^{-1}\right)\mathrm{\hslash }}\right)(3)$

The intraband transition plays a leading role in the low frequency THz band rather than the interband transition. Here, the conductivity of graphene can be explained by the Drude model. For $E_f\gg k_{B}T$, the electrical conductivity of graphene can be expressed as Eq. 4 [44, 45]:

${\sigma }_g=\frac{e^2{E}_f}{\pi {\mathrm{\hslash }}^2}\frac{j}{\omega +j{\tau }^{-1}}(4)$

The relative dielectric constant is [46].

${\epsilon }_g=1+\frac{j{\sigma }_g}{{\epsilon }_0\omega t_g}(5)$

where, ${\epsilon }_{\mathit{0}}$ is the vacuum dielectric constant and t_g is the thickness of graphene. According to the above equations of conductivity and the dielectric constant of graphene, the calculated data can be imported into CST software and graphene modeling can be completed. We set t_g as $\mathit{1}\mathrm{n}\mathrm{m}$, temperature at 293 $\mathrm{K}$ and relaxation time as 0.5 $\mathrm{p}\mathrm{s}$. In the simulation, we established S-parameters, through which we can get the reflection and transmission of the entire system, $\left(\omega \right)={\left|S_{\mathit{11}}\left(\omega \right)\right|}^{\mathit{2}}$, $T\left(\omega \right)={\left|S_{\mathit{21}}\left(\omega \right)\right|}^{\mathit{2}}$, and the absorption is $A\left(\omega \right)=\mathit{1}-R\left(\omega \right)-T\left(\omega \right)$.

Results and discussion

The absorption of the air-spaced graphene metasurface sensor are studied by the frequency domain solver based on the finite element algorithm in the CST Microwave Studio software. In order to improve the accuracy and simulation speed of structure discretization, adaptive grid is used to divide the sensor structure. Owing to the symmetric structure, the TE direction is the same as the TM direction. When the THz wave is incident vertically ($theta=\mathit{0}°$), no analyte in the air layer (the real part of the air layer dielectric constant $Re=\mathit{1}$, and the imaginary part $Im=\mathit{0}$), the long and short radius of the inner elliptical ring are $R_{in}=\mathit{19}\mu \mathrm{m}$ and $R_{out}=\mathit{0.65}{R}_{in}\mu \mathrm{m}$, the thickness of the air layer is $h_{\mathit{2}}=\mathit{180}\mu \mathrm{m}$ and the Fermi level $E_f=\mathit{1}\mathrm{e}\mathrm{V}$, the absorption spectrum is shown in Figure 2. From the absorption spectrum, two resonance peaks M1 and M2 with high absorption rates of 94.9 % and 79% in the frequency range of 0.1 ∼ 2.0 THz were observed. The resonant frequencies of the two resonant peaks are M1 = 0.95 THz and M2 = 1.53 THz.

FIGURE 2

FIGURE 2. A Absorption spectrum of graphene-based THz metasurface sensor at $h_{\mathit{2}}=\mathit{180}\mu \mathrm{m}$.

Equivalent model analysis

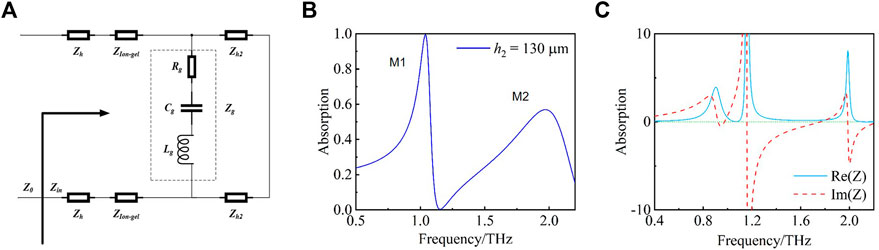
According to transmission line theory, the graphene-based metasurface is equivalent to an RLC series circuit, which is shown in the Figure 3A. The equivalent impedance is Z_g, Z_g = R_g + j $\omega$ L_g + 1/(j $\omega$ C_g). In addition, on the basis of the transmission line theory, the ion-gel layer and the dielectric layer both are equivalent to a lossy transmission line, and the electrical impedances are Z_Ion-gel and Z_h, respectively, and the magnitudes are related to the thickness and dielectric constant. Since the thickness of the metal reflective layer is greater than the skin depth of the metal aluminum in the THz wave, the THz wave cannot penetrate the reflective layer, so the metal reflective layer is equivalent to a lossless short-circuit wire, and the impedance Z_gold = 0. The equivalent electrical impedance of the sensor is Z_in, and the free space electrical impedance is Z₀. Figure 3A shows the equivalent circuit model of the designed graphene-based THz sensor. According to the impedance matching theory, when Z_in = Z₀, the impedance matching condition is satisfied, and the THz wave at the resonance frequency is absorbed by the sensor [47].

FIGURE 3

FIGURE 3. (A) Equivalent circuit model. (B) Absorption spectrum at $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$ (C) Impedance matching spectrum.

Since the transmission coefficient of the sensor S₂₁ = 0, the complex impedance Z of the sensor can be calculated by the reflection coefficient S₁₁, and the calculation formula of the complex impedance Z is Eq. 6 [48]:

$Z=\frac{1+S_{11}}{1-S_{11}}(6)$

Figure 3B shows the absorption spectrum of graphene-based THz metasurface sensors when $h_2=130\mu \mathrm{m},$ and $R_{in}=19\mu \mathrm{m}$. The complex impedance frequency spectrum of the sensor is shown in Figure 3C. It can be clearly seen that a good impedance match with the free space around 0.98 THz and 1.97 THz, which result in two high absorption rate resonance peaks.

Electric field distribution analysis

We set the inner radius of the elliptical ring to be $R_{in}=\mathit{19}\mu \mathrm{m}$, $E_f=\mathit{1}\mathrm{e}\mathrm{V}$, $h_{\mathit{2}}$ varies from 120 to 200 μm at 10 μm intervals. As can be seen from Figure 4A, in this structure, under the action of TE THz wave, the graphene-based metasurface acts as a resonant unit, interacting with THz wave to generate surface plasmon resonance (SPR), accompanied by the electromagnetic field around the resonant unit. This resonance is a Fano-like linear resonance due to the double elliptical ring structure. When we set $h_{\mathit{2}}=\mathit{180}\mu \mathrm{m}$, two absorption peaks M1 and M2 were located at 0.95 THz and 1.53 THz, and the absorption were 94.9% and 79%, respectively. In order to explain the resonance mechanism of the graphene-based THz metasurface sensors, the electromagnetic field distribution of the sensor is analyzed. First, the electric field distribution of graphene-based THz metasurface sensor at resonance frequency M1 and M2 is shown in Figures 4B,C. It can be seen that the electric fields at the two resonance peaks are both enhanced at the boundary of the middle part, indicating that local electric field enhancement occurs, and we can see that the local enhancement of the absorption peak M1 is more than that of M2, so there is a higher absorption.

FIGURE 4

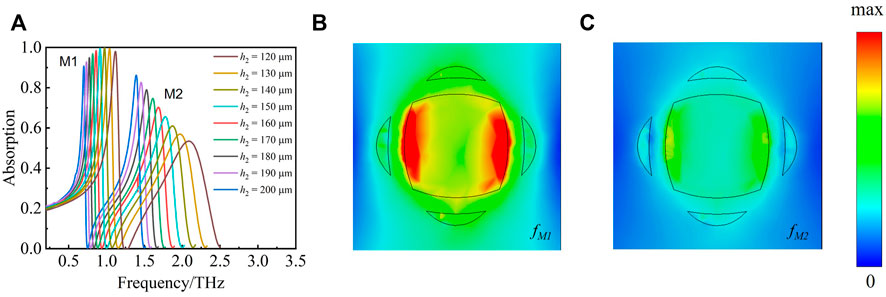
FIGURE 4. (A) The graph of the absorption lines corresponding to $h_{\mathit{2}}$ from 120 to 200 $\mu m$. Electric field distribution of graphene-based THz metasurface sensor at $h_{\mathit{2}}=\mathit{180}\mu \mathrm{m}$ resonant frequency: (B) f_M1; (C) f_M2.

Tunable performance analysis of graphene

Dynamic adjustment of the resonant frequency is a unique advantage of graphene-based THz metasurface sensors. The graphene-based THz metasurface sensors proposed in this study contains an ion-gel layer, and the positive and negative electrode of the bias voltage are connected to the ion-gel layer, and the metal reflective layer, respectively.

The Fermi level of graphene $E_f$ can be adjusted by changing the magnitude of the bias voltage, which can change the electrical conductivity of graphene to achieve the purpose of adjusting the resonant frequency of the sensor. Herein, the relationship between the Fermi level E_f and the voltage $V_b$ is: $\left|E_f\right|\approx {\hslash {\nu }_f\left(\pi N\right)}^{\mathit{1}/\mathit{2}}=\hslash {\nu }_f{\left(\pi {\epsilon }_{\mathit{0}}{\epsilon }_r\left|V_b\right|/d_{\mathit{1}}\right)}^{\mathit{1}/\mathit{2}}\propto V_b^{\mathit{1}/\mathit{2}}$, where ${\nu }_f$, N, and ${\epsilon }_r$ are the Fermi velocity, total carrier density and relative permittivity of dielectric layer, respectively. Then, E_f can reach a specific value by applying a specific applied voltage. The structure parameters are fixed as $R_{in}=\mathit{19}\mu \mathrm{m}$, $h_{\mathit{2}}=\mathit{200}\mu \mathrm{m}$, and $\theta =\mathit{0}°$. We change E_f from 0 to 1.0 eV, with the interval of 0.2 eV, and analyze the absorption spectra. The simulation results are shown in Figure 5B. The maximum absorption of resonance peak M1 increases from 69.8% corresponding to 0 eV to 99.9% corresponding to 0.4 eV, and the resonant frequency increases from 0.36 THz to 0.7 THz as the E_f increases from 0 to 1.0 eV. The resonance frequency of M1 shows an obvious blue shift. The maximum absorption of resonance peak M2 increases from 23.7% corresponding to 0 eV to 86.1% corresponding to 1.0 eV, and the resonant frequency moves from 1.01 THz to 1.39 THz as the E_f increases from 0 to 1.0 eV. The frequency shift curves of the two peaks are similar. According to the relationship between the Fermi level E_f and the voltage V_b, the higher E_f, leads to higher number of N, and contribute to the increase of plasmonic oscillation, which leads to the enhancement of the maximum absorption.

FIGURE 5

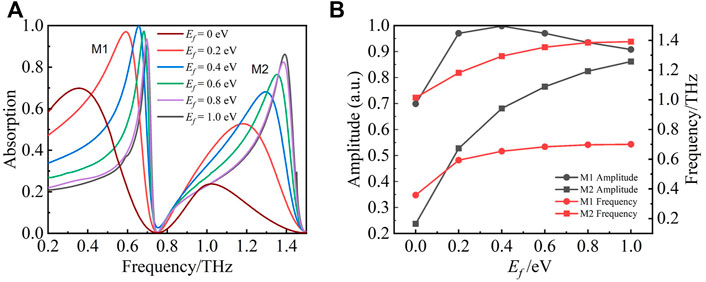
FIGURE 5. (A) The absorption spectra corresponding to the Fermi level (E_f) from 0 to 1.0 eV. (B) Line graph of maximum absorption and resonant frequency of absorption corresponding to the Fermi level (E_f) from 0 to 1.0 eV.

In addition, in the Figure 5A, it can be seen that the width of the working frequency band becomes narrower with the increase of E_f. The working bandwidth mainly depends on how fast Z₀ Re( $\sigma$ _g) and Z₀ Im( $\sigma$ _g) + g cot $\phi$ change with the angular frequency, and the fastest changes of conductivity for continuous graphene is related to cot $\phi$ = cot( $\frac{\omega }{c}$ gd₁), Z₀, g, d₁ and c are constants [46, 49]. From the Figure 5A, we can see that with the increase of E_f, the resonance frequency of the absorption peak begins to increase, because the frequency f and the angular frequency $\omega$ are proportional. In addition, since the cotangent function is a monotonically decreasing function, the operating bandwidth increases with resonant frequency gradually narrows as the resonant frequency increases. The above results show that the graphene-based THz metasurface sensor has high sensitivity tuning ability.

The influence of graphene geometric parameters on the absorption

The influence of graphene geometric parameters on the absorption were also investigated. We set $h_{\mathit{2}}=\mathit{180}\mu \mathrm{m}$, $theta=\mathit{0}°$, $\mathrm{a}\mathrm{n}\mathrm{d}{E}_f=\mathit{1}$ eV. We keep the outer ring radius R_out unchanged, and gradually increasing the inner ring radius R_in. The absorption spectrum with different inner ring radius $R_{in}$ of the graphene-based THz metasurfaces is plotted in Figure 6A. It can be seen that when the R_in increase from $\mathit{19}\mu \mathrm{m}$ to $\mathit{22}\mu \mathrm{m}$, the resonance frequency and the maximum absorption of M1 and M2 have a certain change. As shown in the Figure 6B, it is found that the maximum absorption of resonance peak M1 increases from 94.9% to 99.9% with the R_in increasing from 19 $\mu \mathrm{m}$ to 22 $\mu \mathrm{m}$. Different from M1, the maximum absorption of the resonance peak M2 decreases from 69.1% to 79% with the R_in increasing from 19 $\mu \mathrm{m}$ to 22 $\mu \mathrm{m}$. In addition, both M1 and M2 are blue-shifted to a certain extent, wherein the resonant frequency of M1 decreases from 0.761 THz to 0.736 THz, and the resonant frequency of M2 moves from 1.53 THz to 1.42 THz. This is because the change in the inner radius affects the plasmon resonance generated by the incident wave on the surface, which in turn affects the distribution of the electric field, and finally changes the absorption rate.

FIGURE 6

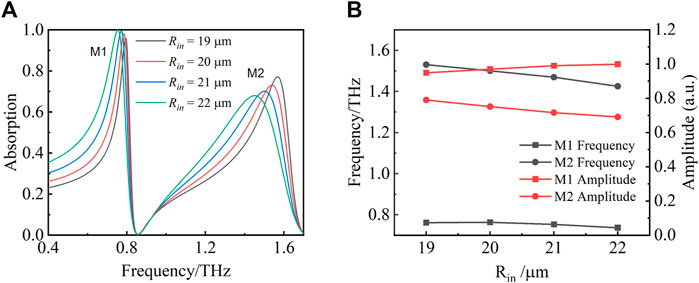
FIGURE 6. (A) The graph of the absorption lines corresponding to R_in from 19 to 22 $\mu m$. (B) Line graph of maximum absorption and resonant frequency of the absorption corresponding to R_in from 19 to 22 $\mu m$.

Insensitive analysis of angle and polarization

The sensitivity of the proposed graphene-based THz metasurface sensor to the THz polarization angle were studied. Figure 7 shows that under the normal incidence of TE polarized THz wave, when the THz wave polarization angle $\theta$ changes from 0° to 50°, the resonant frequency of M1 increases from 0.7 THz to 1.0 THz, simultaneously, the resonant frequency of M2 increases from 1.39 THz to 1.99 THz. It can be found that, as $\theta$ increases to $\mathit{50}°$, the frequency shift of the two resonance peaks is not large. In addition, the maximum absorption of resonance peak M1 drops from 99.9% corresponding to $\theta =\mathit{40}°$ to 90.6% corresponding to $\theta =\mathit{0}°$, and the maximum absorption of resonance peak M2 drops from 86.2% corresponding to $\theta =\mathit{0}°$ to 57.7% corresponding to $\theta =\mathit{50}°$. It is obviously that the absorption change range of the resonance peak M1 is small and relatively stable, and the absorption rate has been kept above 90%. The absorption of the resonance peak M2 starts to increase after 30°, when $\theta =\mathit{50}°$, the absorption rate is 57.7%, the absorption of the resonance peak M2 is relatively stable before 30°, and the absorption drop does not exceed 15%, which indicate that the proposed graphene-based THz metasurface sensor is insensitive to a wide angle of incidence.

FIGURE 7

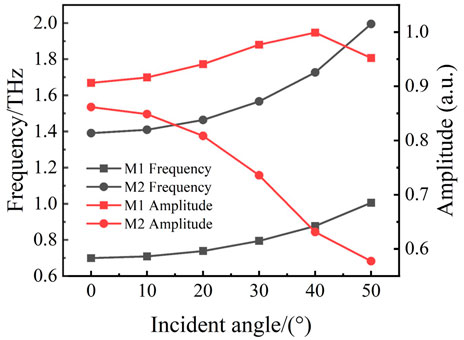
FIGURE 7. A Line graph of maximum absorption and resonant frequency of the absorption corresponding to incident angle from 0° to 50°.

Sensing performance of the proposed graphene-based THz metasurface sensor

Owing to the resonances,graphene-based THz metasurfaces are more sensitive to changes in the dielectric environment [50]. Therefore, the proposed graphene-based THz metasurface sensor can be used for sensing. During the sensor detection process, the analyte is placed in the air layer between the graphene layer and the metal layer, due to the change of the dielectric environment of the sensor surface, the sensor absorption spectrum will change. The thickness of the air layer affects the dielectric constant of the surrounding environment of the sensor, which will affect the sensing characteristics of the sensor. The strength of the sensor resonance absorption depends on the degree of matching between the equivalent impedance of the sensor and the impedance of free space. By adjusting the thickness of the air layer, the equivalent impedance of the sensor can be changed to make it well matched with the impedance of free space, thereby enhancing the absorption of THz wave. For this reason, this section studies the effect of air layer height on sensor characteristics with other parameters unchanged. In order to analyze the thickness of the air layer, the graphene Fermi level $E_f=\mathit{1}\mathrm{e}\mathrm{V},$ $R_{in}=\mathit{19}\mu \mathrm{m}$, $\theta =\mathit{0}°$, the real part of the dielectric constant of the air layer $Re=\mathit{1}$, and the imaginary part of the dielectric constant $Im=\mathit{0}$ .The absorption spectra of the proposed sensor with the thickness of the air layer h₂ increasing from 120 $\mu \mathrm{m}$ to 200 $\mu \mathrm{m}$ are studied, as shown in Figure 8B. The Figure 8A is a color chart with a total thickness of 120 um to 200 um of the air layer, and the trend of M1 and M2 can be clearly seen from the figure. As h₂ increasing from 120 $\mu \mathrm{m}$ to 200 $\mu \mathrm{m}$ , the resonance frequency of M1 decreases from 1.12 THz to 0.7 THz, and the resonance frequency of M2 decreases from 2.09 THz to 1.39 THz. Furthermore, when Re increases from 1 to 2 with a step size of 0.2, and the sensitivity of the sensor with different thicknesses are investigated. According to Figure 8B, we can see that the frequency shifts of the resonance peak M1 and the resonance peak M2 are basically the same. As shown in Figures 8C,D, it can be seen that the frequency shift sensitivity S₁ of the resonance peaks M1 and M2 both showed a decreasing trend with the increase of the thickness of the air layer h_2. The frequency shift sensitivity S₁ is calculated by $=\Delta f/\Delta Re$ , where $\Delta f$ is the frequency shift of resonance absorption peak and $\Delta Re$ is the real variations of the dielectric constant of resonance absorption peak. The results show that when the frequency of the two resonance peaks is within 2 THz, the minimum thickness of the air layer is $h_{\mathit{2}}=130\mu \mathrm{m}$. In addition to the $S$ above, $FOM$ is another important parameter of the device, which can be defined as [51]

$FOM=\frac{\Delta f}{\Delta n\cdot FWHM}=\frac{S}{FWHM}(7)$

where $FWHM$ is the full-width at half-maximum for the resonance absorption peak.

FIGURE 8

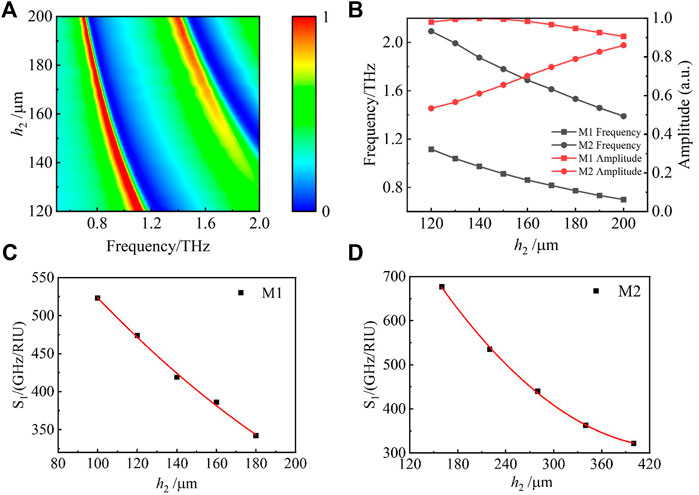
FIGURE 8. (A) Color graph of graphene-based THz metasurface sensor as the change of air layer. (B) Line graph of maximum absorption and resonant frequency of the absorption lines corresponding to h₂ from 0° to 50°. (C) (D) Line graph of frequency shift sensitivity of resonance peak M1 and M2 corresponding to Re from 1 to 2.

The sensing performance are analyzed when $h_{\mathit{2}}=130\mu \mathrm{m}$. The results are shown in Figures 9A,B, when the real part of the permittivity $Re$ increases from 1 to 2 in steps of 0.2 and as the imaginary part of the permittivity $Im$ increases from 0 to 0.1 in steps of 0.01. From Figure 9A, we can see that with the real part of the permittivity $Re$ increases from 1 to 2 in steps of 0.2, the resonance peaks M1 and M2 have a certain frequency shift and amplitude shift. We calculate the sensitivity S, FOM and Q [52] of M1 and M2. As a comparison, the results are shown in the Tables 1, 2, the frequency shift sensitivity of the resonance peak M1 decreases from 450 GHz/RIU o 203 GHz/RIU, and the frequency shift sensitivity of the resonance peak M2 drops from 717 GHz/RIU to 377 GHz/RIU. In addition, according to the Tables 1, 2, the amplitude sensitivity change of the resonant peak M2 is larger than that of the resonant peak M1, indicating that M2 has a high frequency shift sensitivity and also has a good absorption amplitude change, which is more suitable for analyte sensing detection. From Figure 9B, it can be seen that with the increase of the imaginary part of the dielectric constant $Im$, the frequency shift of the resonance peaks M1 and M2 is not large, and the amplitude change of M2 is larger than that of M2, which indicates that M2 is more suitable for sensing detection.

FIGURE 9

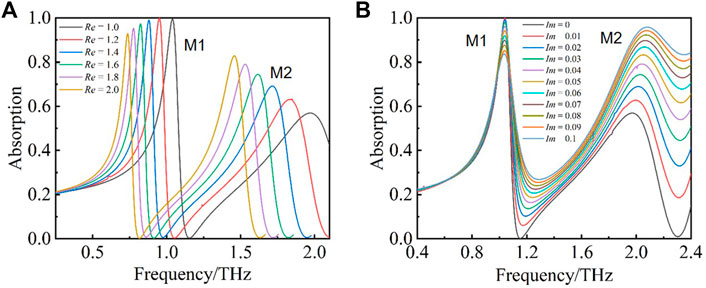
FIGURE 9. (A) Absorption lines of the graphene-based THz metasurface sensor when $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$ corresponding to $Re$ from 1 to 2. (B) Absorption lines of the graphene-based THz metasurface sensor when $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$ corresponding to $Im$.

TABLE 1

TABLE 1. Q, FOM, S₁, S₂ when the resonant peak M1 changes with Re at $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$.

TABLE 2

TABLE 2. Q, FOM, S₁, S₂ when the resonant peak M2 changes with Re at $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$.

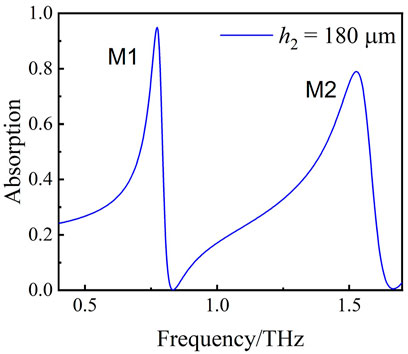
According to Figures 10A,B, we can see that M1 and M2 reach the maximum absorption when $h_{\mathit{2}}=\mathit{140}\mu \mathrm{m}$ and $h_{\mathit{2}}=\mathit{280}\mu \mathrm{m}$, respectively, and the sensing performance of the proposed sensor are studied at these two thicknesses. It can be seen from Figure 10C that when $h_{\mathit{2}}=\mathit{140}\mu \mathrm{m}$, the maximum frequency shift sensitivity of M1 can reach 419 GHz/RIU, and the maximum frequency shift sensitivity of M2 can reach 696 GHz/RIU. Compared with $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$, the two peaks have a slight decrease in sensitivity. It can be seen from Figure 10D that when $h_{\mathit{2}}=\mathit{280}\mu \mathrm{m}$, the maximum frequency shift sensitivity of M2 can reach 440 GHz/RIU, and the maximum frequency shift sensitivity of M2 can reach 232 GHz/RIU. Compared with $h_{\mathit{2}}=\mathit{130}\mu \mathrm{m}$, the two peaks have a larger decrease in sensitivity. According to the above results, we can infer that when the two absorption peaks reach the maximum absorption, the frequency shift sensitivity is still as high as about 450 GHz/RIU.

FIGURE 10

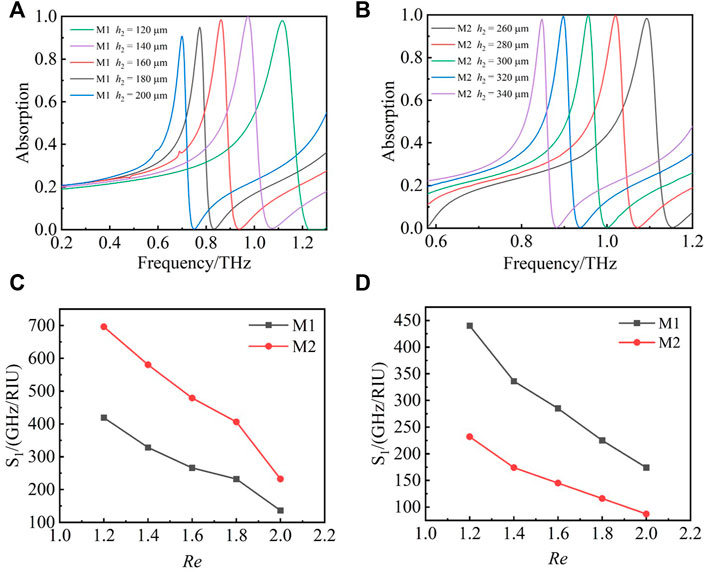
FIGURE 10. (A) Absorption line of the resonance peak M1 as h₂ varies from 120 to 200 $\mu \mathrm{m}$. (B) Absorption line of the resonance peak M2 as h₂ varies from 260 to 340 $\mu \mathrm{m}$. (C) Line graph of S₁ of the absorption corresponding to $Re$ from 1 to 2 when $h_{\mathit{2}}=\mathit{140}\mu \mathrm{m}$. (D) Line graph of S₁ of the absorption corresponding to $Re$ from 1 to 2 when $h_{\mathit{2}}=\mathit{280}\mu \mathrm{m}$.

Conclusion

In summary, a graphene-based THz metasurface sensor with an air spacer is proposed. The absorption spectrum of this sensor was studied. The resonance mechanism was analyzed by impedance matching and electric field distribution. There is a good linear relationship between the absorption peak and the dielectric environment of the sensor surface at 0∼2 THz, and the frequency shift sensitivity of the two resonance peaks M1 and M2 can reach 450 GHz/RIU and 717 GHz/RIU, respectively. By changing the thickness of the air layer, when the two resonance peaks reach the maximum absorption, the frequency shift sensitivity is still as high as close to 450 GHz/RIU. The influence of structural parameters and incident angle on the absorption spectra is studied, it is found that the structural parameters and incident angle have little effect on the device within a certain range, and analyte detection can still be achieved. The above results show that the sensor has good stability and reliability. The graphene-based THz metasurface sensor can be used for analyte sensing, which broadens the application range of THz functional devices.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

HH and BQ conceived and led the design; BQ and XZ finished the whole manuscript writing and the manuscript modification, YW, XH, and YZ contributed to the proofreading, revised the article format, and all authors listed approved it for publication.

Funding

This work was supported in part by the Natural Science Foundation of Shaanxi Province under Grant 2020JZ-48; Youth Innovation Team of Shaanxi Universities(21JP084), and by the National Natural Science Foundation of China (61975163).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhang X, Xu Q, Xia L, Li Y, Gu J, Tian Z, et al. Terahertz surface plasmonic waves: a review. Adv Photon (2020) 2:014001. doi:10.1117/1.AP.2.1.014001

CrossRef Full Text | Google Scholar

2. Jiang T, Chen RZ, Zheng X, Xu ZJ, Tang YH. Photo-induced excitonic structure renormalization and broadband absorption in monolayer tungsten disulphide. Opt Express (2018) 26:859. doi:10.1364/oe.26.000859

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Wu XJ, Quan BG, Pan XC, Xu XL, Lu XC, Gu CZ, et al. Alkanethiol-functionalized terahertz metamaterial as label-free, highly-sensitive and specificbiosensor. Biosens Bioelectron X (2013) 42:626–31. doi:10.1016/j.bios.2012.10.095

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang AX, Wang JF, Zhang JQ, Wang WJ, Xu CL. Ultra wide-angle and broad-band metamaterial absorber based on magneto-electric dipole structure. J Phys D Appl Phys (2021) 54:335102. doi:10.1088/1361-6463/ac0071

CrossRef Full Text | Google Scholar

5. Hu YZ, Tong MY, Xu ZL, Cheng XG, Jiang T. Metamaterials: Bifunctional spatiotemporal metasurfaces for incident angle‐tunable and ultrafast optically switchable electromagnetically induced transparency (small 21/2021). Small (2021) 17:2170097. doi:10.1002/smll.202170097

CrossRef Full Text | Google Scholar

6. Han JG, Tian Z, Gu JQ, He MX, Zhang WL. Composite metamaterials with tunable chiral properties at terahertz frequencies. Chin Opt Lett (2011) 9:s10401–310403. doi:10.3788/COL201109.S10401

CrossRef Full Text | Google Scholar

7. Zhou T, Chen S, Zhang X, Zhang X, Hu H, Wang Y. Electromagnetically induced transparency based on a carbon nanotube film terahertz metasurface. Opt Express (2022) 30:15436–45. doi:10.1364/OE.457768

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang JF, Qu SB, Zhuo X, Song X, Qiu ZJ, Hua M, et al. Experimental verification of left-handed metamaterials composed of electric and magnetic resonators. Acta Phys Sin (2010) 27:1847. doi:10.7498/aps.59.1847

CrossRef Full Text | Google Scholar

9. Yang J, Qi L, Li B, Wu L, Shi D, Ahmed U, et al. A terahertz metamaterial sensor used for distinguishing glucose concentration. Results Phys (2021) 26:104332. doi:10.1016/j.rinp.2021.104332

CrossRef Full Text | Google Scholar

10. Wang JF, Qu SB, Xu Z, Zhang JQ, Yang YM, Ma H, et al. A candidate three-dimensional GHz left-handed metamaterial composed of coplanar magnetic and electric resonators. Photon Nanostructures - Fundamentals Appl (2008) 6:183–7. doi:10.1016/j.photonics.2008.08.001

CrossRef Full Text | Google Scholar

11. Karmakar S, Kumar D, Varshney RK, Chowdhury DR. Strong terahertz matter interaction induced ultrasensitive sensing in Fano cavity based stacked metamaterials. J Phys D Appl Phys (2020) 53:415101. doi:10.1088/1361-6463/ab94e3

CrossRef Full Text | Google Scholar

12. Chen T, Zhang D, Huang F, Li Z, Hu F. Design of a terahertz metamaterial sensor based on split ring resonator nested square ring resonator. Mater Res Express (2020) 7:095802. doi:10.1088/2053-1591/abb496

CrossRef Full Text | Google Scholar

13. Zhu WR, Zhao XP, Gong BY. Left-handed metamaterials based on a leaf-shaped configuration. J Appl Phys (2011) 109:093504. doi:10.1063/1.3583544

CrossRef Full Text | Google Scholar

14. Sun R, Li W, Meng T, Zhao G. Design and optimization of terahertz metamaterial sensor with high sensing performance. Opt Commun (2021) 494:127051. doi:10.1016/j.optcom.2021.127051

CrossRef Full Text | Google Scholar

15. Tan S, Yan F, Wang W, Zhou H, Hou Y. Ultrasensitive sensing with three-dimensional terahertz metamaterial absorber. J Opt (2018) 20:055101. doi:10.1088/2040-8986/aab66e

CrossRef Full Text | Google Scholar

16. Zhang HY, Cao YY, Liu YZ, Li Y, Zhang YP. A novel graphene metamaterial design for tunable terahertz plasmon induced transparency by two bright mode coupling. Opt Commun (2017) 391:9–15. doi:10.1016/j.optcom.2017.01.008

CrossRef Full Text | Google Scholar

17. Wang BX, He Y, Lou P, Xing W. Design of a dual-band terahertz metamaterial absorber using two identical square patches for sensing application. Nanoscale Adv (2020) 2:763–9. doi:10.1039/c9na00770a

CrossRef Full Text | Google Scholar

18. Geng Z, Zhang X, Fan Z, Lv X, Chen H. A route to terahertz metamaterial biosensor integrated with microfluidics for liver cancer biomarker testing in early stage. Sci Rep (2017) 7:16378–11. doi:10.1038/s41598-017-16762-y

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yao H, Mei H, Zhang W, Zhong S, Wang X. Theoretical and experimental research on terahertz metamaterial sensor with flexible substrate. IEEE Photon J (2022) 14:1–9. doi:10.1109/jphot.2021.3124414

CrossRef Full Text | Google Scholar

20. Geng Z, Zhang X, Fan Z, Lv X, Chen H. A route to terahertz metamaterial biosensor integrated with microfluidics for liver cancer biomarker testing in early stage. Sci Rep (2017) 7:16378. doi:10.1038/s41598-017-16762-y

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu XL, Song L, Shi YL, Yang YP, Xie SS, Li W. Light-induced dielectric transparency in single-walled carbon nanotube films. Chem Phys Lett (2005) 410:298–301. doi:10.1016/j.cplett.2005.05.078

CrossRef Full Text | Google Scholar

22. Xu W, Xie L, Zhu J, Tang L, Singh R, Wang C, et al. Terahertz biosensing with a graphene-metamaterial heterostructure platform. Carbon (2019) 141:247–52. doi:10.1016/j.carbon.2018.09.050

CrossRef Full Text | Google Scholar

23. Chen CX, Can S, Schalch J, Zhao XG, Duan GW, Averitt RD, et al. Ultrathin terahertz triple-band metamaterial absorbers: Consideration of interlayer coupling. Phys Rev Appl (2020) 14:054021. doi:10.1103/physrevapplied.14.054021

CrossRef Full Text | Google Scholar

24. Schalch J, Duan G, Zhao X, Zhang X, Averitt R. Terahertz metamaterial perfect absorber with continuously tunable air spacer layer. Appl Phys Lett (2018) 113:061113. doi:10.1063/1.5041282

CrossRef Full Text | Google Scholar

25. Shrekenhamer D, Chen WC, Padilla WJ. Liquid crystal tunable metamaterial absorber. Phys Rev Lett (2013) 110:177403. doi:10.1103/PhysRevLett.110.177403

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wang L, Ge S, Hu W, Nakajima M, Lu Y. Graphene-assisted high-efficiency liquid crystal tunable terahertz metamaterial absorber. Opt Express (2017) 25:23873–9. doi:10.1364/OE.25.023873

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wang RX, Li L, Liu JL, Yan F, Tian FJ, Tian H, et al. Triple-band tunable perfect terahertz metamaterial absorber with liquid crystal. Opt Express (2017) 25:32280–9. doi:10.1364/oe.25.032280

CrossRef Full Text | Google Scholar

28. Yin Z, Lu Y, Xia T, Lai W, Yang J, Lu H, et al. Electrically tunable terahertz dual-band metamaterial absorber based on a liquid crystal. RSC Adv (2018) 8:4197–203. doi:10.1039/c7ra13047c

CrossRef Full Text | Google Scholar

29. Dicken MJ, Aydin K, Pryce IM, Sweatlock LA, Atwater HA, Walavalkar S, et al. Frequency tunable near-infrared metamaterials based on VO₂ phase transition. Opt Express (2009) 17:18330–9. doi:10.1364/OE.17.018330

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Lu C, Lu Q, Gao M, Lin Y. Dynamic manipulation of THz waves enabled by phase-transition VO₂ thin film. Nanomaterials (2021) 11:114. doi:10.3390/nano11010114

CrossRef Full Text | Google Scholar

31. Zhao Y, Chen C, Pan X, Zhu Y, Holtz M, Bernussi A, et al. Tuning the properties of VO₂ thin films through growth temperature for infrared and terahertz modulation applications. J Appl Phys (2013) 114:113509. doi:10.1063/1.4821846

CrossRef Full Text | Google Scholar

32. Zhu HF, Du LH, Li J, Shi QW, Peng B, Li ZR, et al. Near-perfect terahertz wave amplitude modulation enabled by impedance matching in VO₂ thin films. Appl Phys Lett (2018) 112:081103. doi:10.1063/1.5020930

CrossRef Full Text | Google Scholar

33. Aslinezhad M. High sensitivity refractive index and temperature sensor based on semiconductor metamaterial perfect absorber in the terahertz band. Opt Commun (2020) 463:125411. doi:10.1016/j.optcom.2020.125411

CrossRef Full Text | Google Scholar

34. Keshavarz A, Zakery A. Ultrahigh sensitive temperature sensor based on graphene-semiconductor metamaterial. Appl Phys A (2017) 123:797–7. doi:10.1007/s00339-017-1399-y

CrossRef Full Text | Google Scholar

35. Tang T, Li C, Luo L, Zhang Y, Li J. Goos–Hänchen effect in semiconductor metamaterial waveguide and its application as a biosensor. Appl Phys B (2016) 122:167–7. doi:10.1007/s00340-016-6447-3

CrossRef Full Text | Google Scholar

36. Zhao XG, Zhang JD, Fan KB, Duan GW, Metcalfe GD, Wraback M, et al. Nonlinear terahertz metamaterial perfect absorbers using GaAs [Invited]. Photon Res (2016) 4:A16–A21. doi:10.1364/prj.4.000a16

CrossRef Full Text | Google Scholar

37. Duan G, Jacob S, Zhao X, Zhang J, Averitt RD, Xin Z. An air-spaced terahertz metamaterial perfect absorber. Sensors Actuators A: Phys (2018) 280:303–8. doi:10.1016/j.sna.2018.07.052

CrossRef Full Text | Google Scholar

38. Xiao BG, Tong SJ, Alexander F, Shi ZM. Tunable electromagnetically induced transparency based on graphene metamaterials. Opt Express (2020) 28:4048–57. doi:10.1364/OE.382485

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Xiao B, Wang Y, Cai W, Xiao L. Design and prediction of PIT devices through deep learning. Opt Express (2022) 30:14985–97. doi:10.1364/OE.449465

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cai WJ, Xiao BG, Yu JB, Xiao LH. A compact graphene metamaterial based on electromagnetically induced transparency effect. Opt Commun (2020) 475:126266. doi:10.1016/j.optcom.2020.126266

CrossRef Full Text | Google Scholar

41. Barzegar-Parizi S, Ebrahimi A. Ultrathin, polarization-insensitive multi-band absorbers based on graphene metasurface with THz sensing application. J Opt Soc Am B (2020) 37:2372. doi:10.1364/josab.396266

CrossRef Full Text | Google Scholar

42. Biabanifard M, Arsanjani A, Abrishamian MS, Abbott D. Tunable terahertz graphene-based absorber design method based on a circuit model approach. IEEE Access (2020) 8:70343–54. doi:10.1109/access.2020.2986682

CrossRef Full Text | Google Scholar

43. Zhang D, Li Z, Fan K, Chen T, Jia B, Pan S, et al. Dynamically tunable terahertz metamaterial sensor based on metal–graphene hybrid structural unit. AIP Adv (2022) 12:025206. doi:10.1063/5.0079964

CrossRef Full Text | Google Scholar

44. Koppens FHL, Chang DE, JavierGarcía F. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett (2011) 11:3370–7. doi:10.1021/nl201771h

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lui CH, Li Z, Mak KF, Cappelluti E, Heinz TF. Observation of an electrically tunable band gap in trilayer graphene. Nat Phys (2011) 7:944–7. doi:10.1038/nphys2102

CrossRef Full Text | Google Scholar

46. Andryieuski A, Lavrinenko AV. Graphene metamaterials based tunable terahertz absorber: Effective surface conductivity approach. Opt Express (2013) 21:9144–55. doi:10.1364/OE.21.009144

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wen Q, Xie Y, Zhang H, Yang Q, Liu Y. Transmission line model and fields analysis of metamaterial absorber in the terahertz band. Opt Express (2009) 17:20256–65. doi:10.1364/OE.17.020256

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Smith DR, Vier DC, Koschny T, Soukoulis CM. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys Rev E (2005) 71:036617. doi:10.1103/PhysRevE.71.036617

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Qi Y, Zhang Y, Liu C, Zhang T, Wang X, Wang L, et al. A tunable terahertz metamaterial absorber composed of elliptical ring graphene arrays with refractive index sensing application. Results Phys (2020) 16:103012. doi:10.1016/j.rinp.2020.103012

CrossRef Full Text | Google Scholar

50. Zhang K, Yuan YY, Ding XM, Ratni B, Burokur SN, Wu Q. High-efficiency metalenses with switchable functionalities in microwave region. ACS Appl Mater Inter (2019) 11:28423–30. doi:10.1021/acsami.9b07102

CrossRef Full Text | Google Scholar

51. Liu BW, Chen S, Zhang JC, Yao X, Zhong JH, Lin HX, et al. A plasmonic sensor array with ultrahigh figures of merit and resonance linewidths down to 3 nm. Adv Mater (2018) 30:1706031. doi:10.1002/adma.201706031

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Park J, Kang JH, Liu X, Brongersma ML. Electrically tunable epsilon-near-zero (ENZ) metafilm absorbers. Sci Rep (2015) 5:15754. doi:10.1038/srep15754

PubMed Abstract | CrossRef Full Text | Google Scholar