Control of coherent extreme-ultraviolet emission around atomic potential through laser chirp

Substantial neutral atoms can tunnel to excited states in an intense laser field and subsequently generate coherent emission through free induction decay. We experimentally observe an enhanced coherent emission in the harmonic slightly below the threshold, which is consistent with the free induction decay of Rydberg states produced by the frustrated tunnelling ionization (FTI) process. We further find that the intensity of the coherent emission significantly depends on the chirp of laser pulses. The simulations based on the strong field approximation model show that laser chirp affects the probability that the returned electrons recombine to the Rydberg states. Our result shows that coherent emission can be controlled by laser chirp, which facilitates understanding the dynamics of the Rydberg atom and coupling mechanism between the below-threshold harmonics and atomic energy level. In addition, the coherent below-threshold FTI emission we observed has small divergence which is good for EUV light source applications.

1 Introduction

The investigations of high-order harmonic generation (HHG) [1, 2] in atomic and molecular systems promote the development of non-linear optics. A bound-state electron can be released from parent ion through the tunnelling ionization process when the instantaneous intense laser external field becomes comparable to the binding Coulomb field. Then, the released electron obtains kinetic energy in the laser field and recollides with the parent ion; subsequently, the kinetic energy of the collision is converted into radiation energy. This widely accepted physical picture called the three-step model [3, 4] has attracted extensive research interest such as atomic and molecular dynamics [5, 6], attosecond science [7–9], and coherent extreme-ultraviolet source [10].

In the previous reports, the above-threshold HHG has been extensively studied, and recent works show that the below (or near)-threshold harmonics (BTH) present complex and interesting phenomena. When the BTH spectrally overlap with the atomic energy levels, resonance-enhanced vacuum ultraviolet (VUV) emission [10] can be generated with phase-matching and high-efficiency. Although BTH generation [11–15] is largely incompatible with the three-step model of HHG, the surprising result is that these harmonics still arise from a non-perturbative process [16]. The cross-correlation frequency resolved optical gating (XFROG) [17] characterization shows that the BTH has a clear non-perturbative negative group delay dispersion (GDD), and the mechanism for BTH generation is similar to the semi-classical re-scattering process responsible for plateau harmonics. It is also found that the effects induced by the Coulomb potential also have a critical impact on these harmonics [11].

Near the threshold of the atomic or molecular ionization, some new coherent extreme-ultraviolet emissions [18, 19] through frustrated tunnelling ionization (FTI) process [20–24] called “FTI emission” have been reported. In the case of FTI, an electron is released from the parent ion by tunnelling ionization and oscillates in the superposition of the Coulomb field and the laser field, which is similar to the first two steps of the three-step model. Nevertheless, when the laser pulse is turned off, the released electrons return to the vicinity of the parent ion with zero kinetic energy, where the wave packets overlap spatially with the Rydberg states [25–27], rather than direct recombination to the ground state as described in the three-step model. Also, even at extreme high-laser intensities, atoms or molecules are not fully ionized and a fraction of them will appear as high-Rydberg states at the end of the laser pulse [28]. In this way, atoms or molecules can be coherently excited and obtain energy by surviving the laser pulse [29] in the Rydberg states and subsequently generate coherent EUV emission through free-induction decay (FID) [30–33]. The FTI emission is generated in the transition between the Rydberg states and the ground state, where the energy difference determines the frequency of emission. The FTI emission can be spatially controlled by adjusting the spatial chirp of driving pulses [18, 19], but the effect of temporal chirp of laser pulses on FTI emission has not been reported.

In this work, we investigate the FTI emission overlapping with HHG around the ionization potential of Kr atoms, I_p, excited by the chirp-controlled laser. The results show that behavior of the spectra can be strongly affected by the temporal chirp of the laser field and totally different for the parts above and below the ionization potential. The part above the I_p always presents the absorption, while the part below the I_p presents the emission which can be tuned by the laser chirp. By solving a one-dimensional time-dependent Schrödinger equation (1D TDSE), it is found that after the ground-state electron is excited, the probability of electron recombination to the Rydberg states is different under the positive and negative chirps. The positive chirp is conducive to electron recombination to the Rydberg states, in which case the probability of the electron returning to the vicinity of the parent ion with zero kinetic energy is higher. The excited state population at chirp coefficient b = 0.03 is about 5 times that of the unchirped laser field and 10 times that of the b = 0.03 laser field. We can control the emission intensity through chirp; furthermore, the FTI emission below the I_p we observed exhibits a small divergence. Our findings provide a new way to observe the complex electron behavior around the ionization potential I_p and to manipulate the FTI emission, contribute to the mechanism of the BTH, and open up the possibility of EUV light source applications such as lithography [34, 35] and EUV spectroscopy.

2 Experimental results

The BTH are driven by a commercial titanium–sapphire laser system (Coherent LEGEND-HE-Cyro, 800 nm, 1 kHz, 40 fs, 10 mJ pulse energy), which can be tuned to generate pulses with different chirps measured 40–300 fs duration (full width at half maxima, FWHM). The laser pulses were focused by a lens with 500 mm focal length to a 2 mm-length cell filled with Kr atoms under constant pressure to generate harmonics. The energy before the focal lens is 0.5 mJ, and the peak laser intensity of the chirp-free 42 fs pulse is about 1.34 × 10¹⁴Wcm⁻². The transmitted beams from the gas cell are filtered by a 300 nm-thick indium (In) foil, and the filtered HHG is collected in a reflection geometry by a spherical mirror which focuses the emissions onto the slit of the VUV spectrometer (McPherson, 234/302) which is located 950 mm away from the gas cell. The spectrometer has been calibrated with a xenon lamp and a mercury vapor lamp. In this experiment, the wavelength of 9th-order harmonic is 88.89 nm, and the corresponding photon energy is 13.9483 eV which is almost equal to the ionization energy of krypton (I_p = 13.9996 eV), which means 9th harmonic can cover many Rydberg states around the ionization potential I_p of Kr atom. Unless otherwise specified, the following experimental conditions are the same.

The existence of the Rydberg states implies differences between the 9th and other harmonics, and we compare different harmonics with the same experimental parameters. Figure 1 shows experimentally measured spectra of the 9th-order harmonic (A) and higher order harmonics (B) from Kr. The upper figures of Figures 1A,B show the harmonic spectra measured by the CCD. The horizontal axis represents the photon energy and the vertical axis is the divergence of the harmonic, which is calculated according to the distance from the gas cell to the CCD. The red line marks the coherence line emissions (4p⁶ → 4p⁵ns) near the Kr ionization energy, and the energy levels for coherence line emissions refer to the NIST Atomic Spectra Database, ASD [36]. The figures below represent the vertical integration of the upper figures, and the horizontal axis is converted to the corresponding wavelength. When acquiring 13th–17th spectra, the indium foil filter is replaced with aluminum foil with the same thickness because of low-transmittance. Compared with the higher order harmonics, the 9th harmonic spectrum exhibits both absorption [labelled as $({}^{2}P_{1/2}^o)8s$, 87.95 nm] and enhanced emission [labelled as $({}^{2}P_{3/2}^o)11s$, 89.96 nm] due to the Kr levels. The photon energy of enhanced emission is lower than the ionization energy I_p (corresponding to the Kr $II[4p^5({}^{2}P_{3/2}^o)]$ limit). It can also be seen from these figures that the divergence of the enhanced emission is ∼1 mrad, close to that of the 9th harmonic, indicating that this is a radiation with good coherence. Comparatively, there is no such structure in the higher order harmonic (13th, 15th, and 17th) spectra. So, the enhancement part of below-threshold 9th harmonic that differs from higher order harmonics is what we care about.

FIGURE 1

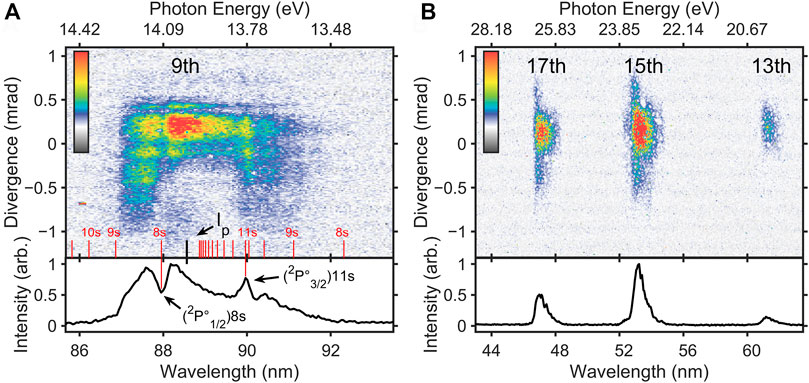
FIGURE 1. Comparison of the 9th-harmonic (A) and higher order harmonic (13th, 15th, and 17th) (B) spectra from krypton. The upper figures show the harmonic spectra measured by the CCD. The horizontal axis represents the photon energy, and the vertical axis is the divergence of the harmonic, which is calculated according to the distance from the gas cell to the CCD. The red line marks the coherence line emissions (4p⁶ → 4p⁵ns) near the Kr ionization energy. The figures below represent the vertical integration of the upper figures, and the horizontal axis is converted to the corresponding wavelength. The indium foil filter was replaced with aluminum foil with the same thickness when acquiring 13th, 15th, and 17th spectra because of low-transmittance.

Typically, the HHG process can be coherently controlled by using a chirped laser [37]. Figure 2 shows the variation of spectrum with the laser chirp, corresponding to the FWHM pulse duration τ from −42 fs to +100 fs, the corresponding laser intensity ranging from 1.34 × 10¹⁴Wcm⁻² to 5.51 × 10¹³Wcm⁻², where “+” and “−” signs indicate the positive and negative chirp, respectively. Apparently, Figure 2 shows that the shape and position of the FTI emission are controlled by the chirp. When the laser pulse is positively chirped, the wavelength position of FTI is fixed, as marked by black dotted circle, depending on the energy level of Kr and the intensity of emission changes with the value of chirp. However, the harmonic will shift with the change of chirp. When the pulse is positively chirped or negatively chirped, the variation range of the intensity is symmetric about the zero-chirp line (dashed line in Figure 2), and the FTI emission does not exhibit this symmetry; the FTI emission can only be observed when the pulse is positively chirped (pulse duration measured +42.8 to +74.1 fs). Despite the same intensity, no FTI radiation was observed under negatively chirped pulse (pulse duration measured −54.2 to −76.2 fs). As can be seen from Figure 2, chirp plays a key role in the spectral intensity of FTI emission.

FIGURE 2

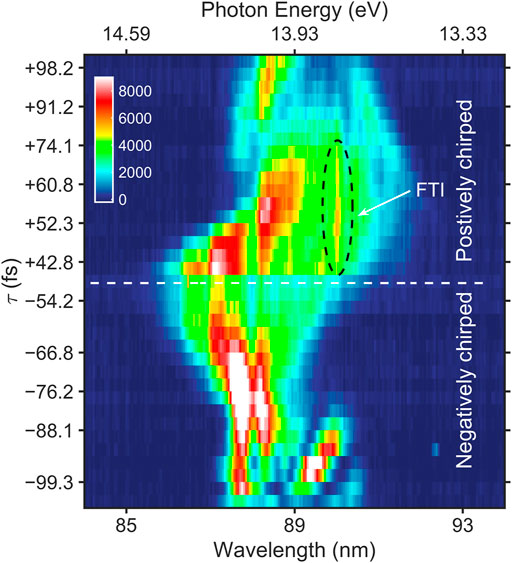
FIGURE 2. Variation of spectrum with laser chirp. The corresponding FWHM pulse duration τ shown as the y-axis varies from −100 fs to +100 fs, where “+” and “−” signs indicate the positive and negative chirp, respectively. The FTI emission is marked by black dotted circles.

To verify whether the enhanced signal is induced by the atomic level, we compare the 9th-harmonic spectra from krypton and argon. In our experimental scheme, the 9th harmonic overlaps the ionization energy and Rydberg-state levels of krypton. But for argon atoms, the photon energy of the 9th harmonic is far below ionization energy. Therefore, when krypton is replaced by argon, the FTI coherent emission will not be observed in the 9th harmonic. Figure 3 displays the comparison of the 9th-harmonic spectra of Kr and Ar under different chirps. In Figure 3A, the levels of Kr near ionization energy are marked above the spectra as red lines, and the FTI coherent emission coincide well with the energy level $4p^5({}^{2}P_{3/2}^o)11s$. Moreover, there are notable absorptions corresponding to the levels $4p^6\to 4p^5({}^{2}P_{1/2}^o)8s$ (87.95 nm) and $4p^6\to 4p^5({}^{2}P_{1/2}^o)9s$ (86.86 nm), implying the transitions from the ground state. The three levels aforementioned are highlighted in a long red line for comparison purposes. The spectral width of the FTI emission at $4p^5({}^{2}P_{3/2}^o)11s$ is ∼0.03 eV, which is comparable to the spectral width of absorption peak at $4p^5({}^{2}P_{1/2}^o)8s$. As seen from the comparison, the 9th harmonic shows a frequency shift, but wavelengths of the absorption and FTI emission are fixed and coincide well with the Kr levels. This suggests that the mechanism of emission at the krypton level is different from that of the 9th-order harmonic generation. For absorption peaks above the threshold, the atom absorbs the 9th harmonic and is excited to the autoionizing state [12, 38], which ionizes almost immediately [39]. The radiation of autoionization propagates at solid angle of 4π, is rarely collected in the spectrometer, and appears as spectral absorption. Figure 3B shows the experimental below-threshold 9th-harmonic spectra generated from Ar, there are only absorptions of the Ar level $[3s^{2}3p^5({}^{2}P°_{3/2})5s]$ (blue line). In addition, the enhanced structure from the Kr level is chirp-dependent.

FIGURE 3

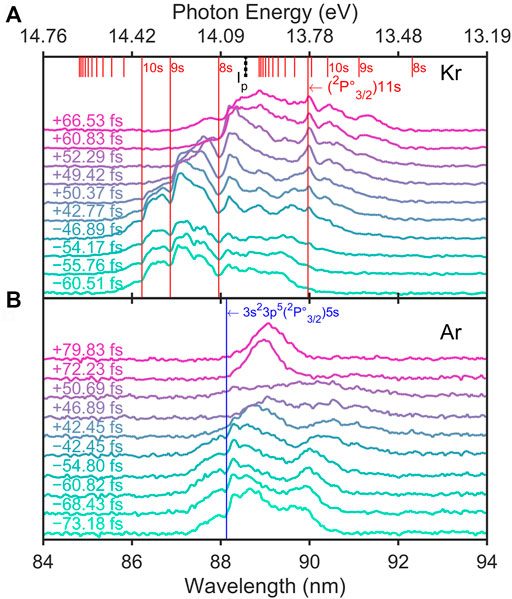
FIGURE 3. Comparison of the 9th-harmonic spectra of Kr (A) and Ar (B) under different chirps. (A) The peak laser intensity of the chirp-free 42-fs pulse was 1.34 × 10¹⁴Wcm⁻². The long red lines are used to highlight absorption and emission under different chirps. (B) There is no fixed structure in the argon harmonic expect absorption of the level Ar $[3s^{2}3p^5({}^{2}P°_{3/2})5s]$ (blue line). The peak laser intensity of the chirp-free 42-fs pulse was 1.88 × 10¹⁴Wcm⁻².

In brief, there are several characteristics of the enhanced coherent emission observed in our experiments. First, the frequency of the enhanced coherent emission is determined by the energy level. So, when we change the chirp of driven pulses, the center wavelength of the enhanced coherent emission remains unchanged, while the 9th-harmonic spectrum drifts a little. Also, there is no enhanced coherent emission from Ar since the 9th harmonic does not cover the levels of Ar atoms. Second, the intensity of the enhanced coherent emission depends on the chirp of driven laser. The chirp is reflected in the temporal shape of the driven photoelectric field. We will analyze how the chirp of driven laser affects the enhanced coherent emission next.

3 Simulation and discussion

As seen in experimental results, the enhanced coherent emission exhibits a small divergence (Figure 1) close to harmonics and its intensity could be controlled by adjusting the temporal chirp of a driving laser pulse, which can be explained by the FTI emission through FID progress [18, 22, 26, 30]. By introducing the concept of electron trajectories, the electron dynamics of FTI progress in the strong laser field could be explained with the strong field approximation theory. In the framework of strong field approximation, the Coulomb field is neglected after the ionization compared to the laser field. In the case of well-known HHG, the wave packet tunnels turn out to be the electron wave packet in the continuum, whose trajectory depends on the ionization time. The electron that tunnels out after the peak of the laser electronic field can be captured to the ground state and lead to harmonic generation. As for FTI progress, we focus on the trajectories of the released electron whose wave packet remains near the parent ion with zero kinetic energy after the laser field. Therefore, only electrons ionized at the appropriate ionization time can recombine to the Rydberg states eventually. The electron that tunnels out near the peak of the laser electric field during every half optical cycle has near-zero kinetic energy after the driving pulse, which is also located near the parent ion and has a high-probability of recombination to the Rydberg states. The chirp dependence of the FTI emission in Figure 2 implies that the probability is also chirp-dependent, causes the temporal shape of driven laser to differ with different chirps, which affect the ionization time of electrons that eventually bind to the Rydberg states. Therefore, the transition probability to the Rydberg state can be expressed as the superposition of ionization rate at the ionization time at every half optical cycle. To simplify the analysis, we assume that Kr atoms are in the ground state before the driving laser (Gaussian beam). The field of linearly polarized pulse with a Gaussian amplitude can be expressed as

$E\left(t\right)=e^{-2\ln 2\times {\left(\frac{t}{\tau }\right)}^2}\times \sqrt{\frac{2I_0}{c{ϵ}_0}}\cos \left[{\omega }_0\left(1+b\frac{t}{\mathrm{\tau }}\right)\times t\right](1)$

where b is the chirp coefficient; I₀ = 6 × 10¹³Wcm⁻² and ω₀ are the peak intensity and frequency of driving laser, respectively; τ = 53fs is the FWHM duration; and ϵ₀ is the vacuum dielectric constant. The parameters of simulation are those when FTI signals can be evidently observed experimentally. The parameter b is used to change the laser chirp. The ionized electron oscillates in the intense laser field after ionization whose trajectory is significantly dependent on the ionization time.

We verify this explanation by solving the 1D TDSE. The soft-core Coulomb potential is given as $V(x)=-1/\sqrt{1.873+x^2}$, the constant 1.873 is used for the ionization potential (I_p = 0.5147 a.u.) of a Kr atom. The Schrödinger equation in a.u. is

$i\frac{\partial }{\partial t}\psi =\left[-\frac{1}{2}\frac{{\partial }^2}{\partial x^2}+V\left(x\right)-x\cdot E\left(t\right)\right]\psi (2)$

where ψ is the wavefunction. The half-length of the absorbing boundary R_abs = 15.9 nm is sufficiently wide to reveal component of the high-lying Rydberg states. Figure 4A shows the temporal evolution of the ground-state krypton atomic populations. The evolution of the wavefunction is shown by |ψ|^0.2, where the value of 0.2 is taken for visualization. It can be seen that the ground state evolves into the superposition of the ground state and excited states when the driving laser is turned off. There is a notable electron population in the vicinity of the ion (±10 nm) where it is overlapped with the Rydberg states. Apparently, some of the electrons are released from the parent ion during the laser field and then are captured to the Rydberg states, which is consistent with FTI as discussed in the previous work [18].

FIGURE 4

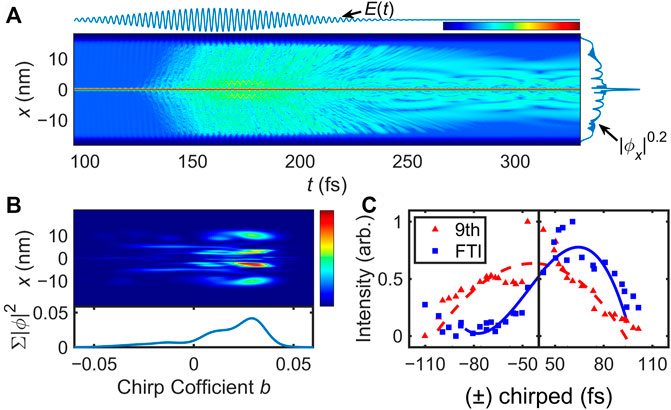
FIGURE 4. (A) Temporal population evolution of a krypton atom exposed to external laser fields in the strong-field tunnelling regime. The top curve is the time domain shape of the laser electric field, and the curve on the right is the populations of krypton when driving laser is off. (B) One-dimensional populations of excited states surviving in different chirped intense laser field. The horizontal axis of the coordinate is the chirp coefficient b in Eq. 1. The curve below shows the integral of populations under different chirp coefficient b. (C) Chirp dependence of the harmonic near threshold (9th, red triangle) and the FTI emission (blue square) observed in experiments. The abscissa is the pulse duration of driven laser which represent different chirps.

The progress of FID [30] suggests that the intensity of FID radiation is related to populations of excited states, which is the high-lying Rydberg states in our study. Previous works have shown that neutrally excited atoms can survive intense laser fields for a long time [20, 29], suggesting that it is possible to accumulate sufficient excited state populations to generate FID radiation under appropriate laser conditions. For qualitative representation, we calculate the one-dimensional population of the first excited state with differently chirped pulses. The chirp coefficient b (Eq. 1) varies in the range of [−0.06, 0.06], which is similar to experimental conditions. Figure 4B displays one-dimensional populations of the first excited state under action of laser with different chirp coefficient b; the curve below displays the integrations of populations under different laser chirps which shows the asymmetric dependence of populations on chirps of driven laser. Our results show that a higher population survived in the positively chirped driving laser than the negative chirped laser. The excited state population at chirp coefficient b = 0.03 is about 5 times that of the unchirped laser field and 10 times that of b = −0.03 laser field. The final position of tunnel-out electron is ∼2.4 nm or ∼10.0 nm away from the parent ion where it is overlapped spatially with the Rydberg states. To confirm the assumption of FID radiation, we compared the chirp dependences of population and experimentally measured the FTI emission. As seen in Figure 4C, normalized intensity of the harmonic generation near threshold (9th, red triangle) indicates a higher efficiency using chirp-free laser, while the FTI emission from the level $4s^{2}4p^5({}^{2}P°_{3/2})11s$ (blue square) is significantly enhanced with small positive chirped lasers, showing the same asymmetry changing with chirp to populations in Figure 4B. The consistency of the calculated population and experimentally measured FTI emission suggests that radiation comes from the FID progress of long-lifetime excited states. In other words, the FTI process can be controlled by adjusting the temporal chirp of a driving laser pulse, including the yield of Rydberg atoms and FID radiation. Although the strong field approximation model could reproduce the FTI emission well, there are still many limitations. First, the effect of chirp is associated with the coefficient b; however, the actual laser pulse duration changes with the chirp. The model does not take into account the possible effect of pulse duration. Second, the recombination process of different excited states was not considered. The model can be improved if different excited states and their phase relation were considered.

4 Conclusion

To conclude, in this work we have investigated the enhanced coherent EUV emission from Rydberg atoms. The emission can be generated using a properly and positively chirped driving laser, under which the excited state population is higher than that of the chirp-free or the negative chirped laser. We have achieved the control of the emission intensity by adjusting the temporal chirp of driving laser. By scanning the chirp, we can identify harmonic spectra drifting at wavelength axis and the emission from the Kr level. In addition, the coherent below-threshold FTI emission we observed has a small divergence which is good for EUV light source applications. These findings suggest a possible support to the progress of extreme-ultraviolet emission summarized as four steps: ionization, oscillation in light field, captured to excited states or autoionizing state, and emission of photon. These results enrich the study of atomic spectroscopy and also give some new ideas with the control of extreme-ultraviolet source.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CY contributed to conceptualization, methodology, validation, formal analysis, investigation, data curation, writing—original draft, and visualization. ZL and FY contributed to validation and investigation. XG contributed to resources. YZ and ZZ contributed to conceptualization, methodology, conceptualization, writing—review and editing, supervision, project administration, and funding acquisition. RL contributed to funding acquisition. All authors contributed to the manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (Grants No. 91950203 and No. 11874374) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB16).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mcpherson A, Gibson G, Jara H, Johann U, Luk TS, Mcintyre IA, et al. Studies of multiphoton production of vacuum ultraviolet-radiation in the rare-gases. J Opt Soc Am B (1987) 4:595–601. doi:10.1364/Josab.4.000595

CrossRef Full Text | Google Scholar

2. Krause JL, Schafer KJ, Kulander KC. High-order harmonic generation from atoms and ions in the high intensity regime. Phys Rev Lett (1992) 68:3535–8. doi:10.1103/PhysRevLett.68.3535

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kulander KC, Schafer KJ, Krause JL. Theoretical model for intense field high-order harmonic generation in rare gases. Laser Phys (1993) 3:359–64.

Google Scholar

4. Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/PhysRevLett.71.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zeng ZN, Cheng Y, Song XH, Li RX, Xu ZZ. Generation of an extreme ultraviolet supercontinuum in a two-color laser field. Phys Rev Lett (2007) 98:203901. doi:10.1103/PhysRevLett.98.203901

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zheng YH, Zeng ZN, Zou P, Zhang L, Li XF, Liu P, et al. Dynamic chirp control and pulse compression for attosecond high-order harmonic emission. Phys Rev Lett (2009) 103:043904. doi:10.1103/PhysRevLett.103.043904

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sansone G, Benedetti E, Calegari F, Vozzi C, Avaldi L, Flammini R, et al. Isolated single-cycle attosecond pulses. Science (2006) 314:443–6. doi:10.1126/science.1132838

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Li J, Ren X, Yin Y, Zhao K, Chew A, Cheng Y, et al. 53-attosecond x-ray pulses reach the carbon k-edge. Nat Commun (2017) 8:186. doi:10.1038/s41467-017-00321-0

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gaumnitz T, Jain A, Pertot Y, Huppert M, Jordan I, Ardana-Lamas F, et al. Streaking of 43-attosecond soft-x-ray pulses generated by a passively cep-stable mid-infrared driver. Opt Express (2017) 25:27506–18. doi:10.1364/OE.25.027506

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chini M, Wang XW, Cheng Y, Wang H, Wu Y, Cunningham E, et al. Coherent phase-matched vuv generation by field-controlled bound states. Nat Photon (2014) 8:437–41. doi:10.1038/nphoton.2014.83

CrossRef Full Text | Google Scholar

11. Xiong WH, Geng JW, Tang JY, Peng LY, Gong Q. Mechanisms of below-threshold harmonic generation in atoms. Phys Rev Lett (2014) 112:233001. doi:10.1103/PhysRevLett.112.233001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Strelkov V. Role of autoionizing state in resonant high-order harmonic generation and attosecond pulse production. Phys Rev Lett (2010) 104:123901. doi:10.1103/PhysRevLett.104.123901

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Xiong WH, Peng LY, Gong QH. Recent progress of below-threshold harmonic generation. J Phys B: Mol Opt Phys (2017) 50:032001. doi:10.1088/1361-6455/50/3/032001

CrossRef Full Text | Google Scholar

14. Yost DC, Schibli TR, Ye J, Tate JL, Hostetter J, Gaarde MB, et al. Vacuum-ultraviolet frequency combs from below-threshold harmonics. Nat Phys (2009) 5:815–20. doi:10.1038/Nphys1398

CrossRef Full Text | Google Scholar

15. Kim S, Jin JH, Kim YJ, Park IY, Kim Y, Kim SW. High-harmonic generation by resonant plasmon field enhancement. Nature (2008) 453:757–60. doi:10.1038/nature07012

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Power EP, March AM, Catoire F, Sistrunk E, Krushelnick K, Agostini P, et al. Xfrog phase measurement of threshold harmonics in a keldysh-scaled system. Nat Photon (2010) 4:352–6. doi:10.1038/Nphoton.2010.38

CrossRef Full Text | Google Scholar

17. Linden S, Giessen H, Kuhl J. Xfrog a new method for amplitude and phase characterization of weak ultrashort pulses. Phys Stat Sol (1998) 206:119–24. doi:10.1002/(sici)1521-3951(199803)206:1<119::aid-pssb119>3.0.co;2-x

CrossRef Full Text | Google Scholar

18. Yun H, Mun JH, Hwang SI, Park SB, Ivanov IA, Nam CH, et al. Coherent extreme-ultraviolet emission generated through frustrated tunnelling ionization. Nat Photon (2018) 12:620–4. doi:10.1038/s41566-018-0255-8

CrossRef Full Text | Google Scholar

19. Mun JH, Ivanov IA, Yun H, Kim KT. Strong-field-approximation model for coherent extreme-ultraviolet emission generated through frustrated tunneling ionization. Phys Rev A (Coll Park) (2018) 98:063429. doi:10.1103/PhysRevA.98.063429

CrossRef Full Text | Google Scholar

20. Nubbemeyer T, Gorling K, Saenz A, Eichmann U, Sandner W. Strong-field tunneling without ionization. Phys Rev Lett (2008) 101:233001. doi:10.1103/PhysRevLett.101.233001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liu H, Liu Y, Fu L, Xin G, Ye D, Liu J, et al. Low yield of near-zero-momentum electrons and partial atomic stabilization in strong-field tunneling ionization. Phys Rev Lett (2012) 109:093001. doi:10.1103/PhysRevLett.109.093001

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Popruzhenko SV. Quantum theory of strong-field frustrated tunneling. J Phys B: Mol Opt Phys (2018) 51:014002. doi:10.1088/1361-6455/aa948b

CrossRef Full Text | Google Scholar

23. von Veltheim A, Manschwetus B, Quan W, Borchers B, Steinmeyer G, Rottke H, et al. Frustrated tunnel ionization of noble gas dimers with rydberg-electron shakeoff by electron charge oscillation. Phys Rev Lett (2013) 110:023001. doi:10.1103/PhysRevLett.110.023001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Popruzhenko SV, Lomonosova TA. Frustrated ionization of atoms in the multiphoton regime. Laser Phys Lett (2021) 18:015301. doi:10.1088/1612-202X/abca43

CrossRef Full Text | Google Scholar

25. Day JO, Brekke E, Walker TG. Dynamics of low-density ultracold rydberg gases. Phys Rev A (Coll Park) (2008) 77:052712. doi:10.1103/PhysRevA.77.052712

CrossRef Full Text | Google Scholar

26. Landsman AS, Pfeiffer AN, Hofmann C, Smolarski M, Cirelli C, Keller U. Rydberg state creation by tunnel ionization. New J Phys (2013) 15:013001. doi:10.1088/1367-2630/15/1/013001

CrossRef Full Text | Google Scholar

27. Piraux B, Mota-Furtado F, O’Mahony PF, Galstyan A, Popov YV. Excitation of rydberg wave packets in the tunneling regime. Phys Rev A (Coll Park) (2017) 96:043403. doi:10.1103/PhysRevA.96.043403

CrossRef Full Text | Google Scholar

28. Li Q, Tong XM, Morishita T, Jin C, Wei H, Lin CD. Rydberg states in the strong field ionization of hydrogen by 800, 1200 and 1600 nm lasers. J Phys B: Mol Opt Phys (2014) 47:204019. doi:10.1088/0953-4075/47/20/204019

CrossRef Full Text | Google Scholar

29. Bing-Bing W, Xiao-Feng L, Pan-Ming F, Jing C, Jie L. Coulomb potential recapture effect in above-barrier ionization in laser pulses. Chin Phys Lett (2006) 23:2729–32. doi:10.1088/0256-307X/23/10/029

CrossRef Full Text | Google Scholar

30. Bengtsson S, Larsen EW, Kroon D, Camp S, Miranda M, Arnold CL, et al. Space-time control of free induction decay in the extreme ultraviolet. Nat Photon (2017) 11:252–8. doi:10.1038/Nphoton.2017.30

CrossRef Full Text | Google Scholar

31. Beaulieu S, Bloch E, Barreau L, Comby A, Descamps D, Geneaux R, et al. Phase-resolved two-dimensional spectroscopy of electronic wave packets by laser-induced xuv free induction decay. Phys Rev A (Coll Park) (2017) 95:041401. doi:10.1103/PhysRevA.95.041401

CrossRef Full Text | Google Scholar

32. Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, et al. Role of excited states in high-order harmonic generation. Phys Rev Lett (2016) 117:203001. doi:10.1103/PhysRevLett.117.203001

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bloch F, Hansen WW, Packard M. Nuclear induction. Phys Rev (1946) 69:127. doi:10.1103/PhysRev.69.127

CrossRef Full Text | Google Scholar

34. Wagner C, Harned N. Lithography gets extreme. Nat Photon (2010) 4:24–6. doi:10.1038/nphoton.2009.251

CrossRef Full Text | Google Scholar

35. Baksh PD, Odstrcil M, Kim HS, Boden SA, Frey JG, Brocklesby WS. Wide-field broadband extreme ultraviolet transmission ptychography using a high-harmonic source. Opt Lett (2016) 41:1317–20. doi:10.1364/Ol.41.001317

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kramida A, Yu Ralchenko , Reader JNIST ASD Team. [Dataset]. NIST atomic spectra Database (ver. 5.8). [Online]. Gaithersburg, MD: National Institute of Standards and Technology (2020). Available: https://physics.nist.gov/asd (Accessed on July 1, 2021).

Google Scholar

37. Lee DG, Kim JH, Hong KH, Nam CH. Coherent control of high-order harmonics with chirped femtosecond laser pulses. Phys Rev Lett (2001) 87:243902. doi:10.1103/PhysRevLett.87.243902

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Milosevic DB. High-energy stimulated emission from plasma ablation pumped by resonant high-order harmonic generation. J Phys B: Mol Opt Phys (2007) 40:3367–76. doi:10.1088/0953-4075/40/17/005

CrossRef Full Text | Google Scholar

39. Lindle DW, Ferrett TA, Becker U, Kobrin PH, Truesdale CM, Kerkhoff HG, et al. Photoionization of helium above theHe+(n=2) threshold: Autoionization and final-state symmetry. Phys Rev A (Coll Park) (1985) 31:714–26. doi:10.1103/physreva.31.714

PubMed Abstract | CrossRef Full Text | Google Scholar