A review of nanoparticle decharging in atmospheric pressure plasma afterglows

Plasma afterglows interacting with dust grains present a dynamic environment in which negatively charged dust grains leaving the plasma bulk experience an environment with plasma conditions transient in space and time. This review focuses on the impact of atmospheric pressure on the physics concerning the interaction between dust grains and the plasma afterglow. The four stage model commonly applied to low pressure dusty plasma afterglows provides a guiding framework for the analysis describing the phases of electron temperature relaxation, ambipolar diffusion, ambipolar-to-free diffusion transition and free diffusion. This work is completed by a non-exhaustive overview of research gaps and opportunities in the young and vibrant field of atmospheric pressure dusty plasma afterglows.

1 Introduction

Dust grains immersed in a plasma environment contribute strongly to the collective behavior by virtue of the electric charge obtained through interactions with the electrons, ions and electric fields. For many applications, from nanoparticle production [1, 2] to contamination control [3, 4], charged dust grains eventually leave the active plasma environment for subsequent processing. As a consequence, charged dust grains experience the transition from the active plasma region, through the ion-rich plasma afterglow with a net positive space charge, into an equilibrium environment containing neutral gas and long-lived radicals.

Early observations [5–7] of dust with residual charges in decaying plasmas at low pressure triggered investigations of dust (de)charging in temporal and spatial afterglow plasmas [8–18]. By contrast, the interaction of nanoparticles with atmospheric pressure afterglow plasmas constitutes a relatively unexplored field compared to low pressure dusty plasma afterglows. Nevertheless, the synthesis of nanocrystals at atmospheric pressure provides a low cost method to produce and deposit nanoparticles [19–22] with a specific structure [23, 24] and optical properties [25, 26], while the deposition of thin films using atmospheric pressure plasmas represents a cost effective alternative to vacuum processes [27–30] and provides the potential to include nanoparticles [20]. With the advent of these upcoming nanotechnologies, the demand for sensing abilities of such nanoparticles (or ultrafine particles) is also increasingly drawing attention [31–34]. Further progress of these technologies is limited by a lack of understanding of the interaction between nanoparticles and afterglow plasmas at atmospheric pressure.

Modeling efforts and experiments on atmospheric pressure afterglow plasmas interacting with dust grains have shown significant progress towards a more detailed understanding of these environments [35–41]. The models and experiments focused on the transition between the bulk plasma, where dust grains are negatively charged, towards an equilibrium gas in which dust grains can be left with residual positive charges. Such charging effects are heavily affected by deviations from bulk plasma properties such as quasi-neutrality, ambipolar diffusion and electron temperatures exceeding those of the gaseous and ion species. In turn, the charge state of nanoparticles strongly influences the aggregation of plasma species and coagulation with other nanoparticles [37]. Consequently, the spatial afterglow of such flow-through plasmas determines largely the resulting size distribution and material structure of nanoparticles synthesized using atmospheric pressure plasma reactors.

This review collects the existing knowledge on atmospheric pressure dusty plasma afterglows following the established model for low pressure dusty plasma afterglows [7, 15, 17, 42–45], and finalizes with a discussion of open gaps in this young and vibrant field of dusty plasma research.

2 Physics of dusty plasma afterglows

In the plasma afterglow, four stages can be identified during which the dust grain charge diminishes due to the decaying plasma conditions [15, 17]: (I) electron temperature relaxation, (II) ambipolar diffusion, (III) ambipolar-to-free diffusion transition, (IV) free diffusion, which are followed by an equilibrium with residual dust charge. In this work, there is no explicit definition of short τ⁰ and long τ^∞ time scales as used in the definitions by Ivlev et al [7] and Couëdel et al [15, 42–44]. Instead, the time scales denoted in this work are calculated for specific plasma conditions that approximate an early (close to the short time scales) or late (before reaching equilibrium where t → ∞) afterglow plasma at atmospheric pressure.

The physics of dust grains interacting with atmospheric pressure plasma afterglows is mostly impacted by the smaller mean free paths (i.e. much higher collision frequencies) compared to vacuum conditions. The mean free path l_sn of a charged or neutral species due to collisions with the neutral gas species is defined as

$l_{s\mathrm{n}}=\frac{1}{n_{\text{n}}{\sigma }_{s\mathrm{n}}},(1)$

for species s, which could be electrons, ions or radicals, for example, where n_n denotes the neutral gas density and σ_sn the collision cross section. As a consequence, the transfer of energy and momentum occurs much more frequently and limits the mobility of the species involved in, for instance, electron temperature relaxation and the currents imposed on dust grains.

2.1 Stage I: electron temperature relaxation

During the first phase (I), the electron temperature drops quickly due to the absence of an active ionization source. This temperature drop is caused by frequent collisions between energetic electrons and neutral gas particles at room temperature, which occurs on a time scale typically about τ_T ∼10^–4 s under low pressure conditions (given for p = 0.4 mbar [15]). The charge fluctuation time scale τ_Q ∼ 10^–6 − 10^–5 s, as given by Couëdel et al [15] for the same conditions, is much smaller than τ_T. This means that the dust charge in the low pressure afterglow remains in quasi-steady state with the plasma conditions. Hence, under vacuum conditions, the relaxation of the electron temperature occurs sufficiently slow with respect to the (nearly temperature-independent) charging time scale so that the magnitude of the dust charge decreases steadily with the decaying plasma conditions [15].

Under atmospheric conditions, this situation differs significantly due to the electron-neutral collisionality. This effect has been accounted for by various models [37, 46], where a global model for the temporal afterglow was used due to the lack of a spatial afterglow model for the electron temperature. Given the scaling of the electron temperature relaxation timescale [15, 47],

${\tau }_{\text{T}}\propto \frac{1}{{\nu }_{\text{en}}}\propto \frac{1}{n_{\text{n}}{\sigma }_{\text{en}}{v}_{\text{e}}},(2)$

where σ_en denotes the electron-neutral collision cross section and $v_{\text{e}}={(8k_{\text{B}}{T}_{\text{e}}/(\pi m_{\text{e}}))}^{1/2}$ the electron thermal velocity, k_B the Boltzmann constant, T_e the electron temperature, and m_e the electron (rest) mass. As can be seen from Eq. 2, τ_T is reduced by the order of magnitude difference in neutral gas pressure for low temperature plasmas. As observed from experiments, the timescale of decay of the effective collision frequency (equivalent to the electron-neutral collision frequency) was on the order of ∼1μs for a helium plasma afterglow entering an air environment [48], and on the order of ∼ 0.1μs for electrons in an argon-oxygen afterglow [49]. Consequently, the electron temperature relaxation time scale is much shorter than that can be expected at low pressure.

The difference in electron temperature relaxation time scale between low and atmospheric pressure conditions implies that the dust charging time scale also needs to be assessed with respect to an enhanced pressure. The ion current experiences collisions much more frequently at atmospheric pressure. To assess the contribution of the collisionless $(I_{\text{i}}^{\text{OML}})$, collision-enhanced $(I_{\text{i}}^{\text{CE}})$ and hydrodynamic $(I_{\text{i}}^{\text{HYD}})$ ion currents, the (capture radius) Knudsen number is used as

${\mathrm{K}\mathrm{n}}_{{\text{R}}_0}=\frac{l_{\text{in}}}{2\alpha R_0},(3)$

with α = 1.22 accounting for the Maxwellian ion energy distribution and R₀ the capture radius, both as defined by Equation [5, 6] in Gatti and Kortshagen [50]. This Knudsen number is at most 0.02 for dust grain radii a_d = 10–300 nm, argon ions in argon at atmospheric pressure σ_in ≈ 5.8 × 10^–19 m⁻² [51], n_n = 2.6 × 10²⁵ m⁻³, plasma density of n_e = n_i = 10¹⁸ m⁻³, and otherwise similar conditions used by Couëdel et al [15]. Hence, this means that only the hydrodynamic ion current contributes significantly to the total ion current. Consequently, the charge fluctuation timescale can be determined using the collisionless electron current (i.e. $I_{\text{e}}^{\text{OML}}$) and the hydrodynamic ion current $I_{\text{i}}^{\text{HYD}}$ by linearization of the current balance,

$4\pi {\epsilon }_0{a}_{\text{d}}\frac{\mathrm{d}V}{\mathrm{d}t}=I_{\text{e}}^{\text{OML}}+I_{\text{i}}^{\text{HYD}},(4)$

where $I_{\text{e}}^{\text{OML}}$ and $I_{\text{i}}^{\text{HYD}}$ are based on the definitions by Gatti and Kortshagen [50], ɛ₀ denotes the vacuum permittivity, and V the dust grain potential. This results in a charge fluctuation time scale at atmospheric pressure expressed as follows,

$\frac{1}{{\tau }_{\text{Q}}^{\text{HYD}}}=\frac{e^2{a}_{\text{d}}{n}_{\text{e}}{v}_{\text{e}}}{4{\epsilon }_0{k}_{\text{B}}{T}_{\text{e}}}\exp \left(\frac{e{V}_{\text{d}}}{k_{\text{B}}{T}_{\text{e}}}\right)-\frac{e{n}_{\text{i}}{\mu }_{\text{i}}\mathrm{sign}\left(V_{\text{d}}\right)}{{\epsilon }_0},(5)$

where e denotes the elementary charge, μ_i = eD_i/T_i the ion mobility, D_i the ion diffusion coefficient, and T_i the ion temperature. From Eq. 5, it can be evaluated that ${\tau }_{\text{Q}}^{\text{HYD}}\approx$ 89 ns for n_e = n_i = 10¹⁸ m⁻³, a_d = 100 nm, T_e = 2 eV, T_i = 0.025 eV, and equilibrium dust floating potential V_d = −0.14 V. Clearly, the charge fluctuation time scale τ_Q is close to the order of the electron temperature relaxation time scale τ_T ∼100 ns, which is vastly different from the ordering at low pressure.

2.2 Stage II: ambipolar diffusion

The second stage concerns the decay of the plasma density, from (the end of) the bulk plasma, until the point at which free diffusion is achieved. Plasma loss is due to ambipolar diffusion onto the reactor walls, recombination at the surface of dust grains and volume recombination of charged species.

Ambipolar diffusion dominates free diffusion as long as the electron Debye length λ_De is much smaller than the reactor size Λ during the early afterglow. In low temperature plasmas, ambipolar diffusion is governed by the ion diffusivity D_i [52, 53], due to the high mobility of electrons μ_i ≪ μ_e, so that

$D_{\text{amb}}=\frac{{\mu }_{\text{i}}{D}_{\text{e}}+{\mu }_{\text{e}}{D}_{\text{i}}}{{\mu }_{\text{i}}+{\mu }_{\text{e}}}\approx D_{\text{i}}\left(1+\frac{T_{\text{e}}}{T_{\text{i}}}\right),(6)$

and the ambipolar diffusion time scale τ_amb boils down to [54]:

${\tau }_{\text{amb}}=\frac{{\mathrm{\Lambda }}^2}{D_{\text{amb}}}=\frac{{\mathrm{\Lambda }}^2{T}_{\text{i}}}{l_{\text{in}}{v}_{\text{i}}\left(T_{\text{i}}+T_{\text{e}}\right)}.(7)$

By evaluation of Eq. 7 for low and atmospheric pressure conditions, one arrives at ambipolar diffusion time scales of ${\tau }_{\text{amb}}^{\text{OML}}\approx$2 × 10^–4 s and ${\tau }_{\text{amb}}^{\text{HYD}}\approx$2 × 10^–2 s for electrons and ions at room temperature. This shows that ambipolar diffusion is much more limited at atmospheric pressure assuming similar conditions for the reduced electric field and mobility, and that the ambipolar diffusion time scales linearly with neutral gas pressure.

The absorption of charged species at the surface of the dust grains provides the second plasma loss mechanism, if the dust density is sufficiently high [55, 56] by assuming here n_d = 10¹³ m⁻³. As the dust grains are negatively charged by the bulk plasma, the decrease of the ion density is governed by the flux of ions necessitated for recombination, Γ_i, lost at the surface of the dust grains, $A_{\text{d}}=4\pi a_{\text{d}}^2{n}_{\text{d}}$:

$\frac{\mathrm{d}{n}_{\text{i}}}{\mathrm{d}t}=-\frac{n_{\text{i}}}{{\tau }_{\text{A}}}=-{\mathrm{\Gamma }}_{\text{i}}{A}_{\text{d}}.(8)$

Under low pressure conditions, the particle absorption time τ_A is thus determined by the OML ion current [15],

${\tau }_{\text{A}}^{\text{OML}}={\left(\pi a_{\text{d}}^2{n}_{\text{d}}{v}_{\text{i}}\left(1+\frac{e{V}_{\text{d}}^{\text{OML}}{T}_{\text{e}}}{T_{\text{i}}}\right)\right)}^{-1}\sim 10^{-2}\text{s},(9)$

where $v_{\text{i}}={(8k_{\text{B}}{T}_{\text{i}}/(\pi m_{\text{i}}))}^{1/2}$ denotes the thermal ion velocity with m_i the ion mass. At atmospheric pressure, p = 1000 mbar, the hydrodynamic ion current is dominant so that the particle absorption time becomes:

${\tau }_{\text{A}}^{\text{HYD}}={\left(4\pi a_{\text{d}}^2{n}_{\text{d}}{\mu }_{\text{i}}\frac{|V_{\text{d}}^{\text{HYD}}|}{{\lambda }_{\text{DL}}}\right)}^{-1}\sim 10^{-2}\text{s},(10)$

where λ_DL denotes the linearized Debye length [57]. Using Eq. 9, 10 for the particle absorption time scales, it can be seen that the ordering

${\tau }_{\text{amb}}^{\text{OML}}\ll {\tau }_{\text{A}}^{\text{OML}}(11)$

differs vastly from the ordering at atmospheric pressure

${\tau }_{\text{amb}}^{\text{HYD}}\sim {\tau }_{\text{A}}^{\text{HYD}}.(12)$

The outcome for low pressure agrees with findings under such conditions following the four stage model [42]. By contrast, the recombination of ions at the dust surface provides a significant sink compared to reactor wall losses at atmospheric pressure.

Third, ion-electron recombination plays a significant role at atmospheric pressure. For the purpose of comparison, the recombination time scale is based on collisional-radiative recombination for Ar⁺ with electrons [58]:

${\tau }_{\text{CR}}=1.29\cdot 10^{38}{n}_{\text{e}}^{-2}{T}_{\text{e}}^{9/2}.(13)$

Under vacuum, n_e = 10¹⁵ m⁻³ and T_e = T_i, the recombination time scale is in the order of seconds already in the early afterglow, while τ_CR ∼ 10^–5 s for n_e = 10¹⁸ m⁻³ and electrons at room temperature. Please note that also dissociative recombination of molecular ions and other three-body processes can become significant and that this analysis is purely illustrative for the comparison. Consequently, electron-ion recombination could play an important role for plasma loss in the afterglow, although its contribution diminishes quickly with decreasing plasma density.

In conclusion, the plasma density decays steadily due to the loss of electrons and ions to the reactor walls and the surface of dust grains, and by volume recombination at atmospheric pressure. Moreover, the dust density, plasma density, dust size and the gas composition can significantly influence the foregoing ordering of time scales and dominance of the associated processes. The steady decay of the plasma density amounts to two important implications. First, the electron Debye length increases during the plasma decay up to a point at which it becomes comparable to the reactor size, i.e. Λ/λ_De ∼ 1. Second, the electron density decay results in an increasing significance of the total dust grain charge to the quasi-neutrality condition, i.e., the Havnes parameter P_H = |q_d|n_d/(en_e) ∼ 1, where the threshold condition is strongly affected by the value of the dust density [53]. Ambipolar diffusion is halted when one of these conditions is met and consequently, charged species transport becomes governed by free diffusion.

2.3 Stage III: ambipolar-to-free diffusion transition

During the third phase (III), a transition from ambipolar to free diffusion occurs when the electron Debye length tends towards the size of the reactor. At this point, ambipolar diffusion is no longer dominantly driving the transport and the ratio of these processes is important to determine the ratio of electron and ion density during the afterglow process. Several models on dust decharging in the low pressure afterglow have accounted for this transition explicitly such as the model by Couëdel et al [42] and Denysenko et al [17]. In both low [42] and atmospheric pressure [41] cases, it has been noted that a minor deviation from ambipolar diffusion, early in the afterglow, can greatly affect the residual dust charge by broadening the dust charge distributions and resulting in positive residual charges.

The ratio of ambipolar and free diffusivity is often based on the dimensionless (squared) ratio of the reactor size Λ and the electron Debye length λ_De [59]. In early studies [59, 60], it was stated already that the transition does not proceed abruptly, but rather that deviations from ambipolar diffusion occur at ratios Λ/λ_De ∼100. Although such studies have been performed decades ago, Λ/λ_De ∼10 is also used to define the ambipolar-to-free diffusion transition in work on the afterglow [61–63]. Nevertheless, in different works [17, 42], the ambipolar-to-free diffusion transition is explicitly accounted for to provide estimates for the dust residual charge. As the authors point out, the accuracy of the diffusion transition is key to determine the dust decharging process, because the losses to dust grains may also affect the transition from ambipolar to free diffusion.

2.4 Stage IV: free diffusion

During the fourth phase (IV), free diffusion occurs when charge separation is allowed on reactor length scales, after which electrons and ions diffuse independently. This is formalized by the condition that the electron Debye length λ_De is similar to the order of the reactor length Λ, i.e. Λ/λ_De ∼ 1. From this moment, the electrons are quickly lost to the reactor walls and dust grains due to the mass difference (i.e. m_i ≫ m_e) at the same temperature. As a consequence, the dust grains are left in a positive space charge region which results in an increasingly less negative dust charge by absorption of ions. In the end, the charge distribution is severely changed compared to the previous phase to such extent that part of the dust grains can become positively charged [42].

The positive ion density is transported to the reactor walls by free diffusion, or absorbed at the surface of the dust grains. The time scale of free diffusion of the ions τ_free is governed by the diffusivity and the reactor length scale,

${\tau }_{\text{free}}=\frac{{\mathrm{\Lambda }}^2}{D_{\text{i}}}\approx 88\times 10^{-3}\mathrm{s},(14)$

for Λ = 1 mm and the ion diffusion coefficient,

$D_{\text{i}}=\frac{3\pi }{16\sqrt{2}}\frac{v_{\text{i}}}{n_{\text{n}}{\sigma }_{\text{in}}}\approx 10^{-5}{\mathrm{m}}^2{\mathrm{s}}^{-1}(15)$

where the parameters were defined already for Eqs. 3–9 for argon ions diffusing in argon gas at atmospheric pressure. Because Λ = 100 mm typically at low pressure, and the pressure typically equals ∼0.1 mbar, the free diffusion time scale for the ions is the same as that at atmospheric pressure.

The loss of ions due to absorption by the dust grains can be evaluated using Fuchs’ theory of aerosol charging, although there is serious debate about the applicability of the theoretical assumptions underlying the model to small particles [40, 64]. Using Fuchs’ theory [65], the neutralization time scale of the dust grains due to ion absorption ${\tau }_{\text{N}}^{\text{HYD}}$ during the free diffusion regime can be assessed using

${\tau }_{\text{N}}^{\text{HYD}}=\frac{1}{n_{\text{i}}{\beta }_{\text{i}}}\approx 10^{-3}\mathrm{s},(16)$

where β_i = 10^–11 m³ s⁻¹ obtained from Suresh et al [41] for n_i = 10¹⁴ m⁻³ at p = 1000 mbar and T_n = 300 K. By comparison of [14–16], it can be concluded that the ions are quickly lost by absorption to the dust grains down to an ion density of about n_i ∼10¹² m⁻³, after which free diffusion to the walls plays an equally significant role. Consequently, this means that the ion density present during this stage is critical in determining the residual dust charge.

The dust residual charge becomes frozen, when the plasma density is insufficient to provide any significant current. The frozen charge condition, as described by Chaubey et al [45] and Ivlev et al [7], states that the charge becomes frozen when τ_L ≲ τ_Q. At very low pressure, plasma loss occurs much faster than charge fluctuations, i.e. τ_L ≪ τ_Q, and the dust charge can be frozen already from the beginning of the afterglow. At atmospheric pressure, however, the plasma loss timescale can exceed the charge fluctuation timescale, which agrees with the scaling of the frozen charge condition with pressure as described by Ivlev et al [7].

In Figure 1, the timescales discussed in this work are depicted as a function of the particle radius a_d in the range of 1–1000 nm, evaluated for three different phases as indicated in the figure caption. The conditions related to phase 1 are similar to those used for evaluation of the electron temperature relaxation stage. It can be seen that the charge fluctuation timescale τ_Q ≲ τ_T in the early afterglow (phase 1 and 2), which means that the charge is in quasi-steady state with the plasma conditions for all sizes depicted. Because the electron temperature relaxation is much faster than the timescales of plasma losses, the phase 2 and 3 timescales are the target of further analysis. These conditions are based on the ambipolar diffusion stage (phase 2) and the free diffusion stage (phase 3). Recombination occurs much faster than the ambipolar and particle absorption losses as ${\tau }_{\text{CR}}^2\ll {\tau }_{\text{amb}}^2$ and ${\tau }_{\text{CR}}^2\ll {\tau }_{\text{A}}^2$, which implies that the plasma density will quickly decrease due to recombination in pure argon. Under conditions where recombination is negligible, the dominant loss process depends strongly on the particle radius due to the intersection point between ${\tau }_{\text{A}}^2$ and the ambipolar timescale ${\tau }_{\text{amb}}^2$ around a_d ∼500 nm. This implies that particles with a larger size will absorb a significant part of the plasma ions, while the smaller particles do not have sufficient time to interact with the ions and thus have their charge frozen earlier in the afterglow. For phase 3, the neutralization timescale ${\tau }_{\text{N}}^3$ is smaller than the free diffusion timescale ${\tau }_{\text{free}}^3$, which indicates that particle decharging also occurs throughout this phase. A detailed calculation of the neutralization timescale, through evaluation of β_i for different particle radii (see Eq. 16), is out of scope for this work, but could provide interesting insight in the relation to the other timescales.

FIGURE 1

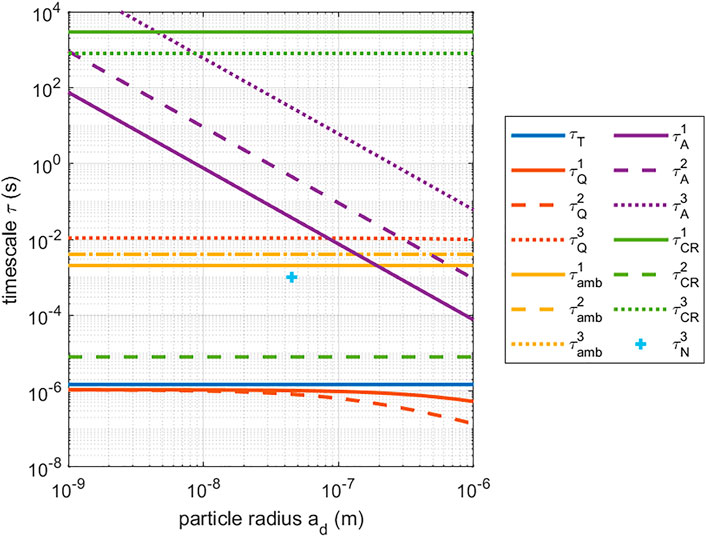
FIGURE 1. Timescales τ (s) as a function of particle radius a_d (m). The timescales have been evaluated for three different conditions. Superscript 1 (phase 1): T_e = 2 eV and n_p = 10¹⁸ m⁻³. Superscript 2 (phase 2): T_e = 0.025 eV and n_p = 10¹⁸ m⁻³. Superscript 3 (phase 3): T_e = 0.025 eV and n_p = 10¹⁴ m⁻³.

3 Discussion

The foregoing analysis of the physics of atmospheric pressure dusty plasma afterglows is related to recent experimental and modelling work in this section to define open gaps in the field.

First, it is noted by various authors that a deviation from ambipolar diffusion early in the afterglow introduces growing differences between the electron and ion density, which greatly affect the final charge distribution of the nanoparticles [37, 41]. In the model by Chen et al [37], for example, the transition from ambipolar-to-free diffusion is simply put as two limiting cases due to the lack of a clear transition model, as stated by the authors. Consequently, an improved understanding of the transition from ambipolar-to-free diffusion could be gained by accurately modeling the ratio of the electron to ion density and the electric field, as both evolve dynamically in the spatial afterglow of flow-through plasmas.

Second, it is stated by multiple authors that accurate knowledge of the (absolute) ion and electron density in the afterglow is required to predict the dust charge distribution [41, 42]. It was found by Suresh et al through a comparison of their model to experiments by Sharma et al [38] that the fraction of charged particles increases with both electron and ion density present at the beginning of the spatial afterglow [41]. This implies that the electron density provides a tuning knob for the dust charge distribution, which shifts to positive residual mean charge for increasing electron density. Additionally, external electric fields have been used to manipulate the dust charge in the afterglow [11, 12, 14, 18, 35, 36, 45, 66]. In various experiments, it was found that a bias voltage can result in positively charged dust grains, or can be used to reduce the dust charge. However, it was noted that different mechanisms could be at play such as a decreased electron loss or thermionic emission from the wall [35]. Hence, the manipulation and measurement of the electron and ion density in future experiments would greatly assist the development of models and physical control of dust charge distributions.

Third, inconsistencies have been noted regarding the charge distribution of dust grains in relation to the dust grain size. In the afterglow, the characteristic charging time takes most time for the smallest dust grains due to the decreasing probability of a collision with charged species. For small nanoparticles with a_d ≲100 nm, the charge fluctuation time scale τ_Q typically exceeds the residence time τ_res in the afterglow meaning that the dust charge is not in a steady state [38]. However, this also suggests that dust particles below a critical size—for which τ_Q ∼ τ_res—should not exhibit a bipolar charge distribution, which is a conclusion opposite to their observations. For larger nanoparticles with a_d ≳100 nm, the dust grains became net positively charged for lower residence times (i.e. due to higher flow velocity) [36], which is in sharp contrast with the idea that shorter interaction time leads to charge distributions with mean negative charge. In conclusion, future endeavors could be targeting the transient dynamics of nanoparticles interacting with afterglow plasmas to capture the physics involved in the charging of small nanoparticles.

Fourth, there are several opportunities for future research that span interest across other fields. The presence of negative ions built from molecular species introduced by a precursor gas could have a major influence on the dust charging [38], but also on the depletion of electrons in the bulk and afterglow plasma [67]. The effect of neutral radicals and nanoparticles is not often mentioned in the foregoing literature, although neutral radicals contribute significantly to surface growth and an abundance of neutral nanoparticles in the bulk plasma already implies that coagulation becomes a significant mechanism for dust growth [68]. The relatively high fluxes compared to typical low pressure plasmas induce significant heating induced by recombination at the dust surface, which leads to increased hydrogen desorption and crystallization of the material [39].

Experimentalists, theoreticians and modellers clearly face many challenges in their effort to understanding dusty plasma afterglows. As the charge of dust particles in the plasma afterglow greatly impacts the material properties such as the crystallinity and size distribution, their combined effort will enable many applications from controlled synthesis of nanosized materials to contamination control at the nanometer scale.

Author contributions

The author of this work declares that this manuscript was drafted in solitude by TS and that the author is solely accountable for the content of this manuscript.

Acknowledgments

The author expresses his gratitude to T.J.M. Donders for fruitful discussions on dusty plasma afterglows and an offline review of this work.

Conflict of interest

Author T.J.A. Staps was employed by Prodrive Technologies B.V.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mangolini L. Monitoring non-thermal plasma processes for nanoparticle synthesis. J Phys D Appl Phys (2017) 50:373003. doi:10.1088/1361-6463/AA812E

CrossRef Full Text | Google Scholar

2. Michael P, Lam YT, Filipe EC, Tan RP, Chan AH, Lee BS, et al. Plasma polymerized nanoparticles effectively deliver dual siRNA and drug therapy in vivo. Sci Rep (2020) 10:12836–14. doi:10.1038/s41598-020-69591-x

PubMed Abstract | CrossRef Full Text | Google Scholar

3. van de Kerkhof M, van Empel T, Lercel M, Smeets C, van de Wetering F, Mark van de Kerkhof A, et al. Advanced particle contamination control in EUV scanners. 10957 (2019) 191–203. doi:10.1117/12.2514874

CrossRef Full Text | Google Scholar

4. Beckers J, Bv M, Blom P, Kroesen G, Peijnenburg T. Particle contamination control by application of plasma. 11323 (2020) 558–63. doi:10.1117/12.2560192

CrossRef Full Text | Google Scholar

5. Dimoff K, Smy PR. Dust induced quenching of an afterglow plasma. Tech Rep (1970) 32:13–4. doi:10.1016/0375-9601(70)90056-3

CrossRef Full Text | Google Scholar

6. Childs MA, Gallagher A. Plasma charge-density ratios in a dusty plasma. J Appl Phys (2000) 87:1086–90. doi:10.1063/1.371983

CrossRef Full Text | Google Scholar

7. Ivlev AV, Kretschmer M, Zuzic M, Morfill GE, Rothermel H, Thomas HM, et al. Decharging of complex plasmas: First kinetic observations. Phys Rev Lett (2003) 90:055003. doi:10.1103/PhysRevLett.90.055003

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Agarwal P, Girshick SL. Sectional modeling of nanoparticle size and charge distributions in dusty plasmas. Plasma Sourc Sci Technol (2012) 21:055023. doi:10.1088/0963-0252/21/5/055023

CrossRef Full Text | Google Scholar

9. Meyer JK, Merlino RL. Evolution of dust clouds in afterglow plasmas. IEEE Trans Plasma Sci IEEE Nucl Plasma Sci Soc (2016) 44:473–8. doi:10.1109/TPS.2015.2504920

CrossRef Full Text | Google Scholar

10. Chaubey N, Goree J. Preservation of a dust crystal as it falls in an afterglow plasma. Front Phys (2022) 10. doi:10.3389/fphy.2022.879092

CrossRef Full Text | Google Scholar

11. Van Minderhout B, Peijnenburg T, Blom P, Vogels JM, Kroesen GM, Beckers J. The charge of micro-particles in a low pressure spatial plasma afterglow. J Phys D Appl Phys (2019) 52:32LT03. doi:10.1088/1361-6463/ab2525

CrossRef Full Text | Google Scholar

12. Van Minderhout B, Van Huijstee JC, Platier B, Peijnenburg T, Blom P, Kroesen GM, et al. Charge control of micro-particles in a shielded plasma afterglow. Plasma Sourc Sci Technol (2020) 29:065005. doi:10.1088/1361-6595/ab8e4f

CrossRef Full Text | Google Scholar

13. van Minderhout B, van Huijstee JC, Rompelberg RM, Post A, Peijnenburg AT, Blom P, et al. Charge of clustered microparticles measured in spatial plasma afterglows follows the smallest enclosing sphere model. Nat Commun (2021) 12:4692. doi:10.1038/s41467-021-23604-z

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Van Minderhout B, Van Huijstee JC, Peijnenburg AT, Blom P, Kroesen GM, Beckers J. Charge neutralisation of microparticles by pulsing a low-pressure shielded spatial plasma afterglow. Plasma Sourc Sci Technol (2021) 30:045016. doi:10.1088/1361-6595/abd81f

CrossRef Full Text | Google Scholar

15. Couëdel L, Mikikian M, Boufendi L, Samarian AA. Residual dust charges in discharge afterglow. Phys Rev E (2006) 74:026403. doi:10.1103/PhysRevE.74.026403

CrossRef Full Text | Google Scholar

16. Alexandrov AL, Schweigert IV, Ariskin DA. Kinetic simulations of argon dusty plasma afterglow including metastable atom kinetics. J Exp Theor Phys (2013) 116:663–72. doi:10.1134/S1063776113030151

CrossRef Full Text | Google Scholar

17. Denysenko IB, Mikikian M, Azarenkov NA. Dust dynamics during the plasma afterglow. J Phys D Appl Phys (2022) 55:095201. doi:10.1088/1361-6463/ac3539

CrossRef Full Text | Google Scholar

18. van Huijstee JCA, Blom P, Peijnenburg ATA, Beckers J. Spatio-temporal plasma afterglow induces additional neutral drag force on microparticles. Front Phys (2022) 0:537. doi:10.3389/FPHY.2022.926160

CrossRef Full Text | Google Scholar

19. Mangolini L, Thimsen E, Kortshagen U. High-yield plasma synthesis of luminescent silicon nanocrystals. Nano Lett (2005) 5:655–9. doi:10.1021/nl050066y

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Holman ZC, Kortshagen UR. A flexible method for depositing dense nanocrystal thin films: Impaction of germanium nanocrystals. Nanotechnology (2010) 21:335302. doi:10.1088/0957-4484/21/33/335302

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kramer NJ, Aydil ES, Kortshagen UR. Requirements for plasma synthesis of nanocrystals at atmospheric pressures. J Phys D Appl Phys (2015) 48:035205. doi:10.1088/0022-3727/48/3/035205

CrossRef Full Text | Google Scholar

22. Hwang SH, Okumura T, Kamataki K, Itagaki N, Koga K, Shiratani M. Size and flux of carbon nanoparticles synthesized by Ar+CH4 multi-hollow plasma chemical vapor deposition. Diamond Relat Mater (2020) 109:108050. doi:10.1016/j.diamond.2020.108050

CrossRef Full Text | Google Scholar

23. Askari S, Levchenko I, Ostrikov K, Maguire P, Mariotti D. Crystalline Si nanoparticles below crystallization threshold: Effects of collisional heating in non-thermal atmospheric-pressure microplasmas. Appl Phys Lett (2014) 104:163103. doi:10.1063/1.4872254

CrossRef Full Text | Google Scholar

24. Coleman D, Lopez T, Yasar-Inceoglu O, Mangolini L. Hollow silicon carbide nanoparticles from a non-thermal plasma process. J Appl Phys (2015) 117:193301. doi:10.1063/1.4919918

CrossRef Full Text | Google Scholar

25. Mangolini L. Synthesis, properties, and applications of silicon nanocrystals. J Vacuum Sci Tech B, Nanotechnology Microelectronics: Mater Process Meas Phenomena (2013) 31:020801. doi:10.1116/1.4794789

CrossRef Full Text | Google Scholar

26. Kortshagen UR, Sankaran RM, Pereira RN, Girshick SL, Wu JJ, Aydil ES. Nonthermal plasma Synth nanocrystals: Fundam principles, Mater applicationsChemical Rev (2016) 116(18):11061–127. doi:10.1021/acs.chemrev.6b00039

CrossRef Full Text

27. Benedikt J, Raballand V, Yanguas-Gil A, Focke K, Von Keudell A. Thin film deposition by means of atmospheric pressure microplasma jet. Plasma Phys Control Fusion (2007) 49:B419–27. doi:10.1088/0741-3335/49/12B/S39

CrossRef Full Text | Google Scholar

28. Lommatzsch U, Ihde J. Plasma polymerization of HMDSO with an atmospheric pressure plasma jet for corrosion protection of aluminum and low-adhesion surfaces. Plasma Process Polym (2009) 6:642–8. doi:10.1002/ppap.200900032

CrossRef Full Text | Google Scholar

29. Lin YC, Wang MJ. Fabrication of hydrophobic/hydrophilic HMDSO films by atmospheric pressure plasma jet deposition. Jpn J Appl Phys (Institute Phys Publishing) (2019) 58. doi:10.7567/1347-4065/aaea6c

CrossRef Full Text | Google Scholar

30. Kuchakova I, Ionita MD, Ionita ER, Lazea-Stoyanova A, Brajnicov S, Mitu B, et al. Atmospheric pressure plasma deposition of organosilicon thin films by direct current and radio-frequency plasma jets. Materials (2020) 13:1296. doi:10.3390/ma13061296

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Brilke S, Resch J, Leiminger M, Steiner G, Tauber C, Wlasits PJ, et al. Precision characterization of three ultrafine condensation particle counters using singly charged salt clusters in the 1–4 nm size range generated by a bipolar electrospray source. Aerosol Sci Tech (2020) 54:396–409. doi:10.1080/02786826.2019.1708260

CrossRef Full Text | Google Scholar

32. Carsí M, Alonso M. A numerical study of bipolar charging and neutralization of ultrafine particles with uniformly generated heterogeneous ions. J Aerosol Sci (2020) 149:105611. doi:10.1016/J.JAEROSCI.2020.105611

CrossRef Full Text | Google Scholar

33. Intra P, Wanusbodeepaisarn P, Siri-achawawath T. Evaluation of the performance in charging efficiencies and losses of ultrafine particles ranging in sizes from 15 to 75 nm in a unipolar corona-based ionizer. J Electr Eng Technol (2021) 16:963–74. doi:10.1007/S42835-020-00623-2

CrossRef Full Text | Google Scholar

34. Saputra C, Kamil AI, Munir MM, Waris A, Novitrian N. The performance of an electrical ionizer as a bipolar aerosol charger for charging ultrafine particles. Aerosol Sci Tech (2021) 56:117–33. doi:10.1080/02786826.2021.1976719

CrossRef Full Text | Google Scholar

35. Dhawan S, Vidwans A, Sharma G, Abuyazid NH, Mohan Sankaran R, Biswas P. Enhancing charging and capture efficiency of aerosol nanoparticles using an atmospheric-pressure, flow-through RF plasma with a downstream DC bias. Aerosol Sci Tech (2020) 54(11):1249–54. doi:10.1080/02786826.2020.1807459

CrossRef Full Text | Google Scholar

36. Husmann E, Thimsen E, Chen X. Particle charge distributions in the effluent of a flow-through atmospheric pressure low temperature plasma. Plasma Sourc Sci Technol (2021) 30:075030. doi:10.1088/1361-6595/ac12c1

CrossRef Full Text | Google Scholar

37. Chen X, Hogan CJ. Nanoparticle dynamics in the spatial afterglows of nonthermal plasma synthesis reactors. Chem Eng J (2021) 411:128383. doi:10.1016/j.cej.2020.128383

CrossRef Full Text | Google Scholar

38. Sharma G, Abuyazid N, Dhawan S, Kshirsagar S, Sankaran RM, Biswas P. Characterization of particle charging in low-temperature, atmospheric-pressure, flow-through plasmas. J Phys D Appl Phys (2020) 53:245204. doi:10.1088/1361-6463/ab7c97

CrossRef Full Text | Google Scholar

39. Lopez T, Mangolini L. On the nucleation and crystallization of nanoparticles in continuous-flow nonthermal plasma reactors. J Vacuum Sci Tech B, Nanotechnology Microelectronics: Mater Process Meas Phenomena (2014) 32:061802. doi:10.1116/1.4899206

CrossRef Full Text | Google Scholar

40. Gopalakrishnan R, Hogan CJ. Coulomb-influenced collisions in aerosols and dusty plasmas. Phys Rev E (2012) 85:026410. doi:10.1103/PhysRevE.85.026410

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Suresh V, Li L, Go Felipe RJ, Gopalakrishnan R. Modeling nanoparticle charge distribution in the afterglow of non-thermal plasmas and comparison with measurements. J Phys D Appl Phys (2021) 54:275205. doi:10.1088/1361-6463/abf70c

CrossRef Full Text | Google Scholar

42. Couëdel L, Samarian AA, Mikikian M, Boufendi L, Mendonça JT, Resendes DP, et al. Influence of plasma diffusion losses on dust charge relaxation in discharge afterglow. AIP Conf Proc (2008) 1041:183–4. doi:10.1063/1.2996828

CrossRef Full Text | Google Scholar

43. Couëdel L, Samarian AA, Mikikian M, Boufendi L. Dust density effect on complex plasma decay. Phys Lett A (2008) 372:5336–9. doi:10.1016/J.PHYSLETA.2008.06.047

CrossRef Full Text | Google Scholar

44. Couëdel L, Mezeghrane A, Samarian AA, Mikikian M, Tessier Y, Cavarroc M, et al. Complex plasma afterglow. Contrib Plasma Phys (2009) 49:235–59. doi:10.1002/CTPP.200910025

CrossRef Full Text | Google Scholar

45. Chaubey N, Goree J, Lanham SJ, Kushner MJ. Positive charging of grains in an afterglow plasma is enhanced by ions drifting in an electric field. Phys Plasmas (2021) 28:103702. doi:10.1063/5.0069141

CrossRef Full Text | Google Scholar

46. Staps TJA, van de Ketterij MI, Platier B, Beckers J. The underexposed effect of elastic electron collisions in dusty plasmas. Commun Phys (2021) 4:1–9. doi:10.1038/s42005-021-00734-w

CrossRef Full Text | Google Scholar

47. Breizman B, Stupakov G, Vekstein G. Diffusion regime of electron-electron collisions in weakly ionized plasmas. Phys Plasmas (2021) 28:030701. doi:10.1063/5.0038623

CrossRef Full Text | Google Scholar

48. Platier B, Staps TJ, Van Der Schans M, Ijzerman WL, Beckers J. Resonant microwaves probing the spatial afterglow of an RF plasma jet. Appl Phys Lett (2019) 115:254103. doi:10.1063/1.5127744

CrossRef Full Text | Google Scholar

49. Staps TJ, Donders TJ, Platier B, Beckers J. Laser-induced photodetachment of negative oxygen ions in the spatial afterglow of an atmospheric pressure plasma jet. Plasma Sourc Sci Technol (2022) 31:025010. doi:10.1088/1361-6595/AC4B66

CrossRef Full Text | Google Scholar

50. Gatti M, Kortshagen U. Analytical model of particle charging in plasmas over a wide range of collisionality. Phys Rev E (2008) 78:046402. doi:10.1103/physreve.78.046402

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Biondi MA. Atmospheric electron–ion and ion–ion recombination processes. Can J Chem (1969) 47:1711–9. doi:10.1139/v69-282

CrossRef Full Text | Google Scholar

52. Amiranashvili S, Yu MY. Ambipolar diffusion in a dusty plasma. Phys Plasmas (2002) 9:4825–8. doi:10.1063/1.1517049

CrossRef Full Text | Google Scholar

53. Denysenko IB, Stefanović I, Sikimić B, Winter J, Azarenkov NA. Discharging of dust particles in the afterglow of plasma with large dust density. Phys Rev E (2013) 88:023104. doi:10.1103/PhysRevE.88.023104

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Limpens R, Platier B, Lassise AC, Staps ATJ, W van Ninhuijs MA, Luiten OJ, et al. Influence of a magnetic field on an extreme ultraviolet photon-induced plasma afterglow. J Phys D Appl Phys (2021) 54:435205. doi:10.1088/1361-6463/ac1885

CrossRef Full Text | Google Scholar

55. Tadsen B, Greiner F, Piel A. On the amplitude of dust-density waves in inhomogeneous dusty plasmas. Phys Plasmas (2017) 24:033704. doi:10.1063/1.4977901

CrossRef Full Text | Google Scholar

56. Greiner F, Melzer A, Tadsen B, Groth S, Killer C, Kirchschlager F, et al. Diagnostics and characterization of nanodust and nanodusty plasmas. Eur Phys J D (2018) 725:811–2. doi:10.1140/EPJD/E2017-80400-7

CrossRef Full Text | Google Scholar

57. Daugherty JE, Porteous RK, Kilgore MD, Graves DB. Sheath structure around particles in low-pressure discharges. J Appl Phys (1992) 72:3934–42. doi:10.1063/1.352245

CrossRef Full Text | Google Scholar

58. Celik Y, Tsankov TV, Aramaki M, Yoshimura S, Luggenhölscher D, Czarnetzki U. Recombination and enhanced metastable repopulation in the argon afterglow. Phys Rev E (2012) 85:056401. doi:10.1103/physreve.85.056401

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Freiberg RJ, Weaver LA. Microwave investigation of the transition from ambipolar to free diffusion in afterglow plasmas. Phys Rev (1968) 170:336–41. doi:10.1103/PhysRev.170.336

CrossRef Full Text | Google Scholar

60. Gerber RA, Gerardo JB. Ambipolar-to-Free diffusion: The temporal behavior of the electrons and ions. Phys Rev A (Coll Park) (1973) 7:781–90. doi:10.1103/PhysRevA.7.781

CrossRef Full Text | Google Scholar

61. Platier B, Limpens R, Lassise AC, Staps TJ, Van Ninhuijs MA, Daamen KA, et al. Transition from ambipolar to free diffusion in an EUV-induced argon plasma. Appl Phys Lett (2020) 116:103703. doi:10.1063/1.5142290

CrossRef Full Text | Google Scholar

62. Phelps AV. The diffusion of charged particles in collisional plasmas: Free and ambipolar diffusion at low and moderate pressures. J Res Natl Inst Stand Technol (1990) 95:407. doi:10.6028/jres.095.035

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Chantry PJ. A simple formula for diffusion calculations involving wall reflection and low density. J Appl Phys (1998) 62:1141–8. doi:10.1063/1.339662

CrossRef Full Text | Google Scholar

64. Gopalakrishnan R, Thajudeen T, Ouyang H, Hogan CJ. The unipolar diffusion charging of arbitrary shaped aerosol particles. J Aerosol Sci (2013) 64:60–80. doi:10.1016/J.JAEROSCI.2013.06.002

CrossRef Full Text | Google Scholar

65. Fuchs NA. On the stationary charge distribution on aerosol particles in a bipolar ionic atmosphere. Geofisica pura e applicata (1963) 56:185–93. doi:10.1007/BF01993343

CrossRef Full Text | Google Scholar

66. Wörner L, Ivlev AV, Couëdel L, Huber P, Schwabe M, Hagl T, et al. The effect of a direct current field on the microparticle charge in the plasma afterglow. Phys Plasmas (2013) 20:123702. doi:10.1063/1.4843855

CrossRef Full Text | Google Scholar

67. Abuyazid NH, Chen X, Mariotti D, Maguire P, Hogan CJ, Sankaran RM. Understanding the depletion of electrons in dusty plasmas at atmospheric pressure. Plasma Sourc Sci Technol (2020) 29:075011. doi:10.1088/1361-6595/AB9CC3

CrossRef Full Text | Google Scholar

68. Le Picard R, Markosyan AH, Porter DH, Girshick SL, Kushner MJ. Synthesis of silicon nanoparticles in nonthermal capacitively-coupled flowing plasmas: Processes and transport. Plasma Chem Plasma Process (2016) 36:941–72. doi:10.1007/s11090-016-9721-6

CrossRef Full Text | Google Scholar