Thermal and solutal energy transport analysis in entropy generation of hybrid nanofluid flow over a vertically rotating cylinder

An investigation of an axisymmetric mixed convective boundary layer flow of silver-titanium dioxide/water ($\mathrm{A}\mathrm{g}-\mathrm{T}\mathrm{i}{\mathrm{O}}_2/{\mathrm{H}}_2\mathrm{O}$) hybrid nanofluid towards vertically and rotating stretching cylinder with entropy generation is conducted. The Cattaneo-Christov theory and joule heating effect are used to analyze the features of thermal energy. Moreover, the magnetic impact and convective boundary conditions on the vertical surface also considered in the current investigation. The developing equations for momentum, energy and entropy generation are modelled and by the usage of similarity variables to transform into the system of nonlinear ordinary differential equations (ODEs). The solutions of nonlinear ODEs are obtained numerically with the assistance of BVP4C MATLAB built-in scheme. The graphical consequences and relevant physical reasoning regarding the velocity, temperature, and concentration profiles are discussed. It is noteworthy that strong estimation of buoyancy ratio and mixed convection parameter enhances axial velocity, but the swirl velocity is diminished. The fluid temperature and concentration both are diminished due to thermal and solutal stratification effects. It is also seen that thermal Biot and Eckert numbers enhance the temperature distribution. Further, the Reynold number improves entropy generation.

1 Introduction

Nanofluids exhibit superior heat transport features to those of regular fluids. The effectiveness of heat exchange and the compactness of lower thermal conductivity fluid are delayed in the process, but many techniques are used to develop heat transport phenomena. One innovative trick is used to improve the heat transport/thermal conductivity of a fluid through the suspension of nanoparticles in the base liquids. Nanofluid thermal conductivity mainly depends upon the volume fraction of nanoparticles. The thermal conductivity of nanoparticles is expected to be greater than that of usual fluids. These nanoparticles are very small, not more than 100 mm. The term nanofluids was first used to refer to the fluids along suspended nanoparticles by Choi [1]. Some experimental outcomes have been obtained by Eastman et al. [2] with respect to the development of thermal conductivity with the suspension of $\mathrm{C}\mathrm{u}\mathrm{O}$ in base fluid water. The transport of the heat and mass of the 3D stagnation point flow of a water-based nanofluid toward an exponentially stretching surface was identified by Rehman and Nadeem [3]. Sheikholeslami [4] present the numerical examination of the $\mathrm{C}\mathrm{u}\mathrm{O}$-water based nanofluid affected by a magnetic field about a porous channel. Bilal et al. [5] surveyed the numerical inspection of MHD and the thermal radiative flow of a Williamson nanofluid influenced by variable thermal conductivity across a stretching cylinder. Maskeen et al. [6] used a stretching cylinder to evaluate the heat transfer features of alumina-coper/water hybrid nanofluid. The heat and mass transport analysis of a chemically reactive Eyring-Powell nanofluid influenced by a Cattaneo-Christov heat flux was performed by Reddy et al. [7] through a stretching cylinder. Ullah et al. [8] explored the collective characteristics of heat sources and the zero mass flux of magnetized nanofluid flow with an activation effect across a rotating and stretchable disk. Khan et al. [9] elaborated a comparison between a linear and exponential stretching surface to identify the rotating impact on a nanofluid flow in stratification conditions. Dawar et al. [10] observed the convective flow of a Williamson nanofluid across the two different geometries with convective boundary conditions. Some meaningful research in the direction of nanofluid is presented in Refs. [11, 12]. Scientists have lately discovered novel techniques to boost thermal conductivity and the heat transport rate of a fluid. One of the best ways to improve the heat conductivity of fluid by the addition of more than two nanoparticles in the convectional fluid, which is said a hybrid nanofluid. A hybrid nanofluid is more beneficial than simple nanofluids. Some key developments in the direction of hybrid nanofluid can be found in Refs. [13–20].

In the modern era, entropy generation is the most valuable subject for the researcher, in which irreversible processes of mass and heat transport occur. The Second Law of Thermodynamics entirely revolves around entropy. The design of the system that depends upon heat transport has a valuable application in the real life of the entropy generation. Entropy minimized energy losses in the system. Heat and mass transport processes occur in heat exchange, heat engines, fluid flow, heat pumps, refrigerators, air conditioners, power plants, anelastic deformation, and substance mixing and expansion, among other sites. Significant work has been done on entropy with application to various fields by Adrian Bejan [21–24]. Mahian et al. [25] elaborated convective heat transport augmentation with the use of nanofluid flow and entropy generation impacts to develop high heat flux cooling devices. Siavashi et al. [26] scrutinized the heat transport and entropy generation characteristics of nanofluid flow across an annular pipe in a two-phase combination model. Rashid et al. [27] observed entropy generation on ferromagnetic fluid flows along the slip and nonlinear radiation impact across a stretching sheet. Khan et al. [28] reviewed the modeling and computational study of hybrid nanofluids subject to entropy generation. Muhammad et al. [29] examined the Darcy–Forchheimer boundary layer flow influenced by activation energy and entropy generation across a curved surface. Recent studies related to the investigation of entropy generation are given in Refs. [30–33].

Heat transportation occurs due to temperature gradients. There are three modes of heat transfer conduction, radiation, and convection. Heat transportation phenomena have many important industrial and engineering applications, such as heat exchange, power generation, nuclear power, refrigeration, petroleum production, and so on. Fourier [34] first developed the law of heat conduction to analyze the rate of heat transport in a system. Ellahi et al. [35] scrutinized the heat transfer rate of a mixed convective boundary layer fluid flow across a vertical permeable slender cylinder. The heat and mass transportation of a non-Newtonian fluid flow influenced by transverse magnetic field and suction/injection effect towards permeable stretching sheet was developed by Sandeep et al. [36]. The heat transfer scrutiny of MHD micropolar fluid flows subject to joule heating and chemical reactions across a stretching sheet were explored by Dawar et al. [37]. Ramadan et al. [38] analyzed that flow and heat transport in a microchannel influenced by gas cooling conditions and thermal creep. Finally, other studies of heat transfer are presented in Refs. [39–48].

The aim of this examination is to study the 3D axisymmetric MHD flow of a viscous nanofluid with nanoparticles generated by vertically rotating a stretching cylinder. The main concern of this existing inquiry is to identify entropy generation evaluation of mixed convective hybrid nanofluid flow with modified Fourier’s and Fick’s law across a rotating and stretching surface. Moreover, convective boundary conditions are also considered to identify a flow regime. The formulated fluid model is converted into a pair of ODEs by adopting appropriate similarity variables. The coupled ODEs are numerically manipulated with the aid of BVP4C MATLAB built-in technique [49–53]. A graphical inquiry into the evolving parameters with respect to temperature distribution, concentration distribution, and velocity profile is established and discussed. The comparison of current outcomes with previous investigation is presented, and a good harmony is shown between them.

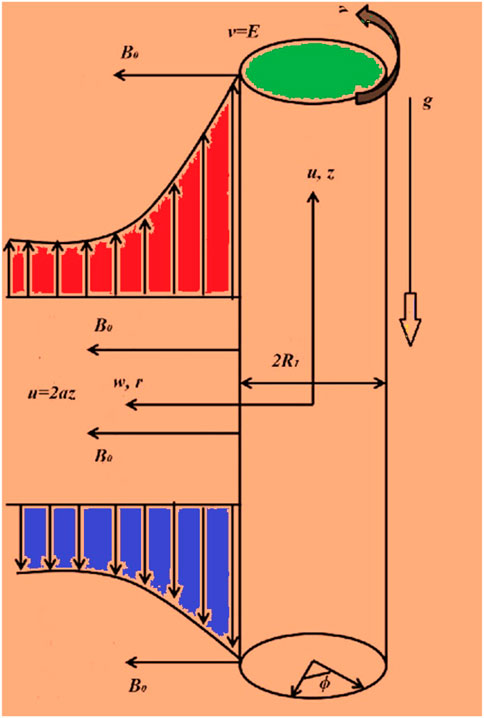
2 Flow modelling

Here, we observe a steady, incompressible, axisymmetric laminar, and mixed convective boundary layer flow of $\mathrm{A}\mathrm{g}-\mathrm{T}\mathrm{i}{\mathrm{O}}_2/{\mathrm{H}}_2\mathrm{O}$ hybrid nanofluid induced by a vertical and rotating stretching cylinder with a double diffusion Cattaneo-Christov and entropy generation impact. The equation of thermal and solutal energy are through the consideration of heat generation/absorption, chemical reaction, and joule heating impact. Furthermore, thermal and concentration convective conditions are enforced on the boundary of the stretching cylinder. A magnetic field ($B_0$) is applied in the direction of the $r-$axis to analyze the effect of the Lorentz force. The stretching cylinder has radius is $R_1$, $r$ is the radial direction, and $z-$axis is measured along the cylinder. The cylinder rotates with an angular velocity and the stretching velocity is directly proportional to the axial distance. Moreover, the concentration and temperature of the surface nanoparticles are ${\stackrel{\sim }{C}}_w$ and ${\stackrel{\sim }{T}}_w$, respectively, and away from the surface they are symbolized by ${\stackrel{\sim }{C}}_{\infty }$ and ${\stackrel{\sim }{T}}_{\infty }$, respectively. The flow geometry and the coordinate axes are shown in Figure 1. Using the above-mentioned supposition with the presence of Boussinesq approximation, the flow equations are followed by [49, 50],

$\frac{\partial \stackrel{\sim }{u}}{\partial z}=-\left(\frac{\stackrel{\sim }{w}}{r}+\frac{\partial \stackrel{\sim }{w}}{\partial r}\right),(1)$

$\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{u}}{\partial r}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{u}}{\partial z}=-\frac{1}{{\rho }_{hnf}}\frac{\partial P}{\partial z}+{\upsilon }_{hnf}\left(\frac{{\partial }^2\stackrel{\sim }{u}}{\partial r^2}+\frac{1}{r}\frac{\partial \stackrel{\sim }{u}}{\partial r}\right)+g^{*}\left(\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\rho }_{hnf}}\left(\stackrel{\sim }{T}-{\stackrel{\sim }{T}}_{\infty }\right)+\frac{{\left(\rho {\beta }_C\right)}_{hnf}}{{\rho }_{hnf}}\left(\stackrel{\sim }{C}-{\stackrel{\sim }{C}}_{\infty }\right)\right)-\frac{{\sigma }_{hnf}{B}_0^2\stackrel{\sim }{u}}{{\rho }_{hnf}},(2)$

$\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{v}}{\partial r}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{v}}{\partial z}+\frac{\stackrel{\sim }{w}\stackrel{\sim }{v}}{r}={\upsilon }_{hnf}\left(\frac{{\partial }^2\stackrel{\sim }{v}}{\partial r^2}+\frac{1}{r}\frac{\partial \stackrel{\sim }{v}}{\partial r}-\frac{\stackrel{\sim }{v}}{r^2}\right)-\frac{{\sigma }_{hnf}{B}_0^2\stackrel{\sim }{v}}{{\rho }_{hnf}},(3)$

$\begin{array}{l}\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{T}}{\partial z}+\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{T}}{\partial r}+{\epsilon }_0\left(\begin{array}{l}2\stackrel{\sim }{u}\stackrel{\sim }{w}\frac{{\partial }^2\stackrel{\sim }{T}}{\partial z\partial r}+{\stackrel{\sim }{u}}^2\frac{{\partial }^2\stackrel{\sim }{T}}{\partial z^2}+\left(\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{w}}{\partial z}+\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{w}}{\partial r}\right)\frac{\partial \stackrel{\sim }{T}}{\partial r}\\ +{\stackrel{\sim }{w}}^2\frac{{\partial }^2\stackrel{\sim }{T}}{\partial r^2}+\left(\stackrel{\sim }{w}\frac{\partial u}{\partial r}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{u}}{\partial z}\right)\frac{\partial \stackrel{\sim }{T}}{\partial z}\end{array}\right)={\alpha }_{hnf}\left(\frac{{\partial }^2\stackrel{\sim }{T}}{\partial r^2}+\frac{1}{r}\frac{\partial \stackrel{\sim }{T}}{\partial r}\right)\\ +\frac{{\sigma }_{hnf}{B}_0^2}{{\left(\rho C_p\right)}_{hnf}}\left({\stackrel{\sim }{u}}^2+{\stackrel{\sim }{v}}^2+2{\epsilon }_0\left(\stackrel{\sim }{u}\stackrel{\sim }{w}\frac{\partial u}{\partial r}+\stackrel{\sim }{v}\stackrel{\sim }{w}\frac{\partial v}{\partial r}\right)\right)+\frac{Q_0}{{\left(\rho C_p\right)}_{hnf}}\left({\epsilon }_0\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{T}}{\partial z}+{\epsilon }_0\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{T}}{\partial r}+\stackrel{\sim }{T}-{\stackrel{\sim }{T}}_{\infty }\right),\end{array}(4)$

$\begin{array}{l}\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{C}}{\partial z}+\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{C}}{\partial r}+{\epsilon }_1\left(\begin{array}{l}2\stackrel{\sim }{u}\stackrel{\sim }{w}\frac{{\partial }^2\stackrel{\sim }{C}}{\partial z\partial r}+{\stackrel{\sim }{u}}^2\frac{{\partial }^2\stackrel{\sim }{C}}{\partial z^2}+\left(\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{w}}{\partial z}+\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{w}}{\partial r}\right)\frac{\partial \stackrel{\sim }{C}}{\partial r}\\ +{\stackrel{\sim }{w}}^2\frac{{\partial }^2\stackrel{\sim }{C}}{\partial r^2}+\left(\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{u}}{\partial r}+\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{u}}{\partial z}\right)\frac{\partial \stackrel{\sim }{C}}{\partial z}\end{array}\right)=D_B\left(\frac{{\partial }^2\stackrel{\sim }{C}}{\partial r^2}+\frac{1}{r}\frac{\partial \stackrel{\sim }{C}}{\partial r}\right)\\ -K_1\left(\stackrel{\sim }{C}-{\stackrel{\sim }{C}}_{\infty }\right)-{\epsilon }_1{K}_1\left(\stackrel{\sim }{u}\frac{\partial \stackrel{\sim }{C}}{\partial z}+\stackrel{\sim }{w}\frac{\partial \stackrel{\sim }{C}}{\partial r}\right),\end{array}(5)$

FIGURE 1

FIGURE 1. Flow diagram of the article.

The related surface and ambient conditions are stated as follows:

$\left(\begin{array}{l}{\stackrel{\sim }{v}}_{sr}\left(r,z\right)=E,{\stackrel{\sim }{u}}_{ss}\left(r,z\right)=2az,\stackrel{\sim }{w}\left(r,z\right)=0,-k_{hnf}\frac{\partial \stackrel{\sim }{T}}{\partial r}=h_f\left({\stackrel{\sim }{T}}_w-\stackrel{\sim }{T}\right),\\ -D_B\frac{\partial \stackrel{\sim }{C}}{\partial r}=h_{g_1}\left({\stackrel{\sim }{C}}_w-\stackrel{\sim }{C}\right),\end{array}\right)asr=R_1,(6)$

$\stackrel{\sim }{u}\to 0,\stackrel{\sim }{v}\to 0,\stackrel{\sim }{T}\to {\stackrel{\sim }{T}}_{\infty },\stackrel{\sim }{C}\to {\stackrel{\sim }{C}}_{\infty },\mathrm{a}\mathrm{s}r\to \infty (7)$

In the above Eqs. 1–6, $\stackrel{\sim }{u}$ and $\stackrel{\sim }{w}$ are the velocity of the fluid in the $z-$ and $r-$ directions, respectively. The symbols ${\nu }_{hnf},{\sigma }_{hnf},g^{*},\left({\beta }_T,{\beta }_C\right),{\epsilon }_0,{\alpha }_{hnf},Q_0,C_p,{\epsilon }_1,{\rho }_{hnf},K_1,h_f,{h_g}_1,$and $D_B$ indicate kinematic viscosity of hybrid nanofluid, electrical conductivity of hybrid nanofluid, gravitational force, thermal and concentration volumetric expansion coefficients, thermal relaxation time, thermal diffusivity, heat generation/absorption coefficient, specific heat, concentration relaxation time, density of fluid hybrid nanofluid, chemical reaction constant, mass diffusivity, coefficient of convective heat transfer, coefficient of convective mass transfer, and mass diffusivity, respectively.

2.1 Hybrid nanofluid model

The experimental relationship for an Ag-TiO/water hybrid nanofluid is given as follows [14],

2.1.1 Hybrid nanofluid dynamic viscosity

$\frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_{s1}-{\varphi }_{s2}\right)}^{2.5}},(8)$

2.1.2 Hybrid nanofluid density

$\frac{{\rho }_{hnf}}{{\rho }_f}=\left(1-{\varphi }_{s1}-{\varphi }_{s2}\right)+{\varphi }_{s1}\frac{{\rho }_{s1}}{{\rho }_f}+{\varphi }_{s2}\frac{{\rho }_{s2}}{{\rho }_f},(9)$

2.1.3 Hybrid nanofluid specific heat capacity

$\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}=\left(1-{\varphi }_{s1}-{\varphi }_{s2}\right)+{\varphi }_{s1}\frac{{\left(\rho C_p\right)}_{s1}}{{\left(\rho C_p\right)}_f}+{\varphi }_{s2}\frac{{\left(\rho C_p\right)}_{s2}}{{\left(\rho C_p\right)}_f},(10)$

2.1.4 Hybrid nanofluid thermal conductivity

$\frac{k_{hnf}}{k_f}=\left[\frac{2k_f+\left(\frac{{\varphi }_{s1}{k}_{s1}+{\varphi }_{s2}{k}_{s2}}{{\varphi }_{s1}+{\varphi }_{s2}}\right)+2\left({\varphi }_{s1}{k}_{s1}+{\varphi }_{s2}{k}_{s2}\right)-2\left({\varphi }_{s1}+{\varphi }_{s2}\right)k_f}{2k_f+\left(\frac{{\varphi }_{s1}{k}_{s1}+{\varphi }_{s2}{k}_{s2}}{{\varphi }_{s1}+{\varphi }_{s2}}\right)-\left({\varphi }_{s1}{k}_{s1}+{\varphi }_{s2}{k}_{s2}\right)+\left({\varphi }_{s1}+{\varphi }_{s2}\right)k_f}\right],(11)$

2.1.4 Thermal and solutal volumetric coefficient

$\begin{array}{l}{\left(\rho {\beta }_T\right)}_{hnf}=\left(1-{\varphi }_{s2}\right)\left\{{\left(\rho {\beta }_T\right)}_{s1}{\varphi }_{s1}+\left(1-{\varphi }_{s1}\right){\left(\rho {\beta }_T\right)}_f\right\}+{\varphi }_{s2}{\left(\rho {\beta }_T\right)}_{s2},\\ {\left(\rho {\beta }_C\right)}_{hnf}=\left(1-{\varphi }_{s2}\right)\left\{{\left(\rho {\beta }_C\right)}_{s1}{\varphi }_{s1}+\left(1-{\varphi }_{s1}\right){\left(\rho {\beta }_C\right)}_f\right\}+{\varphi }_{s2}{\left(\rho {\beta }_C\right)}_{s2},\end{array}(12)$

Here, s1 and s2 specify the silver (Ag) and titanium dioxide (TiO₂) nanoparticles, respectively. Further, the solid volume fraction of Ag is represented by ${\varphi }_{s1}$ and TiO₂ with ${\varphi }_{s2}$.

Table 1 presents the thermo-physical features of convectional fluid and hybrid nanofluid, as follows:

TABLE 1

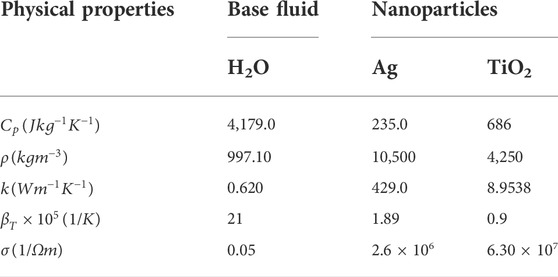
TABLE 1. Thermophysical characteristics of base liquid and nanoparticles [14].

2.2 Similarity variables

The applicable similarity variables are signified as in [50]:

$\begin{array}{l}\eta =\frac{r^2}{R_1^2},v=Eg\left(\eta \right),u=2azf{\left(\eta \right)}^{\prime },w=-a{R}_1\frac{f\left(\eta \right)}{{\eta }^{1/2}},\\ \frac{\left(T-T_{\infty }\right)}{\left(T_w-T_{\infty }\right)}=\theta \left(\zeta \right),\frac{\left(C-C_{\infty }\right)}{\left(C_w-C_{\infty }\right)}=\chi \left(\eta \right).\end{array}(13)$

Using Eq. 12, Eqs. 2–10 take the following form:

$\frac{\raisebox{1ex}{${\mu }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\left(\eta f^{‴}+f^{″}\right)-\frac{\mathrm{R}\mathrm{e}}{2}\frac{M\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}{f}^{\prime }+\lambda \mathrm{R}\mathrm{e}\left(\theta +N_{1}h\right)+\mathrm{R}\mathrm{e}\left(f{f}^{″}-f{\prime }^2\right)=0,(14)$

$\frac{\raisebox{1ex}{${\mu }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\left(2{\eta }^2{g}^{″}+2\eta g^{\prime }-\frac{g}{2}\right)-\mathrm{R}\mathrm{e}\left(\frac{M\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}g+2\eta f{g}^{\prime }+fg\right)=0,(15)$

$\frac{\raisebox{1ex}{$k_{hnf}$}\!\left/ \!\raisebox{-1ex}{$k_f$}\right.}{\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.}\left(\eta {\theta }^{″}+\theta ″\right)+\mathrm{P}\mathrm{r}\mathrm{R}\mathrm{e}\left[\begin{array}{l}\frac{\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.M{E}_c}{\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.}\left({f^{\prime }}^2+g^2-2{\epsilon }_t\left(f{f}^{\prime }{f}^{″}+g{g}^{\prime }f\right)\right)\\ +\frac{D_c}{\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.}\left(\theta -2{\epsilon }_{t}f{\theta }^{\prime }\right)+f{\theta }^{\prime }-2{\epsilon }_t\left(f^2{\theta }^{″}+f{f}^{\prime }{\theta }^{\prime }\right)\end{array}\right]=0,(16)$

$\eta h^{″}+h^{\prime }+S_c\mathrm{R}\mathrm{e}f{h}^{\prime }-2{\epsilon }_c{S}_c\mathrm{R}\mathrm{e}\left(f^2{h}^{″}+f{f}^{\prime }{h}^{\prime }\right)+2S_c{R}_c\mathrm{R}\mathrm{e}\left({\epsilon }_{c}f{h}^{\prime }-h\right)=0,(17)$

The convenient conditions are as follows:

$\left(f^{\prime }\left(1\right)=1,f\left(1\right)=0,g\left(1\right)=1,h^{\prime }\left(1\right)=B_c\left(h\left(1\right)-1\right),{\theta }^{\prime }\left(1\right)=\frac{k_f}{k_{hnf}}{B}_e\left(\theta \left(1\right)-1\right)\right),(18)$

$\left(f^{\prime }\left(\infty \right)\to 0\leftarrow g\left(\infty \right),h\left(\infty \right)\to 0\leftarrow \theta \left(\infty \right)\right).(19)$

The parameters involved are given as Reynold number $\mathrm{R}\mathrm{e}\left\{=\raisebox{1ex}{$a{R}_1^2$}\!\left/ \!\raisebox{-1ex}{$2{\upsilon }_f$}\right.\right\}$, magnetic parameter $M\left\{=\raisebox{1ex}{${\sigma }_f{B}_0^2$}\!\left/ \!\raisebox{-1ex}{${\rho }_{f}a$}\right.\right\}$, and mixed convection parameter $N_1\left\{=\frac{Gr}{G{r}^{*}}\right\}$. The Grashof numbers for temperature and concentration are $Gr\left(=\raisebox{1ex}{$g{\beta }_T\left(T_w-T_{\infty }\right)z^3$}\!\left/ \!\raisebox{-1ex}{${\upsilon }_f^2$}\right.\right)$ and $G{r}^{*}\left(=\raisebox{1ex}{$g{\beta }_C\left(C_w-C_{\infty }\right)z^3$}\!\left/ \!\raisebox{-1ex}{${\upsilon }_f^2$}\right.\right)$, respectively, and the parameters of the buoyancy ratio $\lambda \left\{=\raisebox{1ex}{$Gr$}\!\left/ \!\raisebox{-1ex}{$\mathrm{R}{\mathrm{e}}_z^2$}\right.\right\}$, local Reynold number ${\mathrm{R}\mathrm{e}}_z\left\{=\raisebox{1ex}{$u_{ss}^{2}z$}\!\left/ \!\raisebox{-1ex}{${\upsilon }_f^2$}\right.\right\}$, thermal relaxation ${\epsilon }_t\left\{={\epsilon }_{0}a\right\}$, concentration relaxation ${\epsilon }_c\left\{={\epsilon }_{1}a\right\}$, and Prandtl number $\mathrm{Pr}\left\{=\frac{{\nu }_f}{{\alpha }_f}\right\}$ are also given.

The above equations hold only for the positive Reynold number, and the solution convergence criteria are very slow for the lower Reynolds numbers. To improve solution convergence, we use the transformation $\eta =e^x$, developed by Fang and Yao [31]. The above ODEs are transformed into following form:

$\frac{\raisebox{1ex}{${\mu }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\left(f_{xxx}-2f_{xx}+f_x\right)-\frac{M{\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.e}^x}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\mathrm{R}\mathrm{e}\frac{f_x}{2}+\lambda \mathrm{R}\mathrm{e}{e}^{2x}\left(\theta +N_{1}h\right)-\mathrm{R}\mathrm{e}{f}_x^2+\mathrm{R}\mathrm{e}f{f}_x-\mathrm{R}\mathrm{e}f{f}_{xx}=0,(20)$

$\frac{\raisebox{1ex}{${\mu }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\left(2g_{xx}-\frac{g}{2}\right)-\frac{M\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}\mathrm{R}\mathrm{e}g+2\mathrm{R}\mathrm{e}f{g}_x+\mathrm{R}\mathrm{e}fg=0,(21)$

$\frac{\raisebox{1ex}{$k_{hnf}$}\!\left/ \!\raisebox{-1ex}{$k_f$}\right.}{\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.}{\theta }_{xx}+\mathrm{P}\mathrm{r}\mathrm{R}\mathrm{e}\left[\begin{array}{l}\frac{\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.M{E}_c}{e^x\left(\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.\right)}\left(f_x^2+e^{2x}{g}^2-\frac{2{\epsilon }_t}{e^x}\left(f{f}_x{f}_{xx}-f{f}_x^2+e^{2x}g{g}_{x}f\right)\right)\\ +\frac{D_c}{\raisebox{1ex}{${\left(\rho C_p\right)}_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.}\left(\theta e^x-2{\epsilon }_{t}f{\theta }_x\right)-\frac{2{\epsilon }_t}{e^x}\left(f^2{\theta }_{xx}+f{f}_x{\theta }_x-f^2{\theta }_x\right)+f{\theta }_x\end{array}\right]=0,(22)$

$h_{xx}+S_c\mathrm{R}\mathrm{e}f{h}_x-2\frac{{\epsilon }_c{S}_c\mathrm{R}\mathrm{e}}{e^x}\left(f^2{h}_{xx}-f^2{h}_x+f{f}_x{h}_x\right)+2S_c{R}_c\mathrm{R}\mathrm{e}\left({\epsilon }_{c}f{h}_x-h{e}^x\right)=0,(23)$

The convenient conditions at the boundary are as follows:

$\left(f_x\left(0\right)=1,f\left(0\right)=0,g\left(0\right)=1,h_x\left(0\right)=-B_c\left(1-h\left(0\right)\right),{\theta }_x\left(0\right)=-B_e\left(1-\theta \left(0\right)\right),\right),(24)$

$\left(\underset{x\to \infty }{\lim }{e}^{-x}{f}_x\left(\infty \right)\to 0,g\left(\infty \right)\to 0,h\left(\infty \right)\to 0,\theta \left(\infty \right)\to 0,\right),(25)$

2.3 Entropy generation

To include irreversibility sources, for present article, entropy generation consists of the heat transport, mass transport, and joule heating impact. The equation of entropy generation is stated as follows:

$S_{gen}^{‴}=\frac{k_{hnf}}{T_{\infty }^2}{\left(\frac{\partial T}{\partial r}\right)}^2+\frac{{\mu }_{hnf}}{T_{\infty }}{\left(\frac{\partial u}{\partial r}\right)}^2+\frac{R_d{D}_B}{C_{\infty }}{\left(\frac{\partial C}{\partial r}\right)}^2+\frac{R_d{D}_B}{T_{\infty }}\left(\frac{\partial T}{\partial r}\right)\left(\frac{\partial C}{\partial r}\right)+\frac{{\sigma }_{hnf}}{T_{\infty }}{B}_0^2{u}^2,(26)$

Entropy generation $N_G$ is the ratio between the entropy generation rate $S^{‴}$ and the characteristic entropy generation rate $S_0^{‴}$, such that:

$S_0^{‴}=\frac{k_f{\left(\Delta T\right)}^2}{{\left(a{T}_{\infty }\right)}^2}.(27)$

$N_G=\frac{k_{hnf}}{k_f}4\eta \theta {\prime }^2+\epsilon \left(\frac{\mathrm{\Sigma }}{\mathrm{\Omega }}\right)4\eta h{\prime }^2+\epsilon \left(\frac{\mathrm{\Sigma }}{\mathrm{\Omega }}\right)4\eta {\theta }^{\prime }{h}^{\prime }+\left(\frac{Br}{\mathrm{\Omega }}\right){\left(\frac{F}{2\eta }+F^{\prime }\right)}^2+M\left(\frac{Br}{\mathrm{\Omega }}\right){f^{\prime }}^2.(28)$

Now, using the transformation $\eta =e^x$ for fast convergence, we get the following form:

$N_G=\frac{k_{hnf}}{k_f}4e^{-x}{\theta }_x^2+\epsilon \left(\frac{\mathrm{\Sigma }}{\mathrm{\Omega }}\right)4e^{-x}{h}_x^2+\epsilon \left(\frac{\mathrm{\Sigma }}{\mathrm{\Omega }}\right)4e^{-x}{\theta }_x{h}_x+\left(\frac{Br}{\mathrm{\Omega }{e}^{2x}}\right){\left(\frac{f}{2}+f_x\right)}^2+M\left(\frac{Br}{\mathrm{\Omega }}\right)e^{-2x}{f}_x^2.(29)$

In the above equation, the parameter of the temperature difference is $\mathrm{\Omega }=\frac{\Delta T}{T_{\infty }}$, $Br=\frac{{\mu }_f{u}_w}{k_f\Delta T}$ is the Brinkman number, $\mathrm{\Sigma }=\frac{\Delta C}{C_{\infty }}$ is the concentration difference parameter, and $\epsilon =\frac{R_d{D}_B{C}_{\infty }}{k_f}$ is the dimensionless constant.

2.4 Skin friction

The quantities of interest, such as skin friction, are very precious for the engineering point of view. No transport of heat and mass rate were observed in the current investigation. The mathematical form of skin fraction is as follows:

$C_f=\frac{{\tau }_w}{{\left(r\mathrm{\Omega }\right)}^2{\rho }_{hnf}},(30)$

In Eq. 29, ${\tau }_w$ is defined as:

${\tau }_w=\frac{{\mu }_{hnf}}{{\rho }_f{v}_w^2}{\left|\frac{\partial u}{\partial r}\right|}_{r=R_1},(31)$

Equation (30) in its dimensionalized form is as follows:

${\left({\mathrm{R}\mathrm{e}}_r\right)}^{0.5}{C}_f=\sqrt{2}{f}^{″},(32)$

${\mathrm{R}\mathrm{e}}_r=\frac{\mathrm{\Omega }{r}^2}{{\upsilon }_f}$ is the Reynolds number.

3 Graphical discussion

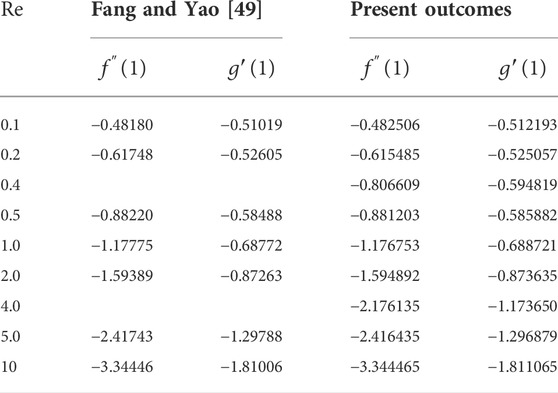
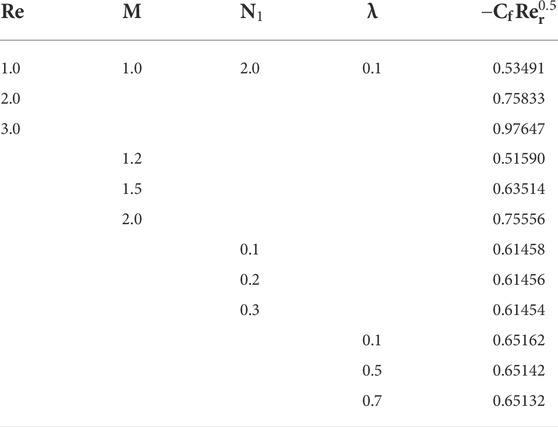
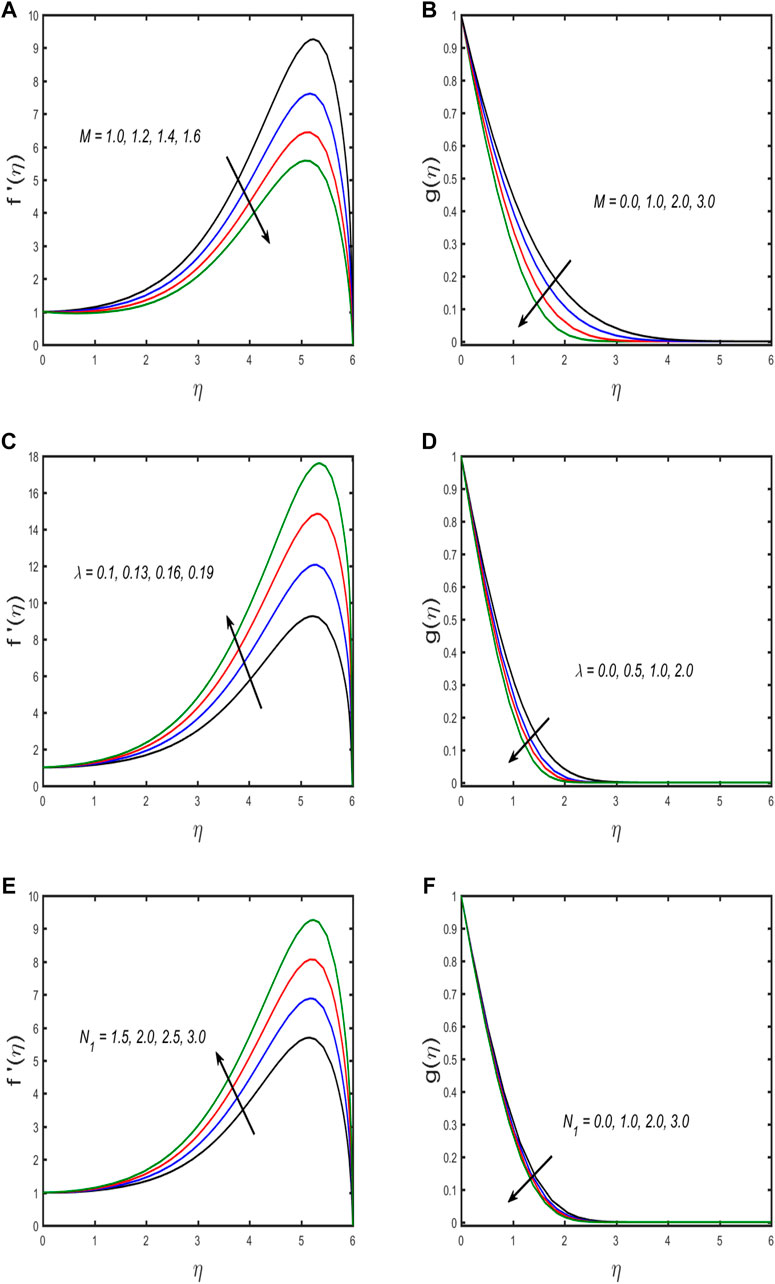
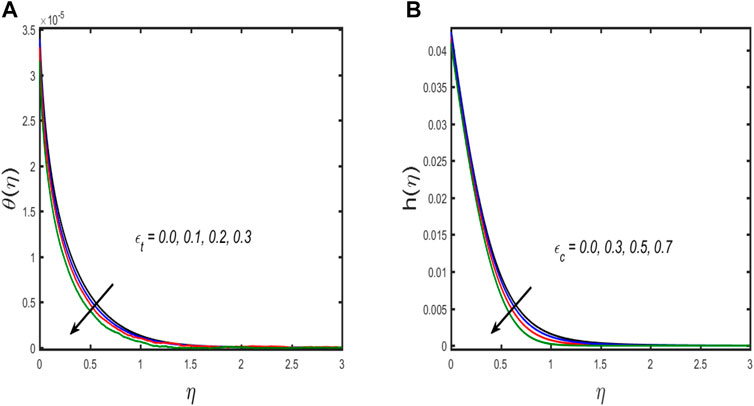
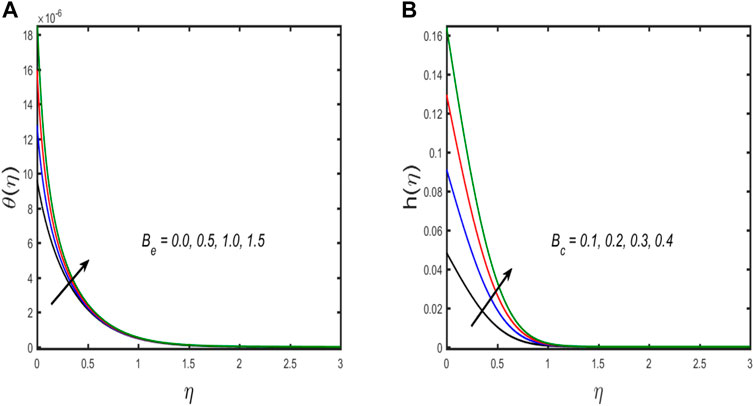
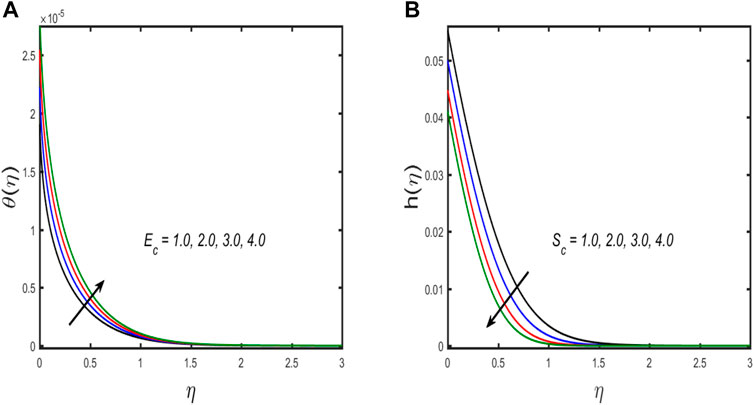
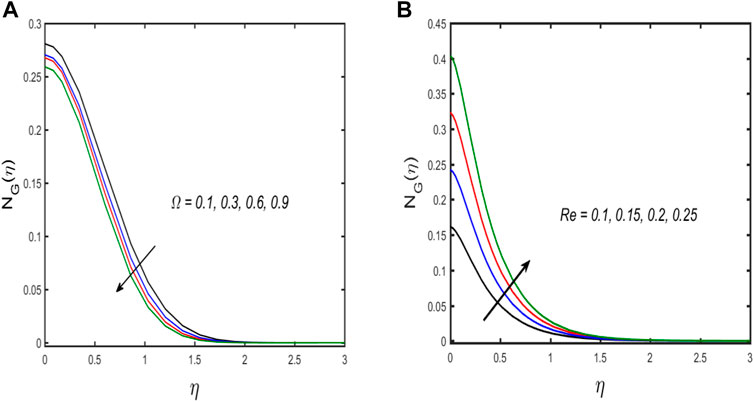
The numerical algorithm BVP4C in MATLAB is used to solve Eqs. 20–23 along with the boundary conditions (Eqs. 24, 25). The Bvp4c technique is only applicable to first-order ordinary differential equations. Thus, we first transform the third and second-order equations into a first-order differential equation with the use of a new variable. References [32–35] are recommended to readers because this system is well-known. Table 2 displays an assessment of the present outcomes in comparison with previously published data. From the table, it can be concluded that the current outcomes show good harmony with the results produced by Fang and Yao [31]. Table 3 presents the tabulated values for skin friction for different emerging parameters. It can be observed from the table that due to enhancement of the estimation of the Reynold number and magnetic parameters, the numerical value of skin friction is enhanced, while it falls due to the enhancement of the value of mixed convection and buoyancy ratio parameters it is reduced. For several growing parameters, graphical results are achieved covering axial and swirl velocity, temperature, and concentration field. Figures 2A,B illustrate the influence of the magnetic parameters on swirl and axial velocity. The figure shows that both fluid velocities diminish with a higher estimation of the magnetic parameter. When the magnetic parameter value is increased, Lorentz force appears, which enhances resistive force in the fluid flow, and as a result, the fluid velocity is reduced. The upshot of the influence of the buoyancy ratio parameter on swirl and axial velocity is discussed in Figures 2C,D. The figure shows that axial velocity improves while swirl velocity declines with growing estimation of the buoyancy ratio parameter, and the same result is found for the mixed convection parameter portrayed in Figures 2E,F. Physically, both buoyancy movement forces and forced convection progress in the same direction, boosting the values of the buoyancy ratio parameter. Thus, because the buoyancy effect produces resistive force to the rotation of fluid particles, the axial velocity of liquid flow grows, while the swirl velocity decreases. A relationship between the temperature and concentration distribution via thermal and solutal stratification is observed in Figures 3A,B. The fluid temperature and concentration are both diminished with thermal and solutal relaxation parameter effects. Physically, the mass and heat transport in the fluid flow are reduced with the dimensionless thermal and solutal relaxation parameter; as a result, both the profiles diminish. Figures 4A,B explore the upshot of thermal and solutal Biot number on temperature and concentration field. Greater convection is caused by an increment in the thermal Biot number, resulting in higher temperature and correlated thickness of boundary layer. The same behavior is seen for the solutal Biot number that is depicted in Figure 4B. The response of the Eckert number on temperature and Schmidt number on concentration profile is observed in Figures 5A,B, respectively. If the Eckert number is strong, the fluid components are more energetic due to energy storage. As a result, there is an upsurge in fluid temperature (see in Figure 5A). Figure 5B discloses the influence of the Schmidt number on concentration distribution. It is seen that by boosting the values of $S_c$ the mass diffusivity is reduced, so the concentration profile shrinks. The upshot of parameter of temperature variance and Reynold number on entropy generation is demonstrated in Figures 6A,B. In Figure 6A, it can be seen that the entropy age diminishes along the temperature variance parameter, although the Reynold number augments the entropy generation described in Figure 6B.

TABLE 2

TABLE 2. Assessment of $f^{″}\left(1\right)$ and $g^{\prime }\left(1\right)$ with previous data, when $N_1=\mathrm{Pr}=0=\lambda =M={\varphi }_1$.

TABLE 3

TABLE 3. Numerical values of $C_f{\mathrm{R}\mathrm{e}}_r^{0.5}$ against the various parameters.

FIGURE 2

FIGURE 2. (A–F) Variation in $f^{\prime }\left(\eta \right)$ and $g\left(\eta \right)$ against $M$, $\lambda$ and $N_1$.

FIGURE 3

FIGURE 3. (A,B) Variation in $\theta \left(\eta \right)$ and $h\left(\eta \right)$ against ${\epsilon }_t$ and ${\epsilon }_c$, respectively.

FIGURE 4

FIGURE 4. (A,B) Variation in $\theta \left(\eta \right)$ and $h\left(\eta \right)$ against $B_e$ and $B_c$, respectively.

FIGURE 5

FIGURE 5. (A,B) Variation in $\theta \left(\eta \right)$ and $h\left(\eta \right)$ against $E_c$ and $S_c$, respectively.

FIGURE 6

FIGURE 6. (A,B) Variation in $N_G\left(\eta \right)$ against $\Omega$ and $\mathrm{R}\mathrm{e}$, respectively.

4 Concluding remarks

In the present analysis, the mixed convection hybrid nanofluid flow is discussed using a modified Fourier and Ficks law. Entropy generation is calculated. Further, the influences of heat generation/absorption, chemical reaction, Joule heating, and the thermal and solutal Biot number are discussed. This analysis presents the thermal characteristics of hybrid nanofluid, which presents many novel applications in the thermal engineering, such as nuclear reactions, heat exchangers, cooling and heating devices, fission and fusion chemical reactions, coolant in machining and manufacturing, thermal extrusion processes, and much more. The bvp4c approach is utilized to solve the problem numerically. The key findings of the present results are as follows:

➢ Axial and swirl velocities are reduced due to Lorentz forces produced by higher magnetic parameters.

➢ The axial velocity of fluid flow is enhanced and the swirl velocity is decreased with the buoyancy ratio parameter, as the buoyancy effect generates resistive force to the rotation of fluid particles.

➢ The temperature field is a growing function of thermal Biot number and the Eckert number but presents a diminishing function of thermal relaxation parameter.

➢ For larger values of the Schmidt number and solutal relaxation, the parameter concentration field is reduced, but for larger solutal Biot numbers, it is enhanced.

➢ Entropy generation is boosted with increased Reynolds number and reduced with falling parameter of temperature difference.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author contributions

SA: conceptualization, methodology, software, formal analysis, writing-original draft preparation. NA: Software, Resources, Writing - review and editing. MK: writing original draft preparation, data curation, investigation, visualization, validation. EA: Funding acquisition, Writing - review and editing, Investigation. ET-E: Funding acquisition, Writing - review and editing, Visualization. KGe: Writing - review and editing, validation. KGu: Methodology, Writing - review and editing. AG: Methodology, Writing - review and editing, Resources.

Acknowledgments

The authors thank the Taif University Researcher for supporting project number TURSP-2020/16, Taif University, Taif, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4331317DSR49.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938. IL (United States): Argonne National Lab. (1995). CONF-951135-29).

Google Scholar

2. Eastman JA, Choi US, Li S, Thompson LJ, Lee. S. Enhanced thermal conductivity through the development of nanofluids. MRS Proc (1996) 457:3. doi:10.1557/proc-457-3

CrossRef Full Text | Google Scholar

3. Ur Rehman F, Nadeem S. Heat transfer analysis for three-dimensional stagnation-point flow of water-based nanofluid over an exponentially stretching surface. J Heat Transfer (2018) 140(5). doi:10.1115/1.4038359

CrossRef Full Text | Google Scholar

4. Sheikholeslami M. Numerical investigation for CuO-H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method. J Mol Liquids (2018) 249:739–46. doi:10.1016/j.molliq.2017.11.069

CrossRef Full Text | Google Scholar

5. Bilal M, Sagheer M, Hussain S. Numerical study of magnetohydrodynamics and thermal radiation on Williamson nanofluid flow over a stretching cylinder with variable thermal conductivity. Alexandria Eng J (2018) 57(4):3281–9. doi:10.1016/j.aej.2017.12.006

CrossRef Full Text | Google Scholar

6. Maskeen MM, Zeeshan A, Mehmood OU, Hassan M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J Therm Anal Calorim (2019) 138(2):1127–36. doi:10.1007/s10973-019-08304-7

CrossRef Full Text | Google Scholar

7. Reddy SRR, Bala Anki Reddy P, Rashad AM. Activation energy impact on chemically reacting Eyring–Powell nanofluid flow over a stretching cylinder. Arab J Sci Eng (2020) 45:5227–42. doi:10.1007/s13369-020-04379-9

CrossRef Full Text | Google Scholar

8. Ullah I, Ullah R, Alqarni MS, Xia WF, Muhammad T. Combined heat source and zero mass flux features on magnetized nanofluid flow by radial disk with the applications of Coriolis force and activation energy. Int Commun Heat Mass Transfer (2021) 126:105416. doi:10.1016/j.icheatmasstransfer.2021.105416

CrossRef Full Text | Google Scholar

9. Khan MN, Nadeem S. A comparative study between linear and exponential stretching sheet with double stratification of a rotating Maxwell nanofluid flow. Surf Inter (2021) 22:100886. doi:10.1016/j.surfin.2020.100886

CrossRef Full Text | Google Scholar

10. Dawar A., Shah Z., Tassaddiq A., Kumam P., Islam S., Khan W. A convective flow of Williamson nanofluid through cone and wedge with non-isothermal and non-isosolutal conditions: A revised buongiorno model. Case Studies in Thermal Engineering (2021) 24:100869. doi:10.1016/j.csite.2021.100869

CrossRef Full Text | Google Scholar

11. Dawar A., Saeed A., Kumam P. Magneto-hydrothermal analysis of copper and copper oxide nanoparticles between two parallel plates with Brownian motion and thermophoresis effects. International Communications in Heat and Mass Transfer (2022) 133:105982. doi:10.1016/j.icheatmasstransfer.2022.105982

CrossRef Full Text | Google Scholar

12. Dawar A., Wakif A., Thumma T., Shah N. A. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. International Communications in Heat and Mass Transfer (2022) 130:105800. doi:10.1016/j.icheatmasstransfer.2021.105800

CrossRef Full Text | Google Scholar

13. Waini I., Ishak A., Pop I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics (2020) 8(4):612. doi:10.3390/math8040612

CrossRef Full Text | Google Scholar

14. Kumar R.N., Gowda R.P., Abusorrah A.M., Mahrous Y.M., Abu-Hamdeh N.H., Issakhov A., Rahimi-Gorji M., Prasannakumara B.C. Impact of magnetic dipole on ferromagnetic hybrid nanofluid flow over a stretching cylinder. Phys Scr (2021) 96(4):045215. doi:10.1088/1402-4896/abe324

CrossRef Full Text | Google Scholar

15. Bakar SA, Arifin NM, Bachok N, Ali FM. Effect of thermal radiation and MHD on hybrid Ag–TiO2/H2O nanofluid past a permeable porous medium with heat generation. Case Stud Therm Eng (2021) 28:101681. doi:10.1016/j.csite.2021.101681

CrossRef Full Text | Google Scholar

16. Salahuddin T, Siddique N, Khan M, Chu YM. A hybrid nanofluid flow near a highly magnetized heated wavy cylinder. Alexandria Eng J (2022) 61(2):1297–308. doi:10.1016/j.aej.2021.06.014

CrossRef Full Text | Google Scholar

17. Dawar A, Bonyah E, Islam S, Alshehri A, Shah Z. Theoretical analysis of Cu-H2O, Al2O3-H2O, and TiO2-H2O nanofluid flow past a rotating disk with velocity slip and convective conditions. J Nanomater (2021) 1–10. doi:10.1155/2021/5471813

CrossRef Full Text | Google Scholar

18. Dawar A, Islam S, Shah Z. A comparative analysis of the performance of magnetised copper–copper oxide/water and copper–copper oxide/kerosene oil hybrid nanofluids flowing through an extending surface with velocity slips and thermal convective conditions. Int J Ambient Energ (2022) 1–19. doi:10.1080/01430750.2022.2063387

CrossRef Full Text | Google Scholar

19. Ramzan M, Dawar A, Saeed A, Kumam P, Watthayu W, Kumam W. Heat transfer analysis of the mixed convective flow of magnetohydrodynamic hybrid nanofluid past a stretching sheet with velocity and thermal slip conditions. Plos one (2021) 16(12):e0260854. doi:10.1371/journal.pone.0260854

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gao J, Liu J, Yue H, Zhao Y, Tlili I, Karimipour A. Effects of various temperature and pressure initial conditions to predict the thermal conductivity and phase alteration duration of water based carbon hybrid nanofluids via MD approach. J Mol Liquids (2022) 351:118654. doi:10.1016/j.molliq.2022.118654

CrossRef Full Text | Google Scholar

21. Bejan A. A study of entropy generation in fundamental convective heat transfer (1979).

Google Scholar

22. Bejan A, Second-law analysis in heat transfer and thermal design. Adv Heat transfer (1982). p. 1–58.

CrossRef Full Text | Google Scholar

23. Bejan A. Entropy generation minimization: The new thermodynamics of finite‐size devices and finite‐time processes. J Appl Phys (1996) 79(3):1191–218. doi:10.1063/1.362674

CrossRef Full Text | Google Scholar

24. Bejan A. Entropy generation minimization: The method of thermodynamic optimization of finite-size systems and finite-time processes. Boca Raton, FL: CRC Press (1996).

Google Scholar

25. Mahian O, Kianifar A, Kleinstreuer C, Moh’d A AN, Pop I, Sahin AZ, et al. A review of entropy generation in nanofluid flow. Int J Heat Mass Transfer (2013) 65:514–32. doi:10.1016/j.ijheatmasstransfer.2013.06.010

CrossRef Full Text | Google Scholar

26. Siavashi M, Bahrami HRT, Saffari H. Numerical investigation of flow characteristics, heat transfer and entropy generation of nanofluid flow inside an annular pipe partially or completely filled with porous media using two-phase mixture model. Energy (2015) 93:2451–66. doi:10.1016/j.energy.2015.10.100

CrossRef Full Text | Google Scholar

27. Rashid M, Khan MI, Hayat T, Khan MI, Alsaedi A. Entropy generation in flow of ferromagnetic liquid with nonlinear radiation and slip condition. J Mol Liquids (2019) 276:441–52. doi:10.1016/j.molliq.2018.11.148

CrossRef Full Text | Google Scholar

28. Khan MI, Alsaedi A, Hayat T, Khan NB. Modeling and computational analysis of hybrid class nanomaterials subject to entropy generation. Comput Methods Programs Biomed (2019) 179:104973. doi:10.1016/j.cmpb.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Muhammad R, Khan MI, Jameel M, Khan NB. Fully developed Darcy-Forchheimer mixed convective flow over a curved surface with activation energy and entropy generation. Comput Methods Programs Biomed (2020) 188:105298. doi:10.1016/j.cmpb.2019.105298

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Riaz A, Bobescu E, Ramesh K, Ellahi R. Entropy analysis for cilia-generated motion of Cu-blood flow of nanofluid in an annulus. Symmetry (2021) 13(12):2358. doi:10.3390/sym13122358

CrossRef Full Text | Google Scholar

31. Riaz A, Abbas T, Zeeshan A, Doranehgard MH. Entropy generation and MHD analysis of a nanofluid with peristaltic three-dimensional cylindrical enclosures. Int J Numer Methods Heat Fluid Flow (2021) 31:2698–714. doi:10.1108/hff-11-2020-0704

CrossRef Full Text | Google Scholar

32. Siddiqui BK, Batool S, mahmood ul Hassan Q, Malik MY. Repercussions of homogeneous and heterogeneous reactions of 3D flow of Cu-water and AL2O3-water nanofluid and entropy generation estimation along stretching cylinder. Ain Shams Eng J (2022) 13(1):101493. doi:10.1016/j.asej.2021.05.007

CrossRef Full Text | Google Scholar

33. Salahuddin T, Imtiaz I, Khan M. Analysis of entropy generation in AA7072-methanol and AA7072+ AA7075-methanol flow near a parabolic surface. Appl Maths Comput (2022) 413:126616. doi:10.1016/j.amc.2021.126616

CrossRef Full Text | Google Scholar

34. Fourier JBJ, Darboux G. Théorie analytique de la chaleur. Vol. 504. Paris: Didot (1822).

Google Scholar

35. Ellahi R, Riaz A, Abbasbandy S, Hayat T, Vafai K. A study on the mixed convection boundary layer flow and heat transfer over a vertical slender cylinder. Therm Sci (2014) 18(4):1247–58. doi:10.2298/tsci110923097e

CrossRef Full Text | Google Scholar

36. Sandeep N, Kumar BR, Kumar MJ. A comparative study of convective heat and mass transfer in non-Newtonian nanofluid flow past a permeable stretching sheet. J Mol Liquids (2015) 212:585–91. doi:10.1016/j.molliq.2015.10.010

CrossRef Full Text | Google Scholar

37. Dawar A, Shah Z, Tassaddiq A, Islam S, Kumam P. Joule heating in magnetohydrodynamic micropolar boundary layer flow past a stretching sheet with chemical reaction and microstructural slip. Case Stud Therm Eng (2021) 25:100870. doi:10.1016/j.csite.2021.100870

CrossRef Full Text | Google Scholar

38. Ramadan KM, Qisieh O, Tlili I. Thermal creep effects on fluid flow and heat transfer in a microchannel gas cooling. Proc Inst Mech Eng C: J Mech Eng Sci (2022) 236(9):5033–47. doi:10.1177/09544062211057039

CrossRef Full Text | Google Scholar

39. Zaydan M, Hamad NH, Wakif A, Dawar A, Sehaqui R. Generalized differential quadrature analysis of electro‐magneto‐hydrodynamic dissipative flows over a heated riga plate in the presence of a space‐dependent heat source: The case for strong suction effect. Heat Trans (2022) 51(2):2063–78. doi:10.1002/htj.22388

CrossRef Full Text | Google Scholar

40. Sohail M, Nazir U, EssamEl-Zahar R, Alrabaiah H, Kumam P, Mousa AAA, et al. A study of triple-mass diffusion species and energy transfer in Carreau–Yasuda material influenced by activation energy and heat source. Sci Rep (2022) 12(1):10219–7. doi:10.1038/s41598-022-13890-y

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Nazir U, Sohail M, Kumam P, Sitthithakerngkiet K, Mousa AAA, Khan MJ, et al. A dynamic assessment of various non-Newtonian models for ternary hybrid nanomaterial involving partially ionized mechanism. Sci Rep (2022) 12(1):10306–15. doi:10.1038/s41598-022-14312-9

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Sohail M, El-Zahar ER, Mousa AAA, Nazir U, Althobaiti S, Althobaiti A, et al. Finite element analysis for ternary hybrid nanoparticles on thermal enhancement in pseudo-plastic liquid through porous stretching sheet. Sci Rep (2022) 12(1):9219–3. doi:10.1038/s41598-022-12857-3

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Hou E, Wang F, Nazir U, Sohail M, Jabbar N, Thounthong P. Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines (2022) 13(2):201. doi:10.3390/mi13020201

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tlili I, Sajadi SM, Baleanu D, Ghaemi F. Flat sheet direct contact membrane distillation study to decrease the energy demand for solar desalination purposes. Sustainable Energ Tech Assessments (2022) 52:102100. doi:10.1016/j.seta.2022.102100

CrossRef Full Text | Google Scholar

45. Zhang J, Sajadi SM, Chen Y, Tlili I, Fagiry MA. Effects of Al2O3 and TiO2 nanoparticles in order to reduce the energy demand in the conventional buildings by integrating the solar collectors and phase change materials. Sustain Energ Tech Assessments (2022) 52:102114. doi:10.1016/j.seta.2022.102114

CrossRef Full Text | Google Scholar

46. Tlili I, Alharbi T. Investigation into the effect of changing the size of the air quality and stream to the trombe wall for two different arrangements of rectangular blocks of phase change material in this wall. J Building Eng (2022) 52:104328. doi:10.1016/j.jobe.2022.104328

CrossRef Full Text | Google Scholar

47. Qi X, Sidi MO, Tlili I, Ibrahim TK, Elkotb MA, El-Shorbagy MA, et al. Optimization and sensitivity analysis of extended surfaces during melting and freezing of phase changing materials in cylindrical Lithium-ion battery cooling. J Energ Storage (2022) 51:104545. doi:10.1016/j.est.2022.104545

CrossRef Full Text | Google Scholar

48. Alzahrani J, Vaidya H, Prasad KV, Rajashekhar C, Mahendra DL, Tlili I. Micro-polar fluid flow over a unique form of vertical stretching sheet: Special emphasis to temperature-dependent properties. Case Stud Therm Eng (2022) 34:102037. doi:10.1016/j.csite.2022.102037

CrossRef Full Text | Google Scholar

49. Fang T, Yao S. Viscous swirling flow over a stretching cylinder. Chin Phys Lett (2011) 28(11):114702. doi:10.1088/0256-307x/28/11/114702

CrossRef Full Text | Google Scholar

50. Ahmed A, Khan M, Ahmed J. Mixed convective flow of Maxwell nanofluid induced by vertically rotating cylinder. Appl Nanosci (2020) 10(12):5179–90. doi:10.1007/s13204-020-01320-2

CrossRef Full Text | Google Scholar

51. Nayak MK, Mabood F, Dogonchi AS, Ramadan KM, Tlili I, Khan WA. Waves in random and complex media (2022). p. 1–22.Entropy optimized assisting and opposing non-linear radiative flow of hybrid nanofluid

CrossRef Full Text | Google Scholar

52. Qin L, Ahmad S, Khan MN, Ahammad NA, Gamaoun F, Galal AM. Thermal and solutal transport analysis of Blasius–Rayleigh–Stokes flow of hybrid nanofluid with convective boundary conditions. Waves in Random and Complex Media (2022) 1–19. doi:10.1080/17455030.2022.2072018

CrossRef Full Text | Google Scholar

53. Ahmad S, Nadeem S. Thermal analysis in buoyancy driven flow of hybrid nanofluid subject to thermal radiation. Int J Ambient Energ (2020) 1–9. doi:10.1080/01430750.2020.1861090

CrossRef Full Text | Google Scholar