- 1Department of Physics, University of Maiduguri, Maiduguri, Nigeria
- 2Department of Physics, Akwa Ibom State University, Uyo, Nigeria
- 3Department of Physics, College of Science, Sultan Qaboos University, Muscat, Oman
- 4Department of Physics, University of South Africa, Johannesburg, South Africa
By employing the extended Nikiforov–Uvarov (ENU) method, we solved the radial Schrodinger equation with the shifted screened Kratzer potential model. The analytical expression of the energy eigenvalues and numerical results were determined for some selected diatomic molecule systems. Variations of the energy eigenvalues obtained with potential parameters and quantum numbers were discussed graphically. Also, variations of different thermodynamic properties with temperature and maximum vibration quantum numbers were discussed extensively. Our results correspond to the results obtained in the literatures. The shifting parameters contribute a great effect to the energy results obtained. It has also been established that there exists a critical temperature at specific entropy values for the selected diatomic molecule systems.
Introduction
Since the inception of quantum mechanics many decades ago, different analytical techniques have been used by different authors to obtain the solutions of the Schrodinger wave equation (SWE), Klein–Gordon equation (KGE), and Dirac equation (DE). Such analytical techniques include the factorization method [1], modified factorization method [2], Nikiforov–Uvarov (NU) method [3], asymptotic iteration method (AIM) [4], Nikiforov–Uvarov functional analysis (NUFA) method [5], and extended Nikiforov–Uvarov (ENU) method [6], among others [7–9]. In recent years, many researchers in quantum mechanics have devoted their interest to finding the solutions of the SWE for different potential models [10–12]. These solutions obtained are either exactly or approximately. In the literature, only a few of these potential models can be solved exactly such as that of a harmonic oscillator and hydrogen atom [13]. It is also well known that the solution obtained from the SWE can be used to study many physical systems such as probability density and information theoretic measures [14–18], thermodynamics properties [19–23], and other applications in physics and chemistry [24–30]. The potential models that have been investigated within the framework of nonrelativistic and relativistic quantum mechanics included the screened Kratzer potential, Hulthen potential, Mobius-square potential, improved screened Kratzer potential, Wood–Saxon potential, Manning–Rosen potential, Yukawa potential, screened Coulomb potential, and others. One of the best potential models used to describe the interaction of a molecular structure in quantum mechanics is the Kratzer potential [31]. The Kratzer potential has many applications in different branches of physics and chemistry such as molecular physics, atomic physics, and quantum chemistry [32]. Recently, Ikot et. al. [33] proposed a screened Kratzer potential and investigated the bound state solution of the SWE with applications to diatomic molecules. In a similar development, Ikot et al. [34] proposed an improved screened Kratzer potential and investigated the bound state solutions of the Klein–Gordon equation with applications to the thermodynamic properties within the nonrelativistic limit. One of the special cases of the improved screened Kratzer is the shifted screened Kratzer potential (SSKP), which is our focal point of concern in this study. This is given in the form:
where
Solutions of the radial Schrodinger equation with the shifted screened Kratzer potential
The radial Schrodinger equation is given as [35]
where
We employ the Greene–Aldrich approximation scheme to deal with the centrifugal barrier as [37]
Substituting Eq. 4 into Eq. 3 and using the coordinate transformation of the form
where
Comparing Eq. 5 and Eq. (A1) of the extended Nikiforov–Uvarov (ENU) [6, 38, 39] method (see the Appendix A section), we have the following polynomials:
Substituting these polynomials into Eq. (A8), we obtain
Here, we have employed a linear function
where the coefficients
By employing Eq. 12, Eq. 11 becomes
By substituting Eqs 7, 13 into Eq. (A7) (see the Appendix A section), we have
From the knowledge of the ENU method, we choose the expression
and
Referring to Eq. (A9) and by substituting Eq. 16, we define the constant
By substituting Eqs 6, 12, 16, 17 into Eq. A12, where
where,
and
Thermodynamic properties of the shifted screened Kratzer potential
The partition function is the starting point usually employed in investigating different thermodynamic properties of diatomic molecule systems. The partition function is known to be a function of temperature, which is obtained via the expression [40–42]
Here,
By substituting Eq. 18 into Eq. 21, we obtain
where
With the help of a Mathematica software, the partition function of the SSKP is obtained as
where
Results and discussions
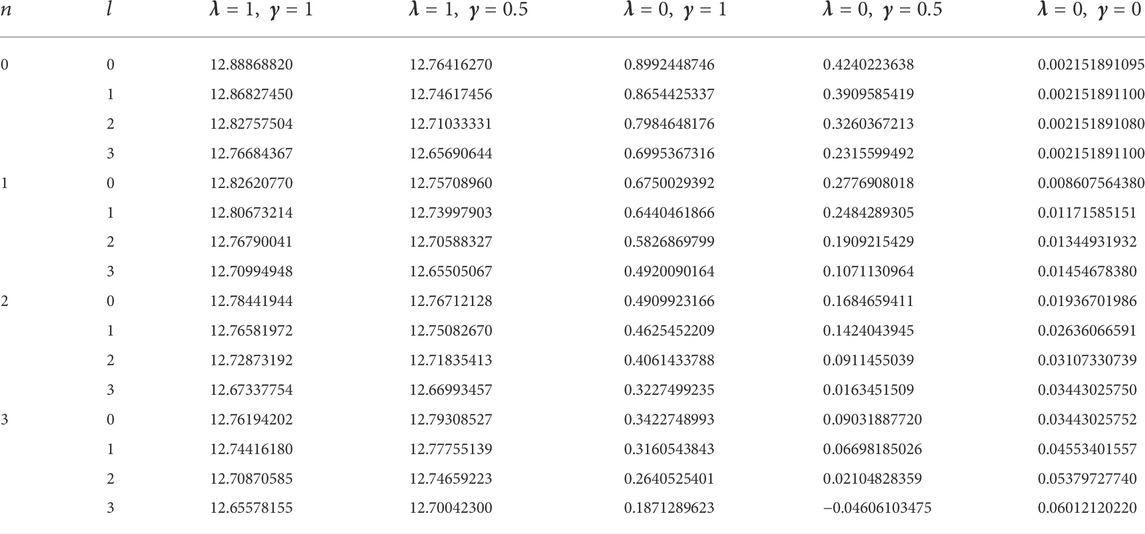
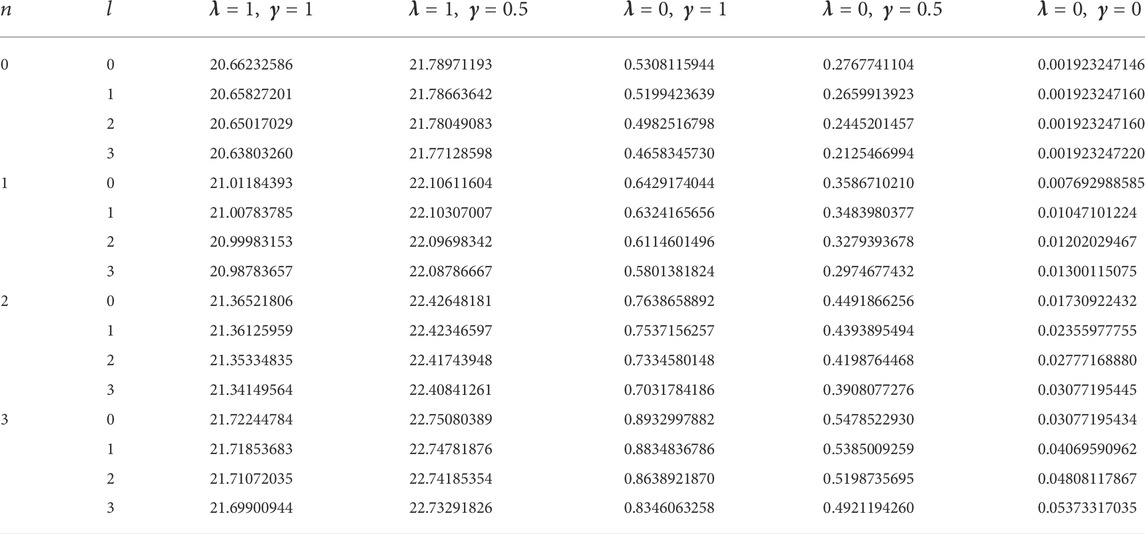
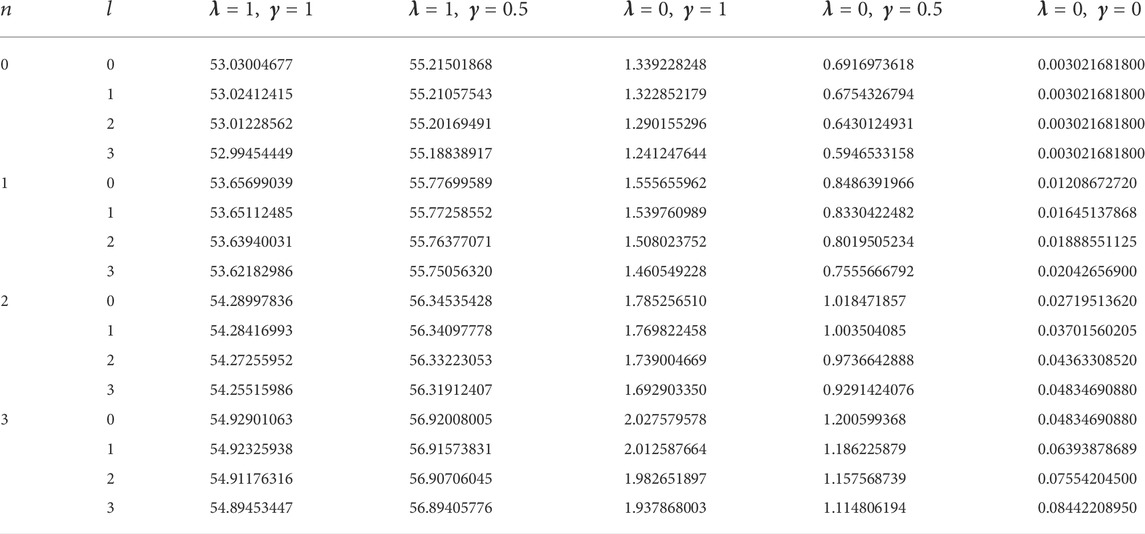
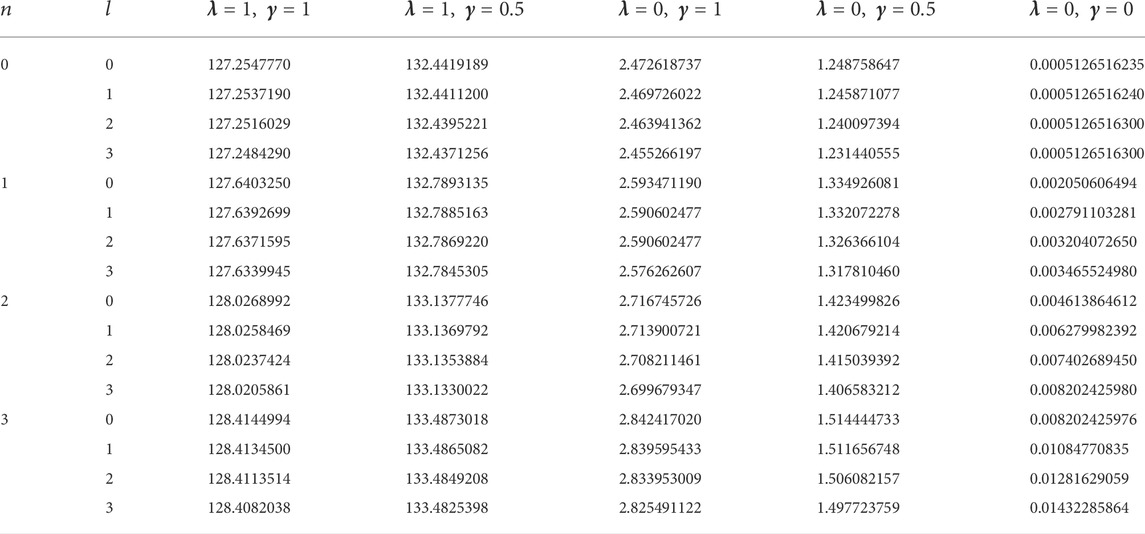
In this study, four diatomic molecule systems were considered. The spectroscopic parameters for the selected molecules are presented in Table 1, as obtained from Ref. [45]. The analytical expression for the energy eigenvalues of the SSKP model is given in Eq. (18). Numerical energy results of the SSKP for the selected diatomic molecules have been computed using the Maple software protocols. These results are presented in Tables 2–5, for various combinations of the shifted parameters. It is worth mentioning here that the following conversions have been adopted throughout our computations:
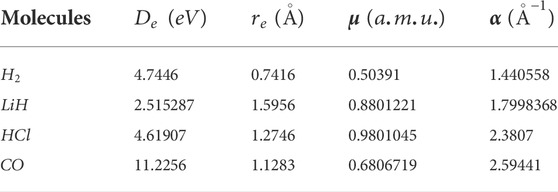
TABLE 1. Spectroscopic parameters for the selected diatomic molecule systems [45].
The variations of the energy eigenvalues of the SSKP with different potential parameters and quantum numbers were considered. Throughout our graphical analysis, the following quantum numbers have been adopted:
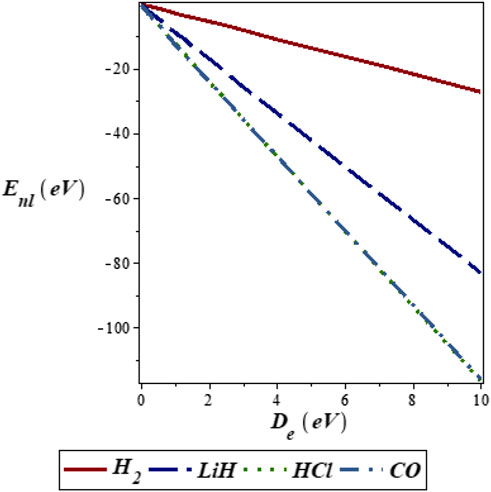
FIGURE 1. Variation of energy eigenvalues of the SSKP with dissociation energy for different diatomic molecule systems with n = 2 and l = 1.
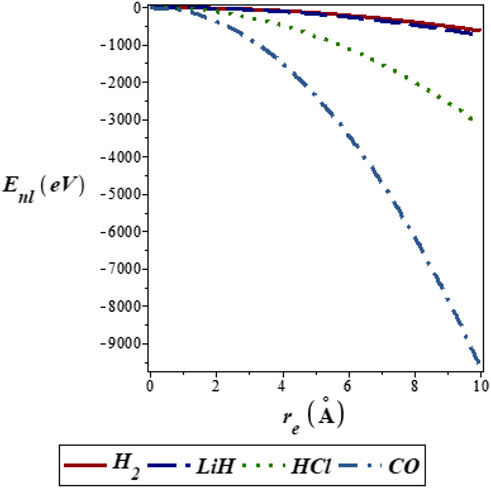
FIGURE 2. Variation of energy eigenvalues of the SSKP with equilibrium bond length for different diatomic molecule systems with n = 2 and l = 1.
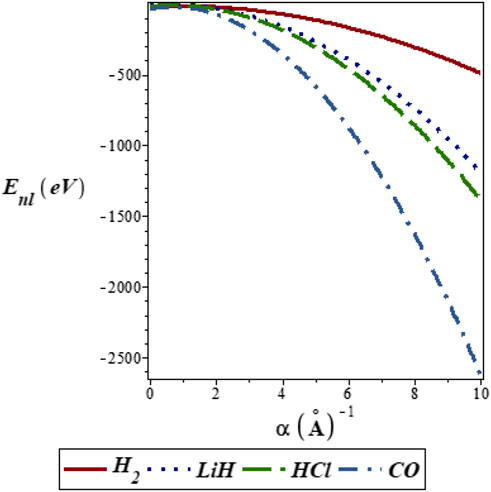
FIGURE 3. Variation of energy eigenvalues of the SSKP with screening parameters for different diatomic molecule systems with n = 2 and l = 1.
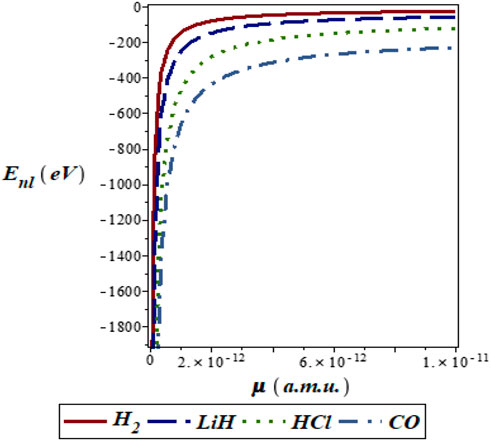
FIGURE 4. Variation of energy eigenvalues of the SSKP with reduced mass for different diatomic molecule systems with n = 2 and l = 1.
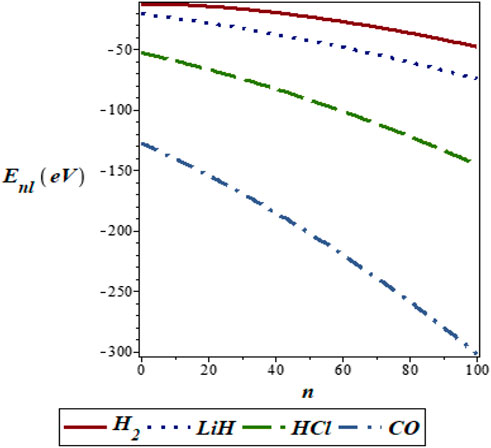
FIGURE 5. Variation of energy eigenvalues of the SSKP with vibrational quantum number for different diatomic molecule systems with l = 1.
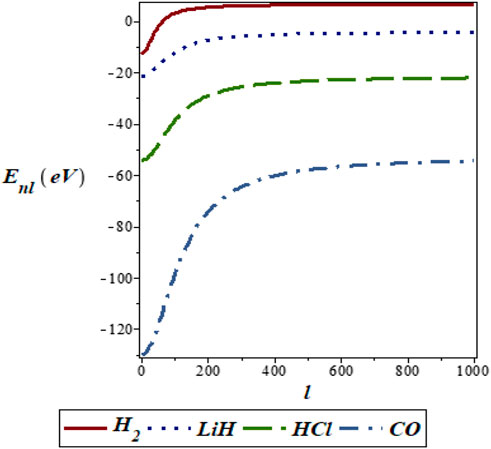
FIGURE 6. Variation of energy eigenvalues of the SSKP with rotational quantum number for different diatomic molecule systems with n = 2.
Furthermore, the variation of different thermodynamic properties of the SSKP with both temperature and maximum quantum number has been evaluated. These were done with the help of the partition function expression obtained in Eq. 24 and other thermodynamic expressions given in Eq. 25.
In Figure 7, we observe a sharp decrease in the partition function of the SSKP at zero temperature for the
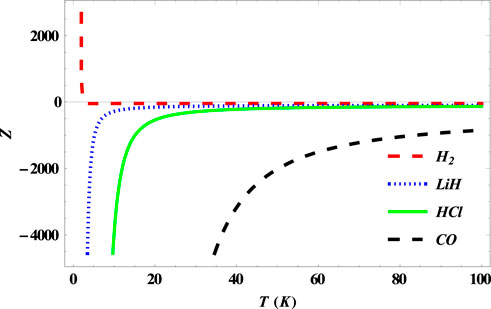
FIGURE 7. Variation of the partition function of the SSKP with temperature for different diatomic molecule systems with n = 2 and l = 1.
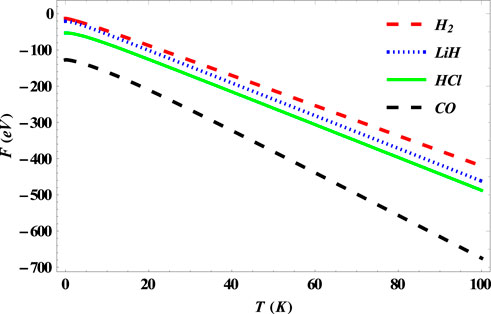
FIGURE 8. Variation of free energy of the SSKP with temperature for different diatomic molecule systems with n = 2 and l = 1.
In Figure 9, there exists a monotonous decrease in the internal energy of the SSKP for the selected diatomic molecule systems toward zero as the temperature increases.
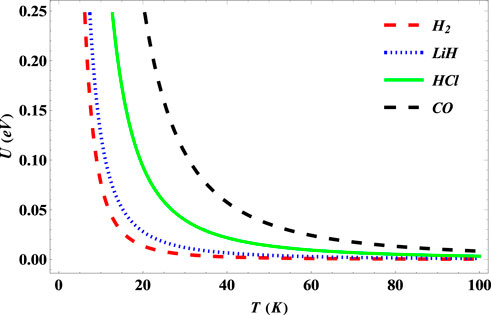
FIGURE 9. Variation of internal energy of the SSKP with temperature for different diatomic molecule systems with n = 2 and l = 1.
The plot of entropy of the SSKP with temperature is shown in Figure 10 for the diatomic molecule systems considered. Here, the entropies of the diatomic molecules increase to unique values, corresponding to a selected diatomic molecule system at a particular temperature. This temperature value corresponding to the peak values of entropy is called the critical temperature. As the temperature increases further, the entropy values begin to decrease gradually. With further increase in the temperature, the entropy of the selected systems remains constant.
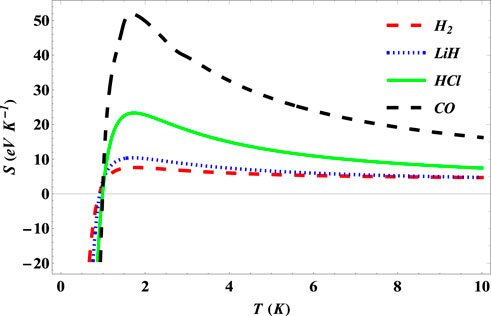
FIGURE 10. Variation of entropy of the SSKP with temperature for different diatomic molecule systems with n = 2 and l = 1.
The specific heat capacities of the SSKP for the selected diatomic molecules are seen to increase monotonously as the temperature increases first (Figure 11). With further increase in the temperature beyond a certain value, the specific heat capacity values for the molecule systems considered remain constant around zero.
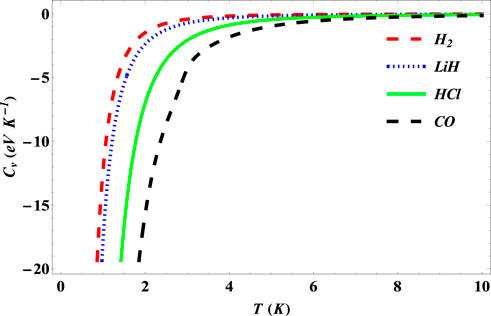
FIGURE 11. Variation of the specific heat capacity of the SSKP with temperature for different diatomic molecule systems with n = 2 and l = 1.
Figure 12 shows the variation of the partition function of the SSKP with maximum vibration quantum number for the selected molecule systems. The partition function here increases with an increase in the maximum vibration quantum number. In Figure 13, the free energy of the SSKP for the selected molecule systems decreases monotonously with the increase in the maximum vibration quantum number. The variation of the internal energy of the SSKP for the different diatomic molecule systems is shown in Figure 14. In this plot, the internal energies for the selected molecule systems first increase slowly at a particular value of the maximum vibration quantum number. With the further enhancement of the maximum vibration quantum number, the internal energies of these diatomic systems begin to decrease monotonously at different paces. Figure 15 shows a monotonous increase in the entropy of the SSKP for the different diatomic molecule systems as the maximum vibration quantum number increases.
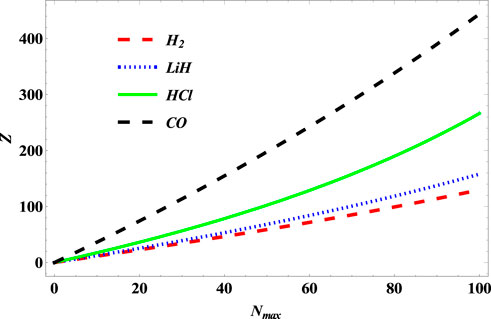
FIGURE 12. Variation of the partition function of SSKP with maximum vibration quantum number for different diatomic molecule systems with n = 2 and l = 1.

FIGURE 13. Variation of free energy of the SSKP with maximum vibration quantum number for different diatomic molecule systems with n = 2 and l = 1.
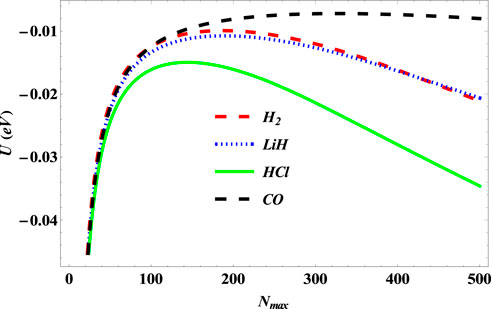
FIGURE 14. Variation of internal energy of the SSKP with maximum vibration quantum number for different diatomic molecule systems with n = 2 and l = 1.

FIGURE 15. Variation of entropy of the SSKP with maximum vibration quantum number for different diatomic molecule systems with n = 2 and l = 1.
In Figure 16, the specific heat capacity of the SSKP is also seen to increase with the increase in the maximum vibration quantum number for the diatomic molecule systems considered. Our results obtained are seen to agree perfectly with previous studies [34], as regards the selected diatomic molecule systems [44].
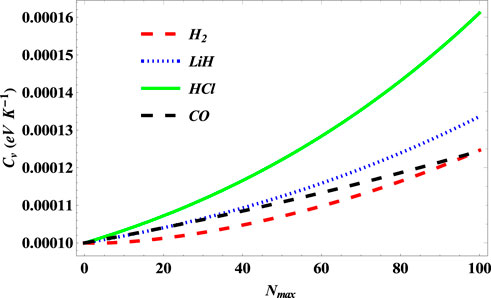
FIGURE 16. Variation of specific heat capacity of the SSKP with maximum vibration quantum number for different diatomic molecule systems with n = 2 and l = 1.
Concluding remarks
In this work, the extended Nikiforov–Uvarov method (ENU) was employed to solve the radial Schrodinger equation for the shifted screened Kratzer potential (SSKP) model and its analytical expression of energy eigenvalues was obtained. With the help of the energy eigenvalues, the expression for the partition function and other thermodynamic properties’ expressions were obtained using the exact method. In this study, four different diatomic molecule systems were employed. These were hydrogen dimer, lithium hydride molecule, hydrogen chloride molecule, and carbon monoxide molecule. With the help of spectroscopic parameters of the selected diatomic molecule systems extracted from available literatures, numerical results of energies of the SSKP were obtained at different quantum states and shifted parameters. The shifted parameters were seen to have a great effect on the energy eigenvalues obtained. In addition, variations of the energy eigenvalues of the SSKP with different potential parameters and quantum numbers were analyzed graphically.
Furthermore, the variations of the partition function and other thermodynamic properties of the SSKP with respect to temperature and maximum vibration quantum number for the diatomic molecule systems considered were studied graphically. The major result obtained lies in the existence of the critical temperature for each of the diatomic molecule system considered. From our results, the SSKP model can be employed to predict the thermochemical properties of different diatomic molecule systems. It is our future intention to study the higher dimensional energies of these diatomic molecule systems in the relativistic regime.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All the authors contributed to the manuscript as follows: 1) NI conceptualized the idea. 2) UO wrote the first draft and computed the thermodynamic functions. 3) NS carried out the literature analysis. 4) MR discussed all the results. 5) GR conducted the proof reading and corrected all the necessary corrections.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Appendix A: Extended Nikiforov–Uvarov method
The extended Nikiforov–Uvarov (ENU) method was proposed by [6, 38, 39] as an extended form of the Nikiforov–Uvarov (NU) method to transform Schrodinger-like equations into a second-order differential equation which has at most four singular points that can be solved analytically. The ENU method is defined as
where
the basic equation given by Eq. A1 becomes a hypergeometric-type equation
Eq. A3 has a particular polynomial solution of the form
with
Here,
with
The polynomials
and
where
According to the condition that polynomial
where
But, if and only if
References
2. Liu JY, Zhang GD, Jia CS. Calculation of the interaction potential energy curve and vibrational levels for the state of molecule. Phys Lett A (2013) 377:1444–7. doi:10.1016/j.physleta.2013.04.019
3. Nikiforov AF, Uvarov VB, Special functions of mathematical physics (Germany: Birkhauser Verlag Basel), A Jaffe, 317 (1988).
4. Ciftci H, Hall RL, Saad N. Construction of exact solutions to eigenvalue problems by the asymptotic iteration method. J Phys A: Math Gen (2005) 38:1147–55. doi:10.1088/0305-4470/38/5/015
5. Ikot AN, Okorie US, Amadi PO, Edet CO, Rampho GJ, Sever R. Few body syst, 62. Berlin, Germany: Springer (2020). p. 9.
6. Karayer H, Demirhan D, Buyukkilic F. Extension of Nikiforov-Uvarov method for the solution of Heun equation. J Math Phys (2015) 56:063504. doi:10.1063/1.4922601
7. Witten E. Dynamical breaking of supersymmetry. Nucl Phys B (1981) 188:513–54. doi:10.1016/0550-3213(81)90006-7
8. Ma ZQ, Xu BW. Quantum correction in exact quantization rules. Europhys Lett (2005) 69:685–91. doi:10.1209/epl/i2004-10418-8
9. Castro E, Paz JL, Martin P. Analytical approximations to the eigenvalues of the Morse potential with centrifugal terms. J Mol Struct THEOCHEM (2006) 769:15–8. doi:10.1016/j.theochem.2005.11.034
10. Jia CS, Diao YF, Liu XJ, Wang PQ, Liu JY, Zhang GD. Equivalence of the Wei potential model and Tietz potential model for diatomic molecules. J Chem Phys (2012) 137:014101. doi:10.1063/1.4731340
11. Jia CS, Yi LZ, Long SW. Relationship of the deformed hyperbolic Kratzer-like and Tietz potential energy models for diatomic molecules. Can J Phys (2014) 92:1258–61. doi:10.1139/cjp-2013-0684
12. Gao J, Zhang MC. Analytical solutions to the D-dimensional Schrödinger equation with the Eckart potential. Chin Phys Lett (2016) 33:010303. doi:10.1088/0256-307X/33/1/010303
13. Liu L, Rana J, Liao S. Analytical solutions for the hydrogen atom in plasmas with electric, magnetic, and Aharonov-Bohm flux fields. Phys Rev E (2021) 103:023206. doi:10.1103/physreve.103.023206
14. Solaimani M, Dong SH. Quantum information entropies of multiple quantum well systems in fractional Schrödinger equations. Int J Quan Chem (2020) 120:e26113. doi:10.1002/qua.26113
15. Shi YJ, Sun GH, Tahir F, Ahmadov AI, He B, Dong SH. Quantum information measures of infinite spherical well. Mod Phys Lett A (2018) 33:1850088. doi:10.1142/s0217732318500888
16. Isonguyo CN, Oyewumi KJ, Oyun OS. Quantum information-theoretic measures for the static screened Coulomb potential. Int J Quan Chem (2018) 118:025620. doi:10.1002/qua.25620
17. Onate CA, Ikot AN, Onyeaju MC, Ebomwonyi O, Idiodi JOA. Effect of dissociation energy on Shannon and Rényi entropies. Karbala Int J Mod Sci (2018) 4:134–42. doi:10.1016/j.kijoms.2017.12.004
18. Amadi PO, Ikot A. N, Ngiangia AT, Okorie US, Rampho GJ, Abdullah HY. Shannon entropy and Fisher information for screened Kratzer potential. Int J Quan Chem (2020) 120:e26246. doi:10.1002/qua.26246
19. Chabi K, Boumali A. Thermal properties of three dimensional Morse potential for some diatomic molecules via Euler-Maclaurin approximation. Rev Mex Fis (2020) 66:110–20. doi:10.31349/revmexfis.66.110
20. Ikot AN, Azogor W, Okorie US, Bazuaye FE, Onyeaju MC, Onate CA, et al. Exact and Poisson summation thermodynamic properties for diatomic molecules with shifted Tietz potential. Indian J Phys (2019) 93:1171–9. doi:10.1007/s12648-019-01375-0
21. Edet CO, Okorie US, Osobonye G, Ikot AN, Rampho GJ, Sever R. Thermal properties of Deng–Fan–Eckart potential model using Poisson summation approach. J Math Chem (2020) 58:989–1013. doi:10.1007/s10910-020-01107-4
22. Okorie US, Ikot AN, Onyeaju MC, Chukwuocha EO. A study of thermodynamic properties of quadratic exponential-type potential in D-dimensions. Rev Mex Fis (2018) 64:608–614.
23. Okorie US, Ikot AN, Chukwuocha EO, Rampho GJ. Thermodynamic properties of improved deformed exponential-type potential (IDEP) for some diatomic molecules. Results Phys (2020) 17:103078. doi:10.1016/j.rinp.2020.103078
24. Jia CS, Zhang LH, Wang CW. Thermodynamic properties for the lithium dimer. Chem Phys Lett (2017) 667:211–5. doi:10.1016/j.cplett.2016.11.059
25. Song XQ, Wang CW, Jia CS. Thermodynamic properties for the sodium dimer. Chem Phys Lett (2017) 673:50–5. doi:10.1016/j.cplett.2017.02.010
26. Jia CS, Wang CW, Zhang LH, Peng XL, Zeng R, You XT. Partition function of improved Tietz oscillators. Chem Phys Lett (2017) 676:150–3. doi:10.1016/j.cplett.2017.03.068
27. Al-Jamel A. Saturation in heavy quarkonia spectra with energy-dependent confining potential in N-dimensional space. Mod Phys Lett A (2018) 32:1850185. doi:10.1142/s0217732318501857
28. Chaturvedi R, Rai AK. Charmonium spectroscopy motivated by general features of pNRQCD. Int J Theor Phys (Dordr) (2020) 59:3508–32. doi:10.1007/s10773-020-04613-y
29. Kher V, Rai AK. Spectroscopy and decay properties of charmonium. Chin Phys C (2018) 42:083101. doi:10.1088/1674-1137/42/8/083101
30. Ibekwe EE, Okorie US, Emah JB, Inyang EP, Ekong SA. Mass spectrum of heavy quarkonium for screened Kratzer potential (SKP) using series expansion method. Eur Phys J Plus (2021) 136:87. doi:10.1140/epjp/s13360-021-01090-y
31. Qiang WC, Hong-Hong C. Ab initio calculations of electronic structure of anatase TiO 2. Chin Phys (2004) 13:2121–5. doi:10.1088/1009-1963/13/12/025
32. Rampho GJ, Ikot AN, Edet CO, Okorie US. Energy spectra and thermal properties of diatomic molecules in the presence of magnetic and AB fields with improved Kratzer potential. Mol Phys (2021) 119:e1821922. doi:10.1080/00268976.2020.1821922
33. Ikot AN, Okorie US, Sever R, Rampho GJ. Eigensolution, expectation values and thermodynamic properties of the screened Kratzer potential. Eur Phys J Plus (2019) 134:386. doi:10.1140/epjp/i2019-12783-x
34. Ikot AN, Okorie US, Rampho GJ, Amadi PO, Edet CO, Akpan IO, et al. Klein–gordon equation and nonrelativistic thermodynamic properties with improved screened kratzer potential. J Low Temp Phys (2021) 202:269–89. doi:10.1007/s10909-020-02544-w
35. Onate CA, Onyeaju MC, Ikot AN, Ebomwonyi O. Eigen solutions and entropic system for Hellmann potential in the presence of the Schrödinger equation. Eur Phys J Plus (2017) 132:462. doi:10.1140/epjp/i2017-11729-8
36. Zhang LH, Li XP, Jia CS. Approximate solutions of the Schrödinger equation with the generalized Morse potential model including the centrifugal term. Int J Quan Chem (2011) 111:1870–8. doi:10.1002/qua.22477
37. Greene RL, Aldrich C. Variational wave functions for a screened Coulomb potential. Phys Rev A (Coll Park) (1976) 143:2363–6. doi:10.1103/physreva.14.2363
38. Karayer H, Demirhan D, Buyukkilic F. Solution of Schrödinger equation for two different potentials using extended Nikiforov-Uvarov method and polynomial solutions of biconfluent Heun equation. J Math Phys (2018) 59:053501. doi:10.1063/1.5022008
39. Karayer H, Demirhan D, Buyukkilic F. Some special solutions of biconfluent and triconfluent heun equations in elementary functions by extended nikiforov–uvarov method. Rep Math Phys (2015) 76:271–81. doi:10.1016/s0034-4877(15)00039-7
40. Servatkhah M, Khordad R, Ghanbari A. Accurate prediction of thermodynamic functions of H2 and LiH using theoretical calculations. Int J Thermophys (2020) 41:37. doi:10.1007/s10765-020-2615-0
41. Horchani R, Jelassi H. Effect of quantum corrections on thermodynamic properties for dimers. Chem Phys (2020) 532:110692. doi:10.1016/j.chemphys.2020.110692
42. Khordad R, Ghanbari A. Theoretical prediction of thermodynamic functions of TiC: Morse ring-shaped potential. J Low Temp Phys (2020) 199:1198–210. doi:10.1007/s10909-020-02368-8
43. Ikot AN, Chukwuocha EO, Onyeaju MC, Onate CA, Ita BI, Udoh ME. Thermodynamics properties of diatomic molecules with general molecular potential. Pramana - J Phys (2018) 90:22. doi:10.1007/s12043-017-1510-0
44. Osobonye GT, Adekanmbi M, Ikot AN, Okorie US, Rampho GJ, Pramana J. Thermal properties of anharmonic Eckart potential model using Euler–MacLaurin formula. Pramana - J Phys (2021) 95:98. doi:10.1007/s12043-021-02122-z
Keywords: shifted screened Kratzer potential (SSKP), extended Nikiforov–Uvarov (ENU) method, partition function, entropy, diatomic molecule system
Citation: Ibrahim N, Okorie US, Sulaiman N, Rampho GJ and Ramantswana M (2022) Solutions of the Schrodinger equation of the shifted screened Kratzer potential and its thermodynamic functions using the extended Nikiforov–Uvarov method. Front. Phys. 10:988279. doi: 10.3389/fphy.2022.988279
Received: 07 July 2022; Accepted: 28 July 2022;
Published: 02 September 2022.
Edited by:
Akpan Ndem Ikot, University of Port Harcourt, NigeriaReviewed by:
Reza Khordad, Yasouj University, IranAkaninyene Daniel Antia, University of Uyo, Nigeria
Copyright © 2022 Ibrahim, Okorie, Sulaiman, Rampho and Ramantswana. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Uduakobong Sunday Okorie, dWR1YWtvYm9uZ29rb3JpZUBha3N1LmVkdS5uZw==
 Nuhu Ibrahim
Nuhu Ibrahim Uduakobong Sunday Okorie
Uduakobong Sunday Okorie Nidhal Sulaiman3
Nidhal Sulaiman3 Gaotsiwe Joel Rampho
Gaotsiwe Joel Rampho