High brilliance γ-ray generation from the laser interaction in a carbon plasma channel

The generation of collimated, high brilliance γ-ray beams from a structured plasma channel target is studied by means of 2D PIC simulations. Simulation results reveal an optimum laser pulse duration of 20 fs for generating photon beams of brilliances up to 10²⁰ s⁻¹mm⁻¹mrad⁻² (0.1 %BW)⁻¹ with photon energies well above 200 MeV in the interaction of an ultra-intense laser (incident laser power P_L ≥ 5 PW) with a high-Z carbon structured plasma target. These results are aimed at employing the upcoming laser facilities with multi-petawatt (PW) laser powers to study the laser-driven nonlinear quantum electrodynamics processes in an all-optical laboratory setup.

1 Introduction

Plasma-based short-wavelength radiation sources have attracted significant attention in past decades, since plasmas enable not only a compact size but also a wide range of physical mechanisms to generate short-wavelength radiations, be it high-harmonic generation, synchrotron radiation, or betatron radiation mechanisms; [1–6]. These highly energetic photon sources have numerous applications for the fundamental research of radiation-reaction force, generation of electron-positron (e⁻e⁺) pairs, photospectroscopy, radiotherapy, and radiosurgery [1]. The main advantage of using laser–plasma interaction for generating short-wavelength radiation sources is to only require an all-optical setup for the experimental realization. With a continued push for increasing the laser intensity further into a regime where radiation reaction and pair-production effects become important, the possibility of generating highly energetic γ-rays in an all-optical setup is becoming an exciting experimental prospect.

Recently, it has been shown that the use of structured plasma targets, for example, a cylindrical target acting as an optical waveguide, is optimal for accelerating electrons and consequently generating γ-photons [7–13]. This scheme is analogous to the betatron radiation generation in an ion channel [2,6,14–16]. However, here, the self-generated magnetic field of the electron beam accelerated in the channel not only causes the generation of γ photons but also enhances the yield of these photons, especially in the so-called radiation-dominated regime. Thus, this scheme not only produces higher yields of γ-photons, but also the self-generated magnetic field helps in collimating the two photon beams generated around the laser propagation axis. This high directionality of the photon beams can be exploited for producing electron–positron pairs by the Breit–Wheeler process in colliding two γ-ray beams setup in a laboratory [11]. Key findings of the scheme are that for high-Z, for example, carbon plasmas at incident powers in the range P_L ≤ 5 PW, the laser-to-photon energy conversion efficiency drops for incident laser power in the excess of P_L ≈ 5 PW [11]. Also, the efficiency of the γ photons generation seems to peak around τ ∼ 45 fs laser pulse duration for laser powers P_L ≤ 10 PW at laser intensity I_L = 5 × 10²² W/cm² [11]. At this laser intensity, radiation reaction can be modeled classically and stochastic effects involved in quantum radiation reaction are negligible[17].

The upcoming laser facilities such as ELI and others 18–21] are expected to provide multi-petawatt laser systems. These multi-petawatt laser systems are to rely on short laser pulse durations τ ∼ 20 fs, as significantly increasing the energy contained in the laser pulse is challenging due to technical reasons associated with material damage, etc. Thus, it is instructive to examine the generation of γ-photons with much shorter laser pulses, for example, τ ≤ 45 fs. Also, these multi-petawatt laser pulses can be focused to smaller beam radii $\le 10\mu$m resulting in laser intensities (I_L ≥ 1 × 10²³ W/cm²) that can enter the so-called quantum-electrodynamic regime, in which radiation reaction has a stochastic nature and it significantly affects the electron dynamics and consequently, γ-photon generation. Moreover, generation of pair-production can also be important in this regime. Motivated by these considerations, we study the generation of γ-photons in a laser–plasma channel, for the laser power exceeding P_L = 5 PW. The plasma channel used is a structured carbon plasma target and the laser pulse has the intensity I_L = 2.65 × 10²³ W/cm². Further, we also chose a conical plasma channel to optimize the generation of γ-photons since conical-shaped targets provide higher laser to plasma electron energy conversion efficiencies [9]. We carry out all simulations for both target geometries for 20 fs and 40 fs pulse durations.

The remainder of this article is organized as follows: in Section 2, we discuss the simulation setup and plasma dynamics and the physical process of γ photon generation. In sections 3.2 and 3.3, we show results from planar and conical plasma channels, respectively. In Section 3.4, we compare our results with previous simulation results. Finally, we conclude the discussions in Section 4.

2 Materials and methods

We carry out 2D particle-in-cell (PIC) simulations, employing the open-source PIC code SMILEI [22]. The simulation domain is 120 × 8 μm (x × y) with a cell size of 0.02 × 0.01 μm simulating a time period of T_sim ≈ 2,500 fs, divided into timesteps of Δt ≈ 0.02 fs. A linearly polarized laser pulse with wavelength λ_L = 0.8 μm impinges on a structured carbon ion plasma target located at x ≥ 10 μm from the left boundary. We use 16 particles per cell for electrons as well as ions. To ensure quasi-neutrality in our simulation, the ion density is chosen to be n_i = n_e/6, where n_e is the plasma electron density. Open boundary conditions are used in the x-direction, while periodic boundary conditions are employed in the y-direction. The laser pulse has a normalized amplitude a₀ = eE₀/mω₀c = eA₀/m_ec² = 350 (corresponding laser intensity I_L ≈ 2.65 × 10²³ W cm⁻²), and a pulse duration of τ = 40 fs as well as τ = 20 fs (measured at FWHM), where e is the electronic charge, c is the velocity of light in vacuum, E₀ (A₀) and ω₀ are the laser electric field (vector potential) and frequency, respectively. The core of the plasma channel has density n_e,ch = 37 n_cr, while the surrounding bulk plasma is denser n_e,B = 184 n_cr, as also simulated before [8,10]. Here, n_cr = m_eω₀/4πe² is the non-relativistic critical plasma density. This type of plasma channel can either be created using modern techniques (see [23]) or they can arise dynamically due to the action of ponderomotive force associated with the laser pre-pulse. The laser pulse has a 2D-Gaussian spatial distribution, and it was focused on the center of the channel’s opening at x = 10 μm and y = 4 μm from the left boundary of the simulation box. To maximize the energy conversion from the laser pulse to plasma electrons, the waist of the pulse w₀ in the focal plane was chosen to be equal to the channel’s entrance radius w₀ = R₀. On increasing the laser waist-radius, one can scan the power dependence $P_L=\pi w_0^2{I}_0/2=\pi R_0^2{I}_0/2$, in our simulations, where I₀ is the peak laser intensity. The first set of simulations was carried out for a planar target that represents a longitudinal cross-section of a cylindrical target with a constant channel radius R(x) = R₀. For a conical target, the radius varies as R(x) = R₀ − (R₀ − R_exit) (x − 10 μm)/L, for x ≥ 10 μm, where L = 110 μm is the channel length and R₀ and R_exit = 0.25 μm for all incident laser powers. In total, the experiment consists of two sets of four simulations. We scanned the incident power for P_L = [5, 10, 15, 20] PW for laser pulse durations of τ = 20 and 40 fs.

The laser pulse parameters were chosen in such a way that they were broadly consistent with the upcoming laser systems at ELI facility, which aim to investigate laser-driven quantum-electrodynamic processes. SMILEI employs a fully stochastic quantum Monte Carlo model of photon emission and pair generation by the Breit–Wheeler process (see [24,25]). The probability of photon generation and pair-creation can be simplified considerably if some assumptions can be enforced, for example, ultra-relativistic particle motion; the electromagnetic field experienced by particles in their rest frames is less intense than the critical Schwinger field and varies slowly over the formation time of a photon, and radiation emission by particle is incoherent [26]. These assumptions are always satisfied in the PIC simulations carried out here. The photon-emission and pair-creation are fundamentally a random-walk process [25–28]. One assigns initial and final optical depths (between 0 and 1) to a photon. This optical depth is allowed to evolve in time following particle motion in the laser field. The time evolution of the optical depth is equal to the production rate of pairs in the laser field [24]. When the final optical depth is reached, a photon is allowed to be emitted by the algorithm. The parameters of emitted particles can be obtained by inverting the cumulative probability distribution function of the respective species (see [27,29]). Production of e⁻e⁺ pairs from photons also utilizes a similar procedure, and pairs are expected to be emitted along the photon propagation direction (see [24]).

2.1 Filamentation of the laser pulse in a plasma channel

As one increases the incident laser power at a fixed laser intensity, the focal spot of the laser pulse increases. For high laser power (and large laser spot-size), the laser pulse becomes susceptible to the laser filamentation instability [30–32]. This issue hitherto has not been discussed in the previous studies so far, even though the filamentary structures in electron plasma density are visible, and they are attributed to the current filamentation instabilities [10]. Transverse laser pulse filamentation can also affect the generation of γ-photons in a plasma channel. Thus, it is instructive to estimate the laser filament and choose the laser spot size which is smaller than the filament size due to the filamentation instability. For the purpose of estimating the filament size of a laser pulse in an underdense plasma, we use the well-known formalism of laser-driven parametric instabilities and use the envelope model of the laser pulse propagation. For including the radiation reaction force in the instability analysis, we follow the approach developed by Kumar et al. [17] by including the dominant term of the Landau–Lifshitz radiation reaction force. The equation of motion for an electron in the laser electric and magnetic fields including the leading order term of the Landau–Lifshitz radiation reaction force is

$\frac{\partial \mathit{p}}{\partial t}+\mathit{\upsilon }\cdot \nabla \mathit{p}=-e\left(\mathit{E}+\frac{1}{c}\mathit{\upsilon }\times \mathit{B}\right)-\frac{2e^4}{3m_e^2{c}^5}{\gamma }^2\mathit{\upsilon }\left[{\left(\mathit{E}+\frac{1}{c}\mathit{\upsilon }\times \mathit{B}\right)}^2-{\left(\frac{\mathit{\upsilon }}{c}\cdot \mathit{E}\right)}^2\right],(1)$

where $\gamma =1/\sqrt{1-{\mathit{\upsilon }}^2},e$ is the electronic charge, m_e is the electron mass, and c is the velocity of light in vacuum. The other terms of the Landau–Lifshitz radiation force are 1/γ times smaller than the leading order term [33].

For theoretical calculations, we use the circularly polarized laser pulse propagating in plasma. The relativistic motion of an electron in a linearly polarized laser pulse involves generation of high harmonics at the fundamental laser frequency. Due to this reason, the Lorentz factor γ of an electron is not constant in time, and analytical treatment of any laser-driven plasma processes becomes intractable in an ultra-relativistic regime. For circularly polarized laser pulse, the gamma factor is constant in time, and it enables analytically tractable results to showcase the influence of radiation reaction on the filamentation instability of a laser pulse in plasma. This has been also done by others in the past while investigating the parametric instabilities of laser pulse in plasmas. A quick comparison with the linearly polarized laser pulse can be made by rescaling the normalized vector potential a₀ as $a_0^{\text{LP}}=a_0^{\text{CP}}/\sqrt{2}$. We expressed the electric and magnetic fields in potentials using a Coulomb gauge in Eq.(1), and wrote the CP laser pulse as $\mathit{A}={\mathit{A}}_{\mathbf{0}}({\mathit{x}}_{\perp },z,t)e^{i{\psi }_0}/2+c.c$, where ψ₀ = k₀z − ω₀t. We assumed that the laser pulse amplitude varied slowly, that is, $\left|\partial {\mathit{A}}_0/\partial t\right|\ll \left|{\omega }_0{\mathit{A}}_0\right|,\left|\partial {\mathit{A}}_0/\partial z\right|\ll \left|k_0{\mathit{A}}_0\right|$, and $|\varphi |\ll |\mathit{A}|,{\omega }_p^2/\gamma {\omega }_0^2\ll 1$, and $\gamma ={(1+e^2|\mathit{A}{|}^2/m_e^2{c}^4)}^{1/2}$, ϕ being the electrostatic potential. We then wrote the transverse component of the quiver momentum from Eq.(1) as

$\frac{\partial }{\partial t}\left({\mathit{p}}_{\perp }-\frac{e}{c}\mathit{A}\right)=-\frac{e\mu {\omega }_0}{c}\mathit{A}\gamma |\mathit{A}{|}^2,(2)$

where ${\omega }_p={(4\pi n_e{e}^2/m_e)}^{1/2}$ is the non-relativistic plasma frequency, and $\mu =2e^4{\omega }_0/3m_e^3{c}^7$. We have assumed |μγ|A|²|≪ 1, which is valid for laser intensities I_L ≤ 10²³ W/cm², for which the influence of radiation reaction force has to be taken into account. The wave equation then reads as

${\nabla }^2\mathit{A}-\frac{1}{c^2}\frac{{\partial }^2\mathit{A}}{\partial t^2}=\frac{{\omega }_p^2}{\gamma c^2}\frac{c}{e}{\mathit{p}}_{\perp },(3)$

where A₀ is the amplitude of the envelope. On collecting the terms containing $e^{i{\psi }_0}$, Eq.(3) yields the dispersion relation for the equilibrium vector potential as ${\omega }_0^2=k_0^2{c}^2+{\omega }_p^{\prime 2}\left(1-i\mu |A_0{|}^2{\gamma }_0/2\right)$, where ${\gamma }_0={(1+e^2{A}_0^2/2m_e^2{c}^4)}^{1/2}$ is the equilibrium Lorentz factor, and ${\omega }_p^{\prime }={(4\pi n_e{e}^2/m_e{\gamma }_0)}^{1/2}$ is the relativistic electron plasma frequency corresponding to the equilibrium propagation of the laser pump. It is evident from the dispersion relation that the radiation reaction term causes damping of the pump laser field. This damping can be incorporated either by defining a frequency or a wavenumber shift in the pump laser by defining a frequency shift of the form ω₀ = ω_0r − iΔω₀, Δω₀ ≪ ω_0r (real part of ω₀) with the frequency shift Δω₀ being $\mathrm{\Delta }{\omega }_0={\omega }_p^{\prime 2}\epsilon {\gamma }_0{a}_0^2/2{\omega }_{0r}$, where ɛ = r_eω_0r/3c, and r_e = e²/m_ec² is the classical radius of the electron. Eq.(3) in the envelope approximation can be expanded as

$2i{\omega }_0\frac{\partial A_0}{\partial t}+c^2{\nabla }_{\perp }^2{A}_0+\frac{{\omega }_p^2}{{\gamma }_0}\left(1-\frac{i\mu |A_0{|}^2{\gamma }_0}{2}\right)A_0=\frac{{\omega }_p^2}{\gamma }\left(1-\frac{i\mu |A{|}^2\gamma }{2}\right)A,(4)$

The left hand side of Eq.(4) represents the equilibrium propagation of the laser pulse in an envelope approximation. While the right hand side of Eq.(4) is the source of perturbation for the filamentation instability. Following the approach in Kumar et al. [32], we wrote A₀ (x_⊥, z, t) = A₀ + δA (x_⊥, z, t), δA = δA_r + iδA_i, and δA_r, δA_i ∼ exp (iq_⊥x_⊥ − iδωt). This yields two equations for real and imaginary parts of perturbation amplitudes δA_r and δA_i, yielding the growth rate Γ = Im (δω) − Δω₀, as

$\mathrm{\Gamma }\approx \frac{q_{\perp }{c}^2}{4{\omega }_0^2}{\left[\frac{{\omega }_p^2{a}_0^2}{2{\gamma }_0^3}-q_{\perp }^2{c}^2\right]}^{1/2}-\frac{\epsilon a_0^2{\omega }_p^2}{{\omega }_0}.(5)$

From here, the reduction in the filamentation growth rate is apparent. Thus, radiation reaction unlike in the case of stimulated Raman scattering [17] does not enhance the growth of the filamentation instability. This is not unexpected since the enhancement in the case of stimulated Raman scattering depends on the simultaneous resonant excitations of Stokes and anti-Stokes modes in the plasma. Radiation reaction force causes mixing of these modes, leading to a higher growth rate of the stimulated Raman scattering. The spatial filamentation instability, as discussed here, is a broadband instability since the growth can occur over a large range of frequencies. Since the mixing of two distinct modes is absent for filamentation instability, radiation reaction does not lead to the enhanced growth rate of filamentation instability but plays the role of a damping force in a plasma. From this equation, we find the filament size to be $q_{\perp }^{-1}\approx (c/\sqrt{2}{\omega }_p)a_0$. For our setup (linearly polarized laser pulse) with a₀ = 350 and n_e,ch = 37n_cr, this yields an approximate size of $q_{\perp }^{-1}\sim 7.3\mu \mathrm{m}$. We expect strong filamentation for a spot-size or channel width exceeding $q_{\perp }^{-1}$, resulting in the loss of efficiency in high-energy photon production. Simulation setup in all cases (also in Heppe [34]) has a spot-size smaller than optimum filament size given by the above scaling to improve the photon generation especially for the pulse duration τ = 20 fs.

3 Results

First, we qualitatively discuss and recapitulate the plasma dynamics involved in the generation of the ultra-strong magnetic field and the high-energy photon emission. Afterwards, we show results on the photon beam properties from a 2D planar target and then from a conical target. The plasma physical processes involved remain qualitatively true for both targets.

3.1 Plasma dynamics and MeV photon emission

The general features of the plasma dynamics involved in the generation of γ-photons qualitatively show similar behavior as discussed before [8,10,11,34]. The laser pulse can accelerate plasma electrons to very high energy in this plasma channel via direct laser acceleration [9]. The current associated with these so-called hot electrons often exceed the so-called Alfvénic current. Consequently, a return plasma current is excited which compensates for the hot electron current and enables their transportation inside the plasma. The magnetic field B_z associated with the hot-electrons can help in generating energetic photons and enables a large laser energy conversion into γ-photons. If these accelerated hot-electrons have transverse dimensions of ∼ c/ω_p, where ω_p is the background plasma frequency corresponding to the surrounding bulk plasma, then a filamentation by the counter-propagating background plasma current also ensues [35]. Since the return plasma current filamentation is associated with the bulk plasma density, the generated quasi-static magnetic field due to the filamentation instability exceeds the magnetic field generated by the forward-moving relativistic electrons in the plasma channel and dominates the generation of high-energy γ-photons by the synchrotron emission mechanism [8,10]. This radiated synchrotron power P_rad is proportional to the emissivity parameter η, that is, P_rad ∝ η². This parameter η reads as

$\eta \equiv \frac{\gamma }{E_s}\sqrt{{\left(\mathbf{E}+\frac{1}{c}\left(\mathbf{v}\times \mathbf{B}\right)\right)}^2-\frac{1}{c^2}{\left(\mathbf{E}\cdot \mathbf{v}\right)}^2},(6)$

where γ is the Lorentz factor for electron; v, its velocity; E and B are local electric and magnetic fields, and E_s ≈ 1.3 × 10¹⁸ Vm⁻¹ is the so called Schwinger field. If one were to only consider the laser electric (E_L) and magnetic (B_L) fields in Eq. 6, the parameter η would be close to zero on account of the Doppler-shifted electric field experienced by the hot-electrons in their rest frame, co-propagating with the laser. However, the plasma magnetic field (B_p) generated due to hot-electrons and dominantly by the return current filamentation can facilitate a non-zero value of the parameter η since now B = B_L + B_p and despite the Doppler shift cancellation of laser electric and magnetic fields, one still has B_p facilitating a non-zero value of η. Consequently, MeV photon generation in a plasma channel can ensue. One may also note that pair-production by these γ-photons in the presence of ultra-intense magnetic fields can also occur. For the parameters considered here, we see negligible pair-production in our simulations. This is in sync with previous PIC simulations. Figure 1 (see also the movie in Supplementary Material) shows the electron density n_e, the azimuthal magnetic field B_z, and a composite figure of n_e (grey) overlaid by the synchrotron emissivity factor η ≥ 0.0004 (red), shortly after the laser pulse hits the target. Due to the ponderomotive force, there is an accumulation of the plasma electron density at the boundary of the channel [13]. The fluctuations associated with the plasma channel boundaries are presumably due to hosing type instabilities associated with the laser pulse propagation in a plasma channel. The plasma electrons become relativistic quickly due to direct laser acceleration [9,13,36]. In the centre of the plasma channel, a strong forward current associated with the electrons is generated [9]. These electrons generate a strong and quasi-static azimuthal magnetic field B_z up to the order of B₀ ∼ 4–7 MT as it propagates along the target’s symmetry axis. As these electrons propagate through the channel, they excite a return plasma current along the plasma channel boundary. As discussed before, the filamentation of the current also causes the generation of quasi-static ultra-strong magnetic field. Since this magnetic field is caused by the Weibel-type filamentation instabilities, it is quasi-static (owing to the Weibel-type instability being aperiodic in a collision-less plasma; see Kumar et al. [35]) and does not propagate deeper into the plasma, as seen in Figure 1B (see also the Supplementary Material). This can be verified from Figure 2 where the strongest radiation emission is shown to occur in the overlapping area of the magnetic field and the high η factor closer to the target surface.

FIGURE 1

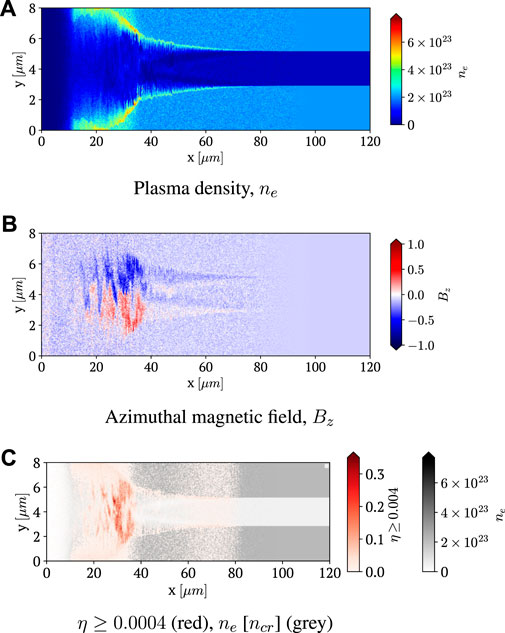
FIGURE 1. (A) Plasma electron density in the units of n_cr, (B) azimuthal magnetic field strength B_z in units of B₀ of the laser field and (C) Plasma electron density (grey) overlaid with emission parameter η ≥ 0.0004 (red) for a simulation with a laser pulse P_L = 5 PW, τ = 40 fs and a₀ = 350 hitting a planar target of C6⁺ plasma at around t ≈ 1400 fs.

FIGURE 2

FIGURE 2. Synchrotron emission parameter η along the symmetry axis (y =4 μm) of the plasma channel over time for simulations of a τ =40 fs laser pulse with incident power P_L =5 PW and a normalized amplitude a₀=350. The colorbar indicates the synchrotron emission power parameter η (6), and is limited to values up to η_max =0.005 (higher values are depicted as η_max) to enhance visibility.

The high-energy photon emission shows a broader angular distribution, albeit with the presence of two well-defined peaks situated around ±45° from the laser propagation direction in the channel as visible in Figure 3. From Figure 3, we can see that high-energy photons (≳ 50 MeV) are concentrated in these two peaks. This occurrence of two peak’s spectra has also been noted before for the case of linearly polarized laser pulse propagation in plasmas [10,37]. The physical reason for two lobes in the case of linearly polarized laser pulse stems from the fact that the laser field attains absolute maximum twice in a laser cycle, causing significant electron heating twice in the same laser cycle. This results in two distinct lobes of radiation emission. While in the case of a circularly polarized laser field, the maximum absolute electric field remains constant in a laser cycle and one only sees a single lobe of emitted radiation [12]. From now onwards, while discussing the properties of the γ-photon beams, we only consider photons emitted within one emission lobe at Φ = 45° ± 10°.

FIGURE 3

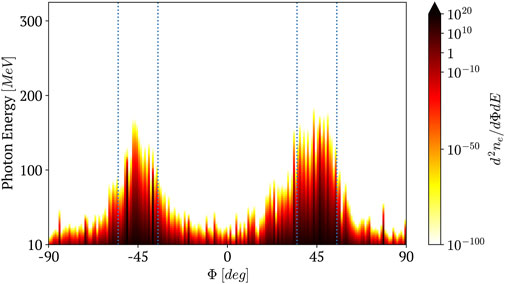
FIGURE 3. Angular distribution of the photon energy spectrum in degree with respect to the channel’s symmetric axis in MeV for a simulation with a laser pulse P_L =5 PW, τ =40 fs, and a₀=350, hitting a cylindrical target of C⁶⁺ plasma, averaged over the duration of the simulation. The dotted blue line indicates the beams defined as the emission cone at Φ =±45°±10°.

Figure 4 shows fractional efficiency of laser-to-photon energy conversion (ɛ) with the laser pulse duration for the incident laser power P_L = 10 PW for the planar target. The choice of P_L = 10 PW becomes clear later while comparing the brilliance of the photon beams. Evidently, the efficiency peaks for the laser pulse duration τ = 20 fs. This is attributed to plasma instabilities associated with the laser pulse propagation not being dominant for the short laser pulse duration of τ = 20 fs. However, for longer laser pulse duration, one can expect the generation of higher energy γ-photons. Thus, from now onwards, we show the γ-photons spectra for two laser pulse durations, for example, τ = 20 and τ = 40 fs.

FIGURE 4

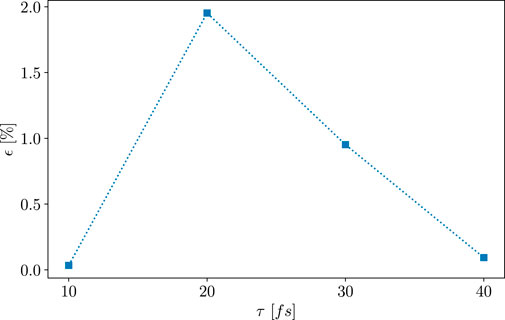
FIGURE 4. τ-scan for a 10 PW laser pulse with a₀=350, regarding conversion efficiency into a collimated high-energy γ-ray beam $(\ge 10\text{MeV})$ with beam width Δθ =20° in percentages for a cylindrical C⁶⁺-ion plasma target.

3.2 Planar target

Figure 5 shows the photon spectra generated for the different laser powers and pulse lengths. The maximum energy emitted by a photon increases with the incident laser power with maximum photon energy emitted $\ge 250$ MeV for P_L = 10 PW laser power. The emitted photon spectra do not show significant deviations with laser power at different pulse lengths.

FIGURE 5

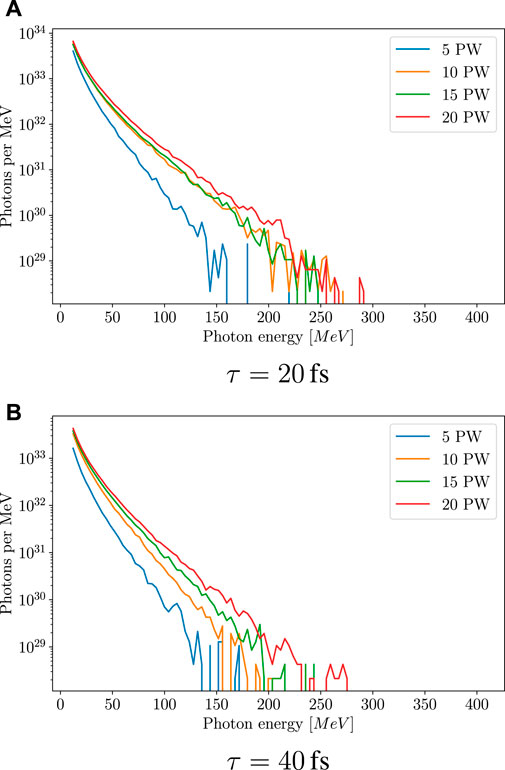
FIGURE 5. Photon emission spectra for photons with energies $\ge 5\text{MeV}$, for a₀=350 laser impacting a planar target C⁶⁺-plasma target. (A) τ = 20 fs and (B) τ = 40 fs

To quantify the quality of the emissions regarding the collimated beams, we take a look at the two distinct radiation lobes as seen in Figure 3. Here, we consider all photons emitted with energies $\ge 1\text{MeV}$ within the angular range described before, that is, only considering one of the two photon beams emitted. Tables 1, 2 give a summary of the brilliance of this single photon beam as well as the laser to collimated γ-ray photon beam (ϵ) energy conversion efficiencies for different laser powers. For a γ-ray photon beam with a cut-off of 1 MeV photon energy, the recorded brilliances are higher for the laser pulse duration τ = 20 fs compared to the pulse duration τ = 40 fs, except for P_L = 10 PW case (see Tables 1, 2). This observation is particularly important. On one hand, the use of a longer laser pulse duration can enhance the highest γ-photon-emitted energy as seen in Figures 5, 6. Moreover, the brilliances for 10 MeV cut-off photon energies are also better for the shorter laser pulse duration τ = 20 fs at all incident laser powers except for P_L = 10 PW. The lower brilliance for τ = 40 fs laser pulse duration is on account of these γ-photons being not as tightly collimated in the angular range Δθ = 20°. This clearly points to the deleterious role of other plasma instabilities such as hosing instability on the radiation emission. The hosing instability can cause laser focus to jitter along the equilibrium propagation direction, resulting in a wide angular radiation emission spectrum. These plasma instabilities associated with the laser propagation are dominant for longer laser pulse durations and consequentially, strongly affect the brilliances for longer pulse duration case. The brilliance of the photon beams seems to be weakly dependent on ϵ. This is presumably due to the higher abundance of low-energy (ϵ_γ ≪ 1 MeV) photons in the lobe. A similar trend is also noted for longer laser pulse duration, for example, τ = 40 fs (see Table 2). The brilliances for 10 MeV photon beam are considerably lower than those for 1 MeV photon beams. This is attributed to the following two reasons: first, relatively low numbers of higher γ-photon ($\ge 10$MeV) generation compared to 1 MeV photons, and second, the spatial distribution of these 10 MeV photons not confined to a small angular range used to record the brilliance. One can also see from Tables 1, 2, that the normalized photon counts ${\tilde{N}}_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}$ normalized to the photon count from the P_L = 5 PW case first show higher photon yields and then start saturating. However, the brilliances of both 1 and 10 MeV γ-photons peak at P_L = 20 PW, hinting that γ-photons are largely generated in a small angular range (Δθ = ±10° around one lobe). The highest γ-ray photon brilliance recoded, that is, $\sim 4.00\times 10^{20}{\text{s}}^{-1}{\text{mm}}^{-1}{\text{mrad}}^{-2}{(0.1\%\text{BW})}^{-1}$ for photon energy cut-off 1 MeV and $\sim 4.38\times 10^{18}{\text{s}}^{-1}{\text{mm}}^{-1}{\text{mrad}}^{-2}{(0.1\%\text{BW})}^{-1}$ for photon energy cut-off 10 MeV are sufficient for the observation of pair-generation due to linear Breit–Wheeler and photon–photon scattering processes envisaged in the upcoming projects [38–40].

TABLE 1

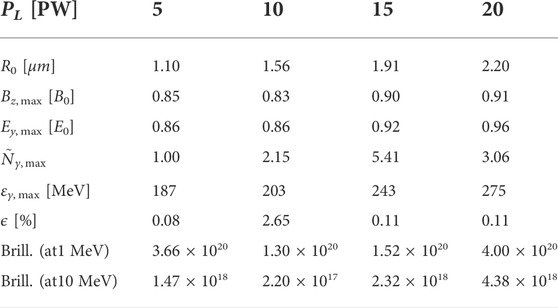
TABLE 1. Table of characteristic simulation results for the planar target with a₀=350 laser pulse of duration τ =20 fs, rounded to second digit, except maximum photon energy ɛ_γ,max. Maximum values depict the overall maximum of that value during the whole simulation. ${\tilde{N}}_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}=N_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}/N_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}^{5\mathrm{P}\mathrm{W}}$ is the maximum photon count during the simulation normalized to the 5 PW case. Brilliance (Brill.) is in units of s⁻¹mm⁻¹mrad⁻²(0.1%BW)⁻¹ with the chosen bandwidth energy corresponding to the energies referred.

TABLE 2

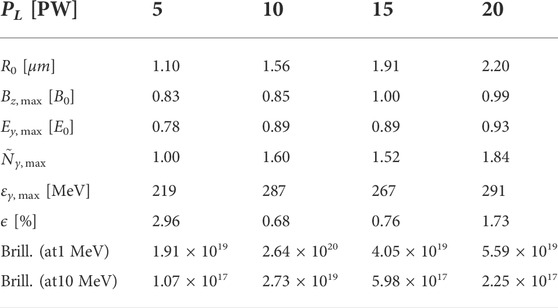
TABLE 2. Table for quantities as in Table 1 but for the laser pulse duration τ =40 fs. The normalized laser pulse amplitude remains the same a₀=350 as in Table 1.

FIGURE 6

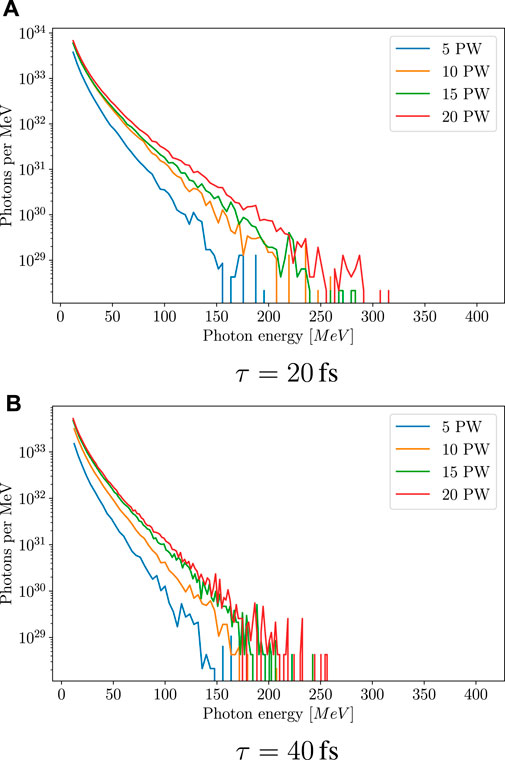
FIGURE 6. Photon emission spectra for photons with energies $\ge 5\text{MeV}$, for a₀=350 laser impacting a conical C⁶⁺-plasma target. (A) τ = 20 fs (B) τ = 40 fs

3.3 Conical target

Figure 6 shows the photon energy spectra for a conical target. The total number of photons is of the same order of magnitude as for the planar target around $\sim 10^{33}{\text{MeV}}^{-1}$. Tables 3, 4 summarize the brilliance for γ-ray beams generated for both 1 and 10 MeV cut-off energies. The conical target, for the laser pulse duration τ = 20 fs, does show higher fraction conversion efficiency of the laser energy to the collimated photon beam. However, this higher fraction does not yield a comparable higher photon brilliance compared to that of the planar target case, as seen in from Table 3. This is again attributed to generation of photons with energies lower than ≪ 1 MeV, which are not shown in Figure 6. However, as in the case of a planar target, one sees the optimal laser pulse duration appears to be τ = 20 fs for generating γ-ray beams of highest brilliance for all incident laser powers and both cut-off energies. The highest brilliance in this case is slightly lower than the planar target case, see Table 1. The enhanced laser energy coupling to electrons in the conical target case (see Yu et al. [41]) does not yield comparable higher photon brilliances. The normalized photon count ${\tilde{N}}_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}$, as shown in Tables 3 and 4, shows a linear increase in photon counts with higher laser power, but the brilliance of the γ-photons does not drastically improve at higher laser power P_L = 20 PW. This suggest that though an efficient laser energy conversion to photons occurs, the laser pulse is subjected to strong jitter, presumably associated with hosing type instabilities, causing the γ-photons to be generated in a large angular range, thereby reducing the brilliance of the γ-photon beam.

TABLE 3

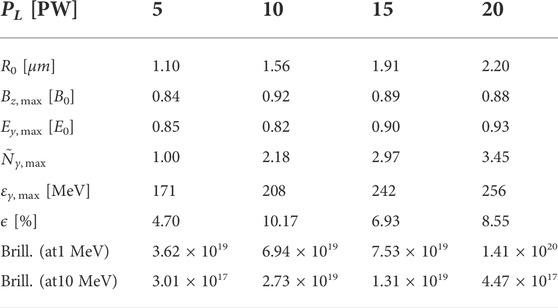
TABLE 3. Table of quantities for a conical target with a₀=350 and the laser pulse duration τ =20 fs.

TABLE 4

TABLE 4. Table of quantities for a conical target as in Table 3 but for the laser pulse duration τ =40 fs.

3.4 Comparison

Our results show similar trends as observed before for heavier plasma ions. For a more intense a₀ = 468, λ = 1 μm pulse with a 15 fs duration using a structured target made of hydrogen plasma and pre-ionized gold [42] achieved brilliance levels of $\sim 10^{24}{\text{s}}^{-1}{\text{mm}}^{-1}{\text{mrad}}^{-2}{(0.1\%\text{BW})}^{-1}$ at photon energies of 58 MeV and generation of photons with maximum energies up to 1.5 GeV. However, the energy conversion in their case lies around 1.45%, which is considerably lower than the highest energy conversion we have observed in our simulations, especially for the conical target, namely, 4% ≲ϵ_beam ≲ 10% using the 20 fs pulse (see Table 3). Similarly, Xue et al. [37] showed that for a₀ = 150, λ = 1 μm pulse of duration τ ≈ 40 fs and brilliance levels of $\sim 10^{21}{\text{s}}^{-1}{\text{mm}}^{-1}{\text{mrad}}^{-2}{(0.1\%\text{BW})}^{-1}$ at 1 MeV can be achieved for a similarly structured target consisting of hydrogen plasma surrounded by Al³⁺ bulk plasma. We observed brilliances of an order of lower magnitude, but this is comparable to the results shown in Figure 7 for hydrogen targets (see Heppe [34]). In a second set of simulations shown by Xue et al. [37], Au-cones filled with a hydrogen plasma produced a two-lobe γ-ray beam with energies up to $\le 420\text{MeV}$ with brilliances of $\sim 10^{21}{\text{s}}^{-1}{\text{mm}}^{-1}{\text{mrad}}^{-2}{(0.1\%\text{BW})}^{-1}$ again at 1 and 10 MeV photon cut-off energies. Also, Wang et al. [43] showed for a₀ = 100, λ = 1 μm, pulse duration τ = 30 fs, and Au⁺⁶⁹-plasma with electron density n_e = 276 n_cr, generations of photons with energy up to $\sim 1.5\text{GeV}$. The generated photon beams had a brilliance of 2.9 × 10²¹ s⁻¹mm⁻¹mrad⁻² (0.1 %BW)⁻¹ at 1 MeV, which is very similar to that in our results. In our simulations carried out before Heppe [34] with similar laser settings (a₀ = 190, λ = 0.8 μm and τ = 40 fs) using the same 2D-cylindrical target but consisting of hydrogen-plasma yielded the same two-lobe distribution we see in Figure 3. Lastly, we can directly compare the case for P_L = 10 PW with the results of Wang et al. [11]; as for all other simulations, the incident power stayed in the regime of P_L ≲ 10 PW in their simulations. Here, using a laser pulse with a₀ = 190, λ = 1 μm, and τ = 35 fs, Wang et al. [11] showed maximum photon energies of $\sim 450\text{MeV}$, while observing a decrease in laser-to-photon energy conversion efficiencies for the incident laser power P_L ≃ 4 PW; a similar trend is also observed in Figure 7 for hydrogen plasmas (see Heppe [34])

FIGURE 7

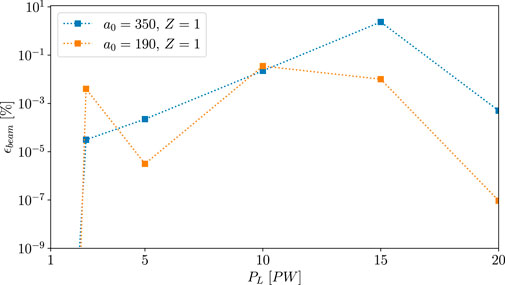
FIGURE 7. Conversion efficiency of the laser energy (τ =40 fs) impacting a Z =1 H⁺-plasma into a high-energy γ-ray beam $(\ge 10\text{MeV})$ with a beam width of ΔΘ =20° in percentages of the total energy for simulations carried out for Heppe [34].

We also compare our results with theoretical predictions on maximum electron energies by Jirka et al. [36], who derived scalings on electron acceleration in the radiation-dominated regime in a plasma channel. As argued by Jirka et al. [36], radiation-reaction force can significantly alter the plasma electron dynamics, and in a best case scenario, electron acceleration to ultra-high energies can occur, as also studied earlier [2,3,9]. Thus, comparing the analytical scalings of electron acceleration by Jirka et al. [36] with the inferred values of the electron energies via synchrotron radiation emission in our simulations is instructive. In our simulations, the condition $E_{\text{field}}\ll E_{\text{channel}}/\mathcal{I}$ is fulfilled. Here, $\mathcal{I}$ denotes the integral of motion including the corrections caused by radiation-reaction force, as defined by Jirka et al. [36],

${\mathcal{I}}_0=1+{\left[\frac{{\omega }_p{\mathfrak{R}}_0}{2c}\right]}^2(7)$

$\mathcal{I}={\mathcal{I}}_0{\left[1+2.3\times 10^{-8}{a}_0^2\frac{{\mathcal{I}}_0}{{\lambda }_0\left[\mu \mathrm{m}\right]}\right]}^{-1}(8)$

${\mathcal{I}}_0$ is the integral of motion without including the radiation reaction force, and ${\mathfrak{R}}_0$, the initial rest distance of the observed electron to the channel center. The mean energy of an electron reads as Jirka et al. [36],

$⟨{\gamma }_{\star }⟩\approx 3/4{\mathcal{I}}^2{\left(\frac{{\omega }_0}{{\omega }_p}\right)}^2,(9)$

Assuming these electrons emit photons by the well-known synchrotron emission, one can write

${\gamma }_{e,\mathrm{m}\mathrm{a}\mathrm{x}}\approx \sqrt{\frac{m_{e}c{\epsilon }_{\gamma ,\mathrm{m}\mathrm{a}\mathrm{x}}}{\hslash eB}},$

where ɛ_γ,max are the maximum measured photon energies as they are denoted in Tables 1 and Figure 3, and we assumed B ≈ B₀, which is approximately in line with the observed field strengths. To compare the predictions with the observations, we plotted their ratio in Figure 8. Interestingly, for low-incident powers of p = 5 PW, our simulations yield photon energies that require electron energies to be $\sim 1.4$ times more than the analytical predictions. The divergence between the analytical scaling and the simulations results on electron acceleration become larger for increasing P. This suggests that additional mechanisms come into the play, that is, the filamentation of the laser pulse as seen in Figure 2. Stronger laser filamentation of the laser pulse can significantly reduce the bulk electron acceleration in the plasma channel. This requires a more thorough investigation in the future. We also observed that 2D simulations can overestimate the energies of accelerated electrons and as a consequence, the resulting photon energies [43].

FIGURE 8

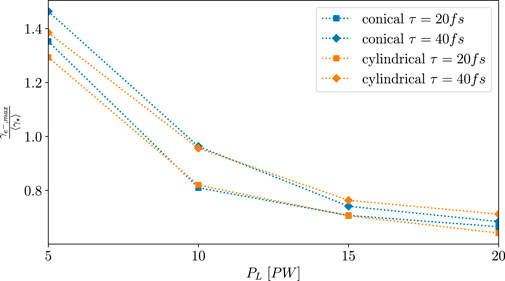
FIGURE 8. Ratio of predicted electron Lorentz factor γ_⋆,max using Eq. 9 to γ_e,max the observed/measured Lorentz factor as function of incident power P_L

4 Discussion and conclusion

We have shown that for incident laser powers (in the range 5–20 PW), one can efficiently convert the laser energy into the photon beams with energies up to $\sim 300\text{MeV}$ in carbon plasmas. The resulting photon beams have brilliances exceeding 10²⁰s⁻¹mm⁻¹mrad⁻² (0.1 %BW)⁻¹, with a single-digit fraction of the laser-to-photon energy conversion efficiencies. Thus, the hitherto unexplored regime of powerful petawatt laser system P_L ≥ 10 PW to generate collimated γ-ray beams appears to be promising. A major result is that the short laser pulse duration τ = 20 fs is preferable over longer pulse duration τ = 40 fs for a large range of incident laser powers. The trend with respect to the laser-to-photon beam conversion efficiencies for incident laser powers is non-linear, strongly hinting at the role of the plasma instabilities associated with the laser pulse propagation in a plasma channel.

We find that the stronger Coulomb forces due to heavier carbon ions reduce the electron acceleration and photon energies compared to the case of hydrogen plasmas. Hence, our results for C⁶⁺-ion plasma (for τ = 40 fs, a₀ = 350) are comparable to the results using a₀ = 190 propagating in a hydrogen plasma channel as shown in Figure 7. Further, we show that the conical target in simulations yields higher laser-to-electron energy conversion efficiency, but it does not strongly improve the angular distribution of the generated photon beams and consequently, their brilliances.

To summarize, we have shown the generation of γ-ray beams with maximum brilliance exceeding 10²⁰ s⁻¹mm⁻¹mrad⁻² (0.1 %BW)⁻¹ for τ = 20 fs for photons with 1 MeV explicitly favoring the shorter pulse length of 20 fs. We have investigated the generation of γ-photons for the laser power P_L > 10 PW in the quantum-electrodynamics regime, where the photon generation is a stochastic effect. For further improvement, the impact of different target compositions, that is, solid shell for the channel instead of bulk plasma [37,42], might offer a way to further improve coupling between laser and plasma electrons as well as the guidance for the accelerated electrons, to improve the photon generation.

4.1 Permission to reuse and copyright

Figures, tables, and images will be published under a Creative Commons CC-BY license, and permission must be obtained for use of copyrighted material from other sources (including re-published/adapted/modified/partial figures and images from the internet). It is the responsibility of the authors to acquire the licenses, to follow any citation instructions requested by third-party rights holders, and cover any supplementary charges.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

NK conceived the project and suggested to CH. CH carried out and analyzed the PIC simulations and discussed the results with NK. NK carried out the theoretical analysis of the filamentation instability. Both authors contributed to the manuscript writing.

Acknowledgments

Results presented here are an extension of the bachelor thesis of CH, submitted to the Heidelberg University; Heppe [34].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.987830/full#supplementary-material

Abbreviations

2D, two-dimensional; PIC, particle-in-cell; keV, kilo electron volt; MeV, mega electron volt; PW, petawatt; FWHM, full-width at half-maximum; BW, bandwidth; MT, mega Tesla.

References

1. Mourou GA, Tajima T, Bulanov SV. Optics in the relativistic regime. Rev Mod Phys (2006) 78:309–71. doi:10.1103/revmodphys.78.309

CrossRef Full Text | Google Scholar

2. Rousse A, Phuoc KT, Shah R, Pukhov A, Lefebvre E, Malka V, et al. Production of a kev x-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys Rev Lett (2004) 93:135005. doi:10.1103/PhysRevLett.93.135005

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kumar N, Tripathi VK. Effect of betatron resonance on plasma wave acceleration of electrons in an ion channel. Europhys Lett (2006) 75:260–6. doi:10.1209/epl/i2006-10110-1

CrossRef Full Text | Google Scholar

4. Liu C, Shen B, Zhang X, Ji L, Bu Z, Wang W, et al. Ultra-bright, well-collimated, gev gamma-ray production in the qed regime. Phys Plasmas (2018) 25:023107. doi:10.1063/1.5005077

CrossRef Full Text | Google Scholar

5. Yu JQ, Hu RH, Gong Z, Ting A, Najmudin Z, Wu D, et al. The generation of collimated γ-ray pulse from the interaction between 10 pw laser and a narrow tube target. Appl Phys Lett (2018) 112:204103. doi:10.1063/1.5030942

CrossRef Full Text | Google Scholar

6. Ji LL, Pukhov A, Nerush EN, Kostyukov IY, Shen BF, Akli KU. Energy partition, γ-ray emission, and radiation reaction in the near-quantum electrodynamical regime of laser-plasma interaction. Phys Plasmas (2014) 21:023109. doi:10.1063/1.4866014

CrossRef Full Text | Google Scholar

7. Zhu X-L, Yin Y, Yu TP, Shao FQ, Ge ZY, Wang WQ, et al. Enhanced electron trapping and γ emission by ultra-intense laser irradiating a near-critical-density plasma filled gold cone. New J Phys (2015) 17:053039. doi:10.1088/1367-2630/17/5/053039

CrossRef Full Text | Google Scholar

8. Stark D, Toncian T, Arefiev A. Enhanced multi-mev photon emission by a laser-driven electron beam in a self-generated magnetic field. Phys Rev Lett (2016) 116:185003. doi:10.1103/PhysRevLett.116.185003

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Vranic M, Fonseca RA, Silva LO. Extremely intense laser-based electron acceleration in a plasma channel. Plasma Phys Control Fusion (2018) 60:034002. doi:10.1088/1361-6587/aaa36c

CrossRef Full Text | Google Scholar

10. Jansen O, Wang T, Stark DJ, d’Humières E, Toncian T, Arefiev AV. Leveraging extreme laser-driven magnetic fields for gamma-ray generation and pair production. Plasma Phys Control Fusion (2018) 60:054006. doi:10.1088/1361-6587/aab222

CrossRef Full Text | Google Scholar

11. Wang T, Ribeyre X, Gong Z, Jansen O, d’Humières E, Stutman D, et al. Power scaling for collimated γ-ray beams generated by structured laser-irradiated targets and its application to two-photon pair production. Phys Rev Appl (2020) 13:054024. doi:10.1103/PhysRevApplied.13.054024

CrossRef Full Text | Google Scholar

12. Luedtke SV, Yin L, Labun LA, Labun OZ, Albright BJ, Bird RF, et al. Creating qed photon jets with present-day lasers. Phys Rev Res (2021) 3:L032061. doi:10.1103/PhysRevResearch.3.L032061

CrossRef Full Text | Google Scholar

13. Huang TW, Zhou CT, Zhang H, Wu SZ, Qiao B, He XT, et al. Collimated gamma photon emission driven by pw laser pulse in a plasma density channel. Appl Phys Lett (2017) 110:021102. doi:10.1063/1.4973972

CrossRef Full Text | Google Scholar

14. Corde S, Ta Phuoc K, Lambert G, Fitour R, Malka V, Rousse A, et al. Femtosecond x rays from laser-plasma accelerators. Rev Mod Phys (2013) 85:1–48. doi:10.1103/revmodphys.85.1

CrossRef Full Text | Google Scholar

15. Mangles SPD, Walton BR, Tzoufras M, Najmudin Z, Clarke RJ, Dangor AE, et al. Electron acceleration in cavitated channels formed by a petawatt laser in low-density plasma. Phys Rev Lett (2005) 94:245001. doi:10.1103/PhysRevLett.94.245001

CrossRef Full Text | Google Scholar

16. Ji Y, Li B, Duan T, Zhou W, Wu F, Zhang Z, et al. Effects of plasma density on laser-generated energetic electron generation and transport in a plasma channel. Phys Plasmas (2018) 25:063114. doi:10.1063/1.5021108

CrossRef Full Text | Google Scholar

17. Kumar N, Hatsagortsyan KZ, Keitel CH. Radiation-reaction-force-induced nonlinear mixing of Raman sidebands of an ultraintense laser pulse in a plasma. Phys Rev Lett (2013) 111:105001. doi:10.1103/PhysRevLett.111.105001

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Aléonard M, Altarelli M, Antici P, Apolonskiy A, Audebert P, Bartnik A, et al. WHITEBOOK ELI – extreme light infrastructure; science and Technology with ultra-intense lasers (andreas thoss). Berlin: THOSS Media GmbH (2011). doi:10.13140/2.1.1227.0889

CrossRef Full Text | Google Scholar

19. Papadopoulos D, Zou J, Le Blanc C, Chériaux G, Georges P, Druon F, et al. The apollon 10 pw laser: Experimental and theoretical investigation of the temporal characteristics. High Pow Laser Sci Eng (2016) 4:e34. doi:10.1017/hpl.2016.34

CrossRef Full Text | Google Scholar

20.[Dataset]. Xcels (2017). Available from: https://xcels.iapras.ru.

Google Scholar

21.[Dataset]. Vulcan (2022). Available from: https://www.clf.stfc.ac.uk/Pages/Vulcan.aspx.

Google Scholar

22. Derouillat J, Beck A, Pérez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei : A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput Phys Commun (2018) 222:351–73. doi:10.1016/j.cpc.2017.09.024

CrossRef Full Text | Google Scholar

23. Fischer J, Wegener M. Three-dimensional optical laser lithography beyond the diffraction limit. Laser Photon Rev (2013) 7:22–44. doi:10.1002/lpor.201100046

CrossRef Full Text | Google Scholar

24.[Dataset]. The Monte Carlo algorithm for pair production, and related tables (2022). Available from: https://smileipic.github.io/Smilei/multiphoton_Breit_Wheeler.html (Accessed August 26, 2022).

Google Scholar

25.[Dataset]. The Monte Carlo algorithm for photon emission, and radiation tables (2022). Available from: https://smileipic.github.io/Smilei/radiation_loss.html (Accessed August 26, 2022).

Google Scholar

26. Nikishov A, Ritus V. Quantum processes in the field of a plane electromagnetic wave and in a constant field 1. Sov.Phys.JETP (1964) 1964:529–41.

Google Scholar

27. Duclous R, Kirk JG, Bell AR. Monte Carlo calculations of pair production in high-intensity laser–plasma interactions. Plasma Phys Control Fusion (2010) 53:015009. doi:10.1088/0741-3335/53/1/015009

CrossRef Full Text | Google Scholar

28. Kirk JG, Bell AR, Arka I. Pair production in counter-propagating laser beams. Plasma Phys Control Fusion (2009) 51:085008. doi:10.1088/0741-3335/51/8/085008

CrossRef Full Text | Google Scholar

29. Lobet M, Ruyer C, Debayle A, d’Humières E, Grech M, Lemoine M, et al. Ultrafast synchrotron-enhanced thermalization of laser-driven colliding pair plasmas. Phys Rev Lett (2015) 115:215003. doi:10.1103/PhysRevLett.115.215003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kaw P, Schmidt G, Wilcox T. Filamentation and trapping of electromagnetic radiation in plasmas. Phys Fluids (1973) 16:1522–5. doi:10.1063/1.1694552

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sheng ZM, Nishihara K, Honda T, Sentoku Y, Mima K, Bulanov SV. Anisotropic filamentation instability of intense laser beams in plasmas near the critical density. Phys Rev E (2001) 64:066409. doi:10.1103/PhysRevE.64.066409

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kumar N, Tripathi VK, Sawhney BK. Filamentation of a relativistic short pulse laser in a plasma. Phys Scr (2006) 73:659–62. doi:10.1088/0031-8949/73/6/021

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Landau LD, Lifshitz EM. The classical theory of fields, vol. 2 of course of theoretical Physics. fourth revised english edn. Oxford, UK: Butterworth-Heinemann (2005).

PubMed Abstract | Google Scholar

34. Heppe C. Short-wavelength radiation generation in ultra-relativistic laser-plasma interaction (Bachelor Thesis). In: Tech. rep. Heidelberg, Germany: Max-Planck-Institute for Nuclear Physics and Universität Heidelberg (2020).

Google Scholar

35. Kumar N, Karmakar A, Pukhov A, Shvets G. Interplay of collisions and temperature on the filamentary structures of a relativistic electron beam in plasmas. Eur Phys J D (2009) 55:415–20. doi:10.1140/epjd/e2009-00102-1

CrossRef Full Text | Google Scholar

36. Jirka M, Vranic M, Grismayer T, Silva LO. Scaling laws for direct laser acceleration in a radiation-reaction dominated regime. New J Phys (2020) 22:083058. doi:10.1088/1367-2630/aba653

CrossRef Full Text | Google Scholar

37. Xue K, Dou ZK, Wan F, Yu TP, Wang WM, Ren JR, et al. Generation of highly-polarized high-energy brilliant γ-rays via laser-plasma interaction. Matter Radiat Extremes (2020) 5:054402. doi:10.1063/5.0007734

CrossRef Full Text | Google Scholar

38. Abramowicz H, Acosta U, Altarelli M, Aßmann R, Bai Z, Behnke T, et al. Conceptual design report for the luxe experiment. Eur Phys J Spec Top (2021) 230:2445–560. doi:10.1140/epjs/s11734-021-00249-z

CrossRef Full Text | Google Scholar

39. He Y, Yeh IL, Blackburn TG, Arefiev A. A single-laser scheme for observation of linear breit–wheeler electron–positron pair creation. New J Phys (2021) 23:115005. doi:10.1088/1367-2630/ac3049

CrossRef Full Text | Google Scholar

40. Kettle B, Hollatz D, Gerstmayr E, Samarin GM, Alejo A, Astbury S, et al. A laser–plasma platform for photon–photon physics: The two photon breit–wheeler process. New J Phys (2021) 23:115006. doi:10.1088/1367-2630/ac3048

CrossRef Full Text | Google Scholar

41. Yu J, Zhou W, Cao L, Zhao Z, Cao L, Shan L, et al. Enhancement in coupling efficiency from laser to forward hot electrons by conical nanolayered targets. Appl Phys Lett (2012) 100:204101. doi:10.1063/1.4718735

CrossRef Full Text | Google Scholar

42. Gu YJ, Klimo O, Bulanov SV, Weber S. Brilliant gamma-ray beam and electron–positron pair production by enhanced attosecond pulses. Commun Phys (2018) 1:93. doi:10.1038/s42005-018-0095-3

CrossRef Full Text | Google Scholar

43. Wang T, Blackman D, Chin K, Arefiev A. Effects of simulation dimensionality on laser-driven electron acceleration and photon emission in hollow microchannel targets. Phys Rev E (2021) 104:045206. doi:10.1103/PhysRevE.104.045206

PubMed Abstract | CrossRef Full Text | Google Scholar