Thermophysical features of Ellis hybrid nanofluid flow with surface-catalyzed reaction and irreversibility analysis subjected to porous cylindrical surface

This study explores the flow irreversibility of the Ellis hybrid nanofluid (containing $CoF{e}_2{O}_4-Ti{O}_2$ nanoparticles) with homogeneous and heterogeneous reactions to a horizontal porous stretching cylinder. The energy transportation aspects are investigated in terms of the influence of joule heating and viscous dissipation. The slip and convective boundary conditions are levied on the cylindrical surface, and the mathematical flow model is transferred to a system of nonlinear ordinary differential equations using suitable transformations. The highly nonlinear systems of equations are numerically solved using the bvp4c approach in MATLAB. The graphical outcomes are obtained and discussed; it is worth noting that incremental estimations of the curvature parameter show opposite behaviors on the Ellis fluid velocity and entropy generation, i.e., the entropy generation profile increases while fluid velocity decreases. The boundary layer thinning shows resistance to impact by elasticity and magnetic field. Further, as the porosity of the liquid phase increases, the momentum of the boundary layer decreases.

Introduction

At present, the development of the human society depends mainly on energy transfer and energy sources. Improvements with regard to generation and utilization of energy can considerably affect the industrial and engineering fields. Advancements in energy transport mechanisms have been investigated, where the thermal capacitances of the base fluids (water, glycols, and engine oil) are boosted by mixing a nanofluid into them. Nanofluids are widely used for community service applications, such as solar cells, nuclear power plants, refrigerators, heat exchangers, and vehicles. Choi and Eastman [1] first proposed the idea of a nanofluid. Advanced and novel applications of nanofluids in domestic refrigerators, power engines, and chillers were then investigated [2]. The thermal and solutal energy transportation towards a stretching surface in a molybdenum disulfide nanoliquid was studied by Waqas et al. [3]. The heat and mass transport features of Cu- and Ag-water across a porous rotating disc affected by thermal radiation, partial slip, and chemical reactions were examined by Reddy et al. [4]. Krishna and Chamkha [5] surveyed the magnetohydrodynamic (MHD) free convective rotating flow of nanofluids (Ag and TiO₂) influenced by the Hall current as well as generation or absorption on a semi-infinite permeable moving plate. The application of the boundary layer flow to nanoparticles along uniform heat flux and heat transport in electronic chips was analyzed by Waqas et al. [6]. Moreover, theoreticians have reported similar studies [6–18]. Hybrid nanofluids are used to enrich the heat transport rates and thermal conductivities of conventional fluids; such hybrid nanofluids are formed by a mixture of nanoparticles immersed in a base fluid to improve the heat transport capacities of the convectional fluids. Turcu et al. [19] and Jana et al. [20] established the idea of hybrid nanofluids that boost the thermal capacitances of regular nanofluids. Devi and Devi [21] presented improved heat transport by distribution of a water-based aluminum oxide ($A{l}_2{O}_3$) and copper hybrid nanofluid subjected to a stretchable surface. The heat and mass transportation aspects of the $A{l}_{2}Cu/H_{2}O$ (alumina-copper/water) hybrid nanofluid toward the stretching cylinder was reported by Maskeen et al. [22]. The solutal and thermal transport features of the transient MHD hybrid nanofluid flow with thermal radiation, chemical reaction, and suction/injection across the extending surface reported by Sreedevi et al. [23]. Other substantial works regarding hybrid nanofluids have also been proposed [24–29].

Chemical reactions are typically categorized into two types as heterogeneous and homogeneous reactions. The processes of burning, fog formation and dispersion, and catalysis occur by such homogeneous and heterogeneous reactions. Homogeneous reactions occur at all phases, while heterogeneous reactions generally occur in confined patches. Chaudhary and Merkin [30] initially proposed the boundary layer flow along the heterogeneous–homogeneous reactions of an isothermal model. Ramzan et al. [31] investigated the electromagnetohydrodynamic hybrid nanofluid flow past two rotating disks along the homogeneous–heterogeneous reaction and its irreversibility analysis. Khan et al. [32] considered the cubic autocatalysis chemical reaction to investigate the flow of magnetized Oldroyd-B fluid across a stretching cylinder. Other investigators have also focused on the influences of the homogeneous–heterogeneous reactions in their recent works [33–38].

The energy losses during an irretrievable process are broadly called as entropy generation. The second law of thermodynamics is considered to measure the energy losses during such irretrievable procedures. Researchers have proposed various approaches to reduce energy losses. The operations of actual systems are unvaryingly related to work losses in accordance with the second law of thermodynamics [39]. Researchers who have investigated entropy generation [40, 41] have deeply analyzed the applications of entropy in several fields. The stagnation point flow of a hybrid nanofluid in the investigation of entropy generation across a stretching sheet was examined by Jakeer and Reddy [42]. Other studies on entropy generation may also be found in literature [43–47].

MHD considerations have many applications in engineering, such as electrical furnaces, nuclear reactors, installation of nuclear accelerators, turbo machinery, and blood flow, and many researchers have investigated their impacts. Ahmad et al. [48] demonstrated the 3D MHD Maxwell nanofluid flow towards a slendering stretching surface affected by joule heating, heat generation, and thermal radiation. Takhar et al. [49] investigated the time-dependent laminar boundary layer flow of an electrically conducting fluid along an aligned magnetic field toward a semi-infinite flat plate. Saeed et al. [50] considered the six-constant Jeffreys nanofluid in an asymmetric channel with inclined magnetic fields to examine the theoretical impact of slip barriers on double diffusion subject to peristaltic flow. The ion and Hall slip impacts on an unstable laminar MHD convective rotating flow of a second-grade fluid across a semi-infinite vertical moving permeable sheet were theoretically investigated by Krishna et al. [51]. Several other researchers [52–59] have also discussed the importance of MHD flows along various geometries.

The main purpose of this work is to explore the 2D boundary layer flow of the Ellis nanofluid (containing $CoF{e}_2{O}_4-Ti{O}_2$ nanoparticles) toward the horizontal porous stretching cylinder under convective and slip boundary conditions. The thermal and solutal transport aspects are investigated with respect to the impacts of viscous dissipation, joule heating, and homogeneous–heterogeneous reactions. The novelty and main contribution of this work involve examining the axisymmetric MHD Ellis hybrid nanofluid flow along homogeneous–heterogeneous reactions and entropy generation effect, which have not been considered in literature thus far. The basic equations developed here are represented as a system of ordinary differential equations (ODEs) using similarity variables. These ODEs are numerically solved using the bvp4c approach in MATLAB. The graphical conclusions are evaluated in terms of velocity, temperature, and homogeneous–heterogeneous (homo–hetero) profiles. Moreover, comparison of the current outcomes with previously reported numerical data shows good agreement.

Mathematical modeling

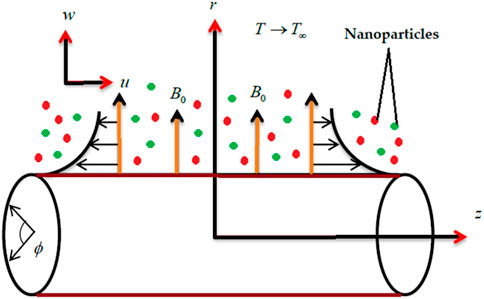
In the mathematical model, we consider a steady 2D laminar incompressible axisymmetric MHD Ellis hybrid nanofluid flow with $CoF{e}_2{O}_4-Ti{O}_2$ nanoparticles across a horizontal porous stretching cylinder. The homogeneous and heterogeneous chemical species are examined to assess the solutal energy transport. The thermal energy transport aspects are discussed under viscous dissipation and joule heating. Figure 1 illustrates that the $z-$axis is chosen as the cylindrical coordinate system and that the $r-$axis is perpendicular to the cylindrical surface. Here, we consider the fluid velocity as $u=u_w=\frac{z{u}_0}{L}$, where $u_0>\mathit{0}$ and $L$ is the length. $B_0$ is the magnetic field that is normal to the cylindrical surface. Additionally, the cylinder temperature is $T_w$ and ambient temperature is $T_{\infty }$.

FIGURE 1

FIGURE 1. Flow diagram of the problem.

The equation of the homo–hetero reaction process is stated as follows [30, 31]:

$C+2D\to 3D,rate=k_{c}a{b}^2.(1)$

The first-order isothermal single reaction is stated as

$C\to D,rate=k_{s}a.(2)$

Here, $C$ and $D$ are the substance species with concentrations $a$ and $b$, respectively. Moreover, $k_s$ and $k_c$ are the constant rates.

Using the above assumption and applying the boundary layer theory, the mathematical flow model is defined as [10, 31]

$\frac{\partial \left(ru\right)}{\partial z}+\frac{\partial \left(rw\right)}{\partial r}=0,(3)$

$u\frac{\partial u}{\partial z}+w\frac{\partial u}{\partial r}=\frac{1}{r{\rho }_{hnf}}\frac{\partial }{\partial r}\left(\frac{r{\mu }_{hnf}}{{\left(\frac{1}{\sqrt{2}{\tau }_0^2}\frac{\partial u}{\partial r}\right)}^{{\alpha }_1-1}+1}\right)-\frac{u}{{\rho }_{hnf}}\left(\frac{{\mu }_{hnf}}{K}+{\sigma }_{hnf}{B}_0^2\right),(4)$

$\begin{array}{l}u\frac{\partial T}{\partial z}+w\frac{\partial T}{\partial r}=\frac{{\alpha }_{hnf}}{r}\left(r\frac{{\partial }^{2}T}{\partial r^2}+\frac{\partial T}{\partial r}\right)+\frac{{\mu }_{hnf}}{{\left(\rho c_p\right)}_{hnf}}\frac{\partial }{\partial r}\left(\frac{1}{1+{\left(\frac{1}{\sqrt{2}{\tau }_0^2}\frac{\partial u}{\partial r}\right)}^{{\alpha }_1-1}}\right){\left(\frac{\partial u}{\partial r}\right)}^2+\frac{{\sigma }_{hnf}{B}_0^2}{{\left(\rho c_p\right)}_{hnf}}{u}^2,\end{array}(5)$

$\begin{array}{l}w\frac{\partial a}{\partial r}+u\frac{\partial a}{\partial z}=D_A^{*}\left(\frac{1}{r}\frac{\partial a}{\partial r}+\frac{{\partial }^{2}a}{\partial r^2}\right)-k_{1}a{b}^2-S{k}_{s}a,\end{array}(6)$

$w\frac{\partial b}{\partial r}+u\frac{\partial b}{\partial z}=D_B^{*}\left(\frac{1}{r}\frac{\partial b}{\partial r}+\frac{{\partial }^{2}b}{\partial r^2}\right)+k_{1}a{b}^2+S{k}_{s}a.(7)$

The appropriate conditions at the boundary are as follows [37]:

$u=-u_w+a_1\frac{\partial u}{\partial r},v=-V_w,T=T_w+c_1\frac{\partial T}{\partial r},\frac{\partial a}{\partial r}=\frac{k_{s}a}{D_A^{*}},\frac{\partial b}{\partial r}=-\frac{k_{s}a}{D_B^{*}},\mathrm{a}\mathrm{t}r=R.(8)$

$u\to 0,a\to a_0,b\to 0,T\to T_{\infty },\mathrm{a}\mathrm{t}r\to \infty (9)$

In Eqs. 3–9, the components of the velocity are $u,v,$ and $w$ in the directions $r,\theta ,$ and $z$, respectively. The symbols ${\rho }_{hnf}$, ${\mu }_{hnf}$, ${\sigma }_{hnf}$, $B_0$, $\left({\tau }_0,{\alpha }_1\right)$, ${\alpha }_{hnf}$, $c_p$, $\left(D_A^{*},D_B^{*}\right)$, $a_1$, $k_1$, and $c_1$ represent the hybrid nanofluid density, dynamic viscosity, electrical conductivity, magnetic field intensity, material constant, thermal diffusivity, specific heat, diffusion coefficient, factor of velocity slip, constant rate, and factor of thermal slip, respectively. The thermophysical characteristics of the hybrid nanofluid with a convectional fluid are listed in Table 1.

TABLE 1

TABLE 1. Thermophysical features of the hybrid nanofluid [24, 30].

Hybrid nanofluid model

The hybrid nanofluid correlation properties of dynamic viscosity, thermal conductivity, heat capacity, density, and electrical conductivity are defined experimentally.

Similarity variables

The applicable similarity variables are as follows [10]:

$\begin{array}{l}\eta =\frac{r^2-R^2}{2R}{\left(\frac{u_w}{z{u}_f}\right)}^{\frac{1}{2}},u=\frac{z{u}_0}{L}{f}^{\prime }\left(\eta \right),w=-\frac{R}{r}{\left(\frac{u_0{u}_f}{L}\right)}^{\frac{1}{2}}f\left(\eta \right),\psi \left(\eta ,z\right)={\left(u_w{u}_{f}z\right)}^{\frac{1}{2}}Rf\left(\eta \right),\\ \theta \left(\eta \right)=\frac{\left(T-T_{\infty }\right)}{\left(T_w-T_{\infty }\right)},g\left(\eta \right)=\frac{a}{a_0},h\left(\eta \right)=\frac{b}{a_0}.\end{array}(10)$

Using the similarity variables in Eq. 10 and Table 2, Eqs. 4–9 can be rewritten as follows:

$\begin{array}{l}\frac{{\mu }_{hnf/{\mu }_f}}{{\rho }_{hnf/{\rho }_f}}\left(\left(1+{\alpha }_1{\left(\beta f^{″}\right)}^{{\alpha }_1-1}\right)\left(1+2\eta \gamma \right)f^{‴}+\gamma \left(3+\left(1+2{\alpha }_1\right){\left(\beta f^{″}\right)}^{{\alpha }_1-1}\right)f^{″}\right)-P_m\frac{{\mu }_{hnf/{\mu }_f}}{{\rho }_{hnf/{\rho }_f}}{\left({\left(\beta f^{″}\right)}^{{\alpha }_1-1}+1\right)}^2{f}^{\prime }\\ \left(\frac{{\mu }_{hnf/{\mu }_f}}{{\rho }_{hnf/{\rho }_f}}{\left({\left(\beta f^{″}\right)}^{{\alpha }_1-1}+1\right)}^{2}M{f}^{\prime }+{\left({\left(\beta f^{″}\right)}^{{\alpha }_1-1}+1\right)}^2\left(f{\prime }^2-f{f}^{″}\right)\right)=0,\end{array}(11)$

$\frac{k_{hnf/k_f}}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\left(\left(1+2\eta \gamma \right){\theta }^{″}+2\gamma \theta \prime \right)+{\mathrm{P}}_r{E}_c\left(\frac{{\sigma }_{hnf/{\sigma }_f}}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}Mf{\prime }^2+\frac{\left(1+2\eta \gamma \right)f^{″2}}{\left(1+{\left(\beta f^{″}\right)}^{{\alpha }_1-1}\right)}\right)+{\mathrm{P}}_{r}f{\theta }^{\prime }=0,(12)$

$\frac{1}{S_c}\left(\left(1+2\eta \gamma \right)g^{″}+2\gamma g\prime \right)+f{g}^{\prime }-K_{c}g{h}^2-K_{vs}g=0,(13)$

$\frac{{\delta }^{*}}{S_c}\left(\left(1+2\eta \gamma \right)h^{″}+2\gamma h\prime \right)+f{h}^{\prime }+K_{c}g{h}^2+K_{vs}g=0.(14)$

The dimensionless forms of the boundary conditions are given as

$\left(\begin{array}{l}f\left(\eta \right)=S_1,f^{\prime }\left(\eta \right)-{\delta }_1{f}^{″}\left(\eta \right)=1,\theta \left(\eta \right)-{\beta }_T\theta \prime \left(\eta \right)=1,\\ K_s^{*}g\left(\eta \right)=g^{\prime }\left(\eta \right),{\delta }^{*}h\prime \left(\eta \right)=K_s^{*}g\left(\eta \right)\end{array}\right),at\eta \to 0.(15)$

$\left(f^{\prime }\left(\eta \right)\to 0,g\left(\eta \right)\to 1,h\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0\right),at\eta \to \infty .(16)$

TABLE 2

TABLE 2. Relationships of hybrid nanofluids [24, 30].

Assuming that the particles of the substances of both species have the same coefficients of diffusion $D_B^{*}$ and $D_A^{*}$, i.e., the ratio of the diffusion parameters $\raisebox{1ex}{$D_A^{*}$}\!\left/ \!\raisebox{-1ex}{$D_B^{*}$}\right.=1$; thus, we have

$h\left(\eta \right)+g\left(\eta \right)=1.(17)$

Eqs. 16, 17 are combined to get

$\frac{1}{S_c}\left(\left(1+2\eta \gamma \right)g^{″}+2\gamma g\prime \right)+f{g}^{\prime }-\left(K_c{\left(g-1\right)}^2+K_{vs}\right)g=0.(18)$

The conditions at the boundary are then given as

$g^{\prime }\left(0\right)=K_s^{*}g\left(0\right),g\left(\infty \right)\to 1.(19)$

The governing parameters here are those of the magnetic field $\left\{M=\raisebox{1ex}{${\sigma }_f{B}_0^{2}z$}\!\left/ \!\raisebox{-1ex}{${\rho }_f{u}_w$}\right.\right\}$, suction $\left\{S_1=V_w{\left(\frac{L}{a{\nu }_f}\right)}^{\frac{1}{2}}>\mathit{0}\right\}$, thermal slip $\left\{{\beta }_T=c_1{\left(\frac{a}{L{\nu }_f}\right)}^{\frac{1}{2}}\right\}$, velocity slip $\left\{{\delta }_1=a_1{\left(\frac{a}{L{\nu }_f}\right)}^{\frac{1}{2}}\right\}$, heterogeneous reaction $\left\{K_s^{*}=\frac{k_s}{D_A^{*}}{\left(\frac{L{\nu }_f}{c}\right)}^{\frac{1}{2}}\right\}$, porosity $\left\{P_m=\frac{z{\mu }_f}{K{u}_w}\right\}$, Schmidt number $\left\{S_c=\frac{{\nu }_f}{D_A^{*}}\right\}$, Eckert number $\left\{E_c=\frac{u_w^2}{c_p\left(T_w-T_{\infty }\right)}\right\}$, material $\left\{\beta =\sqrt{\frac{u_0^3{r}^2{z}^2}{2{\tau }_0^4{R}^2{L}^3{\mu }_f}}\right\}$, curvature $\left\{\gamma =\sqrt{\frac{L{\mu }_f}{u_0{R}^2}}\right\}$, and Prandtl number $\left\{{\mathrm{P}}_r=\frac{{\nu }_f}{{\alpha }_f}\right\}$.

Entropy generation

Entropy generation is defined in terms of the magnetic field, joule heating, and viscous dissipation. The equation of entropy generation is as follows:

$S_{gen}=\frac{k_{hnf}}{T_{\infty }^2}{\left(\frac{\partial T}{\partial r}\right)}^2+\frac{{\mu }_{hnf}}{T_{\infty }}\left(\frac{1}{1+{\left(\frac{1}{\sqrt{2}{\tau }_0^2}\frac{\partial u}{\partial r}\right)}^{{\alpha }_1-1}}\right){\left(\frac{\partial u}{\partial r}\right)}^2+\left(\begin{array}{l}\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}\frac{B_0^2{u}^2}{T_{\infty }}+\frac{R{D}_A^{*}}{T_{\infty }}\left(\frac{\partial T}{\partial r}\right)\frac{\partial a}{\partial r}\\ +\frac{R{D}_A^{*}}{a_0}{\left(\frac{\partial a}{\partial r}\right)}^2+\frac{R{D}_B^{*}}{T_{\infty }}\left(\frac{\partial b}{\partial r}\frac{\partial T}{\partial r}\right)\\ +\frac{{\mu }_{hnf}}{k{T}_{\infty }}{u}^2+\frac{R{D}_B^{*}b}{a_0}{\left(\frac{\partial b}{\partial r}\right)}^2\end{array}\right),(20)$

$N_G=\frac{S_{gen}}{S_0}(21)$

The entropy generation $N_G$ is the ratio of the entropy generation rate $S_{gen}$ to the properties of the entropy generation rate $S_0$, such that

$\begin{array}{l}{N}_G=\frac{k_{hnf}}{k_f}\left(1+2\gamma \eta \right){\alpha }_2\theta {\prime }^2+\frac{\raisebox{1ex}{${\sigma }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_f$}\right.}{\raisebox{1ex}{${\rho }_{hnf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}MBrf{\prime }^2+\frac{{\mu }_{hnf}}{{\mu }_f}\left(\frac{Br\left(1+2\gamma \eta \right)}{1+{\left(\beta f^{″}\right)}^{{\alpha }_1-1}}\right)\\ +\left(\left(1+2\gamma \eta \right)\left(\frac{L_1+L_2}{{\alpha }_2}\right)g{\prime }^2+\left(L_1-L_2\right)\left(1+2\gamma \eta \right){\theta }^{\prime }g\prime \right).\end{array}(22)$

where ${\alpha }_2=\frac{\Delta T}{T_{\infty }}$ is the temperature ratio parameter and $Br=\frac{{\mu }_f{u}_w}{k_f\Delta T}$ is the Brinkman number. Moreover, $L_1$ and $L_2$ are defined as $L_1=\frac{R{D}_A^{*}{a}_0}{k_f}$ and $L_2=\frac{R{D}_B^{*}{a}_0}{k_f}$.

Result and discussion

The numerical solution to the above problem is obtained using bvp4c in MATLAB. Table 3 shows a comparison of the velocity gradient $f^{″}\left(0\right)$ with the results of Ramesh et al. [37] and Bhattacharyya et al. [57] in the absence of ${\alpha }_1$, $\beta$,${\varphi }_1$, and ${\varphi }_2$ by taking $S_1=2.6,\mathrm{Pr}=0.5$. The results of this study are in good agreement with the previously published results. The influences of distinct parameters, such as the curvature, magnetic, porosity, thermal slip, suction, surface-catalyzed, homogeneous reaction, and temperature ratio parameters, as well as the Brinkman number on the velocity, temperature, homo–hetero reaction, and entropy generation profile are discussed in Figures 2–7.

TABLE 3

TABLE 3. Justification of $f^{″}\left(0\right)$ results in the absence of ${\alpha }_1$, $\beta$, ${\varphi }_1$, and ${\varphi }_2$, with $S_1=2.6,\mathrm{Pr}=0.5$.

FIGURE 2

FIGURE 2. (A–D) Outcomes of $f^{\prime }\left(\eta \right)$, $\theta \left(\eta \right)$, $g\left(\eta \right)$, and $N_G\left(\eta \right)$ against $\gamma$.

FIGURE 3

FIGURE 3. (A,B) Outcomes of $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ against $M$.

FIGURE 4

FIGURE 4. (A,B) Outcomes of $f^{\prime }\left(\eta \right)$ against ${\alpha }_1$ and $P_m$.

FIGURE 5

FIGURE 5. (A,B) Outcomes of $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ against $S_1$ and $B_t$, respectively.

FIGURE 6

FIGURE 6. (A,B) Outcomes of $g\left(\eta \right)$ against $K_c$ and $K_{vs}$.

FIGURE 7

FIGURE 7. (A,B) Outcomes of $N_G\left(\eta \right)$ against ${\alpha }_2$ and $Br$.

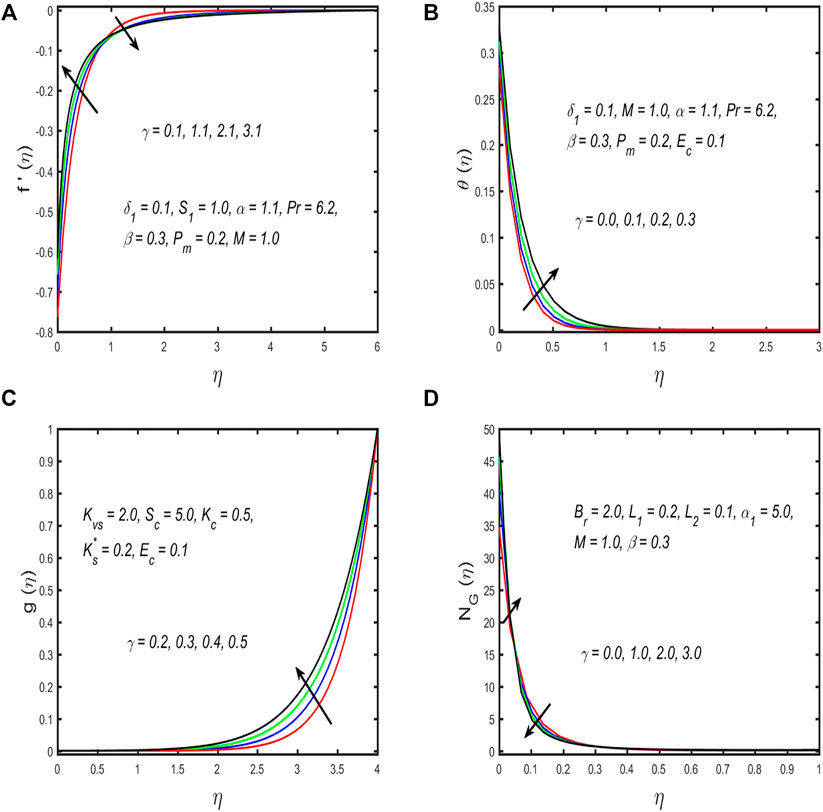
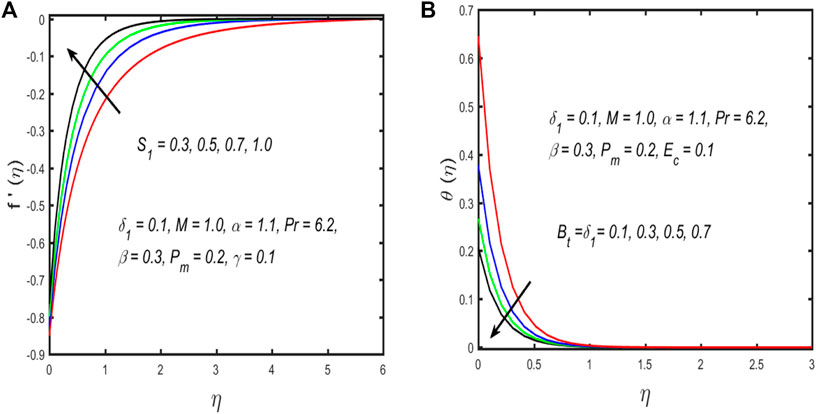
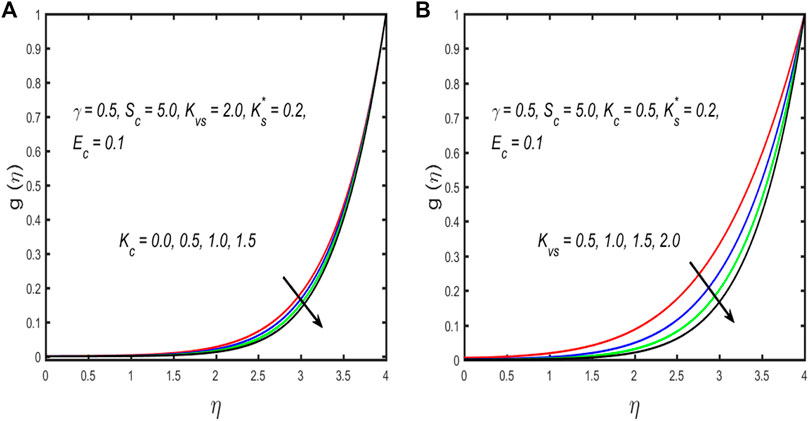
Figures 2A–D show the impacts of the curvature parameter on the velocity, temperature, homo–hetero reaction, and entropy generation profile. From Figure 2A, it is observed that the fluid velocity profile displays a dual trend with increase in the curvature parameter; for a higher value of the curvature parameter, the fluid velocity near the surface increases, while diminishing away from the boundary. The radius and curvature of the cylinder are inversely proportional; therefore, the radius of the cylinder reduces as the curvature parameter increases. As a result, the contact of the Ellis fluid along the cylinder surface decreases, and the surface supports a small resistance owing to the Ellis fluid particles; further, increasing values of $\gamma$ decrease the Ellis velocity of the fluid. Figure 2B shows how the fluid temperature increases when the curvature parameter increases. Physically, increasing values of $\gamma$ (curvature parameter) reflect the increasing thermal boundary layer thickness, which result in increased heat transmission and fluid temperature. Similarly, the curvature parameter improves the concentration and entropy generation distribution, as shown in Figures 2C,D. The impacts of the magnetic parameter on the fluid velocity and temperature are shown in Figures 3A,B. It is noted that the fluid velocity increases as the corresponding thickness of the boundary layer decreases; this is attributed to the fact that the increment in the magnetic field parameter produces a Lorentz force, which enhances the resistance of fluid flow. Consequently, the fluid velocity of the Ellis hybrid fluid diminishes. From Figure 3B, it is obvious that the fluid temperature condenses by stronger estimation of the magnetic parameter. Figures 4A,B show the effects of the material constant and porosity parameter on fluid velocity. The influence of the material constant is observed in Figure 4A, where the velocity reduces and the related thickness of the boundary increases with improvement in the value of the material parameter. The impact of $P_m$ on the velocity distribution of the Ellis hybrid nanofluid is shown in Figure 4B. As the porosity of the liquid phase increases, the momentum boundary layer decreases. Additionally, as we move farther from the bounded surface, the fluid velocity is unaffected by the porosity of the boundary. The effects of the suction and thermal slip parameters on velocity and temperature are respectively shown in Figures 5A,B. Figure 5A presents the velocity characteristics to obtain a better estimate of the suction parameter. The thickness of the momentum boundary layer appears to decrease as a result of this; the drag force develops while the suction parameter increases, which causes the thickness of the momentum boundary layer to reduce. As the thermal and velocity slip parameters increase, the wall temperature decreases, as shown in Figures 5A,B. The velocity slip parameter partially reflects the increment of the conversion of the dragging force on the stretching wall toward the liquid; as the thermal slip parameter increases, it produces a decaying trend in the thermal layer thickness, indicating that even small amounts of heat are transferred to the liquid that has leaked from the surface. Figure 6A shows the properties of the homogeneous reaction parameter’s strength on the $g\left(\eta \right)$ plot. The trend of the $g\left(\eta \right)$ plot diminishes with increment of the homogeneous reaction parameter. The performance of $g\left(\eta \right)$ for the surface-catalyzed reaction is depicted in Figure 6B. The reactants gain a greater surface area for the reaction to proceed through the use of porous media. The reaction rate is additionally accelerated by the surface-catalyzed reaction; hence, increasing the surface-catalyzed reaction lowers $g\left(\eta \right)$ more quickly. In Figures 7A,B, the outcomes of the temperature ratio parameter and Brinkman number on entropy generation are shown; it can be observed from the figures that the entropy generation distribution is boosted by increments to the temperature ratio parameter and Brinkman number.

Concluding remarks

The $CoF{e}_2{O}_4-Ti{O}_2\backslash water$ Ellis hybrid nanofluid flow was explored in a permeable horizontal cylinder through the combined impacts of joule heating, homogeneous–heterogeneous reactions, and slip boundary conditions. The highly nonlinear ODEs were numerically solved using bvp4c in MATLAB. The following are the conclusions of this study:

➢ The curvature parameter shows dual behaviors for fluid velocity and entropy generation as the temperature and nanoparticle concentration of the fluid increase.

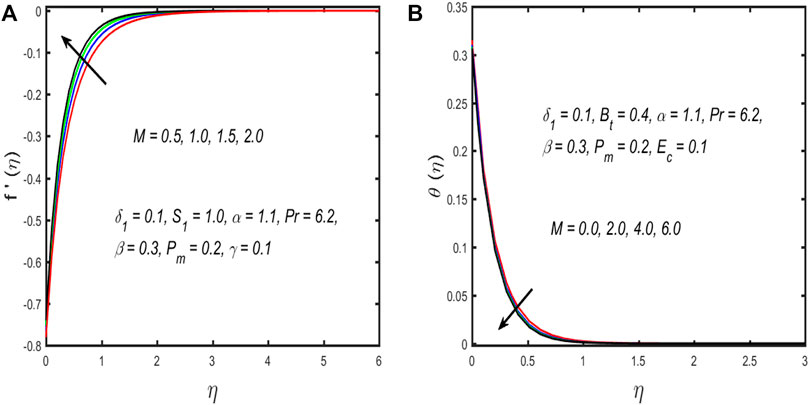
➢ The momentum boundary layer thickness reduces with stronger estimations of the magnetic and porosity parameters.

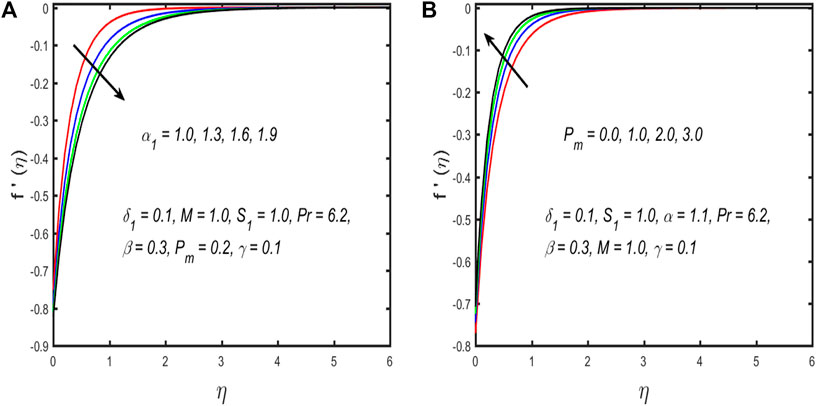
➢ The fluid velocity improves with the suction parameter but diminishes for stronger estimation of the material parameter.

➢ The fluid concentration decreases as the surface-catalyzed and homogeneous reaction parameters increase.

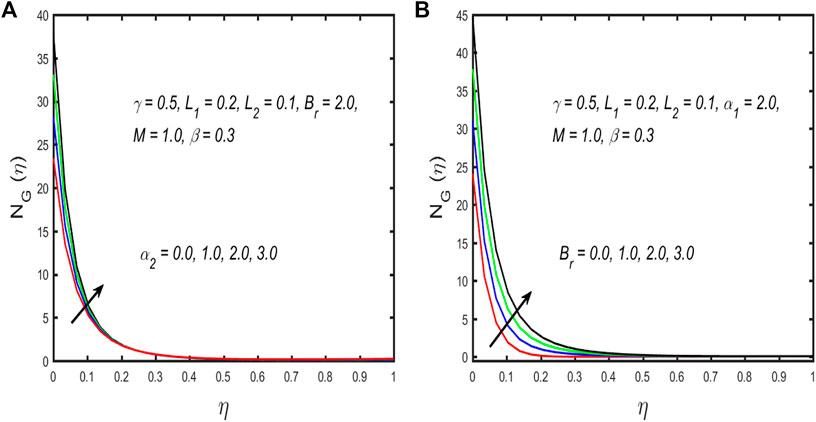
➢ The entropy generation profile is improved by the temperature ratio parameter and Brinkman number.

➢ The thermal and velocity slip parameters reduce the temperature distribution.

Finally, we note that our work was built on the Ellis model for fluid rheology using the unique behaviors of the straightforward power-law model. In particular, as the flow rate in the basic state is zero, the power-law model predicts either a zero or an infinite critical estimate for the Darcy–Rayleigh number, as stated in Barletta and Nield [60]. However, the application of the Ellis model results in a nonsingular trend as the basic flow rate approaches zero, reaching the same critical estimate of the Darcy–Rayleigh number in the case of a Newtonian fluid.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

MK: Writing-Original Draft Preparation, Data Curation, Investigation, Visualization, Validation. NA: Help in computation. SA: Conceptualization, Methodology, Software, Formal Analysis, Writing-Original Draft Preparation. ME; Review the modeling of the problem. ET-e; Improve the physical discussion. KG: Performs the critical review. KAG; Help in coding. MY; Help in problem formulation.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Program under grant no. RGP. 2/19/43. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4331317DSR68). The authors thank to Taif University Researcher for Supporting project number (TURSP-2020/16), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

1. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938. IL (United States): Argonne National Lab. (1995).

Google Scholar

2. Saidur R, Leong KY, Mohammed HA. A review on applications and challenges of nanofluids. Renew Sustain Energ Rev (2011) 15(3):1646–68. doi:10.1016/j.rser.2010.11.035

CrossRef Full Text | Google Scholar

3. Waqas H, Khan SA, Alghamdi M, Muhammad T. Numerical investigation for radiative transport in magnetized flow of nanofluids due to moving surface. Math Probl Eng (2021) 1–10. doi:10.1155/2021/1705736

CrossRef Full Text | Google Scholar

4. Reddy PS, Sreedevi P, Chamkha AJ. MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction. Powder Technol (2017) 307:46–55. doi:10.1016/j.powtec.2016.11.017

CrossRef Full Text | Google Scholar

5. Krishna MV, Chamkha AJ. Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys (2019) 15:102652. doi:10.1016/j.rinp.2019.102652

CrossRef Full Text | Google Scholar

6. Waqas H, Khan SA, Farooq U, Muhammad T, Alshehri A, Yasmin S. Thermal transport analysis of six circular microchannel heat sink using nanofluid. Sci Rep (2022) 12(1):8035–19. doi:10.1038/s41598-022-11121-y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Khan MN, Nadeem S. A comparative study between linear and exponential stretching sheet with double stratification of a rotating Maxwell nanofluid flow. Surf Inter (2021) 22:100886. doi:10.1016/j.surfin.2020.100886

CrossRef Full Text | Google Scholar

8. Khan MN, Ahmad S, Nadeem S. Flow and heat transfer investigation of bio–convective hybrid nanofluid with triple stratification effects. Phys Scr (2021) 96(6):065210. doi:10.1088/1402-4896/abf305

CrossRef Full Text | Google Scholar

9. Alqarni MS, Yasmin S, Waqas H, Khan SA. Recent progress in melting heat phenomenon for bioconvection transport of nanofluid through a lubricated surface with swimming microorganisms. Sci Rep (2022) 12(1):8447–17. doi:10.1038/s41598-022-12230-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Rooman M, Jan MA, Shah Z, Alzahrani MR. Entropy generation and nonlinear thermal radiation analysis on axisymmetric MHD Ellis nanofluid over a horizontally permeable stretching cylinder. Waves in Random and Complex Media (2022) 1–15. doi:10.1080/17455030.2021.2020934

CrossRef Full Text | Google Scholar

11. VeeraKrishna M, Subba Reddy G, Chamkha AJ. Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates. Phys Fluids (2018) 30(2):023106. doi:10.1063/1.5010863

CrossRef Full Text | Google Scholar

12. Chamkha AJ, Mohamed RA, Ahmed SE. Unsteady MHD natural convection from a heated vertical porous plate in a micropolar fluid with Joule heating, chemical reaction and radiation effects. Meccanica (2011) 46(2):399–411. doi:10.1007/s11012-010-9321-0

CrossRef Full Text | Google Scholar

13. Khan Y, Akram S, Athar M, Saeed K, Muhammad T, Hussain A, et al. The role of double-diffusion convection and induced magnetic field on peristaltic pumping of a johnson–segalman nanofluid in a non-uniform channel. Nanomaterials (2022) 12(7):1051. doi:10.3390/nano12071051

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Akram S, Razia A, Umair MY, Abdulrazzaq T, Homod RZ. Double‐diffusive convection on peristaltic flow of hyperbolic tangent nanofluid in non‐uniform channel with induced magnetic field. Math Methods Appl Sci (2022). doi:10.1002/mma.8188

CrossRef Full Text | Google Scholar

15. Akram S, Athar M, Saeed K. Numerical simulation of effects of soret and dufour parameters on the peristaltic transport of a magneto six-constant jeffreys nanofluid in a non-uniform channel: A bio-nanoengineering model. Eur Phys J Spec Top (2022) 231(3):535–43. doi:10.1140/epjs/s11734-021-00348-x

CrossRef Full Text | Google Scholar

16. Akram S, Athar M, Saeed K, Umair MY. Nanomaterials effects on induced magnetic field and double-diffusivity convection on peristaltic transport of Prandtl nanofluids in inclined asymmetric channel. Nanomater Nanotechnology (2022) 12:184798042110486. doi:10.1177/18479804211048630

CrossRef Full Text | Google Scholar

17. Waqas H, Khan SA, Muhammad T, Naqvi SMRS. Heat transfer enhancement in stagnation point flow of ferro-copper oxide/water hybrid nanofluid: A special case study. Case Stud Therm Eng (2021) 28:101615. doi:10.1016/j.csite.2021.101615

CrossRef Full Text | Google Scholar

18. Krishna MV, Chamkha AJ. Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int Commun Heat Mass Transfer (2020) 113:104494. doi:10.1016/j.icheatmasstransfer.2020.104494

CrossRef Full Text | Google Scholar

19. Turcu R, Darabont AL, Nan A, Aldea N, Macovei D, Bica D, et al. New polypyrrole-multiwall carbon nanotubes hybrid materials. J optoelectronics Adv Mater (2006) 8(2):643–7.

Google Scholar

20. Jana S, Salehi-Khojin A, Zhong WH. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim Acta (2007) 462(1-2):45–55. doi:10.1016/j.tca.2007.06.009

CrossRef Full Text | Google Scholar

21. Devi SA, Devi SSU. Numerical investigation of hydromagnetic hybrid Cu–Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int J Nonlinear Sci Numer Simulation (2016) 17(5):249–57. doi:10.1515/ijnsns-2016-0037

CrossRef Full Text | Google Scholar

22. Maskeen MM, Zeeshan A, Mehmood OU, Hassan M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J Therm Anal Calorim (2019) 138(2):1127–36. doi:10.1007/s10973-019-08304-7

CrossRef Full Text | Google Scholar

23. Sreedevi P, Sudarsana Reddy P, Chamkha A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl Sci (2020) 2(7):1222–15. doi:10.1007/s42452-020-3011-x

CrossRef Full Text | Google Scholar

24. Acharya N, Maity S, Kundu PK. Framing the hydrothermal features of magnetized TiO2–CoFe2O4 water-based steady hybrid nanofluid flow over a radiative revolving disk. Multidiscipline Model Mater Structures (2019) 16(4):765–90. doi:10.1108/mmms-08-2019-0151

CrossRef Full Text | Google Scholar

25. Ramesh GK, Shehzad SA, Rauf A, Chamkha AJ. Heat transport analysis of aluminum alloy and magnetite graphene oxide through permeable cylinder with heat source/sink. Phys Scr (2020) 95(9):095203. doi:10.1088/1402-4896/aba5af

CrossRef Full Text | Google Scholar

26. Farooq U, Waqas H, Muhammad T, Khan SA. Heat transfer enhancement of hybrid nanofluids over porous cone. Int J Chem Reactor Eng (2022) 20(4):465–73. doi:10.1515/ijcre-2021-0109

CrossRef Full Text | Google Scholar

27. Qin L, Ahmad S, Khan MN, Ahammad NA, Gamaoun F, Galal AM. Thermal and solutal transport analysis of Blasius–Rayleigh–Stokes flow of hybrid nanofluid with convective boundary conditions. Waves in Random and Complex Media (2022) 1–19. doi:10.1080/17455030.2022.2072018

CrossRef Full Text | Google Scholar

28. Ahmad S, Nadeem S, Khan MN. Enhanced transport properties and its theoretical analysis in two-phase hybrid nanofluid. Appl Nanoscience (2021) 12(3):309–16. doi:10.1007/s13204-020-01634-1

CrossRef Full Text | Google Scholar

29. Waini I, Khan U, Zaib A, Ishak A, Pop I. Thermophoresis particle deposition of CoFe2O4-TiO2 hybrid nanoparticles on micropolar flow through a moving flat plate with viscous dissipation effects. Int J Numer Methods Heat Fluid Flow (2022). doi:10.1108/hff-12-2021-0767

CrossRef Full Text | Google Scholar

30. Chaudhary MA, Merkin JH. A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dyn Res (1995) 16(6):311–33. doi:10.1016/0169-5983(95)00015-6

CrossRef Full Text | Google Scholar

31. Ramzan M, Riasat S, Alotaibi H. EMHD hybrid squeezing nanofluid flow with variable features and irreversibility analysis. Phys Scr (2022) 97(2):025705. doi:10.1088/1402-4896/ac49b1

CrossRef Full Text | Google Scholar

32. Khan M, Yasir M, Alshomrani AS, Sivasankaran S, Aladwani YR, Ahmed A. Variable heat source in stagnation-point unsteady flow of magnetized Oldroyd-B fluid with cubic autocatalysis chemical reaction. Ain Shams Eng J (2022) 13(3):101610. doi:10.1016/j.asej.2021.10.005

CrossRef Full Text | Google Scholar

33. Puneeth V, Manjunatha S, Makinde OD, Gireesha BJ. Bioconvection of a radiating hybrid nanofluid past a thin needle in the presence of heterogeneous–homogeneous chemical reaction. J Heat Transfer (2021) 143(4). doi:10.1115/1.4049844

CrossRef Full Text | Google Scholar

34. Elattar S, Helmi MM, Elkotb MA, El-Shorbagy MA, Abdelrahman A, Bilal M, et al. Computational assessment of hybrid nanofluid flow with the influence of hall current and chemical reaction over a slender stretching surface. Alexandria Eng J (2022) 61(12):10319–31. doi:10.1016/j.aej.2022.03.054

CrossRef Full Text | Google Scholar

35. Gul H, Ramzan M, Chung JD, Chu YM, Kadry S. Multiple slips impact in the MHD hybrid nanofluid flow with Cattaneo–Christov heat flux and autocatalytic chemical reaction. Sci Rep (2021) 11(1):14625–14. doi:10.1038/s41598-021-94187-4

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zainal NA, Nazar R, Naganthran K, Pop I. Flow and heat transfer over a permeable moving wedge in a hybrid nanofluid with activation energy and binary chemical reaction. Int J Numer Methods Heat Fluid Flow (2021) 32:1686–705. doi:10.1108/hff-04-2021-0298

CrossRef Full Text | Google Scholar

37. Ramesh GK, Manjunatha S, Roopa GS, Chamkha AJ. Hybrid (ND-Co3O4/EG) nanoliquid through a permeable cylinder under homogeneous-heterogeneous reactions and slip effects. J Therm Anal Calorim (2021) 146(3):1347–57. doi:10.1007/s10973-020-10106-1

CrossRef Full Text | Google Scholar

38. Tahir W, Althobaiti N, Kousar N, Alhazmi SE, Bilal S, Riaz A. Effects of homogeneous-heterogeneous reactions on Maxwell ferrofluid in the presence of magnetic dipole along a stretching surface: A numerical approach. Mathematical Problems in Engineering (2022). doi:10.1155/2022/4148401

CrossRef Full Text | Google Scholar

39. Keenan JH. Availability and irreversibility in thermodynamics. Br J Appl Phys (1951) 2(7):183–92. doi:10.1088/0508-3443/2/7/302

CrossRef Full Text | Google Scholar

40. Bejan A. Entropy generation minimization: The new thermodynamics of finite‐size devices and finite‐time processes. J Appl Phys (1996) 79(3):1191–218. doi:10.1063/1.362674

CrossRef Full Text | Google Scholar

41. Bejan A. Entropy generation minimization: The method of thermodynamic optimization of finite-size systems and finite-time processes. CRC Press (2013). doi:10.1201/9781482239171

CrossRef Full Text | Google Scholar

42. Jakeer S, Reddy PBA. Entropy generation on EMHD stagnation point flow of hybrid nanofluid over a stretching sheet: Homotopy perturbation solution. Phys Scr (2020) 95(12):125203. doi:10.1088/1402-4896/abc03c

CrossRef Full Text | Google Scholar

43. Khosravi R, Rabiei S, Khaki M, Safaei MR, Goodarzi M. Entropy generation of graphene–platinum hybrid nanofluid flow through a wavy cylindrical microchannel solar receiver by using neural networks. J Therm Anal Calorim (2021) 145(4):1949–67. doi:10.1007/s10973-021-10828-w

CrossRef Full Text | Google Scholar

44. Mumraiz S, Ali A, Awais M, Shutaywi M, Shah Z. Entropy generation in electrical magnetohydrodynamic flow of Al2O3–Cu/H2O hybrid nanofluid with non-uniform heat flux. J Therm Anal Calorim (2021) 143(3):2135–48. doi:10.1007/s10973-020-09603-0

CrossRef Full Text | Google Scholar

45. Li YX, Khan MI, Gowda RP, Ali A, Farooq S, Chu YM, et al. Dynamics of aluminum oxide and copper hybrid nanofluid in nonlinear mixed Marangoni convective flow with entropy generation: Applications to renewable energy. Chin J Phys (2021) 73:275–87. doi:10.1016/j.cjph.2021.06.004

CrossRef Full Text | Google Scholar

46. Riaz A, Almutairi S, Alhazmi SE, Saleem A, Nadeem S, Abdelrahman A. Insight into the cilia motion of electrically conducting Cu-blood nanofluid through a uniform curved channel when entropy generation is significant. Alexandria Eng J (2022) 61(12):10613–30. doi:10.1016/j.aej.2022.04.011

CrossRef Full Text | Google Scholar

47. Bhatti MM, Riaz A, Zhang L, Sait SM, Ellahi R. Biologically inspired thermal transport on the rheology of williamson hydromagnetic nanofluid flow with convection: An entropy analysis. J Therm Anal Calorim (2021) 144(6):2187–202. doi:10.1007/s10973-020-09876-5

CrossRef Full Text | Google Scholar

48. Ahmad S, Khan MN, Nadeem S, Rehman A, Ahmad H, Ali R. Impact of Joule heating and multiple slips on a Maxwell nanofluid flow past a slendering surface. Commun Theor Phys (2021) 74(1):015001. doi:10.1088/1572-9494/ac3bc8

CrossRef Full Text | Google Scholar

49. Takhar HS, Chamkha AJ, Nath G. Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field. Int J Eng Sci (1999) 37(13):1723–36. doi:10.1016/s0020-7225(98)00144-x

CrossRef Full Text | Google Scholar

50. Saeed K, Akram S, Ahmad A, Athar M, Imran M, Muhammad T. Impact of partial slip on double diffusion convection and inclined magnetic field on peristaltic wave of six-constant Jeffreys nanofluid along asymmetric channel. Eur Phys J Plus (2022) 137(3):364. doi:10.1140/epjp/s13360-022-02553-6

CrossRef Full Text | Google Scholar

51. Krishna MV, Ahamad NA, Chamkha AJ. Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alexandria Eng J (2021) 60(1):845–58. doi:10.1016/j.aej.2020.10.013

CrossRef Full Text | Google Scholar

52. Chamkha AJ. MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl Math Model (1997) 21(10):603–9. doi:10.1016/s0307-904x(97)00084-x

CrossRef Full Text | Google Scholar

53. Chamkha AJ, Khaled ARA. Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid‐saturated porous medium. Int J Numer Methods Heat Fluid Flow (2000) 10(5):455–77. doi:10.1108/09615530010338097

CrossRef Full Text | Google Scholar

54. Takhar HS, Chamkha AJ, Nath G. Unsteady mixed convection flow from a rotating vertical cone with a magnetic field. Heat Mass Transfer (2003) 39(4):297–304. doi:10.1007/s00231-002-0400-1

CrossRef Full Text | Google Scholar

55. Akram S, Athar M, Saeed K, Razia A. Impact of slip on nanomaterial peristaltic pumping of magneto-Williamson nanofluid in an asymmetric channel under double-diffusivity convection. Pramana - J Phys (2022) 96(1):57–13. doi:10.1007/s12043-021-02287-7

CrossRef Full Text | Google Scholar

56. Ahmad S, Nadeem S. Analysis of activation energy and its impact on hybrid nanofluid in the presence of Hall and ion slip currents. Appl Nanosci (2020) 10(12):5315–30. doi:10.1007/s13204-020-01334-w

CrossRef Full Text | Google Scholar

57. Bhattacharyya K, Gorla RSR. Boundary layer flow and heat transfer over a permeable shrinking cylinder with surface mass transfer. Int J Appl Mech Eng (2013) 18(4):1003–12. doi:10.2478/ijame-2013-0062

CrossRef Full Text | Google Scholar

58. Ramesh K, Riaz A, Dar ZA. Simultaneous effects of MHD and Joule heating on the fundamental flows of a Casson liquid with slip boundaries. Propulsion Power Res (2021) 10(2):118–29. doi:10.1016/j.jppr.2021.05.002

CrossRef Full Text | Google Scholar

59. Vaidya H, Rajashekhar C, Prasad KV, Khan SU, Riaz A, Viharika JU. MHD peristaltic flow of nanofluid in a vertical channel with multiple slip features: An application to chyme movement. Biomech Model Mechanobiol (2021) 20(3):1047–67. doi:10.1007/s10237-021-01430-y

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Barletta A, Nield DA. Linear instability of the horizontal throughflow in a plane porous layer saturated by a power-law fluid. Phys Fluids (2011) 23(1):013102. doi:10.1063/1.3532805

CrossRef Full Text | Google Scholar

Nomenclature

$r,\theta ,z$ Axis coordinates

${\left(\rho C_p\right)}_{hnf}$ Heat capacity

${\sigma }_{hnf}$ Electrical conductivity

${\tau }_o,{\alpha }_1$ Material constants

$B_o$ Magnetic field intensity

$T_{\infty }$ Ambient temperature

$D_{A^{*}},D_{B^{*}}$ Variable diffusion coefficients of chemical species $C$ and $D$

$C,D$ Chemical species

$k_1,k_s$ Reaction rates

$k_{hnf}$ Thermal conductivity

$S$ Interfacial surface area

$a_1,c_1$ Arbitrary constants

$M$ Magnetic parameter

$\gamma$ Curvature parameter

${\varphi }_2$ Volume fraction of nanoparticles ($Ti{O}_2$)

$Ti{O}_2$ Titanium oxide

${\varphi }_{hnf}$ Hybrid nanoparticle volume fraction

$Br$ Brinkman number

$Ec$ Eckert number

$S_1$ Suction parameter

$B_T$ Thermal slip parameter

$N_G$ Entropy generation

${\alpha }_2$ Temperature ratio parameter

$u,v,w$ Velocity components

$K$ Permeability of porous medium

$u_{\infty },u_w$ Free stream and wall velocities

$T_w$ Wall temperature

${\rho }_{hnf}$ Hybrid nanofluid density

${\alpha }_{hnf}$ Hybrid nanofluid thermal diffusivity

${\upsilon }_{hnf}$ Kinematic viscosity of hybrid nanofluid

$a$ Concentration of $C$

$b$ Concentration of $D$

$\eta$ Similarity variable

$\mathrm{Pr}$ Prandtl number

$K_{vs}$ Surface-catalyzed parameter

$\beta$ Material parameter

$P_m$ Porosity parameter

${\varphi }_1$ Volume fraction of nanoparticles ($CoF{e}_2{O}_4$)

$CoF{e}_2{O}_4$ Cobalt ferrite

$S_c$ Schmidt number

$K_c$ Parameter of homogeneous reaction

$K_{s^{*}}$ Parameter of heterogeneous reaction

${\delta }_1$ Velocity slip parameter

${\delta }^{*}$ Ratio of the diffusion coefficient

${\mu }_{hnf}$ Dynamic viscosity

$S_0$ Characteristic entropy generation rate