- 1Department of Mathematics, College of Sciences, King Khalid University, Abha, Saudi Arabia
- 2Department of Mathematics, Division of Science and Technology, University of Education, Lahore, Pakistan
- 3Department of Computer Science, University of Chakwal, Chakwal, Pakistan
- 4Department of Information Sciences, Division of Science and Technology, University of Education, Lahore, Pakistan
- 5Faculty of Engineering and Technology, Future University in Egypt, New Cairo, Egypt
In this analysis, the authors reveal the effects of electro-osmosis on the multiphase flow of Carreau fluid in a microchannel in the presence of Hall currents and solid particles. Moreover, the compliant channel walls are subject to oscillation occurring at the surface. To investigate the problem quantitatively, mathematical models for fluid phase and particulate phase have been structured. A lubrication approach is adopted due to laminar flow and the small dimensions of the channel. To produce the data, a system of differential equations is produced with the help of a numerical process performed on Mathematica through a built-in NDSolve tool. The results are presented graphically to examine the effects of various physical factors on the flow quantities. From pictorial discussion, it is gathered that the Helmholtz–Smoluchowski velocity parameter and the presence of an increasing amount of solid particles increasing the heat exchange while producing electro-kinetic energy. It is also found that velocity is a direct function of solid particles and compliant walls, but an inverse link is seen in the presence of electro-kinetic energy. Such studies can be employed with microfluidic devices and \may also be productive in medical and mechanical research.
Introduction
For a long time, many scientists have considered peristaltic transport in fluid mechanics to identify its importance in medical fields (in general) and hydrodynamics (in particular). A pumping flow is created by waves spread along the adaptable channel walls. This procedure encounters numerous organic frameworks involving transportation using plane muscles, e.g., the motion of food along the intestinal tract, the transportation of urine, the course of blood in the capillaries, and so on. This subject has received extensive analysis (for various liquids and various channels). The peristaltic transport system attracted additional interest following the examination performed by Latham [1]. Then, Fung and Yih [2] added a commitment to the major investigation of the peristaltic scheme by utilizing the fixed flow frame exhibited by Shapiro et al. [3] in moving frame transformations. Following that, a few examinations were performed to measure the way that peristalsis of different liquids behaves, using lubrication technology (see Refs. [4–8]).
Studies containing two-phase flow due to newly added solid fragments in a base liquid using a variety of conduits has been conducted by many researchers. The hypothetical investigation of these frameworks is vital in actual peculiarities, such as fluidization, lunar debris streams, paint splashes, atomic reactor cooling, and disintegration. The uses of such streams can be seen in medication and geoscience. The hypothesis of particulate-fluid mixture has been used to examine organic streams like those of blood [9, 10]. Recently, the concatenation of an induction of particles in fluids has been identified by numerous researchers. Bhatti et al. [11] explored the issue of a pumping stream with wall slip. This stream was incited by a sinusoidal wave. They likewise examined the endoscopic impacts on the dual phase solution. Srivastava and Srivastava [12] analyzed the peristaltic scheme of rheological fluid utilizing a Casson stress matrix. In a further review, they utilized a particulate-fluid suspension streaming in a body with a pumping procedure [13]. Misra and Pandey [14] developed a particle-fluid flow study in a round and hollow cylinder, in which the stream is produced by a progressive wave. Yamane et al. [15] dealt with the consistent advancement of a particulate solution in a rotating pipe. Later, Bhatti et al. [16] utilized a blood coagulation structure to observe the intensity of motion in a dusty fluid considering a changeable thickness for a wavy movement of fluid. Akbar et al. [17] introduced a numerical model prompted by a ciliary movement within the sight of a magnetic field with a copper type of nano particles. Rashed and Ahmed [18] recently published a work on the peristaltic flow of a dusty liquid concentration of nanofluid across a bended enclosure and produced the reading that large Eckert numbers introduce increased heat and speed of fluid and dusty phases.
Most commonly used liquids are non-Newtonian in their behavior. From raw petroleum unsheathing to the materials business, from thermoplastic industry to medication, and from the assembly of different lubricants to biological blood streams, we intensely rely upon the various types of non-Newtonian liquids. Different numerical tensors for non-linear liquids have been presented by specialists, with reference to the physical and warm qualities of these liquids. Akbar and Nadeem [19] worked on the creeping movement of the Jeffrey stress model by considering a variable viscosity model and heat exchange phenomenon. In this study, it is found that the Jeffrey fluid model imposes an opposite impact on amount of pressure increase, but the heat transfer rate is enhanced in case of variable viscosity attributes. Nazeer et al. [20] investigated two phase flows of non-Newtonian fluid in a heated, inclined conduit, having compliant walls and permeable medium. A lubrication approximation is taken into account to achieve the final form of the flow model exhibiting the physical face of the study. The results of that work have been constructed as follows: the permeability of the free space exerts an inverse impact on temperature of the fluid, and due to radiation effects, the velocity is declines. Saleem et al. [21] described an electro-osmotic analysis for a multiphase flow of a Jeffrey stress model. Tiny spherical particles are considered in the base fluid, and the exact results are framed. The conclusion suggests that electro-kinetic energy can be suitably increased by providing the amount of zeta potential. Riaz and Sadiq [22] published a solid particulate-liquid suspension of the Eyring–Powell expression through a curved channel. The problem is managed with the application of linearity and smoothness constraints. Perturbation technology is adopted to evaluate the analytical data and the result is produced that the presence of solid particles decreases the fluid’s speed as well as its pressure profile. The most common practically used fluid model is the Carreau fluid model, but in the literature, work with this model is rare due to its complicated mathematical stress expression. This model is very useful for its dual characteristics, in that it behaves as a Newtonian at low shear rates and as a non-Newtonian fluid for the median rate of applied stress. Noreen et al. [23] investigated heat exchange analysis in pumping the transport of Carreau fluid flowing in an inclined geometry and suggested that this model be linked to a blood flow in capillary and microvessels. It is claimed that stream boluses are less dragged for Carreau fluid than viscous fluid. Recently, Asha and Belery [24] solved the problem of the peristaltic pumping of Carreau fluid in the presence of Joule’s heating by employing a multi-step DTM, and their results showed that the Grashof number reduces the velocity in half of the channel and increases in the other half, while temperature distribution is enhanced by heat absorption factor and the Brickman number. Further work on Carreau fluid can be found in [25–28].
Electroosmotic studies have been seen to a significant degree for many years. The principal gadget-like Microelectromechanical System (MEMS) was the microfluidic innovation collected during the 1980s. Such devices can be applied across a range of contexts containing natural and physiological sectors, where microfluidic items are termed LOCs (lab-on-chip devices). LOC devices can be utilized equally well for various targets, including physical therapeutics and microbial or toxic contamination. Currently, an there is a recognized need for minimal, straightforward, and cheap homogenized hardware for drug dispersal and DNA-based investigation in light of the requirement for viable, quick, and appreciable standardized quality of microfluidics. Devices are often used that drive liquid all through an entire network utilizing electroosmosis. Electroosmosis addresses the electrolyte stream across a channel with an external voltage unit limit. In a few organic, clinical, and producing systems, electroosmosis creates, including the dialysis of liquids, porous layers, zoological cycles, movement in human skin, a tube/waterway stream, and methods of separation. Yasmeen and Iqbal [29] presented electrical double layer (EDL) effects on the heat and mass convection analysis of a viscous fluid in a porous medium with consideration of peristaltic pumping. The authors found that the electro-osmosis factor can help reduce the permeability of the medium. In the work of Tripathi et al. [30], the unsteady flow of a viscous fluid is established through electro-osmosis and peristalsis. In this article, the authors find that electric potential is an inverse function of EDL, and the strong electric field puts an inverse impact on wall stress. Prakash and Tripathy [31] incorporated the EDL mechanism for a Phan–Thien–Tanner fluid in an asymmetric peristaltic enclosure using Poisson–Boltzman expression and established that the fluid flow is extensively affected by EDL thickness and electric field strength. Further work on electro-osmosis can be found in [32, 33].
Examination of the literature finds no study on the peristaltic mechanism of Carreau model multiphase flow with Hall currents and electroosmotic pumping. The rheological effects of the non-Newtonian (Carreau) and electro-kinetic properties of EDL make the problem more applicable in various clinical and mechanical fields. The current analysis focuses the numerical study of heat transfer in pumping flow of particulate-liquid (Carreau fluid) in the presence of EDL effects and Hall currents in a compliant channel. The equations are modeled using suitably applied lubrication theory and scaling transformations of a non-dimensionlization procedure. The achieved non-linear coupled differential equations are handled by a numerical approach using an in-house command of Mathematica. The results are elaborated pictorially by sketching the curves of velocity and temperature profiles against various factors. Moreover, the current analysis is compared with the results in the literature to establish the validity of the findings.
Mathematical structure
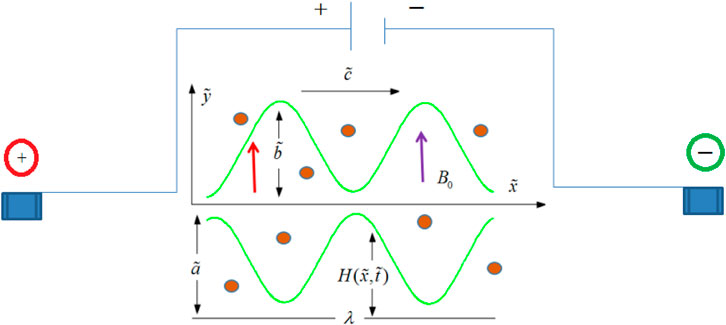
Let us assume an unsteady particulate-fluid transport of non-linear Carreau fluid containing tiny solid particles of non-variable density in a two-dimensional micro peristaltic channel. An external battery is attached to the fluid phase container to produce electro-kinetic energy in the fluid phase. For simplicity, we neglect the effects of electro-osmosis on a particulate phase and a thermal profile. The walls of the conduit are taken to be oscillating at the surfaces. Geometrically, the waves are propagating along a horizontal axis
A constant extrinsic magnetic strength
where
The fluid phase with velocity decomposition as
The aforementioned relation contains the velocity vector
where σ is the fluid’s electric conductivity and
where
For the particulate phase with velocity
Electro-osmotic phenomenon
An electric potential is generated due to the presence of EDL on channel surfaces, whose mathematical structure is developed with the following Poisson relation [29–33]:
where
The aforementioned expression contains the bulk concentration of ions as
The Boltzman equation is transformed as:
Introducing the subsequent non-dimensional quantities
After incorporating aforementioned transformations, Eqs. 2–4, 8–10 become
where
with normalized boundary conditions defined as:
The potential obtained can be found by solving Eq. 23 along with the boundary conditions given in Eq. 24 as
Considering the lubrication strategy, we finally obtained the following velocity and temperature expressions for dual phases:
The imposed surface constraints are manufactured as:
Their corresponding boundary conditions in dimensionless form are:
The expressions for the particulate viscosity and drag coefficient are reported in [33].
Compliant wall conditions
The oscillating boundaries are displayed as [34]:
where
In the aforementioned equation,
Numerical results and discussion
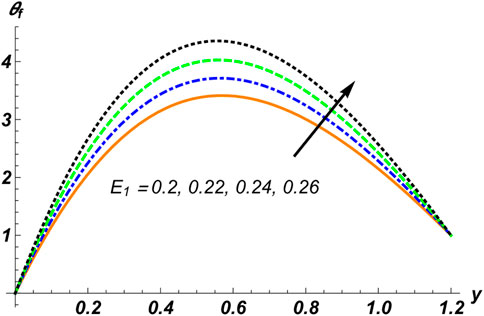
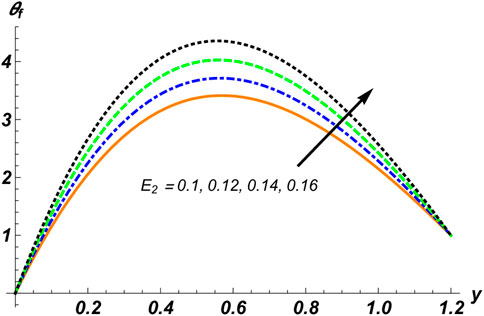
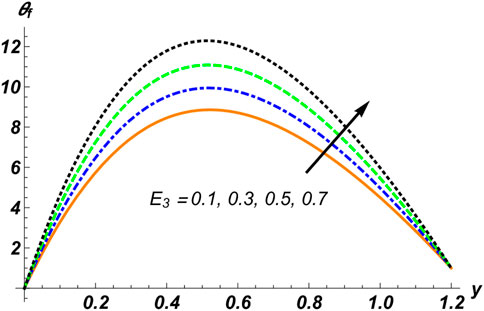
Eqs. 28, 29 are nonlinear coupled differential equations whose exact solution is a very difficult task, so a numerical solution for the considered problem was developed using the computational software Mathematica with the built-in NDSolve tool. The data obtained numerically have been plotted for various physical factors. Here, we discuss the results of various considerable profiles of the problem graphically by sketching plots against some key parameters of the study while keeping others fixed. For this, graphs of temperature profile
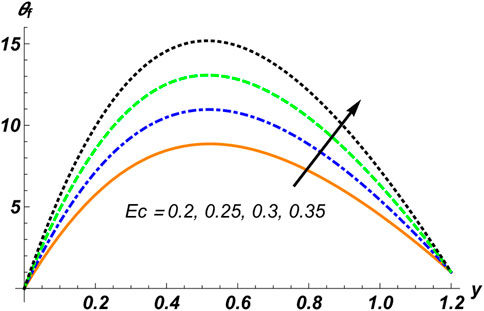
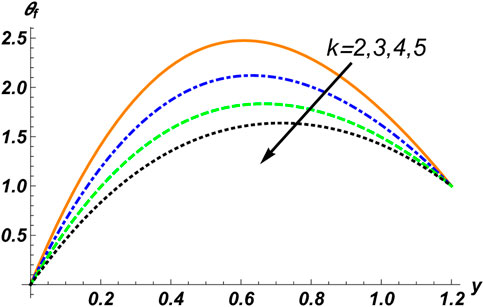
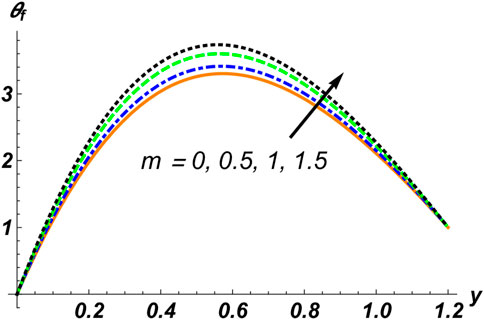
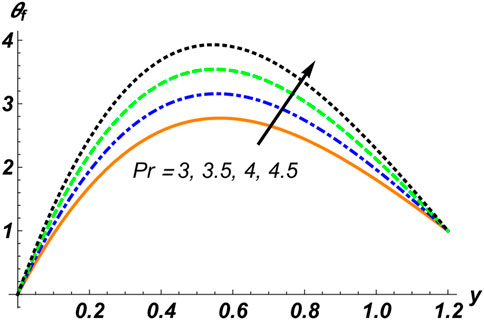
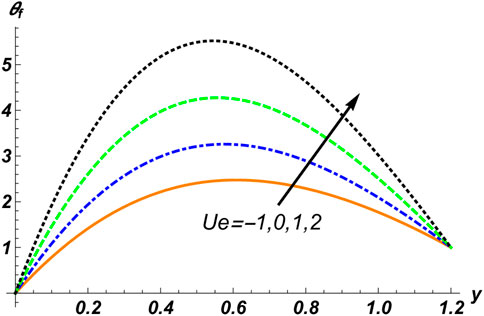
Figures 2–4 are manipulated for the parameters
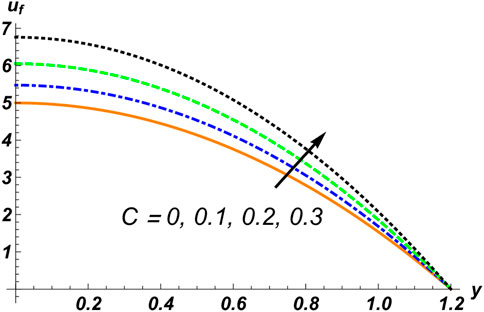
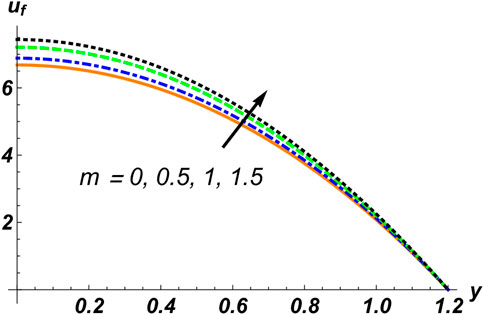
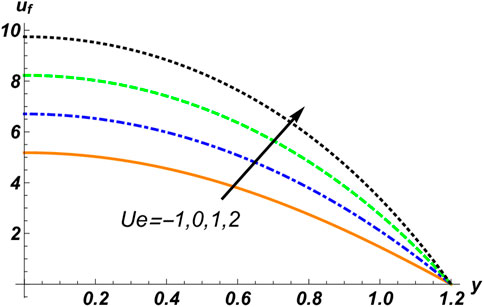
Velocity graphs are shown in Figures 10–15. Figure 10 presents the solid particle concentration C, which affects the velocity of the fluid in an increasing manner, such that if we increase the concentration of solid particles, the velocity of the fluid increases. The kind of observation can be obtained in Figures 11 and 12, which indicate the reflection of the compliant wall parameters
Conclusion
A numerical investigation is conducted to analyze the theoretical study of peristaltic flow of a Carreau fluid model in a channel with thermally induced compliant walls in the presence of electro-osmosis and Hall current effects. To estimate the effects of different valuable factors of the flow problem, graphs have been sketched that show the monotonic variation of temperature and velocity profiles. From the graphical presentation, we draw some key findings, listed as follows:
1. Temperature distribution increases with the concentration of solid particles, the rigidity of the walls, the Hall current factor, the Helmholtz–Smoluchowski velocity, and the Prandtl number.
2. The magnetic field, the electro-kinetic parameter, and the Weissenberg number have an inverse relationship with thermal exchange.
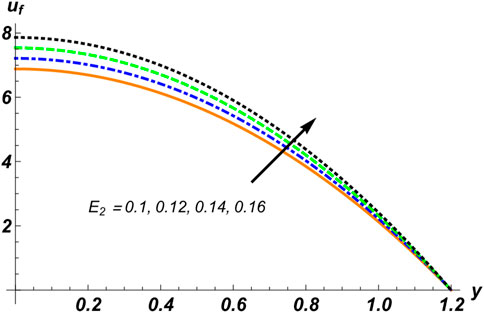
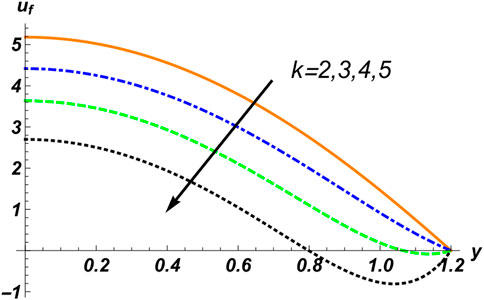
3. The velocity of the fluid phase is directly proportional to the distribution of solid particles, the compliant wall factor, the Hall current parameter, and the Helmholtz–Smoluchowski velocity.
4. The magnetic field, the electro-kinetic parameter, and the Weissenberg number are in inverse relation to the fluid’s velocity.
5. Future work can be performed on this problem by inserting heat and mass transfer effects and elaborating the entropy generation in the flow.
6. It is also notable that this study can be validated in relation to the previous relevant literature by neglecting the electro-osmotic effects. Moreover previous study on the topic [30] can be evaluated with a numerical technique of parallel shooting, and the current data are collected using the built-in Mathematica tool NDSolve to produce a more authentic numerical reading.
7. In future, we can discuss entropy generation and mass transfer effects to obtain new results.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups. [Project under grant number (RGP.2/116/43)].
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Latham TW. Fluid motions in a peristaltic pump. Doctoral dissertation, Massachusetts Institute of Technology (1966).
3. Shapiro AH, Jaffrin MY, Weinberg SL. Peristaltic pumping with long wavelengths at low Reynolds number. J Fluid Mech (1969) 37(4):799–825. doi:10.1017/s0022112069000899
4. Salahuddin T, Khan I, Malik MY, Khan M, Hussain A, Awais M. Internal friction between fluid particles of MHD tangent hyperbolic fluid with heat generation: Using coefficients improved by Cash and Karp. Eur Phys J Plus (2017) 132(5):205–10. doi:10.1140/epjp/i2017-11477-9
5. Sridhar V, Ramesh K, Gnaneswara Reddy M, Azese MN, Abdelsalam SI. On the entropy optimization of hemodynamic peristaltic pumping of a nanofluid with geometry effects. In: Waves in random and complex media (2022). p. 1–21.
6. Abdelsalam SI, Mekheimer KS, Zaher AZ. Dynamism of a hybrid Casson nanofluid with laser radiation and chemical reaction through sinusoidal channels. Waves in Random and Complex Media (2022) 1–22. doi:10.1080/17455030.2022.2058714
7. Khan M, Salahuddin T, Malik MY, Khan F. Arrhenius activation in MHD radiative Maxwell nanoliquid flow along with transformed internal energy. Eur Phys J Plus (2019) 134(5):198. doi:10.1140/epjp/i2019-12563-8
8. Khan M, Salahuddin T, Malik MY. Implementation of Darcy–forchheimer effect on magnetohydrodynamic carreau–yasuda nanofluid flow: Application of von kármán. Can J Phys (2019) 97(6):670–7. doi:10.1139/cjp-2018-0547
9. Bhatti MM, Zeeshan A. Study of variable magnetic field and endoscope on peristaltic blood flow of particle-fluid suspension through an annulus. Biomed Eng Lett (2016) 6(4):242–9. doi:10.1007/s13534-016-0226-2
10. Bhatti MM, Zeeshan A, Ellahi R. Study of heat transfer with nonlinear thermal radiation on sinusoidal motion of magnetic solid particles in a dusty fluid. J Theor Appl Mech (2016) 46(3):75–94. doi:10.1515/jtam-2016-0017
11. Bhatti MM, Zeeshan A, Ijaz N. Slip effects and endoscopy analysis on blood flow of particle-fluid suspension induced by peristaltic wave. J Mol Liquids (2016) 218:240–5. doi:10.1016/j.molliq.2016.02.066
12. Srivastava LM, Srivastava VP. Peristaltic transport of blood: Casson model—II. J Biomech (1984) 17(11):821–9. doi:10.1016/0021-9290(84)90140-4
14. Misra JC, Pandey SK. Peristaltic transport of a particle-fluid suspension in a cylindrical tube. Comput Math Appl (1994) 28(4):131–45. doi:10.1016/0898-1221(94)00134-0
15. Yamane K, Nakagawa M, Altobelli SA, Tanaka T, Tsuji Y. Steady particulate flows in a horizontal rotating cylinder. Phys Fluids (1998) 10(6):1419–27. doi:10.1063/1.869858
16. Bhatti MM, Zeeshan A, Ellahi R. Heat transfer analysis on peristaltically induced motion of particle-fluid suspension with variable viscosity: Clot blood model. Comp Methods Programs Biomed (2016) 137:115–24. doi:10.1016/j.cmpb.2016.09.010
17. Akram J, Akbar NS, Maraj E. Chemical reaction and heat source/sink effect on magnetonano Prandtl-Eyring fluid peristaltic propulsion in an inclined symmetric channel. Chin J Phys (2020) 65:300–13. doi:10.1016/j.cjph.2020.03.004
18. Rashed ZZ, Ahmed SE. Peristaltic flow of dusty nanofluids in curved channels. Comput Mater Continua (2021) 66(1):1012–26. doi:10.32604/cmc.2020.012468
19. Akbar NS, Maraj EN, Noor NFM, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. doi:10.1016/j.csite.2022.102124
20. Nazeer M, Al-Zubaidi A, Hussain F, Duraihem FZ, Anila S, Saleem S. Thermal transport of two-phase physiological flow of non-Newtonian fluid through an inclined channel with flexible walls. Case Stud Therm Eng (2022) 35:102146. doi:10.1016/j.csite.2022.102146
21. Saleem S, Subia GS, Nazeer M, Hussain F, Hameed MK. Theoretical study of electro-osmotic multiphase flow of Jeffrey fluid in a divergent channel with lubricated walls. Int Commun Heat Mass Transfer (2021) 127:105548. doi:10.1016/j.icheatmasstransfer.2021.105548
22. Riaz A, Sadiq MA. Particle–fluid suspension of a non-Newtonian fluid through a curved passage: An application of urinary tract infections. Front Phys (2020) 8:109. doi:10.3389/fphy.2020.00109
23. Noreen S, Kausar T, Tripathi D, Ain QU, Lu DC. Heat transfer analysis on creeping flow Carreau fluid driven by peristaltic pumping in an inclined asymmetric channel. Therm Sci Eng Prog (2020) 17:100486. doi:10.1016/j.tsep.2020.100486
24. Asha SK, Beleri J. Peristaltic flow of Carreau nanofluid in presence of Joule heat effect in an inclined asymmetric channel by multi-step differential transformation method. World Scientific News (2022) 164:44–63.
25. Maqbool K, Manzoor N, Ellahi R, Sait SM. Influence of heat transfer on MHD Carreau fluid flow due to motile cilia in a channel. J Therm Anal Calorim (2021) 144(6):2317–26. doi:10.1007/s10973-020-10476-6
26. Vajravelu K, Sreenadh S, Saravana R. Combined influence of velocity slip, temperature and concentration jump conditions on MHD peristaltic transport of a Carreau fluid in a non-uniform channel. Appl Math Comput (2013) 225:656–76. doi:10.1016/j.amc.2013.10.014
27. Alsemiry RD, Sayed HM, Amin N. Mathematical analysis of Carreau fluid flow and heat transfer within an eccentric catheterized artery. Alexandria Eng J (2022) 61(1):523–39. doi:10.1016/j.aej.2021.06.029
28. Bilal Ashraf M, Haq SU. The convective flow of Carreau fluid over a curved stretching surface with homogeneous-heterogeneous reactions and viscous dissipation. Waves in Random and Complex Media (2022) 1–15. doi:10.1080/17455030.2022.2032867
29. Yasmin H, Iqbal N. Convective mass/heat analysis of an electroosmotic peristaltic flow of ionic liquid in a symmetric porous microchannel with soret and dufour. Math Probl Eng (2021) 1–14. doi:10.1155/2021/2638647
30. Tripathi D, Bhushan S, Bég OA. Unsteady viscous flow driven by the combined effects of peristalsis and electro-osmosis. Alexandria Eng J (2018) 57(3):1349–59. doi:10.1016/j.aej.2017.05.027
31. Prakash J, Tripathi D. Study of EDL phenomenon in Peristaltic pumping of a Phan-Thien-Tanner Fluid through asymmetric channel. Korea-aust Rheol J (2020) 32(4):271–85. doi:10.1007/s13367-020-0026-1
32. Akram J, Akbar NS, Tripathi D. Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J Comput Sci (2022) 62:101696. doi:10.1016/j.jocs.2022.101696
33. Akram J, Akbar NS, Tripathi D. Entropy generation in electroosmotically aided peristaltic pumping of MoS2 Rabinowitsch nanofluid. Fluid Dyn Res (2022) 54(1):015507. doi:10.1088/1873-7005/ac4e7b
34. Alsharif AM, Abdellateef AI, Elmaboud YA, Abdelsalam SI. Performance enhancement of a DC-operated micropump with electroosmosis in a hybrid nanofluid: Fractional cattaneo heat flux problem. Appl Math Mech (2022) 43(6):931–44. doi:10.1007/s10483-022-2854-6
Keywords: Carreau fluid, elastic compliant walls, hall currents, electro-osmois, multiphase flow, numerical results
Citation: Alqarni MM, Riaz A, Firdous M, Lali IU, El-Din EMT and Rahman Su (2022) Hall currents and EDL effects on multiphase wavy flow of Carreau fluid in a microchannel having oscillating walls: A numerical study. Front. Phys. 10:984277. doi: 10.3389/fphy.2022.984277
Received: 01 July 2022; Accepted: 11 August 2022;
Published: 06 October 2022.
Edited by:
Muktish Acharyya, Presidency University, IndiaReviewed by:
Sara Abdelsalam, British University in Egypt, EgyptNoreen Sher Akbar, National University of Sciences and Technology (NUST), Pakistan
Copyright © 2022 Alqarni, Riaz, Firdous, Lali, El-Din and Rahman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arshad Riaz, YXJzaGFkLXJpYXpAdWUuZWR1LnBr
†These authors have contributed equally to this work
 M. M. Alqarni1†
M. M. Alqarni1† Arshad Riaz
Arshad Riaz