- 1Jiangxi Province Key Laboratory of Fusion and Information Control, Department of Physics, Nanchang University, Nanchang, China
- 2School of Physics and Materials, Nanchang University, Nanchang, China
- 3NCU-ASIPP Magnetic Confinement Fusion Joint Lab, Institute of Fusion Energy and Plasma Application, Nanchang University, Nanchang, China
- 4Department of Electronic Information Engineering, Nanchang University, Nanchang, China
A feasible multi-party quantum private comparison (MQPC) protocol based on
1 Introduction
Secure multi-party computation (SMC) was introduced by the famous Millionaires’ problem in 1982 [1], where two millionaires want to compare their wealth and learn who is wealthier without revealing their actual property. With the combination of quantum mechanics and information science, researchers have found that processing information using quantum systems has led to many striking results, such as teleportation of quantum states and quantum algorithms that are exponentially faster than their known classical counterpart. Therefore, the quantum version of SMC has once again set off a research boom. As a particular instance of quantum SMC (QSMC), quantum private comparison (QPC) has wide applications in private bidding and auctions, secret ballot elections, commercial business, identification.
Right after Yao’s millionaire problem, [2] designed an efficient and fair protocol to determine whether two millionaires are equal rich. However, as proved by [3], a quantum two-party secure computation is impossible. Therefore, a third party (e.g., a semi-honest third party) is often involved to help them achieve the task in a QSMC protocol. The semi-honest quantum third party (TP) will always follow the process of the protocol honestly. He will not prepare other types of particles (e.g., GHZ state, single photon) and conspire with any participants or outside eavesdroppers to steal the participants’ privacies. But the TP is curious to know the participants’ privacies, and try to extract their private information from he knows.
In 2009, the first QPC protocol was proposed by based on Bell states [4]. With decoy particle technology, one-way hash function and unitary operation, this protocol can compare the equality. In 2010, [5] devised a novel QPC protocol to compare the equality based on GHZ states, where the unitary operation is necessary. These early QPC protocols can only compare the equality. In 2011, a new QPC protocol was presented by [6] to compare the size relationship of privacies, where the information of size was encoded into the phase of GHZ state. In 2013, Lin et al. also designed a protocol to compare the size relationship based on the
Fortunately, in 2013, the first MQPC protocol was proposed based on GHZ states by [8]. Suppose there are
To make the implementation of the protocol easier, a new MQPC protocol to compare the size relationship among many participants’ privacies is proposed. The
2 The proposed MQPC protocol based on d-dimensional bell states
Assume there are
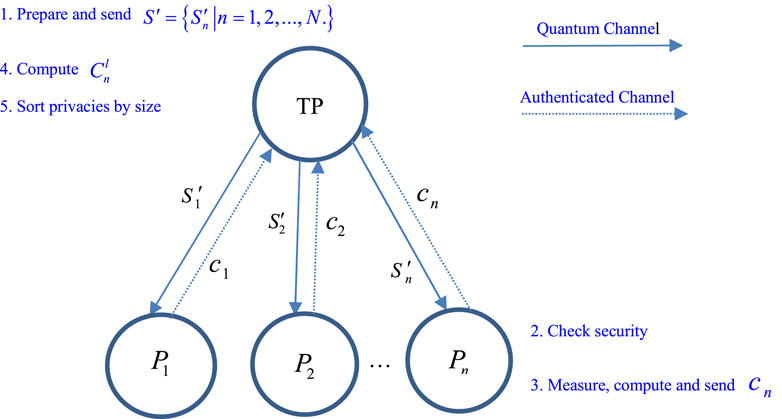
FIGURE 1. The schematic figure of the proposed protocol. The TP needs to implement steps 1, 4, 5 and each participant needs to implement steps 2, 3.
2.1
Bell state, used to describe the four maximal entangled states in two-qubit system, is the most basic quantum entangled state. Compared with other quantum entangled states, Bell state is the easiest to prepare in experiment. Therefore, Bell state is widely used to design quantum cryptographic protocol. In a
where
where
2.2 The proposed MQPC protocol
Step 1: According to Eq. 1, the TP randomly prepares
Based on these prepared Bell states in Eq. 3, he will record the
To prevent eavesdropping, TP will prepare
Step 2: After all the quantum sequences have been received by the corresponding participants, TP will announce the position and the measurement basis of each decoy particle in sequence
Step 3: After removing these decoy particles, each participant will measure the remaining particles with Z basis and record them as
Then, Participant
Step 4: When confirming all sequences embedded privacy data have been received, TP will measure the particles in each sequence
Here,
Step 5: After TP obtaining sequence
Then, he can obtain
For the
3 Correctness analysis
3.1 Output correctness
The quantum resource used in the protocol is the
Therefore, based on Eqs 4, 5 and 6, the Eq. 9 can be deduced
From Eq. 10, one can see that the value of
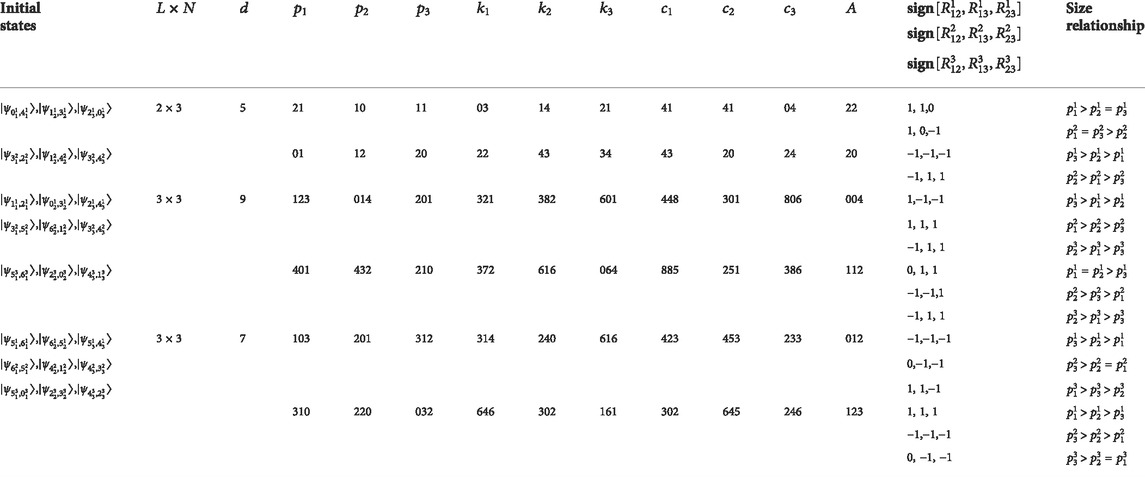
3.2 Examples
Here, some examples are given for illustration the presented protocol without considering the eavesdropping checking. Let
Step 1: TP randomly prepares
First, he records
Step 2: Suppose that no eavesdropper is detected; then, move to Step 3.
Step 3: After removing these decoy particles, Participants
Therefore, after all participants encode their privacies according to Eq. 4, Participants
Step 4: When confirming that the encoding information from all participants has been received, the TP will measure the particles in sequence
Step 5: TP will finish sorting the privacies by size as follows
Similar to Eq. 13, the TP can obtain
Apparently, the size relationship that TP sorts without knowing participants’ privacies is consistent with the actual data (
4 Security analysis
Assumed that the quantum and authentical channels are the ideal channels, that’s to say, there is no noise in the channel and the particles can be sent to the receivers. In this section, the security of the proposed protocol will be analyzed from both external and internal attack. It is shown that no private information has been leaked according to the security analysis.
4.1 External attack
Eve, an external attacker, may attempt to acquire information from the participants including TP. In Step 1, Sequence
4.2 Internal attack
Case 1 Internal attack from
Suppose participant
Case 2 Internal attack from TP
From Section 2.2, one can know that TP is both the sender of quantum information and the receiver of all encrypted information. Therefore, he can obtain more information than other attackers during the protocol execution. Significantly, due to TP semi-honesty, that the only thing he can do is try to extract the information from the received ciphertext
5 Discussion
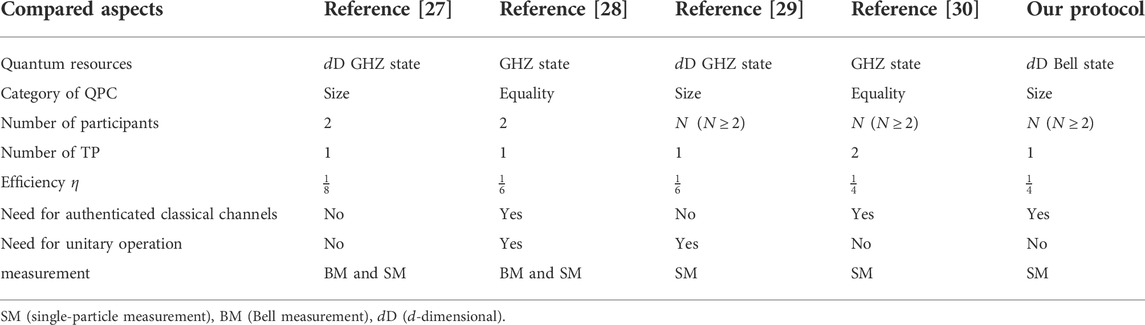
In Table 2, the proposed protocol is compared with some other similar protocols with the following aspects: quantum resource used, category of QPC (size or equality), number of participants, number of TP, need for the authenticated classical channel, need for unitary operation, measurement involved, and qubit efficiency
In Ref. [27], we proposed a new QPC protocol to compare the size relationship of privacies between two participants. The quantum resources used in the protocol are
In Ref. [28], the authors presented a new QPC protocol to compare the equality of privacies between two participants. The quantum resources used are GHZ states. First, the TP needs
In Ref. [29], a novel MQPC protocol for comparing the size relationship among
In Ref. [30], the authors proposed a new MQPC protocol to compare the size relationship among
In our protocol, a new MQPC protocol to compare the size relationship among
From Table 2, one can see that, like the protocols in [27, 29], our protocol can compare the size relationship among privacies, while in [28, 30] they can only compare the equality. When it comes to the MQPC, Refs. [27, 28] are useless. Compared with these protocols listed in Table 2, the unitary operation is not necessary, and only single-particle measurement is required in our protocol. Additionally, our protocol ensures the highest qubit efficiency only with the help of one TP. Table 2 clearly shows that the performance of the proposed protocol is better than these similar QPC protocols. However, it has to be said that the high dimensional quantum state is not easy to obtain experimentally at present. Therefore, we still need to work harder to realize the protocol based on the high dimensional quantum state in experiment.
6 Conclusion
Based on the
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
BW: Conceptualization, methodology, investigation, formal analysis, writing—original draft; L-HG: validation, writing- reviewing and editing S-QL: Conceptualization, funding acquisition, resources, supervision, writing—review and; editing.
Funding
This work is supported by the National Natural Science Foundation of China Grant No. 62161025, the Project of Scientific and Technological Innovation Base of Jiangxi Province Grant No. 20203CCD46008, and the Jiangxi Provincial Key Laboratory of Fusion and Information Control Grant No. 20171BCD40005.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Yao AC. Protocols for secure computations. In: Proceedings of 23rd IEEE Symposium on Foundations of Computer Science (SFCS’08); 03-05 November 1982. Washington, DC, USA: IEEE (1982). p. 160–4. doi:10.1109/SFCS.1982.38
2. Boudot F, Schoenmakers B, Traore J. A fair and efficient solution to the socialist millionaires’ problem. Discrete Appl Math (2001) 111:23–36. doi:10.1016/s0166-218x(00)00342-5
3. Lo HK. Insecurity of quantum secure computations. Phys Rev A (Coll Park) (1997) 56:1154–62. doi:10.1103/physreva.56.1154
4. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42:055305. doi:10.1088/1751-8113/42/5/055305
5. Chen XB, Xu G, Niu XX, Wen QY, Yang YX. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt Commun (2010) 283:1561–5. doi:10.1016/j.optcom.2009.11.085
6. Jia HY, Wen QY, Song TT, Gao F. Quantum protocol for millionaire problem. Opt Commun (2011) 284:545–9. doi:10.1016/j.optcom.2010.09.005
7. Lin S, Sun Y, Liu XF, Yao ZQ. Quantum private comparison protocol with d-dimensional Bell states. Quan Inf Process (2013) 12:559–68. doi:10.1007/s11128-012-0395-6
8. Chang YJ, Tsai CW, Hwang T. Multi-user private comparison protocol using GHZ class states. Quan Inf Process (2013) 12:1077–88. doi:10.1007/s11128-012-0454-z
9. Luo QB, Yang GW, She K, Niu WN, Wang YQ. Multi-party quantum private comparison protocol based on $$d$$ d -dimensional entangled states. Quan Inf Process (2014) 13:2343–52. doi:10.1007/s11128-014-0805-z
10. Wang QL, Sun HX, Huang W. Multi-party quantum private comparison protocol with $$n$$ n -level entangled states. Quan Inf Process (2014) 13:2375–89. doi:10.1007/s11128-014-0774-2
11. Zhang B, Liu XT, Wang J, Wang J, Tang CJ. Cryptanalysis and improvement of quantum private comparison of equality protocol without a third party. Quan Inf Process (2015) 14:4593–600. doi:10.1007/s11128-015-1145-3
12. Ji ZX, Zhang HG, Fan PR. Two-party quantum private comparison protocol with maximally entangled seven-qubit state. Mod Phys Lett A (2019) 34:1950229. doi:10.1142/s0217732319502298
13. Zhou NR, Xu QD, Du NS, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional Bell states. Quan Inf Process (2021) 20:124. doi:10.1007/s11128-021-03056-6
14. Liu W, Wang YB, Wang XM. Quantum multi-party private comparison protocol using d-dimensional bell states-dimensional bell states. Int J Theor Phys (Dordr) (2015) 54:1830–9. doi:10.1007/s10773-014-2388-y
15. Ye CQ, Ye TY. Multi-party quantum private comparison of size relation with d-level single-particle states-level single-particle states. Quan Inf Process (2018) 17:252. doi:10.1007/s11128-018-2021-8
16. Cao H, Ma WP, Lü LD, He YF, Liu G. Multi-party quantum privacy comparison of size based on d-level GHZ states. Quan Inf Process (2019) 18:287. doi:10.1007/s11128-019-2401-8
17. Ye TY, Hu JL. Multi-party quantum private comparison based on entanglement swapping of bell entangled states within d-level quantum system. Int J Theor Phys (Dordr) (2021) 60(4):1471–80. doi:10.1007/s10773-021-04771-7
18. Daniel BS, Constantin B, Patrick JC, Norbert L, Ryan MC, Junji U, et al. Self-referenced continuous-variable quantum key distribution protocol. Phys Rev X (2015) 5:041010. doi:10.1103/physrevx.5.041010
19. Liu XS, Long GL, Tong DM, Li F. General scheme for super dense coding between multi-parties. Phys Rev A (Coll Park) (2002) 65:022304. doi:10.1103/physreva.65.022304
20. Liu ZH, Chen HW, Xu J, Liu WJ, Li ZQ. High-dimensional deterministic multiparty quantum secret sharing without unitary operations. Quan Inf Process (2013) 11:1785–95. doi:10.1007/s11128-011-0333-z
21. Lo HK, Ma X, Chen K. Decoy state quantum key distribution. Phys Rev Lett (2005) 94:230504. doi:10.1103/PhysRevLett.94.230504
22. Wang XB. Beating the photon-number-splitting attack in practical quantum cryptography. Phys Rev Lett (2005) 94:230503. doi:10.1103/PhysRevLett.94.230503
23. Deng FG, Li XH, Zhou HY. Efficient high-capacity quantum secret sharing with two-photon entanglement. Phys Lett A (2008) 372(12):1957–62. doi:10.1016/j.physleta.2007.10.066
24. Deng FG, Long GL, Liu XS. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys Rev A (Coll Park) (2003) 68(4):042317. doi:10.1103/physreva.68.042317
25. Bennett CH, Brassard G. Quantum cryptography: Public-key distribution and coin tossing. In: Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing; 14-16 Nov. 2005. Bangalore. India: IEEE Press (1984). p. 175–9.
26. Shor PW, Preskill J. Simple proof of security of the BB84 quantum key distribution protocol. Phys Rev Lett (2000) 85(2):441–4. doi:10.1103/physrevlett.85.441
27. Wang B, Liu SQ, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional GHZ states. Chin Phys B (2022) 31:010302. doi:10.1088/1674-1056/ac1413
28. Xu QD, Chen HY, Gong LH, Zhou NR. Quantum private comparison protocol based on four-particle GHZ states. Int J Theor Phys (Dordr) (2020) 59:1798–806. doi:10.1007/s10773-020-04446-9
29. Huang SL, Hwang T, Gope P. Multi-party quantum private comparison with an almost-dishonest third party. Quan Inf Process (2015) 14:4225–35. doi:10.1007/s11128-015-1104-z
Keywords: multi-party quantum private comparison, size relationship, d-dimensional bell state, qubit efficiency, semi-honest quantum third party
Citation: Wang B, Gong L-H and Liu S-Q (2022) Multi-party quantum private size comparison protocol with d-dimensional Bell states. Front. Phys. 10:981376. doi: 10.3389/fphy.2022.981376
Received: 29 June 2022; Accepted: 15 July 2022;
Published: 22 August 2022.
Edited by:
Tianyu Ye, Zhejiang Gongshang University, ChinaReviewed by:
Run-hua Shi, North China Electric Power University, ChinaMingxing Luo, Southwest Jiaotong University, China
Yuling Chen, Guizhou University, China
Copyright © 2022 Wang, Gong and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: San-Qiu Liu, c3FsZ3JvdXBAbmN1LmVkdS5jbg==
 Bing Wang
Bing Wang Li-Hua Gong
Li-Hua Gong San-Qiu Liu
San-Qiu Liu