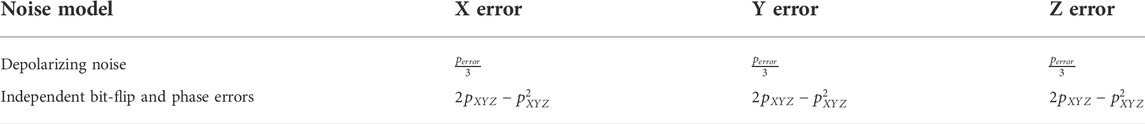Determining quantum topological semion code decoder performance and error correction effectiveness with reinforcement learning

Quantum error correction technology is a vital method to eliminate noise during the operation of quantum computers. To solve the problem caused by noise, in this paper, reinforcement learning is used to encode defects of Semion codes, and the experience replay technique is used to realize the design of decoder. Semion codes are quantum topological error correction codes with the same symmetry group ${\mathbb{Z}}_2$ as Kitaev toric codes, we used the topological characteristics of error correction codes to map qubits to multi-dimensional space, and error correction accuracy of the decoder is calculated to be 77.5%. Calculate the threshold of topological quantum Semion code, depending on the code distance, resulting in different thresholds, p_threshold = 0.081574 when the code distance is d = 3, 5, 7 and threshold p_threshold = 0.09542 when the code distance is d = 5, 7, 9. And we design the $\mathbb{Q}$-network to optimize the cost of quantum circuit gates and compare the size of the cost reduction under different thresholds. Reinforcement learning is an important method for designing Semion code decoders and optimizing numerical values, providing more general error models and error correction codes for future machine engineering decoders.

1 Introduction

Quantum computing and quantum information have made tremendous progress over the years, and technologies based on quantum communication and quantum error correction (QEC) are developing rapidly [1–4]. The robustness of quantum memory to outer noise and noise removal is an extremely significant resource for quantum fault tolerance [5–9]. Among quantum memories, Among quantum memories, Kitaev toric code [10] is the first proposed topological torus code, which is a simple two-dimensional lattice gauge theory with the ${\mathbb{Z}}_2$ gauge group. A double-Semion model is a model with the same gauge group theory as Kiteav but with not the same topological properties [11,12]. Although the double Semion model and Kitaev have the same standard set, there are some differences. Double Semion codes weave two elementary quasiparticle excitations that will give ± i phase, showing the statistic of anyons, while Kitaev toric codes only give a ±1 phase factor. The topological order provides a wide range of new topological codes with non-Pauli stabilizers, such as error correction codes: Semion code, which is topologically ordered, respect the stabilizer formalism, but due to Pauli X and Pauli Z existing in the square operator, it is not Pauli’s code, it can not be represented as a tensor product of Pauli matrices, so it is not Calderbank-Shor-Steane (CSS) code [13].

Threshold is an effective means of characterizing fault tolerance performance. Specifically, when the physical error rate of qubits is lower than a certain threshold, quantum error correction can be applied to perform effective quantum computing, and the logical error rate can be suppressed to an arbitrarily low level. Due to the fragile nature of quantum information, future universal quantum computers could diagnose syndromes based on the logic qubits of stabilizers. To prevent error propagation and logical failures, a decoder needs to be designed that provides a set of recovery operations to correct errors given a specific syndrome, must include the corresponding error statistics [13] for any given syndrome, and must account for the defects of the syndrome due to measurement errors of the stabilizer, requiring QEC. At present, there are many decoders designed based on topological codes, not only toric codes [14,15], but also color codes [16,17]. The logical qubit is composed of a large number of entangled physical qubits. It can prevent local disturbance caused by errors such as bit flips when the logic operation requires global changes.

Reinforcement learning (RL) combined with deep learning has achieved great success in many fields [18–20]. Techniques from machine learning have begun to find applications in various fields of quantum physics and to fast solve decoding problems [21–23], decoders of many kinds of neural networks have been proposed, although such methods have obvious advantages, it promises extremely fast decoding times, flexibility relative to underlying code and noise models, and the ability to scale to large code distances, there is room for improvement and application. At present, there are many decoders designed based on toric codes and color codes [24,25], but few decoders based on Semion code are involved. Although the performance of our proposed decoder is not better than the current decoder, its value lies in the show that it is feasible to implement the design of Semion code using RL. The paper studies a decoder to find the optimal error correction strategy for quantum topological Semion codes. In the field of quantum computing, it is necessary to try to measure the logical errors generated by the decoder given the syndrome, and to detect the logical errors generated by the decoder through intelligent algorithms. We apply deep learning to quantum computing, decoding for future universal self-training devices provides ideas.

The following contents are arranged as follows. In Section 2, a brief background on quantum topological Semion codes and RL. In Section 3, an algorithm was designed for quantum topological Semion codes. In Section 4, analysis of error correction performance, and conclude in Section 5.

2 Background

2.1 Quantum topological semion code

The double Semion model plays a principal role in the fields of gapped systems and new topological orders [26], and the Semion code is an error correction code that needs to be studied in depth in topological codes. Semion code is a QEC code with the characteristics of the double Semion model. The Semion code has a topological protection effect on quantum information and will not affect the global error due to local errors. Semion code is a non-CSS and non-Pauli topological code described as a hexagonal lattice Λ. We map the qubits in three-dimensional space and use the topology of the code to convert qubits into qubits in multi-dimensional space. The edges represent physical qubits and the vertices represent stabilizer operators. The vertex operator is represented by V_Q, and vertex Q is represented as shown in Figure 1(1), and the Pauli Z operator is represented as:

$V_Q=Z_i{Z}_j{Z}_k(1)$

FIGURE 1

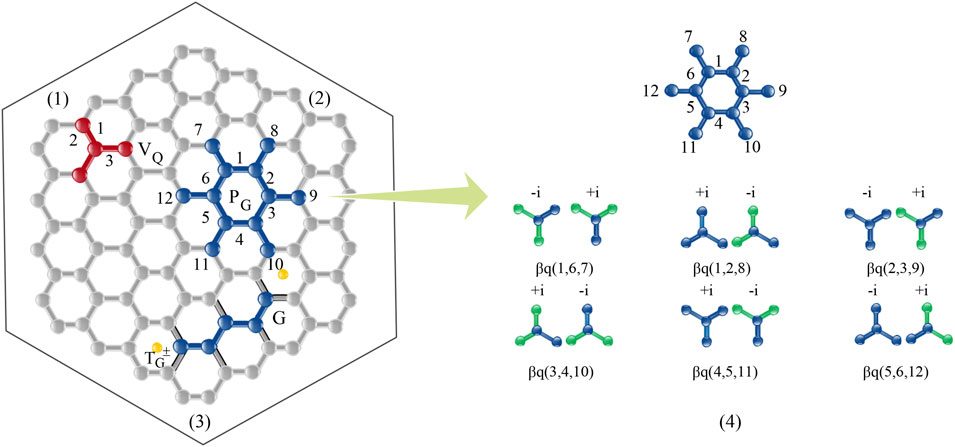
FIGURE 1. Hexagonal lattice diagram, the outermost hexagonal frame is only for aesthetics and does not represent a bounded hexagonal diagram. (1)Vertex operator V_Q. (2)Plaquette operator P_G, the plaquette operator not only includes the blue hexagon, but also the outputting legs connecting the hexagon. (3)The path G of the positive or negative chirality string operator $T_G^{\pm }$ is represented by the blue path, the connecting line represents the $T_G^{\pm }$ support Conn(G), and the yellow dots represent a pair of vertex excitations generated at the endpoints of the path G. (4)Phase factor diagram expanded from (2).

Plaquette operator is represented by P_G, and apply the Pauli X operator on the sides of the hexagon:

$P_G=\prod _{k\in \partial G}{X}_k\sum _{\vec{j}}{p}_G\left(\vec{j}\right)|\vec{j}\rangle \langle \vec{j}|(2)$

$\vec{j}$ in the above formula represents the bit string of a state on the basis of calculation, ∂G belongs to the edge of the plaquette boundary, the value of $p_G(\vec{j})$ is {±1, ±i}. The diagonal operator ${\sum }_{\vec{j}}{p}_G(\vec{j})|\vec{j}\rangle \langle \vec{j}|$ acts on the twelve qubits in Figure 1(2).

2.2 Reinforcement learning

RL problems consider an agent that interacts with the environment [27]. The agent can manipulate and observe parts and perform a sequence of actions to accomplish a particular problem. Through RL, we can find the optimal policy of the action subject in the system. The optimal policy is the policy that proxies the best return in the process of interacting with the system. Discrete problems are usually considered. At each time step t, the environment can be represented by a state s_t ∈ S, where S is the state space. Given a state, the agent can choose to perform an action a_t ∈ A, where A is the action space. According to the result after the agent selects the action, the state is updated accordingly, entering a new state s_t+1, and providing the agent with feedback on the action selection in the form of reward r_t+1, starting from time t, the return R_t = r_t+1 + λr_t+1 + λ²r_t+1 + ⋯, where λ ≤ 1 is the discount factor that quantifies how one wants to value immediate and subsequent returns [28]. There will be a constant return r = 1 for each step. To formalize the agent’s decision-making process, we define the agent’s policy as π, and π(a, s) is the probability that the agent chooses a_t = a when the state is in s_t = s. By using a measure of discounted cumulative reward, the value of any given state depends not only on immediate rewards from that state following a particular policy but also on expected rewards in the future.

3 Algorithmic process

3.1 Explore semion code

As shown in Figure 1(4), the subscript q runs over the vertices belonging to the plaquette G. β_q can be represented by twelve qubits as

$\begin{array}{ll}\hfill {\mathrm{\Sigma }}_{q\in G}{\beta }_q& =i^{n_7^{+}\left(n_1^{+}{n}_6^{-}-n_1^{-}{n}_6^{+}\right)}{i}^{n_8^{-}\left(n_1^{-}{n}_2^{-}-n_1^{+}{n}_2^{+}\right)}\hfill \\ \hfill & =i^{n_9^{-}\left(n_2^{+}{n}_3^{+}-n_2^{-}{n}_3^{-}\right)}{i}^{n_{10}^{+}\left(n_3^{-}{n}_4^{+}-n_3^{+}{n}_4^{-}\right)}\hfill \\ \hfill & =i^{n_{11}^{-}\left(n_4^{-}{n}_5^{-}-n_4^{+}{n}_5^{+}\right)}{i}^{n_{12}^{-}\left(n_5^{+}{n}_6^{+}-n_5^{-}{n}_6^{-}\right)}\hfill \end{array}(3)$

and

$n_i^{\pm }=\frac{1}{2}\left(1\pm Z_i\right)(4)$

According to the above analysis, $p_G(\vec{j})$ can be clearly defined as

$\sum _j{p}_G\left(\vec{j}\right)|\vec{j}\rangle \langle \vec{j}|=\prod _{k\in \partial G}{\left(-1\right)}^{n_{k-1}^{-}{n}_k^{+}}\prod _{q\in G}{\beta }_q(5)$

Therefore, according to the above reasoning, we add β_q to $P_G^{\prime }$ on each vertex, and we can obtain a $P_G^{\prime }$ expression that conforms to the entire Hilbert space.

$P_G^{\prime }=\prod _{k\in \partial G}{X}_k\prod _{k\in \partial G}{\left(-1\right)}^{n_{k-1}^{-}{n}_k^{+}}(6)$

$P_G^{\prime }$ satisfies the commutate [29] principle of the operator, and the plaquette operator allows the definition based on stability topological error-correcting code in agent form.

The same as the string operator in Kitaev toric code, T^Z in Semion code is expressed as a string operator that generates grid excitation [30], that is, T^Z is a string of Z operators. Each stabilizer commutes with these operators except the grid operator at the end of the string, and the string X produces the string operator of the vertex excitation, as shown in Figure 1(3). We commute the characters on the path G. The string is marked as $T_G^{+}$ and is supported by coon. $T_G^{+}$ can only act on the coon set of qubits non-trivially. According to the constraints: (1)The square of the string operator is 1. (2)It must be determined by exchanging with the stabilizer. The system of linear equations can be withdrawn from $F(\vec{j})$,

$F\left(\vec{j}\right)=F\left(\vec{j}\oplus \vec{i}\right)(7)$

the qubit of $F(\vec{j})$ in Coon(G) [11] is 0, and the ⊕ sign represents the sum of the remainder of the bit string to Z. The value of $F(\vec{j})$ is {±1, ±i}. So the string $T_G^{+}$ is:

$T_G^{+}=\prod _{k\in G}{X}_k\sum _{j}F\left(\vec{j}\right)|\vec{j}\rangle \langle \vec{j}|(8)$

The quasiparticle vertex excitation behavior generated by $T_G^{+}$ is the same as that of anyons.

The positive chirality string is defined as T⁺, the negative chirality string is T⁻, and the negative chirality string can be got by calculating the T^Z string operator, that is, T⁻ = T^ZT⁺. The operator commutes with the Z operator, and the Z operator and T^± do not commute. In conclusion, the commutation principle to be followed is:

$\left[T^{\pm },T^{\pm }\right]=0,\left[T^{\mp },T^{\pm }\right]=0,\left[T^Z,T^{\pm }\right]=0(9)$

The Hamiltonian is used as the coding space, Semion codes are alike to Kitaev toric codes, with vertex and plaquette operators. Embedding the Semion code in Kitaev toric code results in two quantum memories with logical qubits. The logical operator consists of $T_L^{+}$ and $T_H^{+}$, H(L) is any homogeneous non-trivial path in the horizontal (vertical) direction, and the other pair logical operator is $T_L^{-}$ and $T_H^{-}$, which are non-self-intersecting or overlapping the composition of each path is shown in Figure 2(1). Two logical qubits of the code require two pairs of logical operators, which are defined as X₁ and X₂:

$X_1=T_H^{-},Z_1=T_L^Z,X_2=T_L^{+},Z_2=T_H^Z(10)$

FIGURE 2

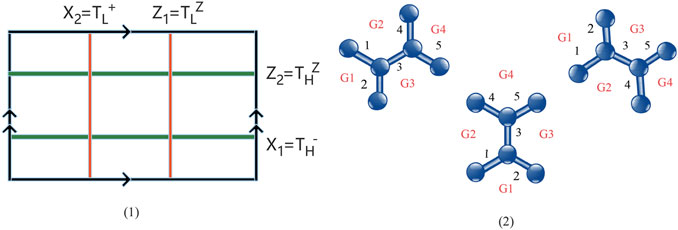
FIGURE 2. (1)Uncomplicated example of two sets of logical operators on a torus, with arrows denoting the identified boundaries. (2)The three possible edge orientations on the X operator can be applied. The qubit marked 3 is influenced in any case, in addition to this, it may leave flux excitations on the four surrounding plaquettes labeled by G1, G2, G3, G4.

The set of these operators satisfies the inverse relationship. The hexagonal lattice makes the distance of the X operator twice that of the Z operator, which can better avoid errors. To perform error correction, the stabilizers have to be measured periodically, and the excitations have to be annihilated by bringing them together using the string operators.

3.2 Build noise models

The error-correcting ability [31] of QEC codes depends on the type and strength of qubit manager errors [32–34]. In the context of topological codes, two error models have been extensively studied, namely depolarizing noise and independent bit-flip and phase errors. In the depolarizing noise model, each qubit has an error according to the following probability (1−p_error) for no error, and $\frac{p_{\mathit{error}}}{3}$ for X, Y, and Z errors. p_error is a parameter between 0 and 1. The model is symmetric between X, Y, Z.

In the independent bit-flip and phase errors, each qubit will be affected by the error, we record the probability of X error, Y error, and Z error as p_XYZ, so the probability of error is $p_{\mathit{error}}=2p_{\mathit{XY\; Z}}-p_{\mathit{XY\; Z}}^2$. As shown in Table 1.

TABLE 1

TABLE 1. Error model.

Assuming that the X operator is applied to a qubit, for three possible edge orientations, the probability of a syndrome error can be obtained, with the “+” sign indicating the excitation on a given plaquette. Table 2 shows the probabilities of calculating a given flux pattern, corresponding to Figure 2(2).

TABLE 2

TABLE 2. Different probabilities of plaquette excitation.

Consider that the error operator of the n-qubit Pauli operator is E. In the stabilizer, errors are detected by measuring the stabilizer generator. If no errors occur, these measurements will output +1 eigenvalues. If an error E occurs, the same as The stabilizer generator against E commutation will output −1, and the output of the stabilizer measurement is the error syndrome. To correct the error, the inverse operator of the error is applied, and in the case of the self-inverse Pauli error, the same operator can be applied [35,36]. The main task of error correction is to determine the correction operator to apply to a given syndrome. The decoder is designed to give an error model and output a correction operator after analyzing the probabilities of all possible errors consistent with the observed syndrome. The optimal decoder is to choose the most suitable correction chain, and this choice will depend heavily on the specific error model.

3.3 Convert to square form

Embed the Semion code into the torus. We improved it and used the Ref. [37] programming framework to map the hexagonal lattice of Semion code to square, Ref. [11] provided an idea for our conversion process. As shown in Figure 3, the left picture is a schematic diagram of a hexagonal lattice, the numbers with blue circles represent half calculations, there are sixteen symbols in total, the red numbers are vertex operators, and there are thirty-two in total. The data outside of the square is the period filling used, which shows the periodic boundary condition of the Semion code. The figure on the right is a converted square lattice, and the numbers with blue circles represent plaquette operators. The “∣” in the figure is to ensure hexagonal space structure. Its value is always recorded as zero and does not correspond to any element measured by the stabilizer. The numbers in the blue circles represent companion calculations. Letters were used to represent vertices and plaquette operators, when the code distance is d, there are 2d² vertices and d² plaquettes, so there are 3d² stabilizers in total. Map the Semion code into a square and choose d = 4, so a square image of 8 × 8 is obtained. We assume that vertex and plaquette operators are marked from right to left and top to bottom. The syndrome of vertex s corresponds to the W_k,m of an image element, where k and m are expressed as follows:

$k=2\times \lfloor \frac{q-1}{2d}\rfloor +1(11)$

$m=\mathit{mod}\left(q-1+\left(1-2d\right)\lfloor \frac{q-1}{2d}\rfloor ,2d\right)+1(12)$

The syndrome of plaquette G corresponds to the W_k,m of the image element, where k and m are expressed as follows:

$k=2\times \lfloor \frac{G-1}{2d}\rfloor +2(13)$

$m=\mathit{mod}\left(2G+\left(1-4d\right)\lfloor \frac{G-1}{d}\rfloor ,2d\right)+1(14)$

FIGURE 3

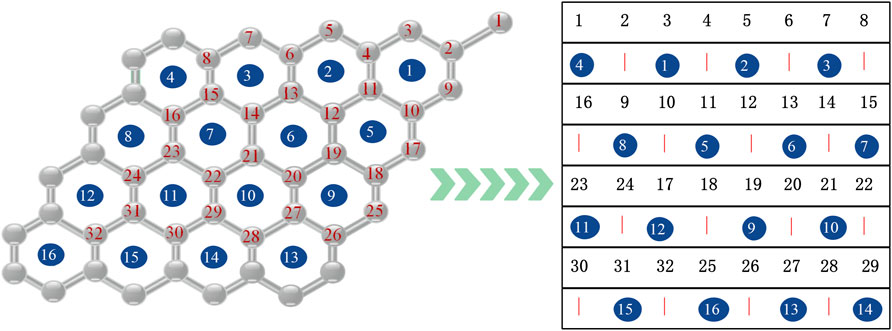
FIGURE 3. Lattice transformation square diagram. The left picture is a schematic diagram of a hexagonal lattice. The numbers with blue circles represent half calculations. There are 16 symbols in total, the red numbers are vertex operators, and there are 32 in total. The figure on the right is a converted square lattice. The numbers with blue circles represent plaquette operators, and red “∣” represents the spatial structure. Extra values do not have any meaning, other numbers are vertices. In the previous figure, letters were used to represent vertices and plaquette operators. Due to the large number here, we use numbers to represent.

3.4 Emulate semion codes decoder

Quantum computers are affected by the noise of the external environment, which makes the operations perform defects. Therefore, an error correction mechanism is needed to improve the defects. The decoding algorithm needs to count the homology of each particle to restore topological information [6,38]. Stabilizer code allows errors to be detected by measuring stable code operators without changing the encoding information and correcting errors by performing recovery operations [39]. If the encoding task has a specific structure, the decoding task can be easier to handle, and an efficient decoder with better performance can be obtained. The topological code stabilizer is geometrically local, and the abnormal return value indicates that some qubits have errors [40]. Local errors can be detected and corrected by encoding quantum information in a non-local manner. Error syndromes consist of measurements of non-trivial stabilizer operators, and syndrome analysis can infer what errors have occurred and how to correct them.

Using the $\mathbb{Q}$ function to represent the action-value function of a set of actions and the cumulative reward of the corresponding transition, update the estimate of $\mathbb{Q}$ using the formula:

$\mathbb{Q}\left(s,a\right)+\delta \left[\left(r+\lambda ma{x}_{a^{\prime }}\mathbb{Q}\left(s^{\prime },a^{\prime }\right)\right)-\mathbb{Q}\left(s,a\right)\right]\to \mathbb{Q}\left(s,a\right)(15)$

where δ < 1 is the learning rate. The action-value function $\mathbb{Q}(s,a)$ represents the payoff of taking action a in state s and following a certain strategy at π. In the next step of $\mathbb{Q}$-learning, $\mathbb{Q}(s,a)=r+\lambda ma{x}_{a^{\prime }}\mathbb{Q}(s^{\prime },a^{\prime })$ is used to quantify $\mathbb{Q}$, s → s′ is the optimal policy to follow for the current estimate of $\mathbb{Q}$. The policy is given by ${\max }_a\mathbb{Q}(s,a)$ taking action a will eventually converge to the optimal policy, and it is quite useful to follow the ɛ-greedy policy, which takes the optimal action for the estimate of $\mathbb{Q}(s,a)$ with probability (1 − ɛ), but take a random action with probability ɛ. For a large state-action space, it is impossible to store a complete action-value function. In deep $\mathbb{Q}$-learning, a deep neural network is used to represent the action-value function. The input layer is the representation of a certain state, and the output layer is possible the value of the action, using $\mathbb{Q}(s,a,\theta )$ to denote the parameterization of the $\mathbb{Q}$-function by the neural network, and θ to denote the network’s complete set of weights and biases.

The RL decoder used is the evaluation of the capability of generated action by an agent through reinforcement information provided by the environment, without telling the agent how to generate corrective action. Since the outer environment offers a little piece of information, an agent must learn through experience. It learns a mapping from the environment state to the behavior so that the selected behavior can get the maximum reward of the environment, and the system dynamically adjusts the parameters. To achieve the maximum enhancement signal. In a larger state-action space, it is impossible to save a complete action-value function, using depth $\mathbb{Q}$-learning, a deep neural network represents the action-value function, and the input layer represents a specific state. The output layer is the value of some earthly actions. This simulation part uses a neural network-based decoder [41,42], uses RL methods to optimize the observation of Semion code syndrome, and gradually proposes the recovery chain of a syndrome.

Training of decoder adopts deep $\mathbb{Q}$-network algorithm, which uses experience playback technology to store experience gained by an agent in the form of a conversion tuple in-memory buffer. A specific process is to first send syndrome to an agent in the action part, according to the defect of $\mathbb{Q}$-network, select action store results in a buffer in the form of a tuple, and then enter the learning process, and use stochastic gradient descent algorithm to reduce $\mathbb{Q}$-network prediction for a gap between target and sample target, according to the requirements of the target network, network parameters are optimized, and then a new training sequence is started, the weight of $\mathbb{Q}$-network is synchronized with the weight of target network. In terms of sample selection, the samples are divided into three independent parts, namely the training set, validation set, and test set. The training set is used to estimate the model, the validation set is used to determine the network structure or parameters that control the complexity of the model, and the test set tests the performance of the final selected optimal model. 50% of the sample is the training set, 25% of the sample is the validation and test sets, and all three parts are randomly selected from the sample.

4 Error correction performance analysis

4.1 Error correction performance

Taking depolarization noise as an example, through the training of the decoder, the data map shown in Figure 4 is obtained. It is found that the performance of the decoder is better, and the accuracy of error correction can reach 77.5%. The decoder in this paper is to calculate the threshold of the Semion code. The logical error rate is drawn in the range of the physical error rate for different code distances, and the threshold is generally determined as the physical error rate value at the intersection of the two. For physical error rates below the intersection of the two, the logical error rate will decrease as the code distance increases. For each physical error rate, the logical error rate is calculated as the average of multiple independent instances, and for experimental certainty, it must be determined that a certain number of logical errors are observed each time in an actual experiment. For the code distance d, the logical error rate p_logical should have the following correspondence:

$p_{\mathit{logical}}=\left(p_{\mathit{error}}-p_{\mathit{threshold}}\right)\times d^{\frac{1}{v_o}}(16)$

where p_error is the physical error rate, p_threshold is the threshold, v_o is the scaling exponent. Based on the above formula, this paper obtains the data graph as shown in Figure 5. It can be observed in Figure 5(1) that when the logical error rate p_logical = 0.31257, the threshold p_threshold = 0.081574. Figure 5(2) can be observed, but when the logical error rate p_logical = 0.2642, the threshold p_threshold = 0.09542. Thresholds vary due to code distances and qubits. It is considered to compare the outcome of this paper with a series of previous estimates of thresholds, some small difference between estimates is reasonable due to not the same execution of decoding algorithms and numerical simulations. As can be seen from the two graphs in Figure 5, when the physical error rate is below the threshold, the greater the code distance the more errors can be corrected, so the logical error rate will be lower. When the physical error rate is above the threshold, although a larger code distance can correct more errors, the logical error rate will be greater as the code itself has more quantum bits and more errors will occur.

FIGURE 4

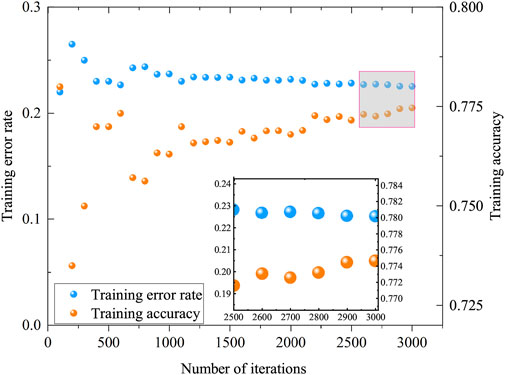
FIGURE 4. The number of training times corresponds to the function of training error rate and training accuracy. The horizontal axis represents the number of training times, and the vertical axis represents the training error rate and accuracy rate. Training error and accuracy are marked in blue and orange, respectively. For accurate viewing, zoom plots are set to make it easier to observe the data.

FIGURE 5

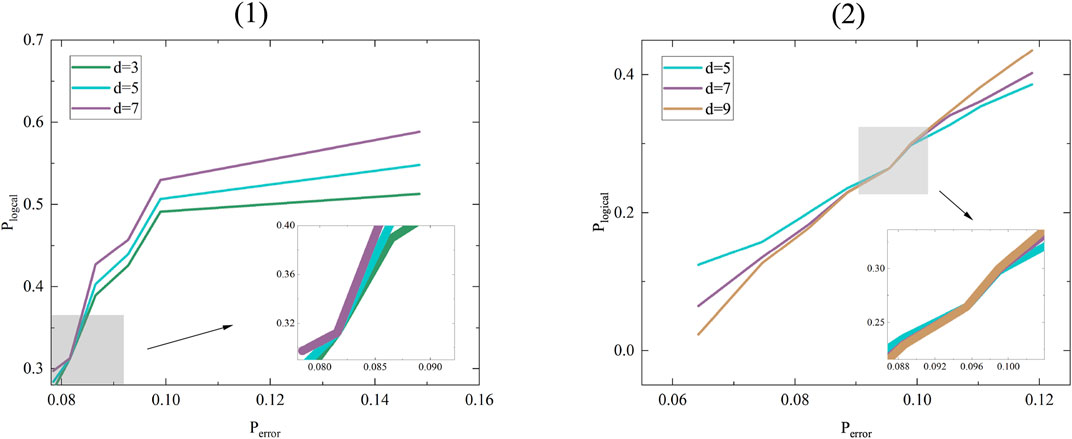
FIGURE 5. (1)Function correspondence of physical error rate p_error, logical error rate p_logical, and code distance d = 3, 5, 7. Threshold p_threshold = 0.081574. (2)Function correspondence of physical error rate p_error, logical error rate p_logical, and code distance d = 5, 7, 9. Threshold p_threshold = 0.09542. The abscissa represents the physical error rate, the ordinate represents the logical error rate. For better numerical analysis, the different code distances d are marked in different colours, d = 3 in green, d = 5 in blue, d = 7 in purple and d = 9 in brown.

Our threshold is significantly lower than that of other papers, this difference seems to be related to the definition of logical error rate, some papers define logical error rate p_logical as the error rate measured per round [43–45], according to the analysis of Ref. [46], with the d increase, the p_error of continuous curve intersection will decrease, and this definition will lead to an overestimation of the threshold. This is roughly the same as the data of some articles. Therefore, it is difficult for this paper to make a conclusive statement on the difference in the results. Nonetheless, this paper achieves the feasibility of implementing $\mathbb{Q}$-networks for Semion code decoders.

4.2 Quantum circuit performance

RL has a good effect on optimization problems. It can extract non-local laws from noise and perform transfer learning in various tasks. Applying this advantage to the cost of qubits passing through the quantum gate can reduce the cost of qubits. The qubits contain auxiliary qubits in the process of comprehensive measurement, and the logic overhead is the cost of auxiliary qubits in the process of comprehensive measurement. In this paper, the $\mathbb{Q}$-network of RL is used to experiment, and the number of simulated qubits ranges from 3 × 10⁷ to 2.1 × 10⁸, and compare the original overhead under different thresholds and the optimized overhead of the $\mathbb{Q}$-network, Figure 6(1) shows that when the threshold is p_threshold = 0.081574, as the number of qubits increases, both the original overhead and the $\mathbb{Q}$-network overhead increase, but the $\mathbb{Q}$-network optimized overhead is significantly lower than the original overhead. Figure 62) shows that when the threshold is p_threshold = 0.09542, as the number of qubits increases, the optimized overhead of the $\mathbb{Q}$-network is also much lower than the original overhead, although when the number of qubits is 2.1 × 10⁸, the optimized $\mathbb{Q}$-network has the overhead is slightly higher than the original, but this does not affect our overall results in the slightest. At the same time, comparing the results under different thresholds in Figure 6, we can find that the larger the threshold, the greater the overhead of the quantum circuit gate.

FIGURE 6

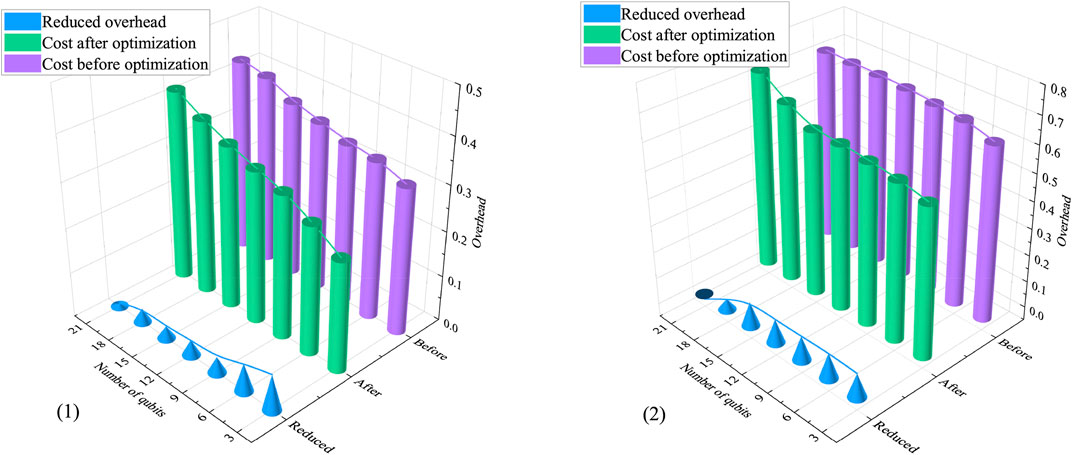
FIGURE 6. Quantum circuit gate overhead data graph. (1)When the threshold p_threshold = 0.081574, the original cost is compared with the optimized cost of the $\mathbb{Q}$-network. (2)When the threshold p_threshold = 0.09542, the original cost is compared with the optimized cost of the $\mathbb{Q}$-network. Among them, the abscissa represents the number of qubits, which is displayed in scientific notation, and the ordinate is the logical cost. The original cost is marked in orange, and the $\mathbb{Q}$-network optimized cost is marked in blue.

5 Conclusion

In this paper, topological QEC codes based on Semion codes in the case of noise are studied. It is a novel error correction method. Make sure that the perturbations of local errors do not destroy the global degrees of freedom through periodic measurement and inspection. Error-correcting codes protect the security and correctness of quantum information. Semion code is more innovative and flexible. The hexagonal lattice is transformed into a quadrilateral lattice through mathematical thinking, and the deep RL algorithm is input to get the error-corrected experimental results. In addition, the optimization problem of quantum circuits is also involved. Of course, this work leaves a lot to be desired. For example, the current Semion code decoder can only be input into the decoder in the form of squares and has not been completely input in the form of hexagonal grids. And we only realized that the RL decoder embedded in Semion code is feasible, but the threshold is not optimal. The follow-up work still needs to be further explored.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

H-WW (First Author): Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing–Original Draft; QC: Data Curation, Writing–Original Draft; Y-JX: Visualization, Investigation; LD: Resources, Supervision; H-YL: Software, Validation Y-MD: Visualization, Writing–Review and Editing H-YM (Corresponding Author): Conceptualization, Funding Acquisition, Resources, Supervision, Writing–Review and Editing.

Funding

Project supported by the National Natural Science Foundation of China (Grant Nos.61772295), Natural Science Foundation of Shandong Province, China (Grant Nos.ZR2021MF049, ZR2019YQ01), Project of Shandong Provincial Natural Science Foundation Joint Fund Application (ZR202108020011).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xin T, Wang B-X, Li K-R, Kong X-Y, Wei S-J, Wang T, et al. Nuclear magnetic resonance for quantum computing: techniques and recent achievements. Chin Phys B (2018) 27:020308. doi:10.1088/1674-1056/27/2/020308

CrossRef Full Text | Google Scholar

2. Zhou N, Zhu K, Zou X. Multi-Party semi-quantum key distribution protocol with four-particle cluster states. Annalen der Physik (2019) 531:1800520. doi:10.1002/andp.201800520

CrossRef Full Text | Google Scholar

3. Ma H-Y, Wang H-F, Zhang S. Implementation of the Grover quantum search algorithm in thermal cavity. J Yanbian University(Natural Science) (2008) 34:27–30. doi:10.16379/j.cnki.issn.1004-4353.2008.01.010

CrossRef Full Text | Google Scholar

4. He Z-X, Fan X-K, Chu P-C, Ma H-Y. Anonymous communication scheme based on quantum walk on Cayley graph. Acta Phys Sin (2020) 69:160301. doi:10.7498/aps.69.20200333

CrossRef Full Text | Google Scholar

5. Terhal BM. Quantum error correction for quantum memories. Rev Mod Phys (2015) 87:307–46. doi:10.1103/RevModPhys.87.307

CrossRef Full Text | Google Scholar

6. Beale SJ, Wallman JJ, Gutiérrez M, Brown KR, Laflamme R. Quantum error correction decoheres noise. Phys Rev Lett (2018) 121:190501. doi:10.1103/PhysRevLett.121.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Huang E, Doherty AC, Flammia S. Performance of quantum error correction with coherent errors. Phys Rev A (Coll Park) (2018) 99:022313. doi:10.1103/PhysRevA.99.022313

CrossRef Full Text | Google Scholar

8. Clemens JP, Siddiqui S, Gea-Banacloche J. Quantum error correction against correlated noise. Phys Rev A (Coll Park) (2004) 69:062313. doi:10.1103/physreva.69.062313

CrossRef Full Text | Google Scholar

9. Poulin D. Stabilizer formalism for operator quantum error correction. Phys Rev Lett (2005) 95:230504. doi:10.1103/PhysRevLett.95.230504

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kitaev AY. Fault-tolerant quantum computation by anyons. Ann Phys (2003) 303:2–30. doi:10.1016/s0003-4916(02)00018-0

CrossRef Full Text | Google Scholar

11. Dauphinais G, Ortiz L, Varona S, Martin-Delgado MA. Quantum error correction with the semion code. New J Phys (2019) 21:053035. doi:10.1088/1367-2630/ab1ed8

CrossRef Full Text | Google Scholar

12. Bullivant A, Hu Y, Wan Y. Twisted quantum double model of topological order with boundaries. Phys Rev B (2017) 96:165138. doi:10.1103/PhysRevB.96.165138

CrossRef Full Text | Google Scholar

13. Fuentes P, Etxezarreta MJ, Crespo PM, Garcia-Frias J. Approach for the construction of non-Calderbank-Steane-Shor low-density-generator-matrix–based quantum codes. Phys Rev A (Coll Park) (2020) 102:012423. doi:10.1103/physreva.102.012423

CrossRef Full Text | Google Scholar

14. Castelnovo C. Negativity and topological order in the toric code. Phys Rev A (Coll Park) (2013) 88:042319. doi:10.1103/physreva.88.042319

CrossRef Full Text | Google Scholar

15. Gu Z-C, Wang Z, Wen X-G. Lattice model for fermionic toric code. Phys Rev B (2014) 90:085140. doi:10.1103/PhysRevB.90.085140

CrossRef Full Text | Google Scholar

16. Sarvepalli P, Robert R. Efficient decoding of topological color codes. Phys Rev A (Coll Park) (2012) 85:022317. doi:10.1103/physreva.85.022317

CrossRef Full Text | Google Scholar

17. Aloshious AB, Sarvepalli PK. Erasure decoding of two-dimensional color codes. Phys Rev A (Coll Park) (2019) 100:042312. doi:10.1103/PhysRevA.100.042312

CrossRef Full Text | Google Scholar

18. Bolens A, Markus H. Reinforcement learning for digital quantum simulation. Phys Rev Lett (2021) 127:110502. doi:10.1103/PhysRevLett.127.110502

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mills K, Michael S, Isaac T. Deep learning and the Schrödinger equation. Phys Rev A (Coll Park) (2017) 96:042113. doi:10.1103/physreva.96.042113

CrossRef Full Text | Google Scholar

20. Zhang Y-H, Zheng P-L, Zhang Y, Deng D-L. Topological quantum compiling with reinforcement learning. Phys Rev Lett (2020) 125:170501. doi:10.1103/PhysRevLett.125.170501

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wu SL, Sun S, Guan W, Zhou C, Chan J, Cheng CL, et al. Application of quantum machine learning using the quantum kernel algorithm on high energy physics analysis at the LHC. Phys Rev Res (2021) 3:033221. doi:10.1103/PhysRevResearch.3.033221

CrossRef Full Text | Google Scholar

22. Juan C, Torlai G. How to use neural networks to investigate quantum many-body physics. PRX Quan (2021) 2:040201. doi:10.1103/PRXQuantum.2.040201

CrossRef Full Text | Google Scholar

23. Baireuther P, Criger B, Beenakker CWJ. Machine-learning-assisted correction of correlated qubit errors in a topological code. Quantum (2017) 2:48. doi:10.22331/q-2018-01-29-48

CrossRef Full Text | Google Scholar

24. Baireuther P, Caio MD, Criger B, Beenakker CWJ, O’Brien TE. Neural network decoder for topological color codes with circuit level noise. New J Phys (2019) 21:013003. doi:10.1088/1367-2630/aaf29e

CrossRef Full Text | Google Scholar

25. Wang H-W, Xue Y-J, Ma Y-L, Hua N, Ma H-Y. Determination of quantum toric error correction code threshold using convolutional neural network decoders. Chin Phys B (2022) 31:10303–010303. doi:10.1088/1674-1056/ac11e3

CrossRef Full Text | Google Scholar

26. Levin MA, Wen X-G. String-net condensation: a physical mechanism for topological phases. Phys Rev B (2005) 71:045110. doi:10.1103/physrevb.71.045110

CrossRef Full Text | Google Scholar

27. Lin T, Su Z, Xu Q, Xing R, Fang D. Deep Q-network based energy scheduling in retail energy market. IEEE Access (2020) 8:69284–95. doi:10.1109/ACCESS.2020.2983606

CrossRef Full Text | Google Scholar

28. Nautrup HP, Delfosse N, Dunjko V, Briegel HJ, Friis N. Optimizing quantum error correction codes with reinforcement learning. Quantum (2019) 3:215. doi:10.22331/q-2019-12-16-215

CrossRef Full Text | Google Scholar

29. Lo H-K, Preskill J. Non-Abelian vortices and non-Abelian statistics. Phys Rev D (1993) 48:4821–34. doi:10.1103/PhysRevD.48.4821

CrossRef Full Text | Google Scholar

30. Forslund DW, Kindel JM, Lindman EL. Parametric excitation of electromagnetic waves. Phys Rev Lett (1972) 29:249–52. doi:10.1103/physrevlett.29.249

CrossRef Full Text | Google Scholar

31. Harada N, Nakanishi K. Exciton chirality method and its application to configurational and conformational studies of natural products. Acc Chem Res (1972) 5:257–63. doi:10.1021/ar50056a001

CrossRef Full Text | Google Scholar

32. Guerreiro T. Molecular machines for quantum error correction. PRX Quan (2021) 2:030336. doi:10.1103/prxquantum.2.030336

CrossRef Full Text | Google Scholar

33. Ahn C, Wiseman HM, Milburn GJ. Quantum error correction for continuously detected errors. Phys Rev A (Coll Park) (2003) 67:052310. doi:10.1103/physreva.67.052310

CrossRef Full Text | Google Scholar

34. Valenti A, van Nieuwenburg E, Huberand S, Greplova E. Hamiltonian learning for quantum error correction. Phys Rev Res (2019) 1:033092. doi:10.1103/PhysRevResearch.1.033092

CrossRef Full Text | Google Scholar

35. Xu X, Benjamin SC, Yuan X. Variational circuit compiler for quantum error correction. Phys Rev Appl (2021) 15:034068. doi:10.1103/PhysRevApplied.15.034068

CrossRef Full Text | Google Scholar

36. Nadkarni PJ, Garani SS. Quantum error correction architecture for qudit stabilizer codes. Phys Rev A (Coll Park) (2021) 103:042420. doi:10.1103/physreva.103.042420

CrossRef Full Text | Google Scholar

37. Andreasson P, Johansson J, Liljestrand S, Granath M. Quantum error correction for the toric code using deep reinforcement learning. Quantum (2019) 3:183. doi:10.22331/q-2019-09-02-183

CrossRef Full Text | Google Scholar

38. Dauphinais G, Poulin D. Fault-tolerant quantum error correction for non-Abelian anyons. Commun Math Phys (2017) 355:519–60. doi:10.1007/s00220-017-2923-9

CrossRef Full Text | Google Scholar

39. Faist P, Nezami S, Albert VV, Salton G, Pastawski F, Hayden P, et al. Continuous symmetries and approximate quantum error correction. Phys Rev X (2020) 10:041018. doi:10.1103/physrevx.10.041018

CrossRef Full Text | Google Scholar

40. Ilya D, Kovalev AA, Pryadko LP. Thresholds for correcting errors, erasures, and faulty syndrome measurements in degenerate quantum codes. Phys Rev Lett (2015) 115:050502. doi:10.1103/PhysRevLett.115.050502

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sasaki H, Horiuchi T, Kato S. Experimental study on behavior acquisition of mobile robot by deep Q-network. J Adv Comput Intelligence Intell Inform (2017) 21:840–8. doi:10.20965/jaciii.2017.p0840

CrossRef Full Text | Google Scholar

42. Wyner A, Ziv J. The rate-distortion function for source coding with side information at the decoder. IEEE Trans Inf Theor (1976) 21:1–10. doi:10.1109/tit.1976.1055508

CrossRef Full Text | Google Scholar

43. Raussendorf R, Harrington J, Goyal K. A fault-tolerant one-way quantum computer. Ann Phys (2006) 321:2242–70. doi:10.1016/j.aop.2006.01.012

CrossRef Full Text | Google Scholar

44. Raussendorf R, Harrington J, Goyal K. Topological fault-tolerance in cluster state quantum computation. New J Phys (2007) 9:199. doi:10.1088/1367-2630/9/6/199

CrossRef Full Text | Google Scholar

45. Bravyi S, Vargo A. Simulation of rare events in quantum error correction. Phys Rev A (Coll Park) (2013) 88:062308. doi:10.1103/physreva.88.062308

CrossRef Full Text | Google Scholar

46. Stephens AM. Fault-tolerant thresholds for quantum error correction with the surface code. Phys Rev A (Coll Park) (2014) 89:022321. doi:10.1103/physreva.89.022321

CrossRef Full Text | Google Scholar