- 1Institute of Atomic and Molecular Sciences, Academia Sinica, Taipei, Taiwan
- 2Department of Chemistry, National Taiwan University, Taipei, Taiwan
- 3Department of Physics, National Taiwan University, Taipei, Taiwan
The Tavis-Cummings (TC) model has been widely used to investigate the collective coupling effect in hybrid light-matter systems; however, the TC model neglects the effect of a dielectric environment (the spectral structure of photonic bath), and it remains unclear whether the TC model can adequately depict the light-matter interaction in a non-homogeneous, dispersive, and absorbing medium. To clarify the ambiguity, in this work, we first connect the macroscopic quantum electrodynamics and the TC model with dissipation. Based on the relationship between these two theoretical frameworks, we develop a guideline that allows us to examine the applicability of the TC model with dissipation. The guideline states that if 1) the generalized spectral densities are independent of the positions of molecules and 2) the generalized spectral densities resemble a Lorentzian function, then the hybrid light-matter system can be properly described by the TC model with dissipation. In order to demonstrate how to use the guideline, we examine the position dependence and the lineshape of the generalized spectral densities in three representative systems, including a silver Fabry-Pérot cavity, a silver surface, and an aluminum spherical cavity. We find that only the aluminum spherical cavity meets the two conditions, i.e., position independence and Lorentzian lineshape, required for the utilization of the dissipative TC model. Our results indicate that the use of the TC model with dissipation to study the collective coupling effect should be done with care, providing an important perspective on resonance energy transfer and polariton chemistry.
Introduction
When a group of molecules (atoms, or quantum emitters) interact with confined electromagnetic fields, several intriguing phenomena emerge and have been successively observed, including the modification of spontaneous decay rates [1–5] and chemical reaction products [6–8]. The collective coupling effects provide scientists with a new strategy to alter and control the physical and chemical properties of molecules. To explore the origin of these phenomena, the Tavis-Cummings (TC) model [9], which describes a collection of N identical molecules interacting equally with a single photonic mode, has been widely used to investigate the collective effect in hybrid light-matter systems [10–16]. It is well-known that the TC model gives the N-times decay rate of single-photon superradiance and the
One possible solution to incorporating the effect of the dielectric environment into hybrid light-matter systems is to establish a theory based on macroscopic quantum electrodynamics (QED) [23–25]. As an effective field theory, macroscopic QED provides a framework of quantized electromagnetic fields in the presence of any arbitrary inhomogeneous, dispersive, and absorbing media. Since its debut, macroscopic QED has been successfully applied to investigate the spontaneous emission [26–32], resonance energy transfer [33–40], Casimir-Polder force [41–45], and van der Waals interaction [46–51] in the presence of dielectric bodies. Moreover, it is recently shown that the macroscopic QED theory can be effectively converted to the cavity QED model with dissipation [52–54]. We believe that the connection between these two theoretical frameworks will provide a new perspective on the utilization of the TC model. However, to the best of our knowledge, there is no detailed discussion on the relationship between the macroscopic QED and the widely adopted TC model. As a result, in this article, our main purpose is to clarify the conditions for the transformation from the macroscopic QED Hamiltonian to the dissipative TC model. Based on the requirements for the transformation, we propose a simple but useful guideline to verify whether molecular emitters (or quantum emitters) in a given dielectric environment can be properly described by the TC model with dissipation. Moreover, our theory will also provide how to estimate the parameters in the dissipative TC model from the macroscopic QED theory.
This article is organized as follows. In Section 2, we recapitulate the few-mode field quantization approach that bridges the macroscopic QED and dissipative cavity QED model [52, 54]. Based on the quantization approach, we establish the connection between the dissipative TC model and macroscopic QED and provide a guideline that allows us to examine the applicability of the TC model for a given hybrid light-matter system. In Section 3, to demonstrate the guideline, we investigate three representative systems: molecules inside a silver Fabry-Pérot cavity, above a silver surface, and inside an aluminum spherical cavity. In Section 4, we summarize the main results of this research.
Methods
Total Hamiltonian based on macroscopic quantum electrodynamics theory
We start from a system composed of a collection of N two-level molecules coupled to polaritons (dressed photons) in an arbitrary dielectric environment. Within the framework of macroscopic QED theory [55, 56], the total Hamiltonian in the multipolar-coupling scheme can be expressed as
The first term corresponds to the molecular Hamiltonian, where ωeg,ζ and
where ɛ0 is the vacuum permittivity, ɛr (r, ω) is the relative permittivity at position r, and c is the speed of light in vacuum. Moreover, the dyadic Green’s function
where
Effective dissipative cavity quantum electrodynamics model based on few-mode field quantization
Next, we adopt the few-mode field quantization approach [52, 54] to convert the macroscopic QED Hamiltonian in Eq. 1 into an effective dissipative cavity QED model. The previous study has shown that the few-mode field quantization approach can equivalently describe the dynamics of the molecules coupled to the polaritons derived from the macroscopic QED Hamiltonian. The concept of the quantization approach is to transform the infinite bosonic vector fields (polariton modes)
where ωph,j is the frequency of the j-th discrete photonic mode, and ℏgζ,j is the coupling strength between the ζ-th molecule and the j-th photonic mode. Within the few-mode field quantization approach, the system dynamics can be described by the master equation as follows [54],
where
The parameters ωph,j, gζ,j, and κph,j in the effective dissipative cavity QED model can be obtained by fitting the generalized spectral density (GSD) matrix
It is worth noting that the diagonal terms of the GSD matrix are associated with the single-point dyadic Green’s functions, which are related to the photonic local density of states [57, 58] and the spontaneous emission rates [26, 29, 58] of the molecular emitters; the off-diagonal terms of the GSD matrix are associated with the two-point dyadic Green’s functions, which are related to the photonic cross density of states [57, 59] and the intermolecular interactions between two molecular emitters [33, 36, 60]. The effective GSD matrix
where
Effective dissipative Tavis-Cummings model
In Section 2.2, we have established an effective dissipative CQED model that can equivalently describe the quantum dynamics of the molecular emitters. Here, we would like to emphasize that the few-mode field quantization approach in Section 2.2 does not assume/limit the number of discrete photonic modes and the number depends on the shape of the generalized spectral densities. In order to provide a guideline that allows us to examine the applicability of the dissipative TC model, we need to connect the effective CQED Hamiltonian in Eq. 4 to an effective TC model and clarify the corresponding required conditions. Recall that the TC model is developed in the framework of the rotating-wave approximation. As a result, we first apply the rotating-wave approximation to eliminate the counter-rotating terms in the interaction part. Moreover, we set ωeg,ζ = ωeg, μζ = μ, Na = 1,
and the effective GSD matrix corresponding to the effective TC model becomes
where
Based on Eqs 6, 9, we find that the transformation from the macroscopic QED Hamiltonian into an effective dissipative TC model requires that all elements of the GSD matrix have to meet the following form,
According to Eq. 10, we have successfully established the connection between the macroscopic QED Hamiltonian [Eq. 1] and the dissipative TC model [Eq. 8]. Here, we emphasize that the GSDs
Numerical demonstration and discussion
In Section 2, we have provided a guideline [Eq. 10] to verify whether light-matter interactions in a given dielectric environment can be properly described by the dissipative TC model. The guideline includes two conditions: first,
Silver Fabry-Pérot cavity
In the first system, we focus on molecules inside a silver Fabry-Pérot cavity, where the cavity comprises two 100 nm-thick silver plates separated by a 600 nm gap in vacuum, as shown in Figure 1A. The molecules are located 300 nm above the lower silver plate, with their transition dipole moments perpendicular to the cavity axis (normal direction of the silver plates). We model the silver Fabry-Pérot cavity via the dielectric function as follows:
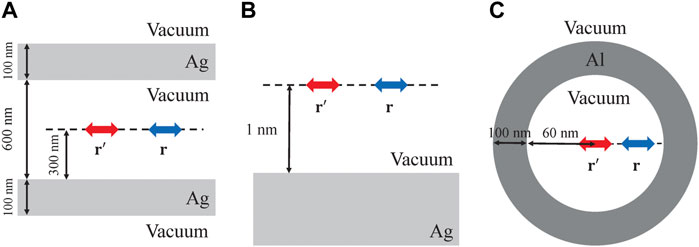
FIGURE 1. Schematic illustrations of molecules (A) inside a silver Fabry-Pérot cavity, (B) above a silver surface, and (C) inside a aluminum spherical cavity. (A) The silver Fabry-Pérot cavity comprises two silver plates in vacuum. The thickness of the silver plates are set to be 100 nm, and the distance between the plates is 600 nm. The molecules are located 300 nm above the lower silver plate, with their transition dipole moments perpendicular to the cavity axis. (B) The distance between the molecules and the silver surface is 1 nm, and the transition dipole moments of the molecules are perpendicular to the normal direction of the silver surface. (C) The aluminum spherical cavity is composed of a hollow sphere in vacuum. The radius of the inner sphere and the thickness of the shell are set to be 60 and 100 nm, respectively. The molecules are inside the sphere, and we set one of them located at the center of the sphere. For simplicity, we set that the transition dipole moments of the molecules in the three systems are the same (the magnitude is 1 Debye and the direction is identical).
The dielectric function of silver ɛAg(ω) is described by the modified Drude model
To validate whether the silver Fabry-Pérot cavity can be described by the dissipative TC model, we examine the Lorentzian lineshape and the position independence of the GSDs by varying the distance between the molecules. The intermolecular distances are set to be 0 nm, 12 nm, and 120 nm, which correspond roughly to 0, 0.01, and 0.1 times the wavelength of the fundamental cavity mode λcav (assumed to be twice the distance between the silver plates), respectively. Note that the GSD does not diverge in the case of 0 nm because the GSD is associated with the imaginary part of a single-point dyadic Green’s function (
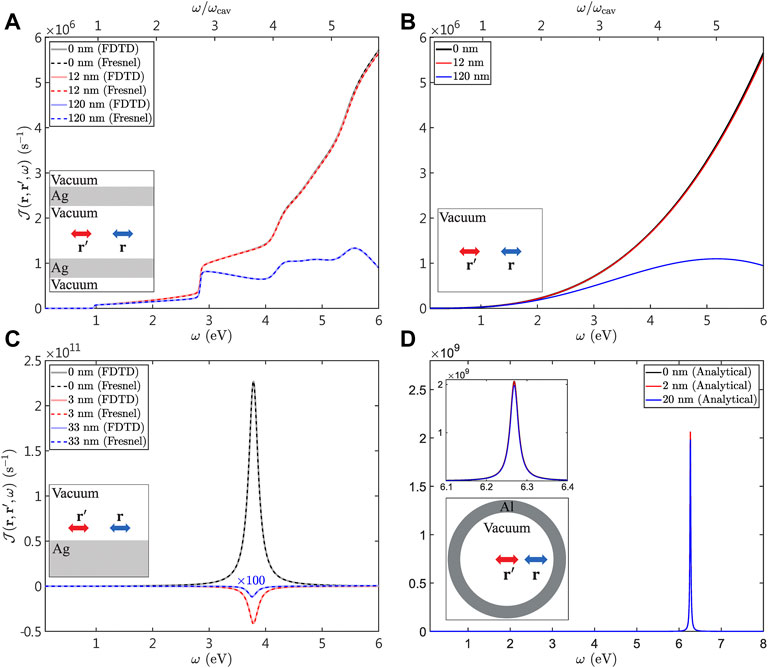
FIGURE 2. Frequency dependence of generalized spectral densities (A) inside a silver Fabry-Pérot cavity, (B) in vacuum, (C) above a silver surface, and (D) inside an aluminum spherical cavity. The magnitude of the transition dipole moments in these systems is set to be 1 Debye.
Our computational results clearly show that the GSDs derived from the two methods are in good agreement with each other, indicating that our computational method and numerical calculations are reliable. More importantly, the GSDs of molecules in the silver Fabry-Pérot cavity exhibit almost the same shape when the intermolecular distances are 0 and 12 nm. Note that we do not show the GSDs between 0 and 12 nm because the GSDs retain their shapes when the intermolecular distance |rζ − rζ′| ≲ 12 nm. In other words, the GSDs in these two cases satisfy the first condition of the guideline given by our theory (position independence). However, the GSDs do not exhibit a Lorentzian lineshape at all, i.e., the second condition of the guideline given by our theory is not satisfied. Therefore, based on our theory, the light-matter interactions in the silver Fabry-Pérot cavity may not be appropriately described by the dissipative TC model.
The GSDs for molecules in the silver Fabry-Pérot cavity (Figure 2A) and in vacuum (Figure 2B) are similar in shape but with a small difference (the step-like characteristics only in the case of the Fabry-Pérot cavity). From a physical point of view, the similarity between the GSDs in the two systems indicates that the confinement of electromagnetic field in the Fabry-Pérot cavity is not well, resulting from the lack of spatial confinement apart from the cavity axis. From a mathematical point of view, the dyadic Green’s function for molecules in the silver Fabry-Pérot cavity
where k0 = ω/c,
Silver surface
In the second system, we consider molecules located 1 nm above a silver surface and their transition dipole moments are perpendicular to the normal direction of the silver surface, as shown in Figure 1B. We model the vacuum-silver system via the following dielectric function:
where ɛAg(ω) is the same as that in the first system. Moreover, the dyadic Green’s functions required for the calculation of the GSDs are obtained based on the same methods as that in the first system.
Following the same procedure in Section 3.1, we calculate the GSDs for different intermolecular distances, as shown in Figure 2C. The distances between the molecules are set to be 0 nm, 3 nm, and 33 nm, which correspond roughly to 0, 0.01, and 0.1 times the resonance wavelength λSPP of the surface-plasmon-polariton mode, respectively. Note that 0.01λSPP corresponds to the near-field condition and 0.1λSPP corresponds to the characteristic distance of plasmon-coupled resonance energy transfer for a surface-plasmon system [38].
Our simulations show that the FDTD method and the Fresnel method give the same curves, which indicates that our computational results are reliable. To verify whether the light-matter interactions for molecules above a silver surface can be adequately described by the dissipative TC model, we apply our theory to examine whether the GSDs in such a system satisfy the Lorentzian lineshape and position independence. First, we find that the GSDs for molecules with the three different intermolecular distances resemble Lorentzian functions, i.e., the second condition is satisfied. Second, obviously, the magnitudes (heights) of the GSDs exhibit significant difference in the cases of three different distances. Even for the case of a very short intermolecular distance (3 nm; 0.01λSPP), the magnitude of the GSD is much smaller than that in the case of 0 nm. In other words, the first condition is not satisfied because the GSDs for molecules above a silver surface strongly depend on their intermolecular distances. Therefore, according to our theory, the dissipative TC model may not be adequate to describe the light-matter interactions between a group of molecules and the surface-plasmon polaritons formed of a silver surface.
Aluminum spherical cavity
In the third system, we focus on molecules inside an aluminum spherical cavity with the same transition dipole moments and set one of them located at the center of the sphere (double red arrow), as shown in Figure 1C. The spherical cavity is made of a hollow aluminum sphere, with the radius of the inner sphere and the thickness of the shell given by 60 and 100 nm, respectively. We model the aluminum spherical cavity via the dielectric function as follows:
where the dielectric function of aluminum ɛAl(ω) is described by the Drude model
The distances between the molecules are set to be 0 nm, 2 nm, and 20 nm, which correspond roughly to 0, 0.01, and 0.1 times the resonance wavelength of the peak position λsph observed in the GSDs, respectively. As shown in Figure 2D, the GSDs of the three different intermolecular distances are nearly the same, satisfying the first condition, i.e., position independence. Moreover, the GSDs in these three cases exhibit a Lorentzian lineshape, namely that the second condition is also met. Therefore, according to our theory, the fulfillment of the two conditions, i.e., position independence and Lorentzian lineshape, implies that the dissipative TC model can adequately describe the collective coupling between the molecules and the cavity photons inside a hollow aluminum sphere. However, we would like to emphasize that the lineshapes of the GSDs are highly sensitive to both the size and material of the sphere. In the Supplemental Material, we demonstrate the GSDs of molecules inside several different spherical cavities and show that their lineshapes can deviate from a single Lorentzian function, i.e., the second condition is not met.
From these three systems, we have demonstrated how to examine the applicability of the dissipative TC model based on the position dependence and the lineshape of the GSDs. It is shown that not all of the hybrid light-matter systems conform to these two conditions, i.e., position independence and Lorentzian lineshape of GSDs. Hence, we would like to emphasize that the use of the TC model (or TC model with dissipation) to study the collective coupling effect in a realistic dielectric environment has to be done with care.
Conclusion
In this study, we show that the macroscopic QED theory can be converted to an effective TC model with dissipation when the following two conditions are met. First, the GSDs should be independent of the positions of molecules. Second, the GSDs should behave like a Lorentzian function. These two conditions together serve as a key guideline to examine the applicability of the dissipative TC model for a given photonic environment. To demonstrate the guideline, we investigate the position dependence and lineshape of GSDs in the three representative systems. In the first system, we focus on molecules inside a silver Fabry-Pérot cavity. In this case, the first condition (position independence) can be satisfied when the intermolecular distance is small; however, the second condition (Lorentzian lineshape) is not met. In the second system, we focus on molecules above a silver surface. In this system, the first condition (position independence) is not satisfied even when the intermolecular distance is small, while the second condition (Lorentzian lineshape) is met. In the third system, we focus on molecules inside an aluminum spherical cavity, and we find that the two conditions (position independence and Lorentzian lineshape) are perfectly matched. Therefore, according to the guideline, we conclude that among these three systems, only the aluminum spherical cavity can be well described by the TC model with dissipation. In addition, it is worth noting that our theory also provide how to estimate the parameters in the dissipative TC model based on Eq. (10). Here, we would like to emphasize that the investigation on the TC model can provide an alternative point of view on the theory of resonance energy transfer based on molecular quantum electrodynamics [64–68] because resonance energy transfer is associated with the dyadic Green’s functions [33, 36, 38] in the GSDs.
The TC model and its extension have been employed to study a variety of physical and chemical systems, but they still suffer from some limitations. Under the conditions that the dissipative TC model is no longer valid, one may improve the model by introducing the position-dependent light-matter couplings [60], the full retarded dipole-dipole interactions [69], or more than one photonic mode to appropriately describe the collective coupling effect. In addition, the dissipative TC model does not include resonant dipole-dipole interactions due to infinite photonic modes and nonradiative processes of the molecular emitters, while these issues may play important roles in polariton chemistry. Nevertheless, based on our results, we believe that revisiting the TC model from a viewpoint of macroscopic QED can still provide a simple but important perspective on quantum optics and polariton chemistry.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Y-TC and L-YH contributed to the conception. Y-TC and M-WL performed the numerical calculations. All authors analyzed the results and contributed to manuscript writing.
Funding
All authors were supported by the Academia Sinica (AS-CDA-111-M02) and the Ministry of Science and Technology of Taiwan (MOST 110-2113-M-001-053).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.980167/full#supplementary-material
References
1. Röhlsberger R, Schlage K, Sahoo B, Couet S, Rüffer R. Collective lamb shift in single-photon superradiance. Science (2010) 328:1248–51. doi:10.1126/science.1187770
2. Goban A, Hung CL, Hood JD, Yu SP, Muniz JA, Painter O, et al. Superradiance for atoms trapped along a photonic crystal waveguide. Phys Rev Lett (2015) 115:063601. doi:10.1103/PhysRevLett.115.063601
3. Zhang Y, Luo Y, Zhang Y, Yu YJ, Kuang YM, Zhang L, et al. Visualizing coherent intermolecular dipole–dipole coupling in real space. Nature (2016) 531:623–7. doi:10.1038/nature17428
4. Kim JH, Aghaeimeibodi S, Richardson CJK, Leavitt RP, Waks E. Super-radiant emission from quantum dots in a nanophotonic waveguide. Nano Lett (2018) 18:4734–40. doi:10.1021/acs.nanolett.8b01133
5. Luo Y, Chen G, Zhang Y, Zhang L, Yu Y, Kong F, et al. Electrically driven single-photon superradiance from molecular chains in a plasmonic nanocavity. Phys Rev Lett (2019) 122:233901. doi:10.1103/PhysRevLett.122.233901
6. Thomas A, Lethuillier-Karl L, Nagarajan K, Vergauwe RMA, George J, Chervy T, et al. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science (2019) 363:615–9. doi:10.1126/science.aau7742
7. Thomas A, Jayachandran A, Lethuillier-Karl L, Vergauwe RM, Nagarajan K, Devaux E, et al. Ground state chemistry under vibrational strong coupling: Dependence of thermodynamic parameters on the rabi splitting energy. Nanophotonics (2020) 9:249–55. doi:10.1515/nanoph-2019-0340
8. Sau A, Nagarajan K, Patrahau B, Lethuillier-Karl L, Vergauwe RMA, Thomas A, et al. Modifying woodward–hoffmann stereoselectivity under vibrational strong coupling. Angew Chem Int Ed (2021) 60:5712–7. doi:10.1002/anie.202013465
9. Tavis M, Cummings FW. Exact solution for an n-molecule—Radiation-field Hamiltonian. Phys Rev (1968) 170:379–84. doi:10.1103/PhysRev.170.379
10. Agarwal GS. Vacuum-field rabi splittings in microwave absorption by rydberg atoms in a cavity. Phys Rev Lett (1984) 53:1732–4. doi:10.1103/PhysRevLett.53.1732
11. Dung HT, Huyen ND. Two atom-single mode radiation field interaction. J Mod Opt (1994) 41:453–69. doi:10.1080/09500349414550451
12. Deng GW, Wei D, Li SX, Johansson JR, Kong WC, Li HO, et al. Coupling two distant double quantum dots with a microwave resonator. Nano Lett (2015) 15:6620–5. doi:10.1021/acs.nanolett.5b02400
13. Deçordi GL, Vidiella-Barranco A. A simple model for a minimal environment: The two-atom tavis–cummings model revisited. J Mod Opt (2018) 65:1879–89. doi:10.1080/09500340.2018.1471172
14. Ribeiro RF, Martínez-Martínez LA, Du M, Campos-Gonzalez-Angulo J, Yuen-Zhou J. Polariton chemistry: Controlling molecular dynamics with optical cavities. Chem Sci (2018) 9:6325–39. doi:10.1039/C8SC01043A
15. Evans RE, Bhaskar MK, Sukachev DD, Nguyen CT, Sipahigil A, Burek MJ, et al. Photon-mediated interactions between quantum emitters in a diamond nanocavity. Science (2018) 362:662–5. doi:10.1126/science.aau4691
16. Angerer A, Streltsov K, Astner T, Putz S, Sumiya H, Onoda S, et al. Superradiant emission from colour centres in diamond. Nat Phys (2018) 14:1168–72. doi:10.1038/s41567-018-0269-7
17. Chikkaraddy R, de Nijs B, Benz F, Barrow SJ, Scherman OA, Rosta E, et al. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature (2016) 535:127–30. doi:10.1038/nature17974
18. Yuen-Zhou J, Menon VM. Polariton chemistry: Thinking inside the (photon) box. Proc Natl Acad Sci U S A (2019) 116:5214–6. doi:10.1073/pnas.1900795116
19. Kéna-Cohen S, Yuen-Zhou J. Polariton chemistry: Action in the dark. ACS Cent Sci (2019) 5:386–8. doi:10.1021/acscentsci.9b00219
20. Hirai K, Hutchison JA, Uji-i H. Recent progress in vibropolaritonic chemistry. ChemPlusChem (2020) 85:1981–8. doi:10.1002/cplu.202000411
21. Xiang B, Xiong W. Molecular vibrational polariton: Its dynamics and potentials in novel chemistry and quantum technology. J Chem Phys (2021) 155:050901. doi:10.1063/5.0054896
22. Yuen-Zhou J, Xiong W, Shegai T. Polariton chemistry: Molecules in cavities and plasmonic media. J Chem Phys (2022) 156:030401. doi:10.1063/5.0080134
23. Gruner T, Welsch DG. Green-function approach to the radiation-field quantization for homogeneous and inhomogeneous kramers-kronig dielectrics. Phys Rev A (Coll Park) (1996) 53:1818–29. doi:10.1103/PhysRevA.53.1818
24. Dung HT, Knöll L, Welsch DG. Three-dimensional quantization of the electromagnetic field in dispersive and absorbing inhomogeneous dielectrics. Phys Rev A (Coll Park) (1998) 57:3931–42. doi:10.1103/PhysRevA.57.3931
25. Scheel S, Knöll L, Welsch DG. Qed commutation relations for inhomogeneous kramers-kronig dielectrics. Phys Rev A (Coll Park) (1998) 58:700–6. doi:10.1103/PhysRevA.58.700
26. Scheel S, Knöll L, Welsch DG. Spontaneous decay of an excited atom in an absorbing dielectric. Phys Rev A (Coll Park) (1999) 60:4094–104. doi:10.1103/PhysRevA.60.4094
27. Scheel S, Knöll L, Welsch DG, Barnett SM. Quantum local-field corrections and spontaneous decay. Phys Rev A (Coll Park) (1999) 60:1590–7. doi:10.1103/PhysRevA.60.1590
28. Dung HT, Knöll L, Welsch DG. Spontaneous decay in the presence of dispersing and absorbing bodies: General theory and application to a spherical cavity. Phys Rev A (Coll Park) (2000) 62:053804. doi:10.1103/PhysRevA.62.053804
29. Wang S, Scholes GD, Hsu LY. Quantum dynamics of a molecular emitter strongly coupled with surface plasmon polaritons: A macroscopic quantum electrodynamics approach. J Chem Phys (2019) 151:014105. doi:10.1063/1.5100014
30. Wang S, Scholes GD, Hsu LY. Coherent-to-incoherent transition of molecular fluorescence controlled by surface plasmon polaritons. J Phys Chem Lett (2020) 11:5948–55. doi:10.1021/acs.jpclett.0c01680
31. Wang S, Lee MW, Chuang YT, Scholes GD, Hsu LY. Theory of molecular emission power spectra. i. macroscopic quantum electrodynamics formalism. J Chem Phys (2020) 153:184102. doi:10.1063/5.0027796
32. Lee MW, Chuang YT, Hsu LY. Theory of molecular emission power spectra. ii. angle, frequency, and distance dependence of electromagnetic environment factor of a molecular emitter in plasmonic environments. J Chem Phys (2021) 155:074101. doi:10.1063/5.0057018
33. Dung HT, Knöll L, Welsch DG. Intermolecular energy transfer in the presence of dispersing and absorbing media. Phys Rev A (Coll Park) (2002) 65:043813. doi:10.1103/PhysRevA.65.043813
34. Dung HT, Knöll L, Welsch DG. Resonant dipole-dipole interaction in the presence of dispersing and absorbing surroundings. Phys Rev A (Coll Park) (2002) 66:063810. doi:10.1103/PhysRevA.66.063810
35. Ding W, Hsu LY, Schatz GC. Plasmon-coupled resonance energy transfer: A real-time electrodynamics approach. J Chem Phys (2017) 146:064109. doi:10.1063/1.4975815
36. Hsu LY, Ding W, Schatz GC. Plasmon-coupled resonance energy transfer. J Phys Chem Lett (2017) 8:2357–67. doi:10.1021/acs.jpclett.7b00526
37. Ding W, Hsu LY, Heaps CW, Schatz GC. Plasmon-coupled resonance energy transfer ii: Exploring the peaks and dips in the electromagnetic coupling factor. J Phys Chem C (2018) 122:22650–9. doi:10.1021/acs.jpcc.8b07210
38. Wu JS, Lin YC, Sheu YL, Hsu LY. Characteristic distance of resonance energy transfer coupled with surface plasmon polaritons. J Phys Chem Lett (2018) 9:7032–9. doi:10.1021/acs.jpclett.8b03429
39. Lee MW, Hsu LY. Controllable frequency dependence of resonance energy transfer coupled with localized surface plasmon polaritons. J Phys Chem Lett (2020) 11:6796–804. doi:10.1021/acs.jpclett.0c01989
40. Wei YC, Lee MW, Chou PT, Scholes GD, Schatz GC, Hsu LY. Can nanocavities significantly enhance resonance energy transfer in a single donor–acceptor pair? J Phys Chem C (2021) 125:18119–28. doi:10.1021/acs.jpcc.1c04623
41. Buhmann SY, Knöll L, Welsch DG, Dung HT. Casimir-polder forces: A nonperturbative approach. Phys Rev A (Coll Park) (2004) 70:052117. doi:10.1103/PhysRevA.70.052117
42. Buhmann SY, Dung HT, Kampf T, Knöll L, Welsch DG. Atoms near magnetodielectric bodies: Van der waals energy and the casimir–polder force. Opt Spectrosc (2005) 99:466. doi:10.1134/1.2055945
43. Buhmann SY, Dung HT, Kampf T, Welsch DG. Casimir-polder interaction of atoms with magnetodielectric bodies. Eur Phys J D (2005) 35:15–30. doi:10.1140/epjd/e2005-00044-6
44. Buhmann S, Welsch DG. Born expansion of the casimir–polder interaction of a ground-state atom with dielectric bodies. Appl Phys B (2006) 82:189–201. doi:10.1007/s00340-005-2055-3
45. Buhmann SY, Welsch DG. Casimir-polder forces on excited atoms in the strong atom-field coupling regime. Phys Rev A (Coll Park) (2008) 77:012110. doi:10.1103/PhysRevA.77.012110
46. Buhmann SY, Welsch DG, Kampf T. Ground-state van der waals forces in planar multilayer magnetodielectrics. Phys Rev A (Coll Park) (2005) 72:032112. doi:10.1103/PhysRevA.72.032112
47. Sambale A, Buhmann SY, Welsch DG, Tomaš MS. Local-field correction to one- and two-atom van der waals interactions. Phys Rev A (Coll Park) (2007) 75:042109. doi:10.1103/PhysRevA.75.042109
48. Buhmann SY, Safari H, Dung HT, Welsch DG. Two-atom van der waals interaction between polarizable/magnetizable atoms near magnetoelectric bodies. Opt Spectrosc (2007) 103:374–87. doi:10.1134/S0030400X07090068
49. Safari H, Welsch DG, Dung HT, Buhmann SY. Interatomic van der waals potential in the presence of a magnetoelectric sphere. Phys Rev A (Coll Park) (2008) 77:053824. doi:10.1103/PhysRevA.77.053824
50. Sambale A, Welsch DG, Dung HT, Buhmann SY. Van der waals interaction and spontaneous decay of an excited atom in a superlens-type geometry. Phys Rev A (Coll Park) (2008) 78:053828. doi:10.1103/PhysRevA.78.053828
51. Safari H, Welsch DG, Buhmann SY, Scheel S. Van der waals potentials of paramagnetic atoms. Phys Rev A (Coll Park) (2008) 78:062901. doi:10.1103/PhysRevA.78.062901
52. Medina I, García-Vidal FJ, Fernández-Domínguez AI, Feist J. Few-mode field quantization of arbitrary electromagnetic spectral densities. Phys Rev Lett (2021) 126:093601. doi:10.1103/PhysRevLett.126.093601
53. Wang S, Chuang YT, Hsu LY. Simple but accurate estimation of light–matter coupling strength and optical loss for a molecular emitter coupled with photonic modes. J Chem Phys (2021) 155:34117. doi:10.1063/5.0060171
54. Sánchez-Barquilla M, García-Vidal FJ, Fernández-Domínguez AI, Feist J. Few-mode field quantization for multiple emitters. Nanophotonics (2022). doi:10.1515/nanoph-2021-0795
55. Buhmann SY, Dispersion Forces I. Springer tracts in modern Physics. Berlin, Heidelberg: Springer Berlin Heidelberg (2012).
57. Carminati R, Cazé A, Cao D, Peragut F, Krachmalnicoff V, Pierrat R, et al. Electromagnetic density of states in complex plasmonic systems. Surf Sci Rep (2015) 70:1–41. doi:10.1016/j.surfrep.2014.11.001
59. Canaguier-Durand A, Pierrat R, Carminati R. Cross density of states and mode connectivity: Probing wave localization in complex media. Phys Rev A (Coll Park) (2019) 99:013835. doi:10.1103/PhysRevA.99.013835
60. Palacino R, Passante R, Rizzuto L, Barcellona P, Buhmann SY. Tuning the collective decay of two entangled emitters by means of a nearby surface. J Phys B: Mol Opt Phys (2017) 50:154001. doi:10.1088/1361-6455/aa75f4
63. Smith DY, Segall B. Intraband and interband processes in the infrared spectrum of metallic aluminum. Phys Rev B (1986) 34:5191–8. doi:10.1103/PhysRevB.34.5191
64. Andrews D. A unified theory of radiative and radiationless molecular energy transfer. Chem Phys (1989) 135:195–201. doi:10.1016/0301-0104(89)87019-3
65. Salam A. The unified theory of resonance energy transfer according to molecular quantum electrodynamics. Atoms (2018) 6:56. doi:10.3390/atoms6040056
66. Jones GA, Bradshaw DS. Resonance energy transfer: From fundamental theory to recent applications. Front Phys (2019) 7. doi:10.3389/fphy.2019.00100
67. Salam A. Ret in a dielectric medium: Insights from molecular qed theory. Mol Phys (2020) 118:e1770882. doi:10.1080/00268976.2020.1770882
68. Salam A. Discriminatory resonance energy transfer mediated by a third molecule. J Phys Chem A (2021) 125:3549–55. doi:10.1021/acs.jpca.0c11053
Keywords: polariton chemistry, Tavis-Cummings model, macroscopic quantum electrodynamics, cavity quantum electrodynamics, generalized spectral density, Fabry-Pérot cavity, surface plasmon plariton
Citation: Chuang Y-T, Lee M-W and Hsu L-Y (2022) Tavis-Cummings model revisited: A perspective from macroscopic quantum electrodynamics. Front. Phys. 10:980167. doi: 10.3389/fphy.2022.980167
Received: 28 June 2022; Accepted: 04 August 2022;
Published: 07 October 2022.
Edited by:
Akbar Salam, Wake Forest University, United StatesCopyright © 2022 Chuang, Lee and Hsu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liang-Yan Hsu, bHloc3VAZ2F0ZS5zaW5pY2EuZWR1LnR3
 Yi-Ting Chuang
Yi-Ting Chuang Ming-Wei Lee 1,3
Ming-Wei Lee 1,3 Liang-Yan Hsu
Liang-Yan Hsu