Time-resolved analysis of transcription kinetics in single live mammalian cells

In eukaryotic cells, RNA polymerase II synthesizes mRNA in three stages, initiation, elongation, and termination, and numerous factors determine how quickly a gene is transcribed to produce mRNA molecules through these steps. However, there are few techniques available to measure the rate of each step in living cells, which prevents a better understanding of transcriptional regulation. Here, we present a quantitative analysis method to extract kinetic rates of transcription from time-lapse imaging data of fluorescently labeled mRNA in live cells. Using embryonic fibroblasts cultured from two knock-in mouse models, we monitored transcription of β-actin and Arc mRNA labeled with MS2 and PP7 stem–loop systems, respectively. After inhibiting transcription initiation, we measured the elongation rate and the termination time by fitting the time trace of transcription intensity with a mathematical model function. We validated our results by comparing them with those from an autocorrelation analysis and stochastic simulations. This live-cell transcription analysis method will be useful for studying the regulation of elongation and termination steps, providing insight into the diverse mechanisms of transcriptional processes.

Introduction

Complex regulation of eukaryotic gene expression starts with transcription, through which information in DNA is copied into mRNA. At the site of transcription, RNA polymerase II (Pol II) reads a DNA code and synthesizes mRNA, and three distinct steps can be considered to comprise the transcription procedure: initiation, elongation, and termination. Initiation is the first step in which Pol II binds to a promoter sequence at the 5ʹ end of a gene [1]. In the elongation step, Pol II reads DNA, synthesizes mRNA, and moves from the 5ʹ end to the 3ʹ end [2]. Termination is the last step in which mRNA and Pol II are released from the 3ʹ end of the gene [3, 4]. Thus, three kinetic rates corresponding to each step can be defined: the initiation rate $c$ (the number of Pol II binding per unit time), the elongation rate $k$ (the number of base pairs transcribed per unit time), and the termination time $T_t$ (the time for mRNA separated from DNA after reaching the transcription end site). Despite many efforts to understand how transcription is regulated, limitations and challenges in quantitative measurement of these three kinetic rates still remain.

In recent years, various RNA sequencing methods have been developed to study elongation and pausing of Pol II at the promoter proximal region, intron-exon junctions, and nucleosomes [5–7]. These methods revealed not only the nascent RNA density in the steady state but also the elongation rate in time-resolved experiments. For such time-resolved measurements, transcription was induced or inhibited to track progression of Pol II after drug treatment, whereby the progression speed of the sequence read density directly reflected the elongation rate [8–11]. Nevertheless, population studies cannot resolve the transcriptional processes occurring at a single gene locus and lack the temporal resolution to investigate fast dynamics in real time.

Live-cell imaging has been applied to study transcriptional dynamics in single cells by labeling mRNA, Pol II, or transcription factors with fluorescent proteins [12, 13]. Fluorescence recovery after photobleaching (FRAP) technique has been used to measure transcriptional kinetic rates by fitting recovery curves with various model functions: half recovery time [14], linear and exponential fitting [15–17], and solutions of rate equations [18–21]. However, there is concern about the accuracy of kinetic modeling using FRAP because recovery curves can be affected by photobleaching, diffusion, and binding of fluorescent particles; additionally, different kinetic models can fit the same experimental data almost equally well [22]. More recently, fluctuation correlation analysis of fluorescently labeled mRNA was used to measure the transcription initiation rate and dwell time of a transcript of a yeast gene [23]. In this analysis, the dwell time consists of the elongation and termination times, which cannot be separated in the steady state. Nevertheless, the authors were able to calculate the elongation rate and the termination time by comparing results from two different constructs bearing a PP7 RNA stem–loop cassette in either the 5ʹ untranslated region (UTR) or 3ʹ UTR [23]. Likewise, another study measured the elongation rate of a reporter gene in living Drosophila embryos by comparing the results from two different positions of an MS2 stem-loop cassette [24]. After that, Coulon et al. developed a dual-color fluctuation correlation analysis for human β-globin reporter mRNA labeled with a PP7 cassette in the second intron and an MS2 cassette in the 3ʹ UTR [25]. Using two autocorrelation functions and a single cross-correlation function, the authors measured the kinetics of transcription and splicing of single mRNAs. Liu et al. also used a two-color MS2/PP7 reporter to infer the initiation rate, elongation rate and termination time of the hunchback gene in developing fruit fly embryos [26]. However, it would be challenging to insert ∼1.5-kb-long MS2 and PP7 cassettes into two different locations in an endogenous gene, which limits the general application of the technique in mammalian cells and tissues.

In this study, we developed a time-resolved transcriptional analysis method to measure the elongation rate and termination time of an endogenous mRNA labeled with one stem–loop cassette. Previously, two knock-in (KI) mouse models, Actb-MBS [27] and Arc-PBS [28], were generated to label β-actin (Actb) and Arc mRNA, respectively. In the former, 24 repeats of the MS2 binding site (MBS) were inserted in the 3′ UTR of the Actb gene [27] (Figure 1A); in the latter, 24 repeats of the PP7 binding site (PBS) were knocked in the 3′ UTR of the Arc gene [28] (Figure 1B). Using mouse embryonic fibroblasts (MEFs) derived from these two mouse models, we investigated the transcriptional dynamics of the Actb and Arc genes. First, by applying our time-resolved analysis method, we measured the elongation rate and the termination time of each transcription allele. Then we measured the initiation rate and the total dwell time using the autocorrelation analysis method [23] and compared the total dwell time with the time-resolved analysis results. We found a highly heterogeneous distribution of the kinetic parameters in each locus of both Actb and Arc genes. Yet, there was a significant difference between Actb and Arc regarding the average transcriptional kinetic rates. This approach allows quantitative measurement of all three kinetic rates of single-color labeled mRNA transcription in live cells, providing opportunities to study diverse transcriptional regulation at the single-allele level with high spatiotemporal resolution.

FIGURE 1

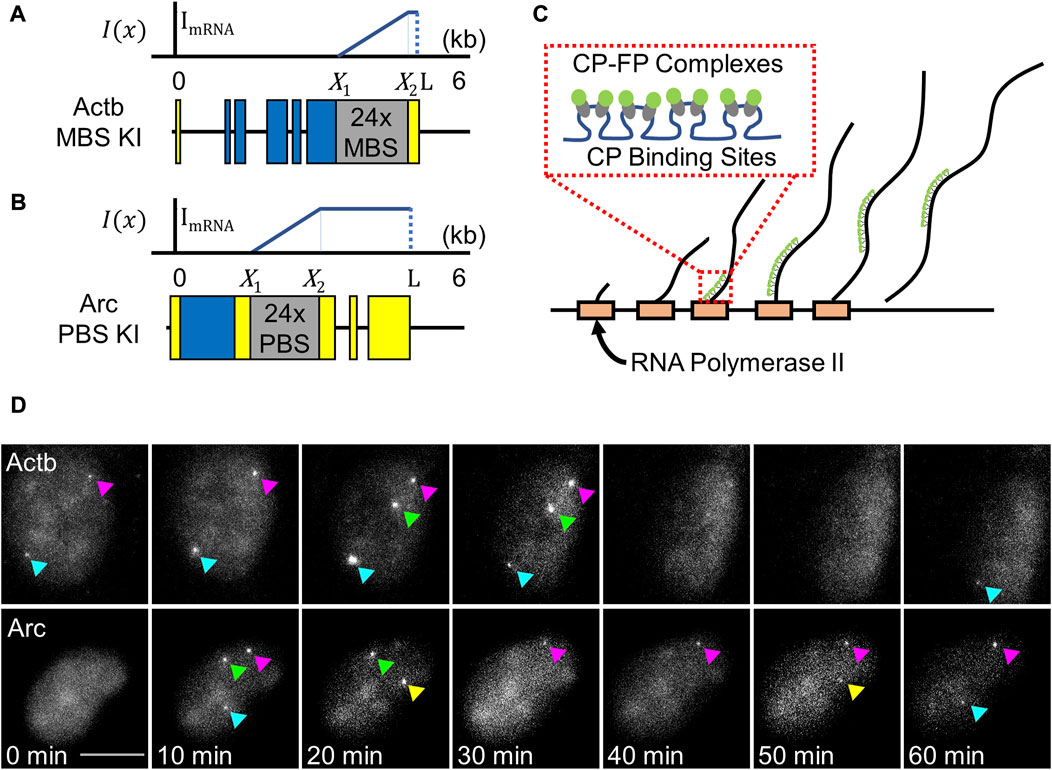
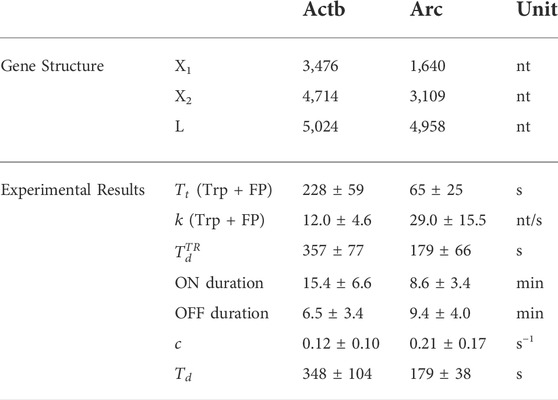
FIGURE 1. Imaging transcription using MS2 and PP7 stem–loop systems. (A,B) Schematic of the Actb-MBS (A) and Arc-PBS (B) knock-in constructs. The fluorescence intensity of a nascent RNA increases as Pol II transcribes the binding sites from $X_1$ to $X_2$. In the post stem–loop region from $X_2$ to $L$, the intensity remains constant (gray: binding sites, blue: coding sequence, yellow: untranslated region). (C) Schematic of nascent RNAs at a transcription site. Multiple capsid proteins fused with fluorescent protein (CP-FP) complexes are bound to a single nascent RNA. (D) Maximum z-projected time-lapse images of serum-stimulated MEFs. Transcription sites are observed as bright points (arrowheads) in the nucleus. Scale bar, 10 μm.

Mathematical models

Time-resolved transcription analysis model

We developed a time-resolved transcription analysis model to determine the transcription elongation rate $k$ and the termination time $T_t$. The dynamics of translation have previously been analyzed using the SunTag system [29] with a mathematical model describing the decreasing fluorescence intensity of a translation site after inhibiting translation initiation [30]. Because RNA stem–loop systems are analogous to the SunTag system, we adapted this model for application to transcriptional dynamics. While translation termination time was not considered in the previous model, we included transcription termination time in our model and derived an analytical function for the decreasing fluorescence intensity after inhibition of transcription initiation.

We assumed that Pol IIs are distributed uniformly on the gene and move toward the 3ʹ end at a constant speed $k$. Although the elongation process can be complex with pausing, traffic jams, backtracking, etc. [31], we sought to measure the average elongation rate $k$ over the entire length of a gene. For simplicity, we modeled transcription termination as a first-order irreversible process with a rate constant $a$. Hence, the number of Pol IIs residing at the 3ʹ end of the gene at time $t$, $N\left(t\right)$ can be calculated as follows.

$\frac{dN\left(t\right)}{dt}=-aN\left(t\right)\to N\left(t\right)=N\left(0\right)e^{-at}(1)$

The transcription termination time was defined as $T_t=1/a$. Suppose that there is no Pol II at the 3ʹ end and that the first Pol II just reaches the end at time $t=0$. With the transcription initiation rate $c$, the number of Pol II reaching the 3ʹ end of the gene during the first time interval Δt is $c\Delta t$. After another time interval Δt, the number of Pol II accumulated at the 3ʹ end becomes

$N\left(\mathrm{n}=2,\Delta t\right)=c\Delta t+c\Delta t{e}^{-\Delta t/T_t}.(2)$

If we assume that Pol II and nascent RNAs fall off at the same time from the 3ʹ end of the gene, Eq. 2 also describes the number of nascent RNAs accumulated at the 3ʹ end at time $2\Delta t$. After an infinite number of Δt intervals, the number of nascent RNAs at the 3ʹ end, $N\left(\infty ,\Delta t\right)$ becomes

$N\left(\infty ,\mathit{\Delta }t\right)=c\mathit{\Delta }t{\displaystyle \sum }_{n=1}^{\infty }{e}^{-\left(n-1\right)\mathit{\Delta }t/T_t}=c\mathit{\Delta }t\frac{1}{1-e^{-\mathit{\Delta }t/T_t}}.(3)$

In the limit that the time interval Δt goes to zero,

$N\left(\infty ,\Delta t\to 0\right)=c{T}_t.(4)$

This result shows that $c{T}_t$ nascent RNAs accumulate at the 3ʹ end in the steady state.

Now let us suppose transcription initiation is blocked at time $t=0$ while in the steady state. After time $t$, the number of nascent RNAs in the 3ʹ end becomes

$N\left(t\right)=c{T}_t{e}^{-t/T_t}.(5)$

Based on the previous study of translational dynamics [30], we set the nascent RNA density as a function of the position on the gene and the time after inhibitor addition. Following the formula for the ribosome probability density in the previous study [30], we first modeled the nascent RNA density function R(x, t) using a Heaviside step function:

$R\left(x,t\right)=\frac{c}{k}H\left(x-kt\right).(6)$

Because $k$ is the elongation rate of Pol II, $c/k$ indicates the number of nascent RNAs per unit length in the Pol II occupied region. The density function in Eq. 6 propagates to the 3′ end direction over time. In this model, however, it is not considered that the nascent RNAs are accumulated at the 3′ end ($x=L$). We expressed the nascent RNA accumulation using a Dirac delta function:

$\delta \left(x-L\right)\cdot c{T}_t\left(H\left(L/k-t\right)+H\left(t-L/k\right)e^{-\left(t-L/k\right)/T_t}\right).(7)$

In Eq. 7, the summation of two Heaviside functions $H\left(L/k-t\right)$ and $H\left(t-L/k\right)e^{-\left(t-L/k\right)/T_t}$ is multiplied by the Dirac delta function. Before the last Pol II enters the 3′ end ($t<L/k$), the amplitude of Dirac delta function (the number of accumulated nascent RNAs) is steady. After the last Pol II enters the 3′ end ($t\ge L/k$), the amplitude decreases exponentially as shown in Eq. 5. Thus, the nascent RNA density at position $x$ and time $t$, $R\left(x,t\right)$ can be described by adding Eq 7 to Eq 6:

$R\left(x,t\right)=\frac{c}{k}H\left(x-kt\right)+\delta \left(x-L\right)\cdot c{T}_t\left(H\left(L/k-t\right)+e^{-\left(t-L/k\right)/T_t}H\left(t-L/k\right)\right).(8)$

This density function is depicted in Figure 2A. The first term in Eq. 8 is the nascent RNA density without the termination time effect. In the second term, the amplitude of the Dirac delta function means the number of accumulated nascent RNAs at position $L$.

FIGURE 2

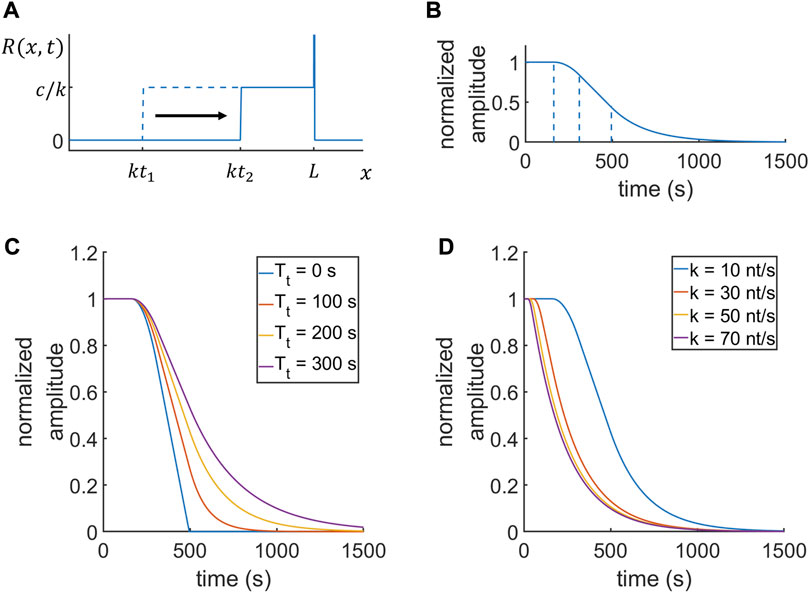
FIGURE 2. Model functional behaviors of the time-resolved transcription analysis. (A) The change in Pol II density distribution from $t_1$ to $t_2$. The transcription initiation inhibitor was added at $t=0$. (B) The model function of the transcription intensity over time after adding the inhibitor. (C,D) The model function calculated for different termination times (C) and elongation rates (D). For (C), the elongation rate was fixed at $k=10$ nt/s, and for (D), the termination time was $T_t=200$ s.

When Pol II starts to transcribe the stem–loop region $\left[X_1,\hspace{0.25em}{X}_2\right]$, the fluorescence intensity of a single nascent RNA $I\left(x\right)$ increases as more stem-loops are synthesized. In the post stem–loop region $\left[X_2\hspace{0.25em},L\right]$, $I\left(x\right)$ remains constant (Figures 1A,B). Then, the intensity with the Pol II position $x$ becomes

$I\left(x\right)=\{\begin{array}{l}0,0\le t<X_1\\ \frac{I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}}}{X_2-X_1}\cdot \left(x-X_1\right),X_1\le t<X_2\\ I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}},X_2\le t<L.\end{array}(9)$

$I_{mRNA}$ is the fluorescence intensity of a single mRNA that is fully transcribed (all 24 stem–loops). Finally, the fluorescence intensity of a transcription site at time $t$, $F\left(t\right)$ can be derived as $F\left(t\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}R\left(x,t\right)\cdot I\left(x\right)dx$. The fluorescence intensity at $t=0$ is

$F\left(0\right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}R\left(x,0\right)I\left(x\right)\cdot dx=I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}}\frac{c}{k}\left(L-\left(X_1+X_2\right)/2+k{T}_t\right).(10)$

The fluorescence intensity at time $t$ becomes

$F\left(t\right)=\{\begin{array}{l}F\left(0\right),0\le t<\frac{X_1}{k}\\ F\left(0\right)-I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}}\frac{c}{k}\frac{1}{2}\frac{{\left(kt-X_1\right)}^2}{X_2-X_1},\frac{X_1}{k}\le t<\frac{X_2}{k}\\ F\left(0\right)-I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}}\frac{c}{k}\left(\frac{1}{2}\left(X_2-X_1\right)+\left(kt-X_2\right)\right),\frac{X_2}{k}\le t<\frac{L}{k}\\ F\left(0\right)-I_{\mathrm{m}\mathrm{R}\mathrm{N}\mathrm{A}}\frac{c}{k}\left(\frac{1}{2}\left(X_2-X_1\right)+\left(L-X_2\right)+k{T}_t\left(1-e^{-\left(t-L/k\right)/T_t}\right)\right),\frac{L}{k}\le t<\infty .\end{array}(11)$

In the Eq. 11, the exponential term in the fourth interval is due to the termination time effect. A normalized fluorescence intensity $F_n\left(t\right)$ is

$F_n\left(t\right)=F\left(t\right)/F\left(0\right)=\{\begin{array}{l}1,0\le t<\frac{X_1}{k}\\ 1-\frac{1}{2}\frac{{\left(kt-X_1\right)}^2}{\left(X_2-X_1\right)\left(L+k{T}_t-\left(X_1+X_2\right)/2\right)},\frac{X_1}{k}\le t<\frac{X_2}{k}\\ \frac{L+k{T}_t-kt}{\left(L+k{T}_t\right)-\left(X_1+X_2\right)/2},\frac{X_2}{k}\le t<\frac{L}{k}\\ \frac{k{T}_t{e}^{-\left(t-L/k\right)/T_t}}{\left(L+k{T}_t\right)-\left(X_1+X_2\right)/2},\frac{L}{k}\le t<\infty .\end{array}(12)$

This is the model function of time-resolved transcription analysis that can be used for fitting experimental data. With the three fitting parameters, $F\left(0\right)$, $k$ and $T_t$, the elongation and termination kinetics can be distinguished in a single-cell experiment.

Autocorrelation analysis model

Larson et al. introduced a mathematical model to analyze transcriptional dynamics using an autocorrelation function of a transcription site intensity trace [23]. We rederived the autocorrelation function in a more concise manner and applied the model to Actb-MBS (Figure 1A) and Arc-PBS (Figure 1B) mRNAs. The autocorrelation function is defined as

$G\left(\tau \right)=\frac{\langle \delta I\left(t\right)\delta I\left(t+\tau \right)\rangle }{{\langle I\left(t\right)\rangle }^2}(13)$

where $\delta I\left(t\right)=I\left(t\right)-\langle I\left(t\right)\rangle$ and $I\left(t\right)$ is the intensity of a transcription site. The bracket denotes the average intensity over time. The experimental data can be fit with the following mathematical model:

$G\left(\tau \right)=\frac{\frac{c}{k_s}{\displaystyle \sum }_{m\le n}^{N+M}{I}_m{I}_{n}P\left(n,t+\tau |m,t\right)}{{\left(\frac{c}{k_s}{\displaystyle \sum }_{m=1}^{N+M}{I}_m\right)}^2}(14)$

where

$\begin{array}{c}N=\frac{X_2-X_1}{l_s}\\ M=\frac{L-X_2}{l_s}\\ k_s=\frac{N+M}{T_d}\end{array}(15)$

$N$ and $M$ are the length of the stem–loop $\left[X_1,\hspace{0.25em}{X}_2\right]$ and the post stem–loop $\left[X_2,\hspace{0.25em}L\right]$ region scaled with the stem–loop size $l_s$. $k_s$ is the effective transition rate of Pol II. $T_d$ is the total dwell time, which includes the elongation time through the fluorescent region (the stem–loop and the post stem–loop region) and the termination time. $I_n$ is the fluorescence intensity of a pre-mRNA after Pol II transcribes the $n$ th stem–loop from the 5ʹ end of the stem–loop region. This pre-mRNA intensity is described as follows:

$I_n=\{\begin{array}{c}n{\bullet I}_{mRNA},0\le n<N\\ N\bullet I_{mRNA},N\le n<N+M\end{array}(16)$

$P\left(n,t+\tau |m,t\right)$ in Eq. 14 is the conditional probability that a Pol II is at position $n$ at time $\left(t+\tau \right)$ given that it has been at position $m$ at time $t$.

Larson et al. approximated the autocorrelation function in Eq. 14 to consider two special cases in which the position of the stem–loop region was at either the 5ʹ or 3ʹ end of an mRNA. Such approximation cannot be applied for Actb-MBS and Arc-PBS mRNAs; the full autocorrelation function in Eq. 14 needs to be used for a general position of the stem–loop region. The autocorrelation function was calculated based on three assumptions: 1) initiation occurs randomly and evenly; 2) Pol II elongates only in one direction from the 5ʹ end to the 3ʹ end, and there is no reverse translocation; and 3) pre-mRNA is released immediately at the 3ʹ end of the gene.

With the assumption that Pol II can progress only in one direction, the probability density of Pol II dwell time $t_n$ in an arbitrary position $n$ can be calculated for the irreversible process.

$\begin{array}{c}n\stackrel{k_s}{{\displaystyle \to }}n+1\\ \frac{d{P}_n\left(t_n\right)}{d{t}_n}=-k_s{P}_n\left(t_n\right)\\ P_n\left(t_n\right)=k_s{e}^{-k_s{t}_n}\end{array}(17)$

The time spent for the transition to the next position is exponentially distributed. If $t_i$ is the time spent for the transition from the $i$ th stem–loop to the $\left(i+1\right)$ th stem–loop, the conditional probability $P\left(n,t+\tau |m,t\right)$ becomes

$P\left(n,t+\tau |m,t\right)=\underset{\tau -{\tau }^{\prime }}{\overset{\infty }{{\displaystyle \int }}}\int \left(k_s{e}^{-k_s{t}_m}\right)\left(k_s{e}^{-k_s{t}_{m+1}}\right)\bullet \bullet \bullet \left(k_s{e}^{-k_s{t}_{n-1}}\right)\left(k_s{e}^{-k_s{t}_n}\right)d^{n-m}t\bullet d{t}_n(18)$

while satisfying constraints given as

$\{\begin{array}{l}{t}_m+t_{m+1}\bullet \bullet \bullet +t_{n-1}={\tau }^{\prime },0{\le \tau }^{\prime }\le \tau \\ {0\le t}_m,t_{m+1},\cdots ,t_{n-1}\\ \tau -{\tau }^{\prime }{\le t}_n\end{array}(19)$

The $\left(n-m\right)$ dimensional integral denoted as $d^{n-m}t$ is $d{t}_m\cdots {dt}_{n-1}$. Each exponential term represents the probability density that Pol II spends time $t_i$ at position $i$. Because Pol II is in the $n$ th stem–loop at time $\left(t+\tau \right)$, if Pol II spends time ${\tau }^{\prime }$ from the $m$ th stem–loop to the $\left(n-1\right)$ th stem–loop, the possible dwell time in the $n$ th stem–loop is from $\tau -{\tau }^{\prime }$ to $\infty$. Then, the conditional probability is described as

$P\left(n,t+\tau |m,t\right)=k_s^{n-m+1}\underset{\tau -{\tau }^{\prime }}{\overset{\infty }{{\displaystyle \int }}}\int \left(e^{-k_s\left(t_1+t_2\bullet \bullet \bullet {+t}_{n-m}\right)}{e}^{-k_s{t}_n}\right)d^{n-m}t\bullet d{t}_n.(20)$

By integrating with $d{t}_n$ first,

$P\left(n,t+\tau |m,t\right)=k_s^{n-m}\int d^{n-m}t\bullet \left(e^{-k_s\left({\tau }^{\prime }\right)}\right)e^{-k_s\left(\tau -{\tau }^{\prime }\right)}=k_s^{n-m}\left(e^{-k_s\tau }\right)\int d^{n-m}t.(21)$

The last integral term is the $\left(n-m\right)$ dimensional volume in the domain denoted in Eq. 19. This domain is a $\left(n-m\right)$-dimensional hyper pyramid in which $(n-m$) segments are perpendicular to each other, and their lengths are $\tau$. The last integral in Eq. 21 is ${\tau }^{n-m}/\left(n-m\right)!$. Finally, the conditional probability becomes

$P\left(n,t+\tau |m,t\right)=\frac{{\left(k_s\tau \right)}^{n-m}{e}^{-k_s\tau }}{\left(n-m\right)!}(22)$

This is the Poisson distribution; $k_s\tau$ is the expected number of stem–loops transcribed during time $\tau$. The autocorrelation function can be calculated by substituting Eq. 22 into Eq. 14. The initiation rate $c$ and the effective transition rate $k_s$ can be obtained by fitting the autocorrelation curve of the experimental data with Eq. 14. Using the $k_s$ value and Eq. 15, we can calculate the total dwell time $T_d$, which includes the elongation time through the fluorescent region (the stem–loop and the post stem–loop region) and the termination time $T_t$. Although we assumed in our derivation that pre-mRNA is released immediately at the 3ʹ end of the gene, the total dwell time calculated from $k_s$ effectively includes the termination time.

Materials and methods

Cell lines and reagents

Two immortalized cell lines, Actb-MBS KI [32] MEFs and Arc-PBS KI [28] MEFs, were used to image Actb and Arc mRNA, respectively. Lentiviral transduction was used to express MCP-GFP and stdPCP-stdGFP [33] fusion proteins in Actb-MBS and Arc-PBS MEFs, respectively. Cells were seeded in glass-bottom dishes in Dulbecco’s modified Eagle’s medium (DMEM) (11995065, Thermo Fisher Scientific, USA) supplemented with 10% fetal bovine serum (FBS) (10082147, Gibco, US), 1% penicillin/streptomycin (Pen/Strep) (15140122, Gibco, US), and 1% GlutaMAX (35050061, Gibco, USA) and incubated at 37°C and 5% CO₂. Prior to imaging, cells were starved for 15–20 h, and the medium was changed to Leibovitz’s L-15 medium without phenol red (21083027 Thermo Fisher Scientific, USA) supplemented with 1% Pen/Strep and 1% GlutaMAX. After placing the cells on a microscope, we stimulated them with a final concentration of 15% FBS. For time-resolved measurement, we blocked transcription initiation by adding 0.5 µM triptolide (T3652, Sigma Aldrich, USA) or 0.3 µM flavopiridol (F3055, Sigma Aldrich, USA) at 10 min after serum stimulation.

Fluorescence microscopy

All images were taken using a wide-field fluorescence microscopy system based on an IX-83 inverted microscope (Olympus) equipped with a UAPON 150×/1.45 NA oil objective (Olympus), iXon Life 888 electron-multiplying charge-coupled device (EMCCD) camera (Andor), SOLA SE u-niR light engine (Lumencor), Chamlide TC top-stage incubator system (Live Cell Instrument), and ET-EGFP filter set (Chroma, ET470/40x, T495lpxr, ET525/50 m). Live-cell imaging was performed at 37°C, and time-lapse z-stack images were taken at an interval of every 8 s over a period of 67 min. Z-stacks were imaged at an interval of 0.5 μm for a total height of 6 μm. The imaging was started right after the inhibitor addition for the time-resolved measurement and serum addition for the auto-correlation analysis (Supplementary Figure S1).

Image analysis

All z-stack images were maximum projected and bleach-corrected via an exponential bleach correction fit using Fiji [34]. Fluorescence intensity time traces of TSs were generated by using HybTrack [35]. The background level was determined by the average intensity of the period in which TS was not automatically detected by HybTrack. For each time trace, transcription ‘ON’ states were distinguished from ‘OFF’ states by two criteria: 1) the TS intensity was higher than 1.5 times the background level, and 2) the durations of both ON and OFF states were equal to or longer than 1 min.

For autocorrelation analysis, we calculated the autocorrelation function of the time traces in the ON-state; time traces longer than the average ON-time were used for analysis. The autocorrelation function was calculated by the multitau algorithm [36]. This algorithm reduces noise in the correlation function at a long lag time. To measure the initiation rate and the total dwell time, we fitted an autocorrelation function of a single ON-time trace with Eq. 14. We used weighted least squares fitting with weights equal to the inverse standard error of the mean. The fitting parameters were the initiation rate $c$ and the effective transition rate of Pol II $k_s$.

For time-resolved measurements after inhibiting transcription initiation, we analyzed time traces showing a plateau followed by a decreasing signal. In our analysis, we assumed that the gene is fully and evenly occupied by Pol IIs before inhibition of transcription initiation; thus, the fluorescence intensity of TS cannot increase after inhibition. Nonetheless, some data exhibited increasing fluorescence intensity after treatment with triptolide; those time traces were considered not to satisfy the condition of our kinetic model. The selected intensity time traces were fit with the model function with a nonlinear least squares method. The fitting parameters were the elongation rate $k$, the termination time $T_t$, and the normalization factor $F\left(0\right)$.

Results

Time-resolved transcription analysis

To label Actb and Arc mRNA with green fluorescent proteins (GFPs), we used the MS2- and PP7-GFP systems, respectively. The MS2-GFP system utilizes highly specific binding between the MS2 bacteriophage capsid protein (MCP) and the MBS RNA stem–loop [37]. Constitutive expression of MCP fused with GFP (MCP-GFP) labeled all endogenous β-actin mRNA in mouse embryonic fibroblasts (MEFs) cultured from Actb-MBS KI mice in which 24 repeats of the MBS were inserted in the 3′ UTR of the β-actin gene [27] (Figure 1A). In a similar manner, endogenous Arc mRNA was visualized by expressing PP7 capsid protein (PCP) fused with GFP (PCP-GFP) in MEFs derived from Arc-PBS KI mice bearing 24 repeats of PBS in the Arc gene 3′ UTR [28] (Figure 1B). In Figures 1A,B, the positions of the start and end of the stem–loop cassettes are denoted as ${\mathrm{X}}_1$ and ${\mathrm{X}}_2$, and the intensity change of a precursor mRNA (pre-mRNA) is shown as a function of the Pol II position $x$. Detailed information of the stem-loop position is described in Table 1. The MS2 or PP7 capsid protein fused with GFP (CP-GFP) complexes carry a nuclear localization sequence (NLS), which targets the protein to the nucleus. When pre-mRNAs are transcribed, multiple CP-GFPs bind to the RNA binding sites (Figure 1C), and the transcription site appears as a bright spot in fluorescence images (Figure 1D, Supplementary Videos S1, S2).

TABLE 1

TABLE 1. Gene structure parameters and measured transcription parameters in this study.

To induce transcription, we starved homozygous Actb-MBS and Arc-PBS MEFs overnight and added serum-containing medium. A few minutes after serum induction, up to four transcription sites appeared in nuclei (Figure 1D). We performed time-resolved experiments by using a small molecule transcription inhibitor, triptolide (Trp) (MW 360.6). It has been shown that triptolide inhibits transcription initiation by preventing transcription bubble formation without significantly affecting the elongation rate [38, 39]. After inhibiting transcription initiation, the region occupied by Pol IIs decreased over time in the direction of elongation (Figure 2A). Then, the normalized intensity of a transcription site declined in 4 steps (Figure 2B). First, the intensity remained constant in $0\le t<X_1/k$ after inhibitor addition. As the last Pol II entered the stem–loop region, the intensity decreased quadratically in the interval of $X_1/k\le t<X_2/k$. After that, the intensity decreased linearly in the time interval of $X_2/k\le t<L/k$ as the last Pol II entered the post stem–loop region. After time $t=L/k$, there were no elongating Pol IIs, and the intensity decreased exponentially due to transcription termination and release of Pol II and mRNA. The model function behaviors for the different values of the termination time $T_t$ and the elongation rate $k$ are shown in Figures 2C,D, respectively. The increase in the termination time $T_t$ resulted in a longer decay time while the time length of the plateau remained the same (Figure 2C). The length of the plateau $X_1/k$ is solely determined by the elongation rate $k$ (Figure 2D), which denotes the speed of Pol II in the pre stem–loop region. Therefore, the elongation rate $k$ and termination time $T_t$ can be acquired by fitting the normalized transcription site intensity of the experimental data with the model function in Eq. 12.

Immediately after adding the initiation inhibitor, we imaged transcription sites in living cells by using fluorescence microscopy. Representative data of the normalized fluorescence intensities of transcription sites in Actb-MBS and Arc-PP7 MEFs are shown in Figures 3A,B, respectively. By fitting the data with Eq. 12, we obtained an average elongation rate of Actb transcription to be 10.4 $\pm$ 2.9 nt/s, which was similar to the elongation rate measured by fluorescence in situ hybridization (FISH) in normal rat kidney (NRK) cells [40]. On the other hand, the average elongation rate of Arc was significantly different from that of Actb; the average elongation rate of Arc transcription was 29.0 $\pm$ 17.0 nt/s, almost 3-fold faster than that of Actb (Figure 3C). Termination times also differed significantly. As illustrated in Figure 3D, the average termination time of Actb mRNA (233 $\pm$ 59 s) was 2.7-fold longer than that of Arc mRNA (86 $\pm$ 27 s).

FIGURE 3

FIGURE 3. Time-resolved analysis of Actb and Arc transcription. (A,B) Representative transcription intensity data (blue dots) and the best fit curves (red lines) of Actb (A) and Arc (B) after the addition of triptolide at $t=0$. (C,D) The elongation rates (C) and termination times (D) of Actb (n = 27 transcription sites) and Arc (n = 10 transcription sites). The mean (red line) and standard deviation (SD, gray box) values are indicated (** $P<0.01$, Wilcoxon rank-sum test).

To validate our measurements, we used another transcription inhibitor, flavopiridol (FP) (MW 438.30), which is known to inhibit cyclin-dependent kinase 9 (Cdk9) in the positive transcription elongation factor b (P-TEFb) complex [41]. This P-TEFb inhibitor FP prohibits Pol II release from the promoter proximal pausing to the productive elongation phase, whereas Trp inhibits new Pol II initiation [8]. Although the mechanisms of inhibition by Trp and FP are different, they result in a similar physical state that inhibits transcription initiation. Using FP with the same procedure as in the Trp experiment, we obtained elongation rate and termination time consistent with the Trp results. We measured the elongation rates of Actb and Arc transcription from the FP experiment as 13.3 $\pm$ 5.6 and 29.0 $\pm$ 15.3 nt/s, respectively, similar to those from the Trp experiment (Figures 4A,B). The termination times obtained from the FP experiments were 223 $\pm$ 59 and 60 $\pm$ 25 s for Actb and Arc transcription, respectively. These values were also consistent with the Trp results (Figures 4C,D). The consistency between the two independent experiments using Trp and FP supports that our time-resolved analysis approach can measure transcriptional elongation and termination kinetics without distinct toxicity effect by the drugs. We determined the average elongation rate and termination time of each gene by pooling the single-allele data set from the Trp and FP experiments (Table 1).

FIGURE 4

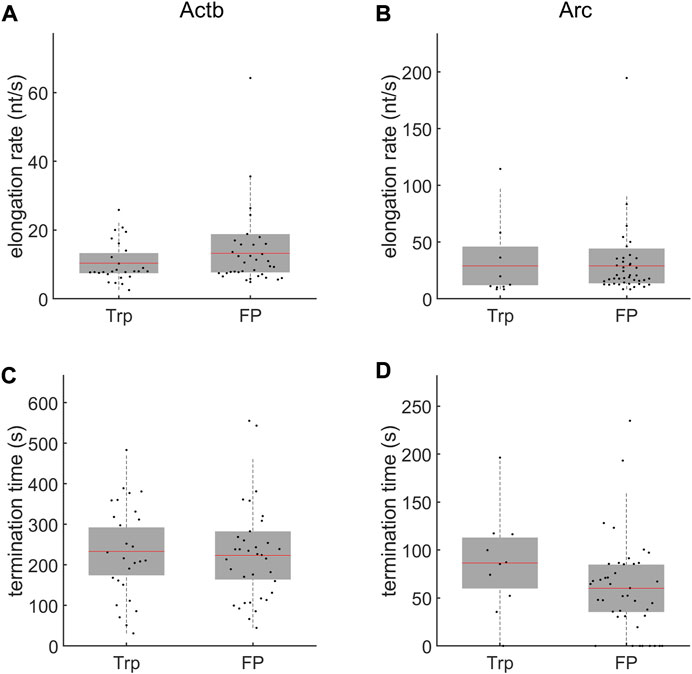
FIGURE 4. Comparison of time-resolved measurements after adding triptolide (Trp) and flavopiridol (FP). (A,B) The elongation rates of Actb (A) and Arc (B). The elongation rates measured after adding Trp and FP were similar for each gene. (C,D) The termination times of Actb (C) and Arc (D). The mean (red line) and standard deviation (SD, gray box) values are indicated. No significant difference was observed between experiments using Trp (n = 27 transcription sites for Actb and 10 for Arc) and FP (n = 35 transcription sites for Actb and 42 for Arc) ($P>0.05$, Wilcoxon rank-sum test).

Autocorrelation analysis

Next, we examined whether the time-resolved results are valid by using the autocorrelation analysis described in the section of mathematical models. For the autocorrelation analysis, we recorded the intensity of transcription sites, which showed bursting transcriptional activity without the initiation inhibitors after serum induction (Figures 5A,B). Both the Actb and Arc genes exhibited stochastic switching between active (ON) and inactive (OFF) states after serum induction. The average duration of the ON-state was 15.4 ± 6.6 min (means ± SD) for Actb, which was significantly longer than the 8.6 ± 3.4 min observed for Arc (p < 0.01, t test; Figure 5C). The duration of the OFF state was 6.5 ± 3.4 min for Actb, shorter than the 9.4 ± 4.0 min for Arc (p < 0.01, t test; Figure 5D). These results demonstrate that Actb exhibits transcriptional bursts more frequently in longer time periods than Arc does.

FIGURE 5

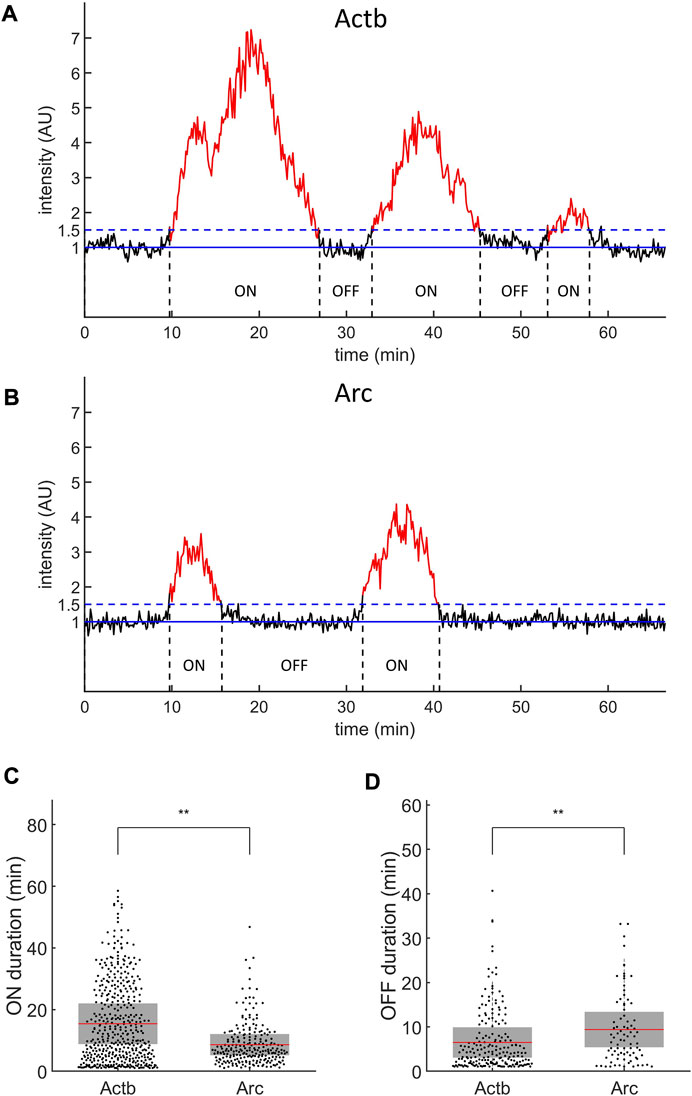
FIGURE 5. Transcription ON and OFF durations of Actb and Arc genes. (A,B) Representative intensity profiles of transcription sites of Actb (A) and Arc (B) genes. The solid blue lines indicate the baseline normalized by the nuclear background. The dashed blue lines indicate the threshold for transcriptional ON (red) and OFF (black) states. AU, arbitrary units. (C,D) ON (C) and OFF (D) durations of Actb (n = 449 for ON and 198 for OFF states) and Arc (n = 234 for ON and 83 for OFF states). The mean (red line) and standard deviation (SD, gray box) values are indicated (* $P<0.05$ and ** $P<0.01$, Wilcoxon rank-sum test).

The initiation rate and total dwell time were measured from the autocorrelation function of transcription intensity traces during ON-times. Because the autocorrelation analysis model was developed for a steady-state condition, we calculated the autocorrelation function from the selected ON-state traces of which durations were longer than the average ON-time of each gene. Then, the selected ON-time duration was 28.9 ± 9.9 min for Actb (183 traces) and 15.5 ± 7.3 min for Arc (82 traces) on average. Before the autocorrelation analysis, we characterized the general behavior of the model function shown in Eq. 14. The autocorrelation amplitude $G\left(0\right)$ in Eq. 14 decreases as either the initiation rate $c$ or the total dwell time $T_d$ increases (Figures 6A,B). The decay time of the autocorrelation function is independent of $c$ (Figure 6A) but increases as $T_d$ increases (Figure 6B). Representative autocorrelation curves of Actb and Arc transcription are depicted in Figures 6C,D, respectively. We plotted $c$ and $T_d$ values obtained from individual ON-traces in Figures 6E,F, respectively. The average initiation rate and total dwell time were $c=$ 0.12 $\pm$ 0.10 s⁻¹ and $T_d=$ 348 $\pm$ 104 s for Actb and $c=$ 0.21 $\pm$ 0.17 s⁻¹ and $T_d=$ 179 $\pm$ 38 s for Arc. These average total dwell times $T_d$ were about 20% of the average of the subjected ON-time duration.

$T_d^{TR}=T_t+\frac{L-X_1}{k}.(23)$

FIGURE 6

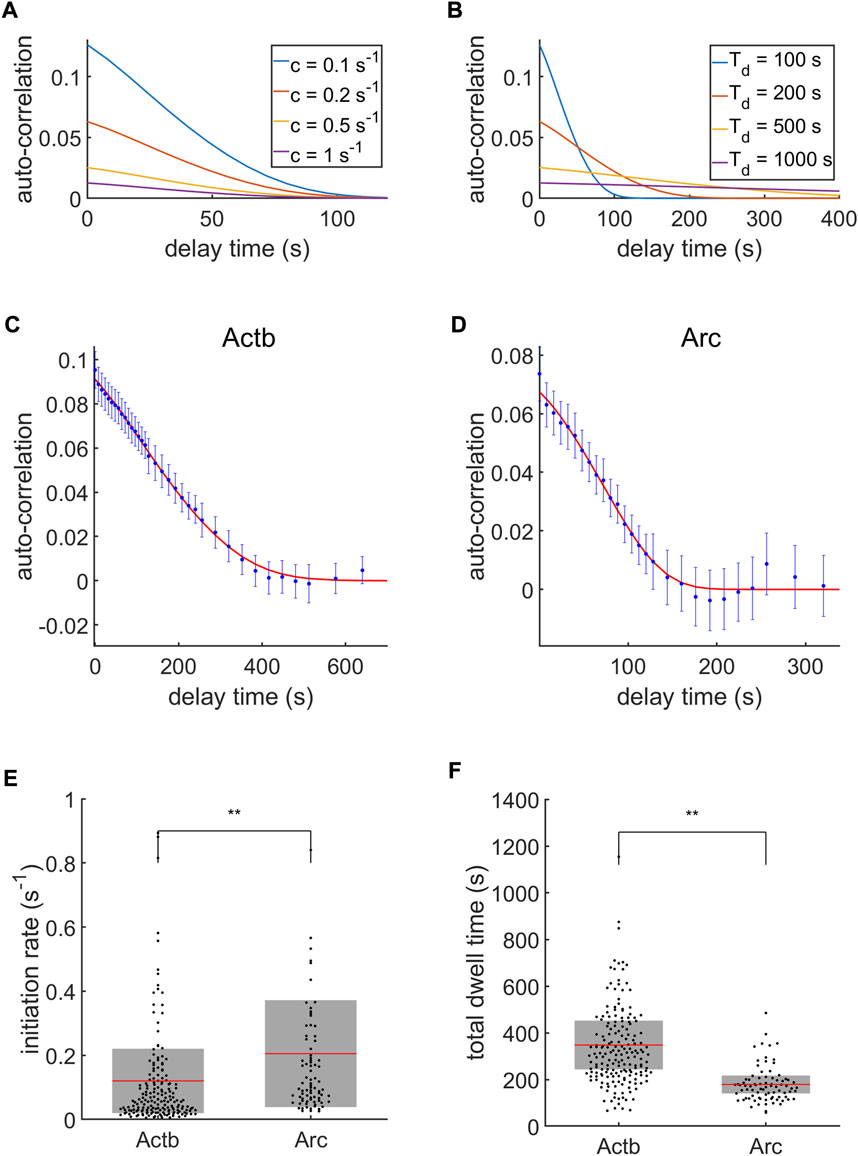
FIGURE 6. Autocorrelation analysis of transcription. (A,B) Autocorrelation model function behaviors with varying initiation rate $c$ (A) and total dwell time $T_d$ (B). The termination time was set to $T_t=0$. For (A), the total dwell time was fixed at $T_d=100$ s, and for (B), the initiation rate was $c=0.1$ s⁻¹. (C,D) Representative autocorrelation data (blue dots) and the best fit curves (red lines) of Actb (C) and Arc (D) transcription. (E,F) The initiation rates (E) and the total dwell times (F) of Actb (n = 183 ON-time traces) and Arc (n = 82 ON-time traces). The mean (red line) and standard deviation (SD, gray box) values are indicated (** $P<0.01$, Wilcoxon rank-sum test).

Next, we compared the total dwell times from the time-resolved measurements with those from the autocorrelation analysis. Using the results of the time-resolved measurements, the total dwell time can be calculated as.

With this, the total dwell times from the time-resolved measurements were calculated as $T_d^{TR}=$ 357 $\pm$ 77 s for Actb and 179 $\pm$ 66 s for Arc transcription. The two different dwell times, $T_d$ and $T_d^{TR}$, obtained from the autocorrelation and the time-resolved analyses, respectively, were quite similar for each gene. We note that the total dwell time was defined as the nascent RNA dwell time in the fluorescence region (stem-loop and post stem-loop regions) in the autocorrelation analysis. In the time-resolved analysis, however, the total dwell time was calculated using the elongation rate $k$ which was measured in the region before the stem-loops. Therefore, we compared $T_d$ and $T_d^{TR}$ under the assumption of a constant Pol II elongation rate $k$ over the whole gene. Although we made such a simple assumption, $T_d$ and $T_d^{TR}$ matched reasonably well.

Error estimation by simulations

Using simulations, we estimated the errors in the time-resolved measurements for each gene structure of Actb and Arc labeled with the stem-loops. The input parameters of the simulations were initiation rate $c$, elongation rate $k$, and termination time $T_t$. For our analytical model, we made a simple assumption of uniform Pol II distribution with a constant initiation rate $c$. However, it is known that the initiation time interval between two Pol IIs is dependent on the promoter dynamics [31, 42]. For a Poissonian promoter, the polymerase initiation time interval follows an exponential distribution. Therefore, we initiated Pol IIs with an exponential time interval $T_{int}$ in computer simulations:

$\mathrm{P}\left(T_{int}\right)=c{\mathrm{e}}^{-c{T}_{int}}(24)$

The mean time interval is $1/c$ as in our time-resolved analytical model.

The elongation process follows the Poisson distribution as shown in Eq. 22. Then, the probability of $x$ nucleotides elongated in time $\Delta t$ is

$\mathrm{P}\left(x\right)=\frac{{\left(k\Delta t\right)}^x}{x!}{\mathrm{e}}^{-k\Delta t}(25)$

In the simulation, the time $\Delta t$ was 8 s, which was the same as the interval of our time-lapse imaging data. Eq. 25 shows that the number of nucleotides elongated by Pol II during $\Delta t$ follows a Poisson distribution with a mean of $k\Delta t$. As Pol II transcribes a stem loop, the intensity of the transcription site increases by a unit brightness. After summation of all pre-mRNA intensities, the simulation generated the intensity time trace of a transcription site. For the simulation of the time-resolved analysis, Pol IIs were distributed at random positions on the gene considering the Poissonian initiation and elongation, and ${cT}_t$ Pol IIs were placed at position $L$ at time $t=0$. The termination time was given as an exponential random value, and there was no newly initiated Pol II after $t=0$. Figure 7 shows the average normalized simulation intensity of Actb 1) and Arc 2) transcription sites (blue dots) when transcription initiation is inhibited at time $t=0$. These intensity time traces were generated by repeating the simulation 100 times with input parameters from the experimental results (Actb: $c=0.12$ s⁻¹, $k=12.0$ nt/s, and $T_t=228$ s. Arc: $c=0.21$ s⁻¹, $k=29.0$ nt/s, and $T_t=179$ s). We fitted the single intensity time traces with the model function from Eq. 12. The red lines in Figures 7A,B show the model function with the average fitted values. The average elongation rate and termination time obtained by fitting the simulation curves were $k=12.4\pm 1.9$ nt/s and $T_t=226\pm 45$ s for Actb; $k=30.6\pm 13.2$ nt/s and $T_t=174\pm 28$ s for Arc. These fitting results are quite similar to their ground truth values used as the input parameters in the simulations.

FIGURE 7

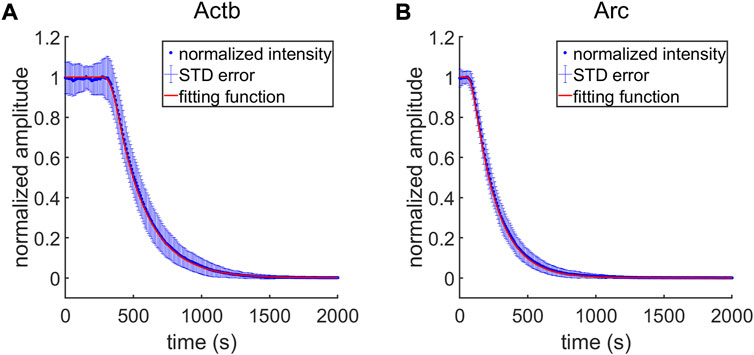
FIGURE 7. Transcription intensities generated by time-resolved computer simulation. (A,B) The averages of normalized transcription intensities are shown as blue dots for each case of Actb (A) and Arc (B) transcription (n = 100 simulations for each gene). The error bar (blue bar) depicts standard deviation of the normalized intensities. The fitting function (red lines) are plotted using the average value of single trace fitting results.

Figure 8 shows the errors in the elongation rate $k$ and the termination time $T_t$ obtained by fitting the simulation results corresponding to various input parameters. The input initiation rate $c$ varied from 0.01 s⁻¹ to 1 s⁻¹ in the $x$-axis. The input elongation rate $k$ varied from 10^0.5 to 10² nt/s in the $y$-axis. The input termination time $T_t$ is shown on top in Figure 8. The error in the output value was defined as $\left|\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}-\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}\right|/\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}$. The color maps in Figure 8 display the errors in the output values of elongation rate $k$ and total dwell time $T_t$. The mean errors are generally larger for shorter termination times $T_t$ and lower initiation rates $c$. Because the assumption of uniformly distributed Pol IIs is not valid for the low $c$ limits, the time-resolved analysis is not appropriate in this realm.

FIGURE 8

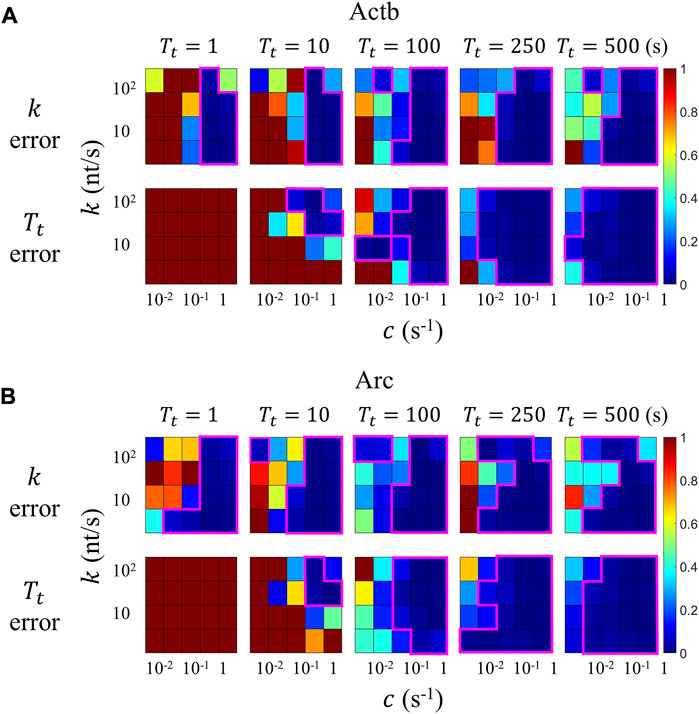
FIGURE 8. Assessment of errors in the time-resolved transcription analysis by using simulations. Simulation input parameters are initiation rate $c$, elongation rate $k$, and termination time $T_t$. (A,B) Mean errors of $k$ and $T_t$ obtained by fitting the results from 100 simulation runs are shown in color maps for Actb (A) and Arc (B). All error values over 1 are displayed in dark red color. Regions with a mean error under 10% are denoted with magenta lines.

The areas inside the magenta lines in Figure 8 indicate the regime in which the mean errors are under 10%. The valid region of the time-resolved model is on the lower and right sides of the color map. The time-resolved analysis of our Actb and Arc transcription data yielded the elongation rate $k$ and the termination time $T_t$ within the valid region of less than 10% error. These results support the overall validity of the elongation rate and termination time measured by the time-resolved method.

Discussion

In this study, we investigated the transcription kinetics of the Actb and Arc genes by using two analysis methods of live-cell imaging. Because transcription initiation, elongation, and termination dynamic factors cannot be measured separately in the steady state, we used Trp and FP to inhibit transcription initiation and performed time-resolved measurements. For simplicity, we assumed that Pol IIs accumulate at the end of the gene for transcription termination and described it as a Dirac delta function in the Pol II density distribution $R\left(x,t\right)$. By fitting our data with this mathematical model, we obtained the elongation rate and the termination time separately and confirmed that the total dwell times of Actb and Arc nascent RNAs were consistent with those from the autocorrelation measurement. To identify the regime where the model function fittings are valid, we checked the error behavior of the time-resolved model with various input parameters. The elongation rates and the termination times of Actb and Arc measured in this study were well within the valid region of our analysis method.

We obtained significantly different elongation rates and termination times for Actb and Arc transcription. The elongation process can include different events such as pausing, traffic jams, backtracking, and so forth [31]. Therefore, the elongation rate obtained in this study represents the overall average elongation rate affected by those complex processes. The Actb and Arc elongation rates were 12.0 $\pm$ 4.6 bp/s and 29.0 $\pm$ 15.5, respectively. So, it appears that Pol II elongation was interrupted more often on the Actb gene than on the Arc. There are many factors that affect the elongation rate of Pol II, such as exon density, nucleosome structure, and CpG content [8, 11]. Previous studies have revealed that Pol II pauses or slows down at intron-exon junctions [8, 9, 11] and that exon density has the greatest effect on the elongation rate among the factors mentioned above [8]. The gene lengths of Actb and Arc are similar (Actb: 3,640 bp, Arc: 3,490 bp), but Actb has 6 exons and Arc has 3. Thus, the exon density of Actb (1.6 exons/kb) is about two times higher than that of Arc (0.9 exons/kb), which could be the reason why the elongation rate of Actb is much slower than that of Arc.

Furthermore, the termination time of Actb (228 ± 59 s) was 3.5-fold longer than that of Arc (65 ± 25 s). There are several different types of transcription termination in mammalian cells [4], and the termination of human Actb transcription occurs by Pol II pause-dependent termination type. This Pol II pausing occurs at the G-rich pause sequence downstream of the poly(A) signal (PAS) [43]. In the human Actb gene, nascent transcripts hybridize to the antisense DNA strand and displace the sense DNA strand, forming a structure called an R-loop [44]. The R-loop is formed prevalently over G-rich pause sites behind the elongation complex and induces Pol II pausing. Senataxin, a DNA-RNA helicase, resolves R-loops to allow the 5ʹ-3ʹ exonuclease Xrn2 to degrade the nascent RNA fragment from the poly(A) cleavage site [44]. Similar to human Actb, mouse Actb also has a G-rich region at 450 nucleotides downstream of the PAS; hence, transcription of mouse Actb is also likely to be terminated by the R-loop-dependent pausing mechanism. We determined the termination time, which was defined as the time from reaching the transcription end site (TES) to the release of mRNA, to be approximately 230 s for mouse Actb. This data provides us with information on the timescale of transcription termination by R-loop-dependent pausing. In contrast, the mouse Arc gene does not have a G-rich region downstream of the PAS and exhibits a much shorter transcription termination time of ∼65 s. Therefore, we presume that Arc transcription termination occurs via a different mechanism. The Arc gene has a viral origin and contains sequences that are related to retrotransposon Gag genes [45, 46]. It is also interesting that the transcription termination time of Arc is similar to that of an HIV-1 RNA reporter gene (63.5 s) in U2OS cells [15]. Our new analysis technique to measure termination time can be useful to unravel diverse transcription termination processes.

We note that our time-resolved model has some limitations due to the simple assumption of uniform transcription initiation and elongation rates. In fact, the initiation and elongation processes are more complex, depending on the promoter dynamics [31, 42]. For instance, the inter-polymerase distance distribution is exponential for a Poissonian promoter and is much more complicated for a bursty promoter. Although Actb and Arc genes exhibit ON and OFF transitions as shown in Figure 5, we investigated the transcriptional activity only during the ON states. Because the average duration of the ON states was sufficiently long, on the order of 10 min for both genes, we were able to analyze the transcription dynamics within a single ON state. The average number of Pol IIs on a gene can be estimated as $c(L/k)+c{T}_t$. Using the data summarized in Table 1, we estimated the average number of Pol IIs on Actb and Arc genes to be 77 and 50, respectively. These numbers are sufficiently large to approximate the Poissonian initiation as a uniform procedure. Therefore, our simple assumption of the uniform Pol II distribution did not result in significant errors for these genes as demonstrated in Figure 8, where we compared our results from the time-resolved analysis with simulation results. However, our simple analysis method may not be generally applicable for a Poissonian promoter with a smaller number of Pol IIs or a bursty promoter with a much faster switching behavior.

The transcription initiation rate was not determined by our time-resolved model because we normalized the decreasing intensity by the plateau level $F\left(0\right)$. If the intensity of a single mRNA $I_{mRNA}$ can be measured, we can calculate the initiation rate $c$ as

$c=\frac{F\left(0\right)}{I_{mRNA}\left(\frac{2L-X_1-X_2}{2k}+T_t\right)}(26)$

Because of the high GFP background in the nucleus, it was difficult to measure the intensities of single mRNA and transcription sites simultaneously in our live-cell experiments. We expect that background-free RNA imaging techniques such as the MS2-PP7 hybrid stem–loop system combined with split-GFP approaches [47, 48] will allow for measuring both single mRNA and transcription site intensities and extracting all three transcription kinetic rates, $c$, $k$, and $T_t$, simultaneously in a single cell.

In addition, we expect this analysis method to be used in conjunction with RNA-targeting CRISPR-Cas systems [49–51], through which we could analyze the transcription kinetics of any endogenous RNA without requiring genetic manipulation. Our time-resolved model function was calculated by integrating the product of the Pol II density function and the fluorescence intensity of a nascent RNA. Such model function for a different RNA tagging system can be easily derived following the same steps described herein. This analysis technique will expand our capability to investigate the transcription kinetics of endogenous genes in a highly quantitative manner.

Data availability statement

The results of experimental and simulation data are uploaded at zenodo (https://zenodo.org/record/7089382#.YyYZCnZByUk), and the source codes for analysis and simulation are uploaded at github (https://github.com/Neurobiophysics/SingleCellTxnDyn).

Author contributions

HP designed research; HC developed the mathematical model and performed all experiments, analysis, and simulations; HC and BL developed software; and HC and HP wrote the paper.

Funding

This work was supported by the Creative-Pioneering Researchers Program through Seoul National University, Howard Hughes Medical Institute (HHMI)-Wellcome International Research Scholar Award from the Wellcome Trust (208468/Z/17/Z), and the Basic Science Research Program through the National Research Foundation of Korea (NRF) grant funded by the Korean government (2020R1A2C2007285). For the purpose of open access, the author has applied a CC BY public copyright license to any Author Accepted Manuscript version arising from this submission.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.977125/full#supplementary-material

References

1. Roeder RG. The complexities of eukaryotic transcription initiation: Regulation of preinitiation complex assembly. Trends Biochem Sci (1991) 16(11):402–8. doi:10.1016/0968-0004(91)90164-q

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Jonkers I, Lis JT. Getting up to speed with transcription elongation by RNA polymerase II. Nat Rev Mol Cel Biol (2015) 16(3):167–77. doi:10.1038/nrm3953

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kuehner JN, Pearson EL, Moore C. Unravelling the means to an end: RNA polymerase II transcription termination. Nat Rev Mol Cel Biol (2011) 12(5):283–94. doi:10.1038/nrm3098

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Proudfoot NJ. Transcriptional termination in mammals: Stopping the RNA polymerase II juggernaut. Science (2016) 352(6291):aad9926. doi:10.1126/science.aad9926

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Core LJ, Lis JT. Transcription regulation through promoter-proximal pausing of RNA polymerase II. Science (2008) 319(5871):1791–2. doi:10.1126/science.1150843

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kwak H, Fuda NJ, Core LJ, Lis JT. Precise maps of RNA polymerase reveal how promoters direct initiation and pausing. Science (2013) 339(6122):950–3. doi:10.1126/science.1229386

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Churchman LS, Weissman JS. Nascent transcript sequencing visualizes transcription at nucleotide resolution. Nature (2011) 469(7330):368–73. doi:10.1038/nature09652

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jonkers I, Kwak H, Lis JT. Genome-wide dynamics of Pol II elongation and its interplay with promoter proximal pausing, chromatin, and exons. elife (2014) 3:e02407. doi:10.7554/elife.02407

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Danko CG, Hah N, Luo X, Martins A, Core L, Lis J, et al. Signaling pathways differentially affect RNA polymerase II initiation, pausing, and elongation rate in cells. Mol Cel (2013) 50(2):778–222. doi:10.1016/j.molcel.2013.05.025

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Fuchs G, Voichek Y, Benjamin S, Gilad S, Amit I, Oren M. 4sUDRB-seq: Measuring genomewide transcriptional elongation rates and initiation frequencies within cells. Genome Biol (2014) 15(5):R69–11. doi:10.1186/gb-2014-15-5-r69

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Veloso A, Kirkconnell KS, Magnuson B, Biewen B, Paulsen MT, Wilson TE, et al. Rate of elongation by RNA polymerase II is associated with specific gene features and epigenetic modifications. Genome Res (2014) 24(6):896–905. doi:10.1101/gr.171405.113

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lenstra TL, Rodriguez J, Chen H, Larson DR. Transcription dynamics in living cells. Annu Rev Biophys (2016) 45:25–47. doi:10.1146/annurev-biophys-062215-010838

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Vera M, Biswas J, Senecal A, Singer RH, Park HY. Single-cell and single-molecule analysis of gene expression regulation. Annu Rev Genet (2016) 50:267–91. doi:10.1146/annurev-genet-120215-034854

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kimura H, Sugaya K, Cook PR. The transcription cycle of RNA polymerase II in living cells. J Cel Biol (2002) 159(5):777–82. doi:10.1083/jcb.200206019

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Boireau S, Maiuri P, Basyuk E, de la Mata M, Knezevich A, Pradet-Balade B, et al. The transcriptional cycle of HIV-1 in real-time and live cells. J Cel Biol (2007) 179(2):291–304. doi:10.1083/jcb.200706018

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Maiuri P, Knezevich A, De Marco A, Mazza D, Kula A, McNally JG, et al. Fast transcription rates of RNA polymerase II in human cells. EMBO Rep (2011) 12(12):1280–5. doi:10.1038/embor.2011.196

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yao J, Ardehali MB, Fecko CJ, Webb WW, Lis JT. Intranuclear distribution and local dynamics of RNA polymerase II during transcription activation. Mol Cel (2007) 28(6):978–90. doi:10.1016/j.molcel.2007.10.017

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ben-Ari Ya., Brody Y, Kinor N, Mor A, Tsukamoto T, Spector DL, et al. The life of an mRNA in space and time. J Cel Sci (2010) 123(10):1761–74. doi:10.1242/jcs.062638

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Darzacq X, Shav-Tal Y, de Turris V, Brody Y, Shenoy SM, Phair RD, et al. In vivo dynamics of RNA polymerase II transcription. Nat Struct Mol Biol (2007) 14(9):796–806. doi:10.1038/nsmb1280

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Dundr M, Hoffmann-Rohrer U, Hu Q, Grummt I, Rothblum LI, Phair RD, et al. A kinetic framework for a mammalian RNA polymerase in vivo. Science (2002) 298(5598):1623–6. doi:10.1126/science.1076164

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yunger S, Rosenfeld L, Garini Y, Shav-Tal Y. Single-allele analysis of transcription kinetics in living mammalian cells. Nat Methods (2010) 7(8):631–3. doi:10.1038/nmeth.1482

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mueller F, Mazza D, Stasevich TJ, McNally JG. FRAP and kinetic modeling in the analysis of nuclear protein dynamics: What do we really know? Curr Opin Cel Biol (2010) 22(3):403–11. doi:10.1016/j.ceb.2010.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Larson DR, Zenklusen D, Wu B, Chao JA, Singer RH. Real-time observation of transcription initiation and elongation on an endogenous yeast gene. Science (2011) 332(6028):475–8. doi:10.1126/science.1202142

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Garcia HG, Tikhonov M, Lin A, Gregor T. Quantitative imaging of transcription in living Drosophila embryos links polymerase activity to patterning. Curr Biol (2013) 23(21):2140–5. doi:10.1016/j.cub.2013.08.054

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Coulon A, Ferguson ML, de Turris V, Palangat M, Chow CC, Larson DR. Kinetic competition during the transcription cycle results in stochastic RNA processing. Elife (2014) 3:e03939. doi:10.7554/elife.03939

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Liu J, Hansen D, Eck E, Kim YJ, Turner M, Alamos S, et al. Real-time single-cell characterization of the eukaryotic transcription cycle reveals correlations between RNA initiation, elongation, and cleavage. Plos Comput Biol (2021) 17(5):e1008999. doi:10.1371/journal.pcbi.1008999

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lionnet T, Czaplinski K, Darzacq X, Shav-Tal Y, Wells AL, Chao JA, et al. A transgenic mouse for in vivo detection of endogenous labeled mRNA. Nat Methods (2011) 8(2):165–70. doi:10.1038/nmeth.1551

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Das S, Moon HC, Singer RH, Park HY. A transgenic mouse for imaging activity-dependent dynamics of endogenous Arc mRNA in live neurons. Sci Adv (2018) 4(6):eaar3448. doi:10.1126/sciadv.aar3448

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Tanenbaum ME, Gilbert L, Qi L, Weissman J, Vale R. A protein-tagging system for signal amplification in gene expression and fluorescence imaging. Cell (2014) 159(3):635–46. doi:10.1016/j.cell.2014.09.039

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yan X, Hoek T, Vale R, Tanenbaum M. Dynamics of translation of single mRNA molecules in vivo. Cell (2016) 165(4):976–89. doi:10.1016/j.cell.2016.04.034

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Dobrzynski M, Bruggeman FJ. Elongation dynamics shape bursty transcription and translation. Proc Natl Acad Sci U S A (2009) 106(8):2583–8. doi:10.1073/pnas.0803507106

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Park HY, Lim H, Yoon YJ, Follenzi A, Nwokafor C, Lopez-Jones M, et al. Visualization of dynamics of single endogenous mRNA labeled in live mouse. Science (2014) 343(6169):422–4. doi:10.1126/science.1239200

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wu B, Miskolci V, Sato H, Tutucci E, Kenworthy CA, Donnelly SK, et al. Synonymous modification results in high-fidelity gene expression of repetitive protein and nucleotide sequences. Genes Dev (2015) 29(8):876–86. doi:10.1101/gad.259358.115

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, et al. Fiji: An open-source platform for biological-image analysis. Nat Methods (2012) 9(7):676–82. doi:10.1038/nmeth.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Lee BH, Park HY. HybTrack: A hybrid single particle tracking software using manual and automatic detection of dim signals. Sci Rep (2018) 8(1):212–7. doi:10.1038/s41598-017-18569-3

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wohland T, Rigler R, Vogel H. The standard deviation in fluorescence correlation spectroscopy. Biophysical J (2001) 80(6):2987–99. doi:10.1016/s0006-3495(01)76264-9

CrossRef Full Text | Google Scholar

37. Bertrand E, Chartrand P, Schaefer M, Shenoy SM, Singer RH, Long RM. Localization of ASH1 mRNA particles in living yeast. Mol Cel (1998) 2(4):437–45. doi:10.1016/s1097-2765(00)80143-4

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Vispé S, DeVries L, Creancier L, Besse J, Breand S, Hobson DJ, et al. Triptolide is an inhibitor of RNA polymerase I and II–dependent transcription leading predominantly to down-regulation of short-lived mRNA. Mol Cancer Ther (2009) 8(10):2780–90. doi:10.1158/1535-7163.mct-09-0549

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Bensaude O. Inhibiting eukaryotic transcription. Which compound to choose? How to evaluate its activity? Which compound to choose? How to evaluate its activity? Transcription (2011) 2(3):103–8. doi:10.4161/trns.2.3.16172

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Femino AM, Fay FS, Fogarty K, Singer RH. Visualization of single RNA transcripts in situ. Science (1998) 280(5363):585–90. doi:10.1126/science.280.5363.585

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Chao S-H, Price DH. Flavopiridol inactivates P-TEFb and blocks most RNA polymerase II transcription in vivo. J Biol Chem (2001) 276(34):31793–9. doi:10.1074/jbc.m102306200

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ali MZ, Choubey S. Decoding the grammar of transcriptional regulation from RNA polymerase measurements: Models and their applications. Phys Biol (2019) 16(6):061001. doi:10.1088/1478-3975/ab45bf

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Gromak N, West S, Proudfoot NJ. Pause sites promote transcriptional termination of mammalian RNA polymerase II. Mol Cel Biol (2006) 26(10):3986–96. doi:10.1128/mcb.26.10.3986-3996.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Skourti-Stathaki K, Proudfoot NJ, Gromak N. Human senataxin resolves RNA/DNA hybrids formed at transcriptional pause sites to promote Xrn2-dependent termination. Mol Cel (2011) 42(6):794–805. doi:10.1016/j.molcel.2011.04.026

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Ashley J, Cordy B, Lucia D, Fradkin LG, Budnik V, Thomson T. Retrovirus-like Gag protein Arc1 binds RNA and traffics across synaptic boutons. Cell (2018) 172(1-2):262–74 e11. doi:10.1016/j.cell.2017.12.022

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Pastuzyn ED, Day CE, Kearns RB, Kyrke-Smith M, Taibi AV, McCormick J, et al. The neuronal gene arc encodes a repurposed retrotransposon Gag protein that mediates intercellular RNA transfer. Cell (2018) 172(1-2):275–88 e18. doi:10.1016/j.cell.2017.12.024

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wu B, Chen J, Singer RH. Background free imaging of single mRNAs in live cells using split fluorescent proteins. Sci Rep (2014) 4:3615. doi:10.1038/srep03615

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Park SY, Moon HC, Park HY. Live-cell imaging of single mRNA dynamics using split superfolder green fluorescent proteins with minimal background. RNA (2020) 26(1):101–9. doi:10.1261/rna.067835.118

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Nelles DA, Fang M, O’Connell M, Xu J, Markmiller S, Doudna J, et al. Programmable RNA tracking in live cells with CRISPR/Cas9. Cell (2016) 165(2):488–96. doi:10.1016/j.cell.2016.02.054

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Yang L-Z, Wang Y, Li SQ, Yao RW, Luan PF, Wu H, et al. Dynamic imaging of RNA in living cells by CRISPR-Cas13 systems. Mol Cel (2019) 76(6):981–97.e7. e7. doi:10.1016/j.molcel.2019.10.024

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Wang H, Nakamura M, Abbott TR, Zhao D, Luo K, Yu C, et al. CRISPR-mediated live imaging of genome editing and transcription. Science (2019) 365(6459):1301–5. doi:10.1126/science.aax7852

PubMed Abstract | CrossRef Full Text | Google Scholar