Abstract
We investigate the over-barrier ionization of hydrogen atoms in intense circularly and elliptically polarized laser fields. By solving the time-dependent Schrödinger equation, we simulate the photoelectron momentum distributions with the peak laser field intensity ranging from tunneling ionization to over-barrier ionization regime. It is shown that the photoelectron momentum distributions reveal a spiral distribution in the over-barrier ionization regime, which is in contrast with the typical donut distribution sculpted by above-threshold ionization peaks in the tunneling ionization regime. To analyze the intriguing photoelectron behavior, we further develop a semi-classical model by considering the non-adiabatic effect and the depletion effect of the ground state. The photoelectron momentum distributions calculated by the semi-classical model agree well with the results of the time-dependent Schrödinger equation. Based on these results, we further explore the relationship between the instantaneous ionization rate and initial transverse momentum in over-barrier ionization. It is worth noting that such a relationship is not easy to be clearly revealed in tunneling ionization regime as the final electron momentum is significantly modified by the inter-cycle interference. Moreover, we also show that the non-adiabatic effect and long-range Coulomb interaction play important roles in the over-barrier ionization.
Introduction
In the strong-field community, when atoms and molecules are exposed in intense laser fields, a series of interesting physical phenomena can be revealed, including the above-threshold ionization (ATI) [1–3], molecular dissociation, Coulomb explosion [4–6], and non-sequential double (multiple) ionization [7–9]. As well known, strong-field ionization can be characterized using the Keldysh parameter [10], where ω, E, are the angular frequency of driving light, electric field strength, and ionization potential of atoms, respectively. When the amplitude of the driving laser field is small (), the ionization is dominated by multi-photon ionization (MPI) [11–13]. In this case, the photoionization tends to be depicted in the frequency picture, and its ionization rate is proportional to , where is the laser intensity and is the number of photons absorbed. When the amplitude of the driving laser field is large (), the Coulomb potential of atoms is pronouncedly bent to be a barrier. Then the electrons can tunnel through the suppressed barrier into the classical region, which is called tunneling ionization (TI) [14–18]. So far, multi-photon ionization and tunneling ionization have been intensively studied.
If the laser intensity further increases, the suppressed Coulomb barrier could be lower than the energy of the ground state atom. The bounded electron would be liberated from the parent ion directly, which is called over barrier ionization (OBI) [19]. The threshold strength of the driving laser field for OBI can be estimated by (Here Z is the charge of the residual ion) [20]. This formula is derived on the assumption that the electrons only move in one-dimensional (1D) Cartesian space. Tong and Lin have developed an empirical formula to describe the ionization rate over a wide range of laser intensity, including the OBI regime [21]. Meanwhile, several experimental and theoretical studies of the OBI have been reported. In Ref. [22], the authors have made a systematic scan of the ionization rate of noble gases from the TI to OBI regime. Using the magneto-optically trapped target reaction microscope (MOTREMI), the photoelectron energy and momentum spectra of single ionization of lithium in the OBI regime have been measured [23], and these results were then analyzed by solving the time-dependent Schrödinger equation (TDSE) [24]. By measuring the electron transverse momentum distributions of the neon atom in 3P2 metastable state near the OBI regime, Ivanov, et al., showed that the cusp-like structure of transverse momentum is independent of laser ellipticity in OBI regime [25, 26]. Recently, by using MOTREMI, the momentum distributions of Rbn+ recoil ions up to have been measured, which exhibit multiband structures as the light field polarization varies from linear polarization to circular polarization [27].
In this paper, we theoretically study the photoionization of hydrogen atoms driven by intense elliptically and circularly polarized laser fields. By solving TDSE, we show that the photoelectron momentum distributions reveal a unique helical structure in the OBI regime, which has been rarely discovered in the MPI and TI regimes. To interpret the underlying mechanism, we further develop a semi-classical model (SCM), in which the depletion effect of ground state wavefunction and non-adiabatic effect have been considered. The simulated results of the SCM and TDSE show a great agreement. We reveal that the photoelectrons emitted in the leading edge of the laser pulse are streaked into momentum-resolved final states, allowing one to establish the time-to-angle mapping. Utilizing the correspondence between the final momentum and ionization moments, we explore the initial condition of ejected photoelectrons. The simulated results indicate that the non-adiabatic effect and long-range Coulomb potential still play important roles in OBI.
Theoretical methods
Quantum simulation
We obtain the photoelectron momentum distributions by numerically solving the TDSE based on the split-operator spectral (SOS) method [28–30]. In principle, the SOS method is suitable for all linear eigenvalue issues involving any number of dimensions, and it does not require special basis functions or potentials in the form of analytic expression. However, to ensure the accuracy of SOS method, an adequate sampling rate in space and time is necessary [31–33].
When an intense laser field interacts with a hydrogen atom, the TDSE within single-electron approximation and dipole approximation is given by (unless otherwise stated, atomic units () are used throughout this paper)where is the electronic coordinate measured from the center of the nucleus and is the synthesized potential imposed on the electron, including the action of hydrogen ion and laser field. The synthesized potential can be written aswhere is the electric field of driving laser pulses. We notice that the synthesized potential reaches its maximum at the distance of . Therefore, if the laser electric field is strong enough, the synthesized potential can be lower than the ionization potential of atoms, namely . In this case, the strong-field ionization enters into the OBI regime. Specifically, for a hydrogen atom ( a.u.), we can estimate that the OBI occurs when the laser field strength is larger than a.u., corresponding to the laser intensity W/cm2.
To find a clear physical picture of the OBI, we use elliptically and circularly polarized laser fields in the simulation. The selection of these two laser fields can avoid the rescattering of ejected electrons so that we can highlight the effect taken by the laser strength. Here, the electric field is given bywhere , and are the laser ellipticity, angular frequency, and carrier envelope phase (CEP), respectively.f(t)=sin2(ωt/2n) is the sine-square temporal envelope, where n is the cycle number of the laser pulse and here it is chosen to be . For a sufficiently strong circularly polarized pulse laser, as the electric field increases the ionization model changes from MPI to TI, and finally to OBI within a single laser pulse, as shown in Figure 1. We have performed a series of simulations with the center wavelength of 800 nm, and the peak intensity varying from 1.1 × 1014 W/cm2 to 6.3 × 1015 W/cm2, corresponding electric field strength changing from 0.04 a.u. to 0.3 a.u.
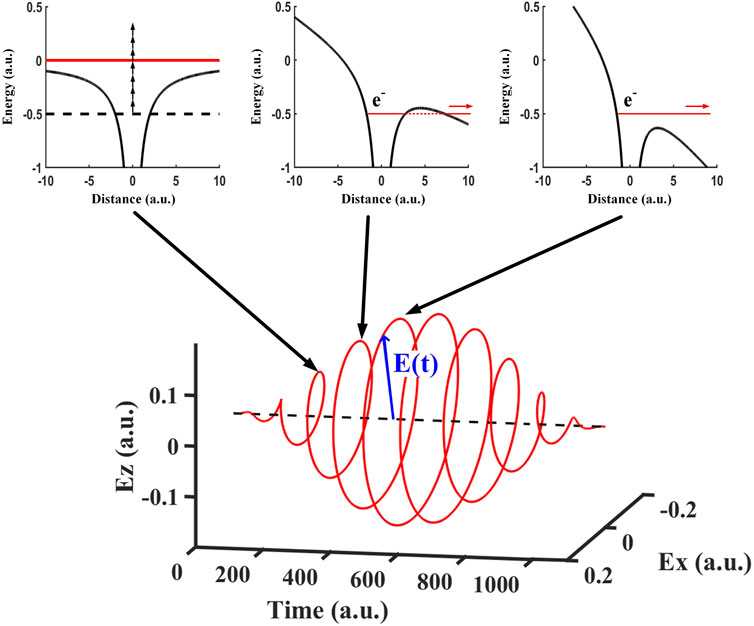
FIGURE 1
The electric field of a circularly polarized pulse laser with the peak electric field strength of 0.2 a.u. Three insets represent three different kinds of ionization and mark the corresponding electric field strength. The blue arrow represents the instantaneous electric field strength.
We utilize a symmetrically split operator algorithm for advancing the solution of TDSE by an incremental time . This can be expressed as
Here, is the initial wavefunction of the electron, which can be prepared by imaginary-time propagation [34]. Eq. 4 is equivalent to a free particle propagation over a half time increment, a phase change from the action of the potential over a total time increment, and a free propagation over the remaining half increment. The operator applied to is difficult to calculate in coordinate space. However, it can be realized by using the band-limited Fourier series representation.
After the electron wavefunction being operated by , we will havewhere is the number of grid points, and is the length of the computational grid. At the end of the pulse, the wave function is propagated for another three cycles to make sure that the low-energy electrons could travel far enough from the parent ion to be collected in calculation. At each time step , we extract the ionized part from the total wave function,where is a smooth absorbing function, and is the boundary to distinguish if the electron is ionized or not. Then the ionized wavefunction would be converted into momentum space.where is the vector potential of the laser field, and analytically propagates under the Volkov Hamiltonian to the end of the simulation,
At last, we obtain the total photoelectron momentum distribution by summing the wave packets in momentum space ionized at different .
Semiclassical model
The physical process of SCM is based on the traditional strong-field ionization model [35–37] with the improvement of the initial momentum distribution and the depletion effect. The initial tunneling coordinates of tunneling electrons are obtained by the saddle-point approximation [38, 39], in which the non-adiabatic effect and phase in the ionization process are included in the SCM [40, 41]. In the saddle-point method, the electron transition amplitude between the ground state and Volkov state is approximated by summing over the quantum orbits [1, 42],where is the classical action and is the saddle point of time, given by
The initial momentum and position are given by , , where is the ionization moment. The motion of released electron is obtained by solving Newton’s motion equations . This kind of practice uses for reference from Coulomb-corrected strong-field approximation, which can deal well with the influence of Coulomb potential [43].
Besides, the depletion of ground state wavefunction cannot be ignored because of the high ionization rate in the intense laser field. We can suppose the instantaneous ionization rate can be expressed by the product of static field ionization rate and residual electron probability.where is the cumulative ionization probability in a laser pulse and is an empirically-corrected formula for static field ionization rate [21]. Here, since the OBI is driven by the circularly and elliptically polarized laser fields, the rescattering effect of electrons is suppressed.
Results and discussion
In Figure 2, we show the two-dimensional photoelectron momentum distributions simulated by TDSE, for a wide range of electronic field strength from a.u. to 0.3 a.u., corresponding to the transition from TI to OBI regime. In the TI regime (Figure 2A), the photoelectron momentum spectrum has a donut-shaped distribution sculpted by an obvious ATI structure resulting from inter-cycle interference [11]. With the conversion of the electric field strength from the TI regime to the OBI regime, the photoelectron momentum spectra show characteristic spiral distributions, along with the disappearance of ATI peaks, as shown in Figures 2B–D. The spiral structures are gradually stretched with the increasing electric field strength. These phenomena have been never revealed in previous works. Additionally, one can find these spiral-shaped structures are nearly overlapped with the negative vector potentials of the driving lasers (the red lines in Figure 2).
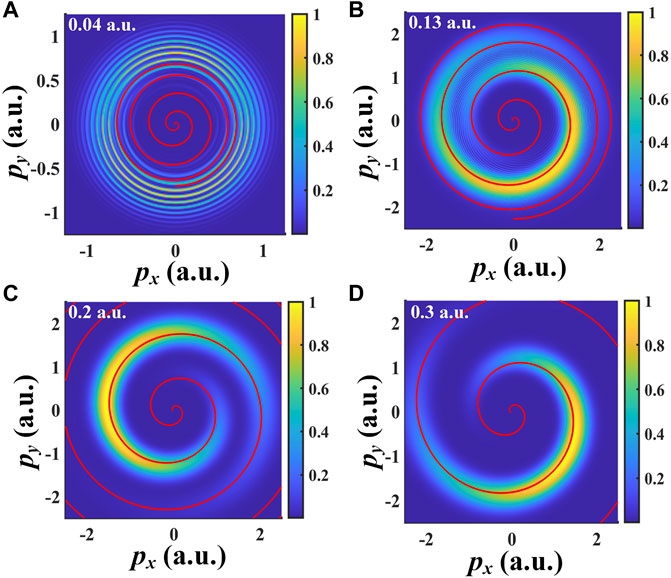
FIGURE 2
The photoelectron momentum spectra calculated by TDSE, corresponding electric field strength are (A) 0.04 a.u. (B) 0.13 a.u. (C) 0.2 a.u. (D) 0.3 a.u. The field-driven momentum is shown by the red line.
Within the strong-field approximation, the final momentum of the measured electron is determined by the negative vector potential , where is the ionization instant [44, 45]. In the OBI regime, the field-strength dependent ionization rate is high enough for saturation so that most electrons are ionized in the rising edge of a laser pulse. Because the shape of the negative vector potential is a spiral curve in the rising edge, the photoelectron distributions show a similar spiral structure in momentum space, as shown in Figures 2B–D. Besides, one can note that the electrons ionized at different moments of the same laser cycle would be mapped into different directions, and the electrons ionized in different laser cycles would be mapped into different radii in momentum space. Therefore, the inter-cycle interference patterns have been suppressed in the OBI regime, resulting in the disappearance of ATI peaks. Moreover, the momentum-resolved final states of electrons mean that one can establish the one-to-one correspondence between final momenta and ionization moments via the relation , which will be helpful to investigate the initial condition of ejected photoelectrons.
To reveal the physical mechanism of OBI, we have further calculated the photoelectron momentum distributions by the SCM including the non-adiabatic effect and the depletion of bound electrons. The simulated results are shown in Figure 3, which agree well with the TDSE simulation. In addition to reproducing the momentum distributions of TDSE, the SCM also offers an intuitive description of the initial condition of the ejected photoelectrons in the OBI regime. In SCM, we can give the instantaneous ionization rate with the depletion effect of bound electrons, as indicated in Figure 4A. In order to compare the ionization rate under the same electric field strength conveniently, we also calculate the ionization rate as a function of the instantaneous electric field, as shown in Figure 4B. The black dotted line represents the threshold to come into the OBI regime for a hydrogen atom ( a.u.). When the electric field is weaker than the threshold field strength, the instantaneous electric field dominates the process, and the rate increases exponentially as the field strength increases. However, if the electric field is larger than the threshold, the increase of ionization rate gradually slows down and even begins to decline due to the depletion effect of bounded electron wavefunction. In the past, the instantaneous ionization rate is only a function of instantaneous electric field strength. But after considering the depletion effect, the pulse envelope, determined by the peak electric strength , also plays an important role. One can note the curve with a.u. (blue circles in Figure 4B) is shifted to the right than the curve with a.u. (purple circles), which means that with higher peak strength, there are more electrons remaining unionized until the laser field reaches a higher intensity. Utilizing the one-to-one correspondence between final momenta and ionization moments, we can extract the ionization rates from the momentum distributions calculated by TDSE, represented by blue and purple lines in Figure 4A,B, which support the conclusions of SCM.
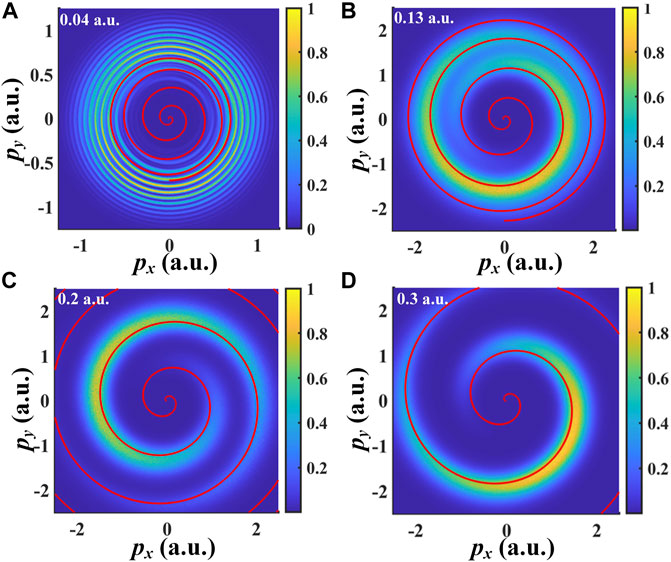
FIGURE 3
The photoelectron momentum spectra calculated by SCM, corresponding electric field strength are (A) 0.04 a.u. (B) 0.13 a.u. (C) 0.2 a.u. (D) 0.3 a.u. The field-driven momentum is shown by the red line.
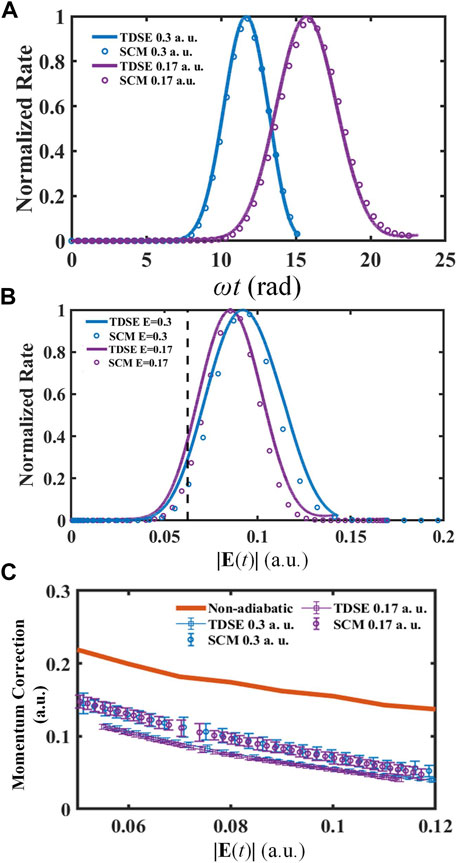
FIGURE 4
The comparisons between TDSE and SCM. (A) The ionization rates normalized by the maximum. The blue and purple lines represent the ionization rates given by TDSE with different peak electric field strengths, 0.3 and 0.17 a.u. The blue and purple circles represent the counterparts in SCM. (B) The same as (A) but the horizontal ordinate is the instantaneous electric field strength in rising edge instead of time. The black dotted line represents the threshold of the OBI regime, a.u. (C) The red line represents the correction of initial transverse momentum deviation from non-adiabatic effect. The bule and purple lines represent the total momentum correction in TDSE, and the blue and purple circles represent the counterparts in SCM.
As seen in SCM, the non-adiabatic ionization coordinates are important ingredients for the simulation. In the next step, we explore the initial transverse momentum deviation, which is included in the difference between the negative vector potential and the most probable final momentum. Taking the non-adiabatic effect into account, one can obtain the correction of initial transverse momentum [46], represented by the red line in Figure 4C. Then it was also influenced by the Coulomb potential in the propagation process after ionized. Therefore, the final momentum can be expressed by , where is the initial transverse momentum deviation and is the correction due to the Coulomb potential. Utilizing the correspondence between the final electron momentum and the ionization moment, one can draw the total corrections of both SCM and TDSE by calculating , which are shown in Figure 4C. Although there is no reliable method to directly obtain the initial transverse momentum deviation from TDSE, the agreement of total correction between SCM and TDSE suggests the correction of initial momentum in SCM is enlightening. Besides, by comparing the results with different peak electric field strengths (0.3 a.u. represented by blue line and circles, and 0.17 a.u. represented by purple line and circles), it is intuitive to find the momentum correction is only dependent on the instantaneous electric field. And as the electric field strength increases, the momentum corrections become smaller. One can see that there is a tiny difference between the results of TDSE and SCM. This discrepancy is caused due to insufficient consideration of the change of barrier width caused by the increase of laser intensity in the SCM.
We further calculate the photoelectron momentum distributions in the OBI regime by using a laser pulse with different ellipticities and CEPs. The results are shown in Figure 5, where the left column is calculated by TDSE and the right column is calculated by SCM. As shown in Figure 5A,B, for an elliptically polarized laser field with a.u., , the shape of electron momentum spectra is squashed along the minor axis due to the change of negative vector potential. There are several extrema of ionization rate because the electric field strength is not monotonous any longer at the rising edge. For a long laser pulse, the CEP is always thought to have no influence. But in the OBI regime, when CEP is varied, the shape of negative vector potential will be rotated and result in a rotated photoelectron momentum spectrum. The results are shown in Figure 5C,D, using a circularly polarized laser with peak electric field strength of 0.2 a.u. and CEP of . This suggests that in order to perform a strong-field ionization experiment with a laser intensity in the OBI regime, the CEP of the pulse laser should be stabilized. Otherwise, the final electron momentum distribution will be averaged by the results of different laser CEPs, and thus it reveals an annulus as shown in Figure 5E,F.
FIGURE 5
The calculated photoelectron momentum distributions for different ellipticities and CEPs. The left column is calculated by TDSE and the right column is calculated by SCM. (A,B) a.u., , ; (C,D) a.u., , ; (E,F) the superposition of photoelectron spectra with different CEPs.
Conclusion
In conclusion, we have theoretically studied the OBI of hydrogen atoms under the intense circularly and elliptically polarized laser pulses. The simulated photoelectron momentum distributions reveal an interesting spiral structure, and such structure can be reproduced by the modified SCM. It suggests that the non-adiabatic effect and depletion of ground state wavefunction are very important in the OBI regime. Utilizing the corresponding relation between the ionization moment and final momentum, we have analyzed the initial condition of ejected photoelectrons. Moreover, the developed SCM has been used in the calculation for the laser pulse with different ellipticities and CEPs. This work presents an intuitive physical picture of the photoionization process in the OBI regime. Due to the momentum-resolved final states of electrons ionized at different moments in one cycle, one can fully resolve the sub-cycle dynamics of photoelectrons in the OBI.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
We thank the support of the National Natural Science Foundation of China (Grant No. 92050201 and 11774013).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Becker W Grasbon F Kopold R Milošević D Paulus G Walther H . Above-threshold ionization: From classical features to quantum effects. Adv Mol Opt Phys (2002) 48:35–98. 10.1016/S1049-250X(02)80006-4
2.
Eberly JH Javanainen J Rza̧żewski K . Above-threshold ionization. Phys Rep (1991) 204(5):331–83. 10.1016/0370-1573(91)90131-5
3.
Schafer K Yang B DiMauro L Kulander K . Above threshold ionization beyond the high harmonic cutoff. Phys Rev Lett (1993) 70(11):1599–602. 10.1103/PhysRevLett.70.1599
4.
Bocharova I Karimi R Penka EF Brichta J-P Lassonde P Fu X et al Charge resonance enhanced ionization ofCO2Probed by laser Coulomb explosion imaging. Phys Rev Lett (2011) 107(6):063201. 10.1103/PhysRevLett.107.063201
5.
Posthumus J Giles A Thompson M Codling K . Field-ionization, Coulomb explosion of diatomic molecules in intense laser fields. J Phys B: Mol Opt Phys (1996) 29(23):5811. 10.1088/0953-4075/29/23/022
6.
Stapelfeldt H Constant E Corkum P . Wave packet structure and dynamics measured by Coulomb explosion. Phys Rev Lett (1995) 74(19):3780–3. 10.1103/PhysRevLett.74.3780
7.
Becker W Liu X Ho PJ Eberly JH . Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev Mod Phys (2012) 84(3):1011–43. 10.1103/RevModPhys.84.1011
8.
Fittinghoff DN Bolton PR Chang B Kulander KC . Observation of nonsequential double ionization of helium with optical tunneling. Phys Rev Lett (1992) 69(18):2642–5. 10.1103/PhysRevLett.69.2642
9.
Walker B Sheehy B DiMauro LF Agostini P Schafer KJ Kulander KC . Precision measurement of strong field double ionization of helium. Phys Rev Lett (1994) 73(9):1227–30. 10.1103/PhysRevLett.73.1227
10.
Keldysh L . Ionization in the field of a strong electromagnetic wave. Sov Phys JETP (1965) 20(5):1307–14.
11.
Agostini P Fabre F Mainfray G Petite G Rahman NK . Free-free transitions following six-photon ionization of xenon atoms. Phys Rev Lett (1979) 42(17):1127–30. 10.1103/PhysRevLett.42.1127
12.
Voronov G Delone G Delone N Kudrevatova O . Multiphoton ionization of the hydrogen molecule in the strong electric field of ruby laser emission. J Exp Theor Phys (1965) 2:237.
13.
Fabre F Petite G Agostini P Clement M . Multiphoton above-threshold ionisation of xenon at 0.53 and 1.06 µm. J Phys B: Mol Phys (1982) 15(9):1353–69. 10.1088/0022-3700/15/9/012
14.
Ge P Han M Deng Y Gong Q Liu Y . Universal description of the attoclock with two-color corotating circular fields. Phys Rev Lett (2019) 122(1):013201–6. 10.1103/PhysRevLett.122.013201
15.
Delone N Krainov VP . Energy and angular electron spectra for the tunnel ionization of atoms by strong low-frequency radiation. J Opt Soc Am B (1991) 8(6):1207–11. 10.1364/JOSAB.8.001207
16.
Corkum P Burnett N Brunel F . Above-threshold ionization in the long-wavelength limit. Phys Rev Lett (1989) 62(11):1259. 10.1103/PhysRevLett.62.1259
17.
Teeny N Yakaboylu E Bauke H Keitel CH . Ionization time and exit momentum in strong-field tunnel ionization. Phys Rev Lett (2016) 116(6):063003. 10.1103/PhysRevLett.116.063003
18.
Han M Ge P Fang Y Yu X Guo Z Ma X et al Unifying tunneling pictures of strong-field ionization with an improved attoclock. Phys Rev Lett (2019) 123(7):073201–5. 10.1103/PhysRevLett.123.073201
19.
Calvert J Goodall S Wang X Xu H Kheifets AS Ivanov I et al Transverse electron momentum distribution in tunneling and over the barrier ionization by strong-field laser pulses. J Phys Conf Ser (2015) 635:19002. 10.1088/1742-6596/635/9/092073
20.
Augst S Strickland D Meyerhofer DD Chin S-L Eberly JH . Tunneling ionization of noble gases in a high-intensity laser field. Phys Rev Lett (1989) 63(20):2212–5. 10.1103/PhysRevLett.63.2212
21.
Tong X Lin C . Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression regime. J Phys B: Mol Opt Phys (2005) 38(15):2593–600. 10.1088/0953-4075/38/15/001
22.
Augst S Meyerhofer DD Strickland D Chin S-L . Laser ionization of noble gases by coulomb-barrier suppression. J Opt Soc Am B (1991) 8(4):858–67. 10.1364/JOSAB.8.000858
23.
Schuricke M Zhu G Steinmann J Simeonidis K Ivanov I Kheifets A et al Strong-field ionization of lithium. Phys Rev A (2011) 83(2):023413. 10.1103/PhysRevA.83.023413
24.
Morishita T Lin CD . Photoelectron spectra and high rydberg states of lithium generated by intense lasers in the over-the-Barrier ionization regime. Phys Rev A (2013) 87(6):063405. 10.1103/PhysRevA.87.063405
25.
Ivanov I . Evolution of the transverse photoelectron-momentum distribution for atomic ionization driven by a laser pulse with varying ellipticity. Phys Rev A (2014) 90(1):013418. 10.1103/PhysRevA.90.013418
26.
Ivanov I Kheifets A Calvert J Goodall S Wang X Xu H et al Transverse electron momentum distribution in tunneling and over the barrier ionization by laser pulses with varying ellipticity. Sci Rep (2016) 6(1):19002–8. 10.1038/srep19002
27.
Yuan J Liu S Wang X Shen Z Ma Y Ma H et al Ellipticity-dependent sequential over-barrier ionization of cold rubidium. Phys Rev A (2020) 102(4):043112. 10.1103/PhysRevA.102.043112
28.
Feit M Fleck J Jr Steiger A . Solution of the schrödinger equation by a spectral method. J Comput Phys (1982) 47(3):412–33. 10.1016/0021-9991(82)90091-2
29.
Feit M Fleck J Jr . Solution of the schrödinger equation by a spectral method II: Vibrational energy levels of triatomic molecules. J Chem Phys (1983) 78(1):301–8. 10.1063/1.444501
30.
Hermann MR Fleck J Jr . Split-operator spectral method for solving the time-dependent schrödinger equation in spherical coordinates. Phys Rev A (1988) 38(12):6000. 10.1103/PhysRevA.38.6000
31.
Fleck JA Morris J Feit M . Time-dependent propagation of high energy laser beams through the atmosphere. Appl Phys (1976) 10(2):129–60. 10.1007/BF00896333
32.
Feit M Fleck J . Computation of mode eigenfunctions in graded-index optical fibers by the propagating beam method. Appl Opt (1980) 19(13):2240–6. 10.1364/AO.19.002240
33.
Feit M Fleck J . Spectral approach to optical resonator theory. Appl Opt (1981) 20(16):2843–51. 10.1364/AO.20.002843
34.
Protopapas M Keitel CH Knight PL . Atomic physics with super-high intensity lasers. Rep Prog Phys (1997) 60(4):389–486. 10.1088/0034-4885/60/4/001
35.
Corkum PB . Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71(13):1994–7. 10.1103/PhysRevLett.71.1994
36.
Paulus GG Becker W Nicklich W Walther H . Rescattering effects in above-threshold ionization: A classical model. J Phys B: Mol Opt Phys (1994) 27(21):L703–8. 10.1088/0953-4075/27/21/003
37.
Min L Geng JW Hong L Deng Y Wu C Peng LY et al Classical-quantum correspondence for above-threshold ionization. Phys Rev Lett (2014) 112(11):113002. 10.1103/PhysRevLett.112.113002
38.
Bleistein N Handelsman RA . Asymptotic expansions of integrals. San Francisco: Ardent Media (1975).
39.
Gribakin G Kuchiev MY . Multiphoton detachment of electrons from negative ions. Phys Rev A (1997) 55(5):3760–71. 10.1103/PhysRevA.55.3760
40.
Han M Ge P Shao Y Liu MM Deng Y Wu C et al Revealing the sub-barrier phase using a spatiotemporal interferometer with orthogonal two-color laser fields of comparable intensity. Phys Rev Lett (2017) 119(7):073201–6. 10.1103/PhysRevLett.119.073201
41.
Li M Geng J-W Han M Liu M-M Peng L-Y Gong Q et al Subcycle nonadiabatic strong-field tunneling ionization. Phys Rev A (2016) 93(1):013402. 10.1103/PhysRevA.93.013402
42.
Salières P Carré B Le Déroff L Grasbon F Paulus G Walther H et al Feynman's path-integral approach for intense-laser-atom interactions. Science (2001) 292(5518):902–5. 10.1126/science.108836
43.
Popruzhenko V . Keldysh theory of strong field ionization: History, applications, difficulties and perspectives. J Phys B: Mol Opt Phys (2014) 47(20):204001. 10.1088/0953-4075/47/20/204001
44.
Reiss HR . Effect of an intense electromagnetic field on a weakly bound system. Phys Rev A (1980) 22(5):1786–813. 10.1103/PhysRevA.22.1786
45.
Faisal FH . Multiple absorption of laser photons by atoms. J Phys B: Mol Phys (1973) 6(4):L89–92. 10.1088/0022-3700/6/4/011
46.
Li M Liu M-M Geng J-W Han M Sun X Shao Y et al Experimental verification of the nonadiabatic effect in strong-field ionization with elliptical polarization. Phys Rev A (2017) 95(5):053425. 10.1103/PhysRevA.95.053425
Summary
Keywords
over-barrier ionization, photoelectron momentum spectrum, time-dependent schrödinger equation (TDSE), semi-classical model, strong field physics
Citation
Wang J, Guo Z, Fang Y, Yu X and Liu Y (2022) Over-barrier ionization of hydrogen atom in intense circular and elliptical laser fields. Front. Phys. 10:976734. doi: 10.3389/fphy.2022.976734
Received
23 June 2022
Accepted
21 July 2022
Published
08 September 2022
Volume
10 - 2022
Edited by
Weifeng Yang, Hainan University, China
Reviewed by
Hongcheng Ni, East China Normal University, China
Yueming Zhou, Huazhong University of Science and Technology, China
Updates
Copyright
© 2022 Wang, Guo, Fang, Yu and Liu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yunquan Liu, yunquan.liu@pku.edu.cn
This article was submitted to Optics and Photonics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.