- 1Department of Physics, National Tsing Hua University, Hsinchu, Taiwan
- 2Center for General Education, Chang Gung University, Taoyuan, Taiwan
- 3Department of Physics, National Tsing Hua University, Hsinchu, Taiwan
- 4Physics Division, National Center for Theoretical Sciences, Hsinchu, Taiwan
- 5Institute of Physics, Academia Sinica, Taipei, Taiwan
First-principles calculation has become one of the most reliable approaches in predicting structural, electronic, and magnetic properties for material applications. Alloys in Heusler structures have also attracted much attention recently since they can be easily synthesized and provide interesting properties for future spintronic applications. In this work, we investigate a series of Fe-based Heusler compounds Fe3−xYxZ (x = 0, 1, 2, 3; Y= Cr, Mn, Co; Z= Al, Ga, Si) with L21- and XA-type structures using first-principles calculations based on density functional theory. According to formation energy calculations and mechanical property analysis, most of the studied Heusler compounds are thermodynamically stable and could be synthesized experimentally. The Co substitution leads Fe3−xCoxZ to a ferromagnetic ground state like Fe3Z with a strong magnetization ranging from 4 to 6 μB/f. u. While replacing Fe with Cr or Mn, the exchange coupling between Cr (Mn) and its neighboring atoms generally tend to be anti-parallel. Among the antiferromagnetic compounds, Mn3Al and Mn3Ga are antiferromagnetic half metal while Mn3Si is ferrimagnetic half metal. These rarely found type of half metals with low magnetic moment and high spin polarization at the Fermi level are important for low energy consumption spintronic applications. The estimated Curie temperatures for Mn3Al, and Mn3Si and Co2FeSi (XA) are in good agreement with previously theoretical values, while for Fe3Al and Fe3Si, they are in good agreement with previous experimental results. The good consistency in Curie temperature demonstrates high reliability of our predictions based on first-principles calculations. As for the topological property aspect, we predict Fe2CrAl and Fe2MnAl as the 3-dimensional Weyl semimetal. Furthermore, Fe2CrSi is predicted to be the magnetic nodal-line semimetal. Interestingly, our mechanical property analysis demonstrates that Co3Si and Fe2CoSi (L21) exhibit ultraelastic metal behavior, which is of high potential in advanced mechanical industry. This work suggests that Heusler compounds are excellent candidates for future spintronics as well as for high-performance ultraelastic metals.
1 Introduction
It is well known that Heusler compounds are intermetallic materials with rich magnetic properties [1–7]. Since the first discovery of the Cu2MnAl Heusler alloys in 1903, it is found that although the compositions of alloy were non-magnetic (NM), the alloy exhibits an adjustable magnetic properties through the treatment of heat and chemical compositions [8]. To date, thousands of members of Heusler compounds have been discovered with a wide range of physical properties, such as half-metallics, ferrimagnets [9–11], ferromagnets [12–14], shape memory alloys [15, 16], and even tunable topological insulators [17, 18]. Also, most Heusler alloys have high Curie temperatures, large saturated magnetization [19, 20], and crystallize in cubic high-symmetry structure. These properties are of high potential for spintronics, energy technologies, and magneto-caloric applications. For spintronic applications, Heusler compounds with full spin polarizability (100%) and high Curie temperatures can be considered as ideal semiconductor spin electron injection sources [21]. In terms of magnetocaloric applications, magnetic materials inherently have magnetocaloric effects due to the interdependence of thermal and magnetic properties. Since the discovery of Ni-Mn-based Heusler compounds with giant magnetocaloric effects, magnetic Heusler compounds have been regarded as candidates in magnetocaloric materials [22]. Finally, for energy applications, most thermoelectric materials are semiconductors with small energy gap. A. Berche et al. has suggested that Fe2VAl Heusler compound exhibits a small energy gap and a decent figure of merit, thus can be regarded as a material for thermoelectric applications [23]. The crystal structure of the traditional Heusler alloy (Figure 1) consists of four interpenetrating face-centered cubic (FCC) lattices with Wyckoff coordinates of A (0, 0, 0), B (1/4, 1/4, 1/4), C (1/2, 1/2, 1/2), and D (3/4, 3/4, 3/4). In general, the traditional Heusler alloys are composed of three kinds of element (ternary Heusler alloy), which can be divided into half Heusler alloys XYZ (No. 216,
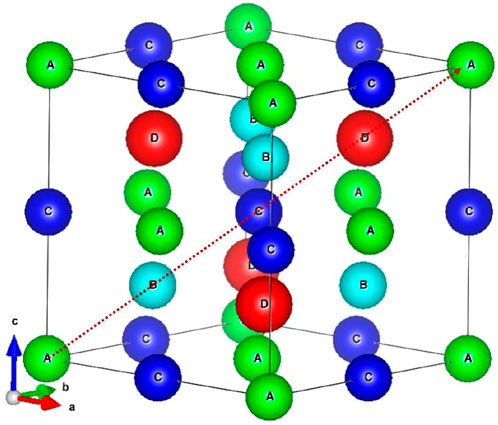
FIGURE 1. Crystal structure of full Heusler alloy. The lattice consists of four fcc sublattices (A–D) with respect to the Wyckoff coordinates of (0, 0, 0) (0.25, 0.25, 0.25, 0.25), (0.5, 0.5, 0.5), and (0.75, 0.75, 0.75), respectively.
Inspired by this, we study the substitution effects in binary and ternary Heusler alloys for a series of Fe-based Heusler compounds Fe4Z (Z= Al, Ga, and Si) by replacing Fe with different 3d elements X = Cr, Mn, and Co, namely, Fe3−xXxZ (x = 0, 1, 2, 3; X= Cr, Mn, Co; Z= Al, Ga, Si) with L21- and XA-type structures using first-principles calculations based on density functional theory. We present in this paper a systematic theoretical investigation including the structural, electronic, magnetic, and mechanical properties of binary and ternary full-Heusler alloys.
2 Computational method
The ideal X2YZ (X, Y= Cr, Mn, Fe, and Co; Z= Al, Ga, and Si) Heusler alloys are in the cubic closely packed structure as shown in Figure 1. Following the previous study by Wang et. al. [42], we assume that one of X atoms sits at A-site, and the other X atom sits at B- or C-site. Therefore, there are two possible structures for the ternary Heusler alloys, i.e. full and inverse Heusler structure with X atom occupied C- and B-site, respectively. For the binary Heusler alloys X3Z (X= Cr, Mn, Fe, and Co; Z= Al, Ga, and Si), it belongs to DO3-type structure with space group
The structural, electronic, and magnetic properties of X2YZ Heusler alloys are calculated by using the density functional theory as implemented in the Vienna ab initio simulation package (VASP) [43, 44]. The Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA) was chosen for the exchange and correlation effects [45, 46]. The Γ-centered Monkhorst-Pack scheme with a k-mesh of 12 × 12×12 is used for the Brillouin zone integration. The self-consistent total energy convergence criterion is set as 1.0× 10–7 eV. In all cases, a plane wave basis set with cut-off energy of 350 eV was used. All the three types of structures are geometrically optimized with the convergence criterion of 1.0 × 10–6 eV. To calculate the ground state total energy of the isolated atom, we use a very large supercell with 20 Å of separation in all x, y, and z directions which should be wide enough to decouple the nearest atom. The calculated ground state spin magnetizations of Cr, Mn, Fe, Co, Al, Ga, and Si isolated atoms are 6.00 μB, 5.00 μB, 4.00 μB, 3.00 μB, 1.00 μB, 1.00 μB, and 2.00 μB, respectively. These calculated ground-state spin magnetic moments of isolated atoms are consistent with those reported by S. Shehada et al. [24], which magnitude can be explained by Hund’s rules.
3 Results and discussion
3.1 Electronic, magnetic, and topological poperties
Listed in Supplementary Table A1 are the calculated lattice constants (Å), cohesive energy (eV/f.u.), and formation energy (eV/f.u.) of the considered Heusler compounds. In order to prevent the flow of paper from being interrupted, all tables are arranged in APPENDIX. The cohesive energy is calculated as the difference between the sum of the ground state total energies (E) of isolated atoms and the total energy of the encountered Heusler compounds, i.e., ∑Eatom − Ebulk. The cohesive energy is the energy required to break alloys into isolated atoms. Consequently, high cohesive energy alloys are relatively stable compared to those with low cohesive energies. The formation energies (Ef) of X2YZ are also calculated using
where Etot,
In general, a negative value of the formation energy indicates that the total energy of the compound is lower than that of its individual components, implying that the compound can be synthesized experimentally under ambient conditions, whereas a positive formation energy means that the synthesis of the material is dependent on extra factors such as pressure, temperature, and/or electromagnetic waves. Practically, the formation energies of certain existing compounds can be positive, such as diamond (0.13 eV/f. u.) [47]. Even with this positive formation energy, diamond can be formed under high pressure and high temperature, while it remains stable under ambient conditions. Therefore, it is still possible to synthesize these Heusler compounds experimentally under certain conditions even if the calculated formation energy is positive.
We first summarize few general remarks regarding lattice constants here. As shown in Supplementary Table A1, we find that the equilibrium lattice constant of X2YAl (X, Y= Cr, Mn, Fe, Co) is larger than those of X2YSi. This is because that the Wigner-Seitz radius of aluminum is larger than that of silicon. Similarly, when substituting the sp element from Al to Ga, in general, except for Cr2FeZ and XA-Fe2MnZ, the equilibrium lattice constant is enlarged due to the slightly larger atomic size of heavier element Ga.
Then we used transition metal atoms Cr, Mn, and Co to replace the Fe atoms in Fe3Z. There are two different types of iron atoms in the unit cell of Fe3Z (Figure 1): the first type Fe atoms (Fe(A) and Fe(C)) in the tetrahedral coordination are surrounded by four Fe and four Z atoms; the second type Fe atom (Fe(B)) in the octahedral coordination is surrounded by eight Fe atoms. Therefore, as one Fe atom of the first type is replaced by Y, XA ternary Heusler alloy is formed and labelled by XA-Fe2YZ (inverse structure). When the second type Fe atom is replaced by Y, L21 ternary Heusler alloy is formed and labelled by L21-Fe2YZ (normal structure).
As a benchmark result, the calculated lattice constants of the binary alloy Fe3Al, Fe3Ga and Fe3Si are 5.736, 5.750 and 5.601 Å, which are in agreement with the value of 5.74, 5.76 and 5.61 Å reported by Gao et. al [30]. As shown in the table, there seems no general trend for the lattice constants among all the above mentioned Cr, Mn, Co substituted Heusler alloys. Interestingly, for all Fe2YZ alloys except Fe2CoAl and Fe2CoGa, the lattice constant of the inverse structure is significantly larger than that of the normal structure. In contrast, for the X2FeZ alloys except Mn2FeAl and Co2FeGa, the lattice constant of the normal structure is larger than that of the inverse structure. This is presumably due to the Coulomb interaction between the nearest atoms. Taking Fe2CrAl as an example, since Cr has fewer d electrons than Fe, the length of Fe-Cr bond will be shorter than that of Fe-Fe bond, which results in that the length of Fe(A)-Cr(B)-Fe(C) will be shorter than that of Fe(A)-Fe(B)-Cr(C).
As for the cohesive energies of the X2YZ Heusler alloys listed in Supplementary Table A1, in general, X2YSi is more stable than X2YAl and X2YGa for all types of ternary and binary Heusler alloys. In order to clearly demonstrate the stability trends of different compounds, we graphically represent the evolutions of the cohesive and formation energy of Fe2XZ, X2FeZ, and X3Z with X, as shown in Figure 2. In terms of transition metal substitution for Fe3Z, the L21-Co2FeZ is the stablest case for all Z in Al, Ga, and Si. Supplementary Table A1 also shows the calculated formation energy, which serves as the indication of the structural stability. Except for Mn2FeSi, the formation energies of all Heusler alloys are negative, indicating that these Heusler alloys are thermodynamically stable and can be synthesized experimentally. In addition, comparing the formation energy of L21 and XA structure, it can be found that Fe2CrZ, Fe2MnZ, and Co2FeZ exhibit lower Ef in L21 than in XA structure. It is known that in Heusler alloys X2YZ, when element Y with fewer 3d electrons than element X, Y prefer to occupy B site, forming L21 structure. Conversely, when Y has more 3d electrons than X, Y tends to occupy A or C site, leading to XA structure [52].
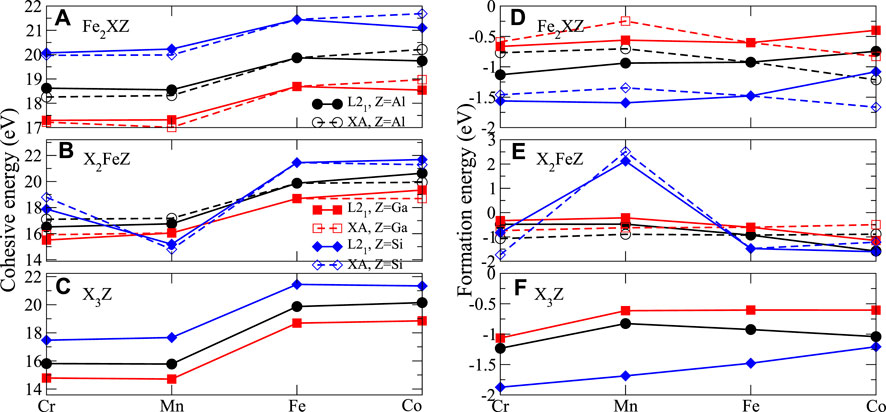
FIGURE 2. Cohesive energies (A–C) and formation energies (D–F) with respect to different Heusler compounds.
Supplementary Table A2 lists the calculated magnetic ground state, total spin moment (mt) (in μB/f. u.), atomic spin magnetic moments, magnetization energy, spin polarization, Curie temperature, as well as the total magnetization derived by Slater-Pauling rule (SP-rule):
where Nv is the total number of valence electrons in the unit cell of all the considered Heusler alloys. For L21-X2YZ, magnetic X1, X2, Y, and nonmagnetic Z positioned at A-, C-, B-, and D-site, respectively. In XA-X2YZ, magnetic X1, X2, Y, and nonmagnetic Z positioned at A-, B-, C-, and D-site, respectively. We consider the ferromagnetic (FM) and three ferrimagnetic configurations: Fi1, Fi2, and Fi3, in which Fi1(2,3) means that the magnetic direction at A-(B-,C-) site is antiparallel to the other 2 magnetic atoms. Then magnetic ground states can be determined by comparing the total energies of these magnetic states. Also, the magnetization energy defined as the total energy difference between magnetic ground state and nonmagnetic state can be obtained.
As can be seen in Supplementary Table A2, many candidates of half metals as indicated by HM are found in this work. Starting with binary Heusler compounds, all the three Mn3Z exhibit half metallic (HM) ground state. Both Mn3Al and Mn3Ga are fully compensated HM antiferromagnets (HM-AFMs), while Mn3Si is HM ferrimagnets. HM-AFMs show not only 100% spin polarization but also zero net magnetization, which is very useful in spintronic applications due to the lower energy consumption. On the other hand, all Fe3Z and Co3Z are metallic ferromagnets, and Cr3Z are metallic ferrimagnets. It is worth noting that the total and atomic magnetizations and the equilibrium lattice constants of Cr3Z, Mn3Z, and Fe3Z obtained in this work are in consistent with previous theoretical results [30]. Moreover, for Fe3Al, Fe3Si, and Mn3Si, our results are also in agreement with previous experimental data [49].
Then we discuss the magnetic properties of the ternary Heusler compounds in Supplementary Table A2. Considering the Fe2YZ series, the magnetic configuration can be mainly divided into ferromagnetic states for Y= Fe and Co, and ferrimagnetic states for Y= Cr and Mn, except for L21-Fe2CrSi and L21-Fe2MnSi (both are FM states). For Y= Cr and Mn, the ferrimagnetic states can be specifically described as Fi2 and Fi3 states for L21-Fe2YZ and XA-Fe2YZ, respectively. There exists a tendency for the spin directions of Cr and Mn to align antiparallel to neighboring atoms. This trend is in agreement with the previous magnetic research [58, 59]. Most X2YZ and Y2XZ have similar magnetic configuration. For example, Co2FeZ and Fe2CoZ are both in the FM ground states, while Cr2FeZ and Fe2CrZ show the FiM ground states, except for L21-Cr2FeGa, L21-Fe2CrSi and XA-Cr2FeSi. For Mn2FeZ compounds, L21-Mn2FeAl, XA-Mn2FeAl, L21-Mn2FeGa, and XA-Mn2FeGa are FiM states, while the others are FM states.
The Fe2YSi alloys series have been studied theoretically and experimentally by Luo et al. [60]. Our results in total magnetic moment and lattice structure agree well with those reported in Ref. [60], except for L21-Fe2MnSi that the magnetic moment is 1 μB smaller than the experimental value. This mainly comes from the antisite disorder relation between Fe and Mn atoms [60]. Luo et al. also show that the magnetic states of Fe2YSi are Fi2, Fi2, FM, and FM with respect to Y = Cr, Mn, Fe, and Co. Among them, the FiM magnetic states of L21-Fe2CrSi and L21-Fe2MnSi are different from our FM states. This discrepancy may results from the difference in lattice constants. To demonstrate that the variation of lattice constant can affect the DOS in Heusler alloys, we show in Figure 3 the DOS of Cr3Z (Z = Al, Ga, and Si) with the lattice constants differing by
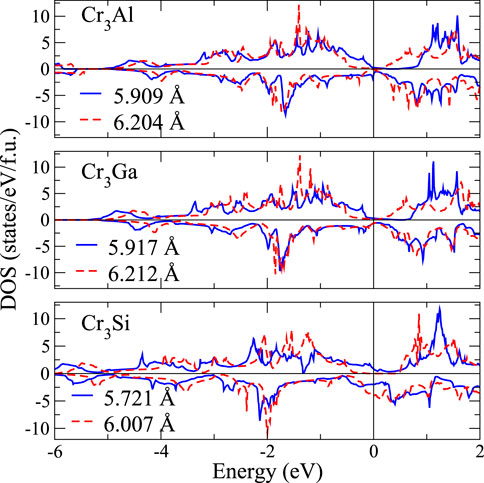
FIGURE 3. The spin-resolved total density of states for (a) Cr3Al, (b) Cr3Ga, (c) Cr3Si at different lattice constants. Blue one (solid line) means the equilibrium lattice constant, and red is one to enlarge +5%.
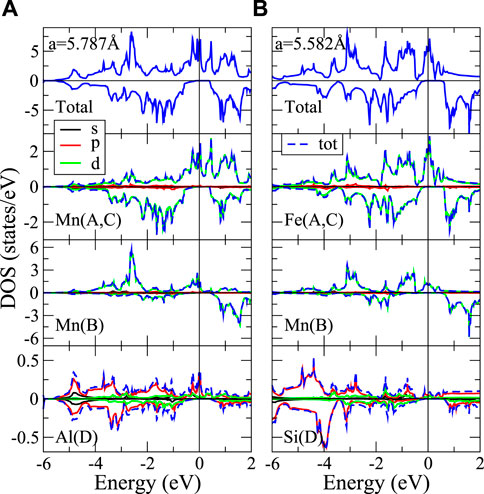
To illustrate the substitution effect on magnetism, we take Fe2YGa as an example for discussion below. Figure 5 shows total DOS and atom-decomposed partial DOS of these compounds. Starting with Fe3Ga, the Fe-3d spin up bands span from the Fermi level down to ∼ − 4 eV with the spin up band energies about 2 eV higher spanning from ∼ − 2 eV to
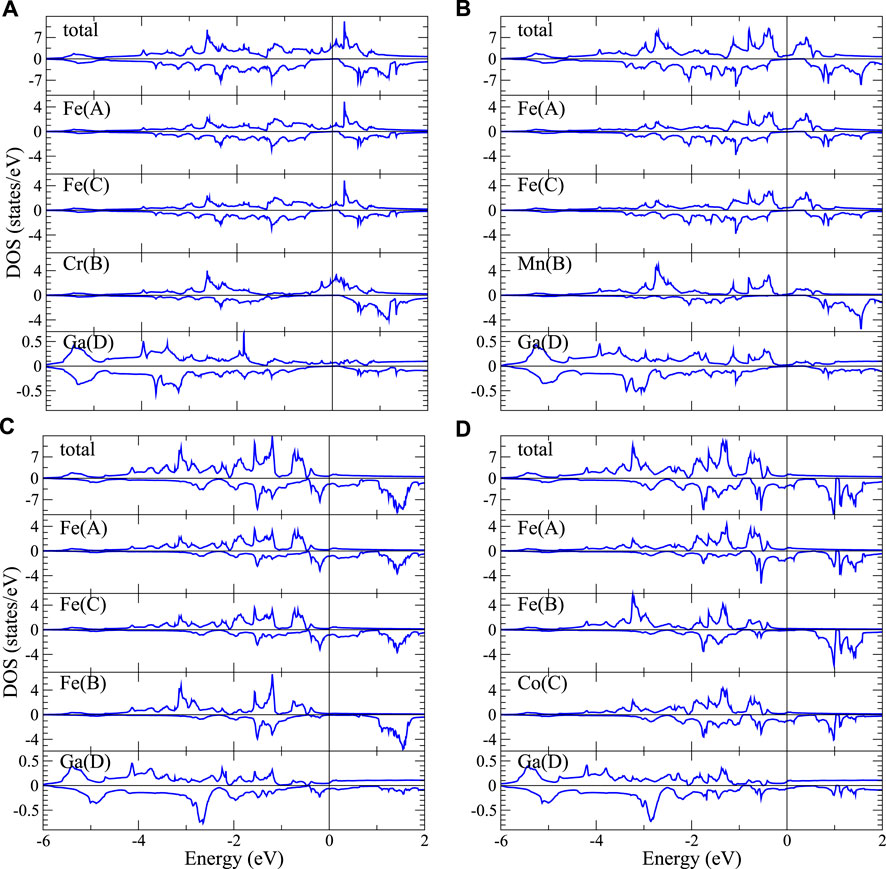
FIGURE 5. Total and atom-decomposed partial DOS of (A) L21-Fe2CrGa, (B) L21-Fe2MnGa, (C) L21-Fe3Ga, and (D) XA-Fe2CoGa.
When we substitute one Fe in Fe3Ga with Cr or Mn, they prefer the B-site to form the normal structure. As shown in Supplementary Table A1, the total energies of Fe2CrGa and Fe2MnGa in normal structure are indeed lower than that in inverse structure. Since Cr and Mn have respectively 2 and 1 fewer valence electrons than Fe, the majority spin band is no longer completely filled. On the other hand, the minority spin band shifts slightly toward lower energy due to the relatively weaker exchange interaction. This effect is stronger in Fe (A, C) and results in much smaller magnetic moments of Fe (A, C) in L21-Fe2CrGa and L21-Fe2MnGa. As shown in Figures 5A,B, the main contributions of DOS at the Fermi level (EF) come from Fe (A, C) and Cr or Mn in the majority spin channel, while the minority spin DOS(EF) are almost vanished, leading to nearly half metals with high spin polarization at EF for L21-Fe2CrGa and L21-Fe2MnGa (99 and 75%, respectively). Similar behavior can be found when Ga is replaced by Al. Further, when Ga is replaced by Si, its spin polarization reaches 100%.
When Fe substitutes for Co, Co atom prefers to occupy the (A, C) sites and forms the inverse structure. Take Co residing in C site as an example (Figure 5D), the total and partial DOS of XA-Fe2CoGa are quite similar to Fe3Ga due to the similar local environment. However, the extra electron from Co occupies the minority spin bands, leading to slightly smaller total magnetic moment in XA-Fe2CoGa (5.13 μB) than Fe3Ga (6.05 μB).
Topological materials are of high research interest in the past decade due to novel phenomena and promising technological applications. We have also studied the topological aspect of obtained band structures for all the Heusler compounds investigated in this work. Interestingly we found few Heusler alloys with topological band structure such as 3-dimensional (3D) Dirac and nodal-line bands shown in Figure 6 and discussed below. Figure 6A shows the band structure of the Fe2CrAl inverse Heusler structure. Among the spin down bands (red-dashed), there exist two parabolic bands around the high symmetric point X about 0.3 eV above EF with one concave up and one concave down. They come across each other along high symmetric lines XΓ and XW, leading to Dirac cone-like linear bands with a crossing node (i.e., the Dirac point) and a small gap, respectively. This is the typical band dispersion of the 3D Dirac semimetal such as Cd3As2 [53] and Na3Bi [54]. Note that the Dirac bands in Cd3As2 and Na3Bi are doubly degenerate non-spin polarized bands. In contrast, the Dirac-like bands of Fe2CrAl here are indeed spin polarized (spin down) single bands as can be seen in Figure 6A. Therefore, Fe2CrAl should belong to the 3D Weyl semimetal category. Owing to the high tunability, Heusler candidate of 3D Weyl semimetal might provide a helpful platform to understanding the relationship between the topology and various physical properties [55, 56].
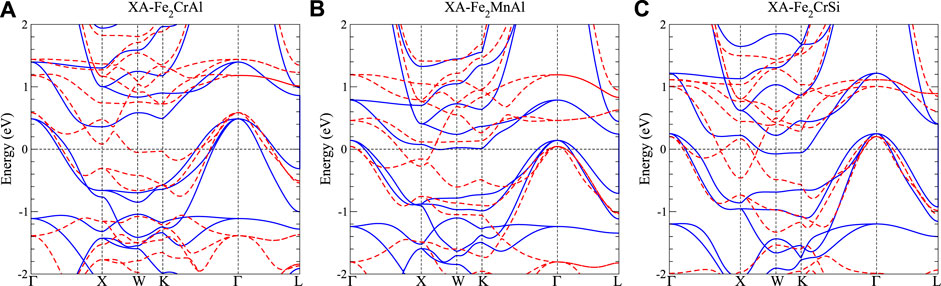
FIGURE 6. Band structure for (A) XA-Fe2CrAl, (B) XA-Fe2MnAl, (C) XA-Fe2CrSi. Blue solid curves denote the spin-up bands, while red-dashed curves indicate spin-down bands. Blue shaded region indicates the continuous gap in the spin up channel.
After replacing Cr with Mn (Figure 6B), the band structure of Fe2MnAl remains similar with the Fermi level shifted upward due to the extra electron of Mn. Consequently, the Weyl point shifts to a lower energy closer to the Fermi level. Further, with Si replacing Al (Figure 6C), the two parabolic bands of Fe2CrSi cross each other linearly through two Weyl-point-like nodes almost at EF. Actually, these two Weyl-point-like nodes would form a nodal ring circulating the high symmetry point X, which is similar to the nodal-line semimetal [56]. Recently, magnetic Weyl nodal-line materials have attracted increasing attention. For example, Ti3C2 has been theoretically predicted as a 2D magnetic Weyl nodal-line material with an extraordinary high Curie temperature above 800 K [57]. In our work, the Curie temperatures of XA-Fe2CrAl, XA-Fe2MnAl, and XA-Fe2CrSi are estimated to be 1,152, 1,026, and 919 K, respectively. Based on our calculations and literature survey [48], the overestimation of Tc by the mean field approximation is less than 50%. Although our calculations may quantitatively overestimate the Curie temperatures, it can be qualitatively declared that these three compounds are ferromagnetic Weyl nodal-line compounds with extraordinary high Tc. According to our research survey, three-dimensional Weyl nodal-line compounds with high Curie temperatures have not yet been reported. Therefore, Fe2CrSi discovered in this work serves as a good platform to study the magnetic Weyl nodal lines.
Further, the above mentioned topology-related bands are all located within the continuous gap with the energies of these crossing points very close to EF (all within 0.3 eV around EF). Such well-behaved topological bands will make experimental measurements on the evolution from 3D Weyl semimetal toward magnetic nodal-line semimetal via ion substitution highly feasible. Thus our work can facilitate the design and prediction of the magnetic topological properties in Heusler alloys.
The Curie temperature Tc of ferromagnets is the temperature that the magnetization of the magnetic material would disappear. High Tc material is also a key ingredient for the spintronic applications. The Tc can be calculated within the mean field approximation (MFA). In the classical Heisenberg model, the Hamiltonian (H) of a spin system can be written by
where Jij is the pair exchange coupling parameter and Si, and Sj represent unit vectors of the magnetization of the spin. Within MFA, the Curie temperature of single lattice can be written as follow
where kB, J0, and J0j denote Boltzman’s constant, average exchange coupling parameter, and pair exchange coupling parameter, respectively.
Theoretically, the exchange parameters J0j can be obtained from the total energy differences of ab initio calculations with different magnetic configurations. For the ferromagnetic materials, the first (nearest) exchange parameters is usually the largest one. Simple evaluation of Tc leads to
In order to establish a level of confidence for our estimated Curie temperatures, below we compared our results with those reported in previous experimental and theoretical works. In 2006, Kubler [48] has calculated the Curie temperature of L21 Mn3Al, Mn3Ga and Co2FeSi, and their values are 342, 482, and 1267 K, respectively. Our obtained Tc for these three compounds are respectively 309, 458, and 1629 K. The deviation from the Kubler’s calculated Curie temperature are 10.7%, 5.2%, and 22%, respectively. In terms of experiments, we also found a fairly early literature [49] documenting that the Curie temperatures of Fe3Al and Fe3Si are 713 and 840 K, respectively. They are also in good agreement with our estimations of 710 and 709 K, respectively. Different from previous experience that mean field approximations usually overestimate the value of Tc, the good agreement obtained in this work is probably due to the highly accurate lattice constants and magnetic moments in comparison with the experimental values. On the other hand, our calculated Tc are higher than the experimental values of 830K and 1261K for XA-Fe2CoAl and L21-Co2FeAl, respectively, as measured by Ahmad [50]. Yet the order of magnitudes remain similar, and the calculated Tc can still be an important indicator for spintronics.
3.2 Mechanical properties
To understand the mechanical properties and stability of a solid, we have calculated the elastic constants and related physical quantities of the Heusler compounds X2YZ as discussed below. Since the Heusler compounds studied in this work all belong to the cubic symmetry, we need only to consider three independent elastic constants, i.e., C11, C12, and C44. These independent elastic constants are determined from the strain-stress relations by introducing finite distortions into the cubic symmetric lattice. Once the elastic constants are obtained, we can determine the bulk modulus B, shear modulus G, Voigt shear modulus GV [61], Reuss shear modulus GR [62], Young’s modulus E, anisotropy factor A, Poisson’s ratio ν, and Pugh’s ratio B/G from the following equations [63]
where GV and GR are derived from different approaches. The GV is based on the assumption of uniform local strain, while the GR is based on the assumption of uniform local stress. These two different approaches have been shown [64] that the Voigt and Reuss shear modulus yield the strict upper and lower bound, respectively. Therefore, the average value of the GV and GR is usually used to characterize the shear modulus.
The mechanical stability criteria for the cubic structure [65] are as follows:
As shown in Supplementary Table A3, all the calculated C44 and B coefficients are positive. Consequently, the mechanical stability will be determined by Eq. 11. If C11 < C12, both A and GR are negative, which indicates the structure is mechanically unstable. Accordingly, most of the studied cases listed in the table are mechanically stable except that Mn3Z, Fe2CoZ (Z = Al, Ga), and Fe2CrSi in L21 structure, and Co2FeZ (Z= Al, Ga) in XA structures are mechanically unstable. For L21-Fe2CrSi, the unstable features can also be found in the Hill shear modulus (G) and Young’s modulus (E). In principle, C11 − C12 can be understood as the elastic constant under the orthogonal distortion of the conserving volume.
Bulk modulus B is also called incompressibility of a material. Supplementary Table A3 shows that most alloys in our study have the B values larger than 160 GPa of steel, indicating stronger incompressibility than steel. Alternatively, higher bulk modulus also means higher hardness. Interestingly, the bulk modulus of Fe3−xYxSi is obviously larger than that of Fe3−xYxAl and Fe3−xYxGa. Further, most of the B values of Fe2CrZ, Fe2MnZ, and Co2FeZ (Z= Al, Ga, Si) in L21 structure are larger than those in XA structure. On the contrary, most of the B values of Cr2FeZ, Mn2FeZ, and Fe2CoZ (Z= Al, Ga, Si) in L21 are smaller than those in XA. Combining these results with those in Supplementary Table A1, we can conclude that Heusler alloys with smaller lattice constants exhibit higher incompressibility.
In material science, shear modulus G is also known as modulus of rigidity. It is used to measure the ability of a material to resist the changes in chemical bonding angle by external force. This modulus is more related to the hardness of a material. In our calculation, the smallest values of shear modulus are 37.6 and 40.2 GPa for L21-Fe2CoSi and Co3Si, respectively. These values are very closed to the shear modulus of Phosphor Bronze (38 GPa) and Brass (40 GPa). The largest value of G is 128 GPa for L21-Fe2MnAl, which is very close to the shear modulus of chromium.
Combining the shear modulus and bulk modulus, the well known Pugh’s ratio [63] of B/G can be used to estimate the failure behavior of compounds. A material is classified to be a ductile matter if B/G > 1.75, otherwise it belongs to a brittle matter. Therefore, L21-Fe2CoSi and Co3Si with the largest B/G values (5.5, 5.2) indicate the most ductile among all compounds in our study. According to this empirical criterion, most of the compounds studied are ductile except for Cr3Al, Cr3Ga, L21-Fe2MnAl, XA-Fe2MnAl, and L21-MnGa with more brittle properties. Interestingly, materials with very huge B/G values are too ductile to be stable. This behavior is consistent with the trend of stiffness that the more stiffness the material, the less ductility it is.
Generally, Young’s modulus E can present the stiffness of the material: a higher value of E indicates the material is stiffer. We found that L21-Fe2CoSi has the smallest Young’s modulus of 106.4 GPa among all the mechanically stable Heusler compounds studied. This ultra low Young’s modulus value is very close to 106±10 GPa of the ultraelastic high-entropy alloys recently reported in Nature [66]. In addition to L21-Fe2CoSi, Co3Si also has a very low Young’s modulus of 113.5 GPa, while remains mechanically stable. As such, these two Heusler alloys are excellent candidates for ultraelastic metals with high potential in advanced mechanical industry.
The Poisson’s ratio provides useful information to understand the characteristics of the bonding forces in a material [67]. It has been proved that ν = 0.25 is the lower limit of the central force solid, and ν = 0.5 is the upper limit of the infinite elastic anisotropy [68]. It has also been suggested to judge the brittleness and ductility as ν < 1/3 and ν > 1/3, respectively [69]. According to the above conditions, apart from the mechanical unstable materials which exhibit negative modulus/anisotropy factor, we found that 3 binary Heuslers Fe3Ga, Co3Ga, Co3Si, 5-L21 Heuslers Cr2FeSi, Fe2MnSi, Mn2FeSi, Fe2CoSi, Co2FeSi, and 4-XA Heuslers Mn2FeGa, Cr2FeSi, Mn2FeSi, Co2FeSi are ductile, and the others are brittle. The anisotropy factor A, as shown in Supplementary Table A3, of a solid can be used to predict whether the considered compounds are mechanical isotropy or anisotropy. A, also called the shear anisotropy factor, is defined as the ratio of the shear modulus between [001] and [1–10] directional stress on the shear plane (110). For the orthorhombic crystal, the shear modulus for a shear system (hkl)[uvw] is given by [70, 71].
where (l11, l12, l13) is the direction of the shear stress, (l21, l22, l23) is the normal vector of the shear plane (hkl), and sij is the elastic compliance constants
Therefore, the elastic anisotropy factor can be defined not only by the shear modulus but also by bulk and Young’s modulus. Moreover, there are other definitions of elastic anisotropy factors such as percentage anisotropy incompressibility and shear [72] anisotropy. The shear anisotropic factors provide a measure of the degree of anisotropy in the bonding between atoms in different planes. As shown in Supplementary Table A3, the value of A for all the studied compounds is not equal to 1, which indicates that they are all elastic anisotropic. The difference of A from 1 (either larger or smaller than 1) provides an indication to estimate the level of elastic anisotropy acquired by the crystals.
To clarify the elastic anisotropy, we also present the orientation dependence of shear modulus and Young’s modulus as shown in Figure 8 and Figure 7, respectively. For the shear modulus, we present all directional values on (110) shear plane. The anisotropy factor A equals to the ratio between the x-intercept and y-intercept of the shear modulus contour. It is clear that L21-Fe2CoAl and Mn3Al (Figures 7B,D, respectively) exhibit very strong anisotropy pattern for the Young’s modulus, which means these materials are not stable. L21-Fe2CrSi (Figure 8B) also exhibit strong anisotropy for the shear modulus.
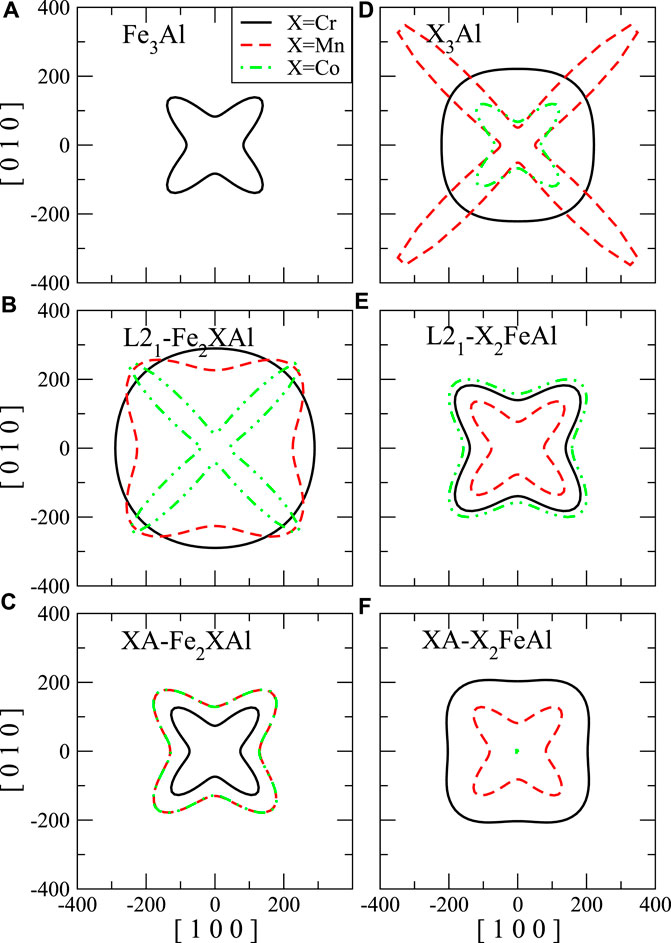
FIGURE 7. The directional Young’s modulus (E, in GPa) with tensile axis rotated from [100] to [010]. The Young’s modulus of binary compound (A) Fe3Al, (D) X3Al. (B) and (C) are the Young’s modulus of Fe2XAl in L21- and XA-structure, respectively. (E) and (F) are the Young’s modulus of X2FeAl in L21- and XA-structure, respectively.
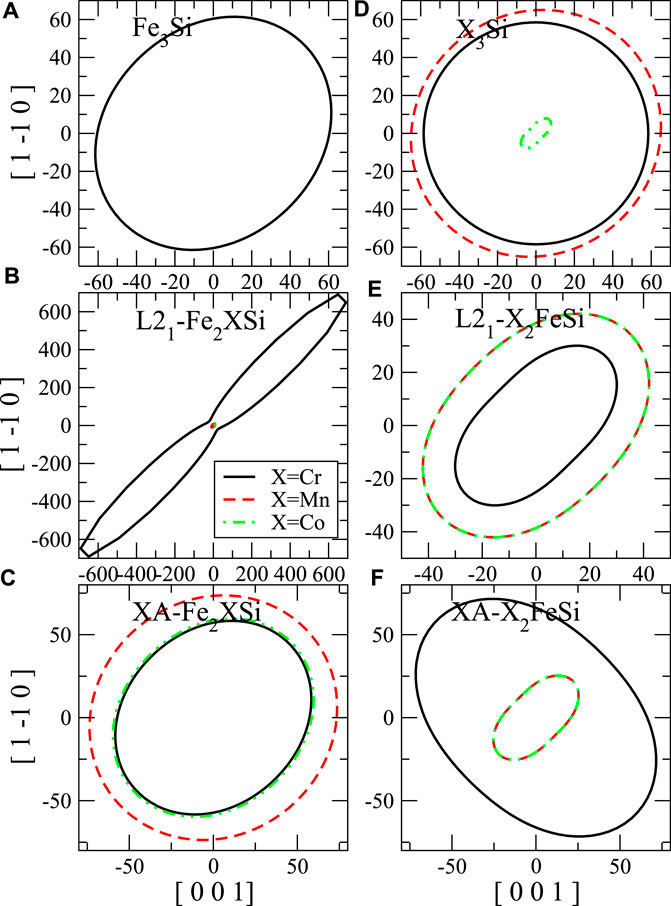
FIGURE 8. Contours of the shear modulus (G, in GPa) for shear stress along [001] to [1–10] on the (110) shear plane. The shear modulus of binary compound (A) Fe3Al, (D) X3Al. (B) and (C) are the shear modulus of Fe2XAl in L21- and XA-structure, respectively. (E) and (F) are the shear modulus of X2FeAl in L21- and XA-structure, respectively.
Supplementary Table A4 lists calculated thermodynamics related results such as the density ρ, longitudinal vl, transverse vt, average vm sound velocity, Debye temperature ΘD, melting temperature Tm, and minimum thermal conductivity κmin. According to the Debye theory, the Debye temperature ΘD of a material correlates to the elastic properties and the thermodynamic properties. Therefore it is of importance to calculate the Debye temperature in this study. The Debye model assumes that the solid is elastic continuum in which all sound waves travel at the same velocity independent of their wavelength. The Debye temperature is the temperature of a crystal’s highest normal mode of vibration. The lattice vibrations also determine the thermodynamic properties such as thermal expansion and melting temperature Tm of a solid. It also corresponds to the structural stability and the strength of bonds. The phase velocity of a solid can be determined from the transverse and longitudinal modes by using elastic constants. In this study, transverse vt and longitudinal vl as well as average vm sound velocity are calculated from Navier’s equation [73] as:
and
The Debye temperature can be estimated from the average elastic wave velocity vm:
where h is the Planck constant, kB is the Boltzmann constant, n is the number of atoms per formula, V is the atomic volume, and vm is the average sound velocity. It is clear that the sound velocity is related to the elastic moduli (B and G).
As shown in Supplementary Table A4, the average sound velocity vm ranges from 1721 to 3,089 m/s2. We can find that G has more influence than B in the magnitude of sound velocity. For instance, among all Fe3−xYxZ, L21-Fe2MnAl has the largest sound velocity and shear modulus, but does not show the largest bulk modulus. Due to the smallest shear modulus, the Debye temperature ΘD of Fe3Ga, Co3Ga, Co3Si, XA-Mn2FeGa, XA-Co2FeSi, XA-Fe2CoGa, and L2 − 1-Fe2CoSi ranging from 249 to 294 K are lower than room temperature. In contrary, the ΘD of L21-Fe2CrAl, Cr3Al, L21-Fe2MnAl, and XA-Fe2MnSi larger than 400 K also come from their largest G, which means that the larger ΘD reflects the higher hardness. Actually, the Debye temperature estimated in this way is usually overestimated than the actual value because the contribution of the optical phonon is ignored here. However, it is still a useful reference in spintronic material design. Further, the melting temperature is a fundamental parameter for the materials being used in heating systems. Materials with high melting temperature are favorable to remain stable against large range of temperature. Fine et al. [74] have studied many cubic metals and compounds and obtained an approximate empirical formula for Tm:
In our calculations, the melting points of 16 alloys are higher than 2000 K, and overall they are higher than 1500 K. Particularly, most of Fe3−xYxZ family show higher melting temperature than stainless steel (1̃700 K). We also find that the melting temperature is highly related to the Debye temperature, i.e., higher ΘD usually correspond to the higher melting temperature.
Beyond Debye and melting temperature, the thermal conductivity is the property of a material that describes its ability to conduct heat. To know if a material is a potential candidate for thermal application, the thermal conductivity needs to be investigated. Thermal conductivity is contributed from electron and phonon (lattice). In this study, we focus on the lattice thermal conductivity for possible thermal-related devices based on Heusler materials. Following the Debye model, Clarke [75] suggested that the theoretical minimum thermal conductivity at high temperatures is in proportional to the mean phonon velocity and the phonon mean free path. The mean phonon velocity is written in terms of the Young’s modulus and its density and the minimum phonon mean free path is the cube root of the volume of a molecule. Therefore, the minimum thermal conductivity κmin can be evaluated as:
where NA is the Avogardo’s number, n is the number of atoms per molecule, ρ is the density, and M is the molecular mass. The calculated minimum thermal conductivity is summarized in Supplementary Table A4. All the κmin values are below 3 W/mK, indicating that these Heusler compounds serve as low lattice thermal conductivity materials. The low thermal conductive material is essential to improve the performance of thermoelectric conversion materials. Furthermore, we also find that L21 structure generally leads to higher thermal conductivity than that given from XA structure, except for Cr2FeAl, Cr2FeSi, Fe2MnSi, and Fe2CoSi. This is because that L21 is more symmetric than XA as suggested by Miyazaki et al [76]. In Eq. 19, kB, NA, and n are constants and density ρ can be in terms of M and equilibrium lattice constant l0. Therefore, κmin is directly proportional to
4 Conclusion
We have investigated a series of Fe-based Heusler compounds Fe3−xYxZ (x = 0, 1, 2, 3; Y= Cr, Mn, Co; Z= Al, Ga, Si) with L21 and XA structure. Based on the calculated formation energies and mechanical property analysis, most of the studied Heusler compounds are thermodynamically stable and could be synthesized experimentally. For the substitution effect, we found that replacing Fe in Fe3Z with Cr, Mn, or Co shows very different trends in magnetic property and spin polarization. For Co substitution, Fe3−xCoxZ remains a ferromagnetic state like Fe3Z with higher total magnetization ranging from 4 to 6 μB/f. u. Whereas replacing Fe with Cr or Mn, the spin moments between Cr(Mn) and its neighboring atoms tend to align antiparallel in most cases with high spin polarization at EF. Furthermore, we predict that Mn3Al and Mn3Ga are antiferromagnetic half metals, while Mn3Si is ferrimagnetic half metal. These rarely found low-moment magnetic materials with high spin polarization at EF are important for spintronics applications due to the lower energy consumption. In addition, an ideal semiconductor spin electron injection source should not only possess a high spin polarizability, but also a high Curie temperature. We found that among all materials in this study, L21-Fe2CrSi and XA-Mn2FeGa satisfy both high spin polarizability (
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
H-LH and J-CT perform the calculations. H-TJ supervise the project. All the three draft the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
This work was supported by the Ministry of Science and Technology, Taiwan. H.-T.J. also thanks support from NCHC, CINC-NTU, AS-iMATE-109-13, and CQT-NTHU-MOE, Taiwan.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.975780/full#supplementary-material
References
1. Graf T, Felser C, Parkin SSP. Simple rules for the understanding of Heusler compounds. Prog Solid State Chem (2011) 39:1–50. doi:10.1016/j.progsolidstchem.2011.02.001
2. Felser C, Hirohata A. Heusler Alloys, properties, growth, applications. Springer Series in Materials Science (2016). p. 222.
3. Bainsla L, Suresh KG. Equiatomic quaternary heusler alloys: A material perspective for spintronic applications. Appl Phys Rev (2016) 3:031101. doi:10.1063/1.4959093
4. Felser C, Wollmann L, Chadov S, Fecher GH, Parkin SSP. Basics and prospective of magnetic Heusler compounds. APL Mater (2015) 2:041518. doi:10.1063/1.4917387
5. Pickett WE, Jagadeesh SM. Half metallic magnets. Phys Today (2001) 54:39–44. doi:10.1063/1.1381101
6. De Groot RA, Mueller FM, Engen PG, Buschow KHJ. New class of materials: Half-metallic ferromagnets. Phys Rev Lett (1983) 50:2024–7. doi:10.1103/physrevlett.50.2024
7. Zhang L, Wang X, Cheng Z. Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-Earth-element-based quaternary Heusler compounds. J Alloys Compd (2017) 718:63–74. doi:10.1016/j.jallcom.2017.05.116
9. Galanakis I, Sasioglu E. High TC half-metallic fully-compensated ferrimagnetic Heusler compounds. Appl Phys Lett (2011) 99:052509. doi:10.1063/1.3619844
10. Kervan N, Kervan S, Canko O, Atis M, Taskin F. Half-metallic ferrimagnetism in the Mn2NbAl full-heusler compound: A first-principles study. J Supercond Nov Magn (2016) 29:187–92. doi:10.1007/s10948-015-3228-x
11. Benea D, Gavrea R, Coldea M, Isnard O, Pop V. Half-metallic compensated ferrimagnetism in the Mn-Co-V-Al Heusler alloys. J Magn Magn Mater (2019) 475:229–33. doi:10.1016/j.jmmm.2018.11.115
12. Asfour I, Rached H, Benalia S, Rached D. Investigation of electronic structure, magnetic properties and thermal properties of the new half-metallic ferromagnetic full-Heusler alloys Cr2GdSi1−xGex: An ab-initio study. J Alloys Compd (2016) 676:440–51. doi:10.1016/j.jallcom.2016.03.075
13. Yalcin BG. Ground state properties and thermoelectric behavior of Ru2VZ (Z=Si, ge, sn) half-metallic ferromagnetic full-Heusler compounds. J Magn Magn Mater (2016) 408:137–46. doi:10.1016/j.jmmm.2016.02.064
14. Kundu A, Ghosh S, Banerjee R, Ghosh S, Sanyal B. New quaternary half-metallic ferromagnets with large Curie temperatures. Sci Rep (2017) 7:1803. doi:10.1038/s41598-017-01782-5
15. Srivastava V, Bhatti KP. Ferromagnetic shape memory heusler alloys. Solid State Phenom (2012) 189:189–208. doi:10.4028/www.scientific.net/ssp.189.189
16. Wang YK, Tung JC. Structural, electronic and magnetic properties of Ni2XAl (X= V, Cr, Mn, Fe, and Co) Heusler alloys: An ab initio study. Phys Open (2020) 2:100008. doi:10.1016/j.physo.2019.100008
17. Singh AK, Ramarao SD, Peter SC. Rare-Earth based half-heusler topological quantum materials: A perspective. APL Mater (2020) 8:060903. doi:10.1063/5.0006118
18. Wang XT, Dai XF, Jia HY, Wang LY, Liu GD, Liu XF, et al. Three-dimensional topological insulators: Case of quaternary heusler compounds. Rare Met (2015) 40:1219–23. doi:10.1007/s12598-014-0421-1
19. Umetsu RY, Kobayashi K, Fujita A, Kainuma R, Ishida K. Magnetic properties and stability of L21 and B2 phases in the Co2MnAl Heusler alloy. J Appl Phys (2008) 103:07D718. doi:10.1063/1.2836677
20. Ozdogan K, Şaşıoğlu E, Aktaş B, Galanakis I. Erratum: Doping and disorder in theCo2MnAlandCo2MnGahalf-metallic heusler alloys. Phys Rev B (2006) 80(2):172412. doi:10.1103/physrevb.80.029901
22. Pfeuffer L, Lemke J, Shayanfar N, Riegg S, Koch D, Taubel A, et al. Microstructure engineering of metamagnetic Ni-Mn-based heusler compounds by Fe-doping: A roadmap towards excellent cyclic stability combined with large elastocaloric and magnetocaloric effects. Acta Mater (2021) 221:117390. doi:10.1016/j.actamat.2021.117390
23. Berche A, Noutack M, Doublet ML, Jund P. Unexpected band gap increase in the Fe2VAl Heusler compound. Mater Today Phys (2020) 13:100203. doi:10.1016/j.mtphys.2020.100203
24. Shehada S, dos Santos Dias M, Guimaraes FSM, Abusaa M, Lounis S. Trends in the hyperfine interactions of magnetic adatoms on thin insulating layers. Npj Comput Mater (2021) 7:87. doi:10.1038/s41524-021-00556-y
25. Bradley AJ, Rogers JM. The crystal structure of the heusler alloys. Proc R Soc A (1934) 144:340. doi:10.1098/rspa.1934.0053
26. Luo HZ, Zhu Z, Ma L, Xu S, Wu G, Liu H, et al. High spin polarization in ordered Cr3Co with the DO3 structure: A first-principles study. Physica B: Condensed Matter (2008) 403:605–10. doi:10.1016/j.physb.2007.09.062
27. Ouyang YF, Tao X, Feng Y, Du Y, Zhong X. First-principles calculations of elastic constants of DO3-Mg3RE (RE = Sc, Y, La, Ce, Lu). Phys Scr (2008) 78:065601. doi:10.1088/0031-8949/78/06/065601
28. Liu H, Guo GY, Hu L, Ni Y, Zu FX, Zhu SC, et al. Bulk and surface half-metallicity: The case of D03-type Mn3Ge. J Appl Phys (2014) 115:033704. doi:10.1063/1.4861875
30. Gao GY, Yao KL. Antiferromagnetic half-metals, gapless half-metals, and spin gapless semiconductors: The D03-type Heusler alloys. Appl Phys Lett (2013) 103:232409. doi:10.1063/1.4840318
32. Wang XT, Chitiboi T, Meine H, Gunther M, Hahn HK. Principles and methods for automatic and semi-automatic tissue segmentation in MRI data. Magn Reson Mater Phy (2016) 412:95–110. doi:10.1007/s10334-015-0520-5
33. Song JT, Wei XM, Zhang JM. The structural, electronic, and magnetic properties of binary heusler alloys ZCl3 (Z = Li, Na, K, Rb) with DO3-type structure from first principle calculations. J Supercond Nov Magn (2019) 32:3217–26. doi:10.1007/s10948-019-5084-6
34. Zhou Y, Zhang JM, Huang YH, Wei XM. The structural, electronic, magnetic and mechanical properties of d0 binary Heusler alloys XF3 (X = Be, Mg, Ca, Sr, Ba). J Phys Chem Sol (2020) 138:109246. doi:10.1016/j.jpcs.2019.109246
35. Hsu LS, Wang YK, Guo GY, Lue CS. Optimal information extraction in probabilistic teleportation. Phys Rev A (Coll Park) (2002) 66:012308. doi:10.1103/physreva.66.012308
36. Galanakis I, Dederichs PH, Papanikolaou N. Origin and properties of the gap in the half-ferromagnetic Heusler alloys. Phys Rev B (2002) 66:134428. doi:10.1103/physrevb.66.134428
37. Kubler J, Fecher GH, Felser C. Understanding the trend in the Curie temperatures ofCo2-based Heusler compounds:Ab initiocalculations. Phys Rev B (2007) 76:024414. doi:10.1103/physrevb.76.024414
38. Kandpal HC, Fecher GH, Felser C. Calculated electronic and magnetic properties of the half-metallic, transition metal based Heusler compounds. J Phys D Appl Phys (2007) 40:1507–23. doi:10.1088/0022-3727/40/6/s01
39. Tung JC, Guo GY. High spin polarization of the anomalous Hall current in Co-based Heusler compounds. New J Phys (2013) 15:033014. doi:10.1088/1367-2630/15/3/033014
40. Huang HL, Tung JC, Guo GY. Lyth bound revisited. Phys Rev D (2015) 91:123532. doi:10.1103/physrevd.91.123532
41. Huang HL, Tung JC, Jeng HT. A first-principles study of rare Earth quaternary heusler compounds: RXVZ (R = Yb, Lu; X = Fe, Co, Ni; Z = Al, Si). Phys Chem Chem Phys (2021) 23:2264–74. doi:10.1039/d0cp05191h
42. Wang X, Cheng Z, Liu G, Dai X, Khenata R, Wang L, et al. Rare Earth-based quaternary Heusler compoundsMCoVZ(M= Lu, Y;Z= Si, Ge) with tunable band characteristics for potential spintronic applications. IUCrJ (2017) 4:758–68. doi:10.1107/s2052252517013264
43. Kresse G, Hafner J. Ab initiomolecular dynamics for open-shell transition metals. Phys Rev B (1993) 48:13115–8. doi:10.1103/physrevb.48.13115
45. Wang Y, Perdew JP. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys Rev B (1991) 44:13298–307. doi:10.1103/physrevb.44.13298
46. Wang Y, Perdew JP. Erratum: Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B (1992) 98:13244. doi:10.1103/physrevb.98.079904
47. Saal JE, Scott K, Muratahan A, Meredig B, Wolverton C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM (2013) 65:1501–9. S. Kirklin NPJ Comput. Mater. 1, 15010 (2015). doi:10.1007/s11837-013-0755-4
48. Kubler J. Ab initioestimates of the Curie temperature for magnetic compounds. J Phys : Condens Matter (2006) 19:9795–807. doi:10.1088/0953-8984/18/43/003
50. Ahmad A, Srimanta M, Srivastava SK, Das AK. Structural, magnetic, and magnetocaloric properties of Fe2CoAl Heusler nanoalloy. J Phys D: Appl Phys (2021) 54:385001.
51. Du Y, Xu GZ, Zhang XM, Liu ZY, Yu SY, Liu EK, et al. Crossover of magnetoresistance in the zero-gap half-metallic Heusler alloy Fe 2 CoSi. EPL (2013) 103:37011. doi:10.1209/0295-5075/103/37011
52. Bansil A, Kaprzyk S, Mijnarends PE. Electronic structure and magnetism of Fe 3 − x V x X (X=Si , Ga, and Al) alloys by the KKR-CPA method. Phys Rev B (1999) 60:13396. doi:10.1103/PhysRevB.60.13396
53. Liu ZK, Jiang J, Zhou B, Wang ZJ, Zhang Y, Weng HM, et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat Mater (2014) 13:677. doi:10.1038/nmat3990
54. Liu ZK, Zhou B, Chen YL. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science (2014) 343:864. doi:10.1126/science.1245085
56. Manna K, Sun Y, Muechler L, Kubler J, Felser C. Heusler, Weyl and berry. Nat Rev Mater (2018) 3:244–56. doi:10.1038/s41578-018-0036-5
57. Zhou F, Liu Y, Kuang M, Wang P, Wang J, Yang T, et al. Time-reversal-breaking Weyl nodal lines in two-dimensional A3C2 (A = Ti, Zr, and Hf) intrinsically ferromagnetic materials with high Curie temperature. Nanoscale (2021) 13:8235–41. doi:10.1039/d1nr00139f
58. Asano S, Yamashita J. Band theory of antiferromagnetic chromium. J Phys Soc Jpn (1967) 23:714–36. doi:10.1143/jpsj.23.714
59. Baltz V, Manchon A, Tsoi M, Moriyama T, Ono T, Tserkovnyak Y. Antiferromagnetic spintronics. Rev Mod Phys (2018) 90:015005. doi:10.1103/revmodphys.90.015005
60. Luo H, Zhu Z, Ma L, Xu S, Liu H, Qu J, et al. Electronic structure and magnetic properties of Fe2YSi (Y = Cr, Mn, Fe, Co, Ni) heusler alloys: A theoretical and experimental study. J Phys D Appl Phys (2007) 40:7121–7. doi:10.1088/0022-3727/40/22/039
62. Reuss A, Angew Z. Berechnung der Fliessgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z Angew Math Mech (1929) 9:49–58. doi:10.1002/zamm.19290090104
63. Pugh SF. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond Edinb Dublin Philosophical Mag J Sci (1954) 45:823–43. doi:10.1080/14786440808520496
64. Hill R. The elastic behaviour of a crystalline aggregate. Proc Phys Soc A (1952) 65:349–54. doi:10.1088/0370-1298/65/5/307
66. He QF, Wang JG, Chen HA, Ding ZY, Zhou ZQ, Xiong LH, et al. A highly distorted ultraelastic chemically complex Elinvar alloy. Nature (2022) 602:251.
67. Koster W, Franz H. Poisson's ratio for metals and alloys. Metallurgical Rev (1961) 6:1–56. doi:10.1179/mtlr.1961.6.1.1
68. Ledbetter MH. Materials at low temperatures. In: Reed RP, Clarck AF, editors. Metals Park, OH: American Society for Metals (1983).
69. Frantsevich IN, Voronov FF, Bokuta SA. Elastic constants and elastic moduli of metals and insulators handbook. In: Frantsevich IN, editor. Kiev: Naukova Dumka (1983).
70. Ghosh G. A first-principles study of cementite (Fe3C) and its alloyed counterparts: Elastic constants, elastic anisotropies, and isotropic elastic moduli. AIP Adv (2015) 5:087102. doi:10.1063/1.4928208
71. Nye JF. Physical properties of crystals: Their representation by tensors and metrices. Oxford, UK: Oxford University Press (1985).
72. Chung DH, Buessem WR. The elastic anisotropy of crystals. J Appl Phys (1967) 38:2010–2. doi:10.1063/1.1709819
73. Schreiber E, Anderson OL, Soga N. Elastic constants and their measurements. 3th ed. New York: McGraw-Hill (1973).
74. Fine ME, Brown LD, Marcus HL. Elastic constants versus melting temperature in metals. Scripta Metallurgica (1984) 18:951–6. doi:10.1016/0036-9748(84)90267-9
75. Clarke DR. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf Coat Technol (2003) 163:67–74. doi:10.1016/s0257-8972(02)00593-5
Keywords: heusler alloy, first principles calculations, half metal, weyl semimetal, dirac semimetal, nodal line semimetal
Citation: Huang H-L, Tung J-C and Jeng H-T (2022) A first-principles study on the effect of Cr, Mn, and Co substitution on Fe-based normal- and inverse-Heusler compounds: Fe3−xYxZ (x=0, 1, 2, 3; Y= Cr, Mn, Co; Z=Al, Ga, Si). Front. Phys. 10:975780. doi: 10.3389/fphy.2022.975780
Received: 22 June 2022; Accepted: 22 August 2022;
Published: 14 September 2022.
Edited by:
Hendrik Ohldag, Stanford University, United StatesReviewed by:
Thomas Feggeler, Berkeley Lab (DOE), United StatesRandy Fishman, Oak Ridge National Laboratory (DOE), United States
Copyright © 2022 Huang, Tung and Jeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Horng-Tay Jeng, amVuZ0BwaHlzLm50aHUuZWR1LnR3; Jen-Chuan Tung, amN0dW5nQG1haWwuY2d1LmVkdS50dw==
 Hung-Lung Huang1
Hung-Lung Huang1 Jen-Chuan Tung
Jen-Chuan Tung Horng-Tay Jeng
Horng-Tay Jeng