Photoelectron momentum distribution of hydrogen atoms in a superintense ultrashort high-frequency pulse

We use a numerically solved time-dependent Schrödinger equation for calculating the photoelectron momentum distribution of ground-state hydrogen atoms in the presence of superintense ultrashort high-frequency pulses. It is demonstrated that the dynamic interference effect within a superintense XUV laser beam has the ability to significantly alter the photoelectron momentum distribution. In our work, a clearly visible dynamic interference pattern is observed when hydrogen atoms are exposed to a superintense circularly polarized laser pulse with a photon energy of ℏω = 53.605 eV, which has previously been found for linearly polarized pulses or the weakly bounded model H⁻ system for circularly polarized pulses. Angular-distorted interference arises for linear superintense XUV pulses of similar intensity. The significant differences in photoelectron momentum distributions that have been seen by linearly and circularly polarized XUV pulses are caused by the Coulomb rescattering phenomenon.

1 Introduction

On account of the fast improvement of strong-pulsed-laser innovation, people are now focusing on a new research region, which uses laser pulses to explore the light and matter interaction in atoms and molecules (Krausz and Ivanov [1]; Sansone et al. [2]). The first characteristic phenomenon of the intense laser-atom interaction, above-threshold ionization (ATI), has been experimentally observed and extensively studied. Free-electron laser (FEL) light sources, such as the Extreme Light Infrastructure (ELI) Kühn et al. [3], have been designed in recent years to generate superintense laser pulses of the order of 10²⁰ W/cm² or stronger. Numerous new physical sciences and incredible phenomena are expected with such extreme intensity Kühn et al. [3] and high frequency Young et al. [4]. When the laser intensity surpasses 3.51 × 10¹⁶ W/cm² (corresponding to 1 atomic unit of laser intensity), the ionization process is stifled until the laser electric field is diminished to a lower intensity, which is the supposed atomic stabilization effect Eberly and Kulander [5].

In an intense polarized linearly high-frequency laser field, the atoms would be at the same ac Stark shift energy level Sussman [6] at a specific time during the rising edge and falling edge of the laser pulse. Thus, the photoelectrons that are delivered by these atoms have frequencies of the same values. Simultaneously, the phase differences between these wave packets that are produced at various moments (say the time − t₁ and t₁ as in the study by Jiang and Burgdörfer [7]) under the effect of atomic stabilization Toyota et al. [8]; Baghery et al. [9]; Jiang and Burgdörfer [7]; Demekhin and Cederbaum [10,11] could remain stable. Then, dynamic interference will appear when the two-electron wave packets superimpose, and the photoelectron spectrum will show an obvious multifringe structure in its ATI peaks Jiang and Burgdörfer [7]; Guo et al. [12].

Theoretically, a simplified model has anticipated the dynamic interference from hydrogen atoms in the ground state Demekhin and Cederbaum [10]; Baghery et al. [9]. Unfortunately, there are minor faults or typos in their models Demekhin et al. [13], and Demekhin and Cederbaum [10] and Baghery et al. [9] gave contradicting conclusions. However, the time-dependent Schrödinger equation (TDSE) fully numerical solution corroborated some predictions of dynamic interference in photoemission by powerful extreme ultraviolet (XUV) linearly polarized pulses Guo et al. [12]; Jiang and Burgdörfer [7]; Wang et al. [14]; Wang and Liu [15].

Scientific research and applications utilize the circularly polarized field in contrast to the linearly polarized field Fu et al. [16]; Bauer and Rzazewski [17]; Toyota et al. [18]. In a linearly polarized field, an electron can get back to its core numerous times; yet in a circularly polarized field, there is no returning event. Such discrepancies can fundamentally affect the electronic dynamics of atoms. Aside from some particular elements, for instance, magnesium Ben et al. [19]; Wang et al. [20], there will be no nonsequential double ionization, and it is difficult to see high harmonic generations with atoms in a circularly polarized field Christov et al. [21].

Despite the fact that the energy spectrum and momentum distribution of photoelectrons produced in strong laser fields with arbitrary polarization have already been documented, such as H⁻ with model potential Toyota et al. [18], the weakly bounded H⁻ system (the model H⁻ has an I_p = 0.76 eV, whose I_p ≤ 1 eV.) differs significantly from the tightly bounded H atom system (H atom has an I_p = 13.6 eV, whose I_p > 10 eV). With the same laser intensity (e.g., 10¹⁷W/cm²) and potential curve, the dynamic interference is readily visible in the weakly bounded excited states (n ≥2, |E_n| ≤ 3.4 eV ≪10 eV) of hydrogen atoms Baghery et al. [9], but it is hardly ever seen in the tightly bounded ground state Baghery et al. [9]; Jiang and Burgdörfer [7].

The current study has looked closely at how a circularly polarized pulse affects dynamic interference and how it differs from a linearly polarized pulse. The explicit demonstration of dynamic interference in the basic photoionization phenomena uses the hydrogen atom, which is unaffected by multiple-electron correlation.

The format of this article is as follows. The theoretical foundation for investigating the ionization of ground-state hydrogen atoms is described in the second part. The impact of different circularly polarized laser pulse strengths on the dynamic interference of photoelectron spectra and momentum distributions is covered in Section 3. The conclusion is found in Section 4. Unless stated differently, the atomic units (a.u.) ℏ = m = e = 1 are used throughout this article.

2 Theory and models

2.1 2D time-dependent Schrödinger equation and 3D time-dependent Schrödinger equation

To describe the ionization of ground-state hydrogen atoms, we will solve the TDSE precisely. The hydrogen atoms’ TDSE when exposed to a laser field is as follows:

$i\frac{\partial \psi \left(\mathit{r},t\right)}{\partial t}=H\psi \left(\mathit{r},t\right).(1)$

The hydrogen atom in the circularly polarized laser field is investigated in the current work using the reduced two-dimensional (2D) TDSE. In the momentum distributions with laser intensity in the perturbation regime (I₀ = 10¹² W/cm²) and stabilization regime (I₀ = 10¹⁸ W/cm²), respectively, we have compared the corresponding results of 2D TDSE with those of 3D TDSE Patchkovskii and Muller [22], as shown in Figure 1.

FIGURE 1

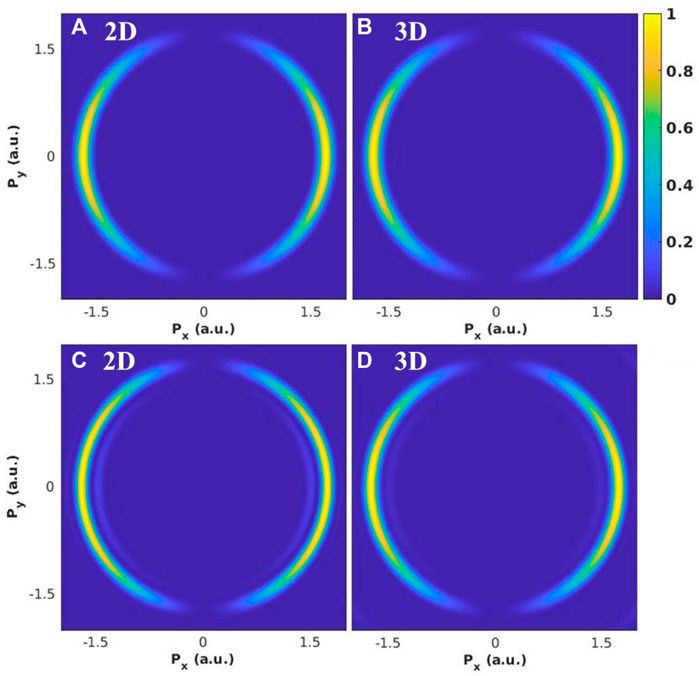
FIGURE 1. (Color online) Numerical results are compared from solving two- and three-dimensional TDSEs. We take the laser parameters as follow: carrier frequency ℏω₀ = 53.605 eV and peak intensities are (A,B) I₀ = 10¹² W/cm², and (C,D) I₀ = 10¹⁸ W/cm², corresponding to the perturbation regime and the stabilization regime. Laser pulse duration τ = 1.5 fs.

All of these findings demonstrate excellent agreement between the perturbation (weak field) and stabilization (strong field) regimes of the 2D (a, c) and 3D (b, d) simulations. Both 2D (Figure 1C) and 3D (Figure 1D) simulations of the stabilization regime show the interference fringes, which have been previously proven Jiang and Burgdörfer [7]; Wang et al. [14].

The 2D TDSE with dipole approximation can be given by:

$i\frac{\partial \psi \left(x,y;t\right)}{\partial t}=H\psi \left(x,y;t\right),(2)$

whose hamiltonian can be written as

$H=T+V\left(x,y\right)+x{E}_x\left(t\right)+y{E}_y\left(t\right),(3)$

where the kinetic energy operator $T=\frac{p_x^2+p_y^2}{2}$ with p_i = −i∂/∂_i (i = x, y) and potential $V(x,y)=-1/\sqrt{x^2+y^2+a}$ is the soft-core potential function of hydrogen atoms, and a = 0.64 is the soft-core parameter to avoid the singularity at origin r = 0 and to obtain the correct ground-state energy E_g = −0.5. In our simulation, the polarized driving laser field is denoted by the variables E_x(t) and E_y(t) for the x-axis and y-axis, respectively. We can write the total time-dependent potential as:

$U\left(t\right)=V\left(x,y\right)+x{E}_x\left(t\right)+y{E}_y\left(t\right).(4)$

We use the splitting operator combined with the fast Fourier transform (FFT) method to solve the TDSE and obtain the initial wave packet by the imaginary time propagation method. The wave function time propagation from t to t + Δt can be expressed as

$\psi \left(t+△t\right)\approx e^{-iT△t/2}{e}^{-iU\left(t+\mathrm{\Delta }t/t\right)△t}{e}^{-iT△t/2}\psi \left(t\right).(5)$

The box sizes are up to 1200 for each dimension, and the step size of time propagation Δt is 0.01. A mask function of the form cos^1/8 was employed to avoid spurious reflections from the boundaries. When the wave function completes the final step of time propagation, we record the ionization part as [1 − M(r)]ψ(x, y; t_f). Here, ψ(x, y; t_f) is the wave function at the last time step. The function expression M(r) for the absorption mask is

$M\left(r\right)=\left\{\begin{array}{c}1,r\le r_b;\hfill \\ \exp \left[-\alpha \left(r-r_b\right)\right],r>r_b,\hfill \end{array}\right.(6)$

where α = 1, $r=\sqrt{(x^2+y^2)}$, and the r_b = 30 (r_b corresponds to the bounded wave function boundary) He et al. [23]. Then, using the fast Fourier transform of the outer wave function, we obtained the photoelectron momentum distribution. Moreover,20 optical cycles make up the pulse duration, while 10 optical cycles can relax due to free field propagation.

2.2 Perturbative superposition model

The laser field is polarized in the xy-plane, as shown in Eq. 4. The associated electric field information of laser pulses is schematically shown in Figure 2. The blue curve represents the electric field of the circularly polarized laser pulse E(t), while the red and golden curves, respectively, depict its projections on the x-axis and y-axis. To put it another way, the E(t) can be split into the two linearly polarized pulses E_x(t) and E_y(t):

$\mathbf{E}\left(t\right)=E_x\left(t\right){\widehat{e}}_x+E_y\left(t\right){\widehat{e}}_y=f\left(t\right)\left[E_x^0\cos \left(\omega t\right){\widehat{e}}_x+E_y^0\cos \left(\omega t+\varphi \right){\widehat{e}}_y\right],(7)$

where ${\widehat{e}}_{x/y}$ is the polarization direction and the ϕ is the relative phase of y-component. When ϕ = ±π/2 and $E_x^0=E_y^0$, we obtain circular pulses, when either $E_x^0$ or $E_y^0$ vanishes, we obtain linear pulses. The pulse profile f(t) is the sine-squared profile, and ω is the central frequency of the laser pulse.

FIGURE 2

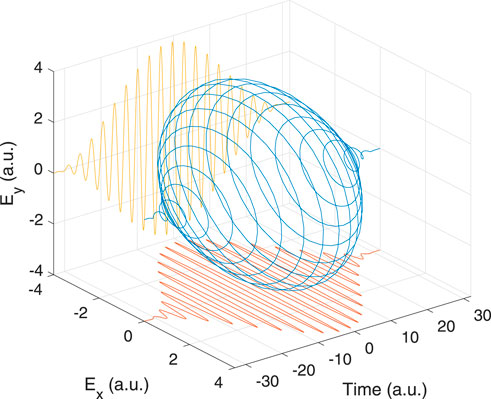
FIGURE 2. (Color online) Schematic electric field of circularly polarized laser pulse E(t) (blue curve) and its projections on the x-axis (red curve) and y-axis (golden curve). In this schematics, we take the laser parameter as follows: carrier frequency ℏω₀ = 53.605 eV, peak intensity I₀ = 10¹⁸ W/cm², and pulse duration τ = 1.5 fs.

The first-order transition amplitudes (in the electric dipole approximation) from an initial bound state ψ₀ is given by Pronin et al. [24]

$A_1=⟨{\psi }_{\mathbf{p}}|\mathbf{E}\cdot \mathbf{r}|{\psi }_0⟩,(8)$

Here, ψ_p describes a final continuum state with electron momentum p and energy E_k = p²/2.

On substituting the electric field E of Eq. 8 with Eq. 7, Eq. 8 is rewritten as Yuan et al. [25]

$A_1=⟨{\psi }_{\mathbf{p}}|E_{x}x+E_{y}y|{\psi }_0⟩=A_1^x\left(\mathbf{p}\right)+A_1^y\left(\mathbf{p}\right),(9)$

where

$A_1^x\left(\mathbf{p}\right)=\langle {\psi }_{\mathbf{p}}|E_{x}x|{\psi }_0\rangle =E_x\langle {\psi }_{\mathbf{p}}|x|{\psi }_0\rangle ,(10)$

$A_1^y\left(\mathbf{p}\right)=\langle {\psi }_{\mathbf{p}}|E_{y}y|{\psi }_0\rangle =E_y\langle {\psi }_{\mathbf{p}}|y|{\psi }_0\rangle .(11)$

which means that the total photoelectron momentum distribution P(p) can be decomposed into two components which are related to the independent E_x and E_y, respectively. The interference terms vanish due to the π/2 phase between them Yuan et al. [25],

$A_1^{\left(x,y\right)}=A_1^{\left(x\right)\ast }{A}_1^{\left(y\right)}+A_1^{\left(x\right)}{A}_1^{\left(y\right)\ast }\propto \cos \left(\varphi \right).(12)$

For circularly polarized pulses, ϕ= ± π/2; thus, the interference term vanishes. Then, we have

$P\left(\mathbf{p}\right)=|A_1{|}^2=|A_1^x\left(\mathbf{p}\right){|}^2+|A_1^y\left(\mathbf{p}\right){|}^2=P_x\left(\mathbf{p}\right)+P_y\left(\mathbf{p}\right).(13)$

The following section of this article will examine how the aforementioned decomposition of the photoelectron momentum distribution is destructed when a sufficiently strong laser field is applied, even for this single-photon ionization.

The photoelectron momentum distribution of hydrogen atoms exposed to a laser pulse with a peak intensity of 10¹⁴ W/cm² is shown in Figure 3. Since atomic stabilization does not take place in this situation with such a high laser frequency and low laser intensity, the dynamic interference effect cannot be observed Gavrila [26]. The photoelectron momentum distribution for hydrogen atoms subjected to the laser with polarization parallel to the x-axis is shown in Figure 3A. The electron momentum distribution is primarily in the x-direction since the laser is polarized along that path. This is an example of a single-photon ionization distribution using the dipole approximation Remetter et al. [27]. In Figure 3B, we display the results for rotating the laser polarization direction to the y-axis (by adding a π/2 phase difference in the carrier of laser electric field): the photoelectron momentum distribution is again mainly in the laser polarization direction, y-direction. When the circularly polarized laser is utilized, as shown in Figure 3C, the momentum distribution only shows one ring. A similar distribution can be achieved in Figure 3D by superposing ψ_x(ɛ) and ψ_y(ɛ) coherently (or adding Figures 3A,B incoherently). The photoelectron energy spectra of the aforementioned four panels are shown in Figure 3E, and these four lines act coincidentally. It is well established, both theoretically and experimentally, that the ponderomotive energy is $U_p=E_0^2/4{\omega }^2\approx 0.005$ eV for the parameters of the present laser field. The photoelectron spectra show an isolated Gaussian profile in Figure 3E for weak-field single-photon ionization, where the ionization process can be explained by the lowest-order perturbation theory (LOPT), and the profile has its peak at the energy E = ℏω − I_p − U_p ≈ 40 eV (I_p is the atomic binding energy).

FIGURE 3

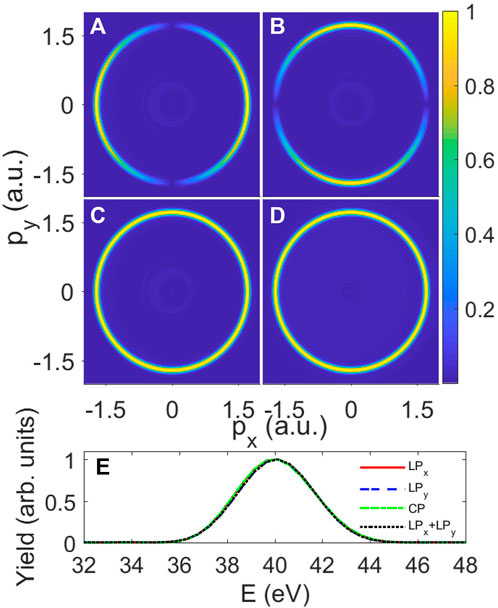
FIGURE 3. (Color online) Photoelectron momentum distribution of hydrogen atoms in the presence of laser pulse with τ₀ = 1.5 fs, carrier frequency ℏω₀ = 53.605 eV, and the peak intensities I₀ = 10¹⁴ W/cm². Graphs (A) and (B) reveal the momentum distributions from the linear polarized x- and y-direction, respectively. Graph (C) shows the result from a circularly polarized laser pulse, while (D) is the momentum distribution from the superposition of (A) and (B) two perpendicular linearly polarized pulses. Panel (E) is the photoelectron spectra of (A) the red solid line, (B) the blue dashed line, (C) the green dashed–dotted line, and (D) the black dotted line.

In the LOPT, the single-photon ionization of hydrogen atoms from the ground state (l = 0 s-wave) by linearly polarized (say along the x-axis) laser pulses can be described by H(1s) + hν → ϵp. The final p-state partial wave (l = 1) has the distribution P_‖(θ) ∝ cos²θ, as shown in Figure 3A. If we rotate the laser polarized direction to the perpendicular direction (along the y-axis), the final momentum distribution is now $P_{\perp }(\theta )\propto {\cos }^2(\frac{\pi }{2}+\theta )={\sin }^2\theta$. The photoelectron angular distribution of single-photon ionization by circularly polarized laser pulses is depicted in the superposition model mentioned earlier as P_cp(θ) ∝ cos²θ + sin²θ = 1, which is constant for all angles and is in excellent agreement with our TDSE simulation of Figure 3C.

3 Results and discussion

We explored the dynamic interference effect in the photoionization of ground-state hydrogen atoms in the presence of superintense linearly and circularly polarized laser pulses based on our ab initio numerical solution of the TDSE. We used the central carrier frequency of the laser pulse at 5 eV. The driving laser pulse has a pulse width of 20 optical cycles and a wavelength of 23 nm. These variables ensure the production of dynamic interference and prevent the complete depletion of the ground state population Guo et al. [12]; Jiang and Burgdörfer [7]; Wang et al. [14].

A straightforward temporal two-path interference scenario can explain this dynamic interference. When the instantaneous ac Stark shift of the initial state coincides at two different times, electron wave packets ejected on the rising and falling edges of the linearly polarized laser pulse can interfere with one another and reach the same final energy. They are temporally separated by a time interval of intense-field stabilization against photoemission Eberly and Kulander [5]; Guo et al. [12]; Jiang and Burgdörfer [7].

In a circularly polarized field, the pulled-out laser-dressed electron cannot move back and forth by the driving laser field, and the atomic stabilization effect is anticipated to be more pronounced Protopapas et al. [28]. In Figure 4, we display the density of wave function in the middle (a) and at the end (b) of the laser pulse and the ionization rate of the ground-state hydrogen. We can see the inner and outer rings, which are probabilities of the photoelectron wave packets produced by the laser pulse in the rising and falling ramp of the pulse, from the spatial distribution for the probability of wave function displayed in Figure 4. Between the inner and outer rings, the vanishing gap indicates the atomic stabilization caused by the ultraintense laser field. Such an effect can be also shown in the ionization rate of the ground state, which has been displayed in Figure 4C. In the rising edge, the ionization rate starts to climb swiftly at t ≈ − 22, the ionization speed reaches its maximum at about t ≈ -18, and then the speed decreases. When the laser electric field profile is near its peak from t = −10 to 10, the ionization process is almost completely stopped. This time zone can be referred to as a stability zone. The gaps between inner and outer wave function rings in Figures 4A,B are produced due to the stabilization time zone. Then on the falling edge of the field profile, the ionization restarts, and finally ionization rate reaches the maximum at the end of a laser pulse.

FIGURE 4

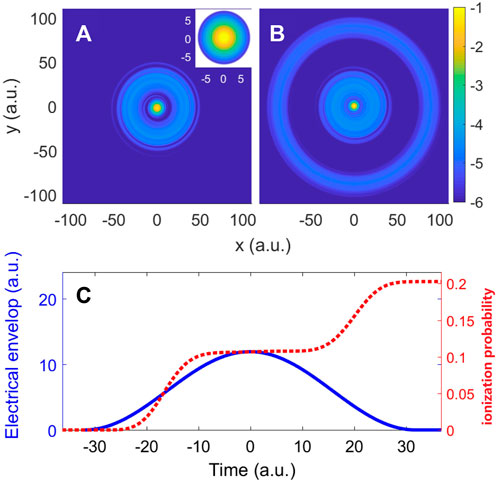
FIGURE 4. (Color online) Probability density of electron in the middle (t = 0) and at the end (t = 32) of a circularly polarized laser pulse in panels (A,B). The initial ground state is plotted as the inset of panel (A). Panel (C) is the time-dependent instantaneous ionization probability (red dashed line) of the ground state of hydrogen atoms in the presence of a laser pulse. The electrical envelope of the laser pulse and the blue solid line are plotted. All parameters are the same as those in Figure 3C, except the peak intensity I₀ = 5 × 10¹⁸ W/cm².

The dynamic interference of photoelectrons can also be anticipated in the ionization induced by circularly polarized laser pulses since the ac Stark shift for energy in a circularly polarized field is similar to that in a linearly polarized field. Additionally, because the ac Stark shift is a cycle-average effect, when the peak intensities of linearly and circularly polarized pulses are equal (e.g., $I_0=E_0^2$), the cycle-averaged intensity of the circularly polarized field (⟨E⟩ = E₀) is almost twice that of the linearly polarized field (⟨E⟩ = 0.707E₀). We could expect a circularly polarized field to produce a larger ac Stark shift of energy than a linearly polarized pulse. However, the ionization in the weak-intensity laser field does not exhibit the blue shift between the findings of the linearly and circularly polarized fields, as seen in Figure 5. As shown in Figure 5, we increase the laser intensity from 5 × 10¹⁶ to 5 × 10¹⁸W/cm². In Figure 5A, there is no obvious modulation in the ATI peak of the momentum spectrum when the laser intensity is relatively low (with I₀ = 5 × 10¹⁶W/cm²).

FIGURE 5

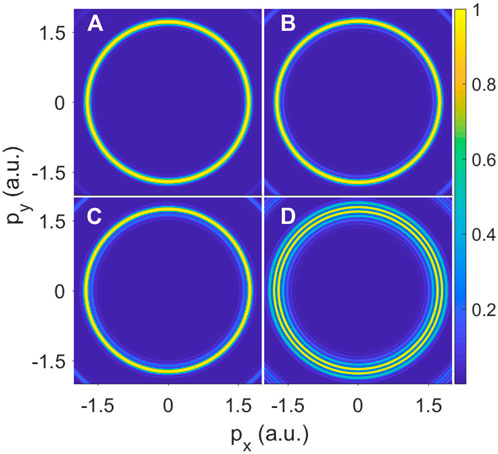
FIGURE 5. (Color online) Normalized photoelectron momentum distribution of hydrogen atoms in the presence of a circularly polarized laser pulse with different intensities: (A) 5 × 10¹⁶, (B) 5 × 10¹⁷, (C) 1 × 10¹⁸, and (D) 5 × 10¹⁸ W/cm². The other parameters are the same as those in Figure 3C.

While the laser intensity is increased to 5 × 10¹⁷ or 1 × 10¹⁸ W/cm² as shown in Figures 5B,C, the multiring structure is found in its momentum distribution. On continuing to increase the laser intensity to 5 × 10¹⁸ W/cm², in Figure 5D, we can observe two bright rings and strongly modulated fringes in the first ATI peak.

Because of the stronger laser field, atomic stabilization occurs sooner and later, resulting in a longer time-delay gap between the wave packet produced on the rising edge of the laser pulse and the one launched on the falling edge of the laser pulse. Furthermore, additional interference fringes are produced as a result of increased phase difference accumulation between rising and falling wave packets due to increased laser intensity. This impact is noticeable in a linearly polarized field Jiang and Burgdörfer [7]. It also implies that the same result can be obtained by decomposing the circularly polarized field into two linearly polarized fields. We will explain how these superposition results coincide with real simulation results in the next two figures (Figures 6, 7).

FIGURE 6

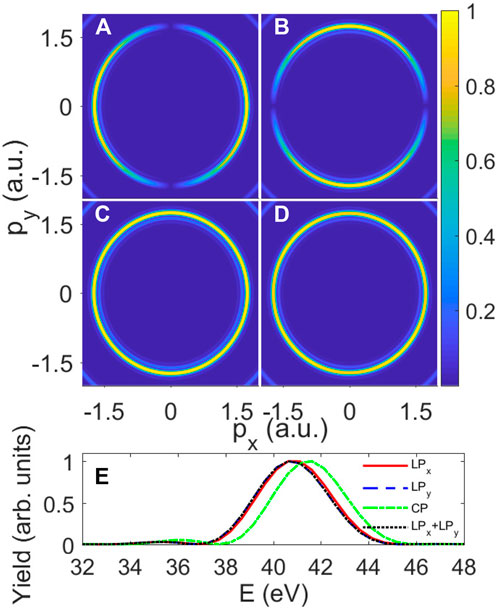
FIGURE 6. Normalized photoelectron momentum distribution of hydrogen atoms in the presence of a circularly polarized laser pulse with different polarization. (A) Linearly alone $x$, (B) Linearly alone $y$, (C) Circularly and (D) superposition of (A,B). Curves in the panel (E) are the photoelectron spectra of (A) the red solid line, (B) the blue dashed line, (C) the green dashed–dotted line, and (D) the black dotted line. Laser intensity is $I_0∼⁼1\times10^{18}$ W/cm$^2$. The rest of laser parameters are the same as those in Figures 3A.

FIGURE 7

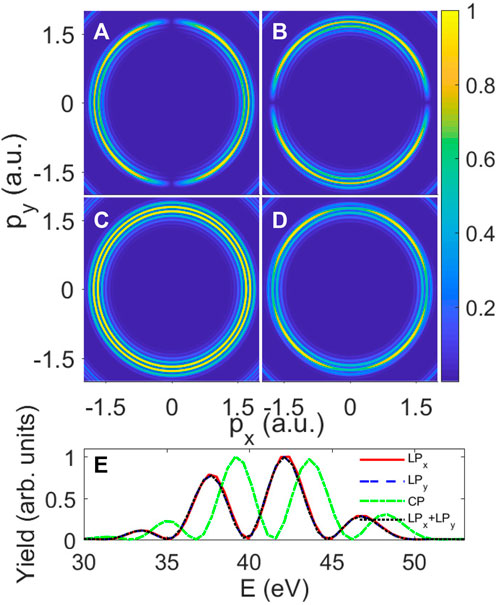
FIGURE 7. Normalized photoelectron momentum distribution of hydrogen atoms in the presence of a circularly polarized laser pulse with different polarization. (A) Linearly alone $x$, (B) Linearly alone $y$, (C) Circularly and (D) superposition of (A,B). Curves in the panel (E) are the photoelectron spectra of (A) the red solid line, (B) the blue dashed line, (C) the green dashed–dotted line, and (D) the black dotted line. Laser intensity is $I＿0～=5\times10^{18}$ W/cm$^2$. The rest of laser parameters are the same as those in Figure 3A.

When the peak intensity of the laser pulse is 1 × 10¹⁸ W/cm², Figure 6 shows the same consequence as Figure 3 illustrates. Although the spectrum is still almost symmetrical, the maximum is constantly moving to higher energies. It has a solitary Gaussian profile, with the peak located at an energy greater than 40 eV. Demekhin et al. have discovered and clarified the underlying physics Demekhin and Cederbaum [10,11]. As usual, this shift follows the intensity envelope of the field Sussman [6]. The circularly polarized field can be decomposed into two perpendicular linearly polarized fields; therefore, each linearly polarized field takes half of the intensity of the circularly polarized field. Compared Figure 6C with Figure 6D, the first-order ATI ring in the circularly polarized laser can be qualitatively in agreement with a model for the superposition of ionization by two linearly polarized pulses, respectively.

As seen in Figure 6E, the peak of the green dashed–dotted curve has larger energy than the peaks of the other curves. This blue shift implies that the atom’s ac Stark shift in a circularly polarized field is greater than the atom’s ac Stark shift in a linearly polarized pulse. This similar blue shift was also discovered in the research by Liang et al. [29]. As the ac Stark shift for energy in a circularly polarized field is similar to that in the linearly polarized field, the dynamic interference of photoelectrons can also be expected in ionization caused by circularly polarized laser pulses. In addition, according to the fact that the ac Stark shift is a cycle-average effect, the cycle-averaged intensity of circularly polarized field (⟨E⟩ = E₀) is about twice that of the linearly polarized field (⟨E⟩ = 0.707E₀) when the peak intensities in linearly and circularly polarized pulses take the same value(e.g., $I_0=E_0^2$). Therefore, we may anticipate that an energy Stark shift induced by a circularly polarized field will be greater than one caused by a linearly polarized pulse. In contrast to the ionization in weak intensity laser field, the blue shift between the data of a linearly polarized field and those of a circularly polarized field, as depicted in Figure 4, is hard to be detected. But as the laser intensity becomes strong (e.g., higher than I₀ = 1 × 10¹⁸ W/cm²), such a blue shift is clearly visible.

When the peak intensity is increased to 5 × 10¹⁸W/cm² in Figure 7, the multipeak structure of photoelectron momentum distribution and photoelectron spectra of hydrogen atoms exposed to laser pulses are seen clearly and intuitively. Higher laser intensities lead to a reduction in the energy difference between nearby interference fringes and an increase in the phase difference between the two electron wave packets, which results in significantly more dynamic interference fringes being recorded. In actuality, two elements are involved in the growing phase difference. First, the time interval between the emission timings t₁ and t_f increases because the atomic stabilizing effect in a high-intensity laser field has earlier beginning and later ending times than what is required for that in a low-intensity laser field. Second, the phase difference increases with the increasing vector potential of the field when a stronger laser field is applied. This effect can be observed in the increased fringes both in momentum distribution shown in Figures 7A,B, and the photoelectron spectrum is shown in Figure 7E.

To further understand the origin of differences among the photoelectron spectra induced by a laser pulse with different kinds of polarization, in Figure 8 we plot the probability densities of the wave function at the middle and the end of the interaction with the laser field at low and high intensity, respectively. When the laser intensity is relatively low, as seen in the top panels (a,b), the probability density shows electrons leave the nuclear core in a dipole pattern. However, at high laser intensity, the electron distribution at the end of the pulse displays two hallows, which denotes an electron scattering from the nuclear center. In order to find the reason for the scattering process occurring at such high laser intensity, we compare the ponderomotive energies (U_p) of two cases. For ℏω = 53.605 eV laser pulses, U_p= 25 eV for I₀ = 5 × 10¹⁷ W/cm² and U_p= 250 eV for I₀ = 5 × 10¹⁸ W/cm². In the low-intensity case, U_p is only 25 eV, which is less than the photoelectron energy ℏω = 40 eV. Therefore, the laser-driven photoelectron is hard to hit the nuclear center. But in the high-intensity case, the U_p, which is up to 250 eV, is much higher than the first-order ATI photoelectron energy. As a result, the photoelectrons will scatter from the hydrogen atom’s Coulomb center and follow and oscillate with the electric field. In other words, the nondipole distribution of photoelectron momentum for the hydrogen atoms in a superintense laser field is mostly caused by Coulomb scattering.

FIGURE 8

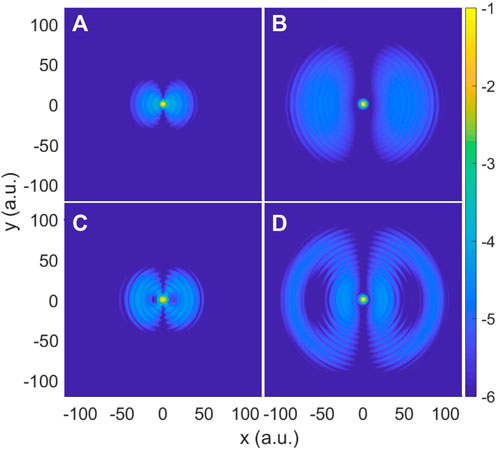
FIGURE 8. (Color online) Probability density of wave function in the middle and at the end of laser pulses. All parameters are the same as those in Figure 3A, except for the peak intensities: (A,B) I₀ = 5 × 10¹⁷ W/cm² and (C,D) I₀ = 5 × 10¹⁸ W/cm².

4 Conclusion

By solving the TDSE of ground-state hydrogen atoms in the presence of superintense laser pulses numerically, the photoelectron momentum distribution with dynamic interference effect is investigated. It has been demonstrated in this study that we can observe dynamic interference effects even in a tightly bounded system when there are circularly polarized pulses present in addition to the linearly polarized laser field. The coherent superposition of two perpendicular, linearly polarized laser pulses with an intensity no higher than I₀ = 10¹⁸ W/cm² can provide a qualitative explanation for the dynamic interference pattern in momentum distribution caused by circularly polarized pulses. However, when the dynamic interference fringes are well separated, such as at I₀ = 5 × 10¹⁸ W/cm², the superposition of the LOPT momentum distribution by linearly polarized pulses and that by a circularly polarized field do not match. This discrepancy results from high-order corrections, including the Coulomb effect, during the photoemission process of linearly polarized laser pulses.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

JW and G-LL contributed equally. AL, L-GJ, and F-ZZ designed the research; G-LL and JW performed time-dependent dynamics simulations; JW, XL, and AL contributed to the analysis of the data; and JW, G-LL, and AL wrote the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China under Grants No.11774131, No.91850114, No.11627807, and No.11604119.

Acknowledgments

Part of the numerical simulation was performed on the high-performance computing cluster Tiger@IAMP at Jilin University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Krausz F, Ivanov M. Attosecond physics. Rev Mod Phys (2009) 81:163–234. doi:10.1103/RevModPhys.81.163

CrossRef Full Text | Google Scholar

2. Sansone G, Benedetti E, Calegari F, Vozzi C, Avaldi L, Flammini R, et al. Isolated single-cycle attosecond pulses. Science (2006) 314:443–6. doi:10.1126/science.1132838

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kühn S, Dumergue M, Kahaly S, Mondal S, Füle M, Csizmadia T, et al. The ELI-ALPS facility: The next generation of attosecond sources. J Phys B: Mol Opt Phys (2017) 50:132002. doi:10.1088/1361-6455/aa6ee8

CrossRef Full Text | Google Scholar

4. Young L, Ueda K, Gühr M, Bucksbaum PH, Simon M, Mukamel S, et al. Roadmap of ultrafast x-ray atomic and molecular physics. J Phys B: Mol Opt Phys (2018) 51:032003. doi:10.1088/1361-6455/aa9735

CrossRef Full Text | Google Scholar

5. Eberly JH, Kulander KC. Atomic stabilization by super-intense lasers. Science (1993) 262:1229–33. doi:10.1126/science.262.5137.1229

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sussman BJ. Five ways to the nonresonant dynamic Stark effect. Am J Phys (2011) 79:477–84. doi:10.1119/1.3553018

CrossRef Full Text | Google Scholar

7. Jiang W-C, Burgdörfer J. Dynamic interference as signature of atomic stabilization. Opt Express (2018) 26:19921–31. doi:10.1364/OE.26.019921

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Toyota K, Tolstikhin OI, Morishita T, Watanabe S. Siegert-state expansion in the kramers-henneberger frame: Interference substructure of above-threshold ionization peaks in the stabilization regime. Phys Rev A (Coll Park) (2007) 76:043418. doi:10.1103/PhysRevA.76.043418

CrossRef Full Text | Google Scholar

9. Baghery M, Saalmann U, Rost JM. Essential conditions for dynamic interference. Phys Rev Lett (2017) 118:143202. doi:10.1103/PhysRevLett.118.143202

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Demekhin PV, Cederbaum LS. Dynamic interference of photoelectrons produced by high-frequency laser pulses. Phys Rev Lett (2012) 108:253001. doi:10.1103/PhysRevLett.108.253001

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Demekhin PV, Cederbaum LS. Ac Stark effect in the electronic continuum and its impact on the photoionization of atoms by coherent intense short high-frequency laser pulses. Phys Rev A (Coll Park) (2013) 88:043414. doi:10.1103/PhysRevA.88.043414

CrossRef Full Text | Google Scholar

12. Guo J, Guo F, Chen J, Yang Y. Pulse duration effect on photoelectron spectrum of atom irradiated by strong high frequency laser. Acta Phys Sin (2018) 67:073202. doi:10.7498/aps.67.20172440

CrossRef Full Text | Google Scholar

13. Demekhin PV, Hochstuhl D, Cederbaum LS. Erratum: Photoionization of hydrogen atoms by coherent intense high-frequency short laser pulses: Direct propagation of electron wave packets on large spatial grids. Phys Rev A (Coll Park) (2017) 95:049903. doi:10.1103/PhysRevA.95.049903

CrossRef Full Text | Google Scholar

14. Wang M-X, Liang H, Xiao X-R, Chen S-G, Jiang W-C, Peng L-Y. Nondipole effects in atomic dynamic interference. Phys Rev A (Coll Park) (2018) 98:023412. doi:10.1103/PhysRevA.98.023412

CrossRef Full Text | Google Scholar

15. Wang N, Liu A. Interference effect of photoionization of hydrogen atoms by ultra-short and ultra-fast high-frequency chirped pulses. Chin Phys B (2019) 28:083403. doi:10.1088/1674-1056/28/8/083403

CrossRef Full Text | Google Scholar

16. Fu LB, Xin GG, Ye DF, Liu J. Recollision dynamics and phase diagram for nonsequential double ionization with circularly polarized laser fields. Phys Rev Lett (2012) 108:103601. doi:10.1103/PhysRevLett.108.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bauer J, Rzazewski K. SFA applied to the nonsequential double ionization of the helium atom by a circularly polarized plane wave. J Phys B: Mol Opt Phys (1996) 29:3351–62. doi:10.1088/0953-4075/29/15/010

CrossRef Full Text | Google Scholar

18. Toyota K, Tolstikhin OI, Morishita T, Watanabe S. Interference substructure of above-threshold ionization peaks in the stabilization regime. Phys Rev A (Coll Park) (2008) 78:033432. doi:10.1103/PhysRevA.78.033432

CrossRef Full Text | Google Scholar

19. Ben S, Guo P-Y, Song K-L, Xu T-T, Yu W-W, Liu X-S. Nonsequential double ionization of mg from a doubly excited complex driven by circularly polarized laser field. Opt Express (2017) 25:1288–95. doi:10.1364/OE.25.001288

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Wang X, Tian J, Eberly JH. Angular correlation in strong-field double ionization under circular polarization. Phys Rev Lett (2013) 110:073001. doi:10.1103/PhysRevLett.110.073001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Christov IP, Murnane MM, Kapteyn HC. High-harmonic generation of attosecond pulses in the “single-cycle” regime. Phys Rev Lett (1997) 78:1251–4. doi:10.1103/PhysRevLett.78.1251

CrossRef Full Text | Google Scholar

22. Patchkovskii S, Muller H. Simple, accurate, and efficient implementation of 1-electron atomic time-dependent Schrödinger equation in spherical coordinates. Comp Phys Commun (2016) 199:153–69. doi:10.1016/j.cpc.2015.10.014

CrossRef Full Text | Google Scholar

23. He P-L, Takemoto N, He F. Photoelectron momentum distributions of atomic and molecular systems in strong circularly or elliptically polarized laser fields. Phys Rev A (Coll Park) (2015) 91:063413. doi:10.1103/PhysRevA.91.063413

CrossRef Full Text | Google Scholar

24. Pronin EA, Starace AF, Frolov MV, Manakov NL. Perturbation theory analysis of attosecond photoionization. Phys Rev A (Coll Park) (2009) 80:063403. doi:10.1103/PhysRevA.80.063403

CrossRef Full Text | Google Scholar

25. Yuan K-J, Chelkowski S, Bandrauk AD. Molecular photoelectron momentum distributions by intense orthogonally polarized attosecond ultraviolet laser pulses. Chem Phys Lett (2015) 638:173–8. doi:10.1016/j.cplett.2015.08.046

CrossRef Full Text | Google Scholar

26. Gavrila M. Atomic stabilization in super-intense laser fields. J Phys B: Mol Opt Phys (2002) 35:R147–93. doi:10.1088/0953-4075/35/18/201

CrossRef Full Text | Google Scholar

27. Remetter T, Johnsson P, Mauritsson J, Varjú K, Ni Y, Lépine F, et al. Attosecond electron wave packet interferometry. Nat Phys (2006) 2:323–6. doi:10.1038/nphys290

CrossRef Full Text | Google Scholar

28. Protopapas M, Lappas DG, Knight PL. Strong field ionization in arbitrary laser polarizations. Phys Rev Lett (1997) 79:4550–3. doi:10.1103/PhysRevLett.79.4550

CrossRef Full Text | Google Scholar

29. Liang J, Jiang W-C, Wang S, Li M, Zhou Y, Lu P. Atomic dynamic interference in intense linearly and circularly polarized xuv pulses. J Phys B: Mol Opt Phys (2020) 53:095601. doi:10.1088/1361-6455/ab7527

CrossRef Full Text | Google Scholar