Impact of strategy conformity on vaccination behaviors

In most of the studies focusing on the conformity of voluntary vaccination decisions, the conformity was always directly modeled as a conformity-driven strategy-updating rule. However, the utility of an individual can also be influenced by the group identity or discrimination behaviors associated with strategy conformity in realities. Thus, a novel utility model of the vaccination game is first formulated in which the influence of strategy conformity is considered. Then, we use the spatial evolutionary game theory to study the dynamics of individual vaccination strategies under the influence of strategy conformity on the scale-free network. The results show that moderate strategy conformity and a high herd immunity threshold have a significant positive effect on vaccination behaviors when the initial vaccination fraction is low. Moreover, for a high initial vaccination fraction, the strong strategy conformity and high herd immunity threshold are more conducive to encourage vaccination behavior. To analyze the model sensitivity, experiments are conducted in the small world network and square lattice network. In addition, we performed the sensitivity analysis on vaccination effectiveness. Finally, the generality of strategy conformity effect is investigated when the myopic strategy updating rule is adopted in the whole population. The result shows that vaccination behaviors can also be promoted under the condition of moderate strategy conformity and low initial vaccination fraction.

1 Introduction

The history of mankind has always been accompanied by a struggle against the epidemic, from the outbreak of the Black Death in the 14th century to the still unresolved COVID-19 [1–9]. Large-scale infectious diseases have caused innumerable damages to human societies. Therefore, the prevention of infectious diseases has great significance for mankind. Vaccination is a significant method to control infectious diseases and numerous researchers have devoted endless efforts to the investigation of this hot topic. For instance, many researchers have proposed some effective immunization strategies based on vaccinations, including random immunization [10], targeted immunization [11], acquaintance immunization [10], and ring immunization [12].

Most of these proposed immunization strategies are based on the assumption that vaccination is mandatory [13]. Practically, the immunization of individuals by vaccinating is more of a voluntary behavior. When deciding whether to vaccinate or not, individuals evaluate a variety of issues, including religion, vaccination cost, and the side effects of vaccination. Therefore, a voluntary vaccination model based on game theory has been proposed to explore influences of immunization on the dynamical process in epidemics [13–18]. Huang et al. [19] proposed a new vaccination update rule: a myopic update rule based on the Fermi function and a new vaccination game. In particular, the utility of risky perception is considered a term of the utility function. [20] built a two-stage game to systematize the process of vaccination with profit-motivated strategy update and transmission of the epidemic. However, the epidemic can hardly be eradicated by a voluntary vaccination policy without incentives [21]. Thus, many works have studied the effect of subsidy policies on vaccination coverage [21–24]. For instance, Zhang et al. [23] found that the targeted subsidy policy is only advantageous when individuals prefer to imitate the subsidized individuals’ strategy. Inspired by previous works on the vaccination subsidy policy, [24] proposed two history information-based subsidy policies and found that history information-based subsidy policies can enhance the vaccination probability of non-hub nodes. In reality, the network structure also plays an important role in the vaccination behavior and the spread of infectious diseases [25]. Thus, many studies have paid attention to the impact of the topology of networks on vaccination behavior [13,16,26–31]. Moreover, Granell et al. proposed a two-layer network, one characterizes the dynamics of the awareness evolves and the other depicts the epidemic process spreads to explore the impact of risk perception on the vaccination behavior [21, 32, 33].

In addition to the aforementioned factors, for an individual, the behaviors of nearing neighbors in networks can also impact its decision-making process, such as conformity (conformity refers to the act of changing one’s behavior to match the responses of others [34]). In reality, individuals can only obtain partial information and have limited computing power, and they usually cannot make decisions with full rationality. There exists compelling evidence in favor of the fact that conformity also plays an important role in the individual decision-making process [35]. Therefore, conformity has been introduced into the social dilemma modeling framework, and some studies have shown that conformity has a significant impact on vaccination behaviors when the conformity is considered in the decision-making process of individuals [36–43]. For instance, Cui et al. presented an evolutionary model to explore the impact of conformity on the prisoner’s dilemma game and found that when the temptation to defect is low and both conformism and local interactions are present, the system can reach high levels of cooperation or even a full cooperation state [37]. Lu et al. discussed the influence of the conformity-driven strategy-updating mechanism on the vaccination behaviors based on the susceptible-infected-recovered (SIR) model [44]. Based on this two-stage model proposed by [20], [45] established a framework considering the conformity-motivated strategy update as well as myopic best response-motivated strategy update on a family network which is demonstrated by a two-layered network. In the proposed studies focusing on the impact of conformity on vaccination behaviors, conformity was always directly modeled as the strategy updating method when an individual makes a vaccination decision.

In reality, individuals are more inclined to cater to the majority to avoid being isolated or get a sense of belonging to the majority. Haque et al. extended the framework of coordination games and incorporate vaccination decisions which is mainly determined by three components, namely, the benefits a node derives from the vaccination, the strategy conformity, and the benefit of herd immunity if a sufficient fraction of individuals is vaccinated [46]. Thus, the utility of individuals can also be affected by the group identity or discrimination behaviors associated with strategy conformity. Motivated by this, to explore the evolution of vaccination behaviors under the influence of vaccination strategy conformity, a novel utility function of vaccination games is formulated to capture the influence. Here, the intensity of strategy conformity (e.g., strong strategy conformity or weak strategy conformity) refers to the intensity of the effect of strategy conformity on utilities. We analyze the vaccination behavior through the imitation-based strategy-updating rule and the utility function. The effects of vaccination cost with different initial vaccination rates on voluntary vaccination behaviors are first explored, and the results show that for a higher initial vaccination fraction, the population is more tolerantly vaccinated with the increase in vaccination cost. Then, we investigate the influences of different strategy conformity intensities on vaccination behaviors. We find that there is no simple linear relationship between the strategy conformity intensity and the vaccination coverage. Furthermore, α − γ phase graphs are performed to explore the joint influence of strategy conformity and herd immunity threshold on vaccination behaviors. The results show that a high herd immunity threshold has a significant positive effect on vaccination behavior, and the most appropriate range of α is diverse for different initial vaccination fractions. Finally, we verify the generality of the impact of strategy conformity on vaccination behaviors by using the myopic strategy updating rule. The result shows that moderate strategy conformity also has a prominent positive effect on vaccination behavior for the low initial vaccination fraction.

This study is organized as follows: in Section 2, we first describe the utility function considering strategy conformity, vaccination cost, and herd immunity. Then, we interpret the model of the vaccination evolutionary process. In Section 3, we mainly analyze the influence of strategy conformity on vaccination behaviors in different scenarios and explained the results. Meanwhile, the sensitivity of the model is analyzed, and the generalization of the influence is also analyzed by the myopic update rule. The conclusions are presented in Section 4.

2 Model

We discuss the effects of conformity on vaccination behaviors by considering a vaccination game in scale-free networks [13,16,47]. In the network, each node represents an individual. The game is the process of voluntary vaccination before the epidemic season, where individuals make decisions between vaccinating or not by comparing their utility in the current season with one of the randomly selected neighbors. Once the epidemic season ends, the utility of individuals in the season is calculated. Similar to previous studies, we suppose that the vaccination is valid permanently in each season and is effective for only one season [16,20,44], especially herd immunity is considered in our model. Herd immunity is a standard notion from mathematical epidemiology: the disease will die out on its own if more than a certain fraction (γ) of nodes is vaccinated in the entire network [46]. When herd immunity is achieved, we call the non-vaccinated individuals as free-riders.

2.1 Utility function

Let s_i denote the vaccination state of individual i, where 0 and 1 indicate vaccination and non-vaccination, respectively. The following utilities are considered in the function:

• Strategy conformity utility

Individuals are more inclined to agree with the majority in real life. When the strategy chosen by an individual is different from the majority, the individual is more likely to be isolated or treated unfairly. Also, as the proportion of the majority increases, so do the negative effects. When an individual chooses the same strategy as the majority, the individual is easier to integrate into the population or get spiritual satisfaction (e.g., collective sense of honor).

Therefore, the utility of individual i obtained from strategy conforming to its neighbors is represented by $\frac{\alpha (N_i-\frac{k_i}{2})}{\frac{k_i}{2}}$, where N_i represents the number of individuals in i’s neighbors who adopt the same strategy x_i and k_i represents the number of the individual i’s neighbors. $N_i-\frac{k_i}{2}$ is the strategy conformity effect to individual i after determining the strategy [39,43,44]. We normalize the expression ($N_i-\frac{k_i}{2}$ divided by $\frac{k_i}{2}$). $\frac{(N_i-\frac{k_i}{2})}{\frac{k_i}{2}}=\frac{(2N_i-k_i)}{k_i}\in [-\mathrm{1,1}]$. $\frac{(2N_i-k_i)}{k_i}=-1$ indicates the strategy chosen by individual i which is different from all neighbors, while $\frac{(2N_i-k_i)}{k_i}=1$ indicates individual i who chooses the same strategy with all its neighbors. The parameter α adjusts the influence intensity of strategy conformity on vaccination decision-making. Here, we refer to $\alpha \frac{(2N_i-k_i)}{k_i}$ as the conformity payoff.

• Utility of vaccinated individuals

The utility of vaccination should be incorporated into the cost of the vaccine C_V (e.g., the opportunity cost of time, economic cost, and the side effects to health) and the (perceived) health benefit C_H[46]. Because the vaccination provides perfect immunity, the vaccinated individual gets the vaccination benefit C_H − C_V regardless of herd immunity. Taking together, the utility of a vaccinated individual i can be expressed as $C_H-C_V+\alpha \frac{(2N_i-k_i)}{k_i}$.

• Utility of free-riders

For a free-rider i, when herd immunity is achieved, it will get the health benefit C_H without any cost. Thus, the utility of a free-rider is as follows: $C_H{s}_i{\mathbb{1}}_{{\sum }_j{s}_j<(1-\gamma )n}+\alpha \frac{(2N_i-k_i)}{k_i}$, where ${\mathbb{1}}_Z$ is an indicator variable, yielding 1 if the condition Z holds and otherwise 0; ∑_js_j is the number of non-vaccinated individuals in the network; and (1 − γ)n is the maximum number of non-vaccinated individuals when herd immunity is achieved. Herd immunity is achieved if ∑_js_j < (1 − γ)n, and the free-rider i (s_i = 1) gets the benefit C_H.

As mentioned previously, both vaccinated individuals and free-riders can get the conformity benefit. Thus, the utility of individual i can be calculated as follows:

$util\left(i\right)=\alpha \frac{\left(2N_i-k_i\right)}{k_i}+\left(C_H-C_V\right)\left(1-s_i\right)+C_H{s}_i{\mathbb{1}}_{\sum _j{s}_j<\left(1-\gamma \right)n}.(1)$

Without loss of generality, we set C_H = 1 in this study. Individuals get benefits according to their own vaccination strategy and whether the herd immunity is achieved or not. To make Eq. 1 easier to understand, we rewrite it as an equivalent piece-wise linear function:

$util\left(i\right)=\left\{\begin{array}{c}\alpha \frac{\left(2N_i-k_i\right)}{k_i}+\left(C_H-C_V\right),s_i=0,\hfill \\ \alpha \frac{\left(2N_i-k_i\right)}{k_i}+C_H{\mathbb{1}}_{\sum _j{s}_j<\left(1-\gamma \right)n},s_i=1\hfill \end{array}\right..(2)$

Note that, on the one hand, vaccinated individuals and free-riders both can obtain the conformity benefit. On the other hand, only the vaccinated individuals can obtain the health benefit when the herd immunity is not achieved.

2.2 Strategy updating rules

We consider two types of strategy updating rules: the imitation rule and the myopic update rule.

Imitation rule: Individual i randomly selects an individual j from its neighbors, and the probability of adopting the neighbor j’s strategy is determined by the following Fermi function. $\frac{1}{K}$ indicates the so-called intensity of selection. Without loss of generality, we keep K = 0.1 in this study [44,45],cc. Note that K = 0 and K = 1 depict the completely deterministic and random selection of individual strategies, respectively:

$P\left(s_i\leftarrow s_j\right)=\frac{1}{1+\mathit{exp}\left[\left(util\left(i\right)-util\left(j\right)\right)/K\right]}.(3)$

Myopic update rule: Individual i updates its own strategy by comparing the strategy s_i and the opposite strategy $\overline{s_i}$. Then, individual i changes the strategy s_i into the opposite strategy $\overline{s_i}$ with the following Fermi-like probability(K = 0.1):

$P\left(s_i\leftarrow \overline{s_i}\right)=\frac{1}{1+\mathit{exp}\left[\left(util\left(i\right)-util\left(\bar{i}\right)\right)/K\right]},(4)$

where $util(\bar{i})$ denotes the utility of the opposite strategy of individual i.

2.3 Simulation procedure

Overall, according to the strategy updating rules discussed previously, the corresponding simulation procedures are summarized in the following steps:

1. Initialization: we simulate this procedure with total population size N = 2000 on the scale-free network and the average degree $<k>=6$. The scale-free network is started from a set of three fully connected nodes and then grows according to the preferential attachment mechanism until the size of the network is 2000 [47]. The initial proportion of vaccinated individuals is V₀ (0 < V₀ < 1), and the vaccinated individuals are randomly chosen within the population. All individuals are fixed with the same rule to update their vaccination strategies.

2. Payoff updates: according to the specific situation of herd immunity and the vaccination behavior of individuals, the utility of each individual is updated.

3. Strategy updates: updating the vaccination strategy of a node according to the strategy updating rule until all nodes are traversed. At this point, the iteration returns to step b or stops after predetermined iterations.

All the results are obtained from an average of over 50 independent realizations. If not otherwise stated, γ = 0.8. Table 1 summarizes the parameters which will be used throughout the study.

TABLE 1

TABLE 1. Summary of parameters.

3 Results and discussion

In this part, we mainly focus on the influence of strategy conformity on vaccination behaviors, when the population adopts the imitation-based strategy-updating rule. First, we plot the vaccination coverage as a function of C_V for the different populations (the populations with different values of α), to analyze the evolution of vaccination behaviors against different vaccination costs. Then, we explore the impact of strategy conformity on the evolution of vaccination behaviors and explain the relevant phenomena. Moreover, a deeper illustration of the co-effects of vaccination costs and initial vaccination fractions is given, by plotting the α − γ phase graphs. Finally, to verify the generality of the strategy conformity influence, we also discuss vaccination behaviors when individuals adopt the myopic strategy updating rule.

3.1 The influence of vaccination cost on vaccination coverage for different strategy conformity intensities

We start by exploring the influence of vaccination cost on vaccination behaviors of the different populations (the populations with different values of α). Due to the existence of conformity effect, the initial vaccination fraction may have an impact on vaccination behaviors. Thus, we plot the results obtained from a lower initial vaccination fraction V₀ = 0.2 (Figure 1A) and a higher initial vaccination fraction V₀ = 0.6 (Figure 1B).

FIGURE 1

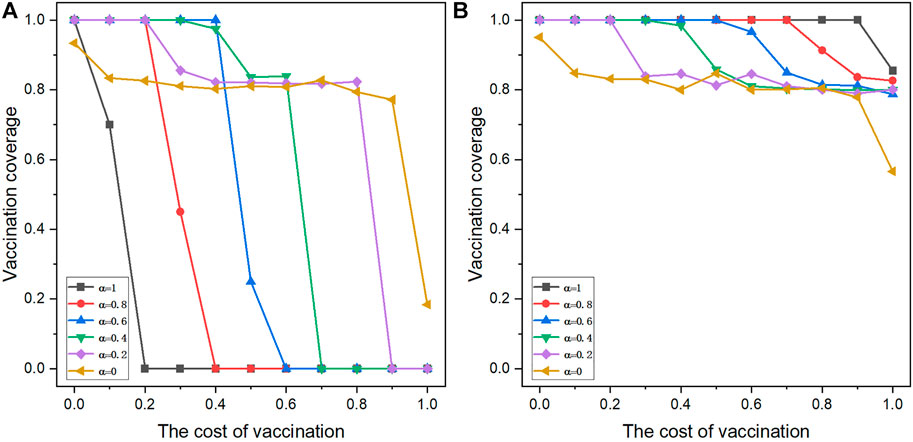
FIGURE 1. Vaccination coverage as a function of the relative cost of vaccination C_V for V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, and C_H = 1.

As shown in Figure 1, first, V₀ has no significant effect on vaccination behaviors of the population when the influence of strategy conformity is not considered (α = 0). Second, one can see that the smaller and larger initial vaccination fractions can lead to two opposite results in the population (α > 0). For the lower initial vaccination fraction V₀ = 0.2 (Figure 1A), stronger conformity has negative effects on vaccination behaviors. In detail, the vaccination coverage in the population with stronger strategy conformity falls to 0 quickly, with an increase in vaccination cost. Interestingly, when C_V < 0.5, the population with intermediate strategy conformity can encourage the vaccination behavior more effectively. When the initial proportion of vaccinated individuals is higher (Figure 1B), one can see a completely opposite result that as the vaccination cost increases, the population has stronger strategy conformity and can have a good tolerance for vaccination behavior. The vaccination coverage in the population with weaker strategy conformity is more negatively impacted by the increase in vaccination cost.

3.2 The influence of strategy conformity on the evolution of vaccination behavior

In order to specifically depict how the last evolutionary stable state is reached for specific values of C_V and V₀ as time passes, a detailed evolution process of vaccination strategies as a function of time steps is plotted for V₀ = 0.2 (panel(a)) and V₀ = 0.6 (panel(b)) in Figure 2 (C_V = 0.3). As shown in Figure 2A, for a lower α ≤ 0.2, the vaccination coverage fluctuates around the herd immunity threshold; for an intermediate 0.4 < α ≤ 0.6, the strategy conformity can encourage the vaccination behavior, and all individuals in the population adopt the vaccination strategy; for a larger α ≥ 0.8, the vaccination behavior is inhibited by the stronger strategy conformity, and the vaccination coverage decreases with the increase of α. When the initial vaccinated fraction of individuals is 60% (Figure 2B), the increase of α significantly improves the vaccination coverage. The phenomenon corresponds to the reality that individuals are more likely to adopt the same strategy as the majority of the population. It is worth noting that for the lower initial vaccination fraction V₀ = 0.2, there is no simple linear relationship between the strategy conformity intensity α and the vaccination coverage, and it can be found that stable vaccination coverage increases first and then decreases as α increases.

FIGURE 2

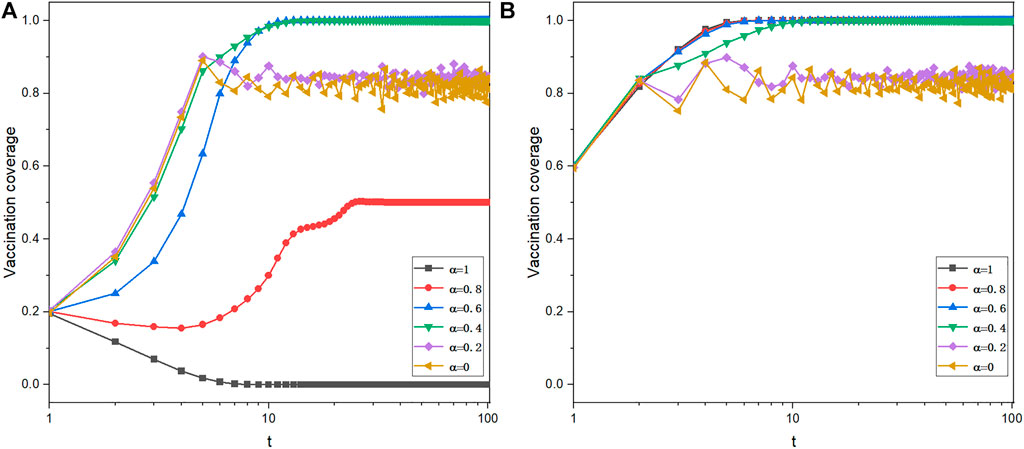
FIGURE 2. Time courses of vaccination coverage for V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, C_V = 0.3, and C_H = 1.

Aiming to further understand the phenomenon in Figure 2A, the state of individuals is divided into four categories based on their strategies in the previous and the current time steps. For three typical populations with α = 1, α = 0.6 and α = 0.2, the fraction evolution of individuals in four states is shown in Figure 3. As shown in Figure 3A, the population with strong strategy conformity has a weak vaccination sentiment, and vaccinated individuals gradually decrease to 0. This is because the non-vaccinated individuals are the majority when the initial vaccination fraction is lower. Also, the stronger strategy conformity leads individuals to follow the majority and not get vaccinated. The result is also consistent with the reality that excessively strong strategy conformity will cause individuals to lose rationality and follow the majority to make irrational behaviors.

FIGURE 3

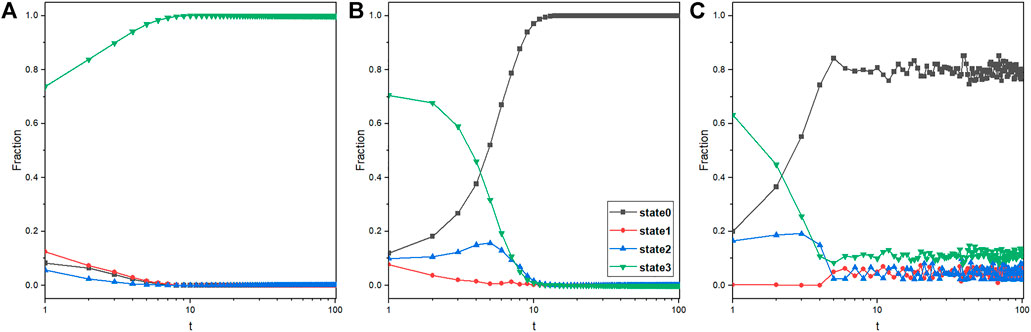
FIGURE 3. Fraction of individuals in different states as a function of time for α = 1 (A), α = 0.6 (B), and α = 0.2 (C). Depicted results are obtained for γ = 0.8, V₀ = 0.2, K = 0.1, C_V = 0.3, and C_H = 1. The state codes are as follows: state0 and state1 represent the vaccinated individuals in the previous epidemic season that still vaccinate and do not vaccinate in the current season, respectively; state2 and state3 represent the non-vaccinated individuals in the previous epidemic season that vaccinate and still do not vaccinate in the current season, respectively.

However, for the low initial vaccination fraction, moderate strategy conformity has a significant positive effect on vaccination behavior in Figure 2A. According to Eq. 2, when the herd immunity is not achieved, the vaccinated individual can get a health benefit compared to the non-vaccinated individual, and they all can get the utility of strategy conformity. For a well-mixed population, taking α = 0.6, C_H = 1, and V_C = 0.2 as an example, the utility of a vaccinated individual is 0.22 higher than the non-vaccinated individual in the beginning. Meanwhile, if the vaccinated individual chooses the non-vaccinated individual to imitate, the probability of adopting a non-vaccination strategy for the vaccinated individual is only 9.98% from Eq. 3. On the contrary, the probability that a non-vaccinated individual will choose to be vaccinated is 90.02%. Therefore, for V_C = 0.2 and α = 0.6, once the vaccinated individuals form clusters (the proportion of vaccinated individuals in the cluster reaches 0.3 or more), the strategy of vaccinated individuals will hardly change. The vaccination behavior also spreads outward from the cluster. As shown in Figure 3B, some vaccinated individuals change their strategies in the beginning. Obviously, these individuals are not in the cluster of vaccinated individuals. However, as the cluster continues to expand, after the third time step, there are few individuals that are in state1 in the network. Moreover, vaccinated individuals are constantly generated in the network. Taken together, this is the reason why the vaccination behavior can be promoted by moderate strategy conformity in the initial stage.

As time goes by, the vaccination coverage increases near the threshold of herd immunity for α = 0.2 in Figure 2A. Also, the vaccination coverage of the population with weak strategy conformity fluctuates around the threshold. To explain the fluctuated vaccination coverage for a low value of α, we analyze the evolutionary process of the state of individuals in Figure 3C. As shown in Figure 3C, the number of individuals who insist on vaccination (state = 0) is increasing at a fast speed in the initial stage. When the vaccination coverage reaches around the value of γ, one can see that the fraction of individuals in all four states fluctuates. This is because some individuals frequently change their strategies between vaccination and non-vaccination. According to Eqs 2, 3, for the weaker strategy conformity, it is hard for any individual to resist the temptation to be free-riders and the benefit of vaccination: When the herd immunity is achieved, even if the vaccinated individuals obtained the full conformity benefit, once they choose to imitate the non-vaccinated individuals without conformity benefit, the probability of the vaccinated individual to be non-vaccinated is 73.21%; when the herd immunity is not achieved, non-vaccinated individuals with full conformity benefit choose to imitate a vaccinated individual without conformity benefit, and the probability of the non-vaccinated individual to be vaccinated is 99.91%. As discussed, when the herd immunity is achieved, the moderate strategy conformity can avoid the emergence of free-riders. Therefore, for α = 0.6, the proportion of individuals who persist in vaccinating keeps increasing and eventually reaches 1 in Figure 3B, and vaccinated individuals rarely change their strategy. In conclusion, for a low initial vaccination fraction, the weaker stronger conformity has a more positive effect on vaccination behavior; when the vaccination coverage increases near the threshold of herd immunity, too weaker conformity cannot inhibit the emergence of free-riders, and the free-riders cause the fluctuation in vaccination coverage. According to our definition of four states, the individual who changes ones strategy can only be in state1 and state2 in Figure 3C. In order to explore the characteristics of individuals who modify their own strategies, we further analyze the degree distribution of individuals with state1 or state2 for the last 50 time steps. According to Figure 4, one can find that individuals who change their strategy almost always have low degrees.

FIGURE 4

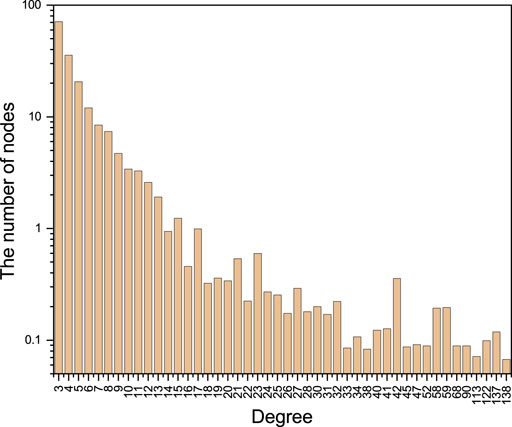
FIGURE 4. Mean of the degree distribution of individuals with state1 or state2 for last 50 time steps in the evolution process of Figure 3 (c). Depicted results are obtained for γ = 0.8, α = 0.2, V₀ = 0.2, K = 0.1, C_V = 0.3, and C_H = 1.

3.3 The co-effect of strategy conformity and herd immunity on vaccination coverage

To better understand the role of the strategy conformity intensity α and herd immunity threshold γ in the vaccination evolutionary process, we plot α − γ phase graphs with different values of C_V and V₀ in Figure 5. One can see that the value of vaccination fraction can be divided into three phases: the yellow phase (full vaccination), the green phase (partial vaccination), and the blue phase (no one vaccinates).

FIGURE 5

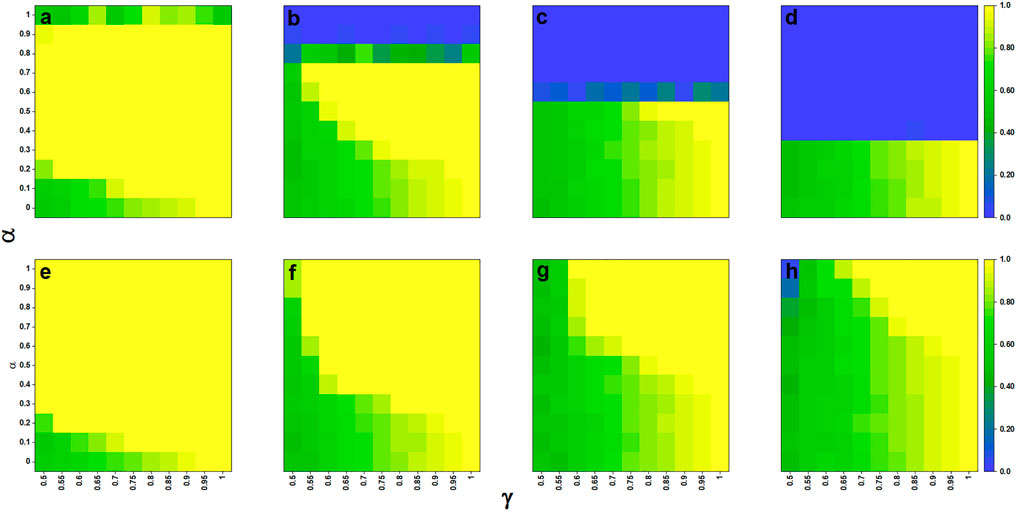
FIGURE 5. α − γ phase graphs, the influence of conformity fraction (α), and herd immunity threshold (γ) on the vaccination coverage. The corresponding value of each point in the figure is the vaccination coverage when the evolution reaches the 100th time step. C_H is fixed at 1. Other parameters corresponding to each image are as follows: (A) V₀ = 0.2 and C_V = 0.1; (B) V₀ = 0.2 and C_V = 0.3; (C) V₀ = 0.2 and C_V = 0.5; (D) V₀ = 0.2 and C_V = 0.7; (E) V₀ = 0.6 and C_V = 0.1; (F) V₀ = 0.6 and C_V = 0.3; (G) V₀ = 0.6 and C_V = 0.5; (H) V₀ = 0.6 and C_V = 0.7.

First, one can find that the α − γ phase graphs correspond to different V₀ showing obvious differences with the increase in vaccination cost. For the convenience of analysis, we divide the initial vaccination fraction into higher initial vaccination fraction (V₀ = 0.2) and lower initial vaccination fraction (V₀ = 0.6) categories. For the lower initial vaccination fraction (as shown in Figures 5A–D), the higher conformity intensity α has strong inhibition effect on population vaccination behavior. Also, there is a clear threshold for α. When α exceeds this threshold, there are no vaccinated individuals in the population. The threshold decreases as the vaccination cost increases. For the higher initial vaccination fraction (As shown in Figures 5E–H), the green areas of the α − γ phase graphs expand from the lower left to the upper right as the vaccination cost increases. Obviously, the vaccination behavior of the population with a higher immunity threshold γ and stronger conformity effect is less inhibited by the increase in vaccine cost C_V.

Then, a pairwise comparison is made of α − γ phase graphs with the same C_V but different initial vaccination rates. For a lower initial vaccination fraction, the part of the phase graph where α is less than the threshold of α is similar to the corresponding position of the phase graph with the same C_V and higher initial vaccination fraction. Therefore, when the value of α is less than the corresponding threshold, the initial vaccination fraction does not affect the final population vaccination coverage. We summarize the results in the phase graphs and put forward two conclusions: first, for a higher initial vaccination fraction, the population which has stronger strategy conformity and higher herd immunity threshold is more conducive to promoting vaccination behavior. Second, for a lower initial vaccination fraction, in order to promote the vaccination behavior, the conformity effect should be weaker than the threshold of α and the herd immunity threshold should be higher.

3.4 Sensitivity analysis

We first discuss the results of the model in other network structures in this part. As shown in Figure 6, the vaccination games are conducted in the Watts–Strogatz (WS) small-world network with a population size N = 2000 and the average degree $<k>=6$. In addition, the probability of rewiring each link is $\frac{1}{5}$ in the network. One can find for the higher initial vaccination fraction that the evolutionary process of vaccination coverage is similar to the results in the scale-free network, while for the lower initial vaccination fraction, vaccination coverage fluctuates around the herd immunity threshold. Particularly, the vaccination coverage in the scenario where α = 1 reaches 1 at about the 700th time step. Then, the evolutionary process of vaccination coverage in the square network with 2000 nodes and each node having four neighbors is plotted in Figure 7. The results show that the vaccination coverage eventually fluctuates around the herd immunity threshold, whatever the initial vaccination fraction is, especially for the higher initial vaccination fraction, the vaccination coverage of some populations with higher α continues to increase and exceeds the herd immunity threshold in the beginning. However, the effect of strategy conformity is still not enough to completely inhibit free-riders, and the vaccination coverage of these populations eventually fluctuates around the herd immunity threshold.

FIGURE 6

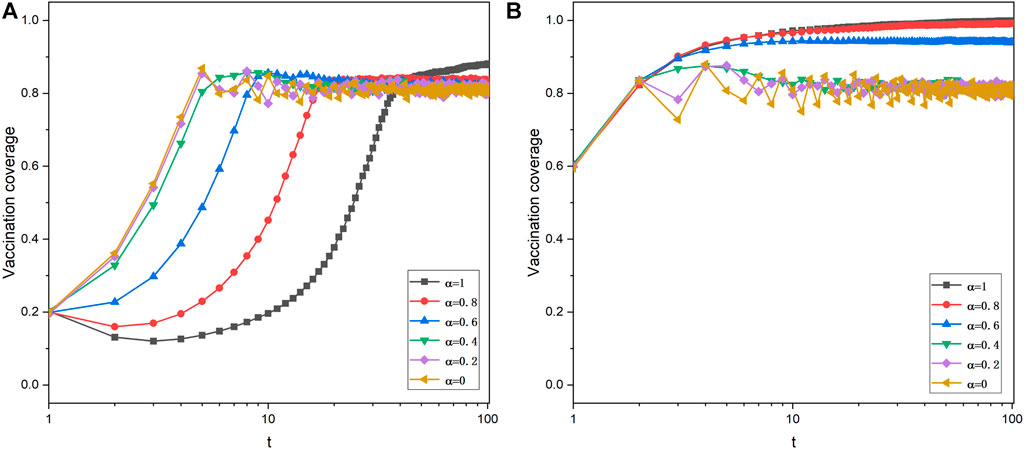
FIGURE 6. Time courses of vaccination coverage in the WS small world network. V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, C_V = 0.3, and C_H = 1.

FIGURE 7

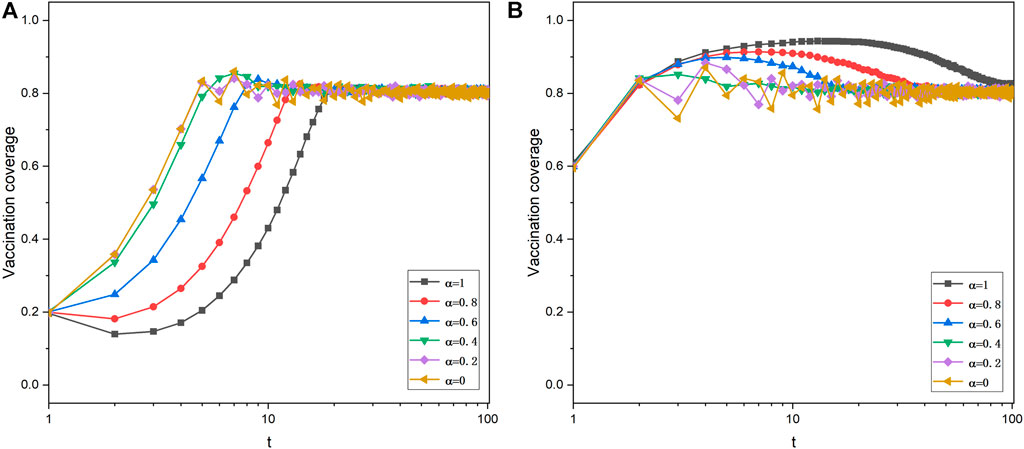
FIGURE 7. Time courses of vaccination coverage in the square lattice network. V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, C_V = 0.3, and C_H = 1.

In the previous section, we assumed that the vaccination can provide perfect immunity for each season. Here, we also explored the influence on the imperfect immunity, and the vaccination coverage for different values of vaccination effectiveness and α on vaccination behaviors is plotted in Figure 8. The vaccination effectiveness V_e represents the probability that the vaccination can provide perfect immunity. For instance, V_e = 0.7 means that vaccinated individuals have a probability of 0.3 not being immunized. In the other words, vaccinated individuals have a 0.3 probability of paying C_V and cannot get C_H. As shown in Figure 8, one can find that more effective vaccination can have a prominent positive effect on vaccination behavior.

FIGURE 8

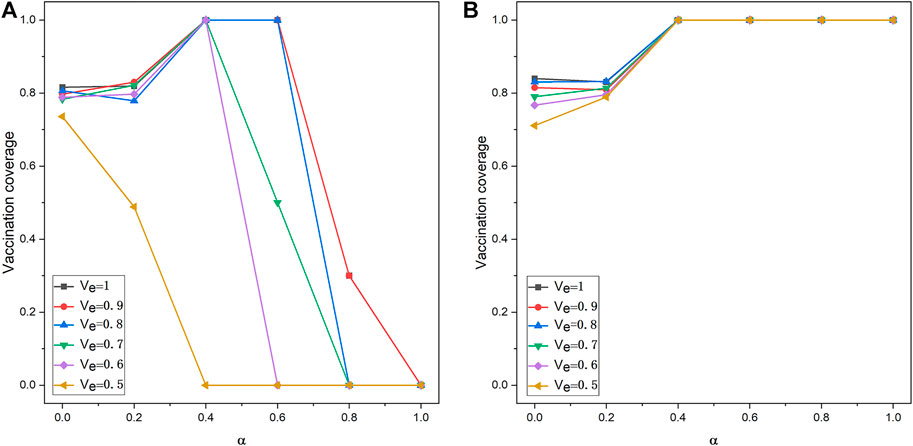
FIGURE 8. Vaccination coverage as a function of the strength of strategy conformity effect α for V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, C_V = 0.3, and C_H = 1.

Finally, to verify the generality of the impact of strategy conformity on vaccination behaviors, when the myopic strategy updating rule is adopted by the population, the evolutionary process of vaccination behaviors is plotted in Figure 9. For α ≤ 0.4, one can see that vaccination behaviors in the population cannot be promoted with an increase in the initial vaccination fraction. As presented in Figure 1, the modest increase of α can effectively stabilize the vaccination behavior of the population and avoid the fluctuation of vaccination coverage near the value of γ.

FIGURE 9

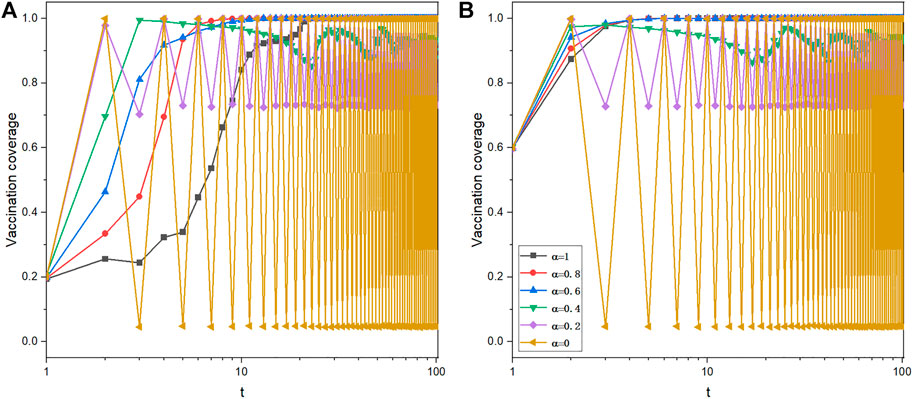
FIGURE 9. Time courses of vaccination coverage when the population adopts the myopic strategy updating rule. V₀ = 0.2 (A) and V₀ = 0.6 (B). Depicted results are obtained for γ = 0.8, K = 0.1, C_V = 0.3, and C_H = 1.

Interestingly, the result of the low initial vaccination rate in Figure 9A is similar to Figure 1A. As the value of α increases, strategy conformity will first promote the occurrence of vaccination behavior. However, when α increases beyond a value, strategy conformity inhibits vaccination behavior. For instance, the vaccination coverage of α = 1 increases more slowly than that of α = 0.8 and α = 0.6. We can still use the conclusions of the previous part to explain the evolutionary process of the vaccination coverage for a low initial vaccination fraction.

4 Conclusion

In this study, we have used the spatial evolutionary vaccination game to explain the influence of strategy conformity on vaccination behaviors. The observation hints that the initial vaccination fraction is an important factor in the dynamics. We have shown that the higher initial vaccination fraction remarkably supports the vaccination behaviors, that is, the population with a higher initial vaccination fraction would have more vaccinated individuals when other conditions were the same. In addition, for the higher initial vaccination fraction, the population which has a stronger conformity effect and higher herd immunity threshold is more conducive to promoting vaccination behaviors. In particular, it is found that too strong or too weak conformity effect is not conducive to vaccination behaviors for a lower initial vaccination fraction. We also analyzed the model sensitivity from the perspective of network structure and vaccine effectiveness. Finally, we verified the generality of strategy conformity influence, and for low initial vaccination fraction, moderate strategy conformity also had a prominent positive effect on vaccination behavior in the myopic update rule. The aforementioned results help understand the impact of strategy conformity on vaccination behavior. We hope that the results of this study will aid the vaccination policy-making for highly infectious diseases, including COVID-19. Meanwhile, we hope that this study can inspire further research on vaccination behavior in complex systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization: TA, JW, XJ, and JZ. Methodology: TA, JW, XJ, and BZ. Software: TA, JW, BZ, and JZ. Visualization: TA and BZ. Formal analysis: TA, JW, and BZ. Writing: TA, JW, JZ, and GC. Funding acquisition: XJ and JZ.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 62002092).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bridbury AR. The black death. Econ Hist Rev (1973) 26:577–92. doi:10.2307/2593699

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Herlihy D, Cohn SH. The Black Death and the transformation of the west. Cambridge: Harvard University Press (1997).

Google Scholar

3. Zhuang Z, Cao P, Zhao S, Lou Y, Yang S, Wang W, et al. Estimation of local novel coronavirus (Covid-19) cases in wuhan, China from off-site reported cases and population flow data from different sources. Front Phys (2020) 8:336. doi:10.3389/fphy.2020.00336

CrossRef Full Text | Google Scholar

4. Zhu J, Jiang Y, Li T, Li H, Liu Q. Trend analysis of Covid-19 based on network topology description. Front Phys (2020) 517. doi:10.3389/fphy.2020.564061

CrossRef Full Text | Google Scholar

5. Duncan CJ, Scott S. What caused the black death? Postgrad Med J (2005) 81:315–20. doi:10.1136/pgmj.2004.024075

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Velavan TP, Meyer CG. The Covid-19 epidemic. Trop Med Int Health (2020) 25:278–80. doi:10.1111/tmi.13383

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Giordano G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, et al. Modelling the Covid-19 epidemic and implementation of population-wide interventions in Italy. Nat Med (2020) 26:855–60. doi:10.1038/s41591-020-0883-7

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ciotti M, Ciccozzi M, Terrinoni A, Jiang W, Wang C, Bernardini S. The Covid-19 pandemic. Crit Rev Clin Lab Sci (2020) 57:365–88. doi:10.1080/10408363.2020.1783198

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Li H, Wang L, Wang Z, Du Z, Yang B, Xia C, et al. Editorial: Mathematical modelling of the pandemic of 2019 novel coronavirus (COVID-19): Patterns, dynamics, prediction, and control. Front Phys (2021) 427doi. doi:10.3389/fphy.2021.738602

CrossRef Full Text | Google Scholar

10. Cohen R, Havlin S, Ben-Avraham D. Efficient immunization strategies for computer networks and populations. Phys Rev Lett (2003) 91:247901. doi:10.1103/PhysRevLett.91.247901

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Pastor-Satorras R, Vespignani A. Immunization of complex networks. Phys Rev E (2002) 65:036104. doi:10.1103/PhysRevE.65.036104

CrossRef Full Text | Google Scholar

12. Müller J, Schönfisch B, Kirkilionis M. Ring vaccination. J Math Biol (2000) 41:143–71. doi:10.1007/s002850070003

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhang H, Zhang J, Zhou C, Small M, Wang B. Hub nodes inhibit the outbreak of epidemic under voluntary vaccination. New J Phys (2010) 12:023015. doi:10.1088/1367-2630/12/2/023015

CrossRef Full Text | Google Scholar

14. Bauch CT, Galvani AP, Earn DJ. Group interest versus self-interest in smallpox vaccination policy. Proc Natl Acad Sci U S A (2003) 100:10564–7. doi:10.1073/pnas.1731324100

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc R Soc B (2005) 272:1669–75. doi:10.1098/rspb.2005.3153

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wang J, Jin X, Yang Y, Chen Q, Wang Z, Ding H. The spread of epidemic under voluntary vaccination with heterogeneous infection rates. Int J Mod Phys C (2021) 32:2150037. doi:10.1142/S0129183121500376

CrossRef Full Text | Google Scholar

17. Wang Q, Du C, Geng Y, Shi L. Historical payoff can not overcome the vaccination dilemma on barabási–albert scale-free networks. Chaos, solitons and fractals (2020) 130:109453. doi:10.1016/j.chaos.2019.109453

CrossRef Full Text | Google Scholar

18. Jusup M, Holme P, Kanazawa K, Takayasu M, Romić I, Wang Z, et al. Social physics. Phys Rep (2022) 948:1–148. doi:10.1016/j.physrep.2021.10.005

CrossRef Full Text | Google Scholar

19. Huang J, Wang J, Xia C. Role of vaccine efficacy in the vaccination behavior under myopic update rule on complex networks. Chaos, Solitons & Fractals (2020) 130:109425. doi:10.1016/j.chaos.2019.109425

CrossRef Full Text | Google Scholar

20. Fu F, Rosenbloom DI, Wang L, Nowak MA. Imitation dynamics of vaccination behaviour on social networks. Proc R Soc B (2011) 278:42–9. doi:10.1098/rspb.2010.1107

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang H, Wu Z, Tang M, Lai Y. Effects of behavioral response and vaccination policy on epidemic spreading-an approach based on evolutionary-game dynamics. Sci Rep (2014) 4:5666–10. doi:10.1038/srep05666

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhang H, Wu Z, Xu X, Small M, Wang L, Wang B. Impacts of subsidy policies on vaccination decisions in contact networks. Phys Rev E (2013) 88:012813. doi:10.1103/PhysRevE.88.012813

CrossRef Full Text | Google Scholar

23. Zhang H, Shu P, Wang Z, Tang M, Small M. Preferential imitation can invalidate targeted subsidy policies on seasonal-influenza diseases. Appl Mathematics Comput (2017) 294:332–42. doi:10.1016/j.amc.2016.08.057

CrossRef Full Text | Google Scholar

24. Ding H, Xu J, Wang Z, Ren Y, Cui G. Subsidy strategy based on history information can stimulate voluntary vaccination behaviors on seasonal diseases. Physica A: Stat Mech its Appl (2018) 503:390–9. doi:10.1016/j.physa.2018.03.003

CrossRef Full Text | Google Scholar

25. Wang Z, Bauch CT, Bhattacharyya S, d’Onofrio A, Manfredi P, Perc M, et al. Statistical physics of vaccination. Phys Rep (2016) 664:1–113. doi:10.1016/j.physrep.2016.10.006

CrossRef Full Text | Google Scholar

26. Cardillo A, Reyes-Suárez C, Naranjo F, Gómez-Gardenes J. Evolutionary vaccination dilemma in complex networks. Phys Rev E (2013) 88:032803. doi:10.1103/PhysRevE.88.032803

CrossRef Full Text | Google Scholar

27. Fukuda E, Tanimoto J, Akimoto M. Influence of breaking the symmetry between disease transmission and information propagation networks on stepwise decisions concerning vaccination. Chaos, Solitons & Fractals (2015) 80:47–55. doi:10.1016/j.chaos.2015.04.018

CrossRef Full Text | Google Scholar

28. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/RevModPhys.87.925

CrossRef Full Text | Google Scholar

29. Guo H, Yin Q, Xia C, Dehmer M. Impact of information diffusion on epidemic spreading in partially mapping two-layered time-varying networks. Nonlinear Dyn (2021) 105:3819–33. doi:10.1007/s11071-021-06784-7

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang Z, Xia C, Chen Z, Chen G. Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans Cybern (2021) 51:1454–62. doi:10.1109/TCYB.2019.2960605

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wang Z, Andrews MA, Wu Z-X, Wang L, Bauch CT. Coupled disease–behavior dynamics on complex networks: A review. Phys Life Rev (2015) 15:1–29. doi:10.1016/j.plrev.2015.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/PhysRevLett.111.128701

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Granell C, Gómez S, Arenas A. Competing spreading processes on multiplex networks: Awareness and epidemics. Phys Rev E (2014) 90:012808. doi:10.1103/physreve.90.012808

CrossRef Full Text | Google Scholar

34. Cialdini RB, Goldstein NJ. Social influence: Compliance and conformity. Annu Rev Psychol (2004) 55:591–621. doi:10.1146/annurev.psych.55.090902.142015

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fiske ST. Social beings: Core motives in social psychology. Hoboken: John Wiley & Sons (2018).

Google Scholar

36. Poland GA, Jacobson RM. Understanding those who do not understand: A brief review of the anti-vaccine movement. Vaccine (2001) 19:2440–5. doi:10.1016/S0264-410X(00)00469-2

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Cui P, Wu Z. Impact of conformity on the evolution of cooperation in the prisoner’s dilemma game. Physica A: Stat Mech its Appl (2013) 392:1500–9. doi:10.1016/j.physa.2012.10.039

CrossRef Full Text | Google Scholar

38. Yang H, Wu Z, Rong Z, Lai Y. Peer pressure: Enhancement of cooperation through mutual punishment. Phys Rev E (2015) 91:022121. doi:10.1103/PhysRevE.91.022121

CrossRef Full Text | Google Scholar

39. Szolnoki A, Perc M. Conformity enhances network reciprocity in evolutionary social dilemmas. J R Soc Interf (2015) 12:20141299. doi:10.1098/rsif.2014.1299

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Javarone MA, Antonioni A, Caravelli F. Conformity-driven agents support ordered phases in the spatial public goods game. EPL (Europhysics Letters) (2016) 114:38001. doi:10.1209/0295-5075/114/38001

CrossRef Full Text | Google Scholar

41. Yang Z, Li Z, Wang L. Evolution of cooperation in a conformity-driven evolving dynamic social network. Appl Mathematics Comput (2020) 379:125251. doi:10.1016/j.amc.2020.125251

CrossRef Full Text | Google Scholar

42. Johnson NF, Velásquez N, Restrepo NJ, Leahy R, Gabriel N, El Oud S, et al. The online competition between pro-and anti-vaccination views. Nature (2020) 582:230–3. doi:10.1038/s41586-020-2281-1

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wang X, Jia D, Gao S, Xia C, Li X, Wang Z. Vaccination behavior by coupling the epidemic spreading with the human decision under the game theory. Appl Mathematics Comput (2020) 380:125232. doi:10.1016/j.amc.2020.125232

CrossRef Full Text | Google Scholar

44. Lu Y, Geng Y, Gan W, Shi L. Impacts of conformist on vaccination campaign in complex networks. Physica A: Stat Mech its Appl (2019) 526:121124. doi:10.1016/j.physa.2019.121124

CrossRef Full Text | Google Scholar

45. Wang X, Gao S, Zhu P, Wang J. Roles of different update strategies in the vaccination behavior on two-layered networks. Phys Lett A (2020) 384:126224. doi:10.1016/j.physleta.2019.126224

CrossRef Full Text | Google Scholar

46. Haque AA-U, Thakur M, Bielskas M, Marathe A, Vullikanti A. Persistence of anti-vaccine sentiment in social networks through strategic interactions. Proc AAAI Conf Artif Intelligence (2021) 35:4812–20.

Google Scholar

47. Barabási A-L, Albert R. Emergence of scaling in random networks. Science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar