Abstract
Physics-informed convolutional recurrent network (PhyCRNet) can solve partial differential equations without labeled data by encoding physics constraints into the loss function. However, the finite-difference filter makes the solution of 2D incompressible flow challenging. Hence, this paper proposes a Fourier filter-based physics-informed convolution recurrent network (named Fourier filter-based PhyCRNet), which replaces the finite-difference filter in PhyCRNet with the Fourier filter to solve the 2D incompressible flow problem. The suggested network improves the accuracy of the partial derivatives, solves the inverse Laplacian operator, and has similar generalization ability due to inheriting the framework of PhyCRNet. Four examples, including the 2D viscous Burger, FitzHugh–Nagumo RD, vorticity and the two-dimensional Navier- Stokes (N-S) equations, validate the correctness and reliability of the proposed Fourier filter-based PhyCRNet.
1 Introduction
Partial differential equations (PDEs), play a crucial role in modeling a wide variety of problems in applied mathematics, physics, biology, chemistry, and engineering technology and thus are widely used to express and interpret the laws involved [1,2]. Although many phenomena can be analyzed and solved through PDEs modeling, such as weather forecasting [3], communication technology [4] and electromagnetic induction [5], in many cases, the analytical solution of PDEs is unavailable, and researchers solve PDEs by numerical methods, i.e., finite-difference, finite volume, and finite element methods [6]. Although some classic numerical methods achieve very high accuracy, the balance between computational cost and accuracy is still a vital issue.
Recently, the rapid development and application of deep learning have provided an alternative solution to PDEs of positive and inverse problems. Theoretically, the universal approximation theorem proves that deep neural networks can simulate arbitrarily complex functions [7]. Due to the development of deep learning and the improvement of computing power, several studies have been proposed utilizing deep learning to solve PDEs [8–15]. The latest related research can be mainly divided into discovering PDEs from data and solving PDEs. The pioneering work in inverse problem research is the sparse regression method introduced by Rudy et al. [8]. On this basis, Long et al [11] proposed an improved neural network, the PDE-Net, to obtain the PDE coefficients and solve PDE. The Physics-informed Neural Network (PINN) proposed by Rassi et al. [16] introduced an innovative approach to encoding physical constraints into loss functions, with many improved PINN versions bring used to solve problems in different scenarios [17–21]. Other researchers propose operator schemes to solve PDEs. For example, Lu et al. [22] introduced a neural network of DeepONets for learning nonlinear operators, while Li et al [23] proposed the Fourier neural operator (FNO) utilizing the Fourier transform, which afforded a much faster solution rate and a stronger generalization ability than other neural networks. Recent research fused neural operators and PINNs to improve the interpretability and speed up the network’s fitting [24,25]. Nevertheless, such a strategy requires quantitative and high-quality training data.
Recent studies have revealed that PDEs can be solved by training the network constraints, such as physical constraints [26,27], without labeled data. However, due to limitations of the network training process, the time extrapolation results are often unsatisfactory. Therefore, researchers have introduced time series prediction deep learning networks in the study to solve PDEs [28–30] with the help of classical numerical methods to solve time-dependent PDEs [31–33]. For instance, the physics-informed based convolutional recurrent network (PhyCRNet) introduced by Ren et al. [30] considers all aspects. Indeed, it starts from the initial conditions without any labeled data, extracts spatial features using a convolutional neural network (CNN) [34], utilizes a convolutional long and short term memory network (ConvLSTM) [35] to learn its evolution, and finally encodes the output values into the loss function through the finite-difference filter for physical constraints. Hence, PhyCRNet solves PDEs using the equations as constraints and supervises the network’s convergence, without high-quality training data.
However, the 2D incompressible flow refers to a flow in which the density remains constant in two-dimensional fluid parcel, which is characterized by stream function and the associated velocity fields and vorticity, as defined by the stream function’s partial derivatives. Typical numerical methods use pseudo-spectral methods to balance the solution rate and accuracy by using the vorticity as the initial field, calculating the partial derivatives in the spectral space, and solving the equations using time iterations [
36–
38]. Nevertheless, calculating the stream function from the vorticity involves calculating the inverse Laplace operator, which is difficult to solve by the finite-difference method. Overall, PhyCRNet has the following disadvantages in solving the 2D incompressible flow problem.
1. The differential accuracy of the finite-difference is not high, resulting in an inaccurate calculation loss function and affecting the convergence speed and accuracy of the solution.
2. Calculating the inverse Laplace operator is challenging when using the finite-difference filter and in the case of calculating the stream function.
3. Finite-difference differential calculation accuracy is related to the grid spacing and the number of cells, and the computational overhead is higher in high-resolution calculations.
Based on these shortcomings, it is necessary to improve the PhyCRNet.
Hence, this paper employs the discrete Fourier transform [39] in the pseudo-spectral method [40] to replace the finite-difference filter in the PhyCRNet and optimize PhyCRNet. The main contribution of this method is solving the problem of efficient solution of the differential operator and the inverse Laplace operator during the vorticity calculation of the stream function in PhyCRNet. In the Fourier filter-based PhyCRNet, we first transform the network’s output into the Fourier space for partial differentiation and calculate the Laplace and the inverse operators, followed by the inverse Fourier transform. Finally, the physical constraints are achieved by encoding and thus effectively solving PhyCRNet’s problem. This improved network has a faster solution than the finite-difference method in large-scale calculations [23].
The remainder of the paper is organized as follows: Section 2 introduces the Fourier filter-based PhyCRNet, while Section 3 provides two examples of two-dimensional viscous Buger’s equation and FitzHugh–Nagumo RD equations to verify the performance of the Fourier filter-based PhyCRNet in solving some basic PDEs. Then, two examples, including the vorticity equation and the 2D incompressible Navier-Stokes equation, demonstrate the advantages of the Fourier filter-based PhyCRNet, finally, Section 5 concludes this work.
2 Methodology
This section introduces the proposed Fourier filter-based PhyCRNet, whose structure describes the PDEs to be solved and then introduces the related algorithms and network frameworks. Finally, the related content of the improved PhyCRNet (namely, Fourier filter-based PhyCRNet) is introduced.
2.1 Problem statement
Our proposed method focuses on the time series prediction and solution of spatiotemporal PDEs. Numerical experimental equations such as Burger’s equation are widely used to verify the method and have the following general form [41,42].where represents the possible solutions found in the time range and the physical space and is the nonlinear operator parameterized with . Also, for the initial and boundary conditions, there are characterizations of the form = 0 and = 0, where represents the boundary interval. The boundary conditions such as Dirichlet and Neumann have not been discussed in this work for the time being.
2.2 PhyCRNet
PhyCRNet proposed by Ren et al adopts ConvLSTM to learn temporal evolution and constructs the network loss function with PDE constraints. It propagates information into future times and solves equations without labeled data as PINN. It has stable extrapolability after training which makes it better than other deep learning methods. For more detailed work on PhyCRNet, refer to the work [30].
2.3 The discrete fourier transform
The discrete Fourier transform (DFT), a fundamental transformation in digital signal processing, is widely used in convolution, image processing, and frequency analysis [43–45]. Its implementation is similar to the continuous Fourier transform, which for a given certain sequence of real numbers , it is represented as a sequence of complex numbers utilizing the discrete Fourier transform. DFT is defined as follows:where . At the same time, the original discrete function can also be reconstructed by the inverse discrete Fourier transform (IDFT), defined as:
By considering the 2-dimensional function as an example, according to Eqs 2, 3:
For the function after the discrete Fourier transform, its corresponding derivative can be quickly obtained in the Fourier space.
Different from the finite difference filter in PhyCRNet to solve the derivative, the spatial derivative is calculated as the product of spectrum and in the wave number domain after the discrete Fourier transforms the function. So, the Fourier filter proposed in this paper is used to calculate spatial derivatives of loss function by discrete Fourier transform. This strategy is more adaptable to solving many PDEs types.
Moreover, the pseudo-spectral method has advantages in solving the 2-dimensional incompressible flow equation [46]. Indeed, given vorticity () and the stream function () at time t, this method first updates ζ forward at time . Then the Poisson equation with periodic boundary is considered as a relationship between the two to update forward at time . The Poisson equation involves the inverse Laplace operator calculation, which is trivial to implement by the discrete Fourier transform when its mean state is known [47]. This is why the discrete Fourier transform is superior to the finite-difference. Assuming that the mean state is one, the inverse Laplace operator is computed as follows:
The improvement proposed in this work is to replace the finite-difference filter in the PhyCRNet with the discrete Fourier transform, and then perform the PDE residual connection to integrate the physical constraints into the neural network (further details are presented in Section 2.4). The resulting network has two advantages. First, it overcomes the inability of PhyCRNet to efficiently solve the inverse Laplace operator. Indeed, the Fourier filter-based PhyCRNet can solve PDEs similar to describing 2D incompressible flows, enhancing the network’s generalization ability. Second, the Fourier transform has higher accuracy than the finite-difference method when calculating high-order partial derivatives, and its computational efficiency is faster in large-scale scientific computing.
2.4 Fourier filter-based PhyCRNet
This section introduces the structure of proposed network. As illustrated in Figure 1, the network consists of the encoding module, time series module, decoding module, input and output connection module and Fourier filtering module. Firstly, the encoding module is used to extract spatial features through CNN and then output to the time series module. Secondly, the time series module captures the time dependence of spatial features and establishes time series relationships. In this way, the network generates the predicted values only under the initial condition. Then, the decoding module reconstructs the discrete output of the time series module by the sub-pixel convolutional layer (pixel shuffle) to achieve the same resolution as the input. In addition, a convolution layer without activation function is added at the end of the module. Finally, the input-output connection module adopts a forward Eulerian method to establish the relationship of and .The Fourier filtering module calculates the spatial derivative involved in the computation of loss function. The Fourier filter calculates the spatial partial derivatives by transforming the input to the spectral space, which turns into a simple multiplication in the frequency domain compared with the finite difference. For more details, please refer to 2.3 for the idea of Fourier filtering and 2.5 for loss construction.
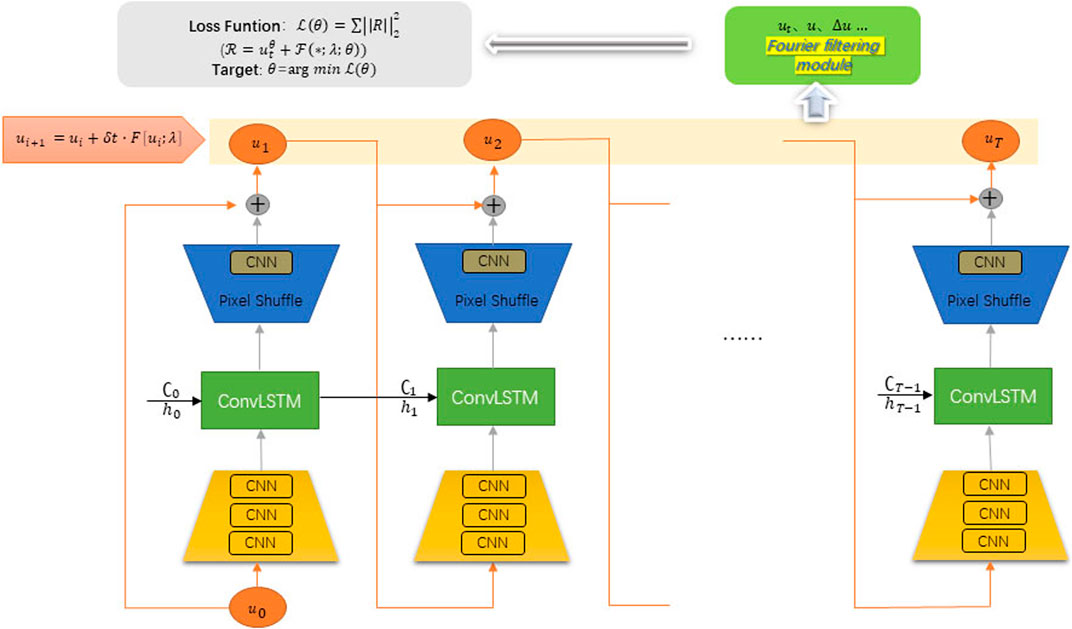
FIGURE 1
The architecture of Fourier filter-based PhyCRNet. It comprises CNN layers with activation functions in the encoder. In the decoder, Pixel Shuffle conducts super-resolution reconstruction to obtain the resolution of the input value, and considers a CNN layer without an activation function for convolution processing. H and C are the hidden state and cell state of ConvLSTM, respectively. All outputs are incorporated into the loss function using DFT and IDFT. Fourier transform loss function with physics-informed.
2.5 Fourier transform loss function with physics-informed
Given that the Fourier filter-based PhyCRNet is trained without labeled data, the loss function construction controlled by the PDEs is significant and must preserve high accuracy and efficiency. The loss function accuracy depends on the partial derivatives, which unlike the chained derivatives of Physics-informed Neural Network (PINN) [16], the Fourier filter-based PhyCRNet uses the Fourier filter formed by the discrete Fourier transform (as introduced in Section 2.3) to calculate the partial derivatives in the PDEs. Hence, we calculate in Eq. 1 and construct the PDEs residual connection to integrate the physical constraints into the loss function of the neural network. Then the PDEs residual connection is formed and the physical constraints are integrated into the loss function in the neural network. As an example, solving the 2-dimensional PDEs, can be defined according to the left side of Eq. 1:where is obtained by traditional numerical methods. The shared network parameter is obtained during training by using the minimization loss function in Eqs 8, 9, defined as the sum of squares of the discrete values of over all spatial and temporal periodswhere denotes the norm.
3 Numerical experiments
This section validates the proposed Fourier filter-based PhyCRNet by utilizing nonlinear PDEs and two PDEs for describing the 2D incompressible fluid flow. The trial involving two nonlinear PDE (2D viscous Burger’s equations and FitzHugh–Nagumo RD equations) verifies that the Fourier filter-based PhyCRNet possesses the capabilities of PhyCRNet. And two 2D incompressible fluid flow PDEs test the feasibility and advantages of Fourier filter-based PhyCRNet. All numerical implementations and constructed networks are coded using Pytorch [48], and all models are trained on an NVIDIA GeForce GTX 3090 with 24 GB of memory.
3.1 Network parameters
The main difference between Fourier filter-based physics-informed convolutional recurrent network (PhyCRNet) and PhyCRNet is the calculation of the partial derivatives, while the other remaining structure is the same. In the encoding part, three convolutional layers are used for feature extraction, with 8, 32, 128 units respectively using a convolutional kernel (44) and a stride of 2 and ReLU function as the activation function. In the decoding part, for the standard connection between the input and output, sub-pixel convolution is performed through pixel shuffle to complete super-resolution reconstruction. Then a convolutional layer is added, using a convolutional kernel (55) and a stride of one to ensure constant resolution without an activation function. The convolution operation in ConvLSTM involves a convolution kernel (33) and a stride of 1. At the same time, the training of both networks are trained using the stochastic gradient descent Adam optimizer [49].
3.2 Evaluation metrics
Three evaluation metrics, mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE), are widely used in the evaluation of deep learning networks. In order to evaluate the solution accuracy of the network in this paper, an accumulative root mean square error (a-RMSE) is defined and the same evaluation metric is used for training and extrapolation.where represents the number of time steps in the period , and represents the full-field a-RMSE. m and n are the resolutions in the spatial region, while and represent the reference solution and the prediction, respectively.
3.3 2D viscous Burger’s equations
Considering the following 2D viscous Burger’s equations with periodic conditions:where is the fluid’s velocity ( and ), is the viscosity coefficient, Δ is the Laplace operator, is the gradient operator, and denotes the initial condition. Here, we set = 0.005, and the spatial region is with a resolution of [128 × 128].
The initial condition is generated in a Gaussian random field, according to where . The experimental reference value is obtained by a pseudo-spectral method with a fourth-order Runge-Kutta method (). PhyCRNet and the Fourier filter-based PhyCRNet both are trained with a relatively large time step () for iterative calculation. In the finite-difference filter module of PhyCRNet, Eq. 12 is used to calculate Δ, and the following difference filter Eq. 13 is used to calculate ▽:
However, in Fourier filter-based PhyCRNet, Eq. 5 is used to calculate ▽, and Δ is calculated by a method similar to Eq. 6, while is calculated by the difference filter in Eq. 14 uniformly. Except for the calculation of spatial derivatives, all parameters are the same as Ref. [30]. The learning rate starts at and decays to 99% every 50 epochs. During the period [0,0.4], PhyCRNet and Fourier filter-based PhyCRNet are trained separately to obtain the numerical solution of the two-dimensional viscous Burger’s equation for 200 time steps. Then, based on the trained model, the solution for the last 200 time steps (within time [0.4, 0.8]) is predicted to verify the model’s extrapolation performance. According to the training method mentioned in [30], we pretrain the model from 100 and then 200 time steps, then extrapolate for another 200 time steps. The relevant codes and data come from open source [30].
Figure 2 depicts four snapshots of taken from the training phase (t = 0.1, 0.3 s) and the extrapolation phase (t = 0.6, 0.8 s), respectively. Each snapshot from top to bottom are reference solutions, predictions by PhyCRNet and ours, and errors of PhyCRNet and ours, respectively. From Figure 2, it can be found that the results of both networks are very agreement with the reference in training and extrapolation. It verifies that the Fourier filter-based PhyCRNet has the same capability to solve basic PDEs as PhyCRNet.
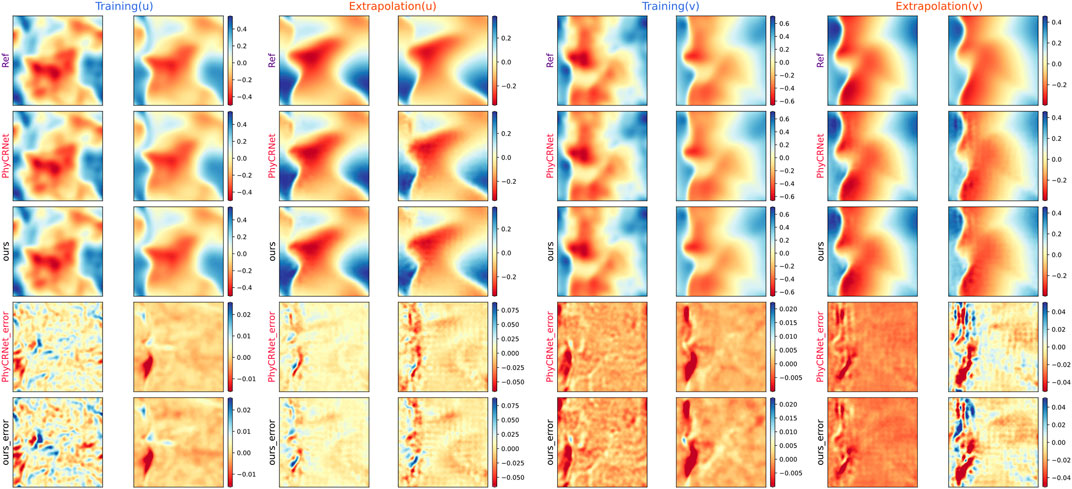
FIGURE 2
The results of Fourier filter-based PhyCRNet and PhyCRNet network solving the two-dimensional viscous Burger’s equation. Four representative moments are selected for comparison as training (t = 0.1, 0.3 s) and extrapolation (t = 0.6, 0.8 s), and the errors across the interval are compared. The subfigures from top to bottom are reference solutions, predictions by PhyCRNet and ours, and errors of PhyCRNet and ours, respectively.
3.4FitzHugh–Nagumo RD equations
Considering the following the FitzHugh–Nagumo (FN) RD equations:
Same as 3.2, except for the Fourier filter, the network hyperparameters and equation coefficients are the same as [30]. and are two interactive components. , , and are equation coefficients by , , and , respectively. The IC is IC_FN1 and the reference solution is calculated using a method in 2D domain of [0.128] for 12,000 time steps () [30]. Two model are trained to solve this PDEs for 200 time steps with time duration of [0, 1.2] and used to achieve the inference for [1.2, 2.4], where . The learning rate is set as 5 × 10–5 and decays by 0.5% every 50 epochs. Besides, we pretrain the model from 100 and then 200 time steps to extrapolate for another 200 time steps.
During training (t = 0.6, 1.2 s) and extrapolation (t = 1.8, 2.4 s) phases, the reference solutions, predicted solutions and error maps are shown in Figure 3. Although FitzHugh–Nagumo RD equations are more complex than Burger’s equation, Fourier filter-based PhyCRNet and PhyCRNet have the same outstanding performance with the truth reference both in training and extrapolation. The error maps of two model exhibit near-perfect results, especially the extrapolation error of the field variable is smaller. Considering that this PDEs has a more complex nonlinear form, the above two neural network methods capture the dynamic evolution process in the long-term, which is different from the traditional forward Euler integration scheme.
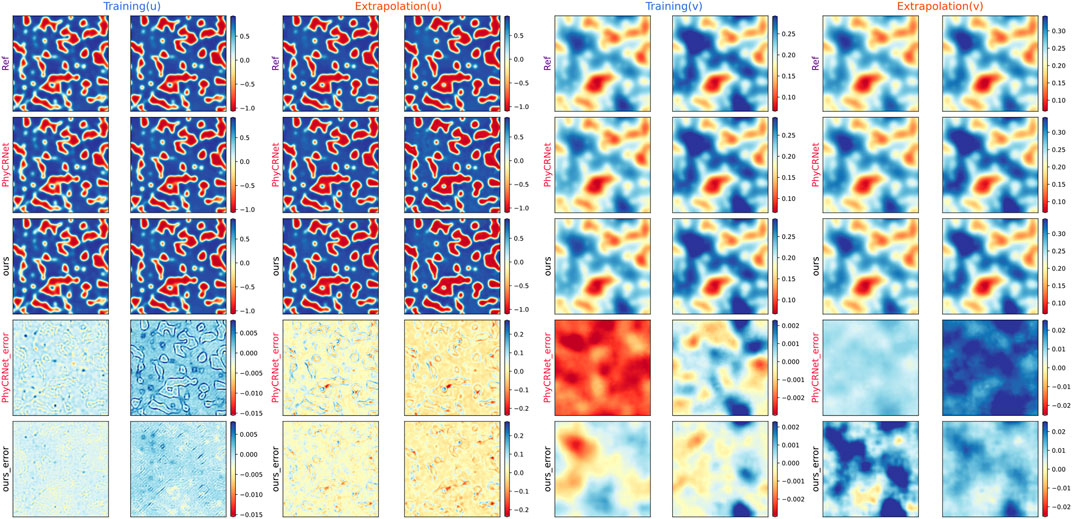
FIGURE 3
The results of Fourier filter-based PhyCRNet and PhyCRNet network solving the FitzHugh–Nagumo RD equations. Four representative moments are selected for comparison as training (t = 0.6, 1.2 s) and extrapolation (t = 1.8, 2.4 s), and the errors across the interval are compared. The subfigures from top to bottom are reference solutions, predictions by PhyCRNet and ours, and errors of PhyCRNet and ours, respectively.
3.5 Vorticity equation
This section focuses on the experimental validation of the Fourier filter-based PhyCRNet to solve the problems that the finite-difference filter of PhyCRNet cannot solve. Since the finite-difference filter cannot solve problems like inverse Laplace operators and there is a time iteration relationship between the input and output modules, the finite-difference method imposes the solution of some PDEs not to have a good propagation relationship between the input and output.
Consider a simple equation for describing 2D incompressible nonviscous fluid flow, namely the vorticity equation, which takes the following formwhere represents the vorticity, the stream function is used to describe the flow of the fluid, and represent the velocity of the fluid in the x and y directions, respectively. The initial flow function for the equation is:where = 0.15. When calculating the reference solution, we calculate and of the initial state from Eq. 17. On the 2D region with a resolution of 256 × 256, a pseudo-spectral method with a fourth-order Runge-Kutta time integral () is used to solve the vorticity equation. The solution reveals that the vorticity moves forward first, then uses the method of Eq. 6 to update the stream function , and then calculates . Using vorticity as a bridge between the input-output connection modules of the network can more effectively capture the time evolution. During network training and extrapolation, the time step is chosen to be . Fourier filter-based PhyCRNet is trained for 100 time steps within [0,0.1] to solve the vorticity equation, and the solution is extrapolated based on the training model for another 100 time steps within time [0.1,0.2]. The learning rate starts at 5 and then decays to 99% every 100 epochs. The entire training time is 6.5 h.
Figures 4, 5 compare the vorticity and velocity fields predicted by Fourier filter-based PhyCRNet and the ground-truth reference values. Four representative time instances are selected for the training (t = 0.025, 0.075 s) and extrapolation (t = 0.125, 0.175 s) phases. From Figures 4, 5, we conclude the following. First, we can see in figures that both the vorticity and velocity fields are close to the true reference during the training and extrapolation phases. Especially in the training phase, many errors are close to zero. As the extrapolation period increases, the error also increases. However, when the extrapolation is at the same training time, the shape of the rotation is still the same. In the region with a larger value, the error becomes larger, but the evolution trend of the solution can still be used as a reference. As the extrapolation time increases, the error also increases. This conclusion is also verified in Figure 8C according to the time-varying a-RMSE.
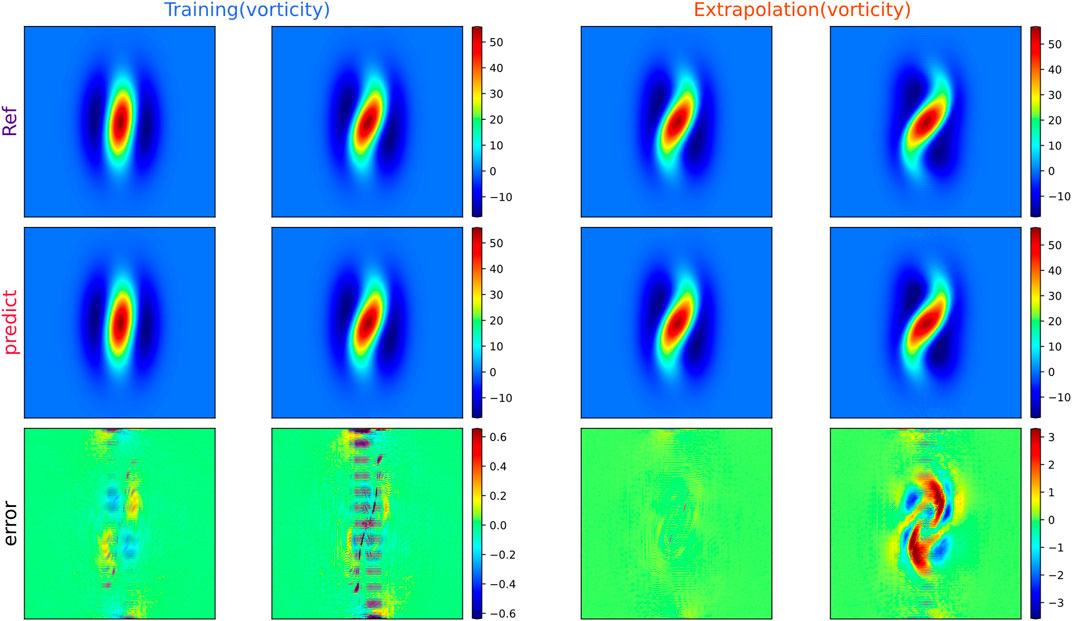
FIGURE 4
The vortex results for solving the vorticity equation with Fourier filter-based PhyCRNet. Four representative moments are selected for comparison, presenting the training (t = 0.025, 0.075 s) and extrapolation (t = 0.125, 0.175 s) maps, and compare the errors across the interval. From top to bottom are reference solutions, predictions and errors.
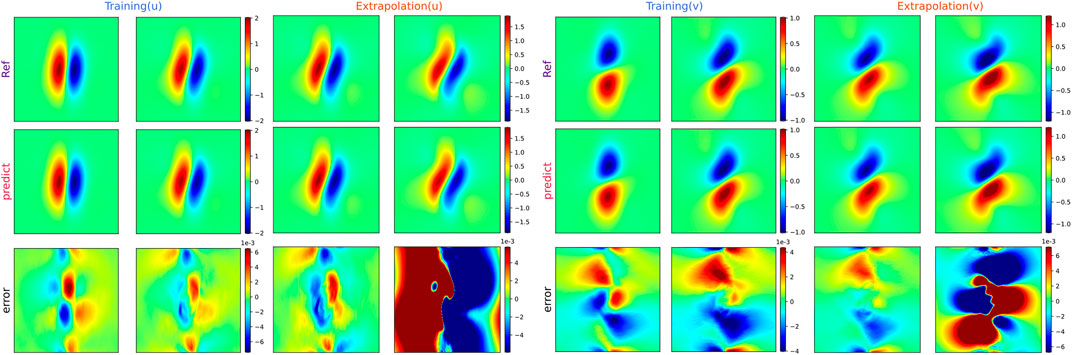
FIGURE 5
The velocity results for solving the vorticity equation with Fourier filter-based PhyCRNet. Four representative moments are selected for comparison, presenting the training (t = 0.025, 0.075 s) and extrapolation (t = 0.125, 0.175 s) maps, and compare the errors of the entire interval. From top to bottom are reference solutions, predictions and errors.
3.6 Two-dimensional Navier-Stokes equation
We consider the 2D Navier-Stokes equations for a incompressible viscous fluid in the form of vorticity on the unit torus [23]:
The reference is all from the open source code of [23]. The initial condition with periodic boundary condition are generated according to , where .We set , and the forcing is kept fixed ). The equation is solved by a pseudo-spectral method, where first, the velocity field is calculated in the Fourier space. The vorticity field is then differentiated, and the nonlinear term is calculated in the physical space. In terms of time, we use the Crank-Nicolson scheme, and the time step is δ. All data are generated on a grid with 256 × 256 resolution. The model is trained for 200 timesteps within the [0, 2] period, and we extrapolate over [2,4], where . The entire training time process lasts 12.5 h.
The vorticity and velocity field predicted by the Fourier filter-based PhyCRNet and the ground-truth are illustrated in Figures 6, 7, respectively. The figures clearly show that the velocity and vorticity fields agree with the ground truth during the training phase. According to the error distribution, the error is minimal and, on many occasions, close to zero. In the extrapolation stage, although the error is increased compared to the training phase, the evolution of the vorticity and velocity fields can still be predicted accurately by the trained model of Fourier filter-based PhyCRNet. This reveals that Fourier filter-based PhyCRNet affords appealing stability.
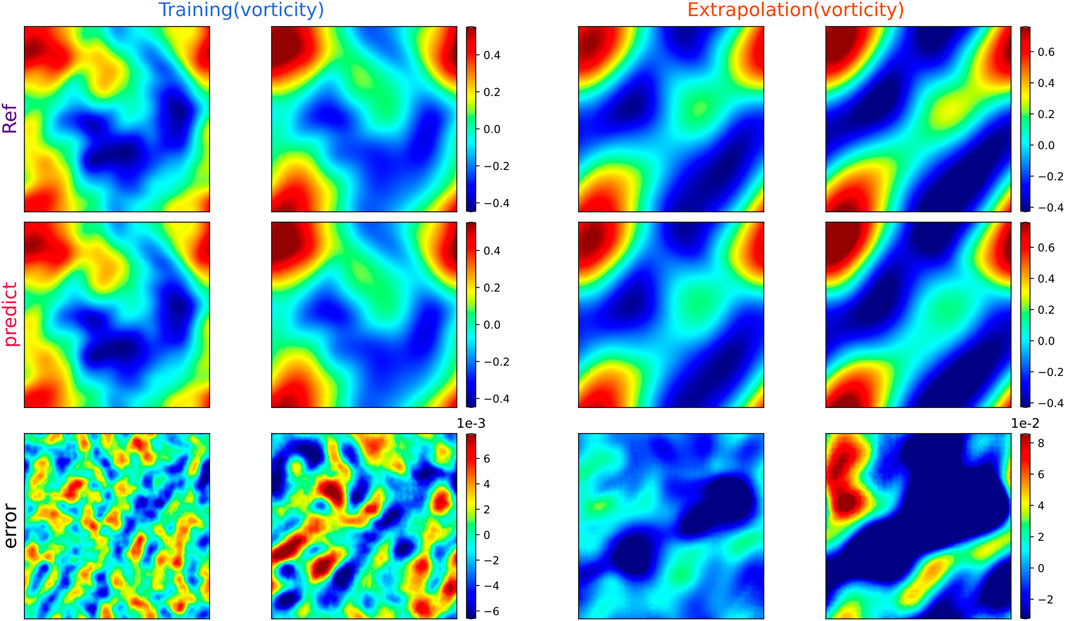
FIGURE 6
The vorticity field results of Fourier filter-based PhyCRNet solving the 2D N_S equation. Four representative snapshots are selected as comparisons, namely training (t = 0.5, 1.5 s) and extrapolation (t = 2.5, 3.5 s), and compared the errors over the entire interval. From top to bottom are reference solutions, predictions and errors.
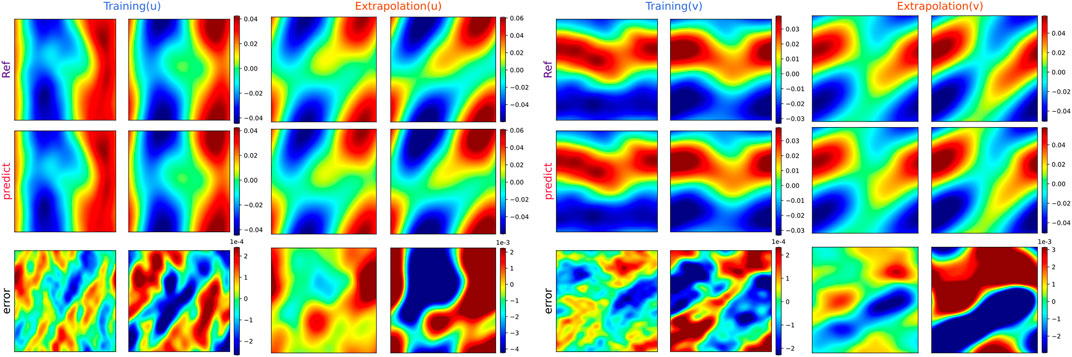
FIGURE 7
The velocity field results of Fourier filter-based PhyCRNet solving the 2D N_S equation. Four representative time instants are selected as comparisons, namely training (t = 0.5, 1.5 s) and extrapolation (t = 2.5, 3.5 s), and compare the errors of the whole interval one by one. From top to bottom are reference solutions, predictions and errors.
3.7 Errors comparison
The error propagation maps of 2D viscous Burger’s equations and FitzHugh–Nagumo RD equations are shown in Figures 8A,B, respectively. The performance of the proposed methods is different in the two experiments. There may be caused by the Fourier filter performs smooth filtering when calculating spatial derivatives and the setting of hyperparameters which is not the optimal setting of Fourier filter based PhyCRNet for solving 2D viscous Burger’s equations. Overall, the errors of both models are on the same level, which indicates that Fourier filter-based PhyCRNet has the same capability to solve the basic PDEs as PhyCRNet.
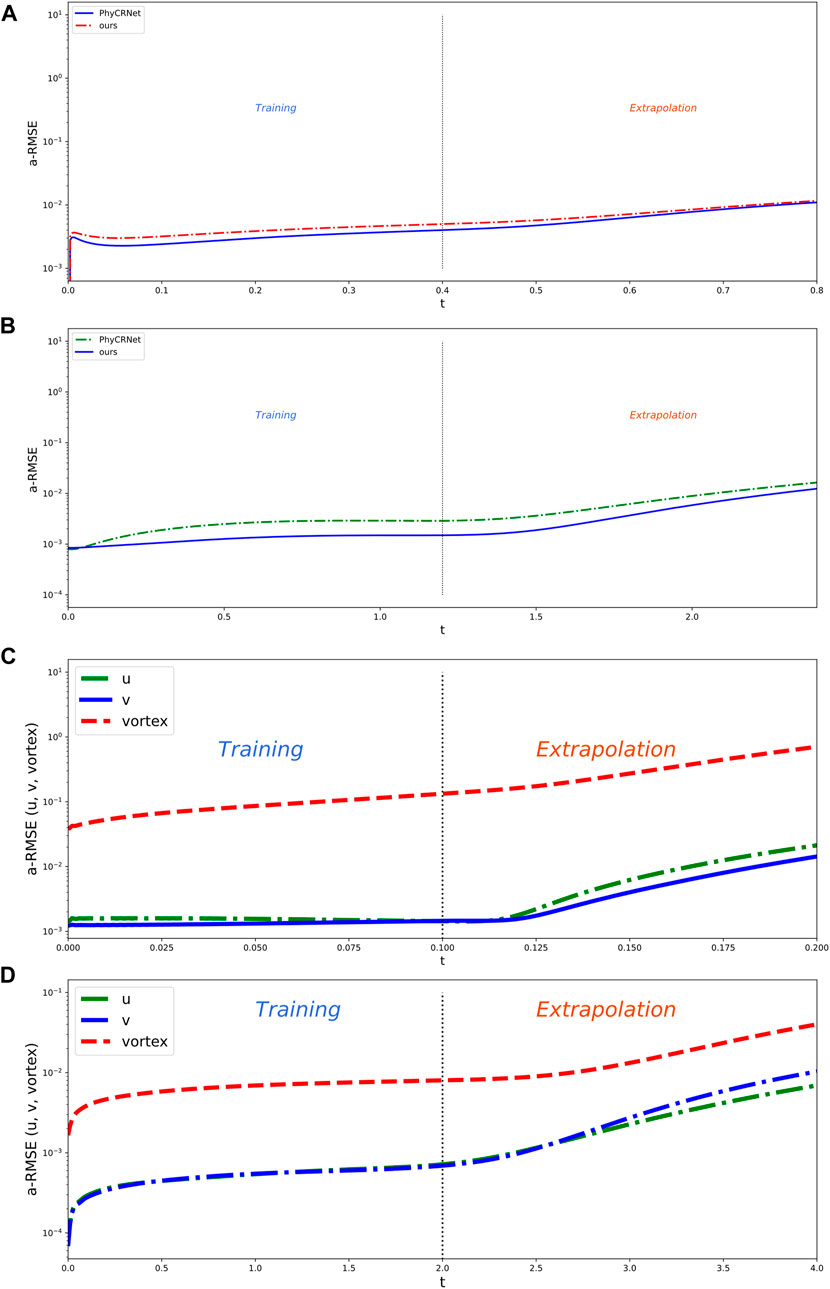
FIGURE 8
The a-RMSE of the four Equations. (A) 2D viscous Burger’s equations; (B) FitzHugh–Nagumo RD equations; (C) Vorticity equation; (D) 2D Navier-Stokes equation.
In Figure 8C, we observe that the errors of vorticity and velocity are very small during the training phase, and the errors gradually increase as the extrapolation time increases. Since both values are not in the same order of magnitude, the a-RMSE of the vorticity is significantly larger than the velocity field, below 0.7 and 0.02, respectively. As shown in Figure 8D, the a-RMSE of vorticity and velocity during the training and extrapolation phases is below 0.04 and 0.01, respectively. This further verifies the effectiveness of the Fourier filter-based PhyCRNet in solving 2D N-S equations.
3.8 Convergence study
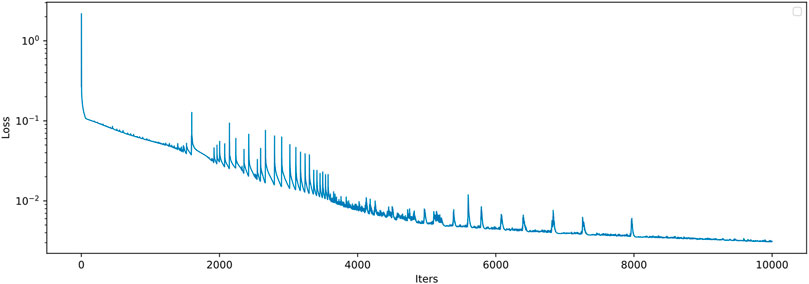
It is significant to conduct the convergence study of the Fourier filter-based PhyCRNet. Fourier method is widely used to solve PDEs, and its convergence has been verified in previous studies (Hald, 1981; Tadmor, 1989; Bardos and Tadmor, 2015). Besides, the convergence of PhyCRNet has been verified. The Fourier filter that replaces the finite difference filter has a higher solution accuracy, so the calculation of the loss function is more accurate. The loss function is used to evaluate the error between the predicted value of the network and the target value. The trained network reaches convergence by back-propagation algorithm [50–52]. According to Eqs 7, 8, the loss function with physical constraints is trained to converge to an acceptable error range, which guarantees the convergence of the network. Therefore, we focus on the loss history of the neural network. Since the loss histories of the four experiments are similar at training phases, we choose the 2D Navier-Stokes equation as the representative example to show the convergence history of the proposed method in Figure 9. It is obvious that as the number of iterations increases, the loss value decreases. However, the convergence trend gradually becomes stable with the iteration. More precisely, the network training has reached a reasonable convergence range after training.
FIGURE 9
The convergence history of Fourier filter-based PhyCRNet.
4 Discussion
As a widely used fluid model, incompressible flow has many variants for different scenarios and there are many traditional numerical methods [
53–
58]. The development of deep learning in recent years has also made rapid progress in the exploration and solution of incompressible flow models [
59–
61]. This paper develops the Fourier filter-based PhyCRNet to solve PDEs. Through four numerical experiments, we verify the capability of our proposed method in the solution of general PDEs and equations describing 2D incompressible flows, respectively. By comparing the predicted values of the Fourier filter-based PhyCRNet with the reference solution, it shows that the proposed network inherits the advantages of PhyCRNet, that is, the ability of extrapolate and encode physical constraints into loss function, and has the following strengths:
1. The calculation of the inverse Laplace operator. It introduces the Fourier filter to calculate the inverse Laplace operator, which the finite-difference filter cannot achieve. In the 2D incompressible flows, the solution is to iterate forward on the vorticity field and update the velocity field after the Laplace inverse operation. The Fourier filter-based PhyCRNet can efficiently solve 2D incompressible flows with the inverse Laplace operator.
2. The accuracy of partial derivatives. It adopts a discrete Fourier transform to calculate partial derivatives improving the solution accuracy. Here we only consider numerical experiments in the periodic domain, but after processing the output with methods such as periodic extension [62,63], the Fourier filter can extend the proposed method to the aperiodic domain.
3. The computational efficient of network. Because of Fourier method, the calculation of the inverse Laplace operator and partial derivatives is very efficient. Due to the small amount of experimental computation and the computational cost of the time series module dominates the entire training process, there is no noticeable performance in the solution of the 2D viscous equation and FitzHugh–Nagumo RD equations.
4. The proposed network exploits the powerful fitting capabilities of deep learning, while avoiding the dependence of the quality of training data. When carrying out network constraints, the fusion of physics-informed adopts the classical numerical method, so the prediction accuracy after training cannot be better than that of the traditional numerical method. Overall, the proposed method provides a reference deep learning method for scientific computing.
5 Conclusion
In this paper, a Fourier filter-based PhyCRNet is proposed by replacing the finite-difference filter with the Fourier filter to improve the accuracy of derivatives and overcome the difficulty of solving the inverse Laplacian operator. The proposed method integrates the physics-informed into the loss function by traditional numerical method to enhance the interpretability and improve the convergence rate. Numerical results demonstrate that the Fourier filter based PhyCRNet not only has the ability to solve general partial differential equations with PhyCRNet, but also is very effective, accurate and easy to implement for 2D incompressible flow. Certainly, the method proposed is not to replace the classical numerical method, but as an emerging field of deep learning to solve partial differential equations, it can bring a new method to scientific computing.
In the future, the proposed network can extend to the solution of problem with irregular regions and various boundary conditions. Furthermore, the graph neural network can be used to replace the convolutional network to extract spatial features more effectively.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
CX, XZ, FY, XC, KP, and JN contributed to the writing of the manuscript and to the interpretation of results. CX: Conceptualization, Writing-Original draft preparation. CX and FY: Software, Validation. XZ, XC, KP, and JN: Writing-Reviewing and Editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
RenardyMRogersRC. An introduction to partial differential equations. Berlin, Germany: Springer Science & Business Media (2006).
2.
PetrovskyIG. Lectures on partial differential equations. Chelmsford, MA, USA: Courier Corporation (2012).
3.
MüllerEHScheichlR. Massively parallel solvers for elliptic partial differential equations in numerical weather and climate prediction. Q J R Meteorol Soc (2014) 140(685):2608–24. 10.1002/qj.2327
4.
NielsenASBrunnerGHesthavenJS. Communication-aware adaptive parareal with application to a nonlinear hyperbolic system of partial differential equations. J Comput Phys (2018) 371:483–505. 10.1016/j.jcp.2018.04.056
5.
RabczukTRenHZhuangX. A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem. Comput Mater Continua (2019) 59:31–55. 10.32604/cmc.2019.04567
6.
HughesTJ. The finite element method: Linear static and dynamic finite element analysis. Chelmsford, MA, USA: Courier Corporation (2012).
7.
HornikKStinchcombeMWhiteH. Multilayer feedforward networks are universal approximators. Neural networks (1989) 2(5):359–66. 10.1016/0893-6080(89)90020-8
8.
RudySHBruntonSLProctorJLKutzJN. Data-driven discovery of partial differential equations. Sci Adv (2017) 3(4):e1602614. 10.1126/sciadv.1602614
9.
LongZLuYMaXDongB. Pde-net: Learning pdes from data. In: International Conference on Machine Learning: PMLR (2018). p. 3208–16.
10.
ZhuYZabarasN. Bayesian deep convolutional encoder–decoder networks for surrogate modeling and uncertainty quantification. J Comput Phys (2018) 366:415–47. 10.1016/j.jcp.2018.04.018
11.
LuLJinPKarniadakisGE. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators (2019). arXiv preprint arXiv:1910.03193.
12.
BruntonSLNoackBRKoumoutsakosP. Machine learning for fluid mechanics. Annu Rev Fluid Mech (2020) 52:477–508. 10.1146/annurev-fluid-010719-060214
13.
GuoYCaoXLiuBGaoM. Solving partial differential equations using deep learning and physical constraints. Appl Sci (2020) 10(17):5917. 10.3390/app10175917
14.
RaissiMYazdaniAKarniadakisGE. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science (2020) 367(6481):1026–30. 10.1126/science.aaw4741
15.
LuLMengXMaoZKarniadakisGE. DeepXDE: A deep learning library for solving differential equations. SIAM Rev Soc Ind Appl Math (2021) 63(1):208–28. 10.1137/19m1274067
16.
RaissiMPerdikarisPKarniadakisGE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys (2019) 378:686–707. 10.1016/j.jcp.2018.10.045
17.
MengXLiZZhangDKarniadakisGE. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput Methods Appl Mech Eng (2020) 370:113250. 10.1016/j.cma.2020.113250
18.
WightCLZhaoJ. Solving allen-Cahn and Cahn-Hilliard equations using the adaptive physics informed neural networks (2020). arXiv preprint arXiv:2007.04542.
19.
BaiYChaoluTBiligeS. Solving Huxley equation using an improved PINN method. Nonlinear Dyn (2021) 105(4):3439–50. 10.1007/s11071-021-06819-z
20.
HaghighatERaissiMMoureAGomezHJuanesR. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput Methods Appl Mech Eng (2021) 379:113741. 10.1016/j.cma.2021.113741
21.
YangLMengXKarniadakisGE. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J Comput Phys (2021) 425:109913. 10.1016/j.jcp.2020.109913
22.
LuLJinPPangGZhangZKarniadakisGE. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell (2021) 3(3):218–29. 10.1038/s42256-021-00302-5
23.
LiZKovachkiNAzizzadenesheliKLiuBBhattacharyaKStuartAet alFourier neural operator for parametric partial differential equations (2020). arXiv preprint arXiv:2010.08895.
24.
LiZZhengHKovachkiNJinDChenHLiuBet alPhysics-informed neural operator for learning partial differential equations (2021). arXiv preprint arXiv:2111.03794.
25.
WangSWangHPerdikarisP. Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Sci Adv (2021) 7(40):eabi8605. 10.1126/sciadv.abi8605
26.
ZhuYZabarasNKoutsourelakisP-SPerdikarisP. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J Comput Phys (2019) 394:56–81. 10.1016/j.jcp.2019.05.024
27.
RaoCSunHLiuY. Physics-informed deep learning for computational elastodynamics without labeled data. J Eng Mech (2021) 147(8):04021043. 10.1061/(asce)em.1943-7889.0001947
28.
GenevaNZabarasN. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. J Comput Phys (2020) 403:109056. 10.1016/j.jcp.2019.109056
29.
HuYZhaoTXuSXuZLinL. Neural-PDE: A rnn based neural network for solving time dependent PDEs (2020). arXiv preprint arXiv:2009.03892.
30.
RenPRaoCLiuYWangJXSunH. PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs. Comput Methods Appl Mech Eng (2022) 389:114399. 10.1016/j.cma.2021.114399
31.
ZhongWJianingZZhongXX. On a new time integration method for solving time dependent partial differential equations. Comput Methods Appl Mech Eng (1996) 130(1-2):163–78. 10.1016/0045-7825(95)00876-4
32.
El-AjouAArqubOAMomaniSBaleanuDAlsaediA. A novel expansion iterative method for solving linear partial differential equations of fractional order. Appl Maths Comput (2015) 257:119–33. 10.1016/j.amc.2014.12.121
33.
ArqubOAHayatTAlhodalyM. Analysis of lie symmetry, explicit series solutions, and conservation laws for the nonlinear time-fractional phi-four equation in two-dimensional space. Int J Appl Comput Math (2022) 8(3):145–17. 10.1007/s40819-022-01334-0
34.
AlbawiSMohammedTAAl-ZawiS. Understanding of a convolutional neural network. In: 2017 international conference on engineering and technology (ICET). Antalya, Turkey: IEEE (2017). p. 1–6.
35.
ShiXChenZWangHYeungDYWongWKWooWC. Convolutional lstm network: A machine learning approach for precipitation nowcasting. Adv Neural Inf Process Syst (2015) 28.
36.
MerileesPE. The pseudospectral approximation applied to the shallow water equations on a sphere. Atmosphere (1973) 11(1):13–20. 10.1080/00046973.1973.9648342
37.
KuHCHirshRSTaylorTD. A pseudospectral method for solution of the three-dimensional incompressible Navier-Stokes equations. J Comput Phys (1987) 70(2):439–62. 10.1016/0021-9991(87)90190-2
38.
KuHCTaylorTDHirshRS. Pseudospectral methods for solution of the incompressible Navier-Stokes equations. Comput Fluids (1987) 15(2):195–214. 10.1016/s0045-7930(87)80004-x
39.
FornbergB. A practical guide to pseudospectral methods. Cambridge: Cambridge University Press (1998).
40.
BracewellRNBracewellRN. The Fourier transform and its applications. New York: McGraw-Hill (1986).
41.
GourlayA. Some recent methods for the numerical solution of time-dependent partial differential equations. Proc R Soc Lond A. Math Phys Sci (1971) 323(1553):219–35.
42.
KreissHOOrtizOE. Introduction to numerical methods for time dependent differential equations. Hoboken, NJ, USA: John Wiley & Sons (2014).
43.
CooleyJWLewisPAWelchPD. The fast Fourier transform and its applications. IEEE Trans Ed (1969) 12(1):27–34. 10.1109/te.1969.4320436
44.
ParksT. DFT/FFT and convolution algorithms. New York: John Wiley fc Sons (1985).
45.
BlahutRE. Fast algorithms for signal processing. Cambridge: Cambridge University Press (2010).
46.
MatykaM. Solution to two-dimensional incompressible Navier-Stokes equations with simple, simpler and vorticity-stream function approaches. driven-lid cavity problem: Solution and visualization (2004). arXiv preprint physics/0407002.
47.
FukaV. Poisfft–a free parallel fast Poisson solver. Appl Maths Comput (2015) 267:356–64. 10.1016/j.amc.2015.03.011
48.
PaszkeAGrossSChintalaSChananGYangEDeVitoZet alAutomatic differentiation in pytorch (2017).
49.
DaK. A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.
50.
RumelhartDEHintonGEWilliamsRJ. Learning internal representations by error propagation. California, USA: California Univ San Diego La Jolla Inst for Cognitive Science (1985).
51.
LeCunYToureskyDHintonGSejnowskiT. A theoretical framework for back-propagation. In: Proceedings of the 1988 connectionist models summer school (1988). p. 21–8.
52.
GohAT. Back-propagation neural networks for modeling complex systems. Artif intelligence Eng (1995) 9(3):143–51. 10.1016/0954-1810(94)00011-s
53.
SolonnikovV. Solvability of the initial-boundary-value problem for the equations of motion of a viscous compressible fluid. J Math Sci (1980) 14(2):1120–33. 10.1007/bf01562053
54.
GigaY. Solutions for semilinear parabolic equations in Lp and regularity of weak solutions of the Navier-Stokes system. J differential equations (1986) 62(2):186–212. 10.1016/0022-0396(86)90096-3
55.
PedloskyJ. Geophysical fluid dynamics. Berlin, Germany: Springer (1987).
56.
LionsP. Mathematical topics in fluid mechanics. Incompressible models, vol. 1. Oxford: Clarendon (1996).
57.
DanchinR. Local and global well-posedness results for flows of inhomogeneous viscous fluids. Adv differential equations (2004) 9(3-4):353–86.
58.
ZhangP. Global smooth solutions to the 2-D nonhomogeneous Navier–Stokes equations. Int Maths Res Notices (2008). 10.1093/imrn/rnn098
59.
JinXCaiSLiHKarniadakisGE. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J Comput Phys (2021) 426:109951. 10.1016/j.jcp.2020.109951
60.
EbrahimijahanADehghanMAbbaszadehM. Simulation of the incompressible Navier–Stokes via integrated radial basis function based on finite difference scheme. Eng Comput (2022) 2022:1–22. 10.1007/s00366-021-01543-z
61.
KashefiAMukerjiT. Physics-informed PointNet: A deep learning solver for steady-state incompressible flows and thermal fields on multiple sets of irregular geometries (2022). arXiv preprint arXiv:2202.05476.
62.
EckhoffKS. Accurate reconstructions of functions of finite regularity from truncated Fourier series expansions. Math Comput (1995) 64(210):671–90. 10.1090/s0025-5718-1995-1265014-7
63.
HuybrechsD. On the Fourier extension of nonperiodic functions. SIAM J Numer Anal (2010) 47(6):4326–55. 10.1137/090752456
Summary
Keywords
fourier filter, convolutional recurrent network, 2D incompressible flow, inverse laplacian operator, physics-informed
Citation
Xiao C, Zhu X, Yin F, Cao X, Peng K and Nie J (2022) Fourier filter-based physics- information convolutional recurrent network for 2D incompressible flow. Front. Phys. 10:971722. doi: 10.3389/fphy.2022.971722
Received
17 June 2022
Accepted
01 September 2022
Published
30 September 2022
Volume
10 - 2022
Edited by
André H. Erhardt, Weierstrass Institute for Applied Analysis and Stochastics (LG), Germany
Reviewed by
Omar Abu Arqub, Al-Balqa Applied University, Jordan
Harsha Vaddireddy, Oklahoma State University Stillwater, United States, in collaboration with reviewer SP
Updates
Copyright
© 2022 Xiao, Zhu, Yin, Cao, Peng and Nie.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fukang Yin, yinfukang@nudt.edu.cn
This article was submitted to Statistical and Computational Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.