Entanglement entropy of the quantum Hall edge and its geometric contribution

Generally speaking, entanglement entropy (EE) between two subregions of a gapped quantum many-body state is proportional to the area/length of their interface due to the short-range quantum correlation. However, the so-called area law is violated logarithmically in a quantum critical phase. Moreover, the subleading correction exists in long-range entangled topological phases. It is referred to as topological EE which is related to the quantum dimension of the collective excitation in the bulk. Furthermore, if a non-smooth sharp angle is in the presence of the subsystem boundary, a universal angle dependent geometric contribution is expected to appear in the subleading correction. In this work, we simultaneously explore the geometric and edge contributions in the integer quantum Hall (IQH) state and its edge reconstruction in a unified bipartite method. Their scaling is found to be consistent with conformal field theory (CFT) predictions and recent results of particle number fluctuation calculations.

1 Introduction

Quantum entanglement is a fundamental and important tool to probe the properties of a variety of physical systems such as black holes in astrophysics, quantum phase transition in condensed matter physics, and photosynthesis in biophysics [1]. In a bipartite system, one usually calculates the von Neumann entropy or the α-Rényi entropy to quantitatively describe the magnitude of the entanglement between two subsystems. Once the system size is smaller than the correlation length, the entropy is proportional to the volume of the system. For a gapped state, it is generally proportional to the area/length of the interface between two subsystems. This is referred to as the area law in a three-dimensional or perimeter law in a two-dimensional system. Heuristically, this could be understood from the fact that an energy gap gives rise to a finite correlation length which defines the scale on which particles inside the subsystem are correlated with the environment. In gapless critical systems, such as quantum Hall edges or critical spin systems which could be described by the conformal field theory (CFT), it is known that the EE has a logarithmic dependence on the boundary length, and the prefactor is related to the central charge of its underlying CFT [2–5].

After the discovery of topological quantum systems, such as the fractional quantum Hall effects [6, 7], it is known that there is an extra correction of the bulk EE which depends on the quantum dimension of the collective excitation in the bulk. It is referred to as the topological EE γ [8, 9], an important quantity to characterize the nontrivial topology of the long-range entangled quantum many-body states. Moreover, Li and Haldane [10] found that the eigenvalue spectra of the reduced density matrix, named the entanglement spectrum, provides more information about the topology since it could be treated as virtual edge excitation spectra at the bipartite boundary. The mechanism of the bulk-edge correspondence [11, 12] could tell us many of the bulk properties. On the other hand, the quantum Hall edge excitation is usually a chiral gapless mode which could be described by (1 + 1)d chiral CFT. Once the cutting line is along the realistic quantum Hall edge with length l_A, a logarithmic type of α-Rényi EE $S_{\text{edge}}\simeq \frac{c+\bar{c}}{12}(1+\frac{1}{\alpha })\log l_A$ [13] with central charge c is expected. For the chiral edge mode, the anti-holomorphic part is $\bar{c}=0$ and thus $S_{\text{edge}}\simeq \frac{c}{12}(1+\frac{1}{\alpha })\log l_A$.

Up to now, the behavior of the EE mentioned previously is under the assumption that the bi-partition has a smooth boundary, such as a circle or an infinite straight line. Once the boundary has a sharp corner, regardless of whether the system is gapped or not, it was found that the corner on the boundary has an important contribution in the EE which was previously explored [14–27] in two-dimensional quantum critical systems and CFT. Recently, it was extended to the gapped topological system such as the integer quantum Hall states [13, 28, 29]. The corner angle dependence of the EE is found to be universal [30]. Therefore, the complete formula of the EE is

$S=aA+b\partial A+\gamma +S_{\mathit{edge}}+S\left(\theta \right)+\mathcal{O}\left(1/L\right),(1)$

in which we include the volume, area, topological, edge, and corner contributions in the first five terms.

In this work, as an example of unification, we consider the quantum Hall state in disk geometry with an open boundary. The fan-shaped bipartite EE with different radius simultaneously gives the contributions from the area law, critical edge mode, and the non-smooth corner. For the integer quantum Hall state, we observed that the corner contribution has similar behavior to the charge cumulation at the cone tip if we put the electrons in a cone-shaped geometry. Moreover, the logarithmic behavior and the central charge are obtained, and the results are immune from the edge reconstruction which conserves the chirality. The robust behavior of the geometric entanglement at the corner could be an explanation of the recent observation that a universal the angle dependence of the particle number fluctuations in a non-smooth bi-partition.

The rest of the article is organized as follows. In Section 2, we revisit the correlation matrix and EE with real space cut in disk geometry. The exact prefactor of the area law is found for α − Rényi entropy with α = 1, 2, 3. In Section 3, the corner contribution is obtained after subtracting the law part by a fan-shaped cut in the bulk. A cone-shaped quantum Hall state reveals the charge cumulation at the cone tip which has similarity to the EE. In Section 4, we consider the fan-shaped bi-partition including the quantum Hall edge. The logarithmic edge contribution could be obtained after subtracting both the area law and corner contribution. The central charge is found robust to any edge reconstructed pattern. Section 5 gives the conclusions and discussions.

2 Entanglement entropy and area law

For a two-dimensional electron gas in a strong perpendicular magnetic field, the typical length scale is the magnetic length $l_B=\sqrt{\hslash /eB}$ which we set to one in the following. The single electron wave function in the symmetric gauge is

$\begin{array}{ccc}\hfill {\varphi }_{n,m}& =\hfill & c_{n,m}^{†}|0\rangle \hfill \\ \hfill & =\hfill & {\left(-1\right)}^n\sqrt{\frac{n!}{2\pi 2^m\left(m+n\right)!}}{L}_n^m\left(\frac{|\mathbf{z}{|}^2}{2}\right){\mathbf{z}}^m{e}^{-|\mathbf{z}{|}^2/4},\hfill \end{array}(2)$

where n, m are the Landau level and the angular momentum index, respectively. In the lowest Landau level with n = 0, the mth orbit is a Gaussian wave package in the radial direction which has the most probable radius at $r_m=\sqrt{2m}$. For a bipartite system, von Neumann entropy is defined as S₁ (ρ_A) = −Trρ_A ln ρ_A once we have the reduced density matrix ρ_A for the subsystem. More generally, the α-Rényi entropies [29] are defined as $S_{\alpha }({\rho }_A)=\frac{1}{1-\alpha }\ln (\text{Tr}{\rho }_A^{\alpha })$ which reduce to the von Neumann entropy in the limit α → 1. Their scaling behaviors with increasing the size of the subsystem A have yielded plentiful interesting results for both gapped and critical systems. Generally, the universality of the entanglement appears when the system length scale, such as the boundary length, is much larger than l_B. Therefore, one usually allows a strong finite size effect for small system sizes. For a many-body system, diagonalizing the ρ_A is usually limited to small systems because of the exponential explosion of its dimension as increasing the system size. Fortunately, for a non-interacting fermionic system which has Slater determinants as its eigenstates, it is known [4, 31] that this could be simplified to calculate the eigenvalues of the single particle correlation matrix $C_{ij}=\text{Tr}({\rho }_A{c}_i^{†}{c}_j),$ where c_i is the single particle operator. Its dimension is the number of orbitals which linearly grow as the system size increases. Furthermore, the correlation matrix is naturally diagonal in case the bipartite cutting conserves the symmetry of its parent wave function, i.e., the circular cutting on a disc or latitude cut on a sphere. In this case, the two types of entropy are defined by its diagonal terms, or its eigenvalues {λ_m} as follows:

$S_1=\sum _m\left[-{\lambda }_m\log {\lambda }_m-\left(1-{\lambda }_m\right)\log \left(1-{\lambda }_m\right)\right],(3)$

$S_{\alpha }=\frac{1}{1-\alpha }\sum _m\log \left[{\lambda }_m^{\alpha }+{\left(1-{\lambda }_m\right)}^{\alpha }\right].(4)$

For a circular bipartite finite disk as shown in Figure 1A, the electron operator for the mth orbital in the lowest Landau level (n = 0), which could be written as [32–34]

$c_m={\alpha }_m{A}_m+{\beta }_m{B}_m,(5)$

where A_m and B_m are the electron operators in subsystem A and its environment B, respectively. ${\alpha }_m^2$ and ${\beta }_m^2$ are the probabilities in the two subsystems. For a circular cut with radius R_A, they are

${\alpha }_m^2={\int }_0^{R_A}{\int }_0^{2\pi }|{\varphi }_{0,m}\left(r,\theta \right){|}^2{d}^{2}r=1-\frac{\mathrm{\Gamma }\left(1+m,\frac{R_A^2}{2}\right)}{\mathrm{\Gamma }\left(1+m\right)}(6)$

and ${\beta }_m^2=1-{\alpha }_m^2$. For the ν = 1 IQH state which does not have topological term γ, if R_A is much smaller than that of the whole disk, namely, the cut edge is far away from the physical edge at $R=\sqrt{2N_e}$, the EE contains only the area law term in Eq. 1 as $S_{\alpha }=b_{\alpha }{l}_A+\mathcal{O}(1/l_A),$ where l_A = 2πR_A is the perimeter of the boundary. In Figure 1B, we plot the b_α = S_α/l_A as increasing the R_A for a system with N_e = 171 electrons. The prefactor b_α, shown as constant values in a large range for R_A > 1 and $R_A<\sqrt{2N_{\mathit{orb}}}\simeq 18.5$, demonstrates a perfect linear behavior of S_α for a smooth cut in the bulk. The prefactor for S₁ is b₁ ≃ 0.203, which is exactly the same as that from a similar study in cylinder geometry where an analytical formula was given as $b_1=\int \frac{d\mu }{2\pi }H[\frac{1}{2}\text{Erfc}(\mu )]\simeq 0.20329081$ in which the integral function is H(x) = −x log(x) − (1 − x) log (1 − x) [35]. We found that the prefactors of the S₂ and S₃ are b₂ = 0.158 and b₃ = 0.142, respectively. Their analytical results could also be obtained by the corresponding integrate function $H_{\alpha }(x)=\frac{1}{1-\alpha }\log (x^{\alpha }+{(1-x)}^{\alpha }),$ which gives b₂ = 0.15843 and b₃ = 0.14213. Moreover, the S_α=2,3/l_A saturates faster than S₁/l_A at small R_A, means the α-Rényi entropy suffers weaker finite size effects than the von Neumann entropy. As a conclusion in this section, we demonstrate that the area law prefactor b_α for IQH is the same for different geometries and could be calculated analytically. This will be applied in the following to subtract the area law term in the non-smooth cut.

FIGURE 1

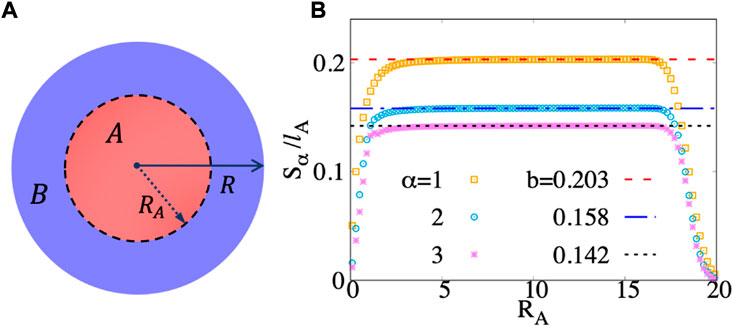
FIGURE 1. (A) Smooth circular cut with radius R_A in a finite disk. (B) Prefactor of the area law for α-Rényi entropies. The well-developed plateau appears when R_A is larger than 1.0l_B and smaller than the radius of the system.

3 Corner contribution

In this section, we consider a non-smooth partition as shown in Figure 2. The subsystem A is a fan-shaped region with a corner angle θ at the center of the disk. Supposing the arc-shaped boundary is far away from the physical edge of the disk, then the EE is still in the area law region. The non-smooth cutting gives one corner of θ-degree at the center and two corners of $\frac{\pi }{2}$-angle at the intersections with the arc. Therefore, the EE in this case is

$S_{\alpha }=b_{\alpha }{l}_A+S_{\alpha }\left(\theta \right)+2S_{\alpha }\left(\frac{\pi }{2}\right)+\mathcal{O}\left(1/l_A\right)(7)$

with the boundary length l_A = 2R_A + θR_A. In order to screen out the pure angle contribution S_α(θ), we subtract the value at θ = π with the same R_A. In this case, we have S_α(π) = 0 and l_A = 2R_A + πR_A. Therefore, the residual entropy is ΔS_α = b_α(θ − π)R_A + S_α(θ) in which the first term could be exactly obtained from the previous section supposing the area law and corner contributions are independent of each other.

FIGURE 2

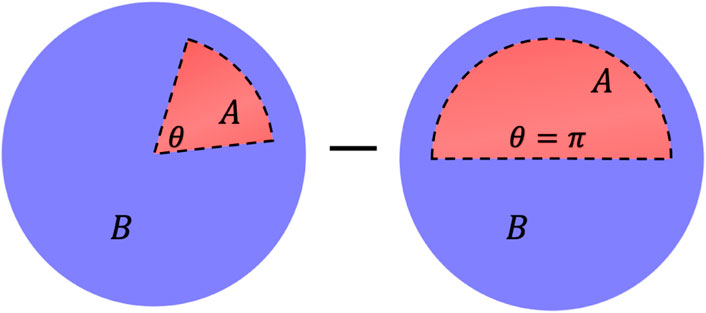
FIGURE 2. The non-smooth cutting schematic diagram of a bipartite finite disk and the subtraction rule is applied to extract pure angle contribution.

In Figure 3, we plot the S_α(θ) = ΔS_α − b_α(θ − π)R_A as a function of the angle θ. A recent work in Ref. 13 discussed a similar bipartition by calculating the Rényi entropy via the cumulants of the particle number in subsystem S_α = ∑_ms_α(m)κ_2m, where κ_m are the even cumulants of the particle number distribution in region A. In particular, κ = κ₂ is the variance of the number of particles in region A which was obtained analytically for the IQH case, namely, $\kappa (\theta )=\frac{\sqrt{N_e}}{{\pi }^{3/2}}+\frac{1}{2{\pi }^2}\ln (\sqrt{N_e}\sin (\frac{\theta }{2}))-\frac{1+(\pi -\theta )\cot \theta }{4{\pi }^2}$. The third term is the corner contribution in the second cumulant. We assume the final S_α obeys the same θ-dependence although the prefactor could be non-analytical. We fit the S_α(θ) [36, 37] with the function S_α(θ) = u_α[1 + (π − θ) cot(θ)] and find that u₁ = −0.0861 (±0.0009), u₂ = −0.0613 (±0.0007) and u₃ = −0.0531 (±0.0006). In [28], the corner contribution was recently calculated in cylinder geometry. While θ → 0, it was found that the divergence of the S₁(θ) behaves as S₁(θ) = −0.0886 (±0.0004)/θ where the coefficient is consistent with our result of u₁ for the bulk corner. It is interesting to know that a refined fit formula was also proposed [29] which gives accuracy fits at both asymptotic limits, namely, $S_{\alpha }(\theta )\simeq {\beta }_1\frac{{(\pi -\theta )}^2}{\theta (2\pi -\theta )}-{\beta }_2[1+(\pi -\theta )\cot \theta ]$ which has an extra θ-dependent term. In our fitting process, the asymptotic behavior in the limit of θ → 0 gives S_α ≃ u_απ/θ. The coefficient u_απ ≃ 0.2705 is qualitatively consistent with the result of 0.276 in [29]. The accuracy in this work could be lower due to missing the correction term and possibly mixing different types of EE on a finite disk.

FIGURE 3

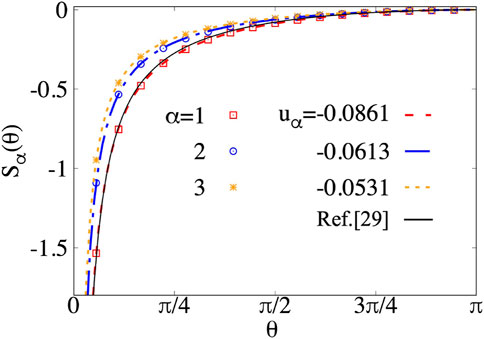
FIGURE 3. θ-Dependence of the corner contribution in Rényi entropy for 171 electrons. After fitting the data by S_α(θ) = u_α [1 + (π − θ) cot(θ)], we find that u₁ = −0.0861 (±0.0009), u₂ = −0.0613 (±0.0007) and u₃ = −0.0531 (±0.0006) which are consistent with the conjecture $S_{\alpha }(\theta )=(1+\frac{1}{\alpha })f(\theta )$.

To look more clearly into the corner contribution of the EE, we treat the correlation matrix as entanglement Hamiltonian. The eigenstate which has the most important contribution in the EE is the one that has an eigenvalue near 1/2. In Figure 4, we plot the single particle density for the state which has an eigenvalue with the smallest $|\lambda -\frac{1}{2}|$. It is interesting to see that for this state, the density mainly concentrates near the boundary of subsystem A, and the sharp corner has a higher density than the smooth edge. We compare two cases with θ = π/3 and θ = 2π/3. It is obvious that the acute angle corner has a much higher density than that of the obtuse angle corner. The behavior of the EE density accumulation at the sharp corner is qualitatively the same as the phenomena of the tip charge accumulation in electromagnetism.

FIGURE 4

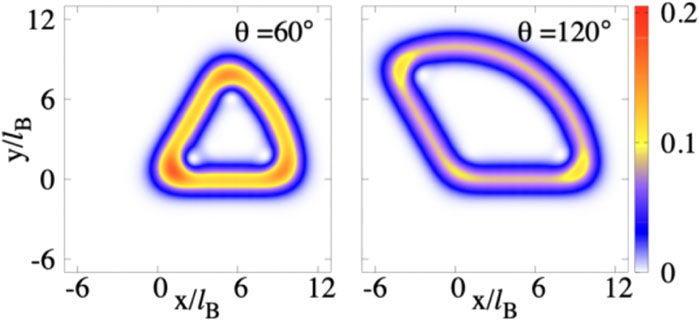
FIGURE 4. Single particle density for the state which has eigenvalue with the smallest $|\lambda -\frac{1}{2}|$. We choose R_A = 10l_B, which is in bulk of a finite disk (with the physical edge $R=\sqrt{342}{l}_B$). We compare two cases with θ = π/3 and θ = 2π/3 and use the same color bar in two cases.

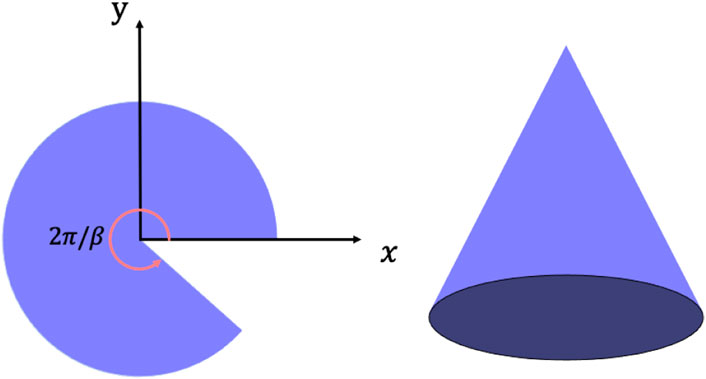
Now we consider a realistic system with a corner. We suppose that the particles live in a fan-shaped geometry and glue it to a cone as shown in Figure 5. The quantum Hall state on a cone has been realized experimentally in synthetic Landau levels for photons [38, 39]. In this case, the Landau wave functions [40–43] come to be

${\varphi }_{n,m}\left(\beta ,\mathbf{z}\right)={\mathcal{N}}_{n,m}{L}_n^{\beta m}\left(\frac{|\mathbf{z}{|}^2}{2}\right){\mathbf{z}}^{\beta m}{e}^{-|\mathbf{z}{|}^2/4},$

where ${\mathcal{N}}_{n,m}={(-1)}^n\sqrt{\frac{\beta n!}{2\pi 2^{\beta m}\mathrm{\Gamma }(\beta m+n+1)}}$. The angle of the system θ = 2π/β could be continuously tuned by varying the parameter β. In this geometry, the wave function of the IQH state is

$|\mathrm{\Psi }\rangle =\prod _{i<j}\left(z_i^{\beta }-z_j^{\beta }\right)\exp \left(-\sum _i|z_i{|}^2/4\right).(8)$

FIGURE 5

FIGURE 5. A cone can be obtained from fan-shaped geometry after gluing two edges together.

In Figure 6, we plot the radial density of the IQH state for different βs. β = 1 corresponds to the original disk geometry which has density $\rho (r)=\frac{1}{2\pi l_B^2}$ at the center. While increasing β or decreasing the θ-angle of the system, the density at the corner tip increases dramatically. From the inserted two-dimensional density profiles, it is obvious that the density at the corner tip cumulates gradually and finally separates from the bulk. The occupation number for each orbital is exactly n_m = 1 for ν = 1 IQH. It is easy to analytically calculate the density at the center ρ(0) = ∑_mn_m|ϕ_0,m (β, 0)|² which is shown in Figure 7. After subtracting the background density with ν = 1, the data are perfectly fitted by f(θ) = 2π/θ − 1 which is the same as that of the EE while θ → 0. Moreover, because of the Pauli exclusive principle of the fermions, the occupation number on each orbital is at most equal to one. Therefore, for other quantum Hall states, such as the fractional quantum Hall states which have ν < 1 at β = 1, the θ → 0 behavior should be universal once the particle number on the 0th orbital reaches one.

FIGURE 6

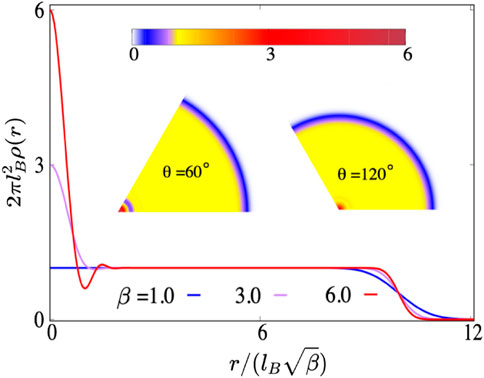
FIGURE 6. Radial density of the IQH state for 50 electrons with βs. β = 1 corresponds to the original disk geometry which has density $\rho (r)=\frac{1}{2\pi l_B^2}$ in the bulk. The two inserted plots are the 2D density profiles for different θs.

FIGURE 7

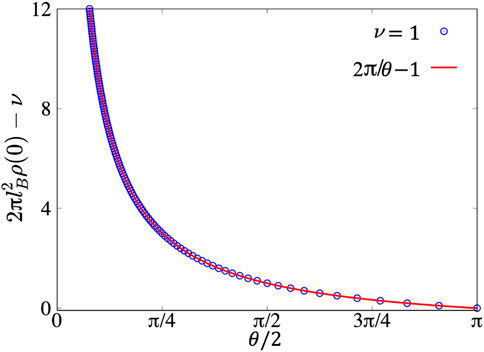
FIGURE 7. Accumulation of density at the tip for IQH state ρ(0). The data are perfectly fitted by f(θ) = 2π/θ − 1.

Therefore, we obtain the exact corner contribution of the EE via the fan-shaped bi-partition in the bulk. We found the 1/θ divergence of the corner contribution near θ → 0 which has similarity to the charge density cumulation at the tip once we put the system on a cone. The similarity between the EE and the local charge density or its fluctuation has been studied in several systems, either the classical or quantum many-body systems [30, 44].

4 Edge contribution and its universality

If we extend the region A in the radial direction to infinity, its arc-shape boundary is the physical edge of the system. As shown in Figure 8, now the EE between A and B contains the area law contribution from the radial boundary, a θ-angle contribution at the center, two $\frac{\pi }{2}$-angle contributions at the intersections, and the edge contribution on the boundary, namely,

$S_{\alpha }=b_{\alpha }{l}_A+S_{\alpha }\left(\theta \right)+2S_{\alpha }\left(\pi /2\right)+S_{\mathit{edge}}+\mathcal{O}\left(1/l_A\right).(9)$

FIGURE 8

FIGURE 8. The same cutting scheme as Figure 2 has the subsystem A containing the physical boundary. A similar subtraction rule is applied to extract the corner and edge contribution.

Similar to the previous section, after subtracting the EE at θ = π, the area law term and S_α(π/2) are eliminated. Now the residual EE contains the corner and edge contributions. ΔS = S_α(θ) + S_edge(θ) − S_edge(π). The CFT predicts [13, 45, 46] that the EE of the chiral edge is equal to $S_{\mathit{edge}}(\theta )=\frac{c}{12}(1+\frac{1}{\alpha })\ln [2R_A\sin (\theta /2)],$ where 2R_A sin (θ/2) is the chordal distance and the central charge c = 1. Therefore, we expect

$\mathrm{\Delta }{S}_{\alpha }=S_{\alpha }\left(\theta \right)+\frac{c}{12}\left(1+\frac{1}{\alpha }\right)\ln \sin \frac{\theta }{2},(10)$

which is independent of the R_A. Here, we suppose the previous results of the corner keep invariant as S(θ) = u_α[1 + (π − θ) cot θ] and fit the data of ΔS by function $p_{\alpha }\ln \sin \frac{\theta }{2}+q_{\alpha }[1+(\pi -\theta )\cot \theta ]$ with parameters q_α and p_α. The results are shown in Figure 9. The result q_α ≃ u_α is expected which shows again that the corner and edge terms are independent. The fitting results p₁ = 0.166, p₂ = 0.126, and p₃ = 0.113 are consistent with the formula $p_{\alpha }=\frac{1}{12}(1+\frac{1}{\alpha })$, and thus c = 1 is verified.

FIGURE 9

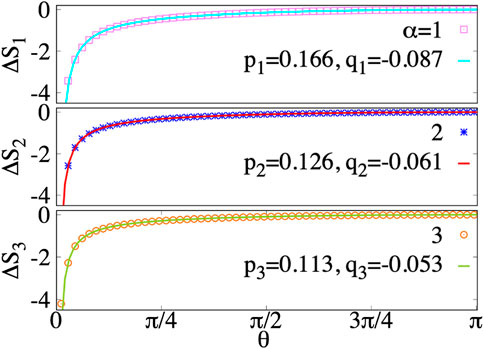
FIGURE 9. θ-Dependence of corner-edge contribution for Rényi entropy. The data are fitted by $p_{\alpha }\ln \sin \frac{\theta }{2}+q_{\alpha }[1+(\pi -\theta )\cot \theta ]$, and the results are p₁ = 0.166 (±0.006), q₁ = −0.087 (±0.001), p₂ = 0.126 (±0.001), q₂ = −0.061 (±0.0002), p₃ = 0.113 (±0.0007), and q₃ = −0.053 (±0.0001).

To see how robust the edge contribution of EE is, we consider the edge reconstruction [47–49] pattern as shown in Figure 10. The system contains two unconnected parts. One is the IQH state at the center with N₁ electrons, the other is the reconstructed part with N₃ electrons, and we assume that they form the same IQH state at ν = 1. In the middle, there are N₂ unoccupied orbitals. In this case, although there are three chiral edge modes, the inner edge of the reconstructed stripe has opposite chirality to that of the other two edges. Therefore, the total chirality is not affected by the edge reconstruction. We follow the same logic of subtracting the EE at θ = π as the unreconstructed case. We fix the total number of orbitals N = N₁ + N₂ + N₃ = 171 and consider several combinations of different {N_i}. The fitting parameters are shown in Table 1. Here we only show the results of S₁, and the results for other S_αs could be expected. It shows that the p₁ and q₁ are very robust and consistent with the previous unreconstructed results.

FIGURE 10

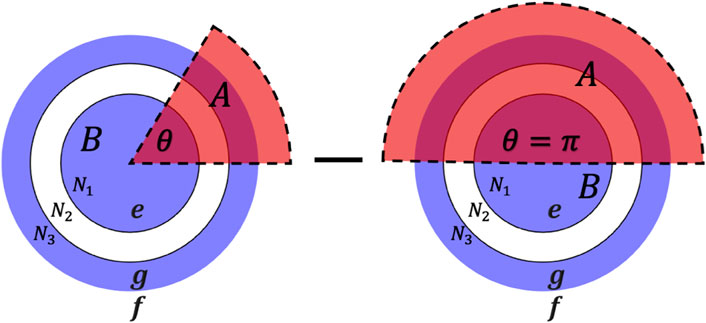
FIGURE 10. Non-smooth cutting schematic diagram of a disk that occurs in edge reconstruction. The system contains two unconnected parts containing N₁ electrons in bulk and N₃ electrons in the edge, respectively, and they are separated by N₂ orbits. There are three chiral edge modes, and the inner edge of the reconstructed stripe has opposite chirality to that of the other two edges. By the same subtraction rule, we extract pure angle contribution and edge contribution.

TABLE 1

TABLE 1. Corner and edge contribution for S₁ of a finite disk in an edge reconstructed pattern. We fix the total number of orbitals N = N₁ + N₂ + N₃ = 171 and consider several combinations of different {N_i}. It shows that the p₁ and q₁ are very robust and consistent with the previous unreconstructed results.

5 Discussions and conclusions

As a conclusion, in the IQH state on a finite disk, we used a simple unified bipartite method to explore the independent EE contributions from the area law, the sharp corner, and the gapless chiral edge contributions. The coefficients of the area law b_α are found to be universal and analytically solvable. With the exact area law term, we obtained the angle dependence of the corner contribution. It has a fixed prefactor, and the behaviors at θ → 0 are consistent with the tip charge accumulation of a realistic IQH liquid on a cone surface. It is similar to recent work of Ref. 30 in which the θ dependence of particle number fluctuations at the corner was found to be universal and has the same 1/θ behavior while θ → 0. While the fan-shaped subsystem contains the edge of the disk, the gapless chiral quantum Hall edge contributes a logarithmic type of EE in which the central charge c in its prefactor is as expected by its underlying CFT. Moreover, we found the edge reconstruction of the IQH does not change any of the prefactors due to the conservation of the chirality.

Here we should note that the correlation matrix method is only applicable to the non-interacting case, such as the IQH state. For the interacting case, namely, the fractional quantum Hall (FQH) states, the direct calculation of the reduced density matrix with breaking the rotational symmetry on a disk is complicated and limited to a small system size. However, as was expected from the charge fluctuation calculations, we believe that our bipartite method is also applicable, and the corner contribution in the FQH states still obeys the same universality, especially in the limit θ → 0 where the charge densities at the tip are the same. The FQH edge also contributes a logarithmic type of EE which has a prefactor with its corresponding central charge.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

DY and YY wrote the EE code and calculated the EE. QL contributed the analysis of IQH on the cone. Z-XH proposed the project and wrote the manuscript.

Funding

This work was supported by National Natural Science Foundation of China Grant No. 11974064, the Chongqing Research Program of Basic Research and Frontier Technology Grant No. cstc2021jcyjmsxmX0081, Chongqing Talents: Exceptional Young Talents Project No. cstc2021ycjh-bgzxm0147, and the Fundamental Research Funds for the Central Universities Grant No. 2020CDJQY-Z003. QL is supported by National Natural Science Foundation of China Grant No. 61988102.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Amico L, Fazio R, Osterloh A, Vedral V. Entanglement in many-body systems. Rev Mod Phys (2008) 80:517–76. doi:10.1103/revmodphys.80.517

CrossRef Full Text | Google Scholar

2. Wen XG. Theory of the edge states in fractional quantum Hall effects. Int J Mod Phys B (1992) 6:1711–62. doi:10.1142/s0217979292000840

CrossRef Full Text | Google Scholar

3. Holzhey C, Larsen F, Wilczek F. Geometric and renormalized entropy in conformal field theory. Nucl Phys B (1994) 424:443–67. doi:10.1016/0550-3213(94)90402-2

CrossRef Full Text | Google Scholar

4. Vidal G, Latorre JI, Rico E, Kitaev A. Entanglement in quantum critical phenomena. Phys Rev Lett (2003) 90:227902. doi:10.1103/physrevlett.90.227902

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Calabrese P, Cardy J. Entanglement entropy and quantum field theory. J Stat Mech : Theor Exp (2004) 0406:06002. doi:10.1088/1742-5468/2004/06/p06002

CrossRef Full Text | Google Scholar

6. Tsui DC, Störmer HL, Gossard AC. Two-dimensional magnetotransport in the extreme quantum limit. Phys Rev Lett (1982) 48:1559–62. doi:10.1103/physrevlett.48.1559

CrossRef Full Text | Google Scholar

7. Laughlin RB. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys Rev Lett (1983) 50:1395–8. doi:10.1103/physrevlett.50.1395

CrossRef Full Text | Google Scholar

8. Kitaev A, Preskill J. Topological entanglement entropy. Phys Rev Lett (2006) 96:110404. doi:10.1103/physrevlett.96.110404

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Levin M, Wen XG. Detecting topological order in a ground state wave function. Phys Rev Lett (2006) 96:110405. doi:10.1103/physrevlett.96.110405

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Li H, Haldane FDM. Entanglement spectrum as a generalization of entanglement entropy: Identification of topological order in non-abelian fractional quantum Hall effect states. Phys Rev Lett (2008) 101:010504. doi:10.1103/physrevlett.101.010504

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chandran A, Hermanns M, Regnault N, Bernevig BA. Bulk-edge correspondence in entanglement spectra. Phys Rev B (2011) 84:205136. doi:10.1103/physrevb.84.205136

CrossRef Full Text | Google Scholar

12. Luo ZX, Pankovich BG, Hu Y, Wu YS. Correspondence between bulk entanglement and boundary excitation spectra in two-dimensional gapped topological phases. Phys Rev B (2019) 99:205137. doi:10.1103/physrevb.99.205137

CrossRef Full Text | Google Scholar

13. Estienne B, Stephan JM. Entanglement spectroscopy of chiral edge modes in the quantum Hall effect. Phys Rev B (2020) 101:115136. doi:10.1103/physrevb.101.115136

CrossRef Full Text | Google Scholar

14. Fradkin E. Field theories of condensed matter physics. Cambridge: Cambridge University Press (2013).

Google Scholar

15. Solodukhin SN. Entanglement entropy, conformal invariance and extrinsic geometry. Phys Lett B (2008) 665:305–9. doi:10.1016/j.physletb.2008.05.071

CrossRef Full Text | Google Scholar

16. Fradkin E, Moore JE. Entanglement entropy of 2D conformal quantum critical points: Hearing the shape of a quantum drum. Phys Rev Lett (2006) 97:050404. doi:10.1103/physrevlett.97.050404

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Casini H, Huerta M. Entanglement entropy in free quantum field theory. J Phys A: Math Theor (2009) 42:504007. doi:10.1088/1751-8113/42/50/504007

CrossRef Full Text | Google Scholar

18. Nishioka T, Ryu S, Takayanagi T. Holographic entanglement entropy: an overview. J Phys A: Math Theor (2009) 42:504008. doi:10.1088/1751-8113/42/50/504008

CrossRef Full Text | Google Scholar

19. Myers RC, Sinha A. Seeing a c-theorem with holography. Phys Rev D (2010) 82:046006. doi:10.1103/physrevd.82.046006

CrossRef Full Text | Google Scholar

20. Kallin AB, Hyatt K, Singh RRP, Melko RG. Entanglement at a two-dimensional quantum critical point: a numerical linked-cluster expansion study. Phys Rev Lett (2013) 110:135702. doi:10.1103/physrevlett.110.135702

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bueno P, Myers RC, Krempa WW. Corner contributions to holographic entanglement entropy. J High Energ Phys (2015) 2015:68. doi:10.1007/jhep08(2015)068

CrossRef Full Text | Google Scholar

22. Faulkner T, Leigh RG, Parrikar O. Shape dependence of entanglement entropy in conformal field theories. J High Energ Phys (2016) 88:1–39. doi:10.1007/jhep04(2016)088

CrossRef Full Text | Google Scholar

23. Laflorencie N. Quantum entanglement in condensed matter systems. Phys Rep (2016) 646:1–59. doi:10.1016/j.physrep.2016.06.008

CrossRef Full Text | Google Scholar

24. Helmes J, Sierens LEH, Chandran A, Krempa WW, Melko RG. Universal corner entanglement of Dirac fermions and gapless bosons from the continuum to the lattice. Phys Rev B (2016) 94:125142. doi:10.1103/physrevb.94.125142

CrossRef Full Text | Google Scholar

25. Chen X, Krempa WW, Faulkner T, Fradkin E. Two-cylinder entanglement entropy under a twist. J Stat Mech (2017) 4:043104. doi:10.1088/1742-5468/aa668a

CrossRef Full Text | Google Scholar

26. Bueno P, Krempa WW. Bounds on corner entanglement in quantum critical states. Phys Rev B (2016) 93:045131. doi:10.1103/physrevb.93.045131

CrossRef Full Text | Google Scholar

27. Krempa WW. Entanglement susceptibilities and universal geometric entanglement entropy. Phys Rev B (2019) 99:075138. doi:10.1103/physrevb.99.075138

CrossRef Full Text | Google Scholar

28. Rozon PG, Bplteau PA, Krempa WW. Geometric entanglement in the integer quantum Hall state at ν=1 with boundaries. Phys Rev B (2020) 102:155417. doi:10.1103/physrevb.102.155417

CrossRef Full Text | Google Scholar

29. Sirois B, Fournier LM, Leduc J, Krempa WW. Geometric entanglement in integer quantum Hall states. Phys Rev B (2021) 103:115115. doi:10.1103/physrevb.103.115115

CrossRef Full Text | Google Scholar

30. Estienne B, Stephan JM, Krempa WW. Cornering the universal shape of fluctuations. Nat Commun (2022) 13:287. doi:10.1038/s41467-021-27727-1

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Peschel I. Calculation of reduced density matrices from correlation functions. J Phys A: Math Gen (2003) 36:L205–8. doi:10.1088/0305-4470/36/14/101

CrossRef Full Text | Google Scholar

32. Sterdyniak A, Chandran A, Regnault N, Bernevig BA, Bonderson P. Real-space entanglement spectrum of quantum Hall states. Phys Rev B (2012) 85:125308. doi:10.1103/physrevb.85.125308

CrossRef Full Text | Google Scholar

33. Dubail J, Read N, Rezayi EH. Real-space entanglement spectrum of quantum Hall systems. Phys Rev B (2012) 85:115321. doi:10.1103/physrevb.85.115321

CrossRef Full Text | Google Scholar

34. Rodriguez ID, Simon SH, Slingerland JK. Evaluation of ranks of real space and particle entanglement spectra for large systems. Phys Rev Lett (2012) 108:256806. doi:10.1103/physrevlett.108.256806

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Rodriguez ID, Sierra G. Entanglement entropy of integer quantum Hall states. Phys Rev B (2009) 80:153303. doi:10.1103/physrevb.80.153303

CrossRef Full Text | Google Scholar

36. Hung LY, Myers RC, Smolkin M. Twist operators in higher dimensions. J High Energ Phys (2014) 10:178. doi:10.1007/jhep10(2014)178

CrossRef Full Text | Google Scholar

37. Bueno P, Myers RC, Krempa WW. Universality of corner entanglement in conformal field theories. Phys Rev Lett (2015) 115:021602. doi:10.1103/PhysRevLett.115.021602

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Schine N, Ryou A, Gromov A, Sommer A, Simon J. Synthetic Landau levels for photons. Nature (2016) 534:671–5. doi:10.1038/nature17943

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Schine N, Chalupnik M, Can T, Gromov A, Simon J. Electromagnetic and gravitational responses of photonic Landau levels. Nature (2019) 565:173–9. doi:10.1038/s41586-018-0817-4

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bueno MJ, Furtado C, Carvalho AMd. M. Landau levels in graphene layers with topological defects. Eur Phys J B (2012) 85:53. doi:10.1140/epjb/e2011-20726-4

CrossRef Full Text | Google Scholar

41. Biswas RR, Son DT. Fractional charge and inter-Landau–level states at points of singular curvature. Proc Natl Acad Sci U S A (2016) 113:8636–41. doi:10.1073/pnas.1609470113

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Can T, Chiu YH, Laskin M, Wiegmann P. Emergent conformal symmetry and geometric transport properties of quantum Hall states on singular surfaces. Phys Rev Lett (2016) 117:266803. doi:10.1103/physrevlett.117.266803

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wu YH, Tu HH, Sreejith GJ. Fractional quantum Hall states of bosons on cones. Phys Rev A (Coll Park) (2017) 96:033622. doi:10.1103/physreva.96.033622

CrossRef Full Text | Google Scholar

44. Jiang N, Li Q, Zhu Z, Hu Z-X. Universal properties of the FQH state from the topological entanglement entropy and disorder effects. Ann Phys (N Y) (2017) 384:225–34. doi:10.1016/j.aop.2017.07.005

CrossRef Full Text | Google Scholar

45. Calabrese P, Cardy J. Entanglement entropy and conformal field theory. J Phys A: Math Theor (2009) 42:504005. doi:10.1088/1751-8113/42/50/504005

CrossRef Full Text | Google Scholar

46. Berthiere C, Krempa WW. Relating bulk to boundary entanglement. Phys Rev B (2019) 100:235112. doi:10.1103/physrevb.100.235112

CrossRef Full Text | Google Scholar

47. Chamon Cde C, Wen XG. Sharp and smooth boundaries of quantum Hall liquids. Phys Rev B (1994) 49:8227–41. doi:10.1103/physrevb.49.8227

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Wan X, Yang K, Rezayi EH. Reconstruction of fractional quantum Hall edges. Phys Rev Lett (2002) 88:056802. doi:10.1103/physrevlett.88.056802

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Wan X, Rezayi EH, Yang K. Edge reconstruction in the fractional quantum Hall regime. Phys Rev B (2003) 68:125307. doi:10.1103/physrevb.68.125307

CrossRef Full Text | Google Scholar