Transport model study of transverse momentum distributions of (anti-)deuterons production in Au+Au collisions at sNN=14.5, 62.4, and 200 GeV

The transverse momentum distributions of deuterons and anti-deuterons in Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV with different centralities are studied within the framework of the UrQMD model combined with the conventional phase-space coalescence model. A strong reversed correlation between R₀ (the maximal relative distances between hadrons) and P₀ (the maximal relative momentum between hadrons) can be seen. It is also time-dependent. The number of particles generated are inconsistent with experimental data for 40, −,60% and 60, −,80% centralities because deuterons have plenty of time to react with other particles, this effect becomes more obvious with the decrease of beam energy. Our results can quantitatively describe the STAR data for 0, −,10%, 10, −,20% and 20, −,40% centralities.

1 Introduction

A great opportunity to explore the properties of strongly interacting substances at extreme densities and temperatures was provided by heavy-ion collisions (HICs) at ultra-relativistic energies [1–5]. More investigation is warranted about the generation mechanism of the particles and fragments in the ultra-relativistic HICs, as it may provide important information on the quantum chromodynamics (QCD) phase transition from quark-gluon plasma (QGP) to hadron gas (HG) [6, 7]. In the past 2 decades, many experiments have been carried out at the Relativistic Heavy Ion Collider (RHIC) near the critical energy for the transition from hadronic matter to QGP [8]. The theoretical studies on the production of particles and anti-particles are been going on for years, for example, the coalescence model, thermal model and transport models [9–21]. In particular, the study of transport phenomena is very important for understanding many fundamental properties [22, 23]. The transverse momentum spectrum of particles produced in high-energy collisions is of great research value because it can provide us with key information about the dynamic freezing state of the interacting system [24]. In the dynamic freezing stage, the effective temperature is not the actual temperature, which describes the sum of the excitation degree of the interacting system and the influence of the lateral flow [25].

The underlying mechanism for the generation of light (anti-) nuclei in relativistic heavy ion collisions is still under investigation. The traditional phase space polymerization method can be widely applied to HICs in large beam energy range [26]. It is of great significance to study deuteron generation at RHIC energy using the traditional coalescence model. In addition, there is a strong correlation between the particle’s coordinates and momentum, and this correlation varies over time. Therefore, the time evolution of the parameter set (R₀, P₀) needs to be scanned within a reasonable range so that the coalescence process produces the same yield [26]. From these experiments, the effect of coalescent parameters on the (anti-)deuteron and its transverse momentum distribution can be observed. The inverse law correlation between R₀ and P₀ should be described in detail in the third section.

In this paper, the Ultra-relativistic Quantum Molecular Dynamics (UrQMD) transport model is adopted to produce the transverse momentum distributions of (anti-)deuterons in Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV, and comparisons were made with experimental data from the STAR collaboration [27]. The main purpose of this work is to study different reaction mechanisms of Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV, such as the effect of coordinate space and momentum space correlation on deuteron and anti-deuteron yields. In the calculation, hadrons with relative distances less than R₀ and relative momentum less than P₀ are considered to belong to a cluster.

2 Ultra-relativistic quantum molecular dynamics transport model and the coalescence model

2.1 The UrQMD model

The UrQMD model is a microscopic multi-body transport method that can be used to study proton-proton (pp), proton-nucleus (pA) and nucleon-nucleus (AA) interactions in the energy range from SIS to LHC. The transport model is based on covariant propagation of color strings, constituent quarks, and double quarks (as string ends) with meson and baryon degrees of freedom [28]. It can combine different reaction mechanisms and give theoretical simulation results of various experimental observations. In this model, by introducing the formation time of hadrons produced by string fragments, the degree of freedom of subhadrons is entered [29–31]. They predominate in the early stages of heavy ion collisions (HICs) with high SPS and RHIC energies.

The UrQMD model and quantum molecular dynamics (QMD) model are based on the parallel principle: hadrons are represented by Gaussian wave packets in phase space, and the phase space of hadrons propagates according to Hamiltonian equations of motion [32],

$\dot{\stackrel{⃗}{r_i}}=\frac{\partial H}{\partial \overrightarrow{p_i}},\dot{\stackrel{⃗}{p_i}}=-\frac{\partial H}{\partial \overrightarrow{r_i}}.(1)$

Here, $\overrightarrow{r_i}$ and $\overrightarrow{p_i}$ are the coordinate and momentum of the hadron i, respectively. The Hamiltonian H consists of the kinetic energy T and the effective interaction potential energy U,

$H=T+U.(2)$

This microscopic transport approach simulates multiple interactions of in-going and newly produced particles, the excitation and fragmentation of color strings and the formation and decay of hadronic resonances. For higher energies, the treatment of subhadronic degrees of freedom is very important. In the current model, these degrees of freedom enter by introducing the formation time of hadrons produced by string fragments. The phase transition to the quark-gluon state is not explicitly incorporated into the model dynamics. However, a detailed analysis of the model in equilibrium state gives an effective Hagedorn type equation of state [33].

In this paper, we mainly study the effect of the correlations between coordinate and momentum spaces on the yields and the transverse momentum distribution of deuteron and anti-deuteron with the cascade mode in the RHIC energy region. In the nextwork, we will focus on the influence of potential on production of light particles in this energy region.

2.2 The coalescence model

The coalescence model describes the formation of hadronic clusters in the kinetic freeze-out stage of a heavy-ion collision. A pair of final (anti-) nucleons with similar momentum can merge to form a deuteron or anti-deuteron with total momentum P [34]. In the calculation, we use a conventional phase space clustering model [35] to construct clusters, in which hadrons with relative distances less than R₀ and relative momentum less than P₀ are considered to belong to a cluster. As a rule of thumb, the parameter set (R₀, P₀) can be selected in the range of (3-4 fm, 0.25–0.35 GeV/c) to describe the experimental data of HICs [26]. In this article, we will investigate the effects of different set of R₀ and P₀ on the yield of (anti-)deuteron over the evolutional time.

3 Time evolution and transverse momentum distributions of the production of (Anti-)deuterons

3.1 The time evolution of (anti-)deuterons

The time dependence of the production of (anti-)deuterons in the mid-rapidity (|y| < 0.3) for 0, −,10% centrality should be considered since they might be produced by different mechanisms. The time evolution of the yield of (anti-)deuterons at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV are shown in Figure 1, Figure 2 and Figure 3, respectively. The blue area represents the range of experimental data. In the view ranges of R₀ and P₀, it is clear that too many deuterons are produced before 40 fm/c at $\sqrt{s_{NN}}$ = 14.5 and at 62.4 GeV, which are unstable and will subsequently fission. In the meantime, too many anti-deuterons are produced before 50 fm/c. If we select parameter sets of (R₀, P₀) (3.8 fm, 0.3 GeV/c), the data can be well described. For $\sqrt{s_{NN}}$ = 200 GeV, the parameter sets of (R₀, P₀) (3.575 fm, 0.285 GeV/c) can be selected. These parameter sets of (R₀, P₀) are commonly used by researchers and are appropriate for this study [7, 26].

FIGURE 1

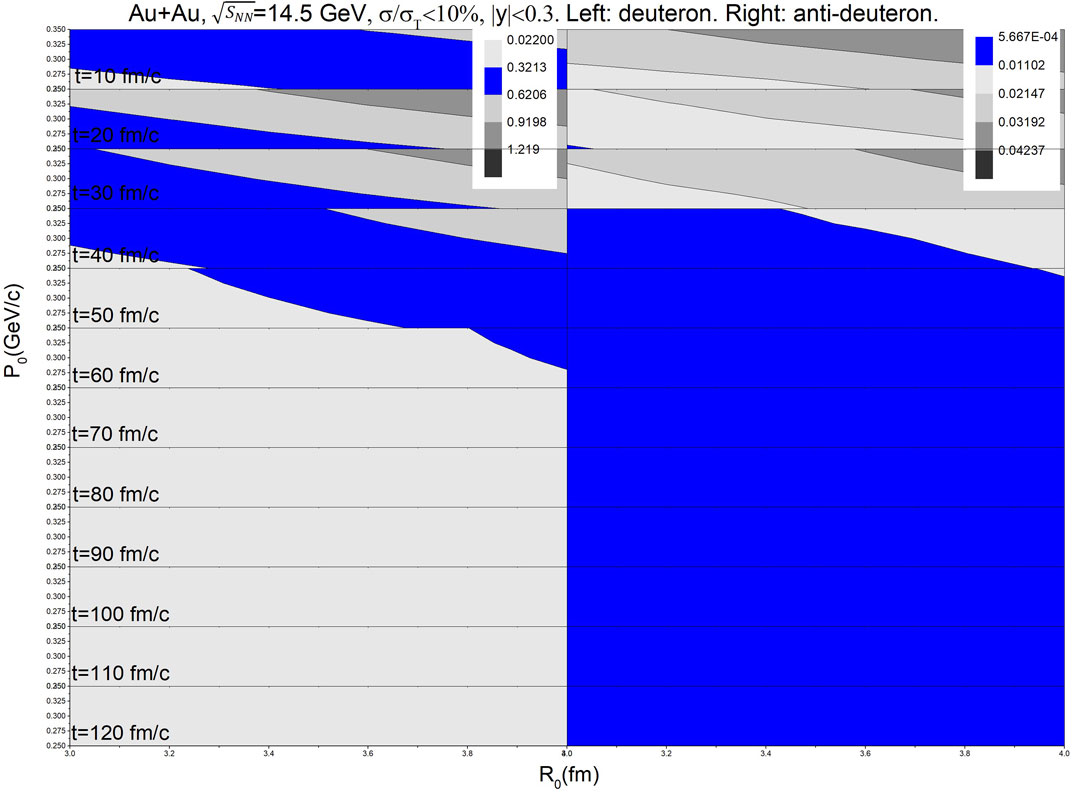
FIGURE 1. Time evolution of R₀-P₀ contour plots of (anti-)deuteron from the central Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5 GeV. The blue areas represent the range of experimental data from the STAR collaboration [27].

FIGURE 2

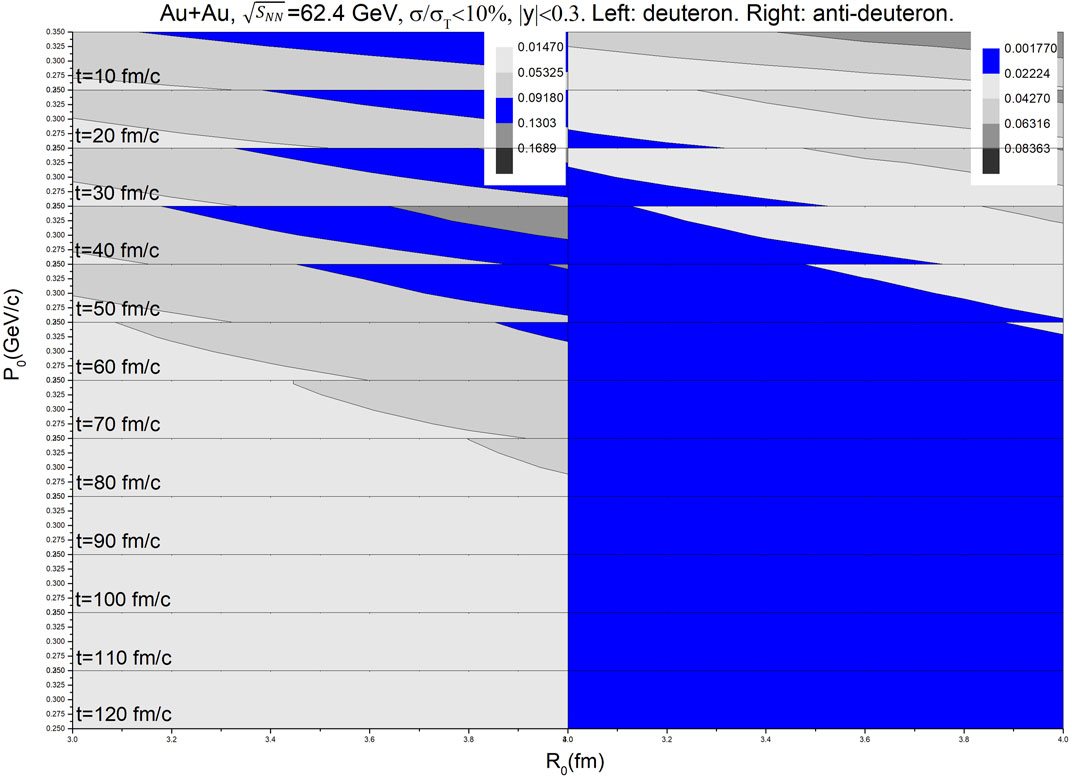
FIGURE 2. Time evolution of R₀-P₀ contour plots of (anti-)deuteron from the central Au + Au collisions at $\sqrt{s_{NN}}$ = 62.4 GeV. The blue areas represent the range of experimental data from the STAR collaboration [27].

FIGURE 3

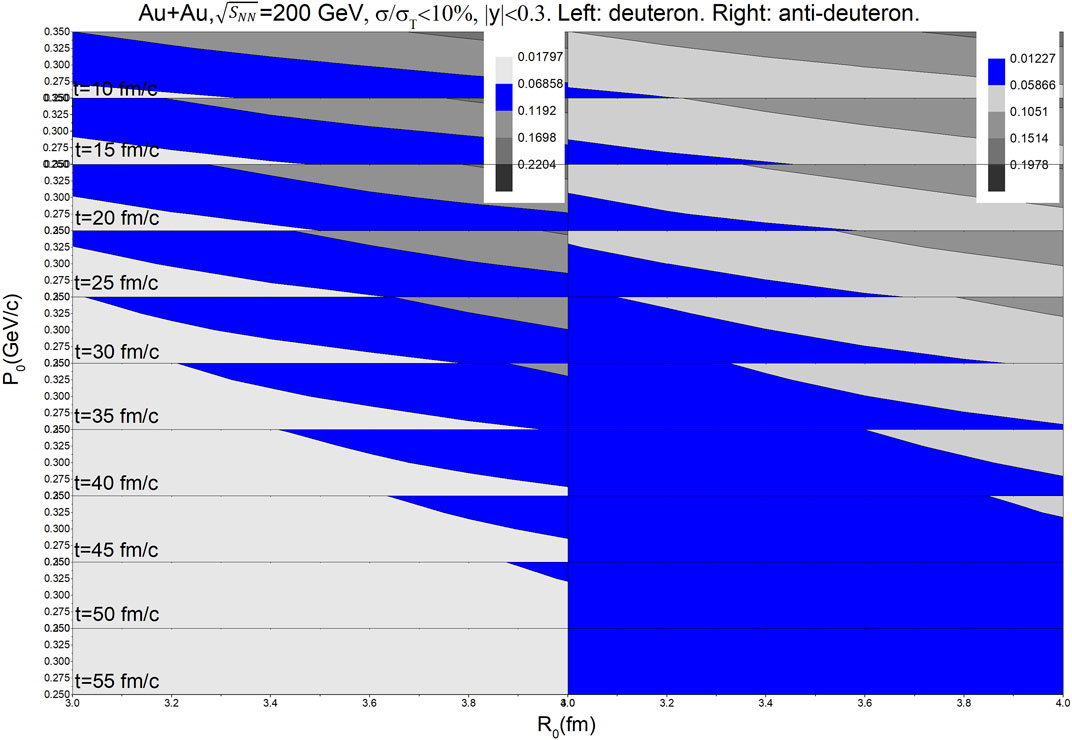
FIGURE 3. Time evolution of R₀-P₀ contour plots of (anti-)deuteron from the central Au + Au collisions at $\sqrt{s_{NN}}$ = 200 GeV. The blue areas represent the range of experimental data from the STAR collaboration [27].

Figure 4 show the yields of (anti-)deuterons as the time evolution in the 0, −,10% centrality Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV at mid-rapidity (|y| < 0.3). The red lines are the results calculated from the cascade mode of UrQMD model. The shaded bands are the experimental data. It can be found that the stopping times should be 50 fm/c for deuterons and 60 fm/c for anti-deuterons for $\sqrt{s_{NN}}$ = 14.5 and 62.4 GeV, and the corresponds stopping times for $\sqrt{s_{NN}}$ = 200 GeV should be 30 fm/c for deuterons and 45 fm/c for anti-deuterons. Therefore, these stopping times are adopted in the following calculations. From Figure 4, one can also find that the deuterons produced at the lower energies need a longer time to be spatially separated [36].

FIGURE 4

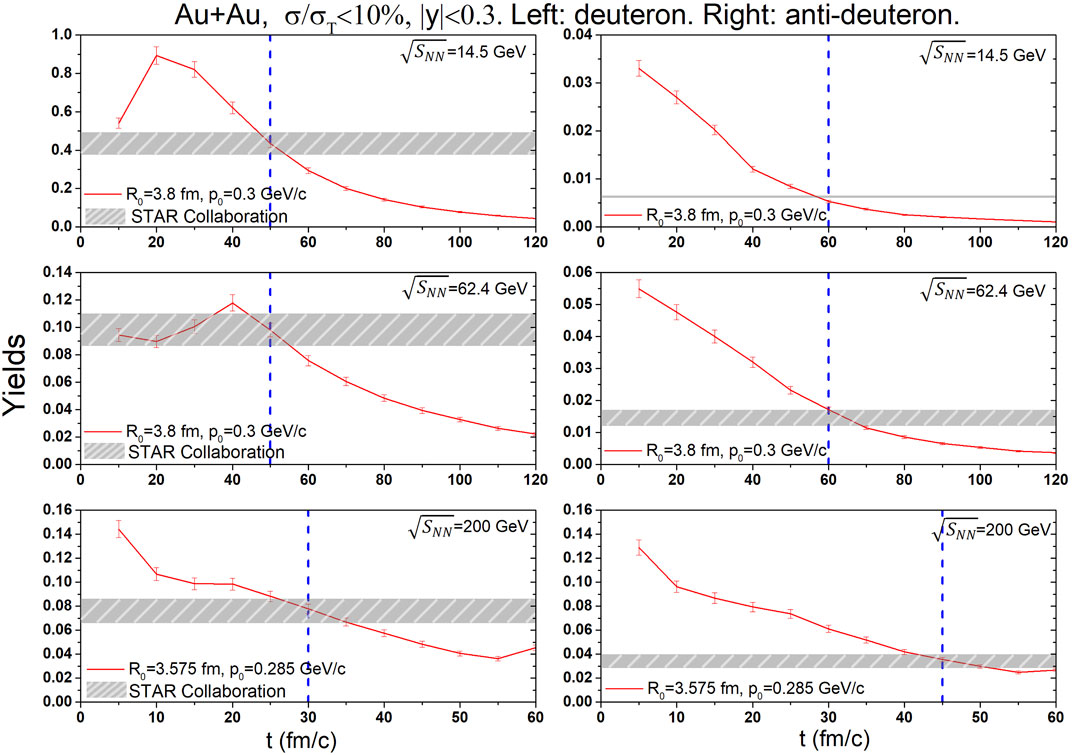
FIGURE 4. The yields of (anti-)deuterons as the time evolution in Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV at mid-rapidity (|y| < 0.3) for 0, − ,10% centrality. The lines are the calculations under certain conditions (R₀, P₀). The shaded bands are the corresponding experimental data which taken from the STAR Collaboration [27]. The dash lines are orientation lines.

The scanning of R₀ and P₀ located in the colored regions of Figure 1, Figure 2 and Figure 3 is useful because they are reliable in the (anti-) deuteron data description of the mid-rapidity region. It is clear that the (anti-)deuteron production rate of RHIC can be well described by the cooperative method of UrQMD + coalescence if the UrQMD stop times are properly combined and the parameter set of (R₀, P₀) in the coalescence is chosen.

3.2 Transverse momentum distributions of (anti-)deuterons

Figures 5–7 show the transverse momentum spectra for deuterons at mid-rapidity (|y| < 0.3) in Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV with 0, −,10%, 10, −,20%, 20, −,40%, 40, −,60% and 60, −,80% centralities. The signs + lines are the results calculated from the cascade mode of the UrQMD model, and the circles are the experimental data. It is found that the calculated results of UrQMD model agree well with the experimental data except for $\sqrt{s_{NN}}$ = 14.5 GeV at the 40, −,60% and 60, −,80% centralities. At $\sqrt{s_{NN}}$ = 14.5 GeV for the 40, −,60% and 60, −,80% centralities, most of our calculations are lower than the experimental data. We know that the deuterons produced at large impact parameter have plenty of time to react with other particles [36], and some of observed deuterons come from the nuclear fragments [27]. The impact of this effect will be further studied.

FIGURE 5

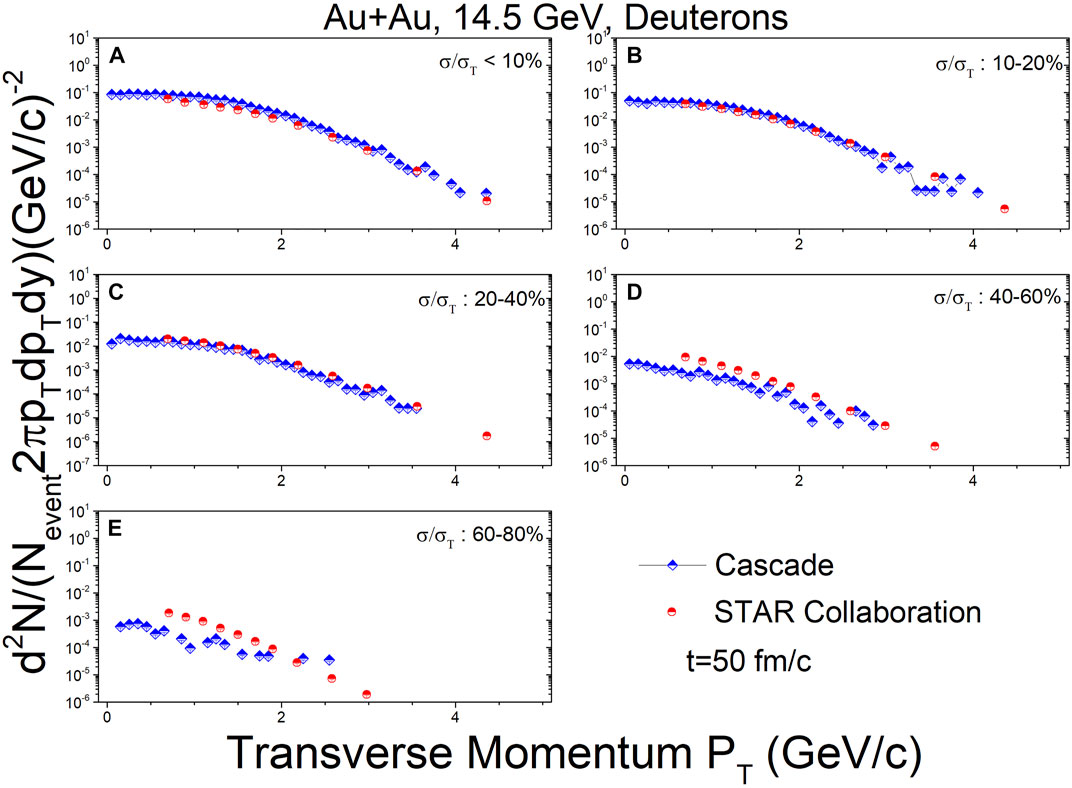
FIGURE 5. In the $\sqrt{s_{NN}}$ = 14.5 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 50fm/c in the deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.8 fm, 0.3 GeV/c).

FIGURE 6

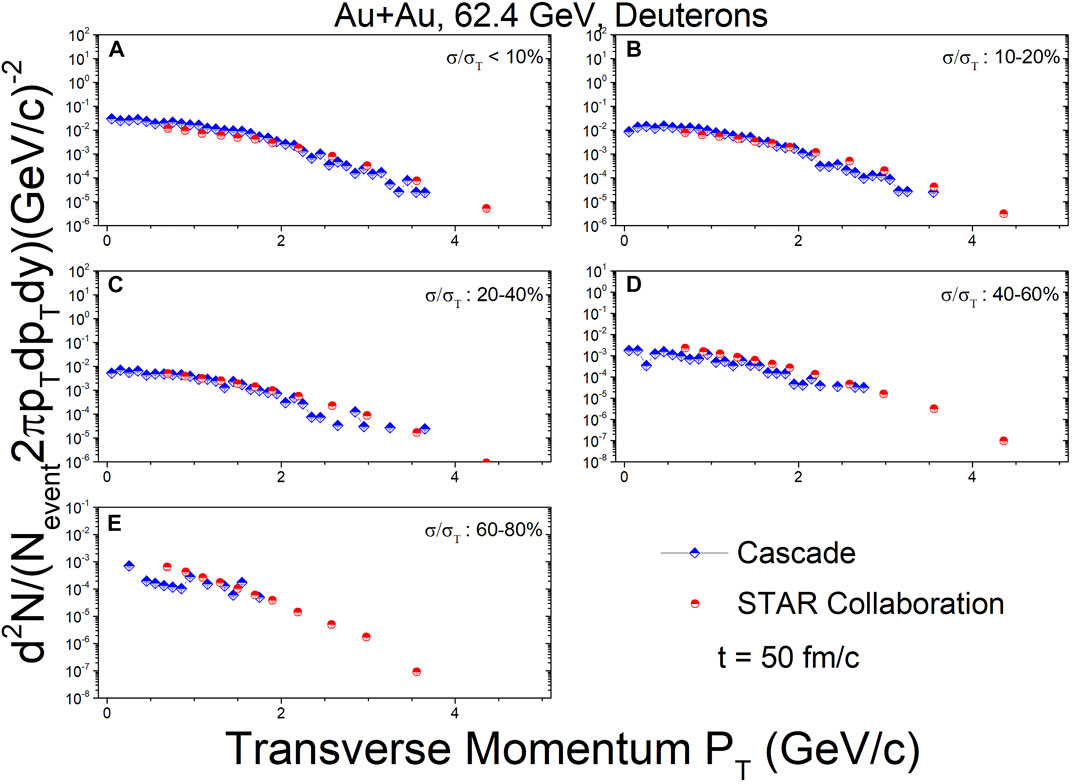
FIGURE 6. In the $\sqrt{s_{NN}}$ = 62.4 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 50fm/c in the deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.8 fm, 0.3 GeV/c).

FIGURE 7

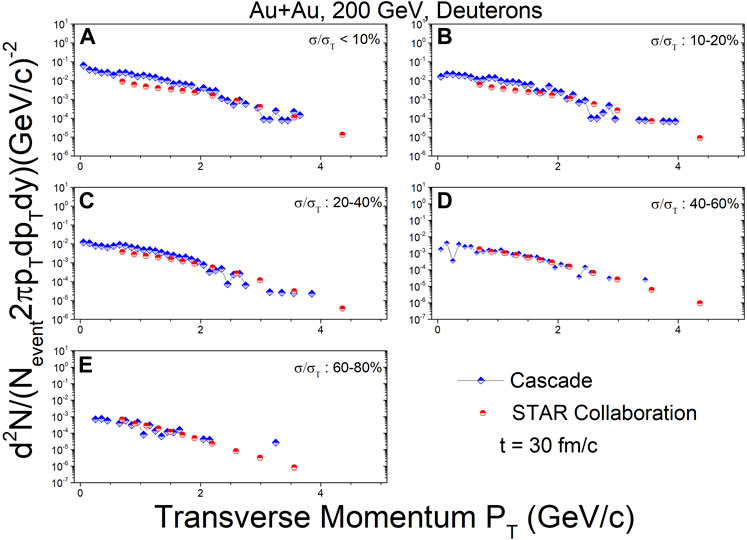
FIGURE 7. In the $\sqrt{s_{NN}}$ = 200 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 30fm/c in the deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.575 fm, 0.285 GeV/c).

Figures 8–10 show the transverse momentum spectra for anti-deuterons at mid-rapidity (|y| < 0.3) in Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV for 0, −,10%, 10, −,20%, 20, −,40%, 40, −,60% and 60, −,80% centralities. The signs + lines are our calculated results using the UrQMD model with cascade mode shown in the every panel. The circles are the experimental data. It is found that the calculations of the UrQMD model are in keeping with the experimental data well at $\sqrt{s_{NN}}$ = 200 GeV. At $\sqrt{s_{NN}}$ = 14.5 GeV, due to anti-deuterons are mainly produced in fireball shells, and the antideuterons produced have a low probability of interacting with other particles, the transverse momentum spectra of anti-deuterons is more. Since the relative suppression of anti-nucleons recedes with increasing energy, anti-deuterons can form much closer to the fireball center. Deuteron and antideuteron formation have the same geometry at energies around $\sqrt{s_{NN}}$ = 200 GeV [34]. Therefore, the theoretical calculation results can describe the experimental data well at $\sqrt{s_{NN}}$ = 200 GeV.

FIGURE 8

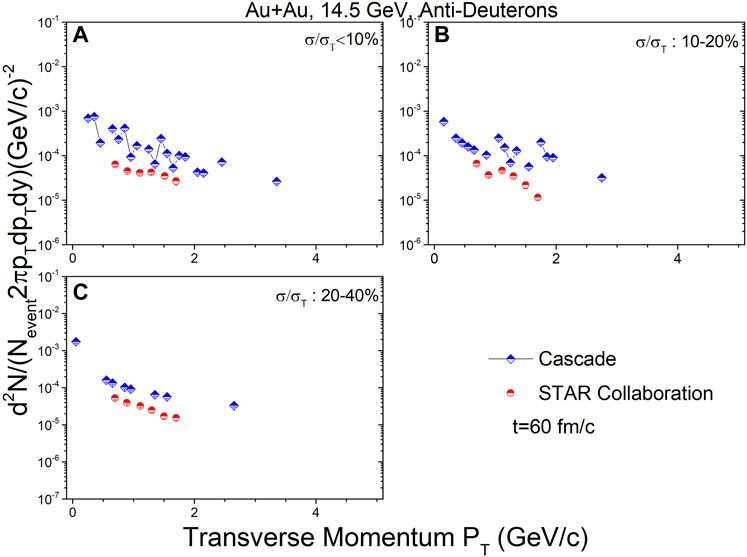
FIGURE 8. In the $\sqrt{s_{NN}}$ = 14.5 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 60fm/c in the anti-deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.8 fm, 0.3 GeV/c).

FIGURE 9

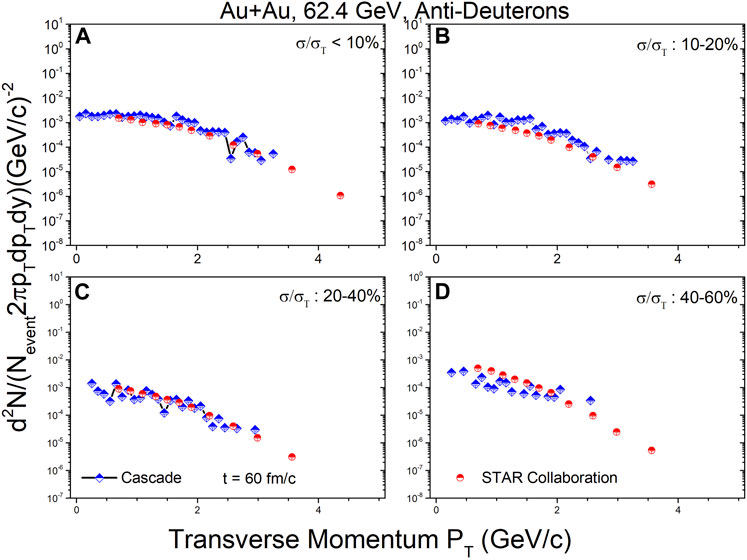
FIGURE 9. In the $\sqrt{s_{NN}}$ = 62.4 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 60fm/c in the anti-deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.8 fm, 0.3 GeV/c).

FIGURE 10

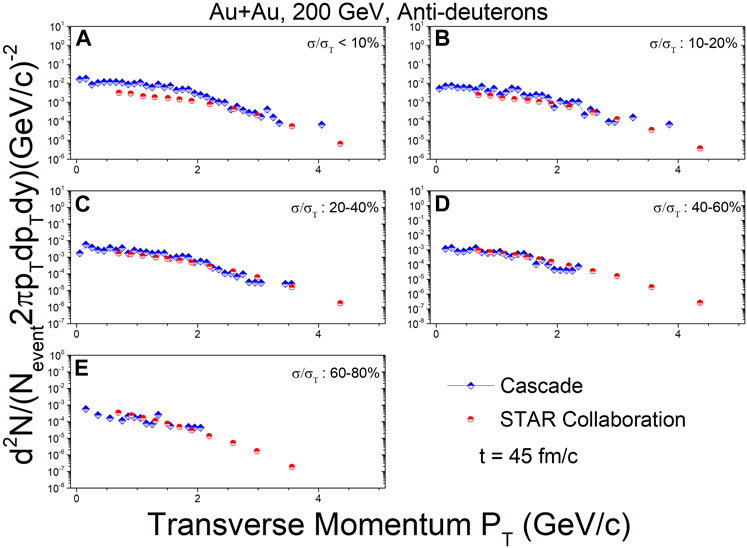
FIGURE 10. In the $\sqrt{s_{NN}}$ = 200 GeV Au + Au collisions, 0, − ,10%, 10, − ,20%, 20, − ,40%, 40, − ,60% and 60, − ,80% centrality in t = 45fm/c in the anti-deuteron transverse momentum spectrum. Calculations are represented by signs + lines. Experimental data from the STAR collaboration [27] are represented as circles. The parameter sets of (R₀, P₀) is (3.575 fm, 0.285 GeV/c).

4 Summary and outlook

In conclusion, we give the time evolution of the (anti-) deuteron in 0, −,10% center Au + Au collisions at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV with the UrQMD model combined with the coalescence. In the coalescence process, the values of the (R₀, P₀) parameter set are surveyed in the ranges (3-4 fm, 0.25–0.35 GeV/c) to describe the experimental data. It is found that there exits a strong reversed correlation between R₀ and P₀ and it is time-dependent. For deuterons, the accepted (R₀, P₀) band in the time period 20–50 fm/c, while for anti-deuterons, the time evolution of the need is greater than 50 fm/c for $\sqrt{s_{NN}}$ = 14.5 GeV, 60 fm/c for $\sqrt{s_{NN}}$ = 62.4 GeV and 35 fm/c for $\sqrt{s_{NN}}$ = 200 GeV. Otherwise, smaller R₀ and P₀ values should be selected. In addition, we also have presented the transverse momentum distributions of (anti-)deuterons for 0, −,10%, 10, −,20%, 20, −,40%, 40, −,60% and 60, −,80% centralities collisions. The results show that the UrQMD + coalescence method can describe the variation experimental data of STAR Collaboration well at $\sqrt{s_{NN}}$ = 14.5, 62.4 and 200 GeV. The transverse momentum spectra of (anti-)deuterons at $\sqrt{s_{NN}}$ = 14.5 GeV are inconsistent with experimental data for 40, −,60% and 60, −,80% centralities, since deuterons have plenty of time to react with other particles, and this phenomenon will become more obvious with the collision energy decreasing. At low collision energies, the emission source size of anti-deuteron is larger than that of deuteron. But the influence mechanism of the spatial separation have yet to be studied in depth, and related work is in progress.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization, XZ; formal analysis, ZH; writing—original draft, YY; writing—review editing, XW.

Funding

This work was supported by the Natural Science Foundation of Guangxi Zhuangzu Autonomous Region of China under Grant Nos. 2021GXNSFAA196052, the Introduction of Doctoral Starting Funds of Scientific Research of Guangxi University of Chinese Medicine under Grant Nos. 2018BS024, and the Open Project of Guangxi Key Laboratory of Nuclear Physics and Nuclear Technology, No. NLK2020-03.

Acknowledgments

We are grateful to the C3S2 computing center in Huzhou University for calculation support. We thank Qingfeng Li and Pengcheng Li for valuable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Alt C. Energy dependence of Λ and Ξ production in central Pb+Pb collisions at 20A, 30A, 40A, 80A, and 158A GeV measured at the CERN Super Proton Synchrotron. Phys Rev C (2008) 78(3):034918. doi:10.1103/PhysRevC.78.034918

CrossRef Full Text | Google Scholar

2. Sun JX, Liu FH, Wang EQ. Pseudorapidity distributions of charged particles and contributions of leading nucleons in Cu-Cu collisions at high energies. Chin Phys Lett (2010) 27(3):032503. doi:10.1088/0256-307x/27/3/032503

CrossRef Full Text | Google Scholar

3. Wang EQ, Liu FH, Rahim MA, Fakhraddin S, Sun JX. Singly and doubly charged projectile fragments in nucleus-emulsion collisions at dubna energy in the framework of the multi-source model. Chin Phys Lett (2011) 28(8):082501. doi:10.1088/0256-307X/28/8/082501

CrossRef Full Text | Google Scholar

4. Li BC, Huang M. Strongly coupled matter near phase transition. J Phys G: Nucl Part Phys (2009) 36:064062. doi:10.1088/0954-3899/36/6/064062

CrossRef Full Text | Google Scholar

5. Liu FH. Anisotropic emission of charged mesons and structure characteristic of emission source in heavy ion collisions at 1–2A GeV. Chin Phys B (2008) 17(3):883–95. doi:10.1088/1674-1056/17/3/025

CrossRef Full Text | Google Scholar

6. Arsenescu R, Baglin C, Beck HP, Borer K, Bussiere A, Elsener K, et al. An investigation of the antinuclei and nuclei production mechanism in Pb + Pb collisions at 158 A GeV. New J Phys (2003) 5:150. doi:10.1088/1367-2630/5/1/150

CrossRef Full Text | Google Scholar

7. Li QF, Wang YJ, Wang XB, Shen CW. Helium-3 production from Pb+Pb collisions at SPS energies with the UrQMD model and the traditional coalescence afterburner. Sci China Phys Mech Astron (2016) 59(3):632002. doi:10.1007/s11433-015-5775-3

CrossRef Full Text | Google Scholar

8. Lao HL, Wei HR, Liu FH, Lacey RA. An evidence of mass-dependent differential kinetic freeze-out scenario observed in Pb-Pb collisions at 2.76 TeV. Eur Phys J A (2016) 52:203. doi:10.1140/epja/i2016-16203-2

CrossRef Full Text | Google Scholar

9. Mrowczynski S, Slon P. Hadron-deuteron correlations and production of light nuclei in relativistic heavy-ion collisions (2016) Available from: http://arxiv.org/abs/nucl-th/1904.08320v2. (Accessed Jun 24, 2019).

Google Scholar

10. Mrowczynski S. Production of light nuclei in the thermal and coalescence models. Acta Phys Pol B (2017) 48:707. doi:10.5506/aphyspolb.48.707

CrossRef Full Text | Google Scholar

11. Mrowczynski S. ⁴He versus ⁴Li and production of light nuclei in relativistic heavy-ion collisions. Mod Phys Lett A (2018) 33:1850142. doi:10.1142/s0217732318501420

CrossRef Full Text | Google Scholar

12. Liu P, Chen JH, Ma YG, Zhang S. Production of light nuclei and hypernuclei at High Intensity Accelerator Facility energy region. Nucl Sci Tech (2017) 28:55. doi:10.1007/s41365-017-0207-x

CrossRef Full Text | Google Scholar

13. Liu FX, Chen G, Zhe ZL, Zhou DM, Xie YL. Light (anti)nuclei production in Cu+Cu collisions at $\sqrt{s_{NN}}$=200 GeV. Eur Phys J A (2019) 55:160. doi:10.1140/epja/i2019-12851-x

CrossRef Full Text | Google Scholar

14. Yuan Y, Li Q, Li Z, Liu F-H. Transport model study of nuclear stopping in heavy-ion collisions over the energy range from0.09Ato160A GeV. Phys Rev C (2010) 81:034913. doi:10.1103/physrevc.81.034913

CrossRef Full Text | Google Scholar

15. Yuan Y. Study of Production of (Anti-)deuteron Observed in Au+Au Collisions at $\sqrt{s_{NN}}$= 14.5, 62.4, and 200 GeV. Advances in high energy Physics (2021) 2021:9305605. doi:10.1155/2021/9305605

CrossRef Full Text | Google Scholar

16. Li P, Wang Y, Li Q. Hongfei Zhang “Accessing the in-medium effects on nucleon-nucleon elastic cross section with collective flows and nuclear stopping. Phys Lett B (2022) 828:2022. doi:10.1016/j.physletb.2022.137019

CrossRef Full Text | Google Scholar

17. Oliinychenko D, Pang L-G, Elfner H, Koch V. Microscopic study of deuteron production in PbPb collisions at $\sqrt{s_{NN}}$2.76 TeV via hydrodynamics and a hadronic afterburner. Phys Rev C (2019) 99:044907. doi:10.1103/PhysRevC.99.044907

CrossRef Full Text | Google Scholar

18. Aichelin J, Bratkovskaya E, Le Fèvre A, Kireyeu V, Kolesnikov V, Leifels Y, et al. Parton-hadron-quantum-molecular dynamics: A novel microscopic n-body transport approach for heavy-ion collisions, dynamical cluster formation, and hypernuclei production. Phys Rev C (2020) 101:044905. doi:10.1103/physrevc.101.044905

CrossRef Full Text | Google Scholar

19. Kireyeu V. Cluster dynamics studied with the phase-space minimum spanning tree approach. Phys Rev C (2021) 103:054905. doi:10.1103/physrevc.103.054905

CrossRef Full Text | Google Scholar

20. Staudenmaier J, Oliinychenko D, Torres-Rincon JM, Elfner H. Deuteron production in relativistic heavy ion collisions via stochastic multiparticle reactions. Phys Rev C (2021) 104:034908. Aticle ID 034908. doi:10.1103/physrevc.104.034908

CrossRef Full Text | Google Scholar

21. Gläßel S, Kireyeu V, Voronyuk V, Aichelin J, Blume C, Bratkovskaya E, et al. Cluster and hypercluster production in relativistic heavy-ion collisions within the parton-hadron-quantum-molecular-dynamics approach. Phys Rev C (2022) 105:014908. doi:10.1103/PhysRevC.105.014908

CrossRef Full Text | Google Scholar

22. Li BC, Fu YY, Wang LL, Liu FH. Dependence of elliptic flows on transverse momentum and number of participants in Au+Au collisions at $\sqrt{\mathrm{\it s_{NN}}}$ = 200 GeV. J Phys G: Nucl Part Phys (2013) 40:025104. doi:10.1088/0954-3899/40/2/025104

CrossRef Full Text | Google Scholar

23. Sombun S, Tomuang K, Limphirat A, Hillmann P, Herold C, Jan S, et al. Deuteron production from phase-space coalescence in the UrQMD approach. Phys Rev C (2019) 99:014901. doi:10.1103/physrevc.99.014901

CrossRef Full Text | Google Scholar

24. Chen YH, Liu FH, Sarkisyan-Grinbaum EK. Event patterns from negative pion spectra in proton-proton and nucleus-nucleus collisions at SPS. Chin Phys C (2018) 42(10):104102. doi:10.1088/1674-1137/42/10/104102

CrossRef Full Text | Google Scholar

25. Waqas M, Liu FH, Li LL, Alfanda HM. Analysis of effective temperature and kinetic freeze-out volume in high energy nucleus-nucleus and proton-proton collisions. Nucl Sci Tech (2020) 31:109. doi:10.1007/s41365-020-00821-7

CrossRef Full Text | Google Scholar

26. Li QF, Wang YJ, Wang XB, Shen CW. Influence of coalescence parameters on the production of protons and Helium-3 fragments. Sci China Phys Mech Astron (2016) 59:672013. doi:10.1007/s11433-016-0120-3

CrossRef Full Text | Google Scholar

27. Adam J. Beam energy dependengce of (anti-)deuteron production in Au+Au collisions at RHIC. Phys Rev C (2019) 99. 064905. doi:10.1103/PhysRevC.99.064905

CrossRef Full Text | Google Scholar

28. Petersen H, Bleicher M, Bass SA, Stocker H. UrQMD-2.3 - changes and comparisons (2022) Available from: http://arxiv.org/abs/0805.0567. (Accessed May 5, 2008).

Google Scholar

29. Andersson B, Gustafson G, Nilsson-Almqvist B. A model for low P(T) hadronic reactions, with generalizations to hadron-nucleus and nucleus-nucleus collisions. Nucl Phys B (1987) 281(1-2):289–309. doi:10.1016/0550-3213(87)90257-4

CrossRef Full Text | Google Scholar

30. Nilsson-Almqvist B, Stenlund E. Interactions between hadrons and nuclei: The lund Monte Carlo, fritiof version 1.6. Computer Phys Commun (1987) 43(3):387–97. doi:10.1016/0010-4655(87)90056-7

CrossRef Full Text | Google Scholar

31. Sjostrand T. High-energy physics event generation with PYTHIA 5.7 and JETSET 7.4. Computer Phys Commun (1994) 82(1):74–89. doi:10.1016/0010-4655(94)90132-5

CrossRef Full Text | Google Scholar

32. Bleicher M, Zabrodin E, Spieles C, Bass SA, Ernst C, Soff S, et al. Relativistic hadron hadron collisions in the ultra-relativistic quantum molecular dynamics model. J Phys G: Nucl Part Phys (1999) 25(9):1859–96. doi:10.1088/0954-3899/25/9/308

CrossRef Full Text | Google Scholar

33. Petersen H, Li Q, Zhu X, Bleicher M. Directed and elliptic flow in heavy-ion collisions from E_beam = 90 MeV/nucleon to E_c.m. = 200 GeV/nucleon. Phys Rev C (2006) 74:064908. doi:10.1103/physrevc.74.064908

CrossRef Full Text | Google Scholar

34. Kittiratpattana A, Wondrak MF, Hamzic M, Bleicher M, Herold C, Limphirat A. Deuteron and antideuteron coalescence in heavy-iom collisions: Energy dependence of the formation geometry. Eur Phys J A (2020) 56:274. doi:10.1140/epja/s10050-020-00269-8

CrossRef Full Text | Google Scholar

35. Kruse H, Jacak BV, Molitoris JJ, Westfall GD, Stoecker H. Vlasov-uehling-uhlenbeck theory of medium-energy heavy ion reactions: Role of mean field dynamics and two-body collisions. Phys Rev C (1985) 31:1770–4. doi:10.1103/physrevc.31.1770

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kireyeu V, Steinheimer J, Aichelin J, Bleicher M, Bratkovskaya E. Deuteron production in ultra-relativistic heavy-ion collisions: A comparison of the coalescence and the minimum spanning tree procedure. Phys Rev C (2022) 105:044909. doi:10.1103/physrevc.105.044909

CrossRef Full Text | Google Scholar