High-dimensional orbital angular momentum entanglement from an ultrathin nonlinear film

Entanglement, as a crucial feature of quantum systems, is essential for various applications of quantum technologies. High-dimensional entanglement has the potential to encode arbitrary large amount of information and enhance robustness against eavesdropping and quantum cloning. The orbital angular momentum (OAM) entanglement can achieve the high-dimensional entanglement nearly for free stems due to its discrete and theoretically infinite-dimensional Hilbert space. A stringent limitation, however, is that the phase-matching condition limits the entanglement dimension because the coincidence rate decreases significantly for high-order modes. Here we demonstrate relatively flat high-dimensional OAM entanglement based on a spontaneous parametric down conversion (SPDC) from an ultrathin nonlinear lithium niobite crystal. The difference of coincidences between the different-order OAM modes significantly decreases. To further enhance the nonlinear process, this microscale SPDC source will provide a promising and integrated method to generate optimal high-dimensional OAM entanglement.

1 Introduction

Light with a helical phase exp (imϕ), which carries orbital angular momentum (OAM), has attracted close attention in the last few decades and found numerous photonic applications, such as high density data storage [1, 2], optical imaging [3–8], holography [9, 10], astrophysics [11, 12], optical manipulation [13–15] and in the optical interferometer for the detection of gravitational waves [16]. In addition, the OAM of light serves, in a sense, as an “alphabet” that allows information to be encoded into the spatial wavefunction of light. The key motivation is that the OAM has potentially an unlimited number of states [17, 18]. In the classical domain, the OAM can increase the capacity of optical communication links ranging from implementation in fibre [19, 20], over-city links [21] and free-space [22], and can also operate in mm-wave [23]. Actually, each OAM mode can be considered as an individual quantum degree of freedom [24, 25]. Quantum mechanically, the OAM occurs in discrete values of mℏ per photon, where m is in principle an unbounded integer. The OAM opens many promising perspectives for quantum communication and computation [26, 27]. Zeilinger’s group firstly realized the OAM-entangled photon pair [28] and verified that the maximum dimension of the OAM entanglement can reach 10,000 [29], which shows the great potential and novel advantage in the high-dimensional quantum information such as teleportation [30] and quantum communication [31–33]. A spontaneous parametric down conversion (SPDC) process is the most common workhorse for the generation of the OAM-entangled photon pairs [34, 35]. Albeit convenient, this process exhibits several drawbacks. For example, photon pairs generated in this way have a non-uniform OAM distribution, which constrains the increase of dimension [26]. The entanglement property of the OAM states is determined by the overlap between the transverse modes of the pump and photon pairs because the transverse intensity profile of the OAM mode depends on its topological charge m. The dimensionality of the two-photon OAM states can be increased with the use of perfect optical vortex (POV) in the pump because the POV is a class of size-invariant modes [36, 37]. The versatile high-dimensional quantum states are generated by using the structured pump [38–40]. Recently, the entangled OAM photon pairs are generated in the multiple SPDC processes by the path identity [41].

In addition, the non-uniformity of OAM entanglement is also restricted by the longitudinal phase mismatching. High-order OAM modes have the larg phase mismatch, which leads to the low generation efficiency. This restriction can be improved by utilizing the microscale flat-optics quantum source [42]. Here we have achieved relatively flat high-dimensional OAM entanglement in an ultrathin film of lithium niobite (LN) via the SPDC, which is impossible in a single bulk source. Being free from the phase matching constraints, the ultrathin source can be fabricated of any materials with large second-order susceptibility. Our method provides a new platform of high-dimensional OAM entanglement on which to investigate fundamental quantum effects but it also has practical applications.

2 Theory

In the paraxial approximation, photons carrying OAM can be described by a Laguerre-Gaussian mode ${\text{LG}}_p^m$. The radial index p shows the number of radial zero crossings and the azimuthal index m is the topological winding number, corresponding to OAM carried by the mode, mℏ per photon. Figure 1A shows the intensity and phase distributions of the LG modes with different OAM. A typical SPDC process, which a Gaussian beam propagating along the x direction pumps a nonlinear crystal with a length of L, as shown in Figure 1B, produces a pair of highly correlated, lower-frequency photons, commonly termed signal and idler photons. The generated two-photon quantum state by the SPDC is given by [43].

$\left|\psi \right.⟩=\iint d{\mathbf{k}}_{s}d{\mathbf{k}}_i\mathrm{\Phi }\left({\mathbf{k}}_s,{\mathbf{k}}_i\right){\widehat{a}}_s^{†}\left({\mathbf{k}}_s\right){\widehat{a}}_i^{†}\left({\mathbf{k}}_i\right)\left|0\right.⟩,(1)$

where $\left|0\right.⟩$ is the multimode vacuum state, while ${\widehat{a}}_s^{†}\left({\mathbf{k}}_s\right)$ and ${\widehat{a}}_i^{†}\left({\mathbf{k}}_i\right)$ are creation operators for the signal and idler modes with the transversal wave vectors k_s and k_i, respectively. $\mathrm{\Phi }\left({\mathbf{k}}_s,{\mathbf{k}}_i\right)$ represents the joint amplitude with the following structure

$\mathrm{\Phi }\left({\mathbf{k}}_s,{\mathbf{k}}_i\right)\propto F\left({\mathbf{k}}_s,{\mathbf{k}}_i\right)\text{sinc}\left(\mathrm{\Delta }kL/2\right),(2)$

where $F\left({\mathbf{k}}_s,{\mathbf{k}}_i\right)$ describes the mode function of the Gaussian pump beam at the input face of the nonlinear crystal. Here we consider only LG modes with p = 0, correspondingly we simplify as ${\text{LG}}_p^m\to {\text{LG}}_m$. One can decompose the quantum state $\left|\psi \right.⟩$ in the base of the eigenstates of the OAM operator under the OAM conservation as

$\left|\psi \right.⟩=\sum _m{C}_{m,-m}{\left|m\right.⟩}_s{\left|-m\right.⟩}_i(3)$

where ${\left|m\right.⟩}_s$ and ${\left|-m\right.⟩}_i$ correspond to the signal and idler modes, respectively. The coincidence amplitudes C_m,−m is written as

$C_{m,-m}=\iint d{\mathbf{k}}_{s}d{\mathbf{k}}_i\mathrm{\Phi }\left({\mathbf{k}}_s,{\mathbf{k}}_i\right){\text{LG}}_m\left({\mathbf{k}}_s\right){\text{LG}}_{-m}\left({\mathbf{k}}_i\right),(4)$

where ${\text{LG}}_m\left(\mathbf{k}\right)$ is the Laguerre-Gaussian mode function in the spatial frequency domain at x = 0. The coincidence probability is $P_{m,-m}={\left|C_{m,-m}\right|}^2$ , which gives the value of the joint detection probability for finding one photon in the signal mode ${\left|m\right.⟩}_s$ and one photon in the idler mode ${\left|-m\right.⟩}_i$ . It is clear that the coincidence probability P_m,−m is mainly determined by the phase matching. If the ${\left|0\right.⟩}_s{\left|0\right.⟩}_i$ mode is assumed to be phase matched, the phase mismatching of high-order OAM modes can be calculated analytically as [42].

$\mathrm{\Delta }kL/2\propto -\left|m\right|\frac{\pi L}{4\lambda }\frac{{\omega }_0^2}{z_R^2}\left(1-\frac{2z_R}{L}\arctan \frac{L}{2z_R}\right),(5)$

where z_R is the Rayleigh range of the mode ${\left|0\right.⟩}_s{\left|0\right.⟩}_i$ and ω₀ is the beam waist of the down-converted beam, respectively. For a type-0 degenerate phase matching process, λ_s = λ_i = 2λ_p is satisfied. We use a common value of λ = 2λ_p to replace λ_s and λ_i. According to Eq. 5, the phase mismatching increase with the topological charge m of the down-converted photon because the high-order modes have a larger divergence angle, which will decrease the longitudinal component of the wave vector, as shown in Figure 1B. Comparing with the mode ${\left|1\right.⟩}_s{\left|-1\right.⟩}_i$, the mode ${\left|5\right.⟩}_s{\left|-5\right.⟩}_i$ suffers from the larger longitudinal phase mismatching and has the lower coincidence probability. In this case, the longer nonlinear crystal will further increase the difference of the coincidence probabilities between the different OAM modes, although it can improve the total efficiency of the photon pairs generated by the SPDC. We calculate the spiral spectrum of the high-dimensional OAM entanglement for the LN crystal with L = 0.6 mm, as shown in Figure 1D. The brightness of photons greatly decreases for the high-order OAM modes, which often limits the usefulness of the high-dimensional OAM entangled states in the quantum experiment. When the length of the nonlinear crystal decreases to L = 6 μm, as shown in Figure 1C, the difference of coincidence probabilities between the different OAM modes is dramatically reduced and the spiral spectrum becomes flat, as shown in Figure 1E. The ultrathin nonlinear crystal not only allows very large longitudinal mismatch, but also leads to a very broad spectrum of emitted photons, both in frequency and in angle [42].

FIGURE 1

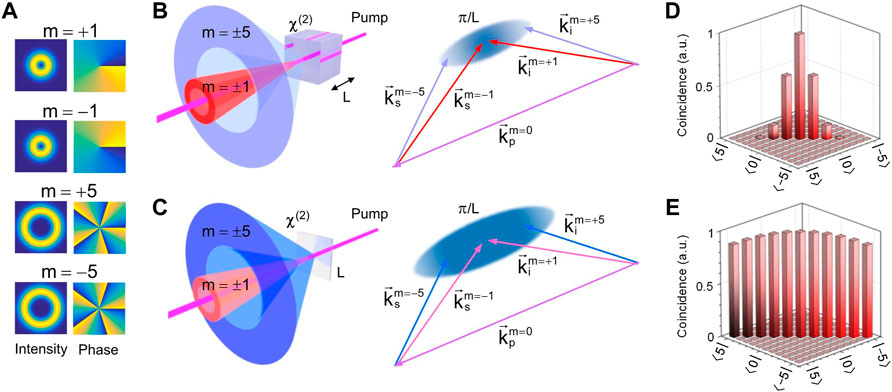
FIGURE 1. (A) The intensity and phase for OAM |m| = 1 and |m| = 5. High-dimensional OAM entanglement from the type-0 SPDC in a thick (B) and ultrathin (C) nonlinear LN crystal orthogonal to the pump (D) and (E) is the simulated spiral spectrum of 11-dimensional OAM entanglement in the nonlinear LN crystal with length of L = 0.6 mm and L = 6 μm respectively. The pump is a Gaussian mode m = 0. The coincidences of the different OAM state are normalized by the coincidence at OAM m = 0.

3 Experimental results

As the experimental setup shown in Figure 2A, we use an x-cut ultrathin film of MgO-doped LN on a fused silica substrate as a nonlinear medium. The LN ultrathin slice had a thickness of ∼6 μm. The pump source is a femtosecond (fs) pulsed laser at a central wavelength of 405 nm, with a pulse duration of ∼140 fs and a repetition rate of ∼80 MHz to create photon pairs at a degenerate wavelength of 810 nm by the SPDC. Benefiting from the largest element d₃₃ of the nonlinear susceptibility tensor, the polarization of the pump fs laser is oriented along the z axis of the ultrathin LN film. Under the condition of type-0 degenerate collinear phase matching, down-conversion photon pairs have the same polarization. The 10 nm narrow bandwidth interference filters (centred at the wavelength of 810 nm) are used to improve the spectral purity of the correlated photon pairs and to block the remaining pump.

FIGURE 2

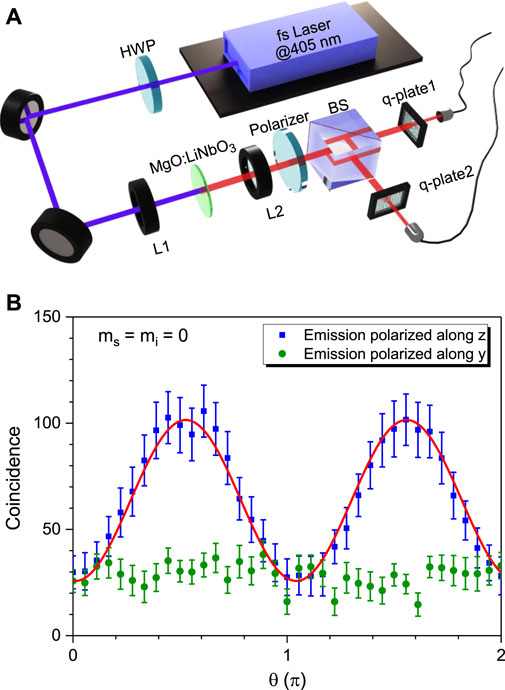
FIGURE 2. (A) The setup used to detect SPDC from the x-cut ultrathin LN film. The pump power is 250 mw. HWP: halfwave plate, BS: beam splitter, L1 and L2: lens (B) The coincidence rate of the fundamental mode (m = 0) versus the pump polarization direction, for the emission polarized along z (blue squares, red fit) and along y (green triangles). θ is the angle between the pump polarization and the y axis. The coincidence time is 1s.

To confirm that the SPDC was mediated by the d₃₃ element of the nonlinear susceptibility tensor, with the pump, signal, and idler photons all polarized along the z axis, we have measured the polarization dependence of the coincidence count, as shown in Figure 2B. The coincidence count depends on the angle θ between the pump polarization and the y axis as sin²θ (blue squares, red fitting curve) and reaches the maximum value only when the signal and idler photons are polarized along the z axis. In contrast, for the emission polarized along the y axis, almost no real coincidences were observed (green circles). Then we use two separate q-plates to transform the incoming field to a fundamental Gaussian mode, which is the unique mode that can be coupled into the single mode fibers, for measuring the OAM of the photon pairs. In the collinear configuration, OAM is conserved in the SPDC, hence we expect the OAMs of the signal and idler photons to be anticorrelated, i.e., the coincidence count is high only when m_s = −m_i. Figure 3 shows the measured coincidence counts for different combinations of signal and idler photon modes. For each combination the polarization-dependent coincidence counts verifies that the correlated photon pairs are generated from the ultrathin LN by the SPDC. Figure 4 shows the spiral spectrum of the 11-dimensional OAM entanglement and it becomes relatively flat comparing with thick nonlinear crystal. The measured coincidence of the high-order OAM state is lower comparing with the theoretical simulation because the collection efficiency decreases with the increment of the OAM sate. In addition, we observe that the SPDC of ultrathin crystal has better robustness for the position of the pump. When the crystal shift 1 mm from the focus of the pump, the decrease of the maximum coincidence counts for difference mode of photon pairs is about 5%.

FIGURE 3

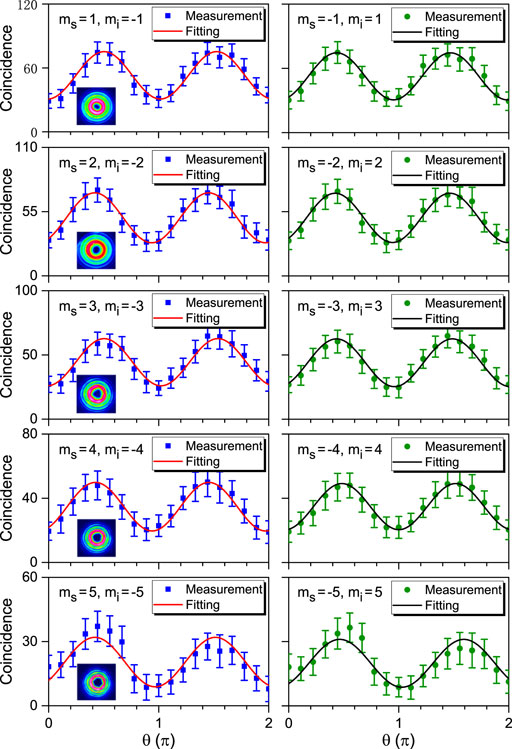
FIGURE 3. The coincidence rate versus the pump polarization direction for different mode combinations of the signal and idler photons from the SPDC. θ is the angle between the pump polarization and the y axis. The coincidence time is 1s. The insets are the intensity distributions for corresponded OAM.

FIGURE 4

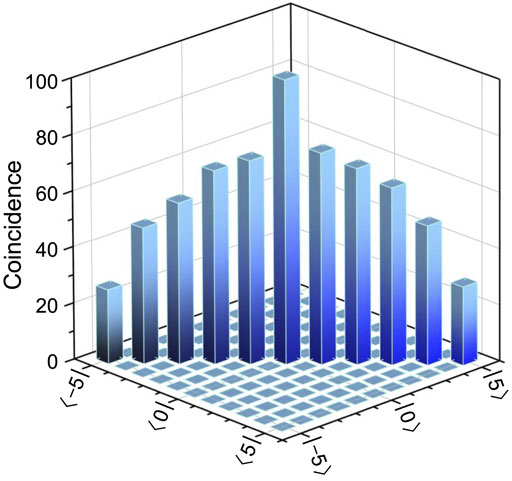
FIGURE 4. The measured spiral spectrum of 11-dimensional OAM entanglement from the SPDC in the ultrathin LN film. The coincidence time is 1s.

4 Conclusion

In conclusion, we have demonstrated the relatively flat high-dimensional OAM entanglement based on the SPDC in the ultrathin LN crystal which allows large longitudinal phase mismatching and decreases the difference of coincidence rate between the different OAM mode. This state might be required for quantum experiment. Although we use the highest nonlinear component available in LN, but the efficiency remained much lower than for phase-matched SPDC in a macroscopic crystal. The generation efficiency can be optimised by using the nonlinear material with the giant second-harmonic generation [45]. Recently, metasurfaces offer an ultracompact and versatile platform for enhancing nonlinear optical processes by designing Bound State in the Continuum (BIC) resonances, which support a high confinement of the optical field within the nonlinear material [46, 47]. Then SPDC efficiency can be dramatically increased when the signal and idler photons are supported by BIC resonances [48] to generate high-dimensional hyperentanglement in the frequency and OAM regimes for increasing the quantum information capacity.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

FD, YL, and H-TW designed experiments, FD performed the theoretical simulations FD dominantly and MW assistantly carried out experiments and analyzed data. FD, YL, and H-TW wrote the manuscript. YL and H-TW. planned and supervised the project. All authors discussed the results.

Funding

This work was supported financially by the National Key R&D Program of China (2019YFA0705000, 2019YFA0308700, 2020YFA0309500), the National Natural Science Foundation of China (12074197, 12074196, 11922406). The authors would like to thank the support by Collaborative Innovation Center of Extreme Optics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ren H-R, Li X-P, Zhang Q-M, Gu M. On-chip noninterference angular momentum multiplexing of broadband light. Science (2016) 352:805–9. doi:10.1126/science.aaf1112

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Xu O-Y, Xu Y, Xian M-C, Feng Z-W, Zhu L-W, Cao Y-Y, et al. Synthetic helical dichroism for six-dimensional optical orbital angular momentum multiplexing. Nat Photon (2021) 15:901–7. doi:10.1038/s41566-021-00880-1

CrossRef Full Text | Google Scholar

3. Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt Lett (1994) 19:780. doi:10.1364/OL.19.000780

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Torner L, Torres JP, Carrasco S. Digital spiral imaging. Opt Express (2005) 13:873. doi:10.1364/OPEX.13.000873

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liu K, Cheng Y-Q, Gao Y, Li X, Qin Y-L, Wang H-Q, et al. Super-resolution radar imaging based on experimental oam beams. Appl Phys Lett (2017) 110:164102. doi:10.1063/1.4981253

CrossRef Full Text | Google Scholar

6. Chu J-Q, Li X-F, Smithwick Q, Chu D-P. Coding/decoding two-dimensional images with orbital angular momentum of light. Opt Lett (2016) 41:1490. doi:10.1364/OL.41.001490

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lee MP, Gibson GM, Bowman R, Bernet S, Ritsch-Marte M, Phillips DB, et al. A multi-modal stereo microscope based on a spatial light modulator. Opt Express (2013) 21:16541. doi:10.1364/OE.21.016541

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Huo P-C, Zhang C, Zhu W-Q, Liu M-Z, Zhang S, Zhang S, et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett (2020) 4:2791–8. doi:10.1021/acs.nanolett.0c00471

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fang X-Y, Ren H-R, Gu M. Orbital angular momentum holography for high-security encryption. Nat Photon (2020) 14:102–8. doi:10.1038/s41566-019-0560-x

CrossRef Full Text | Google Scholar

10. Ren H-R, Fang X-Y, Jang J, Burger J, Rho J, Maier SA, et al. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat Nanotechnol (2020) 15:948–55. doi:10.1038/s41565-020-0768-4

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lavery MPJ, Speirits FC, Barnett SM, Padgett MJ. Detection of a spinning object using light’s orbital angular momentum. Science (2013) 341:537–40. doi:10.1126/science.1239936

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Berkhout GCG, Beijersbergen MW. Method for probing the orbital angular momentum of optical vortices in electromagnetic waves from astronomical objects. Phys Rev Lett (2008) 101:100801. doi:10.1103/PhysRevLett.101.100801

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Padgett M, Bowman R. Tweezers with a twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

14. Dholakia K, Cizmar T. Shaping the future of manipulation. Nat Photon (2011) 5:335–42. doi:10.1038/nphoton.2011.80

CrossRef Full Text | Google Scholar

15. Huang S-Y, Zhang G-L, Wang Q, Wang M, Tu C-H, Li Y-N, et al. Spin-to-orbital angular momentum conversion via light intensity gradient. Optica (2021) 8:1231. doi:10.1364/OPTICA.435475

CrossRef Full Text | Google Scholar

16. Bondarescu M, Thorne KS. New family of light beams and mirror shapes for future ligo interferometers. Phys Rev D (2006) 74:082003. doi:10.1103/PhysRevD.74.082003

CrossRef Full Text | Google Scholar

17. Wang J. Twisted optical communications using orbital angular momentum. Sci China Phys Mech Astron (2019) 62:34201. doi:10.1007/s11433-018-9260-8

CrossRef Full Text | Google Scholar

18. Bozinovic N, Yue Y, Ren Y-X, Tur M, Kristensen P, Huang H, et al. Terabitscale orbital angular momentum mode division multiplexing in fibers. Science (2013) 340:1545–8. doi:10.1126/science.1237861

PubMed Abstract | CrossRef Full Text | Google Scholar

19. He C, Shen Y, Forbes A. Towards higher-dimensional structured light. Light Sci Appl (2022) 11:205. doi:10.1038/s41377-022-00897-3

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Wang A-D, Zhu L, Chen S, Du C, Mo Q, Wang J, et al. Characterization of ldpc-coded orbital angular momentum modes transmission and multiplexing over a 50-km fiber. Opt Express (2016) 24:11716. doi:10.1364/OE.24.011716

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Krenn M, Fink M, Fickler R, Zeilinger A. Twisted photon entanglement through turbulent air across vienna. Proc Natl Acad Sci U S A (2015) 112:14197–201. doi:10.1073/pnas.1517574112

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yan Y, Xie G-D, Lavery MPJ, Huang H, Ahmed N, Bao C-J, et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat Commun (2014) 5:4876. doi:10.1038/ncomms5876

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Xie G-D, Ren Y-X, Yan Y, Huang H, Ahmed N, Li L, et al. Experimental demonstration of a 200-gbit/s free-space optical link by multiplexing laguerre-Gaussian beams with different radial indices. Opt Lett (2016) 41:3447. doi:10.1364/OL.41.003447

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Fabre C, Treps N. Modes and states in quantum optics. Rev Mod Phys (2020) 92:035005. doi:10.1103/RevModPhys.92.035005

CrossRef Full Text | Google Scholar

25. Shen Y, Rosales-Guzman C. Nonseparable states of light: From quantum to classical. Laser Photon Rev (2022) 16:2100533. doi:10.1002/lpor.202100533

CrossRef Full Text | Google Scholar

26. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: New quantum perspectives in high dimensions. Light Sci Appl (2017) 7:17146. doi:10.1038/lsa.2017.146

CrossRef Full Text | Google Scholar

27. Erhard M, Krenn M, Zeilinger A. Advances in high dimensional quantum entanglement. Nat Rev Phys (2020) 2:365–81. doi:10.1038/s42254-020-0193-5

CrossRef Full Text | Google Scholar

28. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature (2001) 412:313–6. doi:10.1038/35085529

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fickler R, Campbell G, Buchler B, Lam PK, Zeilinger A. Quantum entanglement of angular momentum states with quantum numbers up to 10, 010. Proc Natl Acad Sci U S A (2016) 113:13642–7. doi:10.1073/pnas.1616889113

PubMed Abstract | CrossRef Full Text | Google Scholar

30. M-Terriza G, Torres JP, Torner L. Twisted photons. Nat Phys (2007) 3:305–10. doi:10.1038/nphys607

CrossRef Full Text | Google Scholar

31. Kong L-J, Liu R, Qi W-R, Wang Z-X, Huang S-Y, Wang Q, et al. Manipulation of eight-dimensional bell-like states. Sci Adv (2019) 5:eaat9206. doi:10.1126/sciadv.aat9206

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhao S-M, Gong L-Y, Li Y-Q, Yang H, Sheng Y-B, Cheng W-W, et al. A large-alphabet quantum key distribution protocol using orbital angular momentum entanglement. Chin Phys Lett (2013) 30:060305. doi:10.1088/0256-307X/30/6/060305

CrossRef Full Text | Google Scholar

33. Hu X-M, Xing W-B, Liu B-H, He D-Y, Cao H, Guo Y, et al. Efficient distribution of high-dimensional entanglement through 11 km fiber. Optica (2020) 7:738. doi:10.1364/OPTICA.388773

CrossRef Full Text | Google Scholar

34. Romero J, Giovannini D, Franke-Arnold S, Barnett SM, Padgett MJ. Increasing the dimension in high-dimensional two-photon orbital angular momentum entanglement. Phys Rev A (2012) 86:012334. doi:10.1103/PhysRevA.86.012334

CrossRef Full Text | Google Scholar

35. Di Lorenzo Pires H, Florijn HCB, Van Exter MP. Measurement of the spiral spectrum of entangled two-photon states. Phys Rev Lett (2010) 104:020505. doi:10.1103/PhysRevLett.104.020505

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Anwar A, Prabhakar S, Singh RP. Size-invariant twisted optical modes for the efficient generation of higher-dimensional quantum states. J Opt Soc Am B (2021) 2976. doi:10.1364/JOSAB.436088

CrossRef Full Text | Google Scholar

37. Canas G, Gomez ES, Baradit E, Lima G, Walborn SP. Engineering entangled photons for transmission in ring-core optical fibers. Front Phys (2021) 9:752081. doi:10.3389/fphy.2021.752081

CrossRef Full Text | Google Scholar

38. Liu S-L, Zhou Z-Y, Liu S-K, Li Y-H, Li Y, Yang C, et al. Coherent manipulation of a three-dimensional maximally entangled state. Phys Rev A (2018) 98:062316. doi:10.1103/PhysRevA.98.062316

CrossRef Full Text | Google Scholar

39. Kovlakov EV, Straupe SS, Kulik SP. Quantum state engineering with twisted photons via adaptive shaping of the pump beam. Phys Rev A (2018) 98:060301. doi:10.1103/PhysRevA.98.060301

CrossRef Full Text | Google Scholar

40. Anwar A, Lal N, Prabhakar S, Singh RP. Selective tuning of hilbert spaces in states encoded with spatial modes of light. New J Phys (2020) 22:113020. doi:10.1088/1367-2630/abc783

CrossRef Full Text | Google Scholar

41. Kyselaa J, Erharda M, Hochrainer A, Krenn M, Zeilinger A. Path identity as a source of high-dimensional entanglement. Proc Natl Acad Sci U S A (2020) 117:26118–22. doi:10.1073/pnas.2011405117

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Okoth C, Cavanna A, Santiago-Cruz T, Chekhova MV. Microscale generation of entangled photons without momentum conservation. Phys Rev Lett (2019) 123:263602. doi:10.1103/PhysRevLett.123.263602

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Torres JP, Alexandrescu A, Torner L. Quantum spiral bandwidth of entangled two-photon states. Phys Rev A (2003) 68:050301. doi:10.1103/PhysRevA.68.050301

CrossRef Full Text | Google Scholar

44. Hua Y-L, Zhou Z-Q, Liu X, Yang T-S, Li Z-F, Li P-Y, et al. Annual-ring-type quasi-phase-matching crystal for generation of narrowband high-dimensional entanglement. Phys Rev A (2018) 97:013836. doi:10.1103/PhysRevA.97.013836

CrossRef Full Text | Google Scholar

45. Abdelwahab I, Tilmann B, Wu Y, Giovanni D, Verzhbitskiy I, Zhu M, et al. Giant second-harmonic generation in ferroelectric NbOI₂. Nat Photon (2022).

CrossRef Full Text | Google Scholar

46. Kang L, Bao H-G, Werner DH. Efficient second-harmonic generation in high Q-factor asymmetric lithium niobate metasurfaces. Opt Lett (2021) 46:633. doi:10.1364/OL.413764

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Yang Q-Y, Liu Y, Gan X-T, Fang C-Z, Han G-Q, Hao Y, et al. Nonlinear bound states in the continuum of etchless lithium niobate metasurfaces. IEEE Photon J (2019) 1–9. doi:10.1109/JPHOT.2020.3024789

CrossRef Full Text | Google Scholar

48. Parry M, Mazzanti A, Poddubny AN, Valle GD, Neshev DN, Sukhorukov AA, et al. Enhanced generation of nondegenerate photon pairs in nonlinear metasurfaces. Adv Photon (2021) 3:55001. doi:10.1117/1.AP.3.5.055001

CrossRef Full Text | Google Scholar