Abstract
Scientific organizations are creating carbon nanotube-based composites like and , which indicate significant response against voltage. Imbalance-based irregularity indices determine the degree of irregularity of a certain molecular structure and, as a result, determine the properties of a molecular substance. In this article, we aim to compute irregularity indices of two nanotubes, and . We produce formulas for the irregularity of these two nanotubes, which are functions depending on the parameters of the structure and . We compare our results graphically and conclude that is more irregular than .
Introduction
The chemical graph theory is rich with novel developments of functions and polynomials to foresee physiochemical aspects of chemical structures without using tools of quantum mechanics. One type of such a function is imbalance-based irregularity indices which determine the molecular complexity of the chemical substance under discussion. Carbon nanotubes are allotropes of carbon with a cylindrical-shaped nanostructure. These cylindrical-shaped carbon particles have amazing properties, which are significant for nanotechnology, optics, electronics, and various fields of material science and development [1–3].
Regarding flexible modulus and elasticity, carbon nanotubes are the stiffest and most grounded materials individually. This quality results from the covalent sp2 bonds framed between the carbon atoms. A multi-walled carbon nanotube was analyzed in 2000, which has a tensile strength of 63 gigapascals. The adaptability and quality of carbon nanotubes make them of potential use in controlling other nanoscale structures, which suggests that they will have a basic activity in nanotechnology building [4–7]. Molecular topologists are interested in studying the complexity, pattern, combinatorial properties, and irregularities of molecular structures. A basic tool is the conversion of the molecular structure into a graph theoretic model, where vertices are used as toms and edges are used as bonds.
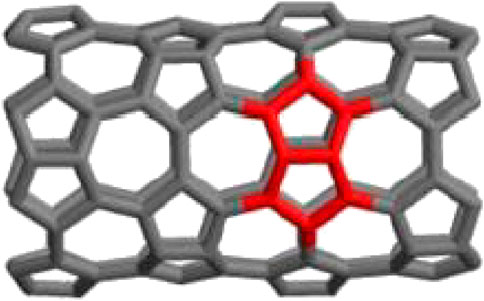
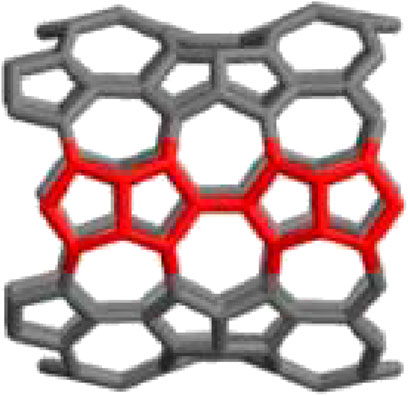
In this article, we aim to compute the imbalance-based degree of irregularity of carbon nanotubes. The molecular graphs of carbon nanotubes and are shown in Figures 1, 2, respectively. One is interested to know the degree of the molecular complexity of these tubes comparatively so that an overview of the properties depending upon the molecular complexity can be understood. By using linear regression, a stochastic relationship can be established between the aforementioned irregularity indices and different properties such as standard enthalpy of vaporization, boiling point, entropy, and acentric factor. The structures of these nanotubes consist of cycles and ( net which is a trivalent decoration constructed by alternating and ) by different compounds. It can cover either a cylinder or a torus.
FIGURE 1
FIGURE 2
The two-dimensional lattice of is shown in Figure 3, and the two-dimensional lattice of is shown in Figure 4.
FIGURE 3
FIGURE 4
In order to proceed with our main objective, we have to be a bit familiar with some notions and notations of the graph theory. We consider only a simple and connected graph G with vertex V, edge set E, and du and dv, the degree of vertices u and v, respectively. A topological invariant is an isomorphism of the graph that preserves the topology of the graph. A graph is said to be regular if every vertex of the graph has the same degree. A topological invariant is called an irregularity index if this index vanishes for a regular graph and is non-zero for a non-regular graph. Regular graphs have been extensively investigated, particularly in mathematics. Their applications in the chemical graph theory initiated the discovery of nanotubes and fullerenes. Paul Erdos stressed the study of irregular graphs for the first time in history in [8]. In the Second Krakow Conference on Graph Theory (1994), Erdos officially posed an open problem as “the determination of extreme size of highly irregular graphs of given order” [9]. Since then, irregular graphs and the degree of irregularity have become one of the core open problems of the graph theory.
A graph in which each vertex has a different degree than the other vertices is known as a perfect graph. The authors of [10] demonstrated that no graph is perfect. The graphs lying in between are called quasi-perfect graphs, in which all except two vertices have different degrees [9]. Simplified ways of expressing irregularities are irregularity indices. These irregularity indices have been studied recently in a novel way [11, 12]. The first such irregularity index was introduced in [13]. Most of these indices used the concept of the imbalance of an edge defined as [14, 15]. The Albertson index, AL(G), was defined by Albertson in [15] as . In this index, the imbalance of edges is computed. The irregularity indices IRL(G) and IRLU(G) are introduced by Vukicevic and Gasparov [16], as and respectively. Recently, Abdoo et al. have introduced a new term “total irregularity measure of a graph G,″ which is defined as [17–19] . Recently, Gutman et al. have introduced the IRF(G) irregularity index of the graph G, which is described as in [20]. The Randic index itself is directly related to an irregularity measure, which is described as in [21]. Further irregularity indices of similar nature can be traced in [21] in detail. These indices are given as , , , , , and . Further details are given in [21–32]. There were various attempts to quantify the irregularity of a graph, of which the Collatz–Sinogowitz index, Bell index, Albertson index, and total irregularity are the best known [13–15]. It has been mathematically proven that no two of these irregularity measures are mutually consistent, namely, that for any two such measures, irrX and irrY, there exist pairs of graphs G1 and G2, such that irrX (G1) > irrX (G2) but irrY (G1) < irrY (G2). People working in related fields have used the aforementioned indices to capture the irregularity of chemical graphs, and occasionally, these indices depict properties such as symmetry and stability of isomers [21].
These irregularity indices have applications in determining the properties of alkane isomers [21]. These applications pushed others to think in this direction. Most recently, authors have computed irregularity indices of chemical substances [33–36]. Hussain et al. established closed forms of the aforementioned irregularity indices for some benzenoid systems in [35] and some nanostar dendrimers in [36]. The present article can be treated as a continuation of the articles [35, 36].
The main results
In this section, we present our main results about the theoretical computation of irregularity indices of the aforementioned nanotubes.
For
the irregularity measures of
are
1
2
3
4
5
6
7
8
9
10
11
12
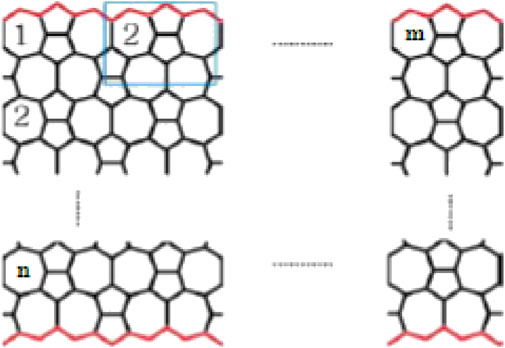
Proof:
In order to prove the aforementioned theorem, we have to consider Figures 1, 3. Table 1 shows the mathematical distribution of the types of edges into two different classes.
Now using Table 1 and the aforementioned definitions, we have
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
TABLE 1
| Number of edges | Number of indices |
|---|---|
Edge partition of the nanotube.
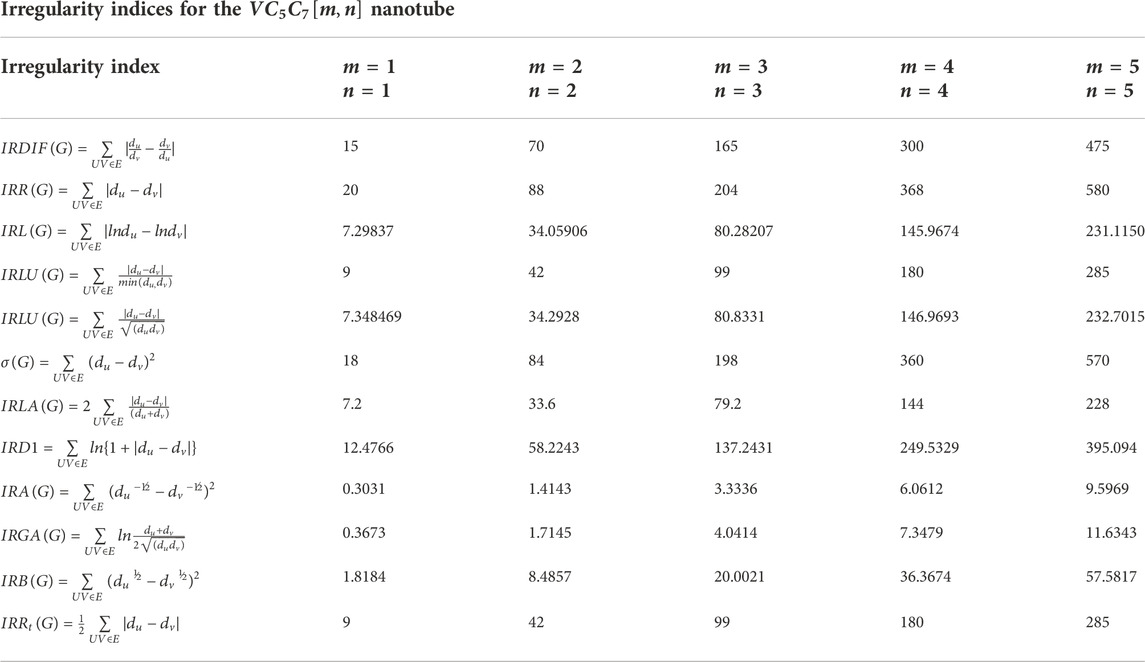
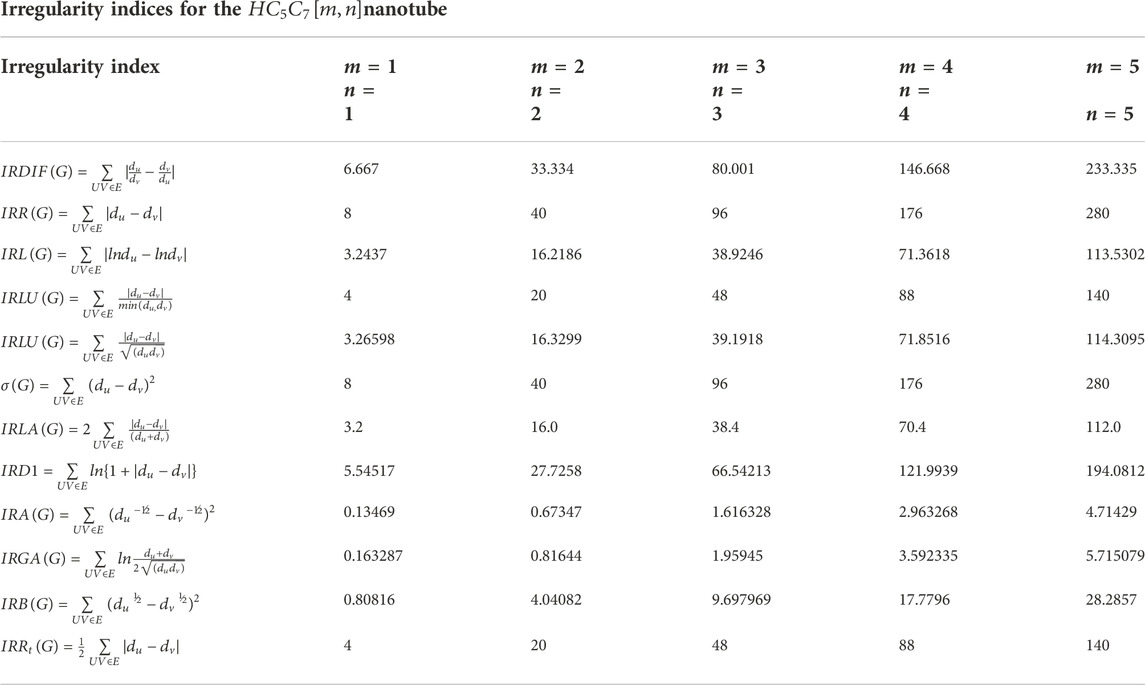
Test values of the irregularity measures of the nanotube VC5C7[m, n] has been given in Table 2. Now, we give our results about for positive values of m and n.
TABLE 2
| Irregularity indices for the nanotube | |||||
|---|---|---|---|---|---|
| Irregularity index | m = 1 n = 1 | m = 2 n = 2 | m = 3 n = 3 | m = 4 n = 4 | m = 5 n = 5 |
| 15 | 70 | 165 | 300 | 475 | |
| 20 | 88 | 204 | 368 | 580 | |
| 7.29837 | 34.05906 | 80.28207 | 145.9674 | 231.1150 | |
| 9 | 42 | 99 | 180 | 285 | |
| 7.348469 | 34.2928 | 80.8331 | 146.9693 | 232.7015 | |
| 18 | 84 | 198 | 360 | 570 | |
| 7.2 | 33.6 | 79.2 | 144 | 228 | |
| 12.4766 | 58.2243 | 137.2431 | 249.5329 | 395.094 | |
| 0.3031 | 1.4143 | 3.3336 | 6.0612 | 9.5969 | |
| 0.3673 | 1.7145 | 4.0414 | 7.3479 | 11.6343 | |
| 1.8184 | 8.4857 | 20.0021 | 36.3674 | 57.5817 | |
| 9 | 42 | 99 | 180 | 285 | |
Test values for the irregularity indices of the nanotube .
For
the irregularity measures of
are
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
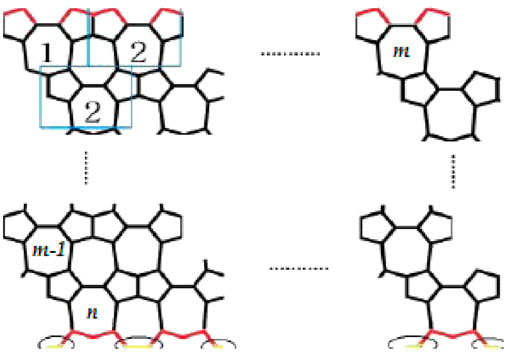
Proof:
In order to prove the aforementioned theorem, we have to consider Figures 2, 4. Table 3 shows the distribution of edges into three different classes.
Now using Table 4 and the aforementioned definitions from Table 1, we have
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
TABLE 3
| Number of edges | Number of indices |
|---|---|
| (2,2) | |
| (3,3) | |
| (2,3) |
Edge partition of the nanotube.
TABLE 4
| Irregularity indices for the nanotube | |||||
|---|---|---|---|---|---|
| Irregularity index | m = 1 n = 1 | m = 2 n = 2 | m = 3 n = 3 | m = 4 n = 4 | m = 5 n = 5 |
| 6.667 | 33.334 | 80.001 | 146.668 | 233.335 | |
| 8 | 40 | 96 | 176 | 280 | |
| 3.2437 | 16.2186 | 38.9246 | 71.3618 | 113.5302 | |
| 4 | 20 | 48 | 88 | 140 | |
| 3.26598 | 16.3299 | 39.1918 | 71.8516 | 114.3095 | |
| 8 | 40 | 96 | 176 | 280 | |
| 3.2 | 16.0 | 38.4 | 70.4 | 112.0 | |
| 5.54517 | 27.7258 | 66.54213 | 121.9939 | 194.0812 | |
| 0.13469 | 0.67347 | 1.616328 | 2.963268 | 4.71429 | |
| 0.163287 | 0.81644 | 1.95945 | 3.592335 | 5.715079 | |
| 0.80816 | 4.04082 | 9.697969 | 17.7796 | 28.2857 | |
| 4 | 20 | 48 | 88 | 140 | |
Test values for the irregularity indices of the nanotube .
Graphical analysis, discussions, and conclusion
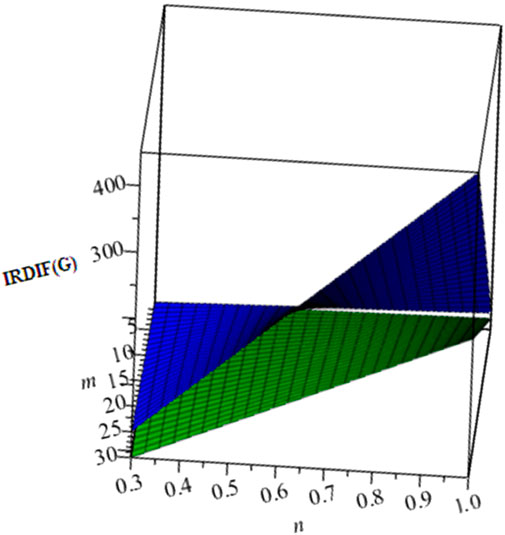
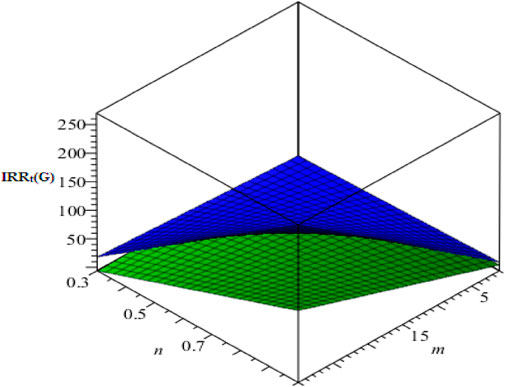
In this section, we present our computational analysis of the irregularity of both of these nanotubes and compare the results obtained. We used 3D graphs in which the Z-axis represents the values of the irregularity indices and the other two axes are devoted to m and n. We used a BLUE graph to show the behavior irregularity indices of , and a GREEN graph shows the graphical behavior irregularity indices of . Following Figure 5 is the irregularity demonstration for the index IRDIF, which shows that is more irregular than .
FIGURE 5
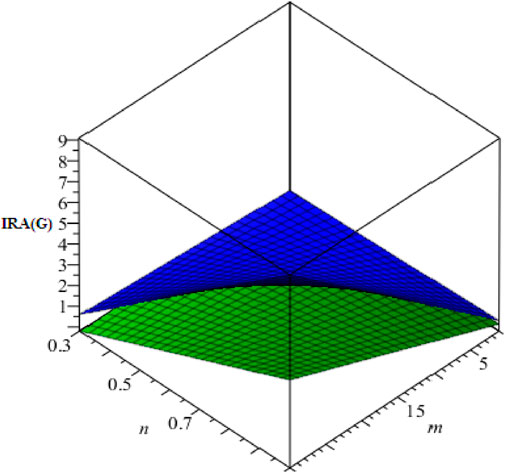
In Figure 6, we give a demonstration for the irregularity index AL. Again it can easily be concluded that is more irregular than . It is evident from the graphs and the two tables where comparative values for the calculated indices are given. Values obtained by most irregularity indices for VC5C7 are higher than those for HC5C7 for the same values of parameters m and n. So, as far as computational irregularity is concerned, VC5C7 is more irregular than HC5C7. The same trends are shown by all other irregularity indices; please see Figures 7, 8. Based on the aforementioned comparative analysis, we conclude that is more irregular than for all irregularity indices discussed in this article. This conclusion can be useful in nano-engineering and electronics.
FIGURE 6
FIGURE 7
FIGURE 8
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
MM conducted the computation and conceived the idea.
Acknowledgments
Author is thankful to professor Liu for technical support. Author is also thankful to the University of Punjab for the support.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
DengHLiXPengQWangXChenJLiY. Monodisperse magnetic single‐crystal ferrite microspheres. Angew Chem Int Ed Engl (2005) 117(18):2782–5. 10.1002/anie.200462551
2.
SomorjaiGABorodkoYG. Research in nanosciences–great opportunity for catalysis science. Catal Lett (2001) 76(1-2):1–5. 10.1023/a:1016711323302
3.
CorriuRJMehdiAReyéC. Molecular chemistry and nanosciences: On the way to interactive materials. J Mater Chem (2005) 15(40):4285–94. 10.1039/b504536n
4.
BaughmanRHZakhidovAADe HeerWA. Carbon nanotubes--the route toward applications. science (2002) 297(5582):787–92. 10.1126/science.1060928
5.
HarrisonBSAtalaA. Carbon nanotube applications for tissue engineering. Biomaterials (2007) 28(2):344–53. 10.1016/j.biomaterials.2006.07.044
6.
De VolderMFTawfickSHBaughmanRHHartAJ. Carbon nanotubes: Present and future commercial applications. science (2013) 339(6119):535–9. 10.1126/science.1222453
7.
LauAKTHuiD. The revolutionary creation of new advanced materials—Carbon nanotube composites. Composites B: Eng (2002) 33(4):263–77. 10.1016/s1359-8368(02)00012-4
8.
ChartrandGErdosPOellermannO. How to define an irregular graph. Coll Math J (1988) 19:36–42. 10.1080/07468342.1988.11973088
9.
MajcherZMichaelJ. Highly irregular graphs with extreme numbers of edges. Discrete Math (1997) 164:237–42. 10.1016/s0012-365x(96)00056-8
10.
BehzadMChartrandG. No graph is perfect. Am Math Mon (1947) 74:962–3. 10.2307/2315277
11.
HoroldagvaBBuyantogtokhLDorjsembeSGutmanI. Maximum sizeof maximally irregular graphs. Match Commun Math Comput Chem (2016) 76:81
12.
LiuFZhangZMengJ. The size of maximally irregular graphs and maximally irregular triangle–free graphs. Graphs Comb (2014) 30:699–705. 10.1007/s00373-013-1304-1
13.
CollatzLSinogowitzU. Spektren Endlicher Graphen Abh Math Sem Univ Hamburg (1957) 21:63
14.
BellFK. A note on the irregularity of graphs. Linear Algebra Appl (1992) 161:45–54. 10.1016/0024-3795(92)90004-t
15.
AlbertsonM. The irregularity of a graph. Ars Comb (1997) 46:219
16.
VukičevićDGraovacA. Valence connectivities versus randić, zagreb and modified zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat Chem Acta (2004) 77:501
17.
AbdoHBrandtSDimitrovD. The total irregularity of a graph. Discr Math Theor Comput Sci (2014) 16:201
18.
AbdoHDimitrovD. The total irregularity of graphs under graph operations. Miskolc Math Notes (2014) 15:3–17. 10.18514/mmn.2014.593
19.
AbdoHDimitrovD. The irregularity of graphs under graph operations. Discuss Math Graph Theor (2014) 34:263–78. 10.7151/dmgt.1733
20.
GutmanI. Topological indices and irregularity measures. J Bull (2018) 8:469. 10.7251/BIMVI1803469G
21.
RetiTSharfdiniRDregelyi-KissAHagobinH. Graph irregularity indices used as molecular discriptors in QSPR studies. MATCH Commun Math Comput Chem (2018) 79:509
22.
HuYLiXShiYXuTGutmanI. On molecular graphs with smallest and greatest zeroth-Corder general randic index. MATCH Commun Math Comput Chem (2005) 54:425
23.
CaporossiGGutmanIHansenPPavlovicL. Graphs with maximum connectivity index. Comput Biol Chem (2003) 27:85–90. 10.1016/s0097-8485(02)00016-5
24.
LiXGutmanI. Mathematical aspects of Randic, Type molecular structure descriptors. In: Mathematical chemistry monographs. Serbia: University of Kragujevac and Faculty of Science Kragujevac: Kragujevac (2006).
25.
DasKGutmanI. Some properties of the second zagreb index. MATCH Commun Math Comput Chem (2004) 52:103–12.
26.
TrinajsticNNikolicSMilicevicAGutmanI. About the zagreb indices. Kemija u industriji: Časopis kemičara i kemijskih inženjera Hrvatske (2010) 59:577
27.
MilicevicANikolicSTrinajsticN. On reformulated Zagreb indices. Mol Divers (2004) 8:393–9. 10.1023/b:modi.0000047504.14261.2a
28.
GuptaCKLokeshaVShwethaSBRanjiniPS. On the symmetric division DEG index of graph. Southeast Asian Bull Math (2016) 40:59
29.
BalabanAT. Highly discriminating distance-based topological index. Chem Phys Lett (1982) 89:399–404. 10.1016/0009-2614(82)80009-2
30.
FurtulaBGraovacAVukičevićD. Augmented zagreb index. J Math Chem (2010) 48:370–80. 10.1007/s10910-010-9677-3
31.
DasKC. Atom–bond connectivity index of graphs. Discrete Appl Math (2010) 158:1181–8. 10.1016/j.dam.2010.03.006
32.
EstradaETorresLRodríguezLGutmanI. An atom–bond connectivity index: Modeling the enthalpy of formation of alkanes. Indian J Chem (1998) 37:849
33.
ZahidIAslamAIshaqMAamirM. Characteristic study of irregularity measures of some Nanotubes. Can J Phys (2019) 97:1125–32. 10.1139/cjp-2018-0619
34.
GaoWAamirMIqbalZIshaqMAslamA. On irregularity measures of some dendrimers structures. Mathematics (2019) 7:271. 10.3390/math7030271
35.
HussainZRafiqueSMunirMAtharMChaudharyMAhmadHet alIrregularity molecular descriptors of hourglass, jagged-rectangle, and triangular benzenoid systems. Processes (2019) 7:413. 10.3390/pr7070413
36.
HussainZMunirMRafiqueSHussnainTAhmadHChel KwunYet alImbalance-based irregularity molecular descriptors of nanostar dendrimers. Processes (2019) 7:517. 10.3390/pr7080517
Summary
Keywords
irregularity index, VC5C7[m,n] and HC5C7 [m,n], nanotubes, imbalance-based irregularity measure, molecular computing
Citation
Munir MM (2022) Irregularity molecular descriptors of and nanotubes. Front. Phys. 10:969598. doi: 10.3389/fphy.2022.969598
Received
17 June 2022
Accepted
22 September 2022
Published
17 November 2022
Volume
10 - 2022
Edited by
Fernando A. Oliveira, University of Brasilia, Brazil
Reviewed by
Weigang Sun, Hangzhou Dianzi University, China
Ali Mehri, Babol Noshirvani University of Technology, Iran
Updates
Copyright
© 2022 Munir.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Mobeen Munir, mmunir.math@pu.edu.pk
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.