- 1Department of automation, Tsinghua University, Beijing, China
- 2Yidu Cloud AI Lab, Yidu Cloud (Beijing) Technology Co., Ltd., Beijing, China
Awareness of epidemics can influence people’s behavior and further trigger changes in epidemic spreading. Previous studies concentrating on the coupled awareness-epidemic dynamics usually ignore the multi-type information and the heterogeneity of individuals. However, the real-world cases can be more complicated, and the interaction between information diffusion and epidemic spreading needs further study. In this article, we propose an individual-based epidemics and multi-type information spreading (IEMIS) model on two-layered multiplex networks considering positive and negative preventive information and two types of heterogeneity: 1) heterogeneity of aware individual’s state which leads to differences in aware transmission capacity and 2) heterogeneity of individual’s node degree which affects the epidemic infection rate. Based on Micro-Markov Chain approach (MMCA), we derive the theoretical epidemic threshold for the proposed model and validate the results by those obtained with Monto Carlo (MC) simulations. Through extensive simulations, we demonstrate that for epidemics with low infectivity, promoting the diffusion of positive preventive information, enhancing the importance ratio of neighbors who are aware of positive information, and increasing social distance among individuals can effectively suppress epidemic spreading. However, for highly infectious diseases, the influence of these factors becomes limited.
Introduction
Pandemics are major threats to human society Morens et al. [1]. Recently, during the COVID-19 pandemic, epidemic-related information diffused by official media, mass media, or relatives and friends has aroused public awareness. Crisis awareness or negative emotions may propagate among individuals. Such awareness can further influence people’s decision-making or behavior, for e.g., wearing masks, reducing physical contact with others, and receiving the vaccination, and as a result, may trigger changes in epidemic spreading Ferguson [2]; Wang et al. [3]; Funk et al. [4]; Funk et al. [5]; Ruan et al. [6]. Therefore, it is necessary to understand the interaction between information diffusion and epidemic propagation, and this topic has gained much attention in recent studies Arefin et al. [7]; Kabir and Tanimoto [8]; Nadini et al. [9]; Hota and Sundaram [10]; Li and Li [11].
Recent studies on the coupled awareness-epidemic dynamics usually used two asymmetrical networks to represent two spreading processes Wang et al. [12]; Jia et al. [13]; Guo et al. [14]; Zhan et al. [15]; Wang et al. [16], Wang et al. [17]. For example, Kabir et al. [18] constructed a two-layer SIR-UA (susceptible-infected-recovered/unaware-aware) model to study the interaction between physical contact and information diffusion on epidemic spreading. Xia et al. [19] considered the influence of mass media in information diffusion in the awareness-epidemic model and derived the epidemic threshold which is correlated with the multiplex network topology. Guo et al. [20] incorporated three types of heterogeneity with the coupled awareness-epidemic spreading model and pointed out that the heterogeneity has two-stage effects on the epidemic threshold. Li et al. [21] used a temporal multiplex network to study the spatial–temporal properties of multiplex networks to the epidemic spreading. Jia et al. [13] proposed a multi-layer activity-driven network that investigates disease diffusion with self-protection awareness. Their results indicate the impact of network structure and propagation parameters on the epidemic threshold. Kabir et al. [22] presented a susceptible –vaccinated– infected–recovered (SIR/V) with the unaware–aware (UA) epidemic model to study the impact of vaccination on epidemic dynamics. Based on their model, they studied the vaccination game with different types of strategy updating rules and different network topologies.
In the real world, the prevalence of public discussion on epidemics varies and does not always bring about a positive effect on the epidemic spreading Depoux et al. [23]; Ahmad and Murad [24]. For instance, individuals may become vigilant or scared and take protective measures when they receive information regarding the pandemic through official media. That is, a positive correlation between the protective measures taken by individuals and the spread of awareness could be built. However, based on the diversification of information, individuals may be affected by misdirected information regarding the disease spreading on social media and thus become irrational to the epidemic. Irrational behaviors including irrational antimicrobial prescribing Parveen et al. [25], irrational beliefs Teovanovic et al. [26], and panic buying Arafat et al. [27] can facilitate the propagation of epidemics by individuals’ improper protective measures. Hence, information diffusion can also lead to a negative correlation between information diffusion and the spread of the epidemic. The issue how the interaction of different types of information influences epidemic propagation has been further studied. To distinguish the impact of different types of information on disease spread, Zhang et al. [28] introduced a nonlinear dependence of the epidemic infection rate representing the effect of different forms of dependence on the coevolving dynamics. In addition, Wang et al. [29] studied the impact of positive and negative epidemic-related information on disease spread. These studies pointed out the significance of information diversity on the propagation of epidemics. However, assumptions for multiple preventive information are still limited and do not consider the individual heterogeneity in the diffusion of information.
Early studies usually assume that individuals are treated equally, namely, individuals have the same response to epidemics after being aware of the protective measures, and each infected or aware individual has the same influence on their neighbors. In fact, the individual differences lie in its characteristics and relationship with the affected neighbors (e.g., number of contacts, states, and intimacy with infected neighbors) Wang et al. [17]; Liu et al. [30]; Guo et al. [31]; Zhang et al. [32]. For instance, highly connected individuals (hub nodes) have higher infectious rates compared with those lowly connected individuals (weak nodes). In other words, individuals who have large social circles are more likely to affect others or be affected by their neighbors. In recent years, there has been an increasing focus on the study of the influence of individual heterogeneity on epidemic dynamics. Guo et al. [33] described the heterogeneity by using degree and k-core measures in three models based on different assumptions. Results showed a difference in the final epidemic size between the k-core measure and the degree measure. Chen et al. [34] proposed a resource-epidemic co-evolution model in order to study the influence of allocation of individual resources on the dynamic of an epidemic. Also, they came to the conclusion that the heterogeneity of self-awareness distribution suppresses the outbreak of an epidemic. Pan and Yan [35] incorporated the heterogeneity of individual response to disease, the heterogeneity of influence in the epidemic network, and the heterogeneity of influence in the information network in a coupled awareness-epidemic spreading model in multiplex networks. Although studies mentioned previously highlight the necessity of considering individual heterogeneity in the information-epidemic multiplex network-based model, such heterogeneity is simple compared to the reality. Therefore, the issue how individual heterogeneity impacts the interplay between epidemics spreading and awareness diffusion requires further study.
Motivated by the aforementioned considerations, we propose an individual-based epidemics and multi-type information spreading (IEMIS) model upon multiplex networks. To investigate the impact of multi-type information, we introduce two types of information: 1) positive and 2) negative preventive information. The diffusion of awareness can reduce or increase the risk of infection depending on its type. Considering that the diffusion speed of awareness is also related to the information type and the epidemic dynamics, the transmission rate of different types of information varies. Moreover, to explore the influence of individual heterogeneity on the interaction between information and disease, two types of heterogeneity are considered: 1) heterogeneity of aware individuals’ states (health state and information type) which contributes to different aware transmission capacities and 2) heterogeneity of individual’s node degree which influences the epidemic infection rate. In this study, we aim to answer the following questions: 1) how do two classes of information affect epidemic spreading when considering individual heterogeneity? 2) how do the two types of individual heterogeneity affect epidemic spreading? and 3) how do the other disease-related or information-related parameters influence the individual heterogeneity?
The remainder of this article is organized as follows. In Section 2, we describe the individual-based epidemics and multi-type information spreading model. In Section 3, we analyze the proposed model by MMCA and derive the analytical expression of the epidemic threshold. In Section 4, we compare the results simulated by MMC and MC methods, validate the accuracy of the MMC method, and investigate the impact of different types of information and individual heterogeneity. In Section 5, we present some concluding remarks for our findings.
Model description
In this article, we proposed an individual-based epidemics and multi-type information spreading model (IEMIS) by two-layered multiplex networks, as presented in Figure 1. The upper layer represents the information diffusion based on the information network, where links represent connections with information spreaders such as friends on Twitter or Facebook, while the lower layer supports the propagation of epidemics, where links denote physical contacts among individuals, e.g., contacts among family members, classmates, or colleagues. Each layer can be represented as a graph G = (V, E), where V and E denote individuals and their links, respectively. The link set X and Y represent the adjacency matrices of epidemic and information networks. The description of key parameters is listed in Table 1. The interactions between the two processes and the corresponding propagation regulations are as follows:
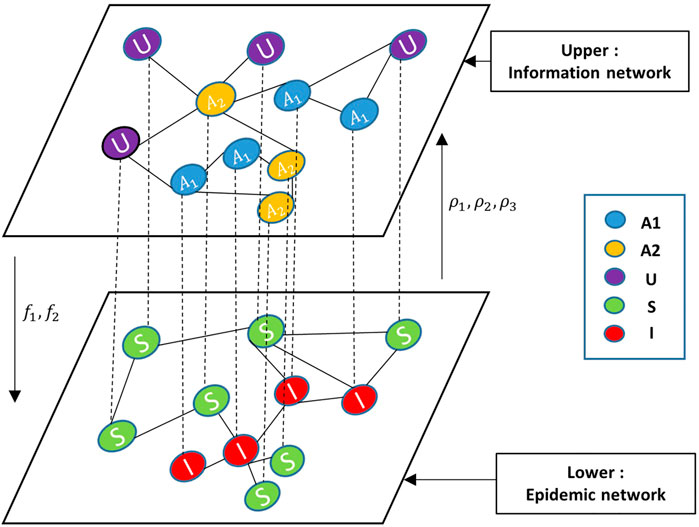
FIGURE 1. Structure of the individual-based epidemics and multi-type information spreading model (IEMIS) in a two-layered network. Nodes in the information network (the upper layer) have three possible states: unaware(U), aware of positive prevention (A1), or aware of negative prevention (A2). Nodes in the epidemic network (the lower layer) have two possible states: susceptible (S) or infected (I). The description of key parameters is listed in Table 1.
Propagation rules
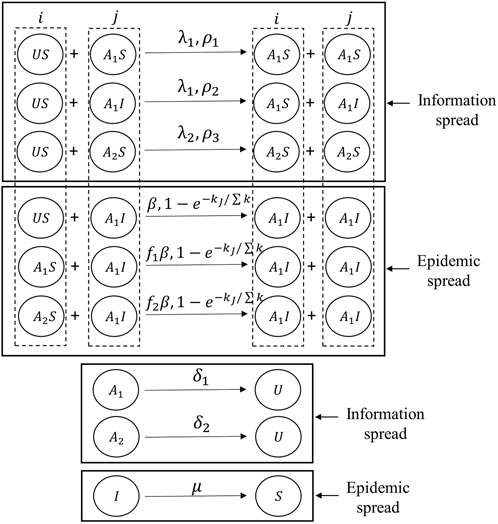
1. Information diffusion. In the upper layer, nodes are separated into three types: unaware (U), aware of positive prevention (A1), and aware of negative prevention (A2). Individuals in state U do not have any awareness about the epidemic prevention. Here, individuals in A1 and A2 are both aware of the disease but take different precautions toward the disease. Individuals in state A1 can take effective precautions toward the disease and have lower infection rates than unaware individuals. On the contrary, individuals in state A2 tend to take irrational preventive measures which lead to higher infection rates than unaware individuals. The unaware individuals can get awareness through contact with neighbors in state A1 (A2) with probability λ1 (λ2). Also, individuals in state A1 and A2 may forget the awareness with probabilities δ1 and δ2, respectively. Moreover, in terms of the awareness-related impact on the epidemic spreading, susceptible individuals whose states are A1 and A2 can influence the probability of being infected by multiplication factors f1 (0 ≤ f1 ≤ 1) and f2 (1 ≤ f2 ≤ 2), respectively. The lower the multiplication factor is, the lower the probability of individuals being infected is, especially when f1 = 0, individuals are fully immune to the infectious disease.
2. Epidemic propagation. In the lower layer, there exist two different health-related states: susceptible(S) and infected (I). Susceptible individuals may be infected with the probability β by infected (I) neighbors when they are unaware of epidemics. The susceptible individuals who are in state A1 and A2 may be infected with probabilities f1β and f2β, respectively. Also, the infected (I) individuals recover with the probability of μ.
3. Heterogeneity of aware individuals’ states. Aware individuals in different states (health state and information type) have different aware transmission capacities. It is known that, in many cases, awareness spread by infected individuals can be more persuasive than healthy people. Neighbors of those infected individuals tend to be more alert to the infectious disease and more willing to take protective measures. In addition, individuals in A1 and A2 states also play different roles in awareness diffusion. We assume that unaware people are more likely to acquire positive preventive information rather than the negative one. Compared with the former studies Wang et al. [29], Wang et al. [17], which assume that aware neighbors have the same contribution on awareness spreading (important ratio of aware individuals
4. Heterogeneity of individual’s node degree. The degree distribution of the epidemic network contributes to the heterogeneity of infection rate for susceptible individuals. The infected individuals with a large node degree mean that they have frequent social activities and are highly connected with their neighbors. Such hub nodes are more likely to be the virus carrier. Hence, the node degree ki is used to represent the impact of infected node i, and ki/∑k is regarded as the influence weight where ∑k is the total degree of the infected neighbors. Figure 3 shows the disease transmission regulation between a susceptible individual and its infected neighbors. Here,
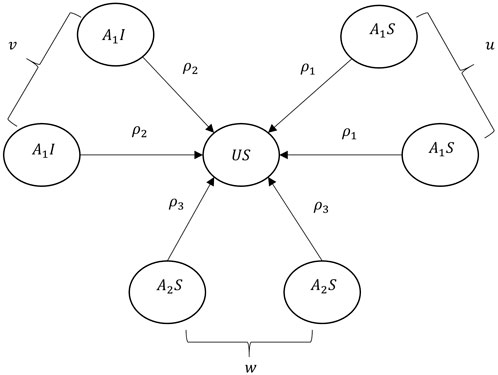
FIGURE 2. Sketch map of the awareness diffusion between unaware individuals and their aware neighbors. u, v, and w denote the number of A1S, A1I, and A2S, respectively. ρ1, ρ2, and ρ3 are the health-related factors.
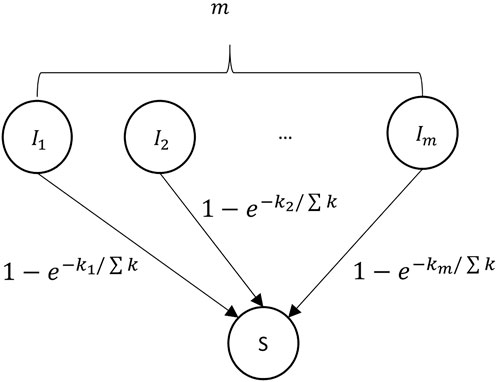
FIGURE 3. Disease transmission regulation among susceptible individuals and their infected neighbors. m represents the number of a susceptible individual’s infected neighbor.
Awareness-epidemic-based dynamics
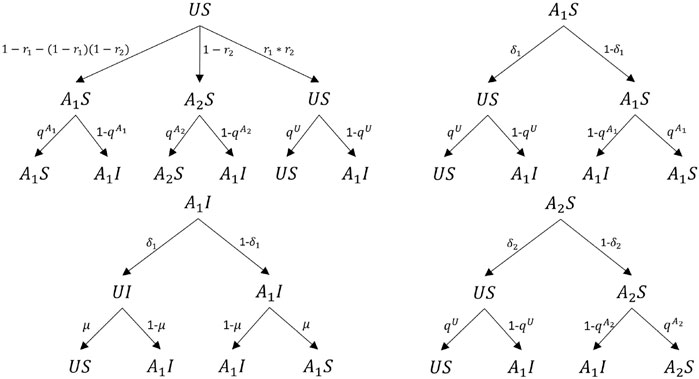
Here, we assume that once an individual is infected, the individual would be aware of the positive preventive information. Considering the combination of health states and awareness states, there are four possible states in our model: 1) US (susceptible individual who is unaware of epidemic), 2) A1S (susceptible individual who is aware of positive preventive information), 3) A2S (susceptible individual who is aware of negative preventive information), and (4) A1I (infected individual who is aware of positive preventive information). The possible state transition procedures are presented in Figure 4. It should be noted that Figure 4 only indicates the state transitions of individual i by its neighbor j who has a transmission capacity of disease or information after a possible epidemic or information spread. That is, Figure 4 only presents changes in the state of individual i. Also, it does not denote a transition in a time step for both the state in epidemic, and information networks of individual i would change in a time step. For example, a susceptible individual who is unaware of the epidemic (US) would be informed by its neighbor j who is in state A1S with a certain probability related to λ1 and ρ1. In addition, we assume that in the upper layer once the unaware individual receives a certain kind of information, the individual will not be able to accept other information at this time step.
Analytical results based on MMCA
In this section, the proposed epidemic model is analyzed, and the epidemic threshold βc is given by MMCA. The probabilities that one individual be in one of the four states at time t can be given as
Let xij and yij be the adjacency matrices of the epidemic and information network, respectively. If a link exists between nodes i and j in the epidemic (information) network, then xij (yij) = 1. Otherwise, xij (yij) = 0. Assuming that the possibilities of becoming infected or aware by neighbors are independent, we define the probability of individual i not being aware of positive or negative information at time t by ri1(t) and ri1(t). In addition,
Here, u represents the number of neighbors of individual i in state A1S, v represents the number of neighbors in state A1I, and w represents the number of neighbors in state A2S. Based on the definition of each state, transition probability trees for the four states (US, A1S, A2S, A1I) are presented in Figure 5. As shown in Figure 5, each individual will transmit its states according to the transition trees and its current state in each time step. Individuals who are aware of the positive (negative) information tend to forget the information with probability δ1 (δ2). μ denotes the probability of being recovered for an infected individual. According to the transition trees, transition equations for individual i by using MMCA are listed in Eq (2):
where
When t → ∞, the model will lead to a steady state and the probabilities for individuals being in each state will be fixed. The solution for Eq 2 should satisfy the following equations:
where
We define Eq 5 to simplify Eq 2. Here,
Ignoring the high-order items, Eq 6 can further be transformed into Eq 7:
Eq 7 can further be reduced to Eq 8 by substituting the first three equations into the fourth one. At the steady state, we assume that
Here, τij is the element of the identity matrix. We define a matrix H whose element is
Results
In this section, we apply the MMCA and the MC method to analyze the interaction between information diffusion and disease spreading Lyubartsev et al. [36]. For the results of MMCA, the stationary fraction of individuals in states I, A1, and A2 are calculated as
We first test the accuracy of MMCA in solving our proposed model by comparing the output with the result of the MC method. Then, we study the impact of multi-type information, heterogeneity of aware individuals’ states, and heterogeneity of individual’s node degree, respectively. Also, the parameters mentioned in the following sections are all used for illustration.
Model validation and the impact of β
Figure 6 presents comparisons between MMCA and MC simulation under different network structures. It shows the proportions of
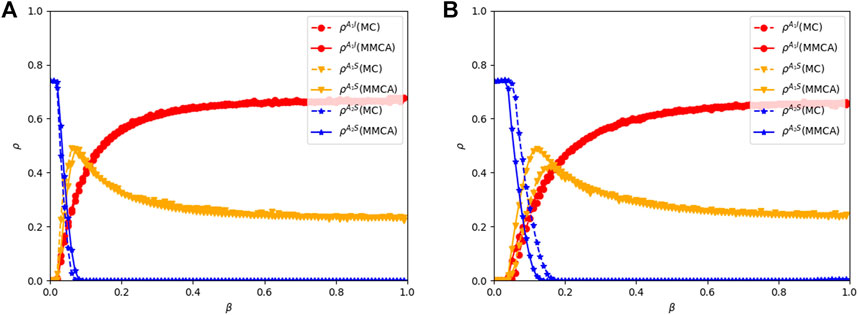
FIGURE 6. Comparison between MMCA and MC simulation. Result shows the proportions of
In addition, the epidemic is more possible to outbreak in the BA-ER networks comparing the epidemic threshold (βc) between Figures 6A, B. However, the difference between the results of two network structures decreases with the increase of β. The comparisons indicate that the structure of the multiplex network influences the final epidemic size but can be negligible when the infectious rate (β) is large, playing a dominant role in the dynamic of awareness-disease spreading.
Impact of multi-type information
Considering the impact of information diversity on the epidemic spreading, f1, f2, λ1, and λ2 are studied in this section, especially f1 and f2 denote the degree of influence of positive or negative information on epidemic spreading, respectively, while λ1 and λ2 represent the probability of positive or negative information diffusion. To investigate the role of f1 and f2, Figure 7 presents the heat map of the proportions of
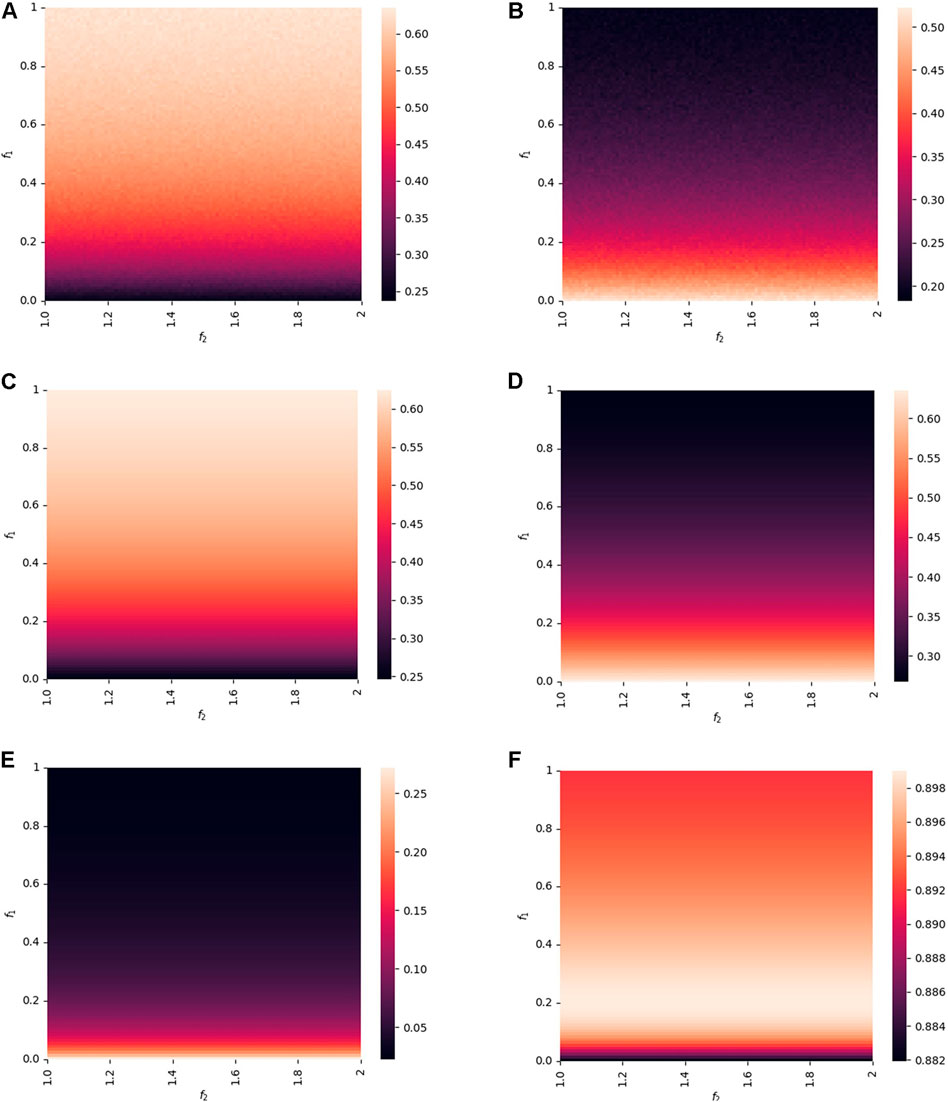
FIGURE 7. Proportions of
Figure 7E presents the impact of f1 on the awareness spreading. When f1 ≤ 0.2,
As for λ1 and λ2 (the impact of awareness diffusion rate for positive and negative preventive information), Figures 8A–D present their influence on the proportion of A1I, A1S, A1, and βc, respectively. As shown in Figure 8A, for the fixed λ2, the final epidemic size decreases with the increase of λ1. Also, increases in positive awareness transmission and epidemic threshold are shown in Figures 8C, D, respectively. The result can be explained that the decrease of λ1 promotes the spread of positive awareness. Moreover, it suppresses the spread of disease for more individuals by taking preventive measures toward the disease, thus decreasing the probability of being infectious. In addition, for the fixed λ1, there is little influence on the epidemic spreading with the variation of λ2, which can be contributed to the same reason as little variation on f2. However, the results do not indicate that the negative awareness-related parameters (e. g. λ2, f2) have little impact on the interplay between epidemics spreading and awareness diffusion under all conditions. In “Supplementary Material S1”, we reset the default values of parameters and incorporate additional simulations to investigate the role of negative awareness-related parameters. In general, based on our model assumption, promoting the diffusion of positive preventive information can help suppress epidemic spreading as well as the epidemic outbreak.
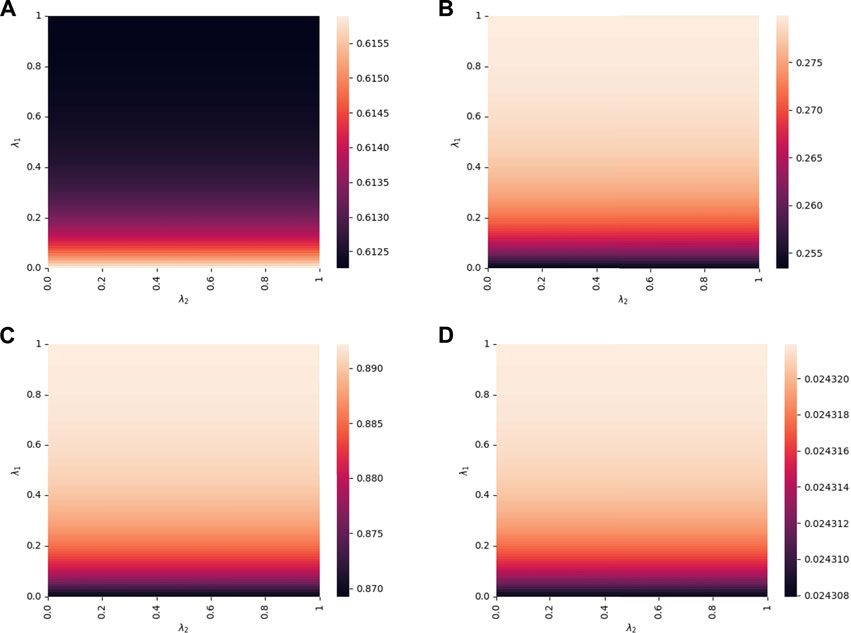
FIGURE 8. Proportions of
Effect of heterogeneity of aware individuals’ states
Apart from multi-type information, heterogeneity of aware individuals’ states (health state and information type) which contributes to different aware transmission capacities is also considered. In the information network, aware neighbors with different health states or different awareness states play different roles in awareness diffusion. ρ1, ρ2, and ρ3 are proposed, representing the importance degree of aware neighbors in A1S, A1I, and A2S, respectively. Figure 9 shows the impact of ρ1, ρ2, and ρ3 on
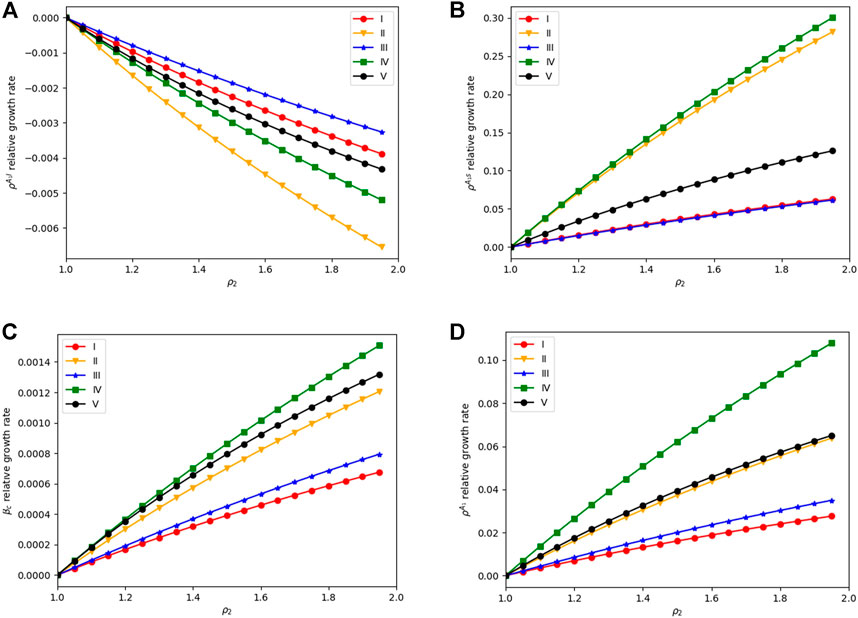
FIGURE 9. ρ1, ρ2, and ρ3 as functions of
Moreover, we also study the result with a higher infection rate (β). However, the variations of ρ2 and ρ3 have little impact on the awareness-disease dynamics in such cases. Therefore, for epidemics with low infectivity (β is small), the importance ratio related to the heterogeneity of information diffusion can have an obvious impact on disease dynamics. To be specific, promoting the importance of A1I neighbors in awareness diffusion while reducing the importance of A2S neighbors can help suppress the epidemic spreading, especially when the recovery rate(μ) and forgotten rate (δ1 and δ2) are relatively large. On the contrary, for epidemics that are highly infectious like SARS or COVID-19, the influence of heterogeneity on the importance ratio of awareness neighbors is limited, making little difference for controlling epidemics.
Effect of heterogeneity of the individual degree
Another aspect of individual heterogeneity taken into account in the proposed model is the individual degree. In the physical layer, infected neighbors with different node degrees have different disease transmissibility. Factor
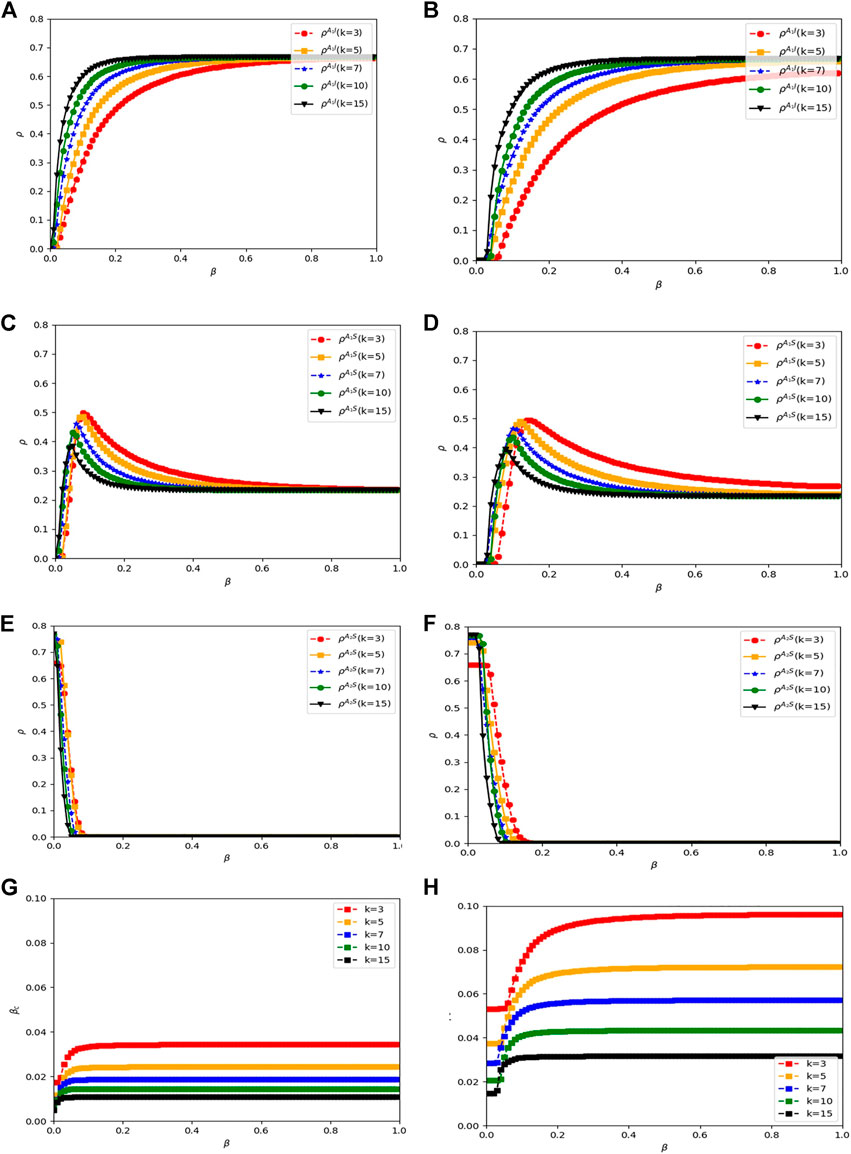
FIGURE 10.
Comparing the results obtained from the ER-BA network with the results obtained from the ER-ER network, the trends for
Conclusion
In this article, we propose an individual-based epidemics and multi-type information spreading (IEMIS) model, mainly considering two factors that can significantly affect the coupled awareness-epidemic spreading but have been rarely studied. The first factor is the multi-type information. The second factor is the individual heterogeneity (including the heterogeneity in awareness diffusion and the heterogeneity in epidemic spreading). Based on MMCA, we give out the analytical epidemic threshold of the proposed model and analyze the impact of information type and individual heterogeneity on the interplay between awareness and epidemic. The results show that the diffusion of positive awareness can help to suppress the epidemic spreading, while the influence of negative awareness is limited for the high proportion of infections leading to an overwhelming propagation of positive information. As for individual heterogeneity, enhancing the importance ratios of aware neighbors who receive positive information can elevate positive awareness spreading and further promote epidemic prevalence. Moreover, lowering the average node degree can effectively suppress epidemic propagation, that is, cutting back social activities or increasing social distances can help control the disease.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
PC, XG, ZJ, and SL contributed to the methodology development and the investigation. LL and JY contributed to funding acquisition. PC and XG contributed to software, formal analysis, and the results presented in this manuscript. YH, YL, and WF contributed to supervision and validation. All authors contributed to the manuscript preparation, review, and editing.
Funding
This work was supported by the Ningbo “2025 S and T Megaprojects” [grant number 2021Z021].
Conflict of interest
Authors ZJ, SL, LL, and JY were employed by Yidu Cloud (Beijing) Technology Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.964883/full#supplementary-material
References
1. Morens D, Folkers G, Fauci A. The challenge of emerging and re-emerging infectious diseases. Nature (2004) 430:242–9. doi:10.1038/nature02759
3. Wang Z, Andrews MA, Wu Z-X, Wang L, Bauch CT. Coupled disease-behavior dynamics on complex networks: a review. Phys Life Rev (2015) 15:1–29. doi:10.1016/j.plrev.2015.07.006
4. Funk S, Salathe M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interf (2010) 7:1247–56. doi:10.1098/rsif.2010.0142
5. Funk S, Gilad E, Jansen VAA. Endemic disease, awareness, and local behavioural response. J Theor Biol (2010) 264:501–9. doi:10.1016/j.jtbi.2010.02.032
6. Ruan Z, Tang M, Liu Z. Epidemic spreading with information-driven vaccination. Phys Rev E (2012) 86:036117. doi:10.1103/physreve.86.036117
7. Arefin MR, Masaki T, Kabir KMA, Tanimoto J. Interplay between cost and effectiveness in influenza vaccine uptake: a vaccination game approach. Proc R Soc A (2019) 475:20190608. doi:10.1098/rspa.2019.0608
8. Kabir KMA, Tanimoto J. Modelling and analysing the coexistence of dual dilemmas in the proactive vaccination game and retroactive treatment game in epidemic viral dynamics. Proc R Soc A (2019) 475:20190484. doi:10.1098/rspa.2019.0484
9. Nadini M, Rizzo A, Porfiri M. Epidemic spreading in temporal and adaptive networks with static backbone. IEEE Trans Netw Sci Eng (2020) 7:549–61. doi:10.1109/tnse.2018.2885483
10. Hota AR, Sundaram S. Game-theoretic vaccination against networked SIS epidemics and impacts of human decision-making. IEEE Trans Control Netw Syst (2019) 6:1461–72. doi:10.1109/tcns.2019.2897904
11. Li X-J, Li X. Perception effect in evolutionary vaccination game under prospect-theoretic approach. IEEE Trans Comput Soc Syst (2020) 7:329–38. doi:10.1109/tcss.2019.2960818
12. Wang H, Ma C, Chen H-S, Zhang H-F. Effects of asymptomatic infection and self-initiated awareness on the coupled disease-awareness dynamics in multiplex networks. Appl Math Comput (2021) 400:126084. doi:10.1016/j.amc.2021.126084
13. Jia M, Li X, Ding L. Epidemic spreading with awareness on multi-layer activity-driven networks. Physica A: Stat Mech its Appl (2021) 579:126119. doi:10.1016/j.physa.2021.126119
14. Guo H, Wang Z, Sun S, Xia C. Interplay between epidemic spread and information diffusion on two-layered networks with partial mapping. Phys Lett A (2021) 398:127282. doi:10.1016/j.physleta.2021.127282
15. Zhan X-X, Liu C, Sun G-Q, Zhang Z-K. Epidemic dynamics on information-driven adaptive networks. Chaos Solitons Fractals (2018) 108:196–204. doi:10.1016/j.chaos.2018.02.010
16. Wang W, Tang M, Yang H, Do Y, Lai Y-C, Lee G, et al. Asymmetrically interacting spreading dynamics on complex layered networks. Sci Rep (2014) 4:5097. doi:10.1038/srep05097
17. Wang W, Liu Q-H, Cai S-M, Tang M, Braunstein LA, Stanley HE, et al. Suppressing disease spreading by using information diffusion on multiplex networks. Sci Rep (2016) 6:29259. doi:10.1038/srep29259
18. Kabir KMA, Kuga K, Tanimoto J. Analysis of SIR epidemic model with information spreading of awareness. Chaos Solitons Fractals (2019) 119:118–25. doi:10.1016/j.chaos.2018.12.017
19. Xia C, Wang Z, Zheng C, Guo Q, Shi Y, Dehmer M, et al. A new coupled disease-awareness spreading model with mass media on multiplex networks. Inf Sci (2019) 471:185–200. doi:10.1016/j.ins.2018.08.050
20. Guo Q, Lei Y, Jiang X, Ma Y, Huo G, Zheng Z, et al. Epidemic spreading with activity-driven awareness diffusion on multiplex network. Chaos (2016) 26:043110. doi:10.1063/1.4947420
21. Li C, Zhang Y, Li X. Epidemic threshold in temporal multiplex networks with individual layer preference. IEEE Trans Netw Sci Eng (2021) 8:814–24. doi:10.1109/tnse.2021.3055352
22. Kabir KMA, Kuga K, Tanimoto J. The impact of information spreading on epidemic vaccination game dynamics in a heterogeneous complex network- A theoretical approach. Chaos Solitons Fractals (2020) 132:109548. doi:10.1016/j.chaos.2019.109548
23. Depoux A, Martin S, Karafillakis E, Preet R, Wilder-Smith A, Larson H, et al. The pandemic of social media panic travels faster than the COVID-19 outbreak. J Trav Med (2020) 27:taaa031. doi:10.1093/jtm/taaa031
24. Ahmad AR, Murad HR. The impact of social media on panic during the COVID-19 pandemic in Iraqi kurdistan: Online questionnaire study. J Med Internet Res (2020) 22:e19556. doi:10.2196/19556
25. Parveen M, Yeasmin M, Molla MMA. Antimicrobial resistance, evidences on irrational anti-microbial prescribing and consumption during covid-19 pandemic and possible mitigation strategies: A Bangladesh perspective (2020). medRxiv. doi:10.1101/2020.10.09.20210377
26. Teovanovic P, Lukic P, Zupan Z, Lazic A, Ninkovic M, Zezelj I, et al. Irrational beliefs differentially predict adherence to guidelines and pseudoscientific practices during the COVID-19 pandemic. Appl Cogn Psychol (2021) 35:486–96. doi:10.1002/acp.3770
27. Arafat SY, Kar SK, Menon V, Kaliamoorthy C, Mukherjee S, Alradie-Mohamed A, et al. Panic buying: An insight from the content analysis of media reports during Covid-19 pandemic. Neurol Psychiatry Brain Res (2020) 37:100–3. doi:10.1016/j.npbr.2020.07.002
28. Zhang Y, Lu X, Cui N, Tang J, Zhang X. Coevolving dynamics between epidemic and information spreading considering the dependence between vigilance and awareness prevalence. Complexity (2021) 2021:1–13. doi:10.1155/2021/5515549
29. Wang Z, Xia C, Chen Z, Chen G. Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans Cybern (2021) 51:1454–62. doi:10.1109/tcyb.2019.2960605
30. Liu Q-H, Wang W, Tang M, Zhang H-F. Impacts of complex behavioral responses on asymmetric interacting spreading dynamics in multiplex networks. Sci Rep (2016) 6:25617. doi:10.1038/srep25617
31. Guo Q, Jiang X, Lei Y, Li M, Ma Y, Zheng Z, et al. Two-stage effects of awareness cascade on epidemic spreading in multiplex networks. Phys Rev E (2015) 91:012822. doi:10.1103/physreve.91.012822
32. Zhang H-F, Xie J-R, Tang M, Lai Y-C. Suppression of epidemic spreading in complex networks by local information based behavioral responses. Chaos (2014) 24:043106. doi:10.1063/1.4896333
33. Guo Q, Lei Y, Xia C, Guo L, Jiang X, Zheng Z, et al. The role of node heterogeneity in the coupled spreading of epidemics and awareness. PLoS One (2016) 11:e0161037. doi:10.1371/journal.pone.0161037
34. Chen X, Gong K, Wang R, Cai S, Wang W. Effects of heterogeneous self-protection awareness on resource-epidemic coevolution dynamics. Appl Math Comput (2020) 385:125428. doi:10.1016/j.amc.2020.125428
35. Pan Y, Yan Z. The impact of individual heterogeneity on the coupled awareness-epidemic dynamics in multiplex networks. Chaos (2018) 28:063123. doi:10.1063/1.5000280
36. Lyubartsev AP, Martsinovski AA, Shevkunov SV, Vorontsov-Velyaminov PN. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J Chem Phys (1992) 96:1776–83. doi:10.1063/1.462133
37. Erdös P, Rényi A. On the Evolution of random graphs, 5. Budapest, Pest, Hungary: Publication of the Mathematical Institute of the Hungarian Academy of Sciences (1960). p. 1776–83.
Keywords: epidemic spreading, information diffusion, multiplex networks, individual heterogeneity, multi-type information
Citation: Chen P, Guo X, Jiao Z, Liang S, Li L, Yan J, Huang Y, Liu Y and Fan W (2022) Effects of individual heterogeneity and multi-type information on the coupled awareness-epidemic dynamics in multiplex networks. Front. Phys. 10:964883. doi: 10.3389/fphy.2022.964883
Received: 09 June 2022; Accepted: 01 July 2022;
Published: 17 August 2022.
Edited by:
Ayse Peker-Dobie, Istanbul Technical University, TurkeyReviewed by:
Linjie Liu, Northwest A and F University, ChinaUmar Farooq, Abdul Wali Khan University Mardan, Pakistan
Copyright © 2022 Chen, Guo, Jiao, Liang, Li, Yan, Huang, Liu and Fan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peiyu Chen, Y3B5MTlAbWFpbHMudHNpbmdodWEuZWR1LmNu
 Peiyu Chen
Peiyu Chen Xudong Guo1
Xudong Guo1 Zengtao Jiao
Zengtao Jiao